Evolution and modulation of intracellular calcium release during long-lasting, depleting depolarization in mouse muscle

Abstract

Intracellular calcium signals regulate multiple cellular functions. They depend on release of Ca²⁺ from cellular stores into the cytosol, a process that in many types of cells appears to be tightly controlled by changes in [Ca²⁺] within the store. In contrast with cardiac muscle, where depletion of Ca²⁺ in the sarcoplasmic reticulum is a crucial determinant of termination of Ca²⁺ release, in skeletal muscle there is no agreement regarding the sign, or even the existence of an effect of SR Ca²⁺ level on Ca²⁺ release. To address this issue we measured Ca²⁺ transients in mouse flexor digitorum brevis (FDB) skeletal muscle fibres under voltage clamp, using confocal microscopy and the Ca²⁺ monitor rhod-2. The evolution of Ca²⁺ release flux was quantified during long-lasting depolarizations that reduced severely the Ca²⁺ content of the SR. As in all previous determinations in mammals and non-mammals, release flux consisted of an early peak, relaxing to a lower level from which it continued to decay more slowly. Decay of flux in this second stage, which has been attributed largely to depletion of SR Ca²⁺, was studied in detail. A simple depletion mechanism without change in release permeability predicts an exponential decay with time. In contrast, flux decreased non-exponentially, to a finite, measurable level that could be maintained for the longest pulses applied (1.8 s). An algorithm on the flux record allowed us to define a quantitative index, the normalized flux rate of change (NFRC), which was shown to be proportional to the ratio of release permeability P and inversely proportional to Ca²⁺ buffering power B of the SR, thus quantifying the ‘evacuability’ or ability of the SR to empty its content. When P and B were constant, flux then decayed exponentially, and NFRC was equal to the exponential rate constant. Instead, in most cases NFRC increased during the pulse, from a minimum reached immediately after the early peak in flux, to a time between 200 and 250 ms, when the index was no longer defined. NFRC increased by 111% on average (in 27 images from 18 cells), reaching 300% in some cases. The increase may reflect an increase in P, a decrease in B, or both. On experimental and theoretical grounds, both changes are to be expected upon SR depletion. A variable evacuability helps maintain a constant Ca²⁺ output under conditions of diminishing store Ca²⁺ load.

To allow contractile activation of skeletal muscle upon action potential depolarization, Ca²⁺ is rapidly released from the sarcoplasmic reticulum (SR) by ryanodine-receptor channels (RyR) that open under the influence of voltage sensors of the transverse (t) tubule membrane. The response of the channels to a single action potential consists of a single peak or spike of release flux. The magnitude and evolution of this flux is determined by a number of mechanisms, which presumably evolved to optimize the signalling function at the activation frequencies that occur during physiological muscle contraction.

A classical approach to the study of the mechanisms that control Ca²⁺ release is the examination of Ca²⁺ transients and release flux caused by prolonged depolarization. These studies were initiated in frog muscle (Baylor et al. 1983; Melzer et al. 1984) and the methods developed for the frog were later adapted to rat (Garcia & Stefani, 1990; Delbono & Stefani, 1993; Garcia & Schneider, 1993) and mouse muscle (Jacquemond, 1997; Szentesi et al. 1997; Wang et al. 1999; Collet et al. 2003; Ursu et al. 2005; Woods et al. 2005). In mammals, the results were generally similar to the frog's, especially in the outline of spatially averaged time course, but differences were found at the ‘local’ sub-sarcomeric level (Shirokova et al. 1998; Csernoch et al. 2004).

Early in the work on frog muscle it was found that upon depolarization, flux followed the now well-known waveform depicted in green in Fig. 4C, including an early peak with half-duration of 10 ms or less at room temperature, followed by a ‘quasi-steady’ or ‘plateau’ phase, which in transients elicited with very long pulses was found to consist of a slow near-exponential decay.

Figure 4.

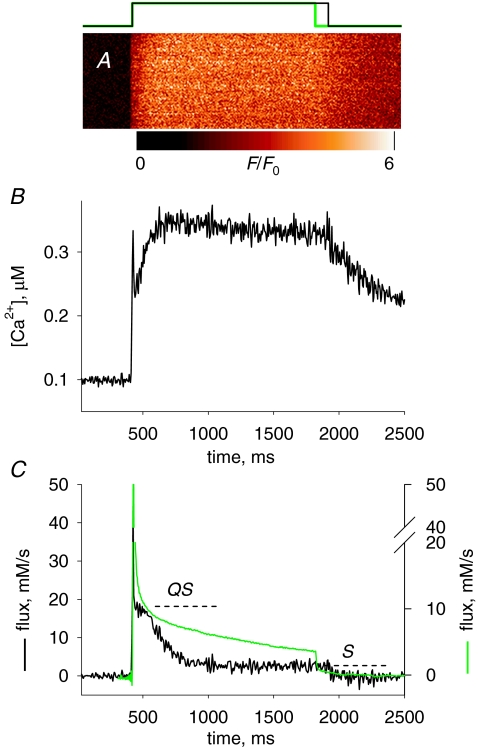
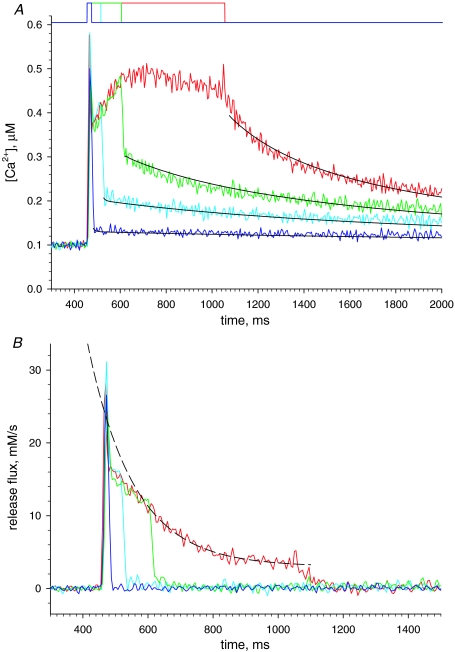
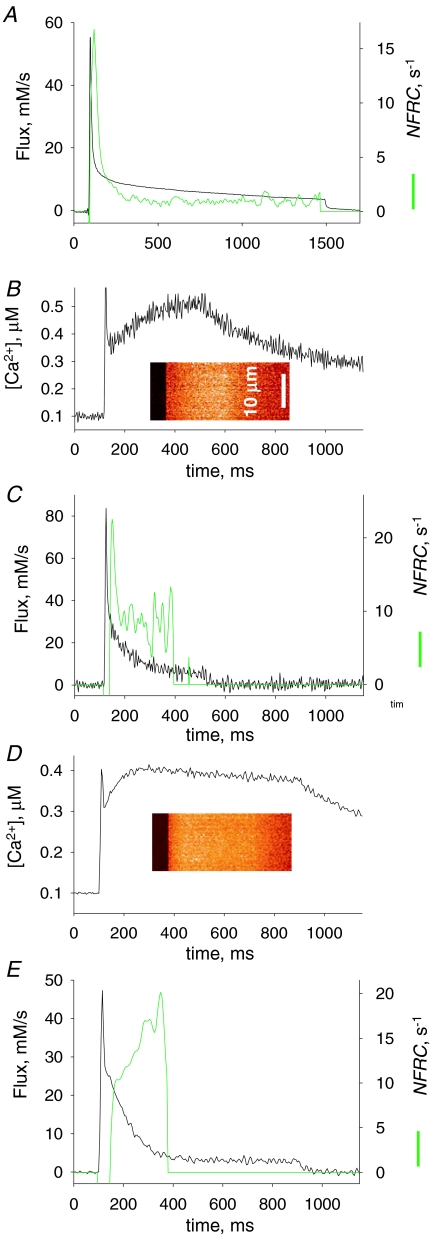
The Ca²⁺ transient and Ca²⁺ release induced by a depolarization of long duration A, normalized line scan F(x,t)/F₀(x) in a cell with rhod-2 stimulated by a 1500 ms pulse to +20 mV (represented in black at top). B, [Ca²⁺]_cyto(t) derived from the averaged fluorescence. Note a virtual stabilization after ∼250 ms. C, black trace, release flux, derived from the record in B. QS is the ‘pedestal’ level reached after a fast relaxation from the peak and S the steady level, also referred to as ‘cycling’ level. Parameters: k_uptake= 4900 s⁻¹, others as in previous figure. Experiment 122606a, record 36. Green trace, flux calculated from Ca²⁺ transient elicited in a frog semitendinosus fibre, voltage clamped in a 2-Vaseline gap, depolarized for 1400 ms to +60 mV (pulse in green at top of figure, data from Pizarro & Ríos, 2004; fibre identifier 1276). Records scaled so that their initial plateaus (QS) overlap.

An account of this waveform starts from the idea that the early peak is due to the opening of release channels controlled by the t membrane voltage sensor, then amplified by opening of other channels activated by Ca²⁺ (for evidence see Jacquemond et al. 1991; Pizarro et al. 1992; Klein et al. 1996; Pape et al. 2002; Brum et al. 2003; Pouvreau et al. 2007). Decay from the high peak is attributed to a Ca²⁺-induced channel closure (or inactivation, ‘CDI’) that is rapid but incomplete, leading to the quasi-steady phase (Baylor et al. 1983; Melzer et al. 1984; Baylor & Hollingworth, 1988; Schneider & Simon, 1988; Jong et al. 1993, 1995; Pape et al. 1995, 1998; Pape & Carrier, 1998; Pizarro & Ríos, 2004; Ríos et al. 2008).

Decay of flux during the quasi-steady phase is attributed to decay in the Ca²⁺ driving force due to depletion in the SR (Schneider et al. 1987). While [Ca²⁺]_SR is undoubtedly reduced during this phase, there is evidence that the openness of the release channels (usually quantified as a release permeability P that is defined precisely later) increases as [Ca²⁺]_SR is reduced. Questions remain regarding the magnitude of the change in P, chiefly because its evaluation requires knowledge of SR Ca²⁺, free or total, with a precision and certainty that are not yet attainable.

In rat and mouse muscles, the waveform of Ca²⁺ release under voltage clamp is qualitatively similar to that of frog muscle, including an initial peak followed by a second phase. ‘Quasi-steady’ would be a misnomer for this phase in the mouse, as Ursu et al. (2005) found that it decays much faster than the corresponding phase in the amphibian, falling by one to two thirds in 100 ms.

In the frog studies, the question of changes in P with SR content has been addressed by applying long-lasting depolarizing pulses to induce Ca²⁺ depletion and examine its consequences (Schneider et al. 1987; Pape et al. 1995, 1998; Pizarro & Ríos, 2004). The same approach has not been used up to now with mammalian muscle.

Here we evaluate the time course of Ca²⁺ release flux during long-lasting depolarizing pulses in mouse muscle. Records of release flux are derived from confocal microscopic line scanning of voltage-clamped cells, a technique that is increasingly favoured as it allows comparison of cellular structure and function (see, for instance, Gouadon et al. 2006; Pouvreau et al. 2007; Paolini et al. 2007; Shen et al. 2007; Legrand et al. 2008), but is not fully characterized yet. Thus, the first goal of the present study is to evaluate the records of release flux derived from confocal microscopy, by comparison with the established (photometric) techniques. It appears that confocal imaging provides a means to derive Ca²⁺ release flux with major advantages and some shortcomings. We then seek to characterize the underlying evolution of SR permeability. Striking differences are found with the corresponding phenomena of frog muscle.

Methods

Isolation of single FDB cells from adult mice

Protocols using mice were approved by the Institutional Animal Care and Use Committee of Rush University, which found them consistent with their ethical standards. The present results were collected from 12 mice (Mus musculus, Black Swiss); 30 others were used at earlier stages for implementation and optimization of techniques used here and in other works of our laboratory. The animals were killed by CO₂ inhalation, and FDB muscles were removed and placed in a 0-Ca Tyrode solution containing 0.2% collagenase (C0130, Sigma) for 55 min at 37°C. After three washes, single fibres were dissociated by gently passing the digested muscle for a few times through Pasteur pipettes. The fibres were kept at 4°C in Tyrode solution plus 2% horse serum. Experiments were carried out at 20–22°C.

Solutions

Composition of the solutions were as follows. Tyrode solution (mm): 140 NaCl, 5 KCl, 2.5 CaCl₂, 2 MgCl₂, 10 Hepes. pH was set to 7.2 with NaOH and osmolality to 320 mosmol kg⁻¹ with NaCl. External solution: 140 mm TEA-CH₃SO₃, 1 mm CaCl₂, 3.5 mm MgCl₂, 10 mm Hepes, 1 μm TTX (citrate), 1 mM 4-AP, 0.5 mm CdCl₂, 0.3 mm LaCl₃, 25 μm BTS (N-benzyl-p-toluene sulphonamide, Sigma-Aldrich Co., St Louis, MO, USA). pH was adjusted to 7.2 with TEA-OH and osmolality to 320 mosmol kg⁻¹ with TEA methanesulphonate. Internal solution (in pipette): 110 mmN-methylglucamine, 110 mm l-glutamic acid, 10 mm EGTA, 10 mm Tris, 10 mm glucose, 5 mm sodium ATP, 10 mm PC, 100 μm rhod-2, 1 mm free Mg, 100 nm free Ca. The effective dissociation constants of EGTA for Ca²⁺ and Mg²⁺ calculated using affinity constants from Martell and Smith and corrections for pH and ionic strength as described by Harafuji & Ogawa (1980) were, respectively, 172 nm and 17 mm; similar results were obtained with the program Maxchelator (Bers et al. 1994). Total concentration of calcium was 3.56 mm and magnesium 7.4 mm. pH was set to 7.2 with NaOH and osmolality to 320 mosmol kg⁻¹ with NMG-glutamate.

Voltage clamp

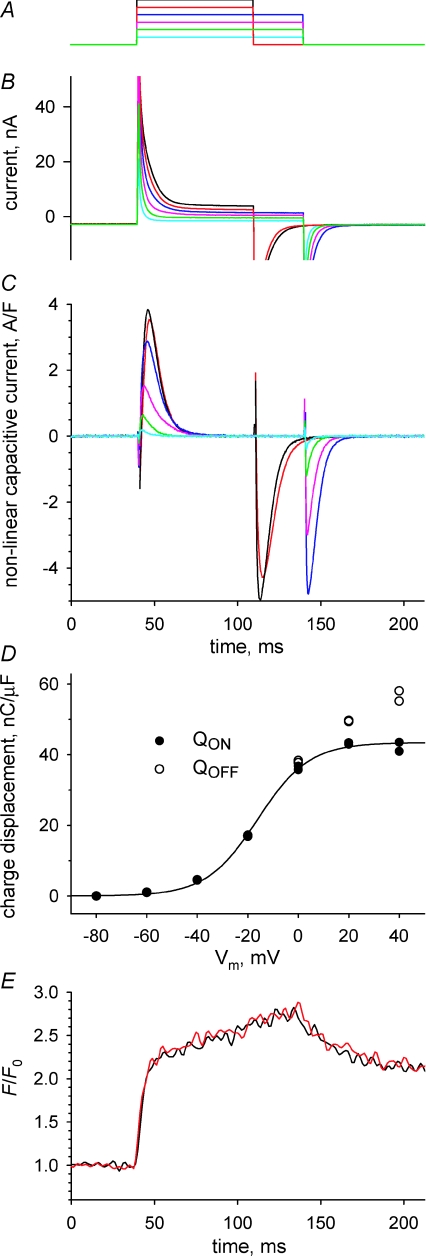
The whole-cell patch clamp technique follows the implementation of Wang et al. (1999), but for the formulation of solutions and other details. We used an Axopatch 200B amplifier (Axon Instruments, Foster City, CA, USA). Data acquisition, pulse generation and synchronization with confocal imaging were performed by a computer running custom software. Pipettes pulled from alkali barium borosilicate glass (Corning; P2000 puller, Sutter Instrument Co., Novato, CA, USA) were heat-polished to a resistance of 600–1200 kΩ. Cells were patched near their centre and were clamped at −80 mV. The clamped cells were stable, as ascertained by stability of series resistance which was analogically compensated, linear capacitance (C_m), charging time constant and holding current, which ranged from 1 to 10 nA in different fibres, but typically stabilized near 2 nA. Speed, spatial homogeneity and graded V_m dependence of the responses are documented below. Actual recording of Ca²⁺ transients was not started before 30 min of stable holding at −80 mV, a time when the concentration of EGTA inside the cell was presumably close to 10 mm, as judged by the abolition of contractile responses (which was also aided by the presence of BTS). Analog compensation of cell capacitance was not used, but command potentials were blunted with 0.6 ms duration ramps, to avoid saturation of the headstage. Figure 1 illustrates membrane currents (Fig. 1B) driven by depolarizing pulses from the holding potential, spanning the range −60 to 40 mV (Fig. 1A), which in these solutions did not activate visible inward ionic currents. Non-linear capacitive and ionic currents were obtained by scaled subtraction of currents in control pulses to −100 mV, which were also used to evaluate C_m. Non-linear capacitive currents (Fig. 1C) were obtained by subtracting from the asymmetric current a sloping baseline fitted starting 40 ms after the beginning or the end of the pulse, respectively, for ON and OFF.

Figure 1.

Membrane currents in a cell voltage clamped through a patch electrode A, depolarizing pulses, applied from a holding potential of −80 mV, to levels between −60 and +40 mV, at 20 mV intervals. These test pulses were intercalated with control pulses to −100 mV. B, total currents, colour-keyed to corresponding test pulses. C, asymmetric currents (difference between test and scaled control currents) after subtraction to both ON and OFF portions of sloping baselines fitted to the records starting, respectively, 40 ms after the leading or trailing edge of the pulse. Currents are normalized to C_m (2.1 nF), evaluated in controls. D, charge transferred at each voltage, in the ON (•) or OFF (◯) transition. Two values of charge, which result from integrations that include or exclude the initial points of wrong polarity, and were indistinguishable in most cases, are plotted at each abscissa. The curve represents the best fit by the ‘Boltzmann’ equation (Methods), with Q_max= 43.4 nC μF⁻¹, V_T=–16.1 mV and K= 10.1 mV. E, normalized fluorescence of rhod-2, imaged while applying a pulse to 0 mV, averaged over 20 μm segments of the line scan, adjacent (red) or 100 μm removed from the patch electrode. Experiment 040308c, records 23–28.

Intramembranous charge transfers Q_ON and Q_OFF were calculated as the time integral of the non-linear capacitive current during the respective transient. The dependence of Q_ON on V_m was fitted with the usual ‘Boltzmann’ function: Q_max/(1 + exp(−(V_m−V_T)/K)) (Fig. 1D). On average in seven cells, the total mobile charge Q_max was 39.2 nC μF⁻¹ (s.e.m.= 2.8), the transition voltage V_T was −18.8 mV (1.4) and the slope factor K was 10.9 mV (0.8), which are all close to the values found in the detailed study of Wang et al. (1999) using a similar single-pipette voltage clamp. C_m was 2.1 nF (0.4). The cells chosen for study were up to 450 μm long and had diameter between 30 and 50 μm. The spatial homogeneity of the clamp was ascertained comparing fluorescence transients at different distances from the pipette. Figure 1E illustrates the evolution of F/F₀ (defined in the following section) averaged over 20 μm of scan next to the pipette (red) or 100 μm away (black).

Confocal imaging and determination of free [Ca²⁺]

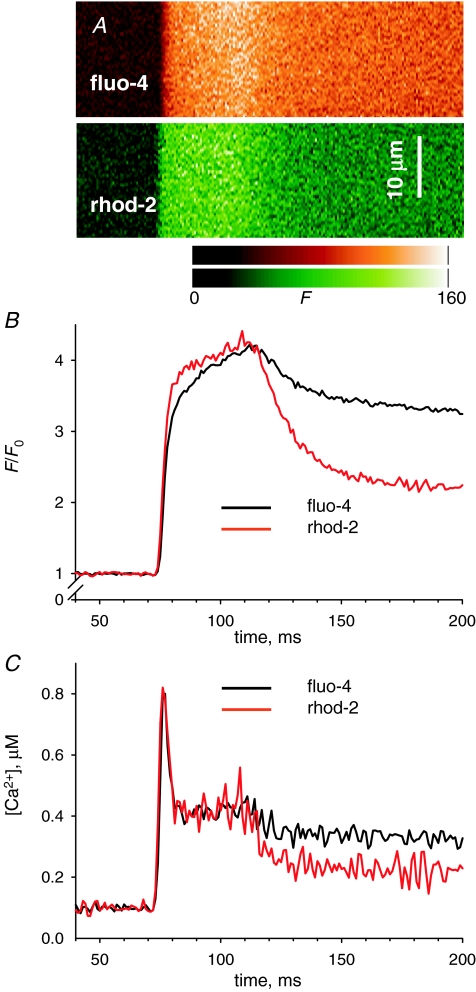
Isolated cells were studied in a plastic chamber with 0.17 μm glass coverslips bottom mounted on a confocal microscope (SP2 AOBS, Leica Microsystems, Exton, PA, USA). Fluorescence of rhod-2 was imaged under excitation at 543 nm, collecting light of intensity F emitted between 562 and 666 nm at 0.13–0.24 μm pixel intervals and line frequency variable between one every 0.5 ms and one every 5 ms. Images were low-pass filtered by convolution with a Chebyshev kernel for a cut-off at 0.5 of the Nyquist frequency (Walraven, 1980). All line scan images consist of 512 lines, thus the sampling time varies from 256 ms at the highest rate to 2.56 s at the lowest. In some cases, images were obtained using two dyes. Figure 2A shows (partially) two line scan images F(x,t) obtained simultaneously for fluo-4 and rhod-2 introduced through the pipette. In all cases, the scanning was parallel to the fibre axis, no more than 30 μm above the bottom surface of the cell. Line scans of voltage-clamped fibres were normalized by the average F₀(x) of F(x,t) during times prior to the pulse. Figure 3A shows a normalized line scan image of rhod-2 fluorescence, i.e. F(x,t)/F₀(x), obtained at a high scan frequency (0.625 ms per line). A line-averaged F(t)/F₀ is calculated by averaging over the x coordinate in the entire x extent of the image, occasionally restricting the range when it included areas outside the cell or otherwise exhibiting an altered response. In the example, only the extent within the bracket was used. Average cytosolic [Ca²⁺](t) is derived from F(t) as

(1)

Figure 2.

Kinetic derivation of [Ca²⁺]_cyto(t) from fluorescence changes A, line scan images of fluorescence of fluo-4 or rhod-2, recorded simultaneously on the same cell, upon depolarization for 50 ms to +20 mV. B, fluorescence averages after normalization by the resting value (as described in Methods). Note that the relative increase by the end of the pulse is the same for both dyes, indicating that both are far from saturation by Ca²⁺. C, [Ca²⁺]_cyto(t) derived from records in B according to eqn (1), with k⁻_fluo-3= 90 s⁻¹ and k⁻_rhod-2= 100 s⁻¹. See further description in text and discussion in Appendix. Experiment 042408a, record 17.

Figure 3.

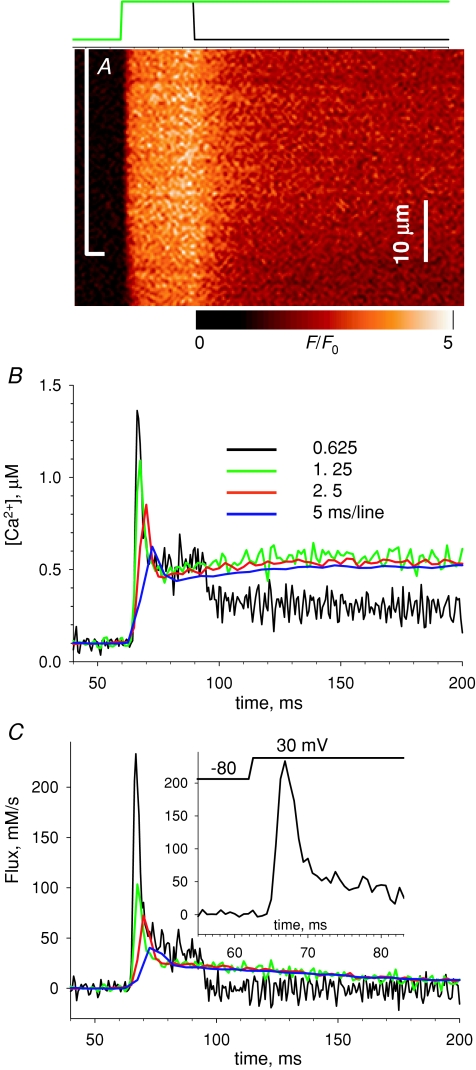
Images acquired at different scan frequencies A, F(t)/F₀ in a cell with rhod-2, stimulated by a 30 ms pulse to + 20 mV, scanned at 0.625 ms line⁻¹. B, [Ca²⁺]_cyto(t), calculated by eqn (1) (black). Three other records, in colour, were derived from images acquired at lower scan frequencies, as listed in the figure. In these cases the depolarizing pulses were 200 ms long, to +30 mV. In all cases, the fluorescence was averaged in the region marked with the bracket in A, to avoid an area of lower intensity. C, release flux records derived from the Ca²⁺ transients in B. Parameters: k_uptake= 6900 s⁻¹, k_E= 14 μm⁻¹ s⁻¹, k⁻_E= 7.0 s⁻¹. EGTA was assumed to be 0.7 of the concentration in the pipette, or 7 mm. Inset, detail of record at the highest frequency. Trace at top marks actual timing of depolarization. Experiment 021408a, records 13, 15, 16, 17.

This equation assumes that the dye is far from saturation by Ca²⁺, which appears justified for rhod-2 considering that [Ca²⁺]_cyto was always much lower than the value of the dye's K_D determined by Escobar et al. (1997) in aqueous solutions. [Ca²⁺]_cyto(0) is assumed equal to that in the pipette (0.1 μm). This assumption was roughly consistent with measurements of resting [Ca²⁺] in three experiments using the SEER ratio fluorescence of indo-1 (Launikonis et al. 2005) introduced via the patch pipette, in which the measured [Ca²⁺]_cyto went from between 33 and 50 nm 10 min after establishing the whole-cell connection to between 84 and 140 nm at 60 min. Since the determination of [Ca²⁺]_cyto in this way depends on a calibration with its own uncertainties (Launikonis et al. 2006), we opted for assuming a constant [Ca²⁺]_cyto(0). It should be noted in this regard that the value of the EGTA kinetic constants fitted inside the cell and used to evaluate release flux result in a dissociation constant for EGTA : Ca greater than that used to formulate the internal solution (a reduction in affinity that has been demonstrated directly for the EGTA-based fluo-3 and is attributed to its engaging in multimolecular reactions; Harkins et al. 1993). If this is the case, then EGTA should be effectively releasing Ca²⁺ as it moves into the cell from the pipette, leading to an increase in [Ca²⁺]_cyto and SR load. Indeed, a slow increase in [Ca²⁺]_cyto was observed in the present experiments, from approximately 40 nm at the beginning to about 110 nm after 60 min; the SR content probably was increasing correspondingly. The accumulated uncertainty in effective affinities and concentrations plus the slow change in [Ca²⁺]_cyto during the experiments, qualify the value of these measurements, which seem adequate as tools for comparison among fibres treated similarly. Comparisons across different experimental platforms instead would be less reliable.

The value of k⁻_rhod-2 was determined by analysis of F(t) in simultaneously obtained images of fluorescence of rhod-2 and fluo-4. Figure 2 illustrates one of two comparison experiments in which both dyes were introduced through the pipette. The images in Fig. 2A were obtained by line interpolation of excitation wavelengths 488 nm (largely absorbed by fluo-4) and 543 nm (absorbed by rhod-2). While exciting with 488 nm light, emission was acquired in the range 500–545 nm. Fluorescence excited by 543 nm light was acquired between 555 and 655 nm. With this protocol, there was essentially no interference between the two dyes. In Fig. 2B are F₁(t)/F₁(0) (from fluo-4 fluorescence) and F₂(t)/F₂(0) (from rhod-2), normalized as described for Fig. 2A. The normalized fluorescence values near the end of the pulse are about the same for both dyes, consistent with both being relatively far from saturation – as in this linear range the relative increase in fluorescence at equilibrium is equal to the relative increase in [Ca²⁺] (i.e. F/F₀=[Ca²⁺]/[Ca²⁺](0)) and should therefore be the same for any dye in its linear range. In Fig. 2C are the records of [Ca²⁺]_cyto(t), derived from the two fluorescence records using eqn (1). The value of k⁻_fluo-4 was set at 90 s⁻¹ (following a determination in frog fibres at room temperature; Shirokova et al. 1996). By trial and error, a k⁻_rhod-2 of 100 s⁻¹ was found to match perfectly the early, fast-changing portion of the Ca²⁺ record. In 10 images of two cells, this value ranged from 99 s⁻¹ to 110 s⁻¹.

The match between the calculations of [Ca²⁺]_cyto(t) using both dyes is good during the early phases, extending essentially to the end of the pulse. After the pulse, the estimate derived from the fluo-4 image remains significantly above that of rhod-2. This discrepancy, which is obviously linked to the fact that the fluorescence of fluo-4 remains higher after the pulse, was observed consistently in all images of both cells studied in this way. In the Appendix it will be shown that the difference cannot be justified with a single-pool model of dye reactions with Ca²⁺. It will also be argued that the reactions of fluo-4 are probably more complex than those of rhod-2. In the following, the reactions of rhod-2 with Ca²⁺ will continue to be described by 1 : 1 stoichiometry in a single pool.

Figure 3C plots [Ca²⁺]_cyto(t) derived from F/F₀ for the image in Fig. 3A (black trace), using eqn (1) with k_{OFF rhod-2}= 100 s⁻¹. Three other Ca²⁺ concentration records are shown, derived from the images of the same cell, obtained at different scan frequencies while longer duration pulses to the same voltage were applied. A lower frequency of scanning results in increasingly blunted calcium records (i.e. increasing error in the estimation of the early peak).

The calculation of Ca²⁺ release flux

Ca²⁺ release flux Ṙ (t) was derived from [Ca²⁺](t) by the removal method (Melzer et al. 1984) in a simplified version nearly identical to that of Schuhmeier & Melzer (2004). The method calculates release flux as that necessary to account for the evolution of [Ca²⁺](t) in a single-compartment model that includes quantitatively specified removal processes. To minimize the unknowns in the removal model, we continued the practice (González & Ríos, 1993; Schuhmeier & Melzer, 2004; Woods et al. 2005) of imposing a large concentration of EGTA via the patch pipette. Provided that [EGTA] is sufficiently high, only four forms of Ca²⁺ must be considered: free, bound to the monitoring dye, bound to EGTA and sequestered in the SR.

The parameters that had to be set to account for the evolution of Ca²⁺ were the rate constants of the reaction with EGTA (k_E and k⁻_E), those of the dye and the rate constant of removal by the SR pump, k_uptake. In conventional applications of the removal method, this is done by routines that change parameter values so that the evolution in the model best fits the measured [Ca²⁺]_cyto(t) in multiple records (see Schuhmeier & Melzer, 2004, for an efficient implementation of this method). Here we further simplified the approach. The removal method – if applied under specific rules described later – yields Ṙ records of reliable kinetics but unreliable scale. In other words, even in the highly simplified situation reached in the presence of high [EGTA] the removal model is over-parametrized. Different sets of parameters yield fits of similar quality, which result in alternative flux records of different magnitude. Prompted by Stephenson (1987), Schneider et al. (1987) found that the alternative Ṙ (t) have essentially the same time course, differing by a scale factor. Therefore, and to make the scale of the results comparable across all fibres, we used the same values of all parameters, except k_uptake, which was set for optimal fit of the evolution of [Ca²⁺](t). The other values were as follows: [Dye]_total and [EGTA]_total were set to 0.5 or 0.7 of the concentrations in the pipette (respectively, for records started after 30 min or 60 min in the whole-cell configuration). Fits to several records in which three parameters were allowed to vary gave values for k_E near 15 (μm s)⁻¹ and k⁻_E near 7.5 s⁻¹. These values were then used for all cells in the present work (with the exception of the study illustrated in Fig. 5), allowing only k_uptake to vary among cells. It should be kept in mind that the best fit value of k_uptake is strongly correlated, near proportionally, to the value of [EGTA], which remains unknown.

Figure 5.

A reliability test of the flux calculation A, [Ca²⁺]_cyto(t) derived from fluorescence of rhod-2 in a cell subjected to the pulses shown at top, to +30 mV for 20, 60, 150 or 600 ms. The black lines represent fits to the OFF portion of the records, with parameters: k_uptake= 7230 s⁻¹, k_E= 11.0 μm⁻¹ s⁻¹, and k⁻_E= 4.90 s⁻¹. EGTA was assumed to be 0.7 of the concentration in the pipette, or 7 mm. B, release flux calculated from records in A. The good quality of the fit of the Ca²⁺ transients is manifested in the fact that calculated Ṙ (t) decay abruptly and monotonically to zero at the end of the pulses. The good fit at intermediate durations (20, 60 and 150 ms) establishes the reliability of the kinetic features of the flux, in particular the change in curvature, at those times. The dashed line, an exponential of time constant 142 ms and asymptote 2.15 mm s⁻¹, fits well the later portion of Ṙ (t), starting 150 ms after the leading edge of the 600 ms pulse. Experiment 091207b, records 21–24.

Consequences of dynamic buffering by high [EGTA]

The elevated [EGTA] used here to simplify the calculation of flux and reduce contractile movement could in principle interfere with the Ca²⁺-mediated interactions among Ca²⁺ channels, including Ca²⁺-induced Ca²⁺ release and Ca²⁺-dependent inactivation. There is, however, a long tradition for the use of high concentrations of EGTA in studies of frog skeletal muscle (e.g. Gonzalez & Ríos, 1993; Pape et al. 1995), which is backed up by evidence that such interference exists (e.g. Jong et al. 1995) but does not change the interactions in essential ways. Thus, the ratio (peak-steady)/steady release flux under voltage clamp depolarization, a measure of the extent of CDI, is nearly constant at [EGTA] between 0 and 40 mm (Rengifo et al. 2002). In skinned muscle fibres of the rat, activated by field stimulation of the resealed t tubules, Posterino & Lamb (2003) found that the presence of BAPTA at 380 μm increases Ca²⁺ release, consistent with interference with CDI, but the effect is not observed at 280 μm. Assuming that the relevant parameter for predicting the dynamic effect of a buffer is its length constant μ (Naraghi & Neher, 1997), which roughly measures a free path for Ca²⁺ from the mouth of the channel, one may calculate a critical length constant μ_B as that of (280 + 380)/2 or 330 μm BAPTA, using the approximation

where D_B and k_B are diffusion coefficient and Ca²⁺ binding rate constant of BAPTA, respectively. The corresponding value μ_E for 10 mm EGTA, using D_E=D_B and k_E= 1.5 μm⁻¹ s⁻¹ (Smith et al. 1984) is 121 nm, which again suggests that the interference by EGTA with Ca²⁺-mediated interactions will be minimal.

Statistics

Statistical significance of the change in the NFRC ratio in Table 1 is established by analysis of the transformed Geary–Hinkley variable t, which in the null hypothesis has a mean = 0 and Gaussian distribution (Hayya et al. 1975).

Table 1.

Average properties of release flux

	1 ms line−1	2 Peak (mm s−1)	3 QS (mm s−1)	4 S (mm s−1)	5 Releasable Ca (mm)	6 NFRC (s−1)	7 NFRC ratio
Average	2.5	50.7	25.6	2.95	3.00	16.2	2.05*
s.e.m.		6.63	3.13	0.33	0.20	1.80	0.19
Average	5	40.8	22.9	2.94	2.88	20.2	2.16*
s.e.m.		5.94	2.82	0.51	0.20	3.20	0.23
Average	All	45.6	24.2	2.95	2.94	18.3	2.11*
s.e.m.		4.38	2.04	0.30	0.14	1.79	0.15

Data derived from 27 images of 18 cells. Top rows, averages and s.e.m. for n= 13 images obtained at 2.5 ms per line, with pulse depolarizations lasting 400 ms to +10 or +30 mV; middle rows, n= 14 images at 5 ms per line, with depolarizations of 800–1500 ms. Bottom rows, averages and s.e.m. for all images, equally weighted. Col. 2: average of peak flux, which is underestimated at these low scanning rates (see text and Fig. 3); col. 3: QS, average of flux at the beginning of ‘quasi-steady’ period (see Fig. 4); col. 4: steady flux at end of decay; col. 5: integral of net flux from beginning of pulse until net flux becomes zero; col. 6: NFRC at the time (200–250 ms into the pulse) at which its calculation stopped because net release fell below 1 mm s⁻¹; col. 7: ratio between NFRC value in col. 6 and the value at its nadir, reached at approximately 30 ms into the depolarizing pulse.

^*Statistically significantly different from 1 at a P < 0.05.

Results

This paper examines the properties of cell-averaged Ca²⁺ transients and Ca²⁺ release flux derived from confocal line scan images of fluorescence in voltage-clamped mouse muscle cells. Two aspects of the technique used here are convenient for a number of reasons but arguably inferior to previously used techniques. Thus, confocal line scanning, by imaging only a thin focal section, reduces the amount of light collected and therefore the signal-to-noise ratio by comparison with the photometric measurements, which collect light from a large volume of cell. Likewise, the single-pipette voltage clamp of a whole cell is expected to be less accurate than multi-electrode clamps including multi-Vaseline gaps and two-pipette voltage clamp (but see Wang et al. 1999 for a description of its advantages), and slower than techniques optimized for speed. The initial results explore these potential limitations. Then the method is used to evaluate release flux and permeability in responses to long-duration pulses.

Speed of polarization and intramembranous charge transfer

Figure 1 documents electrophysiological records of total current (panel B) and intramembranous charge movement current (panel C) under voltage pulses in panel A. As detailed in Methods, fibres were voltage clamped with a large-bore glass electrode, which introduced a solution with high Ca²⁺ buffer, ionic substitutions to improve voltage clamp, and the monitoring dye. In this example, the cell had been allowed to equilibrate with the solution in the pipette for 40 min. The temporal evolution suggests good voltage control, made possible by near-complete blockade of ionic currents. The temporal limitations of the single-pipette voltage clamp are more apparent in the asymmetric (test minus scaled control) current records. Especially for large depolarizing pulses the asymmetric current has the wrong polarity, indicating incorrect subtraction of linear capacitive current, for approximately 0.5 ms during fast voltage transitions. This was not due to saturation of the headstage (see Methods). The full duration at half maximum of the ON charge movement current was on average 7.7 ms at +40 mV. This is longer than in voltage clamp experiments designed to optimize clamp speed (e.g. 4.5 ms in experiments with ‘silicone clamp’, Pouvreau et al. 2004; or 6 ms in 2-Vaseline gap, Szentesi et al. 1997). The transfer of intramembranous charge at each voltage was independent of the setting of analog series resistance compensation. The total mobile charge, evaluated by the parameter Q_max, was near the high end of values reported in previous work, suggesting that the voltage sensor was fully reprimed from voltage-dependent inactivation. According to Jacquemond (1997), the linear capacitance measured in the experiment illustrated, 1.9–2.1 nF, should correspond to a homogeneously polarized cell of 0.448 × 10⁻³ cm². The cell in the example, with radius 18.5 μm and length 415 μm, had an area of 0.482 × 10⁻³ cm² (calculated assuming cylindrical shape). Therefore the measured linear capacitance is consistent with a near-homogeneous polarization of this cell. The spatial profile of the line scans (graph in Fig. 1E) indicated near-homogeneous release in the 120 μm covered by the line scan, consistent again with homogeneity of the clamp.

Comparison of records derived from line scans of different frequency

A major goal in the experiments was to characterize the evolution of Ca²⁺ flux in release events lasting a long time, designed to cause substantial depletion of the SR. To avoid dye bleaching and fibre damage, the increase in the scanning time was accomplished by decreasing the scan frequency while keeping constant the number of lines per image. Predictably, such changes in scan frequency had drastic effects on the kinetics of the acquired records, a consequence studied quantitatively in experiments illustrated in Fig. 3. Panel A shows a normalized line scan image of fluorescence (i.e. F(x,t)/F₀(x)) of rhod-2 in a cell subjected to a 30 ms duration pulse to +30 mV. As in every experiment reported here, the fibre was immobilized by the combination of BTS and high buffer. The image was obtained at a scan frequency (0.625 ms per line) close to the maximum available to this system.

Figure 3B plots the spatially averaged evolution of free cytosolic calcium concentration, [Ca²⁺]_cyto(t), in black, derived kinetically from the fluorescence (eqn (1) in Methods). Three other time courses of calcium concentration are plotted, derived from line scans of the same cell obtained at different frequencies while 200 ms duration pulses to the same voltage were applied. As the peak of [Ca²⁺] is very brief (see also Fig. 2), lower frequencies of scanning result in increasingly blunted [Ca²⁺] records.

Figure 3C plots release flux Ṙ (t) corresponding to the Ca²⁺ transients in Fig. 3B. The frequency of line scanning affects severely the evaluation of the rapidly changing early stages of flux. Obviously the early portion of the flux record cannot be evaluated at scan frequencies of 1.25 ms line⁻¹ or lower. At 0.625 ms line⁻¹ (or 0.5 ms line⁻¹, not shown) the records typically peak 4–5 ms into the pulse (see inset in Fig. 3C) and reach values between 98 and 217 mm s⁻¹ (average = 147 mm s⁻¹, s.e.m.= 15 mm s⁻¹ at +10 to +30 mV in 8 cells). As discussed in the next section, this value is model dependent, but the kinetics is not.

In eight experiments we quantified the blunting effect by comparing release flux elicited by equal pulses, derived from images at 2.5 or 0.5 ms per line. The ratio of peaks at 2.5 and 0.5 ms per line was 2.4 (range 2.0–2.9) while the level immediately after the fast relaxation from the peak, labelled ‘QS’ in Fig. 4, and the final steady level were not significantly affected. In conclusion, the level of the ‘pedestal’ that follows the peak and the evolution of Ṙ (t) afterwards do not depend on the scanning frequency. The study of this evolution is the goal of the rest of the present work.

Kinetics of Ca²⁺ release elicited by depolarizations of long duration

Figure 4A is an image of a cell subjected to a +10 mV depolarization for 1500 ms, a much longer duration than in the previous figures. Figure 4B plots the corresponding [Ca²⁺]_cyto(t). Consistently, the transients start with a fast peak that relaxes to a lower level, followed by a slower rise to a level that remains steady (or decreases slightly) for as long as the pulse is maintained. As shown in the previous section, the temporal resolution used in the records of Fig. 4 resulted in severe underestimation of the early peak in [Ca²⁺]_cyto.

Figure 4C plots release flux Ṙ (t) derived from the calcium record in Fig. 4A. While records of release flux in mouse fibres under voltage clamp have been presented in earlier work (for review see Collet et al. 2004; also Ursu et al. 2005; Woods et al. 2005), the present work is the first to use these long-lasting depolarizations. Ṙ (t) is best described in comparison with the flux in a frog muscle fibre, represented in the green trace (reproduced with modifications from Fig. 6 of Pizarro & Ríos, 2004).

Figure 6.

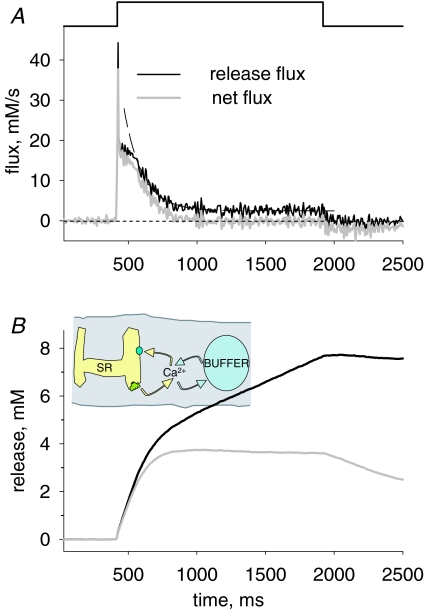
The calculation of total releasable SR calcium A, flux Ṙ (t) reproduced from Fig. 4 (black trace) and net flux Ṙ (t) (grey trace). Ṙ_net approaches zero after approximately 300 ms, a time at which the ‘cycling’ condition depicted in the cartoon is reached. Dashed line, exponential fit starting 100 ms after its beginning; time constant = 133 ms and asymptotic value = 2.47 mm s⁻¹. B, time integrals of the records in A. At the time when the cycling condition is reached, the integral of Ṙ_net becomes essentially constant at a maximum that defines Ca_SR, the releasable SR calcium.

As in the frog, Ṙ in the mouse goes through a large initial peak followed by abrupt descent to a much lower level (named ‘pedestal’ or ‘quasi-steady’). However, unlike the frog, and as shown earlier by Ursu et al. (2005) with briefer depolarizations, the mouse muscle cannot maintain the pedestal level for long; flux decays rapidly, to a true steady state that in this case is 2.47 mm s⁻¹. The initial level after the peak, often visible as a shoulder in the long-duration flux records, is referred to as QS (because ‘quasi-steady’, which fits in the frog, would not suit the briefly sustained level observed in the mouse).

The decay of Ṙ (t) in frog muscle is approximately exponential (see examples in Pizarro & Ríos, 2004). In the example of Fig. 4C an exponential decay to 1.25 mm s⁻¹ of time constant 1.08 s practically overlaps with the slow decay phase (not shown). In the mouse, the decay is kinetically more complex. For the mouse record in Fig. 4C, reproduced in the black trace in Fig. 6A, the decay is best described as sigmoidal; in fact, a single exponential (of time constant 133 ms, dashed trace in Fig. 6A) fits the time course after a lag or ‘shoulder’ of about 100 ms. The significance of this sigmoidicity (and more generally of separation from a single exponential decay) is explored later.

Experiments illustrated in Fig. 5 were designed to assess whether the shoulder is a reliable finding rather than an artifact of the analysis, by exploiting a property of the flux calculation algorithm. Schneider et al. (1987) demonstrated that the ‘removal’ method – which consists of fitting a common-pool model of material transfer (Melzer et al. 1984, 1987) – quantified the evolution of flux reliably, provided that the model fitted well Ca²⁺ waveforms at various pulse durations covering the range of interest. In other words, if the removal model (with any set of parameters) fitted correctly the evolution of [Ca²⁺]_cyto after pulses of various durations, then the kinetics of the derived Ṙ (t) would be reliable – and model independent – at those durations.

This test is illustrated in Fig. 5, which in panel A shows the Ca²⁺ transients elicited with pulses of various durations to the same voltage and the uniformly good fit with the removal model during times post-Ca²⁺ release (thin lines). In Fig. 5B are the Ṙ (t) records derived from these Ca²⁺ transients. Here the goodness of fit translates to a flux that decays rapidly to zero after the end of the pulse and then remains at zero. The sigmoidicity is clearly visible in the record corresponding to the longest pulse, and is supported by the good fit at durations that span the shoulder. Records with similar kinetic properties (but different scale, i.e. roughly differing from the ones shown by a constant factor) could be obtained with different parameter values; thus, for example, a duplication of the assumed concentration of EGTA (from 7 to 14 mm) accompanied by duplication of the rate constant of Ca²⁺ removal by the pump, k_uptake, resulted in a flux roughly scaled up by a factor of 2. In conclusion, while the scale of the computed flux depends steeply on the assumptions for parameter values, the kinetic properties are robust. The sigmoidicity was also found to be independent of scan location in the cell, time after patching, and changes in fit parameters that conserved the goodness of fit. It cannot be explained as a consequence of contractile motion or dye saturation (conditions that were largely avoided in the present work).

In the example and all other cases in the present study the sigmoidal decay of Ṙ (t) led to a value Ṙ (∞), clearly greater than zero, which remained virtually constant for the longest pulses applied (1.8 s). The straightforward interpretation, illustrated in the cartoon of Fig. 6, is that the steady flux – the cycling flux – corresponds to a balance between release via open RyRs and uptake by the SERCA pump while [Ca²⁺]_cyto and [Ca²⁺]_SR remain constant. At this time the Ca²⁺-binding molecules of SR and cytosol, represented by BUFFER in the cartoon, are in true binding equilibrium. This phase, during which Ṙ is essentially constant, should eventually be terminated by inactivation of the t membrane voltage sensor (which for frog muscle has characteristic times greater than 10 s; Brum et al. 1988). A similar cycling phase has been proposed for amphibian muscle, but is more difficult to demonstrate given the much slower decay in the amphibian (Pizarro & Ríos, 2004).

Release flux in the cycling condition, Ṙ (∞), is equal and opposite to the unidirectional flux via the SR pump, p(∞). Since a simple relationship is assumed between pump flux and [Ca²⁺]_cyto, it is possible to calculate p(t) during the whole transient and thereby obtain a net release flux, Ṙ_net, as the sum Ṙ (t) + p (t), which is represented in grey in Fig. 6A. It is then simple to compute the total releasable calcium by integration of Ṙ_net. This is illustrated in Fig. 6B, where the integral of Ṙ (t) is the grey trace and that of Ṙ is the black. As Ṙ tends to a positive constant, its integral grows linearly beyond a certain point in time. The integral of net flux instead stabilizes at a constant value, which is by definition the releasable Ca²⁺.

Table 1 lists averages of quantitative aspects of release flux from 27 records in 18 cells. Results are with pulses to +10 or +30 mV (pooled in spite of small differences between the two sets), with durations of 400–1800 ms. Results are presented in two groups, from images acquired at different scanning frequency, but only peak flux is significantly different between the groups. For the images at 2.5 ms line⁻¹, the average peak is 50.7 mm s⁻¹ and the average QS, 24.2 mm s⁻¹. Had the images been acquired at the highest available frequency, the peak should have reached 122 mm s⁻¹. (As stated before, the average peak of Ṙ determined directly at the highest available scan frequency was 147 mm s⁻¹.)

As listed in the table, the average releasable Ca²⁺ (expressed, like the other measures of flux, in terms of the aqueous myoplasmic volume) was 2.94 mm. The asymptotic or cycling flux was 2.95 mm s⁻¹. A comparison of this value with the level QS of flux after the peak has interesting implications. A value of 2.95 mm s⁻¹ is more than 10% of the average QS. If the release permeability had remained constant during the pulse and all the decay in Ṙ was due to depletion, an asymptotic value of flux greater than 10% of its initial value would imply that more than 10% of the content remained in the SR when the cycling condition was reached. As we shall see, the release permeability appears to increase at least 2-fold with progressive depletion; if this is the case, the limiting value of [Ca²⁺]_SR in a maximally depleting pulse must be less than 10% of its initial value.

It is also worth noting that in spite of the presence of about 10 mm EGTA in the cytosol, the SERCA pump is capable of maintaining a large removal flux (equal to the measured Ṙ (∞), 2.95 mm s⁻¹) and rapidly restoring the initial content after voltage-operated release terminates. After the end of a depleting pulse it takes less than 100 s to recover the initial content, as demonstrated by comparing the responses to paired pulses at variable intervals (not shown).

A quantitative index of non-linear SR emptying

While sigmoidicity – and a ‘shoulder’– are obvious in some records, in others they are not, especially if the flux record is noisy. It was therefore important to find a quantitative measure of this feature, which could be applied systematically and objectively. Curvature was considered first because sigmoidicity implies a change in the sign of the curvature. However, the calculation of curvature (iterated differentiation) increases the noise greatly. Moreover, sigmoidicity is an extreme case of separation from an exponential decay, which is the more relevant feature. A different index was found instead, which has the added virtue of a specific meaning in terms of the physics of transport. The index is the (minus) time derivative of flux, divided by net flux; we call it NFRC, for normalized flux rate of change. Formally:

(2)

which as shown in the Discussion satisfies approximately the following equality:

(3)

where P is release permeability (defined in the Discussion), ϕ is surface-to-volume ratio of the SR and B is SR buffer power (total over free SR calcium concentration). NFRC is a lagging indicator of P/B; it will follow the changes of P/B unless the logarithmic derivative term becomes sizable (which only occurs during the early rise to peak flux, see Discussion and Fig. 9). In particular, NFRC will be constant when P and B are constant; in those cases the decay is trivially exponential, with time constant equal to NFRC⁻¹. NFRC is therefore a generalization of the exponential rate constant to cases where the decay of flux is not exponential.

Figure 9.

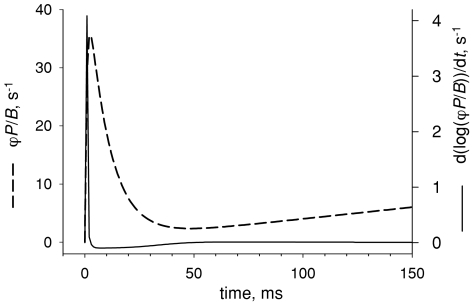
Comparison of two terms in NFRC Dashed curve, the function defined by eqn (12), which imitates the putative evolution of ϕP/B. According to eqn (9) this function constitutes the first term of the NFRC. Continuous curve, second term in NFRC (calculated using the same equation). Note different scales. According to this simulated evolution, NFRC and ϕP/B are essentially identical except at the earliest times.

The use of NFRC is illustrated in Figs 7 and 8. In Fig. 7A is the fluorescence image, in B the derived [Ca²⁺]_cyto(t) and in C the flux, elicited by a 400 ms pulse to +20 mV. In this example, the shoulder in Ṙ is present but small. The green trace is the NFRC, which displays large and fast-changing phases at the very beginning of release (consistent with a rapidly changing permeability), followed by a positive and rising phase that persists while the calculation is possible. At later times, as net flux tends to zero the calculation becomes meaningless (we set the plot to 0 when Ṙ_net dips below 1 mm s⁻¹).

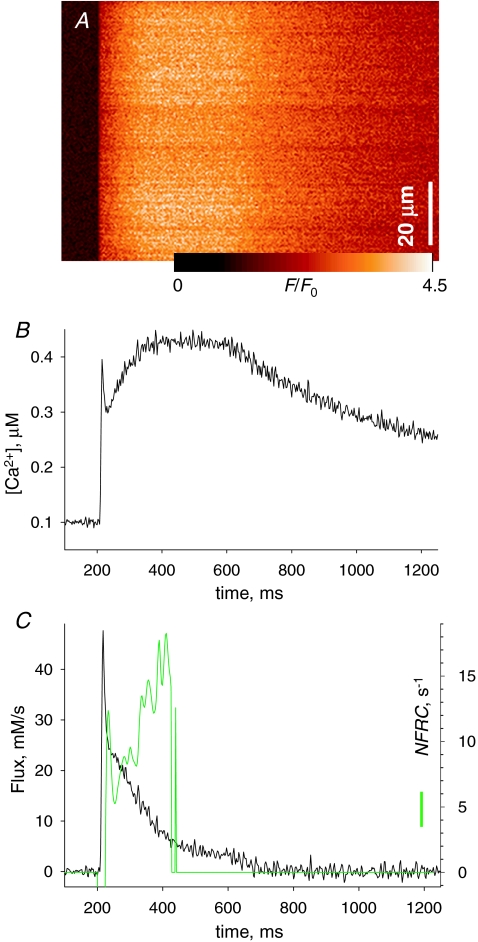
Figure 7.

The NFRC, an index of non-exponential decay of release flux A, F(x,t)/F₀(x) in a cell with rhod-2 stimulated by a 400 ms pulse to 0 mV. B, [Ca²⁺]_cyto(t) derived from the averaged line scan. C, black trace, Ṙ (t) derived from the record in B, showing a ‘shoulder’ or sigmoidal decay following the early peak. Green trace, NFRC(t), calculated according to eqn (2). Note its steady growth following an initial interval of fast biphasic change, cotemporal with the early peak of flux. Calculation of NFRC is stopped when Ṙ_net, not shown, falls below 1 mm s⁻¹. k_uptake= 6150 s⁻¹; other parameters as in Fig. 3. Experiment 021408a, record 25.

Figure 8.

Varied evolutions of NFRC A, black trace, Ṙ (t) in a frog fibre, reproduced from Fig. 4. Green trace, NFRC(t). Note that it becomes essentially constant during the quasi-steady phase of the flux. B, line scan image and [Ca²⁺]_cyto(t) in a mouse fibre. C, Ṙ and NFRC(t), derived from records in B. Note that the decay of Ṙ in this case has no ‘shoulder’ and seems exponential (it is well fitted by an exponential of time constant 110 ms, not shown). Accordingly, the NFRC becomes essentially constant after the initial phase of rapid change. k_uptake= 4010 s⁻¹; other parameters as in Fig. 3. Identifier 101906a, record 21. D and E, line scan image, Ca²⁺ transient, release flux and NFRC(t) in another mouse cell. This cell represents frequent cases in which the decay of the Ṙ (t) record had little evidence of a shoulder, but NFRC(t) still increased during the pulse. k_uptake= 8210 s⁻¹; other parameters as in Fig. 3. Identifier 022008b, record 25.

Other examples of the evolution of this index are in Fig. 8. In panel A is NFRC(t) for the frog release record of Fig. 4, which is superimposed for reference. In frog records, the early peak of NFRC is followed by a descent to a low and steady value; in this case the value is approximately 1 s⁻¹, which of course corresponds to the rate constant of the exponential decay phase of Ṙ.

In a few cases in the mouse (3 out of 37 images in 2 out of 22 fibres), we observed transients as the one in Fig. 8B and C, in which the NFRC evolved much as in the frog, with a steady phase following the early peak (implying that the evolution of flux was approximately exponential).

Finally, in many cases (illustrated in Fig. 8D and E) the flux did not exhibit a clear shoulder but the NFRC still increased during the pulse. These cases constitute the best justification for the use of the index, which proved more sensitive and informative than the observation of sigmoidicity. While sigmoidicity is the eye-catching feature, an increasing NFRC reveals where in the record Ṙ is decaying more rapidly than a first order process, and the degree by which the rate factor is changing.

Table 1 lists in column 6 the NFRC at the time (200–250 ms into the pulse) when its calculation stopped because net release fell below 1 mm s⁻¹. This value was always close to its maximum in the said interval. The average, 18.3 s⁻¹, is more than an order of magnitude greater than typical rate constants of flux decay in frog muscle. In the last column is the relative increase, that is, the ratio between the value at 200–250 ms and the nadir that occurs (at about 30 ms) after the initial peak in permeability. On average, NFRC (or ϕP/B) increases more than 2-fold in this interval.

Discussion

The present results extend work of other laboratories on the properties of voltage-induced Ca²⁺ release in mouse muscle cells under voltage clamp. Carried out on enzymatically dissociated cells from the FDB, they focus specifically on the evolution of release flux during pulses of much longer duration than used previously. By concentrating on this range of stimuli, they provide a view of the evolution of release flux and permeability under conditions of varying SR Ca²⁺ content, and therefore contribute to our understanding of the modulatory effects of load on Ca²⁺ release flux.

The present technique has kinetic limitations

Peak release flux induced by action potential in fast twitch mouse muscle has been evaluated using photometry of large cell segments, at 140–150 mm s⁻¹ (Hollingworth et al. 1996), 212 mm s⁻¹ (Baylor & Hollingworth, 2003) or 320 mm s⁻¹ (Woods et al. 2004). Evaluations of the peak during high voltage clamp pulses in mouse muscle fibres range from 175 mm s⁻¹ using fura-2 (or 209 mm s⁻¹ with a faster dye; Ursu et al. 2005) to 320 mm s⁻¹ with a fast non-ratiometric dye (Woods et al. 2005). There is also an estimate of ∼9 mm s⁻¹ in silicon clamp experiments that did not use EGTA (Collet et al. 2004), which falls well below the range of the others, probably because the calculation depends crucially on intrinsic buffer properties that were not measured. The peak value in the present experiments is close to that reported by Ursu et al. (2005); however, when evaluated with exactly the same parameter values used in the latter study, our estimate is reduced. It is less than the 320 mm s⁻¹ reported by Woods et al. (2005) and the time to peak flux is 1–1.5 ms longer. The reasons for the generally lower values obtained in the present work may be a slower voltage transition plus the documented effect of scanning speed, which even at the highest frequency may not be sufficient to fully reflect the kinetics of release flux.

A tentative conclusion is that conventional (pinhole) scanning confocal microscopy, as used here, does not match whole-cell photometry for speed and signal-to-noise ratio. Faster confocal techniques (including resonant galvanometer scanning or the slit-scanner trademarked LIVE by Zeiss Inc.) combined with faster dyes (as in Woods et al. 2005) should further improve temporal resolution.

Unlike the early peak, we found that the kinetics of the later stages of release flux, starting roughly 20 ms after the beginning of the pulse, is well defined and independent of the rate of image acquisition. This property allowed us to obtain line scans during periods of seconds without obvious bleaching or alteration of electrical properties. Pulses of up to +60 mV and 1.8 s were applied, for periods as long as 120 min (starting 30 min after whole-cell patching), without major changes in holding current or linear membrane capacitance.

One of the outcomes of the long-lasting transients of Ca²⁺ release was a measure of total releasable Ca²⁺, which averaged approximately 3 mm (in terms of aqueous myoplasmic volume). This estimate is similar to that of Ursu et al. (2005) in similarly treated mouse muscle fibres. While the numbers agree, the agreement may have been helped by compensating errors; indeed, the study cited used an internal solution of lower [Ca²⁺], which should have led to a lower SR load, but at the same time extrapolated the flux, assuming that it would decay exponentially at the rate measured in the first 100 ms, which as we argued before, should underestimate the rate of decay and therefore overestimate the content. Fryer & Stephenson (1996) used myofilament force as a monitor of Ca²⁺ content in rat fibres and estimated SR content in fast-twitch EDL muscle at 1.01 mm in terms of fibre volume, or 1.42 mm in terms of myoplasmic volume. The 2-fold greater content measured in the present work could be due to a steady release of Ca²⁺ from EGTA as it enters the myoplasm (see Methods) in the presence of low Ca²⁺ leak from the SR, due in turn to a low concentration of ADP imposed in turn by having creatine phosphate and no creatine in the pipette solution (Macdonald & Stephenson, 2001). Thus, in our conditions the SR would be close to its maximal Ca²⁺ capacity, while Fryer & Stephenson (1996) estimated that the SR was at one-third saturation in their case. All these estimates therefore seem to be in rough agreement; it should be kept in mind, however, that the present calculation of releasable Ca²⁺ is based on the integration of flux, the scale of which is not robustly determined (as discussed in Methods and Results).

The ‘plateau’ that follows the peak of Ca²⁺ release decays rapidly

As first observed in the mouse by Ursu et al. (2005) and Woods et al. (2005), after the early peak elicited by a large depolarization, flux returned to a much lower ‘pedestal’ (Ursu et al. 2005), which is analogous to the quasi-steady level described in frog and rat muscle. The present evaluation of this pedestal is consistent with the earlier data (24 mm s⁻¹ on average, versus 20 mm s⁻¹ in the study of Ursu et al. (2005)). As shown in Fig. 4B and in various examples by Ursu et al. (2005), this pedestal is much more rapidly decaying than in comparable records of frog or rat. While the early 100–150 ms of this decay could be fitted by exponential functions of time constants between 100 and 220 ms, the single exponential was not a good description of Ṙ (t) during long-duration pulses. In most cases, illustrated in Figs 4–8, the decay appeared sigmoidal or exponential after a lag.

Before attributing any particular meaning to such non-exponential decay it was necessary to ascertain that it was a model-independent feature of Ṙ. To this end we used a property of the removal algorithm, described in Results in reference to Fig. 5, namely that the algorithm describes well the kinetics of release flux provided that a condition of ‘detailed fit’ is met (Schneider et al. 1987). The condition was clearly met in four cells, thus establishing the non-exponential decay of Ṙ as a true feature. In some cases, two of which are illustrated in Fig. 8, the evolution was not obviously different from an exponential decay. To generalize the observation and make it objective, we generated a quantitative index, the NFRC.

A quantitative index of non-exponential decay

The reason for recording Ṙ elicited by pulses of long duration was to directly evaluate the flux at the very different [Ca²⁺]_SR levels that prevail at rest and after a long depolarization. As stated, the decay of Ṙ was not exponential. This formal property of the evolution of flux is interesting because it implies changes in SR release permeability (or buffering power) and is therefore an indication of modulation of Ca²⁺ release and the release channel.

While the non-exponential kinetics of the decay of flux was often obvious, in other cases it was not. A relatively simple transform of Ṙ provided an index of its separation from an exponential time course. It is defined as the time-dependent ratio of the (minus) rate of change of flux over the net flux, and is accordingly called the normalized flux rate of change, formally defined by eqn (2).

It will be demonstrated that NFRC has a simple physical meaning. For this purpose we use nomenclature of Shirokova et al. (1995) as follows:

Free Ca²⁺ concentration in the SR: [Ca²⁺]_SR.

Total Ca²⁺ concentration in the SR: [Ca]_SR= total calcium content/SR volume.

SR buffering power for Ca²⁺: B=[Ca]_SR/[Ca²⁺]_SR.

Total SR calcium concentration in terms of accessible cytosolic volume (equivalently, the concentration change that all calcium in the SR would produce if dissolved in the cytosolic volume):

(4)

The depletion-corrected release flux (González & Ríos, 1993), frequently used as a measure of SR release ‘permeability’, is defined as

Using the definitions above, depletion-corrected flux can be factored as

The first factor in Ṙ is a conventionally defined flux m. Given these expansions

(5)

In earlier theoretical analyses, the depletion-corrected flux is loosely termed ‘permeability’. The definition eqn (5) refines the analysis, demonstrating that the depletion-corrected flux includes three factors: a true permeability P, defined as flux per unit area and unit concentration gradient (with dimensions [space]×[time]⁻¹), the Ca²⁺ buffering power of the SR, which has been proposed to change with [Ca²⁺]_SR (Pape et al. 2007; Launikonis et al. 2006) presumably following changes in the aggregation state of calsequestrin (e.g. Park et al. 2004), and the geometric factor ϕ. The main reason for ϕ to change would be a net gain or loss of osmolytes. Given that the total reduction of [Ca²⁺] is at most 1 mm, it is difficult to imagine a net change in osmolarity greater than 1 or 2% of the initial value; hence the reason for a changing depletion-corrected flux must be found in P or B.

Solving eqn (5) for flux and differentiating with respect to time

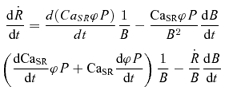(6)

By definition, eqn (6) divided by net flux yields the NFRC. Net flux Ṙ_net is Ṙ + p, where p is SR pump flux, a negative quantity estimated as part of the numerical computation of Ṙ. In turn Ṙ_net is the (minus) rate of change of Ca_SR. Therefore, using eqn (6)

(7)

which can be rewritten as

(8)

During the first 200–250 ms of a pulse, the release flux is large and only slightly greater than the net flux (i.e. the pump rate is negligible by comparison). At such times eqn (8) simplifies to

(9)

At later times Ṙ continues to decay and the approximate eqn (9) becomes invalid. Later Ṙ_net tends to 0 and NFRC is no longer determined.

According to eqn (8) and approximation eqn (9), NFRC is an approximate measure of ϕP/B. If ϕP/B is constant, then NFRC is equal to ϕP/B.

The use of NFRC should be clear after this derivation. The common goal in the analyses of Ca²⁺ release modulation is to determine release permeability. A common obstacle is that [Ca]_SR, the denominator in the definition of permeability, is generally not knowable, as the remnant load after a long pulse is not defined by the present methods. By including an additional differentiation step, the definition of NFRC effectively removes the unknown constant from the equation. This is easy to see if ϕP/B is constant. Differentiating both members in eqn (5) with respect to time under this assumption yields

(10)

therefore

(11)

The left side of eqn (11) is by definition the NFRC and the right side is ϕP/B. If this is a constant, Ṙ (t) is an exponential decay to Ṙ (∞) and NFRC its exponential rate constant.

If ϕP/B changes with time, then NFRC will change essentially following ϕP/B, as the derivative term in eqn (9) is very small. It is only during the times of extremely rapid evolution of P/B that this term becomes large. How close the NFRC follows P/B is illustrated by a simple example: combining 1st and 0th order activation and inactivation variables (m, n, h) we generate a hypothetical evolution of ϕP/B that includes an initial peak followed by a slower increase:

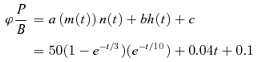(12)

This is the dashed curve in Fig. 9. The continuous trace in the figure is the logarithmic term in the NFRC, calculated from ϕP/B using eqn (9) (note different scales). With this evolution, which is not unlike experimental NFRC records shown in the previous figures, NFRC and ϕP/B are essentially identical except at the earliest times.

In the examples, a constant NFRC (or ϕP/B) prevails during essentially the whole ‘quasi-steady’ portion of the frog record (Fig. 8A) and the mouse record in Fig. 8C, which represents one of three exceptional cases observed in mouse fibres. In all three cases, the (constant) value of NFRC was much greater than the typical rate constants of frog flux records, consistent with a greater relative permeability in the mammal.

By far the most common case for the mouse was an increase in NFRC, which could be followed for at least 200 ms after the early phases of flux. Although changes of up to 4-fold were observed, the average increase of NFRC from the nadir to the value after 200 ms was 111%. During this interval, NFRC was typically more than 10 times greater than in the frog. This implies either that the release permeability increases, the buffering capacity of the SR decreases, or both. Of course, this results in a comparatively much greater ability of the SR to empty its Ca²⁺ content –ϕP/B measures the ‘evacuability’ of the SR.

Comparison with other results

In spite of years of work, there is no consensus as regards the evolution of release permeability when the SR content changes. Early observations of Baylor & Hollingworth (1988) and Hollingworth et al. (1992) on the effect of high concentrations of fura-2 in frog muscle bolstered the idea of a Ca²⁺-dependent inhibitory effect (a CDI). Such a negative feedback mechanism predicts an increase of permeability with depletion of Ca²⁺ in the SR, secondarily to a reduction in unitary current and a consequent reduction in the local elevation of [Ca²⁺]_cyto near release sites. This prediction was largely upheld in experiments by Chandler and co-workers (Jong et al. 1993; Pape et al. 1995, 1998), leading Pape & Carrier (1998) to estimate an increase in release permeability by about 7-fold when Ca_SR was reduced below 400 μm. On the other hand, Schneider et al. (1987), Jacquemond et al. (1991) and Shirokova et al. (1996) interpreted their results as evidence of essential constancy of permeability during long-duration pulses. Later Pizarro & Ríos (2004), combining approaches of the two camps, found evidence of a more modest increase in permeability (about 2.5-fold) upon extreme depletion.

In our present estimate in the mouse, ϕP/B (which is directly comparable with ‘permeability’ of the earlier works) increased substantially, by 250% in the example of Fig. 7, by 111% on average, during the time when it was measurable (i.e. before net release flux became too close to zero).

There is one other estimate, by Ursu et al. (2005), of the effects of SR content on release permeability in the mouse. These authors concluded against ‘a substantial increase in permeability with depletion’. However, we read their Fig. 7G and H as evidence of an increase in steady permeability by 68% (the ‘pedestal’ value of permeability went from 0.011 ms⁻¹ at rest to 0.018 ms⁻¹ when the SR content was reduced by 80%). As all estimates based on an extrapolation to full depletion, the one by Ursu et al. (2005) depends on the residual value of Ca_SR assumed to remain at the time of the test pulses. Small errors in this value will change substantially the evaluation of permeability. In our view, these errors explain the difference in evaluation of the change in permeability in frog muscle between Pape & Carrier (1998) and Pizarro & Ríos (2004) and may explain the differences between the present estimates and the earlier work in the mouse.

Another interesting precedent is the study of Posterino & Lamb (2003) on rat EDL. The contractile force in the response to an action potential in skinned fibres was essentially constant and independent of [Ca]_SR as this variable was changed from ‘full load’, estimated at 3–4 mm, to a value below the ‘endogenous’ load, close to 1 mm. The observation was taken as evidence of a constant integrated release of Ca²⁺ in an action potential, regardless of the concentration gradient that drives it, which implies an essentially inverse proportionality between load and permeability, in qualitative agreement with our present results.

The significance of an increase in evacuability of SR calcium

Rather than a change in permeability – a property of the SR membrane – the increase in NFRC implies an increase in the ratio P/B (eqn (9)), which is a property of the organelle. This index, with dimensions of inverse time, reflects the ability of the SR to empty itself of calcium, the evacuability of the SR. On experimental and theoretical grounds, both P and B could be expected to change in the right direction to result in an increase of P/B. An increase in P with depletion may occur if the increase in local [Ca²⁺]_cyto associated with release causes either closure of open channels or inactivation of closed ones (e.g. Pape et al. 1998; Pizarro & Ríos, 2004), as depletion would reduce the local increase in [Ca²⁺]_cyto. In regard to changes in B, the buffering power of aqueous suspensions of calsequestrin is known to depend on the aggregation state of calsequestrin (Park et al. 2003, 2004) and decrease when calsequestrin depolymerizes. Since decreasing [Ca²⁺] leads to depolymerization of calsequestrin in aqueous suspensions, it is expected that depletion-causing Ca²⁺ release will have the same effect inside the SR, with the consequent reduction in B. In qualitative agreement with this expectation, and based on Ca²⁺-dependent changes in light absorption by tetramethyl-murexide trapped in the SR, Pape et al. (2007) concluded that the buffering power of the SR of frog muscle is maximum at the resting value of [Ca²⁺]_SR and decreases upon release.

An increase in evacuability should increase fractional release of Ca²⁺ per action potential under conditions that cause SR depletion, such as exercise leading to myogenic fatigue (review by Allen et al. 2008). An increase in evacuability probably underpins the maintenance of the nearly constant output of Ca²⁺ per twitch over a wide range of SR loads observed in rat muscle (Posterino & Lamb, 2003). However, in that study Ca²⁺ output per twitch could not be maintained at loads reduced slightly below resting level, while strenuous exercise reduces [Ca²⁺]_SR well below resting levels. The present study shows that the increase in evacuability with depletion continues up to the lowest levels of load that could be explored, which suggests that the phenomenon could help reduce the fatiguing effects of the changes in load, even if release per twitch cannot be maintained.

The growth in the ability of the SR to empty itself as Ca²⁺ is released is in complete contrast with the situation in cardiac muscle, where depletion reduces the openness of RyR channels and is thought to be the dominant agent of termination of Ca²⁺ release (e.g. Stern & Cheng, 2004). It is becoming increasingly clear that the rules determining the control of Ca²⁺ release in skeletal and cardiac muscle are very different, and therefore the control mechanisms must be different. One mechanistic difference, established in a recent bilayer study, is the essential failure of the skeletal isoform of calsequestrin (isoform 1) to modulate the channel activity of the skeletal isoform of the RyR (M. Fill, Rush University, personal communication), in contrast with the strong modulation observed with the cardiac pair (Qin et al. 2008). A teleological justification has been put forward (Ríos et al. 2008): that the ‘anterograde’ regulation active in skeletal muscle, whereby permeability is regulated by released Ca²⁺ at the cytosolic aspect of the channels, reflects preference for maintaining a constant output in a release event, while the ‘retrograde’ regulation of cardiac muscle, where permeability is controlled by Ca²⁺ inside the SR, results in conservation of the content of the store, for a plausible gain in long-term stability of Ca²⁺ output. While skeletal muscle can rest, the heart cannot.

Appendix 1

Complex behaviour of fluo-4 in the cytosol of muscle fibres

The purpose of this Appendix is to show that fluo-4 and rhod-2 salts do not provide comparable measures of the Ca²⁺ concentration in the cytosol, either because they do not constitute single pools of molecules with homogeneous properties or because they compartmentalize into areas or organelles with different [Ca²⁺].

Figure A1 shows raw fluorescence, F₁(t) and F₂(t) of fluo-4 and rhod-2, averaged over space in simultaneous line scans acquired while the cell was subjected to a depolarizing voltage clamp pulse. Note first that the gains of the photomultipliers that amplify the signals have been adjusted, so that the resting intensities of fluorescence F₁(0) and F₂(0) are equal. They will be represented indifferently as F₀.

Figure A1.

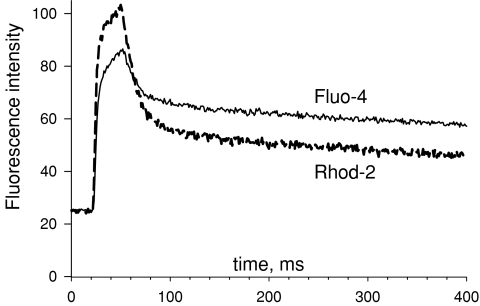
Fluorescence intensity of fluo-4 and rhod-2 during a Ca²⁺ transient Line-averaged intensities of fluorescence in line scan images of fluo-4 or rhod-2, recorded simultaneously on the same voltage-clamped cell, upon depolarization for 30 ms to +20 mV. The photomultiplier gains were adjusted so that the initial average intensity would be the same for both dyes. Plotted are averages of raw intensity, not normalized to resting fluorescence. The crossing of records after the pulse is inconsistent with one-pool models of the dye reactions. See Appendix text for details. Identifier 042408b, record 10.

If these signals are due to 1 : 1 reactions of the dyes in single pools of homogeneous properties with a homogeneous cytosolic Ca²⁺, eqn (A1), the standard kinetic expression for [Ca²⁺] in solution as a function of fluorescence of a dye that binds calcium one-to-one, will apply:

(A1)

When the concentration is changing slowly, an approximation applies:

Relative to the initial concentration, the time-dependent value is:

(A2)

The near-equality applies, as F_min≈ 0 for both dyes used.

Using the fact that F₀ is the same for both dyes, eqn (A2) simplifies to

(A3)

Further simplification results from the fact that rhod-2 is very far from saturation at the times of interest, hence F_max2−F₂≈F_max2−F₀ and

(A4)

At all times during or after the pulse F₁ > F₀; therefore F₂/F₁ must always be greater than 1. The fact that it becomes less than 1 (see Fig. A1) cannot be explained under the single-pool hypothesis.

A heuristic way of presenting the contradiction is to note that F₀ is equal for both dyes, which implies that F_max/K_D is the same in both cases (a result of the adjustment of photomultiplier tube gains). Since this is the factor that relates F to [Ca²⁺] in the limit of low saturation, F₁, which increases less than F₂ as [Ca²⁺] increases beyond [Ca²⁺](0) during the pulse, and is therefore the dye signal that is closest to saturation, should remain below F₂ at all times of slow concentration change. Instead, F₁ eventually overtakes F₂, which implies that the single-pool model must be abandoned.

One variant of the model, suggested by S. M. Baylor (University Pennsylvania) and consistent with properties of fluo-3 reported by Hollingworth et al. (2000), is the presence of multiple dye forms that respond differently to [Ca²⁺]_cyto. As demonstrated by Harkins et al. (1993), a large fraction of fluo-3 is bound to proteins of the cell, and has lower affinity for Ca²⁺. In the presence of an elevated [Ca²⁺]_cyto, the greater Ca²⁺ affinity of the protein-free dye will drive a redistribution of bound into free form and a secondary increase in signal, following the kinetics of dye redistribution. If this phenomenon were quantitatively greater for fluo-3 (and fluo-4) than rhod-2, due for instance to a greater protein affinity, then F₁ would eventually overtake F₂, as observed.

An alternative modification of the single-pool model is to assume preferential entry of fluo-4 into compartments that pick up Ca²⁺ during the pulse, with mitochondria as a main possibility. This explanation, however, would predict a change in spatial pattern of the normalized signal, with F₁ remaining disproportionately elevated at locations consistent with the placement of mitochondria in the sarcomere (i.e. the I band). Such spatial segregation of the increase in fluorescence was not observed.

In conclusion, the difference in evolution of the signals from fluo-4 and rhod-2 is more likely to reflect a late change in the effective affinity of one of the dyes, rather than migration into (or away from) a compartment or organelle with [Ca²⁺] greater than the cytosol. While there is no direct evidence against the participation of rhod-2 in complex reactions similar to those described for fluo-4, the fact that its signal returns more rapidly to resting values suggests a lesser involvement than that of fluo-4. On this basis we tentatively retain the single-pool, one-to-one model to derive [Ca²⁺]_cyto from the signal of rhod-2.