A Non-Parametric Vessel Detection Method for Complex Vascular Structures

Abstract

Modern medical imaging techniques enable the acquisition of in-vivo high resolution images of the vascular system. Most common methods for the detection of vessels in these images, such as multiscale Hessian-based operators and matched filters, rely on the assumption that at each voxel there is a single cylinder. Such an assumption is clearly violated at the multitude of branching points that are easily observed in all but the most focused vascular image studies. In this paper, we propose a novel method for detecting vessels in medical images that relaxes this single cylinder assumption. We directly exploit local neighborhood intensities and extract characteristics of the local intensity profile (in a spherical polar coordinate system) which we term as the polar neighborhood intensity profile. We present a new method to capture the common properties shared by polar neighborhood intensity profiles for all the types of vascular points belonging to the vascular system. The new method enables us to detect vessels even near complex extreme points, including branching points. Our method demonstrates improved performance over standard methods on both 2D synthetic images and 3D animal and clinical vascular images, particularly close to vessel branching regions.

1 Introduction

The detection and quantification of arteriogenesis associated with coronary occlusion is critical for management of patients with cardiovascular disease. Modern medical imaging systems including micro X-ray Computed Tomography (microCT) and Magnetic Resonance Angiography (MRA) provide the capability to non-invasively image the arteriogenesis process of forming collateral vessels in vivo [5, 12, 17, 27]. An automated quantification and in vivo evaluation of arteriogenesis using vascular images would facilitate our understanding of the pathophysiology and could potentially allow in vivo monitoring of therapeutic interventions [4, 21, 31, 32, 42]. However, accurate and robust quantification of vascular images still remains a problem because of the geometrical complexity of vascular structures.

The analysis of vascular images can be divided into four steps: (i) Feature Extraction – detect vessel points; (ii) Geometric Model – connect the vessel points to form vascular trees; (iii) Quantify properties of the vascular tree; and in the case of serial imaging, (iv) quantify differences in these properties over time. For example, a typical vascular segmentation algorithm may consist of a combination of the first two steps in addition to image preprocessing steps. In most cases the methods rely on the detection of local tubular structures based on the local intensity characteristics. Then, global segmentation methods, varying from level sets [6, 20, 22, 41], region growing [13, 26, 30], to Kalman or particle filters [48], are applied to finally segment vascular structures via the global connectivity constraints.

Most image analysis research in this field has focused almost exclusively on the geometric model. The feature extraction process, whether implemented as a separate step or incorporated within the tracking/level set evolution framework, has for the most part used methods based on operators relying on the single cylinder model. Many published techniques, which include matched filters [9, 33], Hessian operator [14, 29] and model-based detection methods [19, 23, 40], suffer from their simple assumption that there exists only one local oriented structure. Some of these methods [9, 33, 23] are especially useful for finding locations of center lines of vessels. However, they perform poorly at points away from vessel center lines, thus reducing their ability to correctly estimate vessel volume. Hessian-based methods [14, 19] are not valid for crossing or branching points, and highly curved vessel points, both of which are essential for measuring vessel connectivity and understanding arteriogenesis. We emphasize that branching points are very common in most angiography problems outside of a few isolated cases of relatively large vessels.

The work presented in this paper focuses exclusively on this first feature extraction step and is aimed at relaxing the single oriented structure assumption common to most published methods. We propose a new method to detect complex vascular structures without the strong single cylinder assumption. We demonstrate that our new algorithm yields significant improvements over previously published methods. In particular, we present a novel “vesselness” measure based on the neighborhood intensity profile in spherical polar coordinates. By “vesselness” measure, we refer to the image in which the image intensity at a certain voxel is proportional to the likelihood that the voxel belongs to a blood vessel in the original image. Instead of assuming a single cylindrical structure at any voxel, we based our approach on the observation that the change of intensities in at least one conical-shaped neighborhood region (whose tip is at the voxel of interest) is very small if these conical region lies in a blood vessel (and high otherwise). This observation holds at both ordinary vessel points, branching points, vessel end-points, and points away from the vessel centerline. This key insight is formalized mathematically using a nonparametric model that does not depend on image derivatives.

The rest of the paper reads as follows: We first give a brief review of the vessel detection and enhancement methods in the literature (Section 2), and then provide additional motivation for our method in Section 3. In Section 4, we define the neighborhood intensity profile in spherical polar coordinates and show that it captures the characteristics of all desired vascular structures (Section 4.1). Next, we derive our new “vesselness” measure based on the intensity profile (Section 4.2). Section 5 describes experimental results for both 2D synthetic and real 3D images (MRA and microCT).

2 Literature Review

Many published approaches for vessel segmentation and tracking are based on filtering vascular structures correctly [1, 18, 48, 34]. We categorize the state-of-the-art vessel detection or enhancement techniques roughly into integral-based and derivative-based methods, both with the addition of multiscale techniques.

The integral-based methods, including matched filters [9, 29, 33], wavelets [45], geometrical moments [28], and model-based inferencing methods [23, 40], are especially useful for finding locations or center lines of vascular structures. However, they do not generate good measures for points away from center lines. Therefore, they either cannot provide accurate estimates for the size or volume of vascular structures or they need extra procedures to have better measures [1, 2, 18, 19, 29]. For example, vessel connectivity constraints [1, 2, 18] improves detection performance with post-processing filtered images.

Among derivative-based methods, Hessian operator based methods [1, 14, 19] are popular as its eigensystem captures the characteristics of tubular structures. Other methods based on the orientation tensor [37] have also been implemented to describe local structures. The idea behind eigenvalue analysis of either Hessian or orientation tensor is to extract the principal directions in which the local structure of the image can be decomposed. This directly gives the direction of smallest curvature, which is the direction of the tubular structure, and avoids the time-consuming line filters in multiple orientations. However, these methods are not valid at branching points because the assumption of the characteristics of the eigen structure does not hold. The decomposition is not valid when there is no longer a simple dominant eigenvector present. Hence, they also have limitations for robust quantification of complex vascular structures, especially when images are noisy, contain branching points, crossing points, and other extreme cases including stenosis and aneurysms.

For the consequent analysis of vascular images, a variety of approaches have been published. For instance, level set methods and topologically adaptable active contour models [6, 20, 22, 25, 35, 36, 41] are very active research subjects. Based on statistical properties of intensities or vessel orientations in images, researchers have demonstrated the effectiveness of the Expectation Maximization (EM) algorithm for the analysis of vascular images [7, 39]. With the integration of local spatial constraints, region-growing approaches have also been illustrated useful in segmenting vasculature in the angiograms [13, 26, 30]. Different minimum cost path techniques [3, 10, 18, 20] provide automatic and robust vessel centerline extraction for vascular analysis after segmentation. Skeleton-based vascular segmentation algorithms [1, 35, 38] were also proposed for both size measurement and the connectivity analysis simultaneously. In most of these methods, they integrate the results from the aforementioned feature extraction methods, which are inadequate at branching points. This is true even for very recently published paper [48], which proposes an elegant and sophisticated geometrical modeling technique with particle filters.

The accuracy of the analysis of the vascular system is determined by the vessel detection or enhancement techniques. The limitations of the aforementioned techniques may result in uncertain, even incorrect vessel tracing or extraction results. In this paper, we propose a new method to detect complex vascular structures without the strong single cylinder assumption. We demonstrate that our new method yields significant improvements over existing techniques, especially at complex extreme cases such as branching points.

The proposed method has the similar motivation as the nonparametic methods implemented for lung nodule detection [43]. It can also be considered as the modification to steerable filters [44, 47, 49] for corner and junction detection in computer vision. In medical image analysis, one-dimensional cores [52] have been proposed for extracting tubular objects, where they also consider local intensities in polar coordinates for finding medial axes at scale. With a corner detector [50], they extend the work to track branches based on the connectivity of extracted cores [51].

3 Motivation

In this section, we first demonstrate the relative inadequacy of a standard approach using Hessian operator for general vascular structure detection. We then provide additional motivation for our proposed algorithm by investigating the intensities within appropriate local neighborhoods of voxels in different places of interest (e.g. center line, branching point, etc.).

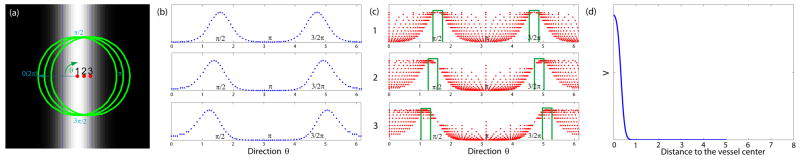
We start with the analysis of a synthetic image (Fig. 1(a)) with a single vessel model. The axis of vessel is the y axis and the section of the vessel begin a Gaussian function $I(x,y)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}}$, where σ = 5. Following the derivation of Frangi’s vesselness measure based on the eigen decomposition of the Hessian matrix (Appendix A) [14], we can get the vesselness measure:

$$V(x)=\{\begin{array}{ll}0\hfill & x^2\ge {\sigma }^2\hfill \\ (1-e^{-{(\frac{{\sigma }^2-x^2}{{\sigma }^4}I(x,y))}^2/2a^2})\hfill & x^2<{\sigma }^2\hfill \end{array}$$

Figure 1.

(a) A synthetic image with a Gaussian profile vessel and 3 labeled points from the vessel center line to vessel boundary (The green circles on the image represent 31×31 local neighborhoods.); (b) The intensity profiles with respect to different directions along the green circles in (a); (c) The variation of the sampled intensities (The ordinates in the plots are proportional to intensity values) with respect to different directions along the circles with varying radii within the green circles in (a): Narrow bands of directions with relatively large intensities and small intensity variations are illustrated by the green bars; (d) The vesselness response using eigen decomposition of the Hessian operator. The abscissa shows the distance to the vessel center.

We plot the response with respect to distance to the vessel center in Fig. 1(d). Clearly, the response drops quickly from the vessel center to the boundary points away from the center. This might cause problems for vascular analysis, especially when the correct estimation of vessel size is important. Multiscale techniques can help alleviate the problem. Another way to overcome this problem is to have an extra post-processing step [19]. By computing the integral of the inner product between the vessel direction (the eigenvector of Hessian matrix corresponding to the eigenvalue close to 0) and image gradients along different directions in multiple scales, the vessel size can be decided by finding the scale with minimum response.

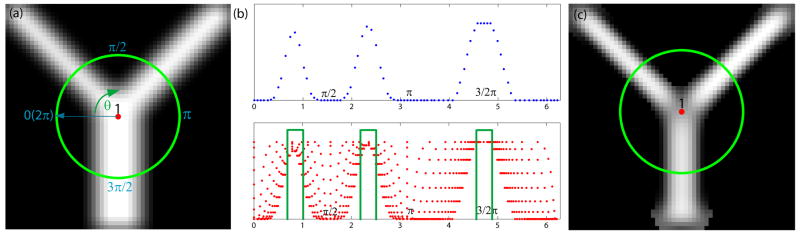
To illustrate another problem of this Hessian-based method, we further examine another synthetic image with a branching model (Fig. 2(a)). For this image, we compute V (x) in multiple scale spaces and the final vesselness measure (Fig. 2(d)) is the maximum of V (x) over multiple scales. The response again drops from the vessel center to the boundary points away from the center. The more serious problem is that this Hessian-based measure is not valid any more at the branching point 1 in Fig. 2(a) due to the ambiguity of the directions of the Hessian eigenvectors.

Figure 2.

(a) A synthetic image with a branching point labeled in the figure (The green circle on the image represents a 31 × 31 neighborhood.); (b) The intensity profile along the green circle and the sampled intensities along different directions within the green circle in (a). Narrow bands of directions with relatively large intensities and small intensity variations are illustrated by the green bars. (c) The vesselness response using eigen-decomposition of Hessian operators in multiple scale spaces [14]

If we directly look at the neighborhood intensities around these points, we find they have some common properties, making it possible to have a measure valid for both center and boundary points. The following observation motivates our new vesselness measure and is critical for appreciating our proposed method.

In Fig. 1(a), we choose 3 points from the vessel center to the boundary point; and the green circles define the local neighborhoods of the selected points. We first plot the intensity profiles with respect to different directions along the green circles in Fig. 1(b). The profiles have the same shape and the only difference is the distance between peaks of intensities. Next, within the green circles in the figure, we take the sampled intensities as the distance from the labeled point increases from 0 to the radius of the green circle. Fig. 1(c) illustrates the variation of the sampled intensities with respect to different directions. We can see that the plots for these points again are similar. One obvious common property is that all of them have two narrow bands of directions where the intensities are relatively large and the variation of intensities is small.

Furthermore, we plot the sampled intensities within the local neighborhood of a branching point in Fig. 2. They have 3 peaks for the intensity profile. More importantly, we can also see multiple narrow bands of directions with relatively large intensities and small intensity variation.

We show the examples in 2D while there are similar phenomena in 3D, which implies that we can design better measures directly based on the local neighborhood intensities. The rest of the section presents the mathematical modeling required to capture the common characteristics of neighborhood intensities for vascular points. We first define Polar Neighborhood Intensity Profile in section 4.1. A new method is proposed to compute the responses for vesselness measures based on Polar Neighborhood Intensity Profile in section 4.2.

4 Methods

4.1 Polar Neighborhood Intensity Profile

The polar neighborhood intensity profile underlies our new vessel enhancement method. We explicitly exploit the characteristics of sampled intensities in an appropriate neighborhood. We show visually that the necessary information deciding whether the points belong to vascular structures can be captured from the variation of neighborhood intensities.

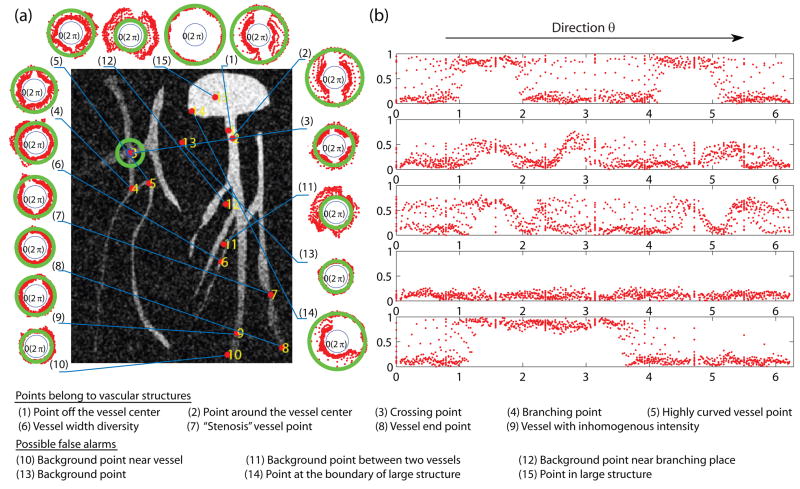
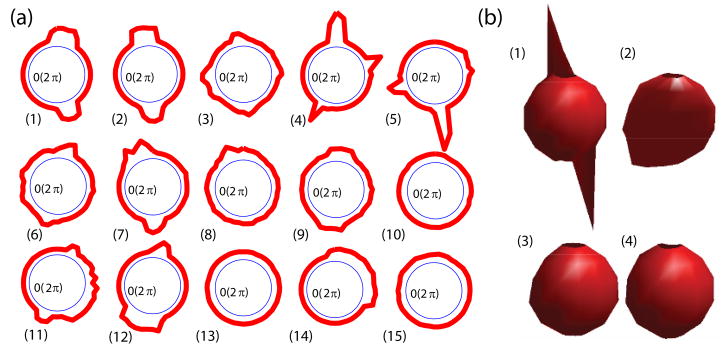
The efficacy of the neighborhood intensity profile is first illustrated by examining a synthetic 2D image containing almost all typical cases encountered in vascular structure analysis (see Fig. 3(a)). We label both vessel points (1–9) and background points (10–15) and plot the sampled intensities in a 31 × 31 neighborhood around each labeled point with respect to the relative direction to that point. We define our polar neighborhood intensity profile as the variation of sampled intensities with respect to the relative direction in polar coordinates.

Figure 3.

A synthetic image with labeled extreme points. The green circle on the image represents a 31 × 31 neighborhood. (a) Polar neighborhood intensity profiles for all the labeled points in polar coordinates: The distances of red points to the origin are proportional to the sampled intensities. The green circle’s radii are proportional to the intensities of the corresponding labeled points. (b) 5 typical cases plotted in Cartesian coordinates: The plots show the sampled intensities along different directions.

A visual inspection of the polar neighborhood intensity profiles (Fig. 3) reveals that for all types of vessel points (1–9), there exists at least one narrow band of relative directions, i.e. constant angle in polar space, in which the variation of intensities along the radial direction is relatively small compared to the other directions. Also, the sampled intensities in the narrow band are above those along close-by directions. On the other hand, for background points, we see that the intensity variation is mostly similar along all directions. Especially note that in the curvilinear regions between two nearby vessels (points 11–12), there are also narrow orientation bands with small intensity variations but the intensities within these bands are relatively low, which also leads to easy classification from true vessel points – this last case hardly occurs in 3D. For points belonging to non-vascular structures illustrated as a large blob in the figure (points 14–15), the polar neighborhood intensity profiles are different from vascular points: they have wide bands of directions with small intensity variation.

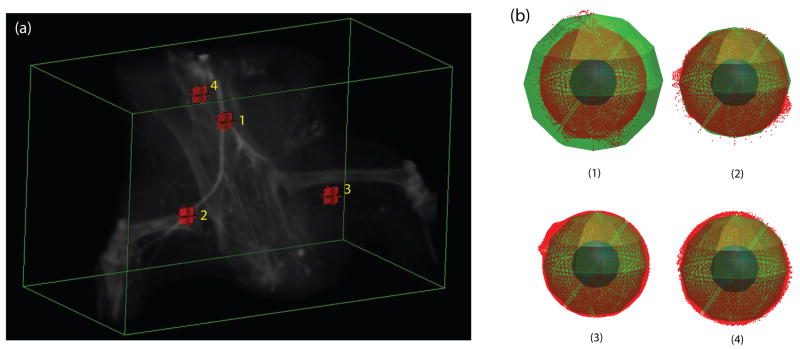
For 3D volumes, we observe the same phenomena and vascular points have tight oriented neighborhood regions with small intensity variation in spherical polar coordinates. Fig. 4 shows the polar neighborhood intensity profiles for points in the hindlimb portion of a 3D mouse vascular contrast-microCT. Hence, in both 2D and 3D cases, there is sufficient information to extract from the neighborhood intensities to measure the probability of having a vessel at an individual voxel, which we will term its “vesselness”. The task now is to mathematically quantify the common property shared by all types of points belonging to different vascular structures: there exist certain oriented neighborhood regions where the intensity variation is relatively small.

Figure 4.

3D polar intensity profiles: (a) Volume rendering of a mouse hindlimb microCT; (b) The sampled intensities in polar coordinates for the labeled points in a 27 × 27 × 27 window. Note the clusters of the sampled intensities (red points) with small variation from the local intensities (green sphere) for vessel points 1–2.

4.2 A Polar Neighborhood Profile “Vesselness” Measure

Based on the polar neighborhood intensity profile, we now derive our new “vesselness” measure, which we will term the polar profile vesselness (PPV) measure. Here we assume that vascular structures are bright in the images. As noted above, previous measures fail for extreme cases, including branching points, because the single cylinder assumption is not adequate to model all the cases in vascular structures. We propose an explicit way to model all possible cases nonparametrically. In this model, voxels will have a high vesselness measure if they satisfy the following two requirements:

1. Tight local orientation clusters with small intensity variation: In the neighborhood of vessel points, there must exist at least one narrow oriented conic zones along which the variation of the intensities is low. We also need to exclude points in non-vascular bright structures where the intensity change is small along all directions.

2. Locally bright structures: Since we are looking for bright vessels, it is important to exclude locally dark structures so that we can distinguish true vessel points from the points between two nearby vessels in 2D images (for example, points 11–12 in Fig. 3).

We derive our new measure in two separate parts in the rest of the section. We focus on the derivation in the three-dimensional case. (The two-dimensional case is similar.)

4.2.1 Tight Orientation Clusters with Small Intensity Variation

Here we introduce our approach to measure the tightness of small variation directions, which is proportional to our new “vesselness” measure and is at the heart of this proposed method. Our measure is based on the observation that there is always certain direction along which the intensity does not change much for vascular points. As indicated in section 4.1, the starting point is to choose an appropriate neighborhood in which we can clearly capture this feature.

We first estimate the intensity variation along relative directions since our objective is to capture the characteristics that the neighborhood intensity variation is small along certain direction from the point of interest. One way to do that is to calculate the average squared intensity deviation along different relative directions θ = {ψ, φ} (ψ and φ are the azimuth and elevation angles; ψ ∈ [0, 2π) and φ ∈ [0,π]) with respect to location of any voxel in the image x = {x₁, x₂, x₃}:

$$\mathit{Dev}(\mathbf{x},\theta )=\int h(\mathbf{u}){(I(\mathbf{x}-\mathbf{u})-I(\mathbf{x}))}^{2}d\mathbf{u},$$ (1)

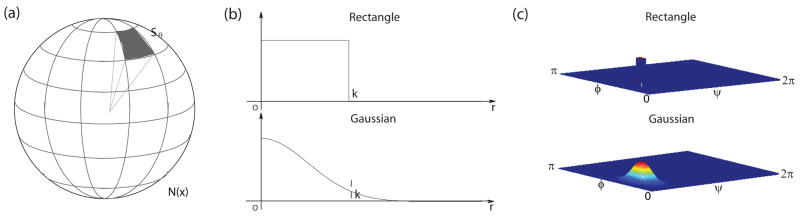
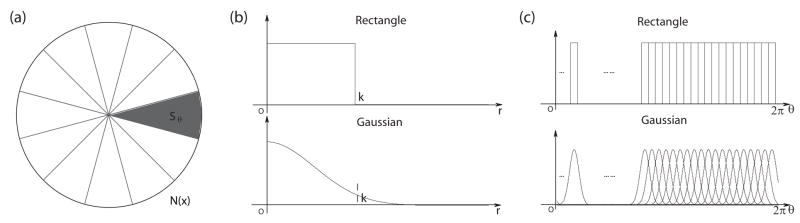
where I is the image intensity and h(u) is a function of relative position of neighborhood points from x defined in a local neighborhood N(x). Different h(u) gives different partition functions or weighting schemes to collect statistics in the neighborhood. We propose to use spherically separable filters h(u) = h_r(u) · h_θ(u) = h_r(r) · h_θ (ψ, φ), where $r=\sqrt{x_1^2+x_2^2+x_3^2}$ is the radial coordinate and ψ = arctan(x₂/x₁), $\phi =arctan(x_3/\sqrt{x_1^2+x_2^2})$. Both the radial and angular parts of the filter can be either a Gaussian function or a simple rectangle function as shown in both Fig. 6 and Fig. 5. We focus on the discussion of the angular part here. The neighborhood region N(x) is uniformly partitioned into n_ψ × n_φ regions along different directions covering the whole sphere as shown in Fig. 6(a). We can select better directions by using spherical barycentric coordinates [46] while the rest of the formulae are exactly the same. (For 2D cases, we have an even simpler partition as shown in Fig. 5(a).)

Figure 6.

Partition 3D neighborhood regions into oriented regions: (a) Partitions; (b) Radial part of the filter (k is the radius/size of the filter); (c) Angular part of the filter

Figure 5.

Partition 2D neighborhood regions into oriented regions: (a) Partitions; (b) Radial part of the filter (k is the radius/size of the filter); (c) Angular part of the filter

For simple average partition functions with rectangle functions for both radial and angular parts, we can calculate the average squared intensity deviation for all sample points u from the local intensity in each region S_θ:

$$\mathit{Dev}(\mathbf{x},\theta )=\frac{1}{\mid S_{\theta }\mid }\sum _{\mathbf{u}\in S_{\theta }}{(I(\mathbf{u})-I(\mathbf{x}))}^2.$$ (2)

For Gaussian functions, the radial part of the filter h_r(r) is shown in both Fig. 6(b) and Fig. 5(b). At each direction, the angular part of the filter h_θ(ψ, φ) is a 2D Gaussian function (Fig. 6(c)). Fig. 5(c) illustrates the simpler forms for the angular part in 2D cases. In the direction of θ = {ψ_i, φ_j}, we have:

$$h_{\theta }(\psi ,\phi )=\frac{1}{2\pi {\sigma }^2}exp(-\frac{D{(\psi ,{\psi }_i)}^2+{(\phi -{\phi }_j)}^2}{2{\sigma }^2}),$$

where D(ψ, ψ_i) = min(|ψ − ψ_i|, |ψ − ψ_j +2π|, |ψ − ψ_j − 2π|) is the minimal circular difference between ψ and ψ_i as the azimuth angle ψ is periodic in [0, 2π). We can get Dev(x, θ) by substituting both radial and angular parts in (1).

Next we express the probability, p_υ (x, θ), of having small intensity variation within the discretized orientation region S_θ as:

$$p_v(\mathbf{x},\theta )=c{e}^{-\beta \mathit{Dev}(\mathbf{x},\theta )},$$ (3)

where c is the normalization factor and β can be set either to a constant, or proportional to the maximum intensity variation along all the directions. Adaptively tuning β helps to get robust results. We can interpret this probability based on the assumption that the noise is normally distributed. Within the orientation regions where there are vascular structures, I(x) is the local intensity of vascular structures and β relates to the variance of the normal distribution. In this sense, this measure is similar to line model based inferencing methods [9] but they compute the generalized likelihood ratio test in the whole neighborhood instead of discretized orientation slabs. They are not adequate for extreme cases because of the single cylinder assumption.

The representative probability density functions in polar coordinates for typical cases, in Figs. 3 and 4, are illustrated in Fig. 7. The plots show clearly that the directions with large probabilities (small intensity variation) correlate with the vessel direction in both 2D and 3D images very well. The density functions for the vascular points are more concentrated than those of background points which are close to uniform distribution.

Figure 7.

Density functions to calculate “vesselness”: (a) The probability density functions in polar coordinates for the points in Fig. 3; (b) The density functions in spherical polar coordinates for the points in Fig. 4.

We use the entropy of the density functions to derive our final measure. The entropy [8] for a given density function measures the spread (or tightness) of the function. The entropy gets smaller when the spread of the distribution decreases. Thus, using the entropy of the density function, we define our tightness measure as:

$$v(\mathbf{x})=e^{-\tau H(p_v)}=e^{\tau \int p_v(\mathbf{x},\theta )log{p}_v(\mathbf{x},\theta )d\theta }.$$ (4)

Here, τ could either be a constant or a function. ¹ In this paper, since the ratio of the number of directions with small intensity variation will be very different for vascular structures and large structures in our experiments, we can simply set τ = 1.

4.2.2 Locally Bright Structures

To account for intensity inhomogeneities in images, we label vessel candidate voxels as being locally brighter than the background.

Intuitively, vessel candidates have to the points whose oriented neighborhood regions with small intensity deviation contain more pixels with high intensities. Hence, we define a brightness function for each pixel x:

$$b(\mathbf{x})=s(\mu (I_{S_{{\theta }_{min}}(\mathbf{x})})-\mu (I_{S_{{\theta }_{max}}(\mathbf{x})})),$$ (5)

where s(d) = 1/(1 + e^−αd) is a sigmoid function; μ(I_Sθmin(x)) is the mean intensity within the orientation region with the minimum deviation; and μ(I_Sθmax(x)) is the mean within the region with the maximum intensity deviation. These values come at no additional computational cost since we have them from the calculation of Dev(x, θ).

Another possible function follows the same derivation of Frangi’s vesselness measure [14]. We simply consider the gray values of μ(I_Sθmin(x)) and set:

$$b(\mathbf{x})=1-e^{-\frac{{\mu }^2(I_{S_{{\theta }_{min}}(\mathbf{x})})}{2\gamma }},$$ (6)

where γ is a constant.

4.2.3 The Polar Profile Vesselness Measure

Finally, our polar profile vesselness measure is the product of the local brightness constraint (equation (5) or (6)) and the local orientation constraint (equation (4)):

$$\mathit{PPV}(\mathbf{x})=b(\mathbf{x})\times v(\mathbf{x})$$ (7)

5 Experimental Evaluation

We perform a detailed evaluation of the performance of our new “vesselness” measure visually and quantitatively on 2D synthetic images and 3D animal vascular images from both MRI (MRA) and micro-CT images.

In Section 5.1, we use 2D synthetic data sets to perform both validation (at increasing level of noise) of the performance of our method as well as a comparison of its performance against that of the standard multiscale Hessian-based vesselness measure [14]. In addition, we perform a sensitivity analysis to demonstrate the relative insensitivity of our new method’s performance to parameter variations.

Next in Section 5.2, we present validation results for our methods against manual segmentations of a set of N = 12 3D MRA lamb pulmonary artery images. We demonstrate that our method yields statistically significant performance improvements over the Hessian method.

Finally, in Section 5.3, we present a set of results using micro-CT rodent images. These results visually demonstrate the improved performance of our method in data with truly complex vascular structures.

We note that, as part of our processing, all the images are first normalized into the range from 0 to 1. In all experiments, we choose the size of neighborhood region k as roughly 2 times larger than the size of the largest desired vessels in images. Based on k and image dimension, we choose the other parameters accordingly.

5.1 Validation and Parameter Sensitivity on 2D Synthetic Data Sets

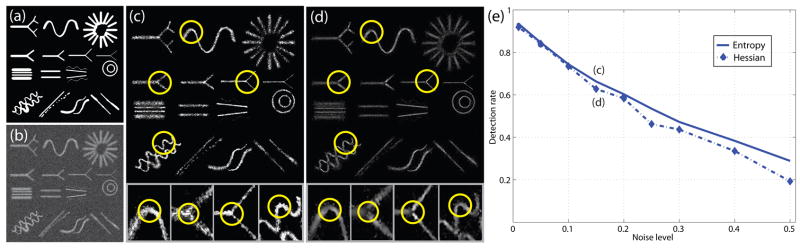
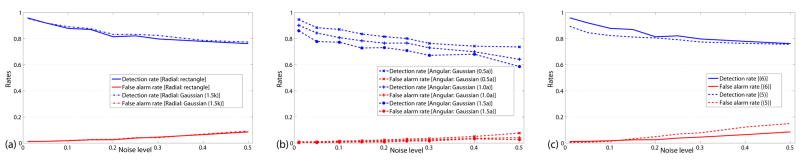
First, we evaluate the new algorithm using a series of 2D synthetic images containing a variety of vascular structures. A series of synthetic images (see Fig. 8) have been derived by adding varying amounts of Gaussian noise, ranging from noise variance of 1% to 50%. We use the phantom image (from [23]) for the performance evaluation. This class of images contains a wide range of different vascular structures as illustrated in Fig. 8(a). We present results from three sets of experiments. First we plot the detection rates (sensitivity) and false alarm rates (1-specificity) of our methods using a fixed threshold with varying noise level (Fig. 9(a, b, c)). Since there are a couple of important parameters involved in our new algorithm, a sensitivity analysis using these images is necessary to show that the algorithm is insensitive to different settings. We therefore perform a sensitivity analysis of the performance of our algorithms with respect to key parameters (Fig. 10(a, b, c)). Afterwards, we compare the performance of our method to a Hessian-based measure obtained by eigen decomposition of multiscale Hessian operators (Fig. 8(c–e)).

Figure 8.

(a) The ground truth synthetic image; (b) A synthetic image with the noise variance of 15%; (c) Our entropy-based measure map with zoomed parts; (d) The standard Hessian-“vesselness” measure map with zoomed parts; (e) Detection rates with false alarm rates fixed at 0.5% for 2 different measures.

Figure 9.

Performance Summary: (a) Detection and false alarm rates of our entropy-based measure with fixed threshold using the same rectangle filter for the angular part; (b) Detection and false alarm rates of our entropy-based measure with fixed threshold using the same rectangle filter for the radial part; (c) Detection and false alarm rates with different brightness functions (5) and (6) with fixed threshold. The terms inside the parentheses with Gaussian filters denote the standard deviations of Gaussian functions. k is the size of filters; a = 2π/n_θ.

Figure 10.

Sensitivity of the algorithm: (a) Sensitivity with respect to k; (b) Sensitivity with respect to n_θ; (c) Sensitivity with respect to β.

(i) Detection and False Alarm Rates

In this first set of experiments, we use the following parameters settings: k = 55, n_θ = 36 and β = 300.0. To calculate detection rates and false alarm rates, we need to threshold our “vesselness” measures. When k is twice larger than the size of the largest desired vascular structure in the images, the angle covered by the directions with small intensity variation cannot be more than π for vascular points. For entropy-based measure, we set the threshold according to the entropy $H_T={\sum }_1^{n_{\theta }/2}2(\mathit{log}(n_{\theta })-\mathit{log}(2))/n_{\theta }$, giving us υ_T = 2/n_θ. The brightness function (6) with γ = 0.015 is used for this set of experiments. Figs. 9(a) and (b) summarize the performance of our algorithm with different filters h(u). Detection rates and false alarm rates are plotted as functions of the noise level. We find that the performance is similar for Gaussian or rectangle filters as the radial part h_r(u) when the effective width of Gaussian filters is comparable to k (Fig. 9(a)). For the angular part h_θ(u), the performance of Gaussian filters depends on the extent of overlap (width of Gaussian functions) between neighboring orientations. When the overlap is small, the performance is close to that of the rectangle filter. While the width of Gaussian functions increases, both the detection and false alarm rates are lower than using rectangle functions for noisy images because of the smoothing effect as shown in Fig. 9(b).

To compare the two different brightness functions defined in equations (5) and (6), we plot the performance of our algorithm using rectangle functions for both the radial and angular part in Fig. 9(c). We choose α = 1000 and γ = 0.015 for the comparison. The plots show that the brightness function (6) is a little bit better for this set of synthetic images because we could miss the low contrast structures when there are bright structures nearby using the sigmoid brightness function (5).

As we have shown, different filter settings lead to similar performance. In the rest of the section, we show the experimental results using rectangle filters for the radial part as well as the angular part with which the fine structures are well preserved. The brightness function uses (6) with γ = 0.015.

(ii) Sensitivity Analysis

We explore here the sensitivity performance of our algorithm with respect to parameter settings. First, although the selection of k can be chosen manually based on the vascular structures in images, we plot the detection and false alarm rates for images with the noise variance of 15% using different k in Fig. 10(a) (n_θ = 36, β = 300). We show that we achieve good performance when k is larger than a certain number, or more specifically, two times of the largest size of a vascular structure.

In this section, we mainly test the performance with different n_θ and β. We set k = 55 and test on images with the noise variance of 15%. The plots of detection rates and false alarm rates with respect to different parameters are given in Fig. 10(b) (β = 300.0) and (c) (n_θ = 36). We can see that when n_θ is beyond a certain value (36 in the figure), the detection rate does not increase. This depends on the image resolution and whether there are enough sample points along different directions to correctly estimate the intensity variation Dev(x, θ). For the parameter β, the false alarm rate increases with increasing β as large β magnifies the difference between orientation slabs and introduces more false positives.

(iii) Comparison with Multiscale Hessian-based Method

For the comparison to multiscale Hessian-based methods, we display the measure maps from our proposed algorithm and Frangi’s algorithm [14]. The results for the synthetic image in Fig. 8(b) are shown in Fig. 8(c) and (d). By comparison, the new measure maps are visually better at branching points and highly curved points as shown in the figure. We also compare their detection rates with fixed false alarm rates of 0.5% in Fig. 8(e). For our new measure, we set the same parameters as in the first set of experiments. We use 12 uniformly sampled Gaussian scales ranging from 0.5 to 12 pixels for the Hessian-based measure. The detection rates at (c), (d) in Fig. 8(e) are obtained based on the measure maps shown in Fig. 8(c) and (d). From the figures, we find that the detection rate decreases faster with the increasing noise level for the Hessian-based measure as it is based on the second derivatives of image intensities.

We further compare our results with the results from a variety of matched filter methods in [23]. As the method in [23] is especially designed for vessel center detection, the true positive and false positive rates in [23] were only measured based on the ground truth of vessel center lines since the method does not perform robustly for the points away from center lines. While our method is designed for all points belonging to vascular structures, we measure the true positive rates and false positive rates using the whole vascular structure. If the true positive rates for our measure are higher than those in [23], it is reasonable to say that our measure has better performance as we treat center line points and points away from center lines in the same way. By comparison, at false alarm rate 0.5%, the true positive rates in this experiment are higher than those in [23] with the false alarm rate being described as “almost zero”.

5.2 Validation on 3D MRA Lamb Data

We further validate our algorithm using a set of 3D MRA lamb images at 1.5T. MRA was performed using a 3D MPRAGE acquisition with 25cm FOV, 1.1mm slice thickness, 128 slices, TE=3ms, TR=24ms, 2 averages, alpha=45°, 192×256 matrix and bandwidth = 220Hz/pixel. The data was then resampled to have isotropic voxel size equal to 0.78125 mm prior to all processing.

The results of both our new method and the Hessian-based method are compared to manual “gold standard” segmentations of a portion of the pulmonary arteries. Manual segmentation of 3D vascular structure is extremely complex and time-consuming. We created a special software tool which is now a part of our BioImage Suite software package (www.bioimagesuite.org) to allow for simultaneous tracing in multiple orthogonal planes, which helps the expert to obtain faithful segmentation results. The validation is performed using the part of the image encompassed by dilating the manual segmentations by 5 voxels. This enables us to compute the detection rates and the false alarm rates from thresholding the vesselness measures within these regions. We set k = 55, β = 800, n_ψ = 16, and n_φ = 8 for our new measure. Multiscale Hessian-based measure is computed in 20 uniformly sampled Gaussian scales ranging from 0.5 to 10 voxels. Note that we compute our new measure by implementing convolutions via the Fast Fourier Transform (FFT) and that the computational time is comparable to the multiscale Hessian-based algorithm.

We implemented our algorithm in MATLAB. The computational time was approximately 4 hours for each MRA image (image size = 101×256×101), on a 2.0 GHz Intel Xeon CPU under Windows XP. The computational time can be reduced substantially by implementing the convolution operations (which take up almost all of the computational time) using hardware acceleration on graphical processing units (GPUs) found on most high end graphics cards. For the implementation of the Hessian-based method, we also used an FFT based-implementation for the convolutions with the appropriate derivatives of the multiscale Gaussian kernels. This enabled the use of relatively large kernel sizes and resulted in significant improvements in the performance of the Hessian based method.

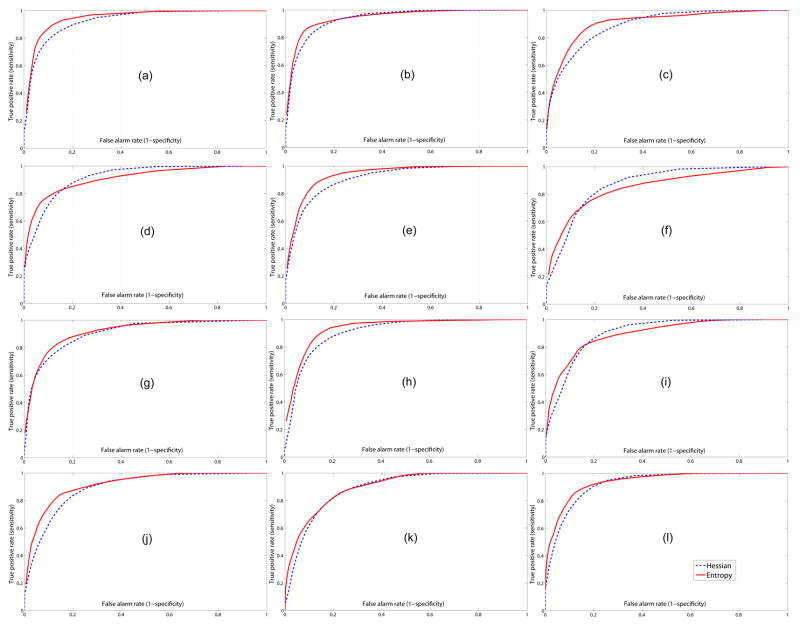
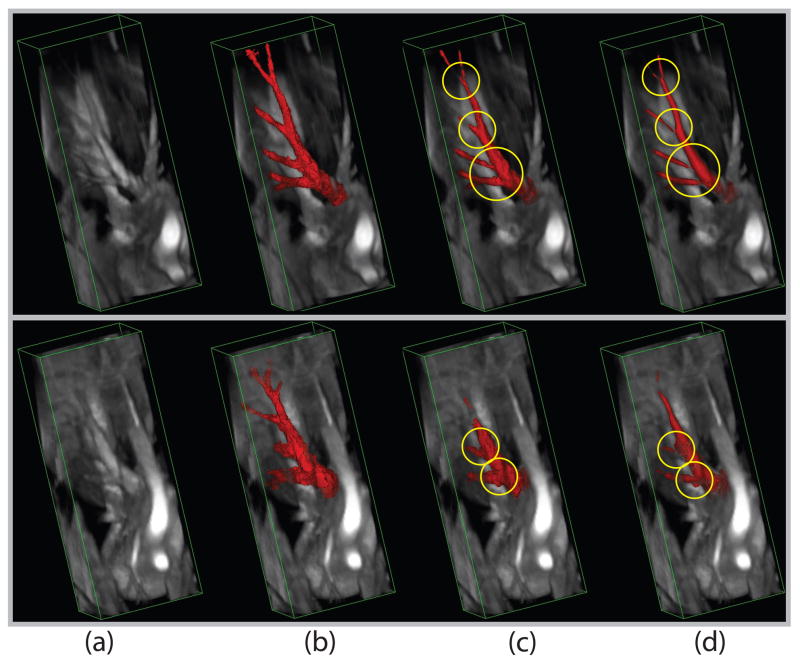
In Fig. 11, we plot the ROC curves for 12 3D images using our new algorithm and the traditional Hessian-based measure [14]. Among 12 curves with entropy-based measures from our new algorithm, 9 of them (except (d), (f), and (i)) are above the corresponding curves from the multiscale Hessian-based algorithm and have better detection performance when the false alarm rates are below 20%. When the false alarm rates are below 10%, all 12 ROC curves from our algorithm are above the corresponding curves from the multiscale Hessian-based algorithm. Table 1 has the average detection rates for our algorithm and the standard multiscale Hessian-based algorithm with false alarm rates fixed at 5%, 10% and 20%. Note that our proposed algorithm’s performance is better than that obtained using the Hessian-based measure. The results at the false alarm rate level of 5% demonstrate statistically significant improvement over the Hessian-based measure (with two-tailed p-value < 0.001). Fig. 12 shows the segmentation surfaces of one good example with the best detection rates (Fig. 11(h)) and one bad example with the worst detection rates (Fig. 11(f)) in 12 volumes by thresholding the measure maps; note especially the improved performance at branching points.

Figure 11.

ROC curves for 12 lamb MRAs for our new entropy-based algorithm and the Hessian-based algorithm [14]

Table 1.

Means and standard deviations of detection rates with false alarm rates fixed at 5%, 10% and 20% for 12 3D lamb MRAs.

	Detection performance (Mean ± STD)
False alarm rate	Our Method	Hessian (Frangi et al [14])
5%	61.23% ± 7.89%	50.96% ± 9.95%
10%	76.40% ± 7.80%	68.17% ± 8.22%
20%	88.57% ± 5.56%	86.01% ± 3.57%

Figure 12.

Volume rendering of 2 MRAs with thresholded vesselness measures: (a) Original image; (b) Ground truth; (c) Our entropy-based measure; (d) The standard Hessian-based measure. Top row: One example with the best detection rates (Fig. 11(h)); Bottom row: One example with the worst detection rates (Fig. 11(f)). Places where the Hessian-based algorithm is not adequate are marked for comparison.

5.3 Vesselness for Micro-CT Rodent Data

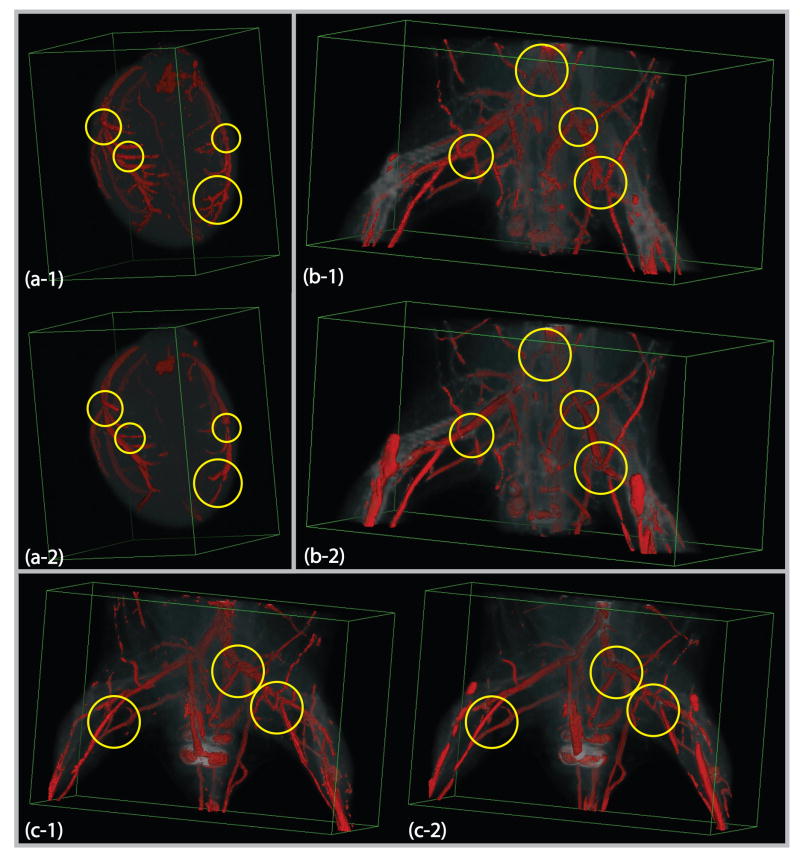
To further investigate the performance, especially at branching places in vascular structures, we implement our new entropy-based measure on a number of ex-vivo 3D small animal micro-CT data sets using barium-sulfate contrast. Images were acquired at a resolution of 100 × 100 × 100μm. We present here three examples for visual comparison. The first is from an excised rat heart with the size 124×119×166. The other two data sets are hindlimb images from two different mice. The sizes are 251 × 131 × 131 and 251 × 131 × 171. We set k = 23, β = 600, n_θ= 12, and n_φ = 6 along the azimuth and elevation directions for our new measure. In Fig. 13(a-1),(b-1) and (c-1), we show the surfaces of the segmentation by thresholding the measure maps. As the mouse hindlimb micro-CTs in (b-1) and (c-1) also contain elongated tubular bone structures, the algorithm can pick up some of bones depending on their size. These figures show that it does look promising for capturing vascular structures displayed in the volumes. In Fig. 13(a-2),(b-2) and (c-2), the multiscale Hessian-based measure is computed in 10 uniformly sampled Gaussian scales ranging from 0.5 to 5 voxels. We see that the Hessian-based algorithm does not give strong responses for branching points in all three data sets. Also, it misses some thin vessels and regions of stenosis for the rat heart data set in Fig. 13(a-2).

Figure 13.

Volume rendering of micro-CT images with thresholded vesselness measure: (a-1) Our new entropy-based measure map for the rat heart data set; (a-2) The standard multiscale Hessian-based measure for the rat heart; (b-1) and (c-1) Our new entropy-based measures for the hindlimb mouse data sets; (b-2) and (c-2) The standard multiscale Hessian-based measures for the mouse data sets. Some of places where the Hessian-based algorithm is not adequate are marked in the figure.

6 Discussion and Conclusions

We have proposed a new polar profile vesselness measure for characterizing vascular structures. This is the first vesselness measure to our knowledge using the information entropy to depict the tightness of oriented clusters with small intensity variation. An important feature of the measure is that it directly exploits the intensity information of underlying structures and does not assume the single cylinder model like other available measures. The new measure is valid for all vascular structures, including points away from the center line, branching points, and other extreme cases. We demonstrate that our new algorithm performs better at those places and the overall detection performance is also marginally better as compared to the conventional multiscale Hessian-based operators, using both 2D synthetic and 3D in vivo lamb MRA acquisitions.

The major limitation of our new method is its relatively high computational cost. We are actively investigating GPU-based implementation of the convolutions to reduce the execution time. Some preliminary testing using the NVIDIA CUDA [53] toolkit suggests that computational improvements of the order of ten to fifty times are possible on modestly priced graphics cards.

Our new vesselness measure is also less smooth than the Hessian-based measure. The most likely source for this is that the Hessian method invokes a parametric model for the data, hence, when the model is correct (the single cylinder assumption) it is able to take advantage of the model to reduce the effect of noise. We use a non-parametric method (no single cylinder assumption) and hence we do not have this luxury. A solution might be to explicitly go to a multi-cylinder type model, either a multi-tensor estimation or a higher order parameterization. The use of a multiple scales might also yield improved performance. At the same time, if we only consider our proposed method as a pre-processing detection step, the relative lack of smoothness could be alleviated if we use global connectivity information for the final segmentation.

As well as providing good results to emphasize vascular structures using the new measure, the intermediate results from the derivation of the measure can also be useful, especially for assisting vessel segmentation and tracking. For example, in the Markov Random Field segmentation framework, the prior probability of the segmentation can be described by a Gibbs distribution of the form $\frac{1}{Z}{e}^{-{\sum }_{c(x)\in C(x)}W(x,c(x))}$ to capture the spatial homogeneity, where C(x) is the set of all possible cliques of x and W(x, c(x)) is known as clique potential [15]. As we can see from Fig. 7, p_υ(x, θ) correlates correctly with the vessel direction, we can have a similar prior probability and let W(x, c(x)) = ∫ p_υ(x, θ)p_υ(c(x), θ)dθ to force the continuity of the vessel direction and help segment vascular structures robustly.

This type of methodology with the use of different neighborhoods – the h(u)’s of equation 1, could also be used in the future to detect regions of different local shape properties such as sheets. The later being useful in the segmentation of the brain cortical gray matter layer as an additional constraint to intensity-based segmentation. In the case of sheets, the neighborhoods would be shaped as half or quarter- discs (as opposed to the conical filters used for vessels).

The current paper provides good results for obtaining a vesselness measure map as a pre-processing step of consequent vessel tracking and connectivity analysis. Our future work includes the enhancement of our new algorithm. For example, the capability to have adaptive parameters for the given images is important. By correctly estimating the largest vessel size, we can automatically choose the kernel size k. We are also interested in using the proposed measures to design better connectivity analysis algorithms and help improve the performance for the analysis of vascular structures.

APPENDIX

A Eigenvalues for a Vessel Model with Gaussian Cross-section

The Hessian matrix of the image $I(x,y)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}}$ is as following:

$$H=\left[\begin{array}{cc}{I}_{xx}& I_{xy}\\ I_{xy}& I_{yy}\end{array}\right]=\left[\begin{array}{cc}-\frac{{\sigma }^2-x^2}{{\sigma }^4}I(x,y)& 0\\ 0& 0\end{array}\right].$$

Therefore, the eigenvalues are ${\lambda }_1=I_{xx}=-\frac{{\sigma }^2-x^2}{{\sigma }^4}I(x,y)$, λ₂=0. Following the same reasoning of getting 3D vesselness measure in [14], we can get the vesselness measure (assuming bright vessels) as

$$V(x)=\{\begin{array}{ll}0\hfill & {\lambda }_1\ge 0\hfill \\ (1-e^{-\frac{{\lambda }_1^2+{\lambda }_2^2}{2a^2}})e^{-\frac{{\lambda }_2^2/{\lambda }_1^2}{2b^2}}\hfill & {\lambda }_1<0\hfill \end{array}=\{\begin{array}{ll}0\hfill & x^2\ge {\sigma }^2\hfill \\ (1-e^{-{(\frac{{\sigma }^2-x^2}{{\sigma }^4}I(x,y))}^2/2a^2})\hfill & x^2<{\sigma }^2\hfill \end{array}$$