Network scaling reveals consistent fractal pattern in hierarchical mammalian societies

Abstract

Recent studies have demonstrated that human societies are hierarchically structured with a consistent scaling ratio across successive layers of the social network; each layer of the network is between three and four times the size of the preceding (smaller) grouping level. Here we show that similar relationships hold for four mammalian taxa living in multi-level social systems. For elephant (Loxodonta africana), gelada (Theropithecus gelada) and hamadryas (Papio hamadryas hamadryas) baboon, successive layers of social organization have a scaling ratio of almost exactly 3, indicating that such branching ratios may be a consistent feature of all hierarchically structured societies. Interestingly, the scaling ratio for orca (Orcinus orca) was 3.8, which might mean that aquatic environments place different constraints on the organization of social hierarchies. However, circumstantial evidence from a range of other species suggests that scaling ratios close to 3 may apply widely, even in species where hierarchical social structures have not traditionally been identified. These results identify the origin of the hierarchical, fractal-like organization of mammalian social systems as a fundamental question.

1. Introduction

Human networks appear to be hierarchically structured (Binford 2001; Hill & Dunbar 2003; Maschner & Bentley 2003), and Zhou et al. (2005) showed that these hierarchical societies were arranged in a coherent set of characteristic group sizes organized according to a geometric series with a preferred scaling ratio close to 3. More recently, Hamilton et al. (2007) have found that within a large sample of hunter–gather societies, the population structure had a scaling ratio closer to 4. Within such hierarchies, it may be that the absolute values of the group sizes are less important than the ratios between successive group sizes; that is, the minimum ‘nucleation’ size may vary but the ratio (of between 3 and 4) might be universal. Claims for this universality among small-scale, hunter–gatherer societies have raised the possibility of a fractal organization underlying human social groups (Mosko 1995; Hamilton et al. 2007). Two key questions remain, however. Firstly, if such hierarchical structures exist within human societies, then what is the actual scaling ratio between successive levels of the network? Secondly, what is the origin of this discrete hierarchy?

Humans are not the only species to live in hierarchical societies, and many animal species have social organizations with a number of identifiable network levels (primates: Kummer 1968, Dunbar & Dunbar 1975; proboscideans: Wittemyer et al. 2005; cetaceans: Ford et al. 2000; birds: Hegner et al. 1982). A key question, therefore, is to determine whether these hierarchical networks have a scaling ratio similar to those observed in humans. For a wide range of primate species, preliminary supporting evidence shows a consistent scaling relationship of 3.15 between grooming clique size (the number of core grooming partners that an average individual has) and total group size (Kudo & Dunbar 2001). Nevertheless, as this is across only two network levels, a more comprehensive analysis is required. To address this, we followed the methodology of Hamilton et al. (2007) to examine the fractal structure of social groups of four mammalian taxa for which appropriate data were available: elephants (Loxodonta africana), gelada (Theropithecus gelada), hamadryas baboons (Papio hamadryas hamadryas) and orca (Orcinus orca). Since there are differences in the fundamental social unit for each of these species (see electronic supplementary material), such an analysis will provide useful insights into the origins of structured societies.

2. Material and methods

(a) Data

Data were collected from published and unpublished sources for all populations of elephants, gelada, hamadryas and orca where detailed information were available on group sizes from at least two levels of the hierarchical network (table 1). The observed group sizes for hamadryas were also supplemented with additional data on grooming cliques from a captive population (Kudo & Dunbar 2001).

Table 1.

Data set of mean group sizes at each grouping level for elephant, gelada, hamadryas, orca and elephants. (Numbers in parentheses indicate samples sizes at each grouping level (M–O Unit: mother–offspring unit; OMU: one-male unit). Data sources are given in the electronic supplementary material.)

species	population	grouping level
elephant		sub-population	clan	bond group	family	M–O unit
Loxodonta africana	Amboseli	(1) 312	(5) 62.4	(3) 23	(32) 9.75	(3) 3.33
gelada		community	band	team	OMU	clique
Theropithecus gelada	Bole	(1) 181	(3) 60.3	(3) 27.0	(10) 17.1	(1) 5.1
	Gich	(1) 278	(2) 139.0		(25) 10.1
	Sankaber	(1) 577	(5) 139.8	(7) 28.7	(46) 13.5
	Arsi		(1) 58		(14) 7.9
	mean	345.3	99.3	27.9	12.2	5.1
hamadryas		troop	band	clan	OMU	clique
Papio hamadryas hamadryas	Eritrea		(6) 139.2		(92) 7.7
	Ethiopia	(2) 255	(3) 73
	Saudi Arabia		(32) 39.6		(90) 6.5
	Awash 1968		(5) 59.4
	Awash 1975		(1) 63	(2) 29.0	(8) 7.3
	Filoha		(1) 165		(24) 4.9
	ErerGota 1971	(1) 232	(3) 77.3	(3) 20.0	(7) 8.6
	ErerGota 1977		(1) 69	(3) 23.0	(10) 6.8
	Captive					(1) 2.9
	mean	243.5	85.7	24.0	7.0	2.9
orca			community	clan	pod	matriline
Orcinus orca	British Columbia		(1) 216	(4) 74.8	(13) 19.8	(53) 5.62

(b) Analysis

We used Horton–Strahler scaling to test for fractal patterns within the data and followed methods similar to that of Hamilton et al. (2007), who used generalized Horton laws (Horton 1945) for calculating the branching ratio (the characteristic ratio of the number of groups of one order to the number of groups in the next higher order). This is done by categorizing the group sizes, g, into numerical orders from the first order (individual animals) to the highest order Ω. For elephant, the orders are (g₁) individual, (g₂) mother–offspring unit, (g₃) family, (g₄) bond group, (g₅) clan and (g₆) sub-population. For gelada and hamadryas, the first five orders are (g₁) individual, (g₂) grooming clique, (g₃) one-male unit, (g₄) team and (g₅) band, with the sixth and top level being community for geladas and troop for hamadryas. For orca, the orders correspond to (g₁) individual, (g₂) matrilines, (g₃) pods, (g₄) clan and (g₅) community.

Following Hamilton et al. (2007), we determine the scaling relation between group sizes across hierarchical orders first by determining the average group size 〈g〉 within order ω across n populations, using $g_i^{(\omega )}$ to denote a group of size g in the ith population, at order ω (Hamilton et al. 2007). In order to find the average branching ratio B, we first determine the mean number of groups per community/troop, and then plot the Horton order ω versus the number of groups per order. The branching ratio is the slope of the semi-log plot of ln[N(g^(ω))], the average number of groups of size g, versus the order ω (cf. Hamilton et al. 2007), with errors estimated by the jackknife technique. Following Hamilton et al. (2007) we estimated the number of groups of size g by dividing the entire population size by the average group size g.

3. Results

As an initial quantitative analysis, we constructed a series of ratios between the mean group sizes at successive levels of the hierarchy for each species, following Zhou et al. (2005). For elephants the mean scaling ratio from mother–offspring unit to subpopulation is 3.25 (2.5, 2.5, 2.76, 4.52), for gelada from grooming clique to community it is 2.94 (2.39, 2.29, 3.60, 3.48), for hamadryas from grooming clique to troop it is 3.06 (2.41, 3.43, 3.57, 2.84) and for orca from matriline to community the mean ratio is 3.40 (3.52, 3.77, 2.89). This suggests that, like humans (Zhou et al. 2005), multi-layered animal societies form groups according to a discrete hierarchy with a preferred scaling ratio of close to 3.

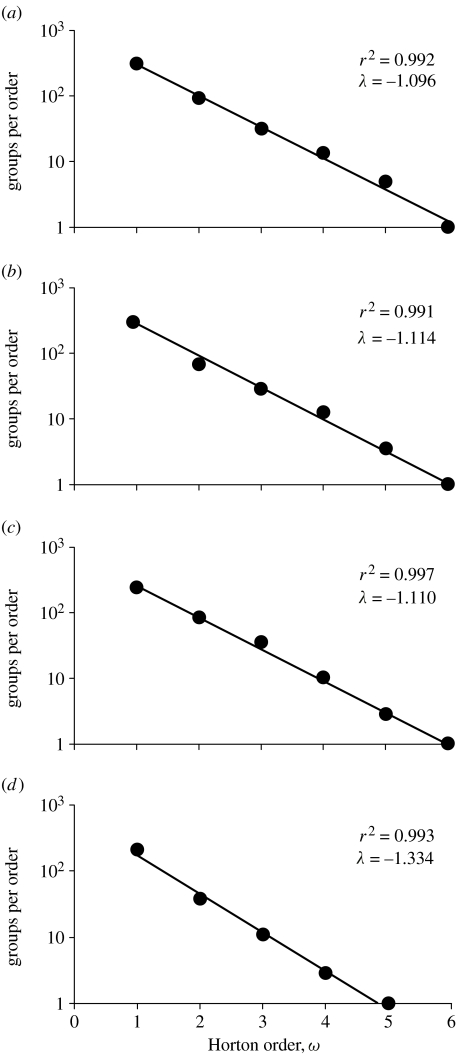
In testing for fractal patterns, figure 1 shows the relationship between Horton order ω and number of groups. In all cases, the number of groups follows a declining exponential form with respect to ω (elephant: r²=0.992; gelada: r²=0.991; hamadryas: r²=0.997; orca: r²=0.993). The linear fits on a semi-log plot indicate that the branching ratio between all levels is consistent, and that the network structure is self-similar for all species. The calculated branching ratios were 2.99±0.10 for elephant, 3.05±0.09 for gelada, 3.04±0.04 for hamadryas and 3.80±0.24 for orca. If mean group sizes are determined via a lognormal mean (the mean of the logged group size values), rather than the arithmetic mean reported above, the branching ratios are virtually identical (gelada: 2.98±0.09; hamadryas: 2.81±0.02; orca: 3.82±0.14; elephant: analysis not possible since only summary dataset is available). Overall, therefore, three species show branching ratios very close to 3, while orcas have a branching ratio between 3 and 4. These findings suggest that consistent branching ratios may be a ubiquitous feature of all hierarchically structured mammalian societies.

Figure 1.

Horton plots of mean number of groups per population for (a) elephants, (b) gelada, (c) hamadryas and (d) orca.

4. Discussion

We have demonstrated that multi-level social systems in four mammalian taxa follow a scaling law similar to that reported recently for humans (Hamilton et al. 2007). Previous studies on humans had reached conflicting conclusions about the precise scaling ratio, however; Zhou et al. (2005) reported a scaling ratio across human group levels of 3, while Hamilton et al. (2007) reported a ratio closer to 4 across a large sample of hunter–gatherers. Our results are consistent with the findings of Zhou et al. (2005), suggesting that a scaling ratio of 3 may be universal across mammalian hierarchical societies.

There is, however, variation in the scaling ratios across species. Elephant, gelada and hamadryas have scaling ratios of almost exactly 3, but in orcas successive layers of the social hierarchy have a scaling ratio of 3.8. Orcas obviously stand out as an aquatic species, and the constraints imposed by their three-dimensional marine environment might create selective pressures on network structure different from those experienced by terrestrial mammals inhabiting an ostensibly two-dimensional world. Comparable information on network structure from further orca populations or other cetacean species such as dolphins (Lusseau et al. 2006), or from non-terrestrial species such as birds (Hegner et al. 1982) may help to elucidate how three-dimensional environments constrain social networks.

However, there is some circumstantial evidence from other mammal species to suggest that a scaling ratio of 3 may be more widespread. Popa-Lisseanu et al. (2008) reported that a population of giant noctule bats (Nyctalus lasiopterus) consisted of three distinct but cryptic social groups suggesting a scaling ratio of 3 from population to social group. Furthermore, the recent proliferation of the application of social network analysis to studies of sociality (Wey et al. 2008) is identifying preliminary evidence for similar patterns in species where hierarchical social structures have previously not been considered. For example, Wolf et al. (2007) used network analysis to identify a social hierarchy with at least three levels in Galápagos sea lions (Zalaphus wollebaeki) with an apparent scaling ratio of 3.7 between community and clique. Similarly, Manno (2008) reported a captive population of Colombian ground squirrels (Spermophilus columbianus) composed of separate communities and subcommunities, with a mean scaling ratio of 2.67 between these levels. Although more systematic analyses for a range of species are clearly required, scaling ratios of close to 3 may be fundamental to mammalian social organization.

What do these consistent scaling ratios mean? Hamilton et al. (2007) suggested that scaling ratios of close to 4 among humans could be derived from an average family size of 4 (two parents and two children). Although this interpretation for humans seems unlikely (such nuclear families are not a universal in human prehistory: Fox 1983), we cannot rule out discrete hierarchies having their origins in the fundamental organization of any social structure (see also Zhou et al. 2005). What remains unclear, however, is whether the constraint that creates the fractal structuring is cognitive (animals can only manage a certain number of relationships at a given level of relationship intensity: see Kudo & Dunbar 2001) or a time constraint (a functional relationship requires a minimum time investment, and constraints on available social time limit the number of relationships an individual can have at a given level of relationship quality: Seyfarth 1977; Dunbar 1996). Determining the origin of these discrete hierarchies thus remains a question of enormous importance that warrants substantial further research.