The optical sensitivity of compound eyes: theory and experiment compared

Abstract

The Land sensitivity equation is a well-known tool for comparing optical performance between eyes. Despite this, the equation has never been experimentally tested. Here, we present, to our knowledge, the first experimental validation of the equation. We have investigated different insect species active at different intensities, and possessing different types of compound eyes, to compare ratios of calculated sensitivities to ratios determined experimentally. Experimental optical sensitivities were measured by adjusting the intensity of an external light source until photoreceptors in the different eyes produced roughly equal numbers of photon responses (‘bumps’) per second. The sensitivity ratios obtained in this manner agree well with those obtained using the equation. We conclude that the Land equation remains an excellent tool for comparing sensitivities between different eyes.

1. Introduction

The Land sensitivity equation (equations (1.1) and (1.2): Kirschfeld 1974; Land 1981) has been widely used to describe and compare the light-gathering capacities of eyes in different organisms living at different light intensities (e.g. Greiner et al. 2004; Frederiksen & Warrant 2008). The equation describes the optical sensitivity of an eye, S (in units of μm² steradians), to an extended source of broad spectral content (Warrant & Nilsson 1998), as found in terrestrial habitats:

$$S={\left(\frac{\pi }{4}\right)}^2{A}^2{\left(\frac{d}{f}\right)}^2\left(\frac{kl}{2.3+kl}\right)(\text{broad}\text{spectrum}).$$ (1.1)

In deep-sea habitats, where daylight is essentially monochromatic, the following expression is more accurate:

$$S={\left(\frac{\pi }{4}\right)}^2{A}^2{\left(\frac{d}{f}\right)}^2(1-{\text{e}}^{-kl})(\text{monochromatic}),$$ (1.2)

where A is the diameter of the eye's aperture; d is the diameter of the photoreceptor (the rhabdom in insects); f is the focal length; k is the absorption coefficient of the photoreceptor; and l is the photoreceptor length. If all lengths have units of μm, then the unit of k is μm⁻¹. Thus, good sensitivity to an extended scene results from a pupil of large area (πA²/4 μm²), and photoreceptors each viewing a large solid angle (πd²/4f² steradians) of visual space and absorbing a substantial fraction of the incident light ((1−e^−kl) for monochromatic light, kl/(2.3+kl) for broad spectrum light).

Despite its appealing simplicity and extensive use, the Land sensitivity equation does have drawbacks. The equation implicitly assumes all light that reaches a photoreceptor is absorbed by that photoreceptor alone, and this is not the case in eyes with low F-number, or in eyes that are poorly focused (Warrant & McIntyre 1990; Stavenga 2003). It also fails to account for waveguiding phenomena in very thin photoreceptors (Stavenga 2003). Nevertheless, if one keeps these drawbacks in mind, the Land equation is still a valuable tool for comparing optical sensitivities in different eyes. Here, we present the first confirmation that its predictions agree well with experiment, using four species of closely related nocturnal and diurnal insects with two different eye designs: Lasioglossum leucozonium (diurnal bee, apposition eyes), Megalopta genalis (nocturnal bee, apposition eyes), Onitis belial (diurnal dung beetle, superposition eyes) and Onitis aygulus (nocturnal dung beetle, superposition eyes).

2. Material and methods

The different species were collected in the following places: L. leucozonium were collected at Revingehed, Sweden; M. genalis were collected on Barro Colorado Island, Republic of Panama; O. belial were collected in the Cabaneros National Park, Spain; and O. aygulus were collected near Cudal, New South Wales, Australia. All insects were kept on a 12 D : 12 L circadian cycle. The preparations for electrophysiology were performed during the light period and the electrophysiology was performed during the dark period.

(a) Electrophysiology

We made intracellular electrophysiological recordings from green-sensitive photoreceptors using an experimental apparatus that has been described elsewhere (Frederiksen et al. 2008). Cell penetration was recognized by a drop of at least 60 mV in baseline potential and the presence of small depolarizations to dim light flashes. A detailed description of the criteria used for judging recording quality can be found in Frederiksen et al. (2008). Once a cell was penetrated we aligned the light stimulus with the optical axis of the cell. The stimulus was produced from a green LED (Roithner Lasertechnik, B5B-433-B525, 6600 mcd, peak transmission of 525 nm). Illumination was provided by a 5 mm wide light guide located 50 mm from the eye (subtending 5.7°). Before starting the recording protocol we allowed the cell to dark adapt for at least 30 min and often much longer. In all insects, recordings were made in the eye region viewing the frontal visual field.

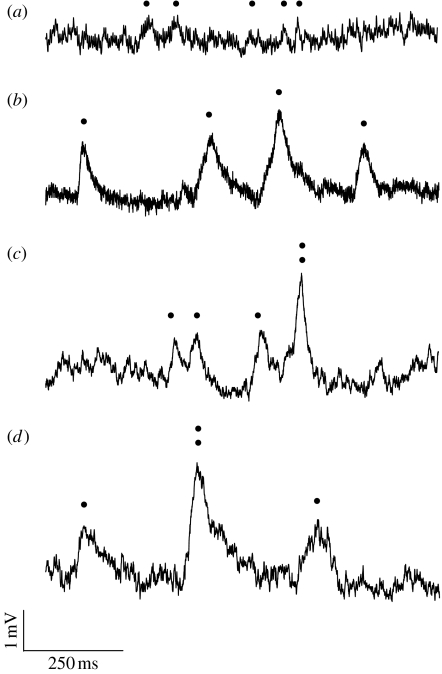
Our recording protocol consisted of a continuous dim light. In each cell and in each species, the intensity, I, of the stimulus was adjusted so that responses to individual photons, or ‘photon bumps’, could be resolved (figure 1). The intensity was then carefully noted. We recorded 60 s of bumps from each cell (eight cells from each species) and calculated the number of bumps produced per second, N. Because the different species have different optical sensitivities, bumps were resolved at different external stimulus intensities (e.g. the less sensitive apposition eyes of L. leucozonium required much higher intensities to produce bumps than the more sensitive superposition eyes of O. aygulus). To be able to compare the rates of bumps in the different cells and in the different species, we calculated the equivalent bump rate, N_eq, that cells would have produced if we had recorded from all cells at the same external intensity. This was done in the following way. First, we located the recording corresponding to the least sensitive cell in the least sensitive species, that is, the recording that resulted in bumps for the highest external stimulus intensity I_L. Second, N_eq was calculated for each recording i (i.e. bump rate N_i recorded at external stimulus intensity I_i) according to:

$$N_{\text{eq}}=N_i\frac{I_{\text{L}}}{I_i},$$ (2.1)

where N_eq is the equivalent bump rate that would have been recorded from the photoreceptor at intensity I_L. Species with higher values of N_eq thus have higher optical sensitivities.

Figure 1.

Recordings of photoreceptor responses to single photons (‘photon bumps’) in four species of insects with different eye types and different activity periods. Halictid bees: (a) L. leucozonium (diurnal, apposition eyes) and (b) M. genalis (nocturnal, apposition eyes). Onitine dung beetles: (c) O. belial (diurnal, superposition eyes) and (d) O. aygulus (nocturnal, superposition eyes). Dots mark bump occurrences.

3. Results

Using data from McIntyre & Caveney (1998) and Greiner et al. (2004), we calculated the optical sensitivity of L. leucozonium, M. genalis, O. belial and O. aygulus using equation (1.2) (table 1). In table 1, we also present N_eq, the equivalent number of bumps (figure 1) produced by the photoreceptor per second at equal stimulus intensities (equation (2.1)). Higher values of N_eq correspond to higher optical sensitivities.

Table 1.

Optical, morphological and physiological properties of the frontal regions of compound eyes in four species of insects: L. leucozonium (L leu: diurnal bee, apposition eyes, n=8), M. genalis (M gen: nocturnal bee, apposition eyes, n=8), O. belial (O bel: diurnal dung beetle, superposition eyes, n=8) and O. aygulus (O ayg: nocturnal dung beetle, superposition eyes, n=8).

symbol	parameter	unit	L leua	M gena	O belb	O aygb
d	distal rhabdom diameter	μm	1.6	8.0	6.5	13
f	focal length	μm	57	97	373	503
A	aperture diameter	μm	20	36	187	613
k	absorption coefficientc	μm−1	0.0067	0.0067	0.0067	0.0067
l	rhabdom length	μm	220	350	32	86
S	optical sensitivity	μm2sr	0.1	4.9	1.3	68
Neq	bumps at equal intensityd	–	13±2	873±93	62±15	3267±980

^aValues for bees were obtained from Greiner et al. (2004).

^bValues for dung beetles were obtained from McIntyre & Caveney (1998).

^cValue for lobster (Bruno et al. 1977).

^dSee §2 for definition.

If we calculate the ratios of the theoretical optical sensitivities (S_species1/S_species2) between all four species and compare them to the corresponding ratios of bump rates at equivalent intensities $(N_{\text{eq}}^{\text{species}1}/N_{\text{eq}}^{\text{species}2})$ we find that there is an almost perfect match (52 versus 51) between the theoretical and experimental ratios for the two dung beetle species (superposition eyes), and only a small mismatch (49 versus 66) for the two bee species (apposition eyes, table 2). However, if we look at the corresponding ratios between the two groups (i.e. compare apposition eyes with superposition eyes) the mismatch becomes substantial (table 2): percentage deviations can exceed 250 per cent. This mismatch can, however, be explained by experimental limitations.

Table 2.

Ratios of sensitivity calculated theoretically (theor) using the Land sensitivity equation (equation (1.2)), and experimentally (exp) using equivalent bump rates at equal intensities (equation (2.1)) in four species of insects: L. leucozonium (L leu: diurnal bee, apposition eyes), M. genalis (M gen: nocturnal bee, apposition eyes), O. belial (O bel: diurnal dung beetle, superposition eyes) and O. aygulus (O ayg: nocturnal dung beetle, superposition eyes). (The error (in per cent)^a between the experimental and theoretical calculations is shown in the rightmost column.)

species ratio	theor	exp	error (%)a
O ayg/L leu	680	248	174
O ayg/O bel	52	51	2
O ayg/M gen	14	3.8	268
M gen/L leu	49	66	34
M gen/O bel	3.8	14	268
O bel/L leu	13	4.7	177

^aThe error was calculated as the deviation in per cent between the experimental and theoretical ratios: |100(S/S)/(N_eq/N_eq)−100%|.

4. Discussion

The theoretical optical sensitivity corresponds well to values obtained experimentally (table 2). There is however a slight mismatch in the comparison between the two bees L. leucozonium and M. genalis. This error can be explained by the fact that the theoretical sensitivity value calculated for L. leucozonium is probably an overestimate. The Land sensitivity equation accounts only for the solid angular field of view (πd²/4f²) of the photoreceptor, implicitly implying that the angular sensitivity function has a square ‘top hat’ shape. This is roughly true for M. genalis (Warrant et al. 2004). However, in L. leucozonium the angular sensitivity functions are more Gaussian shaped, leading to a lower photon catch. The theoretical sensitivity value is thus an overestimate.

These differences in angular receptive field shape in M. genalis and L. leucozonium are sufficient to explain the mismatch between theory and experiment in the two bees, but they are not sufficient to explain the much larger differences that occur when comparisons are made between the bees and the dung beetles. Differences in the spectral sensitivities of green-sensitive photoreceptors in the four species may differ slightly, leading to different absorption rates from our monochromatic stimulus. Moreover, there are two assumptions implicit in Land's equation that are not entirely accounted for by our experimental apparatus. The first assumption is that the stimulus is an extended source. Our stimulus, subtending 5.7° at the corneal surface, is too small to be considered fully extended, especially for the superposition eyes. The second assumption is that all light which is gathered by the optics and focused onto one rhabdom will remain within this rhabdom, being absorbed by it alone (Land 1981). This is far from the truth in many eyes of low F-number, as the refracting superposition eyes of the Onitine dung beetles studied here (Warrant & McIntyre 1990, 1991). Unlike the refracting superposition eyes of the hawkmoth Macroglossum stellatarum (Warrant et al. 1999), whose rhabdoms are optically isolated by a sheath of reflective trachea, the rhabdoms of most Onitis sp. are unsheathed (Caveney 1986).

In Onitis, when light from an extended source is focused onto the target rhabdom, rays from the most peripheral facets in the superposition aperture will reach it with a large angle of incidence. Owing to the lack of rhabdom sheathing, this light will not be trapped in the target rhabdom by total internal reflection but will instead leak to neighbouring rhabdoms, where it will also be absorbed (Warrant & McIntyre 1991). The same principle is true for all other rhabdoms in the eye, and their superposition apertures. Light that leaks out from the target rhabdom is compensated for by light leaking in from neighbouring rhabdoms. Thus, the net effect of this light leakage between neighbouring rhabdoms is that the image will be equally bright irrespective of whether the rhabdoms are optically isolated or not (Warrant & McIntyre 1991). However, the lack of isolation will radically reduce spatial resolution (Warrant & McIntyre 1990). This maximized image brightness, however, only occurs for extended sources. Had our stimulus been larger and truly extended, light leakage between rhabdoms would have been greater and measured bump rates in O. aygulus and O. belial would have been higher. The experimental ratios between O. aygulus and M. genalis, and between O. belial and L. leucozonium, would then have been in much better agreement with those calculated theoretically. This observation, together with the close match of theory and experiment between O. aygulus and O. belial, and between M. genalis and L. leucozonium, allows us to conclude that the Land equation remains an excellent tool for comparing optical sensitivities between different eyes.