Electronic Control of the ‘Bailar Twist’ in Formally d⁰-d² Molybdenum tris(dithiolene) Complexes: A Sulfur K-edge XAS and DFT Study

Abstract

Sulfur K-edge x-ray absorption spectroscopy (XAS) and density functional theory (DFT) calculations have been used to determine the electronic structures of a series of Mo tris(dithiolene) complexes, [Mo(mdt)₃]^z (where mdt = 1,2-dimethylethene-1,2-dithiolate(2-) and z = 2-, 1-, 0), with near trigonal-prismatic geometries (D_3h symmetry). These results show that the formally Mo^IV, Mo^V, and Mo^VI complexes actually have a (d_z²)² configuration, that is, remain effectively Mo^IV despite oxidation. Comparisons with the XAS data of another set of Mo tris(dithiolene) complexes, [Mo(tbbdt)₃]^z (where tbbdt = 3,5-di-tert-butylbenzene-1,2-dithiolate(2-) and z = 1-, 0), show that both neutral complexes, [Mo(mdt)₃] and [Mo(tbbdt)₃], have similar electronic structures while the monoanions do not. Calculations reveal that the “Bailar twist” present in the crystal structure of [Mo(tbbdt)₃]^1- (D₃ symmetry) but not [Mo(mdt)₃]^1- (D_3h symmetry) is controlled by electronic factors which arise from bonding differences between the mdt and tbbdt ligands. In the former, configuration interaction between the Mo d_z² and a deeper energy, occupied ligand orbital, which occurs in D₃ symmetry, destabilizes the Mo d_z² to above another ligand orbital which is half-occupied in the D_3h [Mo(mdt)₃]^1- complex. This leads to a metal d¹ configuration with no ligand holes (ie. d¹[L₃]^0h) for [Mo(tbbdt)₃]^1- rather than the metal d² configuration with one ligand hole (ie. d²[L₃]^1h) for [Mo(mdt)₃]^1-. Thus, the Bailar twist observed in some metal tris(dithiolene) complexes is the result of configuration interaction between metal and ligand orbitals and can be probed experimentally by S K-edge XAS.

1. Introduction

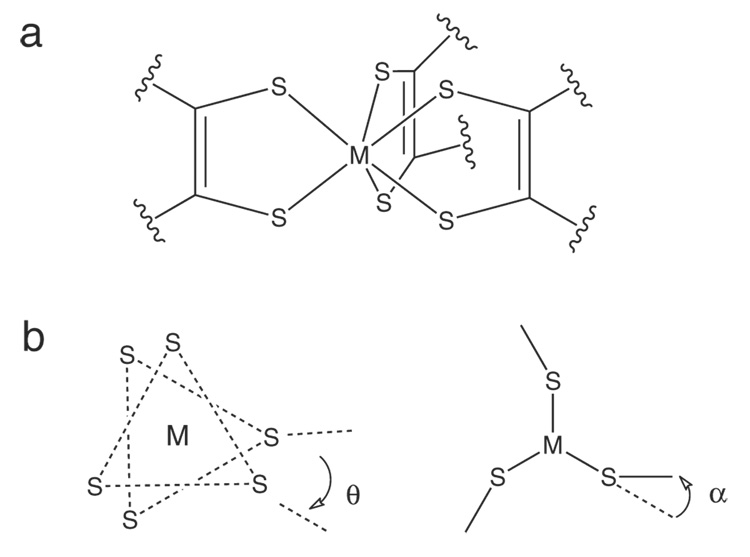
The first six-coordinate complexes shown to adopt a trigonal prismatic structure (D_3h point group) instead of the usual octahedral geometry were metal tris(dithiolene) complexes¹ such as [Re(S₂C₂Ph₂)₃], [W(S₂C₂Ph₂)₃], and [Mo(S₂C₂H₂)₃].^2–4 In these complexes, three sulfur atoms, one from each ligand, are essentially co-planar (forming two S₃ planes) and the M-S₆ core forms a trigonal prism (Scheme 1a). Gray and coworkers proposed that factors contributing to the stability of this structure were interactions between the metal d_z² and in-plane sulfur sp²-hybridized orbitals 120° from the M-S bond and interactions between the metal d_xy & d_x²−y² orbitals and out-of-plane sulfur p orbitals.⁵ In this model, addition of electrons would destabilize the trigonal prism and cause a rotation about the C₃ axis towards octahedral symmetry (Scheme 1b, θ). Indeed, crystallographic investigations showed that tris(dithiolene) complexes such as [Mo(mnt)₃]^2- (mnt = maleonitriledithiolate(2-)) and [Mo(bdt)₃]^1- (bdt = benzene-1,2-dithiolate(2-)) adopt a geometry between trigonal prismatic and octahedral;^6,7 however, there are some notable exceptions such as [Mo(mdt)₃]^z (mdt = 1,2-dimethylethene-1,2-dithiolate(2-), z = 2-, 1-), where the Mo-S₆ trigonal prism is maintained throughout the series, and [Ta(bdt)₃]^1-, which is isoelectronic with [Mo(S₂C₂H₂)₃] but forms a distorted octahedron.^8–10 Another factor thought to stabilize the trigonal prism was inter-ligand sulfur-sulfur bonding. However, this was refuted by comparing the S-S distances in the trigonal prismatic complexes [Mo(bdt)₃] and [Nb(bdt)₃]^1- with those of the distorted complexes [Zr(bdt)₃]^2-, [Mo(mnt)₃]^2-, and [W(mnt)₃]^2-.^11–14

Scheme 1.

(a) The trigonal prismatic structure of metal tris(dithiolenes) and (b) the Bailar twist (θ) and chelate fold (α) distortions.

Rotation about the C₃ axis from O_h (θ = 60°) to D_3h (θ= 0°), which is the pathway used to explain the racemization of certain octahedral tris(chelate) complexes, is known as a Bailar twist (Scheme 1b, θ).¹⁵ Another distortion away from D_3h symmetry observed in tris(dithiolene) complexes involves “folding” the S-C-C-S ligand plane away from the S-M-S plane, resulting in a C_3h symmetry.^3,13,16 Since this distortion affects the planarity of the chelate ring, it is referred to as the “chelate fold” in this paper. Electronic factors contributing to this distortion in metal tris(dithiolene) complexes have been discussed by Harris and Campbell.¹⁷ Similar folding distortions have also been observed in bis(cyclopentadienyl)-ML_n complexes with a single dithiolene ligand and other Mo mono-dithiolene complexes.^18,19

In addition to the different geometric structures of complexes with dithiolene ligands, it has also been found that dithiolene complexes have interesting redox properties, specifically the question of ligand- vs. metal-based oxidation (ie. non-innocent vs. innocent). Recent studies have shown that many dithiolene complexes have inverted bonding descriptions^20,21 with ligand orbitals being redox active (non-innocent behavior) while most metal complexes have traditional metal-based redox active orbitals (normal bonding).

Mononuclear active sites of certain molybdoenzymes contain two pyranopterin-dithiolene ligands and one or two exogeneous or endogenous ligands.²² As such, they have the potential for non-innocent behavior, although this has not been observed with the protein-bound sites or their synthetic analogues.²³ Mo tris(dithiolene) complexes provide a firm background for dissecting the electronic and geometric contributions of the pyranopterin-dithiolene ligand to Mo-S bonding in Mo enzymes without the added complications of oxygen ligands. Additionally, calculations of the reaction pathway for synthetic models of these enzymes show that they proceed through a trigonal prismatic transition state.^24–26

The ligand K-edge XAS methodology developed by our group provides a direct experimental probe of metal-sulfur bonding in complexes and enzymes.²⁷ The S 1s electron can be excited to unoccupied S 4p orbitals and to the continuum by using tunable synchrotron radiation at an energy around 2474 eV, resulting in an electric-dipole-allowed edge feature. Transitions to unoccupied metal-based orbitals are typically at a lower energy than this feature and gain intensity through mixing with S 3p orbitals. Specifically, the intensity of these pre-edge features, D₀, is given by:

$$D_0(S1s\to {\psi }^{*})=\mathit{\text{const}}{\left|\langle S1s|\mathbf{r}|{\psi }^{*}\rangle \right|}^2=\frac{{\alpha }^{2}h}{3n}{I}_s,$$

where r is the transition dipole operator, ψ^* is the antibonding orbital corresponding to metal-ligand bonding ${\psi }^{*}=\sqrt{1-{\alpha }^2}|M_d\rangle -\alpha |S_{3p}\rangle$, α² is the covalency (ie. amount of sulfur character mixed into the metal d orbitals), h is the number of holes in the acceptor orbitals, and n is the number of absorbing atoms. I_s is the intensity of the electric dipole allowed S 1s → 3p transition and has been shown to have a linear relationship with the S 1s → 4p transition energy; therefore, I_s can be estimated from experimental S K-edge data.²⁸

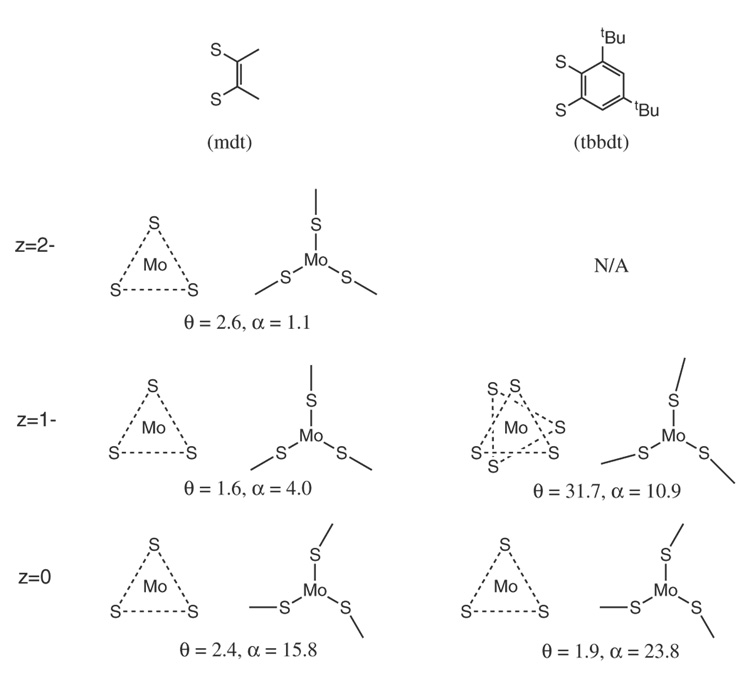
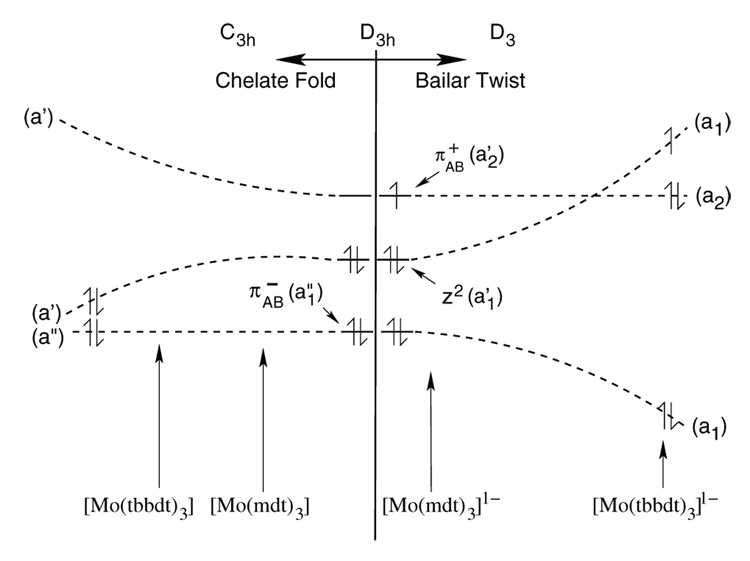
In this paper, S K-edge XAS coupled with density functional theory calculations are used to develop an electronic structure description of a series of three Mo tris(dithiolene) complexes, [Mo(mdt)₃]^z (z = 2-, 1-, 0), which is then compared to an analogous series with a different dithiolene ligand, [Mo(tbbdt)₃]^z (tbbdt = 3,5-di-tert-butylbenzene-1,2-dithiolate(2-) and z = 1-, 0).²⁹ Scheme 2 illustrates the extent of Bailar twist (θ) and chelate fold (α) in these complexes. [Mo(tbbdt)₃]^1-, but not [Mo(mdt)₃]^1-, has a Bailar twist and both [Mo(mdt)₃] and [Mo(bdt)₃] have chelate folds. Differences in electronic structure are determined and provide insight into the electronic control of the amount of Bailar twist (and chelate folds) observed for formally d⁰-d² metal tris(dithiolene) complexes.

Scheme 2.

Average amount of Bailar twist (θ) and chelate fold (α) in the five complexes spanning the three oxidation states and two ligands used in the study. Values reported are from crystallographic data.

2. Experimental

Sample Preparation

The complexes [Mo(mdt)₃]^z (z = 2-, 1-, 0) were prepared as described in references 8 and 9.

X-ray absorption measurements and data analysis

S K-edge and Mo L₃-edge spectra were measured at the Stanford Synchrotron Radiation Laboratory under ring conditions of 3 GeV and 80–100 mA. The measurements utilized the 54-pole wiggler beamline 6-2 operating in high field mode of 10 kG with a Ni-coated harmonic crystal monochromator. Details of the beam line optimization for S K-edge XAS studies were published elsewhere.³⁰ The solid samples were ground in an inert atmospheres (N₂) dry glovebox at less than 1 ppm O₂ and dispersed as thinly as possible on a Mylar tape to minimize the possibility of fluorescence self-absorption effects. A 6 µm thick, sulfur-free polypropylene window was used to prevent sample exposure to air upon mounting in the sample chamber. The photon energy was calibrated to that of the first pre-edge feature of Na₂S₂O₃•5H₂O at 2472.02 eV. Scans were averaged using MAVE, which is part of the EXAFSPAK suite of programs,³¹ and a smooth background of a second-order polynomial was subtracted from the average spectrum.

Normalization of the S K-edge data was accomplished by fitting the post-edge region with a flat first-order polynomial and scaling the data such that the value of this fit function is 1.0 at 2490 eV. Since the post-edge region also contains intensity from the Mo L₃ edge, the data were further scaled such that the region between the S K-edge and Mo L₃-edge had the same intensity as the corresponding region of a tungsten dithiolene complex. Fits to the pre-edges were modeled by pseudo-Voigt peak shapes using the program EDG_FIT³¹ with a fixed 1:1 ratio of Lorentzian to Gaussian contributions. Error in the total pre-edge peak areas ranges from ~2% for well-resolved pre-edges to ~10% for unresolved pre-edges. In addition, normalization procedures can introduce ~5% error in the total pre-edge peak areas. Conversion between peak area and sulfur covalency was accomplished using the equation D₀ = (α²h·I_s)/18 where D₀ is the peak area, h is the number of holes in the corresponding molecular orbital, α² is the sulfur covalency, and I_s is the transition dipole integral as determined using a previously described method.²⁸ Error in determining I_s from the S 1s → 4p transition results in ±2–4% deviation from the reported covalency value.

The raw Mo L₃-edge data were truncated at energies less than 2503 eV and greater than 2600–2620 eV to remove the S K- and Mo L₂-edges. The resulting spectra were normalized by fitting the post-edge region with a flat first-order polynomial and scaled such that the value of this fit function is 1.0 at 2530.0 eV.

Electronic structure calculations

Density functional calculations were performed using the Gaussian 03 package.³² Gaussian calculations were performed using the pure functional BP86 (Becke GGA exchange^33,34 with Perdew 1986 non-local correlation³⁵). The LanL2DZ basis set, which is double-ζ quality with an effective core potential (ECP) for core functions,^36–38 was used for Mo during optimizations. The SDD basis set, which is triple-ζ quality with an effective core potential (ECP) for core functions,³⁹ was used for Mo atoms in calculations at optimized structures. The LanL2DZ basis set was found to give similar molecular orbital compositions and ligand field splittings as the SDD basis set, and was used for Mo atoms in single-point calculations of structures with systematic distortions. The 6–311G(d) basis set was used for the sulfur, carbon, and hydrogen atoms for all calculations, except the optimization of [Mo(mdt)₃]^2- with counter-ions where the 6–31G(d) basis set was used for the nitrogen, carbon, and hydrogen atoms and the 6–311G(d) basis set was used for sulfur atoms. The crystal structure of (Et₄N)₂[Mo(mdt)₃] was used as the initial structure during the optimization of [Mo(mdt)₃]^2- with counter-ions without any geometric constraints. D_3h structures were obtained by using the Opt=Follow keyword during an optimization that started from an initial D_3h guess. Distortions from D_3h symmetry along the Bailar twist were done systematically in 5 degree increments. Molecular orbital compositions were analyzed using Mulliken population analysis⁴⁰ as implemented in PyMOlyze.^41,42

3. Results and Analyses

3.1. S K-edge XAS

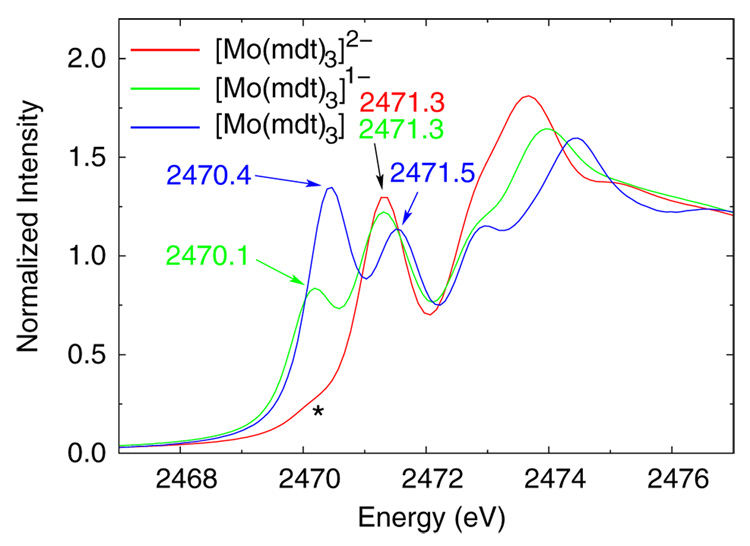
The sulfur K-edge XAS spectra for the [Mo(mdt)₃]^z (z = 2-, 1-, 0) complexes are shown in Figure 1. The dianionic complex (red) has a resolved pre-edge at ~2471.3 eV and a higher-energy pre-edge (~2472.8 eV) that is not resolved from the edge. There is also a small shoulder at ~2470.1 eV (denoted by an asterisk) due to an oxidized impurity (about 10%). The monoanionic complex (green) also has a resolved pre-edge at ~2471.3 eV and an unresolved pre-edge feature at ~2472.8 eV (like the dianionic complex), as well as an additional lower-energy pre-edge peak at ~2470.1 eV, which is consistent with an extra hole due to 1e⁻ oxidation. The neutral complex (blue) also has two resolved features (~2470.4 and ~2471.5 eV) like the monoanionic complex, although both peaks are at slightly higher energy and the lower-energy pre-edge feature has almost twice the intensity consistent with a second valence hole. There is also a pre-edge peak at ~2472.8 eV that is not completely resolved from the rising edge.

Figure 1.

Normalized S K-edge XAS data of the dianionic (red), monoanionic (green), and neutral (blue) [Mo(mdt)₃]^z complexes. The dianionic complex contains an oxidized impurity which is labeled with an asterisk.

There are three contributions to the energy of a ligand pre-edge: the effective nuclear charge (Z_eff) of the metal, ligand Z_eff, and ligand field. An increase in metal Z_eff (ie. oxidation) stabilizes the metal d manifold which decreases the energy of the pre-edge feature, while an increase in ligand Z_eff stabilizes the ligand 1s orbitals which increases the energy of the pre-edge. A stronger ligand field destabilizes the metal d manifold which also increases the energy of the pre-edge. The pre-edge features of the [Mo(mdt)₃]^z (z = 2-, 1-, 0) complexes have approximately the same energy through the series, which is in contrast to the ~1.0 eV decrease in pre-edge observed upon oxidation of a ferrous tetrathiolate.⁴³ Specifically, in going from [Mo(mdt)₃]^2- to [Mo(mdt)₃]^1-, there is no change in the energy of the pre-edge at ~2471.3 eV, and in going from [Mo(mdt)₃]^1- to [Mo(mdt)₃], the energy of this pre-edge increases by 0.23 eV. A fraction of this increase can be attributed to an increase in ligand field strength (~0.10–0.15 eV, Section 3.2), so the remaining ~0.1 eV increase in pre-edge energy indicates that the sulfur Z_eff increases, that is, the dianion and monoanion undergo ligand-based oxidation. This same behavior was also observed for a series of Ni bis(dithiolene) complexes.²⁰ Furthermore, since the increase in pre-edge energy due to ligand oxidation is small, these results indicate that the additional positive charge is delocalized among the ligand atoms.

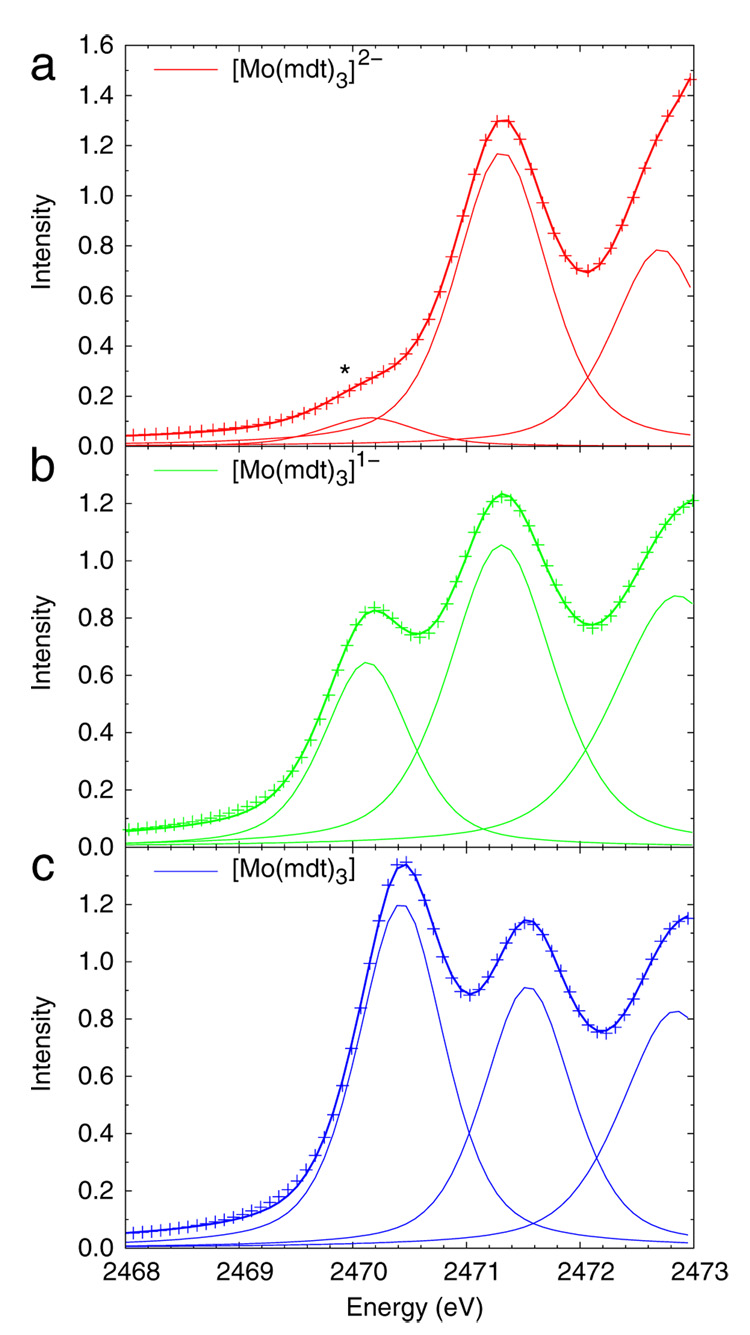
As presented in the Introduction, the intensities of the pre-edge features are proportional to the sulfur character in the unoccupied and half-occupied acceptor orbitals. The dipole integral, I_s, can be estimated from the S 1s → 4p transition.²⁸ The feature in the 2_nd derivative spectra (Figure S1) corresponding to this transition is broad and occurs at about the same energy (~2476.7 eV) in all three complexes; therefore, this energy was used to estimate the dipole integral for all three complexes (I_s = 14.22).²⁸ This approximation is reasonable because the redox-active molecular orbital (vide infra) has equal contributions from all three ligands (ie. the extra positive charge from oxidation is distributed among six sulfur atoms) so only a small change in the 1s → 4p transition energy is expected and observed. Representative fits of the resolved pre-edges of the Mo tris(dithiolene) complexes are shown in Figure 2, and the corresponding ground state sulfur 3p characters obtained from the areas under the pre-edge features are presented in Table 1. The resolved pre-edge (~2471.3 eV) of the dianionic complex (Figure 2a) has 36% S 3p character, which corresponds to about 50% total ligand character (vide infra). The same pre-edge in the monoanionic complex (Figure 2b) has similar sulfur and total ligand character, while the lower-energy pre-edge (~2470.1 eV) has about 75% S 3p character and reflects a ligand-based molecular orbital which also has contributions from carbon and hydrogren atoms (vide infra) for a total of 100% ligand character. Thus, in going from the dianion to the monoanion, the ligands are oxidized. In the neutral complex (Figure 2c), the lower-energy pre-edge (~2470.4 eV) has nearly twice the intensity of the same peak in the monoanionic complex, which is evalulated to 69% S 3p character, or about 85% total ligand character (vide infra), and is consistent with a second ligand-based oxidation. It will be shown in section 3.3 that the decrease from 100% to 85% total ligand character in going from the monoanion to the neutral complex is the result of the chelate fold present in the latter (Scheme 2, left).

Figure 2.

Representative fits of the resolved pre-edges of the (a) dianionic, (b) monoanionic, and (c) neutral [Mo(mdt)₃]^z complexes. The asterisk in the spectrum of the dianion denotes the extra feature due to the oxidized impurity.

Table 1.

Pre-edge peak energies (E), relative energies (RE), intensities (D₀), number of holes in respective orbital (h, vide infra), and covalencies of the S K-edge data for [Mo(mdt)₃]^z (Figure 2).

Z	E (eV)	RE (eV)	D0	h	S 3p (%)
−2	2471.31	0.00	1.13	4	36*
−1	2470.13	0.00	0.59	1	75
	2471.31	1.18	1.16	4	37
0	2470.43	0.00	1.09	2	69
	2471.54	1.11	0.85	4	27

^*corrected for ~10% impurity

Both the energies and intensities of the pre-edges for this series show that the dianionic and monoanionic complexes undergo ligand-based oxidations. Therefore, the formally Mo^V and Mo^VI complexes have the same number of electrons in the d manifold as the Mo^IV complex (ie. d² configurations).

3.2. Mo L₃-edge XAS

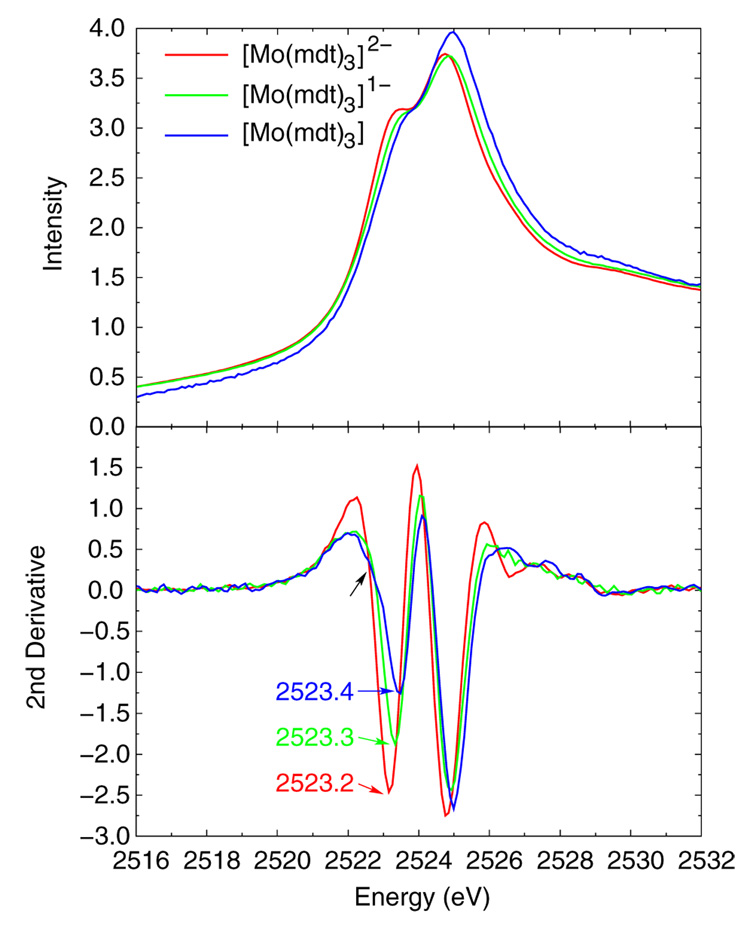
Figure 3 shows the normalized Mo L₃ edges (top) for the [Mo(mdt)₃]^z (z = 2-, 1-, 0) complexes, and the corresponding second derivatives (bottom). Each complex clearly has two peaks due to transitions from the Mo 2p to two groups of molecular orbitals with significant Mo d character, and the energies of these features increase by 0.10–0.15 eV for each oxidation in the series. Our group has previously shown that ligand field effects, and not the effective charge on the metal, are dominant contributions to the energies of metal pre-edges.⁴⁴ Consistent with the results of that study, the 0.10–0.15 eV increase in the energy of the Mo L₃ edge reflects a 0.03 Å decrease in Mo-S bond length (Table 2) in going from the dianion (red) to the monoanion (green). As mentioned in the previous section, the neutral complex (blue) has a chelate fold distortion, and thus, a different ligand field than the D_3h monoanionic complex. This would account for the additional increase in energy of the Mo L₃ edge of the neutral complex compared to that of the monoanion. There is also a low-energy shoulder on the ~2523.4 eV feature in the second derivative spectrum of only the neutral complex (black arrow in bottom panel of Figure 3) which is the result of low symmetry mixing due to the chelate fold (vide infra).

Figure 3.

Normalized and second derivative Mo L₃-edge XAS data of the dianionic (red), monoanionic (green), and neutral (blue) [Mo(mdt)₃]^z complexes. Note that there is a low-energy shoulder present in the data of the neutral complex (black arrow).

Table 2.

Crystal and DFT-optimized structures of the [Mo(mdt)₃]^z complexes. Average values are reported.

	[Mo(mdt)3]2-		[Mo(mdt)3]1-		[Mo(mdt)3]
	Crystal	DFT	Crystal	DFT	Crystal	DFT
Mo-S (Å)	2.40	2.44	2.37	2.42	2.37	2.41
S-C (Å)	1.75	1.78	1.73	1.75	1.73	1.73
S-Mo-S (°)	79.2	80.0	80.5	80.6	81.3	81.1
Bailar Twist (°)	2.6	5.9/19.6*	1.6	1.0	2.4	0.0
Chelate Fold (°)	1.1	0.2	4.0	0.3	15.8	14.9

^*Optimization without counterions results in a significant Bailar twist

3.3. Density Functional Theory Calculations

Spin-unrestricted density functional theory calculations were performed on models derived from the crystal structures of [Mo(mdt)₃]^z (z = 2-, 1-, 0) in order to further investigate the electronic structure intepretations obtained from the above spectroscopic results. Geometry-optimized structural parameters were in reasonable agreement with the crystal structures, which are presented in Table 2. The average Mo-S bond lengths are calculated to be 2.41–2.44 Å, which are 0.04–0.05 Å longer than in the crystal structures, and follow the correct trend of decreasing length as the complexes are oxidized. The S–C bond lengths are calculated to be 1.73–1.78 Å, which is up to 0.03 Å longer than in the crystal structures, and again follow the same trend of decreasing length as the complexes are oxidized. The S-Mo-S chelate angles are 80.0–81.1° which are in good agreement with experimental structures. The optimized structure of the dianionic complex has a 19.6° Bailar twist compared with a 2.6° Bailar twist observed in the crystal structure. Inclusion of two Et₄N⁺ counter-ions in the optimization of the dianionic complex resulted in a near trigonal-prismatic structure with only a small Bailar twist (5.9°). The calculated energy difference between these two structures (without counter-ions) is small (~2.7 kcal/mol) and there is no appreciable difference in the electronic structures at these two geometries, which indicate that crystal packing forces are more important than electronic factors (ie. inter-ligand repulsion, vide infra) in determining the crystal structure of the dianionic complex. Indeed, studies of dianionic W tris(dithiolene) complexes have shown that the amount of Bailar twist is dependent upon the counter-ion.⁴⁵ Since the crystal structure of [Mo(mdt)₃]^2- is trigonal prismatic, the calculation without the Bailar twist will be used for the remainder of this study. The optimized structures of the monoanionic and neutral complexes have essentially no Bailar twist (1.0° and 0.0°, respectively) which are in good agreement with experimental data (1.6° and 2.4°, respectively). Finally, the dianionic and monoanionic complexes have very little chelate fold in their optimized structures (0.2° and 0.3°, respectively, compared with 1.1° and 4.0° experimentally) while the neutral complex has a calculated chelate fold of 14.9°, which agrees with the crystal structure (15.8°).

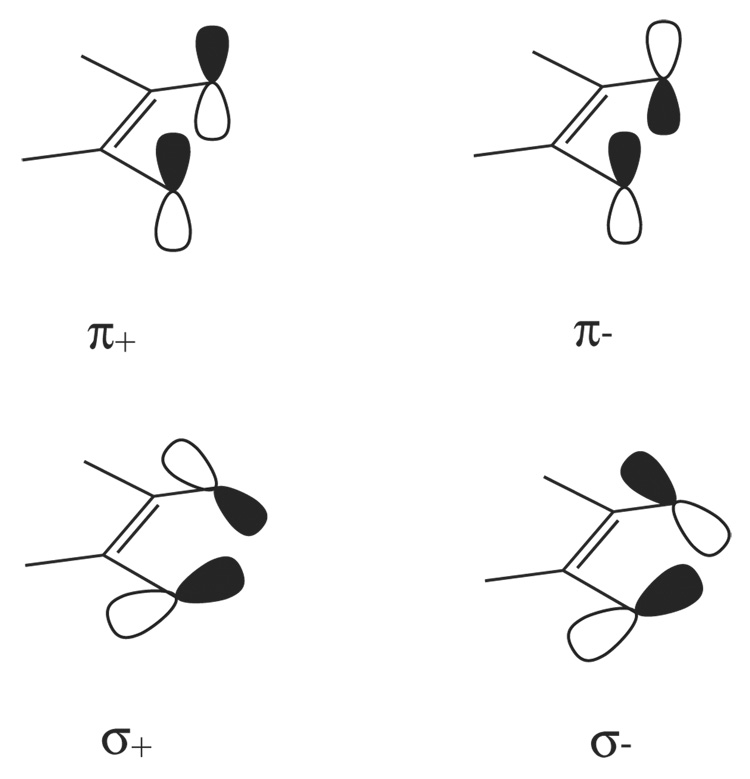
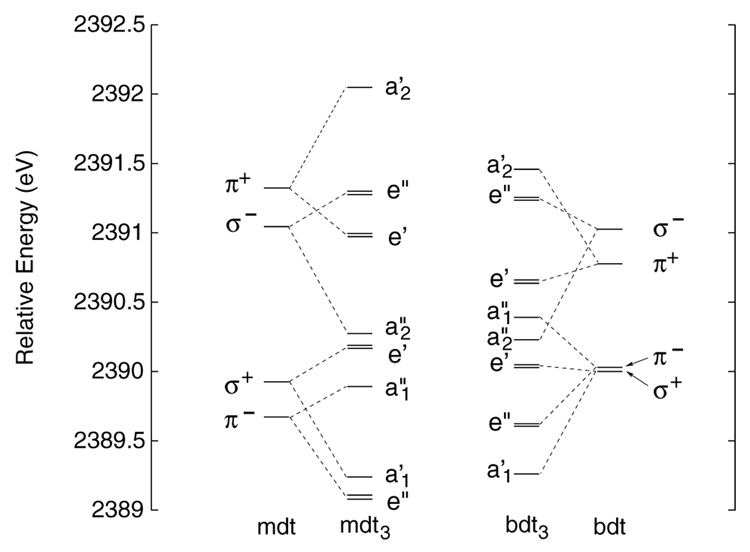
In order to describe the qualitative electronic structure descriptions of the [Mo(mdt)₃]^z complexes, it is helpful to first consider the valence orbitals of the dithiolene ligands. A single mdt ligand has four filled valence molecular orbitals that are derived from four S p orbitals (Scheme 3). The symmetric (+) and anti-symmetric (−) combinations of the two S p orbitals that are out of the S-C-C-S plane have anti-bonding and bonding interactions with the C-C double bond, respectively, and are denoted π⁺ and π⁻. The two in-plane S p orbitals (nearly perpendicular to the C-S bond) also form symmetric (+) and anti-symmetric (−) combinations, denoted σ⁺ and σ⁻, and are about 90% S p character. In the mdt₃ framework of the [Mo(mdt)₃] D_3h complexes, these four orbitals have bonding (B) and anti-bonding (AB) interactions with the orbitals on the other two ligands resulting in four degenerate and four non-degenerate (twelve total) filled valence molecular orbitals (Figure 4, left middle).

Scheme 3.

The four occupied valence orbitals of the dithiolene ligand arising from the symmetric (+) and anti-symmetric (−) combinations of in-plane (σ) and out-of-plane (π) sulfur p orbitals.

Figure 4.

Valence molecular orbitals for the mono- and tris-dithiolene frameworks of mdt and bdt ligands calculated based on the structural parameters of the neutral complexes in D_3h symmetry.

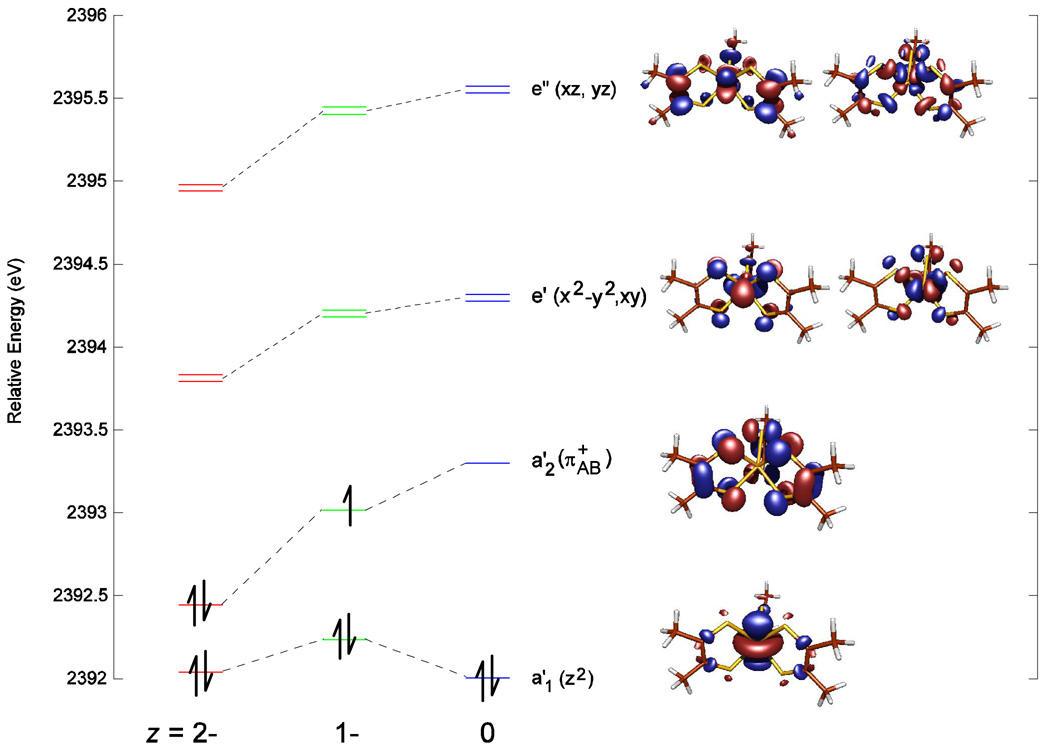
Figure 5 presents the calculated electronic descriptions of the [Mo(mdt)₃]^z complexes. The approximate D_3h ligand field splits the Mo d orbitals into three sets, each separated by 1.2–2.0 eV: z² (a₁') < x²−y²,xy (e') < xz,yz (e”). The a₁' Mo d_z² orbital is primarily non-bonding, so it is the lowest-energy Mo d orbital. The Mo d_xy,x²−y² orbitals primarily have π interactions with mdt₃ orbitals of e’ symmetry, which are comprised of the bonding combination of π⁺ ditholene orbitals (π⁺_B). The Mo d_xz,yz orbitals are highest in energy and primarily have σ interactions with mdt₃ orbitals of e” symmetry, which are comprised of the bonding combination of σ⁻ dithiolene orbitals (σ⁻_B). In addition, there is a ligand-based molecular orbital with a₂' symmetry comprised of the inter-ligand anti-bonding combination of three π⁺ orbitals, denoted π⁺_AB, which is energetically near but above the Mo d_z² orbital. In all three complexes, the Mo d_z² orbital remains doubly-occupied, with one and two holes appearing on the ligand π⁺_AB orbital (a₂’) after each oxidation, which agrees with the ligand-based oxidation description determined by S K-edge XAS. This inverted bonding scheme with the ligand π⁺_AB orbital above the Mo d_z² orbital is due to strong repulsive ligand-ligand interactions, which are also found in metal bis(dithiolene) complexes.²⁰

Figure 5.

Molecular orbital diagram of [Mo(mdt)₃]^z (z = 2-, 1-, 0) showing the five Mo d orbitals and the redox-active ligand π⁺_AB orbital. Energies are relative to the sulfur 1s orbitals and symmetry labels are for D_3h.

For the dianionic complex, the peak at ~2471.3 eV in the S K-edge data (Figure 2, red) is assigned as the transition to the e’ orbitals in Figure 5 (left). It is calculated to have 38% S p character in these orbitals (Table 3) which is in excellent agreement with the experimental value of 36% (Table 1). The remaining electron density is predominately on the Mo d_xy,x²−y² orbitals (52%) and C/H atoms (8%). The ligand π⁺_AB orbital (a₂’ symmetry) has 70% S p and 30% C/H characters and the Mo d_z² orbital (a₁’ symmetry) has 71% Mo d, 10% S p, and 13% C/H characters. Both of these orbitals are occupied, so the electron configuration is d² (electron pair in Mo d_z²) with no holes on the tris(dithiolene) framework (ie. d²[L₃]^0h).

Table 3.

Molecular orbital composition of the [Mo(mdt)₃]^z complexes near the HOMO-LUMO gap. Unoccupied orbitals are shown in bold.

		Mo d (%)	Mo s (%)	Mo p (%)	S p (%)	S s/d (%)	C/H (%)
z=2-	e'	52	0	0	38	1	8
	a2'	0	0	0	70	0	30
	a1'	71	1	0	10	6	13
z=1-	e'	51	0	1	40	1	6
	a2' (beta)	0	0	0	67	0	33
	a2' (alpha)	0	0	0	67	0	33
	a1'	77	2	0	4	8	11
z=0	e'	49	0	1	42	1	6
	a2'	15	0	0	54	1	30
	a1'	63	1	0	11	8	18

The peak at ~2471.3 eV in the S K-edge data for [Mo(mdt)₃]^1- is also assigned as the transition to the e’ orbitals. These orbitals are calculated to have 40% S p character (Table 3), which is in good agreement with the experimental value of 37% (Table 1), with the remaining electron density predominately on the Mo d_xy,x²−y² orbitals (51%) and C/H atoms (6%). The lower-energy pre-edge at ~2470.1 eV in Figure 2 (middle) is assigned as the transition to the half-filled ligand π⁺_AB orbital with a₂’ symmetry. This orbital is calculated to have 67% S p character, which is in good agreement with the experimental value of 75%, and the remaining 33% is on the C/H atoms. The calculated energy splitting between these two orbitals (a₂’ and e’) is 1.2 eV which is the same as the energy difference observed between the two resolved pre-edges. Finally, the filled Mo d_z² orbital (a₁’ symmetry) has 77% Mo d, 4% S p, and 11% C/H characters. Therefore, the electron configuration is also d² with a hole shared among the ligands (ie. d²[L₃]^1h), which is the same electronic structure description determined by S K-edge XAS.

Table 3 also includes the electronic structure description of [Mo(mdt)₃]. The transition to the e’ orbitals occurs at ~2471.5 eV in the S K-edge data. There is 42% S p character in these orbitals, which is somewhat larger than the experimental value of 27%, with the remaining electron density on the Mo d_xy,x²−y² orbitals (49%) and on the C/H atoms (6%). The peak at ~2470.4 eV in the data is due to a transition to the unoccupied ligand π⁺_AB orbital. The calculated value (54%) is smaller than the experimental (69%) S p characters and the remaining electron density is on Mo d orbitals (15%) and C/H atoms (30%). Note that these two peaks overlap and some differences between experiment and calculation can reflect the distribution of overlapping intensity between the two experimental transitions. The total calculated S p character (96%) is in good agreement with the total experimental value (96%). The energy difference between these two orbitals is calculated to be 1.0 eV which is also in reasonable agreement with the energy difference between the corresponding pre-edge features (1.1 eV). Finally, the filled Mo d_z² orbital has 63% Mo d, 11% S p, and 18% C/H characters. Therefore, the electron configuration is d² with two holes on the tris(dithiolene) framework (ie. d²[L₃]^2h), again in agreement with the results from S K-edge XAS.

The decrease in S p and the increase of Mo d character in the ligand π⁺_AB orbital in going from the monoanion to the neutral complex (67% S p and 0% Mo d to 54% S p and 15% Mo d) is mirrored by a similar decrease of metal character in the filled Mo d_z² orbital, and is the result of the chelate fold present in the neutral complex (15.8°). When the complex is distorted from D_3h to C_3h due to the ligand bend (Scheme 1b, α), the ligand π⁺_AB and Mo d_z² orbitals, which transform as a₂’ and a₁’ in D_3h, respectively, become a’ in C_3h and can undergo configuration interaction. This mixes metal character into the ligand-based LUMO and is observed experimentally, both as a decrease in the S p character compared to the monoanion (from 75% to 69%) and as a shoulder on the low-energy side of the feature at ~2523.4 eV in the 2^nd derivative of the Mo L₃-edge spectrum of the neutral complex (black arrow in bottom panel of Figure 3). Indeed, calculations show that if D_3h symmetry is imposed on the neutral complex, this mixing no longer occurs and the S p character in the ligand π⁺_AB orbital increases to 64% with a corresponding decrease in Mo d character to 0%. This configuration interaction in the neutral complex stabilizes the occupied Mo d_z² orbital and destabilizes the unoccupied ligand π⁺_AB orbital, resulting in a net stabilization of the C_3h distorted complex (vide supra).

4. Discussion

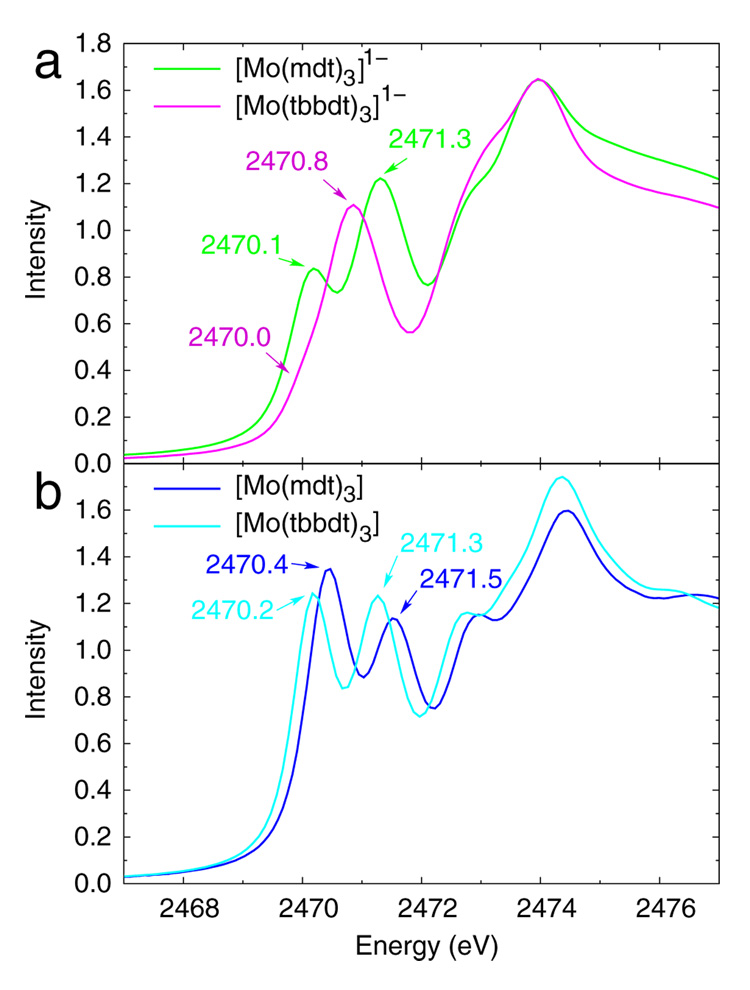
Sulfur K-edge data coupled with DFT calculations show that the [Mo(mdt)₃]^z (z = 2-, 1-) complexes undergo ligand-based oxidations, that is, the formally Mo^IV, Mo^V, and Mo^VI complexes all have d² electron configurations (ie. Mo^IV). This is in contrast to the electronic structure description recently proposed²⁹ for two Mo tris(dithiolene) complexes, [Mo(tbbdt)₃]^z (where z = 1-, 0), illustrated in Scheme 2 (right). In that proposed model, the monoanionic complex has a d¹ configuration with no ligand holes (ie. d¹[L₃]^0h) and the neutral complex is d¹ anti-ferromagnetically coupled to an unpaired electron in a ligand orbital (ie. d¹[L₃]^1h), that is, both are described as Mo^V complexes. The S K-edge XAS data of the [Mo(tbbdt)₃]^z (z = 1-, 0) complexes are compared with the data from this study in Figure 6, and show that the monoanionic complexes (Figure 6a) have different electronic structures, while those of the neutral complexes (Figure 6b) are similar.

Figure 6.

Normalized S K-edge XAS data of (a) [Mo(mdt)₃]^1- (green) and [Mo(tbbdt)₃]^1- (purple), and (b) [Mo(mdt)₃] (dark-blue) and [Mo(tbbdt)₃] (light-blue). The [Mo(tbbdt)₃]^z data are from reference ²⁹.

The energies and intensities of the two resolved pre-edges of the S K-edge data for the [Mo(tbbdt)₃]^z (z = 1-, 0) complexes are presented in Table 4. The spectrum of [Mo(tbbdt)₃]^1- has a shoulder (~2470.0 eV) on the low-energy side of the main pre-edge peak (~2470.8 eV). This feature is clearly present in the second derivative spectrum (Figure S2), and based on the intensity, is due to a transition to a dominately metal-based orbital with some sulfur covalency, which is consistent with a d¹[L₃]^0h configuration proposed in other studies.^29,46 The corresponding pre-edge (~2470.1 eV) of [Mo(mdt)₃]^1- complex, which has a d²[L₃]^1h configuration (vida supra), has 0.53 units of additional intensity. This extra intensity is similar to the amount gained after ligand-based oxidation in going from [Mo(mdt)₃]^2- to [Mo(mdt)₃]^1- (0.59 units), which indicated that one ligand-based hole is worth ~0.6 units of intensity. In going from [Mo(tbbdt)₃]^1- to [Mo(tbbdt)₃], the lowest pre-edge feature (~2470.0 and ~2470.2 eV for the monoanion and neutral, respectively) increases in intensity by 0.85 units. This indicates that approximately 1.4 ligand-based holes have been created upon oxidation of [Mo(tbbdt)₃]^1-.

Table 4.

Pre-edge peak energies (E) and intensities (D₀) for [Mo(mdt)₃]^z and [Mo(tbbdt)₃]^z.

	E (eV)	D0
[Mo(mdt)3]1-	2470.13	0.59
	2471.31	1.16
[Mo(mdt)3]	2470.43	1.09
	2471.54	0.85
[Mo(tbbdt)3]1-	2470.02	0.06
	2470.85	1.21
[Mo(tbbdt)3]	2470.18	0.91
	2471.26	0.89

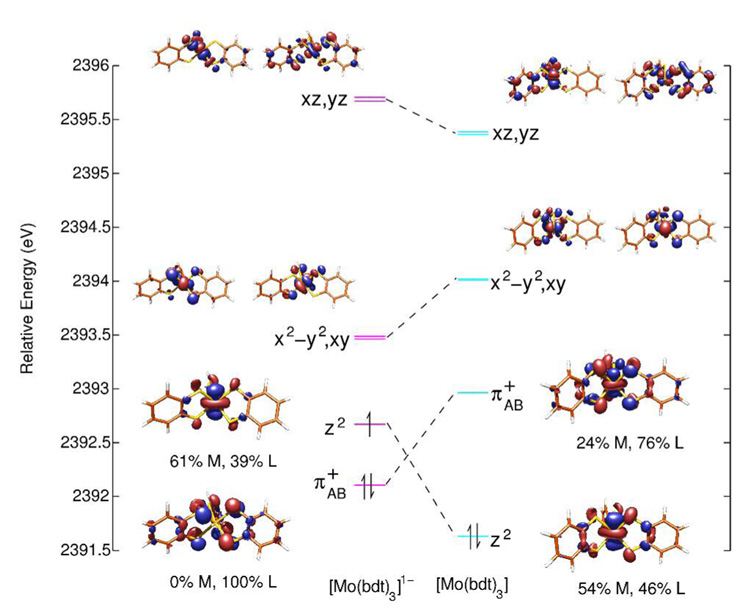
While pre-edge intensities provide a direct probe of the ligand contribution to the molecular orbitals associated with complex oxidation, it is also useful to consider the differences in S K-edge pre-edge energies among these complexes. The pre-edge at ~2471.3 eV in the spectrum of [Mo(mdt)₃]^1- is assigned to a transition to the e’ orbitals (vide supra), and is 0.46 eV higher in energy than the corresponding feature in the spectrum of [Mo(tbbdt)₃]^1- (Table 4). This is qualitatively consistent with a lower metal Z_eff (ie. less oxidized) in the former complex, that is, d²[L₃]^1h and d¹[L₃]^0h configurations for [Mo(mdt)₃]^1- and [Mo(tbbdt)₃]^1-, respectively. Specifically, in going from [Mo(tbbdt)₃]^1- to [Mo(mdt)₃]^1-, there is ~0.2 eV decrease due to ligand field (Figure S4) and ~0.1 eV increase due to ligand-based oxidation (vide supra); therefore, the energy increases by ~0.6 eV due to metal reduction (ie. going from d¹[L₃]^0h to d²[L₃]^1h). This is approximately 35% of the energy shift due to changes in metal Z_eff observed for other complexes with sulfur-containing ligands which undergo metal-based oxidation (1.6–2.0 eV).^20,28,43 Indeed, calculations indicate that the metal center is only partially reduced (0.61 e⁻, Table 5) in going from [Mo(bdt)₃]^1- (where bdt = benzene-1,2-dithiolate(2-), which is a reasonable model for the tbbdt ligand) to [Mo(mdt)₃]^1-.

Table 5.

Total metal and ligand hole character (%) in the redox-active molecular orbital of the [Mo(mdt)₃]^z and [Mo(bdt)₃]^z complexes. Sulfur character is listed in parentheses.

	Metal	Ligands
[Mo(mdt)3]1-	0	100 (67)
[Mo(mdt)3]	30	170 (110)
[Mo(bdt)3]1-	61	39 (22)
[Mo(bdt)3]	47	153 (98)

In going from [Mo(tbbdt)₃]^1- to [Mo(tbbdt)₃], the e’ pre-edge feature increases in energy by 0.41 eV. Approximately 0.1 eV of this increase is due to change in ligand field (Figures S4 and S5). Since this pre-edge shifts to higher energy, it must undergo ligand-based oxidation which accounts for ~0.1 eV of this increase. Therefore, ~0.2 eV of this increase is due to a decrease in metal Z_eff (ie. reduction) which is approximately 10% of the shift expected due to metal-based oxidation. From the calculations in Figure 7, upon oxidation of [Mo(tbbdt)₃]^1-, the metal d_z² orbital shifts down in energy and becomes doubly occupied, with an unoccupied ligand-based orbital at higher energy (ie. complex oxidation leads to metal-based reduction). However, the metal center is only partially reduced (0.14 e⁻, Table 5) in going from [Mo(bdt)₃]^1- to [Mo(bdt)₃] because of the covalency of the Mo-S bonds. This reflects the values in Figure 7, where the monoanion has a metal d_z² hole with 61% metal character, while the neutral complex has two ligand π⁺_AB holes with 24% metal character each. These results are qualitatively consistent with the analysis of the intensity differences for [Mo(tbbdt)₃]^1- and [Mo(tbbdt)₃] which indicated that approximately 1.4 ligand-based holes are created upon oxidation of the monoanion.

Figure 7.

Molecular orbital diagram of [Mo(bdt)₃]^z (z = 1-, 0) showing the five Mo d orbitals and the ligand π⁺_AB orbital. Energies are relative to the sulfur 1s orbital.

In order to elucidate the origin of the changes in electronic structure upon oxidation of [Mo(mdt)₃]^1- relative to [Mo(tbbdt)₃]^1-, one must note the differences in crystal structures (Scheme 2 and Table 6). Both neutral complexes and [Mo(mdt)₃]^1- have similar trigonal prism structures and lack any significant Bailar twist, while [Mo(tbbdt)₃]^1- is distorted 32° towards the octahedral limit. Additional DFT calculations were performed on structures with systematic distortion along the Bailar coordinate (0°–40°) to further evaluate the effect of this distortion.

Table 6.

Crystal structures of the monoanionic and neutral [Mo(mdt)₃]^z and [Mo(tbbdt)₃]^z complexes. Average values are reported.

	[Mo(mdt)3]1-	[Mo(mdt)3]	[Mo(tbbdt)3]1-	[Mo(tbbdt)3]
Mo-S (Å)	2.37	2.37	2.38	2.36
S-Mo-S (°)	80.5	81.3	81.3	81.5
Bailar Twist (°)	1.6	2.4	31.7	1.9
Chelate Fold (°)	4.0	15.8	10.9	23.8

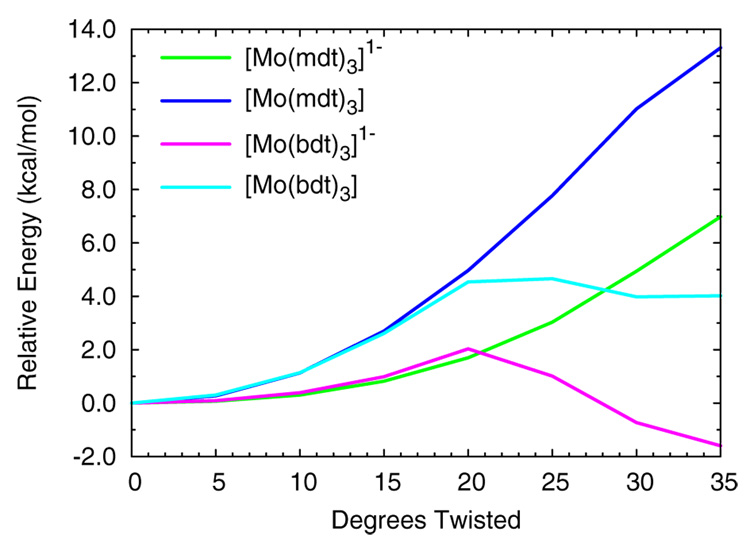
Figure 8 shows the total electronic energies of the monoanionic and neutral complexes [Mo(mdt)₃]^z and [Mo(bdt)₃]^z as a function of degrees twisted towards the octahedral limit. All four complexes increase in energy between 0° and 20° with the slopes of the neutral complexes about twice as large as the monoanions. As the complexes are distorted along the Bailar coordinate, the inter-ligand interactions are disrupted (Figure 4, left, mdt → mdt₃), which stabilizes the anti-bonding ligand π⁺_AB orbital (a₂’) and destabilizes its bonding partner, denoted π⁺_B (e’). Since the π⁺_AB orbital is half-occupied and unoccupied in the monoanionic and neutral complexes, respectively (Figure 5), and the π⁺_B orbital is filled, a net increase in total electronic energy is observed for these complexes, with the energies of the neutral complexes increasing about twice as fast as those of the monoanions. For a Bailar twist of more than 20°, [Mo(bdt)₃]^1- (pink) decreases in energy and [Mo(bdt)₃] (light blue) stops increasing in energy while the energies of [Mo(mdt)₃]^1- (green) and [Mo(mdt)₃] (blue) continue to increase. These trends indicate that there is a major change in the electronic structures of [Mo(bdt)₃]^1- and [Mo(bdt)₃], but not [Mo(mdt)₃]^1- or [Mo(mdt)₃], after a Bailar twist of ~20°.

Figure 8.

The total electronic energies of [Mo(mdt)₃]^z and [Mo(bdt)₃]^z (z = 1-, 0) as a function of the amount of Bailar twist distortion.

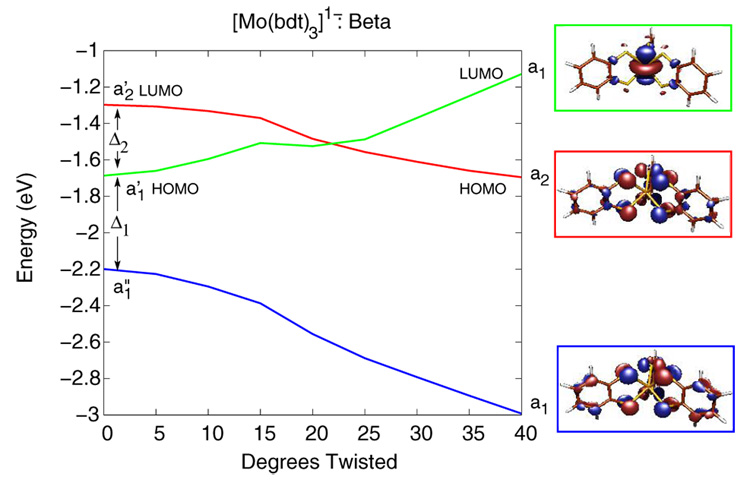
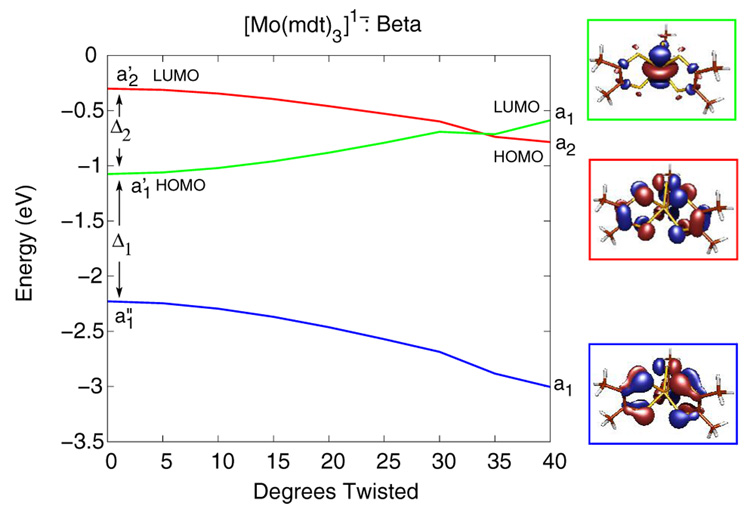
Figure 9 and Figure 10 show Walsh-type correlation diagrams for the three valence β-spin (or spin-down) orbitals of [Mo(bdt)₃]^1- and [Mo(mdt)₃]^1-, respectively, that have significant changes in energy along the Bailar twist. This distortion lowers the symmetry of these complexes from D_3h to D₃. In both [Mo(mdt)₃]^1- and [Mo(bdt)₃]^1-, the occupied Mo d_z² orbital (a₁' in D_3h, green line) and the occupied ligand π⁻_AB orbitals (a₁” in D_3h, blue line) transform as a₁ in D₃ symmetry, and thus, can mix when the complexes are distorted along the Bailar twist. This interaction destabilizes the Mo d_z² orbital while stabilizing the ligand π⁻_AB orbital. The unoccupied ligand π⁺_AB orbital (a₂' in D_3h, red line) transforms as a₂ in D₃ and cannot mix with the a₁ orbitals, but decreases in energy as the repulsive anti-bonding inter-ligand interactions are decreased along the Bailar twist (vide supra). In both complexes, the occupied β-spin Mo d_z² orbital (green line) is eventually destabilized to higher energy than the β-spin ligand π⁺_AB orbital (red line) and becomes unoccupied. This charge-transfer process of moving an electron from the Mo d_z² to a ligand hole occurs around 20° in [Mo(bdt)₃]^1- (Figure 9), which explains the decrease in energy after 20° for [Mo(bdt)₃]^1- in Figure 8; therefore, the observed Bailar twist in [Mo(tbbdt)₃]^1- has an electronic origin. For [Mo(mdt)₃]^1-, this level crossing and the associated charge-transfer process does not occur until about 35° (Figure 10) and does not compensate the increase of energy resulting from the Bailar twist distortion (Figure 8); therefore, the D_3h structure is favored.

Figure 9.

Walsh-type correlation diagram of the β-spin orbitals of [Mo(bdt)₃]^1- as a function of amount of Bailar twist. This distortion causes configuration interaction between the Mo d_z² (green line) and ligand π⁻_AB (blue line) orbitals, which eventually causes the Mo d_z² orbital to have a higher energy than the ligand π⁺_AB orbital (red line).

Figure 10.

Walsh-type correlation diagram of the β-spin orbitals of [Mo(mdt)₃]^1- as a function of amount of Bailar twist. This distortion causes configuration interaction between the Mo d_z² (green line) and ligand π⁻_AB (blue line) orbitals, which eventually causes the Mo d_z² orbital to have a higher energy than the ligand π⁺_AB orbital (red line).

This provides an explanation for the differences between the S K-edge XAS data for [Mo(mdt)₃]^1- and [Mo(tbbdt)₃]^1- (Figure 6a). The Bailar twist in [Mo(tbbdt)₃]^1- shifts the Mo d_z² orbital energetically above the unoccupied ligand π⁺_AB orbital due to configuration interaction with the occupied ligand π⁻_AB orbital resulting in a metal hole, and thus, no intense pre-edge appears at ~2470 eV. The lack of Bailar twist in [Mo(mdt)₃]^1- leaves the Mo d_z² orbital below the ligand orbital resulting in a ligand hole and the additional pre-edge feature present at ~2470 eV.

The differences in amount of Bailar twist needed for this metal-to-ligand charge transfer is the result of the energy spacing between these three molecular orbitals. In [Mo(mdt)₃]^1-, the energy separations between these three orbitals, Δ₁ and Δ₂, are about 1.1 and 0.8 eV, respectively (Figure 10, left), while in [Mo(bdt)₃]^1-, Δ₁ and Δ₂ are about 0.5 and 0.4 eV, respectively (Figure 9, left). In order to understand these differences, the orbital energy spacings of the mdt₃ and bdt₃ ligand frameworks were investigated with DFT calculations on structures derived from the D_3h neutral complexes. Figure 4 shows the molecular orbital diagram for the mono- and tris-dithiolene ligand frameworks, with the mdt ligands on the left and the bdt ligands on the right. The orbital diagram for the mdt ligand (left) has four valence MOs as described above, and similar MOs are present in the bdt ligand (right). The energy difference between the π⁺ and π⁻ orbitals is, however, much larger for the mdt ligand (~1.7 eV) than the bdt ligand (~0.8 eV) due to the amount of π conjugation in the latter. This decreases the strength of bonding/anti-bonding interactions of the out-of-plane S p orbitals with the π orbitals of the C-C bond (Scheme 3,π). In the tris(dithiolene) framework, the energy splitting between the π⁺_AB (a₂') and π⁻_AB (a₁”) orbitals is now ~2.2 eV for mdt₃ and ~1.1 eV for bdt₃, which is only a net increase of ~0.5 and ~0.3 eV, respectively, compared to the orbital energy splitting in a single ligand. Therefore, the difference in energy spacings, Δ₁ and Δ₂, in [Mo(mdt)₃]^1- vs. [Mo(bdt)₃]^1- are primarily due to the fundamental differences between the mdt and bdt ligands, and the Bailar twist in [Mo(tbbdt)₃]^1- can be attributed to the nature of the tbbdt ligand.

It is interesting to consider why the neutral complexes do not Bailar twist. The Mo d_z² (a₁' in D_3h) and ligand π⁻_AB orbitals (a₁” in D_3h) in [Mo(mdt)₃] and [Mo(bdt)₃] can also mix because of a Bailar twist (both transforming as a₁ in D₃), eventually causing the β-spin Mo d_z² orbital to become unoccupied by transferring its electron to the ligand π⁺_AB orbital as discussed above for the monoanionic complexes (Figure 9 and Figure 10). However, the energy stabilization from this metal-to-ligand charge transfer, which results in a d¹[L₃]^1h configuration, is not enough to overcome the net increase in energy due to disruption of inter-ligand interactions (which are net bonding interactions because of the unfilled ligand π⁺_AB orbital) from a Bailar twist in the neutral complexes (Figure 8); therefore, these complexes do not undergo a Bailar twist.⁴⁷ In addition, the neutral complexes have significant chelate fold (Scheme 2 and Table 6) which provides a favorable distortion pathway that maintains the trigonal prismatic Mo-S₆ core. As mentioned in section 3.3 for [Mo(mdt)₃], this distortion from D_3h to C_3h results in the configuration interaction between the Mo d_z² (a₁’ in D_3h) and the ligand π⁺_AB (a₂’ in D_3h) orbitals since both transform as a’ in C_3h. For the neutral complexes, this mixing stabilizes the filled Mo d_z² orbital and destabilizes the unoccupied ligand π⁺_AB orbital, which lowers the energy of the complex. This model is similar to the one proposed by Harris and Campbell for the ligand bending observed in the neutral complexes,¹⁷ but with the Mo d_z² orbital higher in energy than the ligand π⁺_AB orbital.

These results show that there are two possible distortions away from the trigonal prism (D_3h symmetry) for formally d⁰ and d¹ tris(dithiolene) complexes. Bailar twist distortions (Figure 11, right) are available for formally d¹ complexes if the energy separation between the metal d_z² orbital and the ligand π⁻_AB (Δ₁) and ligand π⁺_AB (Δ₂) orbitals are small enough such that the filled metal d_z² becomes higher in energy than the ligand π⁺_AB orbital with limited distortion along the Bailar twist. This model predicts that, in general, formally d¹ tris(dithiolene) complexes with bdt-type ligands (ie. have significant π delocalization) have structures with Bailar twists, while complexes with mdt-type ligands are trigonal prismatic because the energy differences Δ₁ and Δ₂ are large for the mdt-type ligand. These electronic differences, associated with the geometric differences, can be observed experimentally by S K-edge XAS. Specifically, complexes with a trigonal prismatic M-S₆ core will have an intense, low-energy pre-edge feature (ie. a ligand-based hole) while the corresponding feature in Bailar twisted complexes will have little intensity (ie. a metal-based hole).

Figure 11.

Diagram showing orbital interactions with chelate fold (left) and Bailar twist (right) distortions for formally d⁰ and d¹ tris(dithiolene) complexes, respectively. The approximate values of the major distortion in the neutral (left) and monoanionic (right) complexes in this study are also indicated. The energy level spacings between these three orbitals affect the amount of each distortion (see text).

Chelate folding distortions (Figure 11, left), but not Bailar twists, are available for formally d⁰ complexes, and the amount of distortion is again dependent on the energy spacing between the metal d_z² and the ligand π⁺_AB orbital (Δ₂).⁴⁸ This model predicts that, in general, formally d₀ tris(dithiolene) complexes with bdt-type ligands also have more chelate fold than mdt-type ligands because the energy difference Δ₂ between these orbitals is smaller for the π delocalized bdt-type ligand. This is observed experimentally for [Mo(tbbdt)₃] (23.8°) vs. [Mo(mdt)₃] (15.8°).

As can be seen from the crystal structure of [Mo(tbbdt)₃]^1- (Scheme 2 and Table 6), it is possible that some complexes have both a Bailar twist (31.7°) and a chelate fold (10.9°), which shows that the two distortions are not mutually exclusive. Ultimately, the potential energy surfaces for metal tris(dithiolene) complexes depend upon whether there is significant π delocalization in the dithiolene ligand and the formal number of metal d electrons.

It is evident from the large spectral differences seen in Figure 6a that the monanionic complexes have different electronic structures. The monoanion with aliphatic dithiolene ligands has a Mo-S₆ core with D_3h symmetry and a d²[L₃]^1h electronic configuration. The monoanion with π delocalized dithiolene ligands has significant a Bailar twist (ie. the Mo-S₆ core with D₃ symmetry) which leads to configuration interaction of the Mo d_z² orbital with a deeper occupied ligand π⁻_AB orbital. This raises the energy of the Mo d_z² orbital above the unoccupied ligand π⁺_AB orbital, resulting in a d¹[L₃]^0h electronic configuration. The similar intensities of the lowest energy pre-edges in Figure 6b indicate that both neutral complexes are described as d² complexes with two ligand holes (ie. d²[L₃]^2h). This leads to the unusual situation that oxidation of a complex (ie. [Mo(tbbdt)₃]^1-) causes a structural change accompanied by a partial reduction of the metal center with increased Mo-S covalency (resulting in a limited change in the metal Z_eff), and further demonstrates the potential non-innocent behavior of dithiolene ligands.

Supplementary Material

SI1. Supporting Information Available.

Second derivative of the normalized S K-edge spectra of the [Mo(mdt)₃]^z complexes and [Mo(tbbdt)₃]^1-; representative fits for the [Mo(tbbdt)₃]^z complexes; comparisons between the normalized and second derivative Mo L₃-edge spectra of monoanionic and neutral complexes; Cartesian coordinates of the optimized structures of the [Mo(mdt)₃]^z and [Mo(bdt)₃]^z complexes; complete reference ³². This material is available free of charge via the Internet at http://pubs.acs.org.