An age-structured model to evaluate the potential of novel malaria-control interventions: a case study of fungal biopesticide sprays

Abstract

It has recently been proposed that mosquito vectors of human diseases, particularly malaria, may be controlled by spraying with fungal biopesticides that increase the rate of adult mortality. Though fungal pathogens do not cause instantaneous mortality, they can kill mosquitoes before they are old enough to transmit disease. A model is developed (i) to explore the potential for fungal entomopathogens to reduce significantly infectious mosquito populations, (ii) to assess the relative value of the many different fungal strains that might be used, and (iii) to help guide the tactical design of vector-control programmes. The model follows the dynamics of different classes of adult mosquitoes with the risk of mortality due to the fungus being assumed to be a function of time since infection (modelled using the Weibull distribution). It is shown that substantial reductions in mosquito numbers are feasible for realistic assumptions about mosquito, fungus and malaria biology and moderate to low daily fungal infection probability. The choice of optimal fungal strain and spraying regime is shown to depend on local mosquito and malaria biology. Fungal pathogens may also influence the ability of mosquitoes to transmit malaria and such effects are shown to further reduce vectorial capacity.

1. Introduction

Malaria is one of the most important parasitic diseases in the world, with more than 500 million clinical cases and over 1 million deaths annually (Snow et al. 2005). A critical factor determining the successful transmission of malaria is the longevity of the adult mosquito relative to the incubation period of the parasite (MacDonald 1957; Smith & McKenzie 2004). The incubation period varies in the field from approximately 10 to more than 20 days, depending on temperature (Patz & Olson 2006), and only a relatively small fraction of mosquitoes naturally live long enough to infect humans. Thus, techniques that reduce adult survival further, such as indoor residual spraying (IRS) with insecticides and the deployment of insecticide-treated nets (ITNs), can cause substantial decreases in malaria transmission (Curtis & Mnzava 2000; Goodman et al. 2001; Guyatt & Snow 2002; Sharp et al. 2002).

Biopesticides containing spores of entomopathogenic fungi have been proposed as possible alternatives to conventional chemical insecticides for use in ITN- or IRS-based strategies (see Thomas & Read 2007). A range of ‘proof of concept’ studies in both laboratory and field have demonstrated that transient exposure of adult mosquitoes to surfaces treated with pathogenic fungal spores can lead to high levels of infection (Scholte et al. 2003a,b, 2005, 2006; Blanford et al. 2005). The resultant impact on adult survival leads to substantial reductions in the potential for malaria transmission (Blanford et al. 2005; Scholte et al. 2005). However, different fungal strains, formulations and application methods can generate a variety of adult mortality patterns that differ from the standard exponential survival distribution assumed in most of the classic models of malaria epidemiology. In some strains, fungal-induced mortality begins soon after infection and average survival times are approximately 3–4 days, while in others mortality commences more slowly, with a distinct lag phase, and average survival times are approximately 10 days (see Scholte et al. 2003a,b, 2005, 2006; Blanford et al. 2005 and figure 1). Beyond knowing greater mortality is beneficial, currently we have little understanding of how different mean life expectancies or shapes of the survival distribution impact on malaria transmission and hence little foundation for selecting one strain or delivery system over another. Moreover, the consequence of different mortality schedules will likely vary depending on epidemiological parameters such as extrinsic incubation period. A further issue is that a relatively slow-acting biopesticide provides very little personal protection from biting at the household level and so the impact on malaria will depend on the extent of community adoption. However, the level of coverage required and how this scales with a factor such as virulence are unclear. Similarly, it has been argued that the persistence time of the fungal pathogens on treated surfaces will be a key factor determining the ultimate viability of the biopesticide approach (Enserink 2005), but what level of persistence or frequency of re-treatment is required to sustain effective control is unknown.

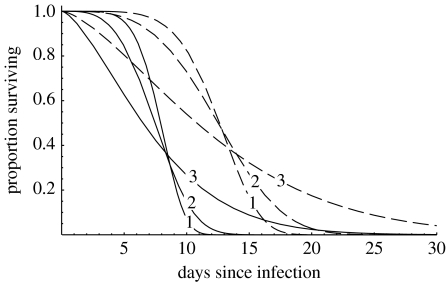
Figure 1.

Patterns of fungal pathogen-induced mortality modelled using a Weibull distribution whose form can be described by the expected time to death (g_F) and by a shape parameter (β). Solid lines correspond to g_F=7.5 days and dashed lines to g_F=12.5 days. Lines labelled 1, 2 or 3 represent β=5.5, 3.5 or 1.5, respectively.

In addition to increased mortality, biopesticides can have other effects on mosquito life history that interact to determine the total impact on malaria transmission. Fungal infection can cause a reduction in blood feeding rate and blood meal size (Koella & Agnew 1997; Blanford et al. 2005; Scholte et al. 2005), which could reduce the transmission rate. There is also evidence that co-infection with the fungal pathogen and the malaria parasite can cause greater than additive mosquito mortality (Blanford et al. 2005; Thomas & Read 2007) and reduced transmissibility of the malaria pathogen (Blanford et al. 2005; Thomas & Read 2007).

At present, therefore, fungal biopesticides hold much promise, but there is limited theoretical understanding and few empirical data to guide their development beyond the proof of concept stage; arguably a situation common to a range of novel vector-control interventions is currently under investigation (e.g. see Rasgon et al. 2003; Sinkins & Gould 2006; Chen et al. 2007; Marrelli et al. 2007). To address this issue, we develop here a new population dynamic model that enables us to explore age-dependent effects in the mosquito–Plasmodium system. We use the model to explore the potential of the fungal biopesticide approach to impact upon malaria transmission and to advance our basic understanding of the interaction in order to aid in the practical development of the technology. More generally, we hope to provide a framework for better understanding of the role of age-dependent factors in the dynamics of malaria.

The classic approach to modelling adult mosquito dynamics, based on the work of Ross (1911) and MacDonald (1957), is to assume that there are just two classes of mosquitoes, susceptibles and infectious (SI models; see Smith & McKenzie 2004). Susceptible mosquitoes become infected at a rate that depends on malaria prevalence in humans, and mosquitoes in each of the two classes die at a constant rate. The models are phrased as ordinary differential equations (ODEs). More realistic ‘SEI’ models also include an exposed class, mosquitoes that carry the malaria pathogen but cannot yet transmit it. Incorporating the relatively fixed duration of the exposed period is difficult within an ODE framework (though see Smith et al. 2004, 2007) and rephrasing the model as delay differential equations (MacDonald 1957; Aron & May 1982; Atkinson et al. 2007; Hancock & Godfray 2007) provides one solution. Here we require a model that includes susceptible, exposed and infectious classes of mosquitoes, and that further divides each class into insects that have or have not been infected by the entomopathogen. Furthermore, we need the probability of death to vary with time since fungal infection. None of the approaches described above are well suited to this, and instead we develop a new age-structured formulation of the SEI model based on integral equations. This allows us to describe the dynamics of each class of mosquito in the presence of age-dependent mortality and to derive expressions for the equilibrium densities that are analytically soluble, at least for limiting cases.

We parametrize the model with literature data on the mosquito–malaria interaction and use it to answer a series of questions relevant to the deployment of a fungal biopesticide. How do different fungal isolates that vary in the pattern of mortality they impose on infected mosquitoes differ in the efficiency with which they reduce malaria transmission? How are these differences affected by the daily probability of fungal infection, and by important details of the mosquito–malaria interaction such as the length of the incubation period? How might interactions between the fungus and the Plasmodium within the adult mosquito influence control strategy? How do factors such as fungal spore persistence in the environment affect the long-term efficacy of a biopesticide application? In §4, we explore how the fungal model might be extended and argue that this approach is generally useful for studying age-specific mortality in vector populations.

2. Model development

(a) Model specification

We make the simplifying assumption that the pre-adult stages of the mosquito can be ignored and that recruitment to the adult stage occurs at a constant rate ϵ. The dynamics of infection by the Plasmodium parasite are treated as an SEI process with the mosquitoes being categorized as susceptible, exposed (but not yet infectious) and infectious. Each of the three categories can be divided into mosquitoes that are uninfected with the fungal pathogen and those that are infected giving six classes of mosquito (a diagram of the model is provided in the electronic supplementary material). Thus, let S₁(t) be the number of susceptible, uninfected mosquitoes at time t, and let S₂(t, u) be the susceptible mosquitoes that were infected with the fungus u days ago. Let E₁(t, p) represent exposed mosquitoes that were infected with the Plasmodium parasite p days ago and E₂(t, p, u) the equivalent class of mosquitoes that picked up the fungal infection u days ago. Finally, let I₁(t) be the density of infectious mosquitoes that have not been infected by the fungus and I₂(t, u) the density of mosquitoes that carried the fungal infection for u days.

In describing the model below, we shall assume that the rate of fungal infection is a constant F, though we shall also analyse numerically a version, where F may vary over time. In applied vector biology, the probability of infection per day (d) is often discussed (sometimes called coverage) and hence we define a quantity c=1−exp(−F) to describe the daily risk of contracting the fungus. We assume that mosquitoes feed solely on humans at a rate a when uninfected and a_F when infected by the fungus. A constant fraction, x, of the human population is infected with malaria, and the probability of transmission from an infected human is b. We use day as the unit of time and assume that it takes the Plasmodium exactly T_E days to mature in a mosquito and become infectious.

In the absence of fungal infection, the mortality rate per day is μ. Mosquitoes infected by the fungus suffer an additional mortality M_F(u) that may vary with u, the time that has elapsed since infection. It is useful to define a series of expressions, θ[·], which will be described in more detail below to represent the probability that a mosquito remains in the same class over different periods of time.

We now write down equations for the number of mosquitoes in the six different classes. Consider first mosquitoes that carry neither the fungus nor Plasmodium,

$$S_1(t)={\int }_0^tϵ{\theta }_{{\text{S}}_1}[t-\tau ]\text{d}\tau ,$$ (2.1a)

where the probability of remaining in this class from day τ to the present is

$${\theta }_{{\text{S}}_1}[t-\tau ]=\text{exp}[-(t-\tau )(\mu +abx+F)].$$ (2.1b)

Mosquitoes become adult at a constant rate, ϵ, and the numbers in the stage are the sum of those maturing at different times in the past multiplied by their probability of avoiding the three risk factors death, malaria infection and fungal infection.

Now consider the class of mosquitoes that have contracted the fungus but not the Plasmodium.

$$S_2(t,u)=S_1(t-u)F{\theta }_{{\text{S}}_2}[u],$$ (2.2a)

where the probability of remaining in this class for u days after fungal infection is

$${\theta }_{{\text{S}}_2}[u]=\text{exp}\left[-{\int }_0^u\mu +M_{\text{F}}(\xi )+a_{\text{F}}bx\text{d}\xi \right].$$ (2.2b)

Because the risk of mortality depends on how long the insect has carried the fungus, u, the population density of this type of susceptibles is now a function of two variables. The number of mosquitoes in this class that were infected u days ago is simply the product of the density of the uninfected susceptible class at that time, the rate of fungal infection and the probability of remaining in the class over the intervening period. The latter is the probability of avoiding both the constant and time-varying risks of mortality, as well as the chance of picking up the malaria infection.

In dealing with the class of mosquitoes exposed to Plasmodium but without the fungal infection, we need to keep track of the length of the time they have carried the parasite, p. Thus,

$$E_1(t,p)=S_1(t-p)abx{\theta }_{{\text{E}}_1}[p],0\le p<T_{\text{E}},$$ (2.3a)

where the probability of remaining in this class for p days after acquiring Plasmodium is

$${\theta }_{{\text{E}}_1}[p]=\text{exp}[-p(\mu +F)].$$ (2.3b)

The number in this class is the density of uninfected susceptibles p days ago multiplied by the risk of acquiring the Plasmodium and the probability of remaining in the class through the intervening period p. The latter is the probability of both avoiding mortality and fungal infection.

The most complicated expression is required for the mosquitoes that are exposed to Plasmodium but not yet infectious, and which are also infected by the fungus. It is necessary to index mosquitoes by the lengths of time they have carried the Plasmodium (p) and the fungus (u).

$$E_2(t,p,u)=H[u,p]E_1(t-u,p-u)F{\theta }_{{\text{E}}_2}[u,u]+(1-H[u,p])S_2(t-p,u-p)a_{\text{F}}bx{\theta }_{{\text{E}}_2}[p,u],0\le p<T_{\text{E}},$$ (2.4a)

where the probability of surviving the last t₁ days, given they have carried the fungal infection for t₀ days, is

$${\theta }_{{\text{E}}_2}[t_1,t_0]=\text{exp}\left[-{\int }_{t_0-t_1}^{t_0}\mu +M_{\text{F}}(\xi )\text{d}\xi \right].$$ (2.4b)

This class is made up of mosquitoes that acquired the fungus first and then the Plasmodium and vice versa. Formally, we define the step function

$$H[u,p]=\{\begin{array}{cc}1,& u\le p,\\ 0,& u>p,\end{array}$$ (2.4c)

to allow us to distinguish these individuals.

The first term in the main expression (2.4a) represents insects that contracted the Plasmodium p days ago and the fungus a shorter period, u days ago. Their numbers at time t are the density of exposed, fungus-free insects u days ago that had at that time carried the Plasmodium for p−u days, multiplied by the risk of fungal infection and the probability of remaining in this class until the present day. The second term represents insects that contracted the fungus first. Their contribution is the density of insects with no Plasmodium that t−p days ago already carried the fungus for u−p days, multiplied by the risks of picking up the malaria parasite, and the probability of remaining in this class until the present day. The probability of remaining in the class is simply the chance of avoiding the time-varying mortality experienced by mosquitoes carrying the fungus.

The density of mosquitoes that carry infectious Plasmodium but are free of the fungus is

$$I_1(t)={\int }_0^t{E}_1(\tau ,T_{\text{E}}){\theta }_{{\text{I}}_1}[t-\tau ]\text{d}\tau ,$$ (2.5a)

where the probability of remaining in this class from day τ to the present is

$${\theta }_{{\text{I}}_1}[t-\tau ]=\text{exp}[-(t-\tau )(\mu +F)].$$ (2.5b)

The first expression is simply the sum of all mosquitoes maturing out of the exposed, fungus-free stage in the past, multiplied by the probability that they remain in this stage. The latter is the probability of avoiding mortality or fungus infection.

The density of the equivalent class of infectious mosquitoes carrying the fungus is

$$I_2(t,u)=I_1(t-u)F{\theta }_{{\text{I}}_2}[u,u]+{\int }_{t-u}^t{E}_2(\tau ,T_{\text{E}},u-(t-\tau )){\theta }_{{\text{I}}_2}[t-\tau ,u]\text{d}\tau ,$$ (2.6)

where the probability of surviving for the last t₁ days given fungal infection occurred t₀ days ago is ${\theta }_{{\text{I}}_2}[t_1,t_0]$. The first term represents insects that entered the infectious stage without the fungus, which they subsequently contracted. Their numbers are the density of infectious, fungus-free mosquitoes u days ago multiplied by the risk of fungal infection and the probability of remaining in the current stage over the intervening u days. The second term represents exposed mosquitoes already carrying the fungus that mature into the infectious class. These insects were all infected by the fungus u days ago but are summed over all the possible dates (τ) on which they might have moved into the infectious class, weighted by the probability that after entering this class they remain there until the present day. The latter probability is simply the chance of avoiding the age-varying mortality.

In the main analysis, we assume

$${\theta }_{{\text{I}}_2}[t_1,t_0]={\theta }_{{\text{E}}_2}[t_1,t_0]=\text{exp}\left[-{\int }_{t_0-t_1}^{t_0}\mu +M_{\text{F}}(\xi )\text{d}\xi \right],$$ (2.7a)

but we also study the case where this class of mosquitoes that are doubly infected by fungus and mature Plasmodium suffer additional mortality, C_F(u), which again depends on the length of time the mosquito has incubated the fungus (u),

$${\theta }_{{\text{I}}_2}[t_1,t_0]=\text{exp}\left[-{\int }_{t_0-t_1}^{t_0}\mu +M_{\text{F}}(\xi )(1+C_{\text{F}}(\xi ))\text{d}\xi \right].$$ (2.7b)

We use this function to explore the consequences of double infections, including increased mortality in infectious mosquitoes and reduced transmissibility of the malaria pathogen. In a constant recruitment model with no density dependence in the adult stage, a mosquito that cannot transmit malaria can be treated as if dead.

(b) Equilibrium densities

Let $S_1^{*}$ be the equilibrium density of S₁(t), the class of mosquitoes carrying neither the fungus nor the pathogen. Let $S_2^{*}(u)$ be the equilibrium density of Plasmodium-free mosquitoes that have carried the fungus u days with $S_2^{**}$, the equilibrium total density of mosquitoes in this class. Define the equilibrium density of the other classes in a similar way. The equilibria for the three mosquito classes without fungal infection are straightforward to calculate,

$$\begin{array}{cc}{S}_1^{*}=\frac{ϵ}{F+abx+\mu };& E_1^{*}(p)=abx{S}_1^{*}\text{exp}(-p(F+\mu )),\\ E_1^{**}=\frac{abx{S}_1^{*}(1-\text{exp}(-T_{\text{E}}(F+\mu )))}{F+\mu };& I_1^{*}=\frac{abx{S}_1^{*}\text{exp}(-T_{\text{E}}(F+\mu ))}{F+\mu }.\end{array}$$ (2.8)

The equilibrium densities of classes with fungal infection depend on the precise form of the age-dependent mortality and cannot be calculated analytically except for simple limiting cases. However, the expressions below can be solved numerically,

$$\begin{array}{l}\begin{array}{l}{S}_2^{*}(u)=S_1^{*}F{\theta }_2[u],S_2^{**}={\int }_0^{\infty }{S}_2^{*}(u)\text{d}u;\\ E_2^{*}(p,u)=H[u,p]E_1^{*}(p-u)F{\theta }_{{\text{E}}_2}[u,u]+(1-H[u,p])S_2^{*}(u-p)a_{\text{F}}bx{\theta }_{{\text{E}}_2}[p,u],\end{array}\hfill \\ E_2^{***}={\int }_0^{\infty }{\int }_0^{T_{\text{E}}}{E}_2^{*}(p,u)\text{d}p\text{d}u;\hfill \\ I_2^{*}(u)=I_1^{*}F{\theta }_{{\text{I}}_2}[u,u]+{\int }_0^u{E}_2^{*}(T_{\text{E}},\tau ){\theta }_{{\text{I}}_2}[u-\tau ,u]\text{d}\tau ,I_2^{**}={\int }_0^{\infty }{I}_2^{*}(u)\text{d}u.\hfill \end{array}$$ (2.9)

(c) Time-varying mortality

To explore the model, we need to specify the additional mortality caused by the fungus, which depends on the length of time the mosquito has been infected (u). We use the Weibull form

$$M_{\text{F}}(u)=\beta {\mu }_{\text{F}}{({\mu }_{\text{F}}u)}^{\beta -1},$$ (2.10)

where μ_F and β are the rate and shape parameters, respectively. Note that if β=1, the dependence on time since infection is lost and overall mortality is exponentially distributed with an average mosquito lifespan of 1/(μ+μ_F). The Weibull distribution is chosen here because it is highly flexible and can be used to describe a wide range of mortality schedules (for related approaches using the Gompertz model, see Clements & Paterson (1981), Charlwood et al. (2000) and Styer et al. (2007)). Figure 1 shows survival curves generated from the Weibull function (equation (2.10)) which describe the range of empirical data on the effects of entomopathogenic fungus formulations on mosquito mortality (Scholte et al. 2003b, 2005, 2006; Blanford et al. 2005).

In exploring the effect of fungal strains with different mortality schedules, we define

$$g_{\text{F}}={\int }_0^{\infty }u\beta {\mu }_{\text{F}}{({\mu }_{\text{F}}u)}^{\beta -1}\text{exp}(-{(u{\mu }_{\text{F}})}^{\beta })\text{d}u.$$ (2.11)

This is the expected time until death due to the fungal infection, given no other mortality. High virulence is equivalent to low values of this measure. When we compare different values of the shape parameter β, we adjust the scale parameter μ_F such that g_F remains constant.

We also model the additional mortality in doubly infected mosquitoes by a Weibull distribution,

$$C_{\text{F}}(u)={\beta }_2{\mu }_{{\text{F}}_2}{({\mu }_{{\text{F}}_2}u)}^{{\beta }_2-1},$$ (2.12)

with different rate $({\mu }_{{\text{F}}_2})$ and shape (β₂) parameters.

(d) Model parameters

The aim of the models developed here is to explore generic issues concerning the application of mosquito fungal pathogens rather than to parametrize a particular fungus–mosquito interaction. Nevertheless we are keen to use biological relevant parameters, and the basic set we employed is shown in table 1. The equilibrium relation between the number of mosquitoes per human m and the recruitment rate m=ϵ/μ (Smith & McKenzie 2004) was used to set a value for ϵ corresponding to a mosquito to human ratio of two (Smith et al. 2004). These parameters are equivalent to an annual entomological inoculation rate of 34.5 (Smith & McKenzie 2004)—an intermediate value consistent with the number of regions in Africa with moderate to high malaria prevalence (Beier et al. 1999; Smith et al. 2007). However, population densities in all mosquito classes scale linearly with the recruitment rate ϵ; so our general results are not contingent on any particular choice of ϵ.

Table 1.

Parameters used in the model.

parameter	description	value	source
ϵ	recruitment to the adult mosquito population	0.2 d−1
F	rate of fungal infection	varies (d−1)
c	daily probability of fungal infection	1−exp(−F)
a	human biting rate of mosquitoes not infected with the fungal pathogen	0.3 d−1	Smith et al. (2004)
aF	human biting rate of mosquitoes infected with the fungal pathogen	varies d−1	Scholte et al. (2006)
b	Plasmodium transmission efficiency (mosquito to human)	0.5	Smith et al. (2004)
b	Plasmodium transmission efficiency (human to mosquito)	0.5	Smith et al. (2004)
x	proportion of humans with transmissible malaria	0.5	Beier et al. (1999)
μ	background mosquito mortality	0.1 d−1	Smith & McKenzie (2004)
TE	time required for Plasmodium incubation	10 d	Smith et al. (2004)
u	time since fungal infection	varies (d)
p	time since Plasmodium infection	varies (d)
μF and β	parameters determining the form of relationship between time since fungal infection and risk of mortality (see text)	vary
${\mu }_{{\text{F}}_2}$ and β2	parameter determining the strength of the effects of co-infection with malaria and the fungal pathogen (see text)	${\mu }_{{\text{F}}_2}$ varies; β2=β	Blanford et al. (2005)
F0 and γ	parameters determining the form of the relationship between fungal infection rate and time since application of the biopesticide (see text)	vary

3. Results

We explore the model by asking a series of questions relevant to mosquito control. We use as a measure of successful intervention the equilibrium or time-averaged density of infectious mosquitoes in a population.

(a) How do the virulence of the fungus and the daily probability of fungal infection affect equilibrium levels of infectious mosquitoes?

As expected both an increased risk of infection and increased fungal virulence decrease the density of infectious mosquitoes (figure 2). For observed values of the average time to death due to the fungus (g_F), which are less than 10 days (Scholte et al. 2003a, 2005; Blanford et al. 2005), the model suggests that, provided fungal infection probability is high enough, virtually all mosquitoes can be killed before they enter the infectious state. As virulence drops (and so g_F increases), the density of infectious mosquitoes rises at first roughly linearly and then asymptotes as the system approaches equilibrium in the absence of the fungus. Increasing the probability of infection per feeding cycle, for example by more intensive biopesticide application, initially improves the efficacy of control, though above a threshold additional reductions in the density of infectious mosquitoes are minimal (figure 3).

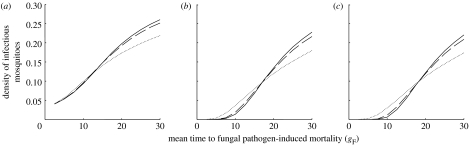
Figure 2.

The equilibrium density of infectious mosquitoes as a function of the mean time to death if the fungus is the only mortality source (g_F; high values imply low virulence) for three values of the daily probability of fungal infection (c=1−exp(−F)): (a) c=0.1, (b) c=0.5 and (c) c=1.0. Solid, dashed and dotted lines represent values of β=5.5, 3.5 and 1.5, respectively; other parameters are the same as given in table 1. In the absence of fungal-induced mortality, the density of infectious mosquitoes is 0.31 for these parameter values.

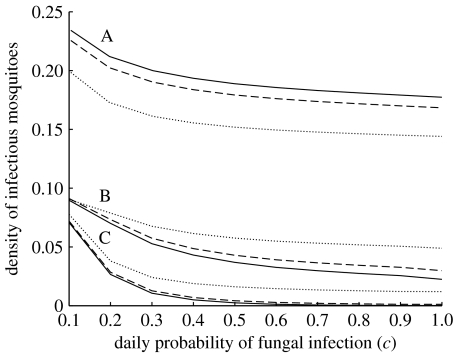
Figure 3.

The equilibrium density of infectious mosquitoes as a function of the daily probability of fungal infection (c=1−exp(−F)). We show three sets of lines, A, B and C, representing virulences of g_F=25.0, 12.5 and 7.5 days, respectively. For each set of curves, solid, dashed and dotted lines represent values of β=5.5, 3.5 and 1.5, respectively.

(b) How does the shape of the fungus mortality function affect equilibrium levels of infectious mosquitoes?

Fungal isolates differ not only in the average time they take to kill the mosquito but also in the form of the mortality function. This can be captured by changing the shape parameter (β) of the Weibull distribution describing fungal mortality while keeping the average time to death due to the fungus (g_F) constant (figure 4). High values of β represent mortality trends that accelerate rapidly following an initial delay, whereas lower values describe mortality that begins to act earlier but then increases more slowly. The effect of changing the shape parameter on the density of infectious mosquitoes is relatively small compared with that of changing virulence (figure 2). When virulence is medium to strong (measured by low values of g_F), higher values of β provide better control (figure 2). The reason for this is that more mortality is concentrated around the mean time of death following fungal infection, and while fewer mosquitoes are killed quickly, fewer mosquitoes escape mortality to become the dangerous long-lived individuals that can potentially transmit the disease. However, if virulence is low (high g_F), then not only are overall levels of control poorer, but also low values of β are better (figure 2). It is now best for mortality to begin as early as possible because many mosquitoes infected with both fungi and Plasmodium will enter the malaria-infectious stage before they succumb to the fungal pathogen. For the experimentally observed range of g_F<10 days (Scholte et al. 2003a, 2005; Blanford et al. 2005), mortality functions with high shape parameters (for constant virulence) are likely to be the most effective.

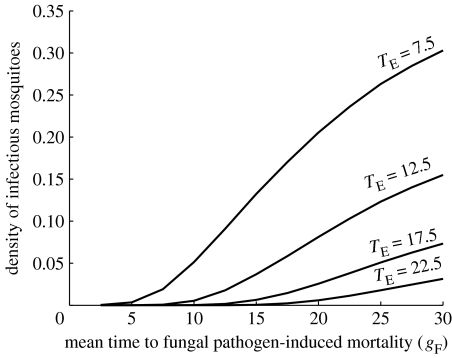
Figure 4.

The equilibrium density of infectious mosquitoes as a function of the mean time to death if the fungus is the only mortality source (g_F; high values imply low virulence) for different values of the Plasmodium incubation period T_E. The shape parameter is assumed to be β=3.5 and the daily probability of fungal infection (c=1−exp(−F)) is c=0.5.

(c) How do differences in the Plasmodium incubation period affect the performance of fungal biopesticides?

The Plasmodium incubation period, T_E, is a key determinant of the rate of malaria transmission. It varies considerably across field sites, largely depending on local temperatures. When incubation periods are long, more time is available to kill mosquitoes after fungal infection before they become infectious with malaria. To explore how the choice of fungal isolate may be influenced by T_E, we varied this parameter across the range of values recorded from malarial areas (see Patz & Olson 2006). As expected, the density of infectious mosquitoes declines with increasing T_E (figure 4). Fungal biopesticides are capable of causing considerable reductions in infectious mosquito density for all T_E levels with greater reductions occurring when fungal-induced mortality occurs quickly compared with the time it takes for the Plasmodium to mature and for the mosquito to become infectious. For this reason, virulence has considerably less impact on the density of infectious mosquitoes when T_E is at the upper limit of its range.

(d) How does the form of the fungal-induced mortality affect biopesticide performance after a single application?

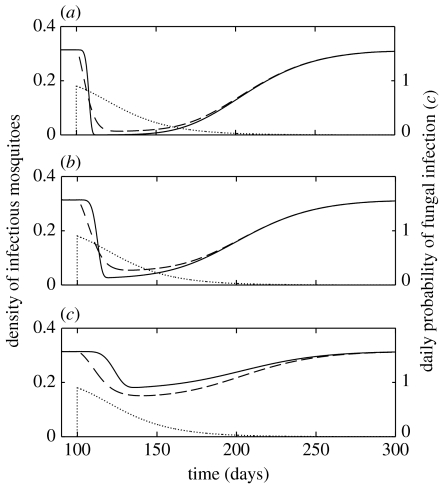
We assume that the mosquito population is at equilibrium with no fungus present and a fungal biopesticide is applied, causing the infection rate F to rise instantly to F₀. We then suppose that the fungal spores decay at a constant rate γ, so that at time τ after spraying the instantaneous infection rate is $F(\tau )=F_0{\text{e}}^{-\gamma \tau }$ (and the daily fungal infection probability, c, can be calculated in the usual manner). The impact of a spray event on the mosquito population is shown in figure 5 for fungal-induced mortality functions of different shape and virulence (equivalent to low values of g_F, the expected average survival time if fungal infection is the only cause of death). Fungal infection does not kill mosquitoes instantly, and thus there is a delay between the time of spraying and the beginning of the drop in infectious mosquito numbers. As virulence increases, the delay in the onset of mortality becomes shorter and the maximum reduction in mosquito density gets larger. For relatively high virulence values (figure 5a,b), a low value of the shape parameter leads to a more rapid drop in infectious mosquito densities. Higher values cause a delayed but then more sustained decrease and overall lead to a slightly better outcome as measured by the cumulative number of infectious mosquitoes present. When virulence is relatively small (figure 5c) a low value of the shape parameter, indicating a rapid onset of mortality, causes both the most rapid and most sustained decrease in infectious mosquito numbers. The reason for this is that with low virulence many mosquitoes die from non-disease causes and the fastest onset of mortality is then most favourable.

Figure 5.

The density of infectious mosquitoes following a single application of biopesticide spray on day 100. Three different values of the mean time to death if the fungus is the only mortality source (g_F; high values imply low virulence) are plotted: (a) g_F=7.5 days; (b) g_F=12.5 days; and (c) g_F=25 days. Solid and dashed lines represent β=5.5 and 1.5, respectively. Dotted lines show the change in the daily probability of fungal infection (c=1−exp(−F)) as a function of time (F₀=2.3 and γ=0.044).

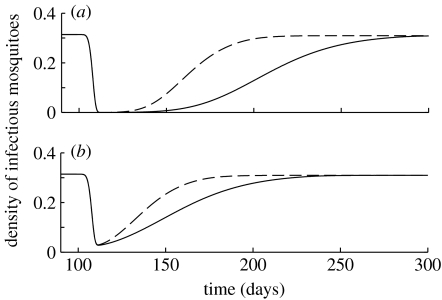
The benefits of spraying are also affected by the maximum infection rate immediately after spraying and by the half-life of spores in the environment (figure 6). A higher initial probability of fungal infection leads to the maximum reduction in density, being maintained for a longer period of time following spraying. As with increased virulence, higher initial infection rates and increased persistence in the environment all act to increase the time it takes for densities of infectious mosquitoes to recover to pre-spray levels. All these factors will tend to reduce the frequency with which the biopesticideneeds to be applied to achieve a sustained reduction in malaria transmission.

Figure 6.

The density of infectious mosquitoes following a single application of biopesticide spray on day 100. Two different values of F₀, the instantaneous transmission rate immediately after spraying, are plotted: (a) F₀=2.3 and (b) F₀=0.22. These values correspond to values of the daily probability of fungal infection (c=1−exp(−F)) of 0.9 and 0.2, respectively. Two values of the fungal spore decay rate γ are shown: γ=0.044 (solid lines) and γ=0.088 (dashed lines). The shape parameter is assumed to be β=5.5 and the virulence is g_F=7.5 days.

(e) What are the effects of reduced feeding rates by fungus-infected mosquitoes?

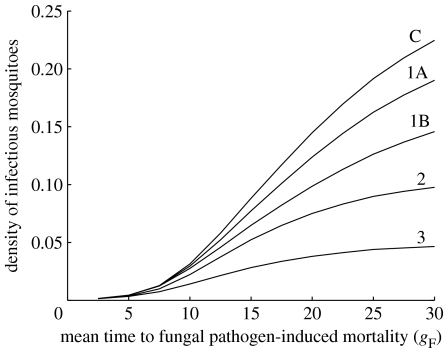
There is evidence that in addition to increasing mortality, the fungus may cause a reduction in mosquito feeding rates (Scholte et al. 2006). We explore this by setting a_F=a/3 and 2a/3, which spans the range of feeding rates reported in Scholte et al. (2006). Such a reduction decreases the density of infectious mosquitoes (figure 7), with the effect being most noticeable if the strain is not highly virulent.

Figure 7.

The density of infectious mosquitoes as a function of the mean time to death if the fungus is the only mortality source (g_F; high values imply low virulence) for different assumptions about the additional effects of the fungus on mosquito biology. The line labelled C describes a situation where the fungus infection has no effect on mosquito feeding rate and where there are no additional effects of co-infection with Plasmodium and the fungal pathogen (a_F=a, ${\mu }_{{\text{F}}_2}=0$; we assume β=3.5 and c=0.3). The lines labelled 1A and 1B show increasing reductions in the human biting rate of fungus-infected mosquitoes to a_F=2a/3; a_F=a/3, respectively. Line 2 approximates an observed increase in the mortality of co-infected mosquitoes (${\mu }_{{\text{F}}_2}=0.09$, β₂=3.5, a_F=a) and line 3 approximates an observed reduction in transmission (${\mu }_{{\text{F}}_2}=0.17$, β₂=3.5, a_F=a).

(f) How do interactions between the fungal pathogen and Plasmodium affect disease-control strategies?

We have focused on the impact of the fungus on adult mortality, as this is known to have a very strong influence on malaria transmission rates. But there is evidence that mosquitoes that carry the fungus are poorer vectors, in part because the presence of the Plasmodium increase the mortality caused by the fungus, but also because Plasmodium transmission may be reduced or blocked by the presence of the fungus (Blanford et al. 2005; Thomas & Read 2007). Further work is needed to characterize precisely these responses, but here we describe an initial investigation of their dynamic consequences. We do this by assuming a multiplicative additional mortality factor (1+C_F(u)) operating on infectious mosquitoes, which depends on the length of time the mosquito has carried the fungus (u). As described in §2, the C_F(u) term can be used to approximate both increased mortality as well as transmission blocking caused by the fungus.

The data on increased mortality due to the fungus reported in Blanford et al. (2005) are too preliminary to estimate both the shape and rate parameters of C_F(u); so we assume that the shape parameter is the same as the basic mortality function, M_F(u), in which case the increased mortality is approximately ${\mu }_{{\text{F}}_2}\approx 0.09$. As shown in figure 7, this additional mortality leads to a very marked reduction in infectious mosquito numbers. Again the data are still preliminary, but the reduction in malaria transmission reported by Blanford et al. (2005) can be approximated by ${\mu }_{{\text{F}}_2}\approx 0.17$. This leads to an even greater reduction in infectious mosquito densities (figure 7), even at low virulences (high g_F). Clearly, these effects may have a major effect on mosquito control and how different fungus strains interact with the Plasmodium should be a high priority for future study.

4. Discussion

It has long been understood that to control malaria, it is necessary to kill only relatively old mosquitoes, and thus any natural or artificial process that accelerates senescence will have strong beneficial effects on disease transmission, while imposing relatively low selection pressures to evolve resistance (MacDonald 1957; Clements & Paterson 1981; Styer et al. 2007; Thomas & Read 2007; Cook et al. 2008). The case analysed here is subtly different in that the cause of mortality increasing with age is a second infection and quantitative models are valuable in disentangling the interactions between the mosquito pathogen and Plasmodium. We have reformulated models of the adult mosquito–Plasmodium interaction to incorporate classes of mosquitoes that have contracted a fungal entomopathogen and thus have an additional mortality risk that increases with age since infection. As a wide variety of age-dependent mortality patterns are possible depending on fungal strain and environmental conditions, we address the question of which type of strain causes the greatest reduction in the density of infectious mosquitoes in different environments for a range of implementation scenarios.

Increased fungal virulence, as measured by the reduction in adult mosquito lifespan, is always beneficial in that it invariably reduces the number of biting mosquitoes and in particular the number of insects that potentially can transmit malaria. For the mosquito and fungus parameters most likely to be used in an implementation programme, the model predicts that substantial reductions in malaria transmission are possible. The benefits of increasing virulence are the greatest when average time to death due to the fungal infection is short. When this is not so, many mosquitoes die from other causes and the marginal benefits of increasing virulence are reduced. Achieving high coverage or equivalently using highly transmissible strains (large F) is also an unqualified benefit.

Fungal strains differ not only in the average time they take to kill the mosquito but also in the temporal pattern of disease-induced mortality. We modelled this by varying the shape parameter of the Weibull distribution, keeping the average time to death (a measure of virulence) constant. High values of the shape parameter indicate that mortality is concentrated around the mean time to death, while with low values the variance in mortality is higher with relatively more early and late deaths. The model predicts that high values of the shape parameter are preferable (keeping virulence constant) for the mosquito and fungus parameters reported in the literature (Scholte et al. 2003a, 2005; Smith et al. 2004; Blanford et al. 2005). Because relatively old mosquitoes transmit malaria, the costs of delaying the onset of mortality are more than compensated for by the fewer number of individuals living into old age. Only in circumstances when the virulence is low, and the average time to death is so long that many fungal-infected mosquitoes are able to transmit malaria, are low values of the shape parameter favoured.

The model also reveals how the relative importance of virulence varies with the incubation period of the parasite (figure 4). As the incubation period increases, it becomes less critical to use a fungal strain with high virulence. For the longest incubation periods recorded in the field, 20 days, even strains with very small effects on average survival time can have a significant impact. Long maturation periods are typically caused by low temperatures, and one might expect this also to disadvantage the pathogen and reduce its time to kill. However, the effect of low temperatures appears less marked on a number of the candidate fungal isolates under investigation compared with the malaria parasite (M. B. Thomas 2007, unpublished data). This points to possible opportunities to use fungal biopesticides at edges of range, for example, where malaria is emerging or re-emerging due to the effects of climate change on extrinsic incubation period (Pascual et al. 2006; Patz & Olson 2006).

With regard to application strategies, the model highlights the advantages of using more virulent strains and those with longer persistence in the environment. Both factors provide the best reduction in infectious mosquitoes after a single spray, and reduce the frequency with which reapplication is necessary. It is encouraging that our models show that even using strains with a low daily probability of fungal infection (approx. 0.1) can lead to significant reductions in the density of infectious mosquitoes and it is relevant that there is normally little benefit in increasing daily infection probability above approximately 0.5–0.6 for a given mortality distribution (figure 3). To explore further the tactical issues of spraying strategy, a more complex model is required that allows the processes determining the daily risk of infection to be disentangled. For example, we would like to know the relative advantages of increasing the number of houses sprayed versus increasing the dose within a house, so that more of the mosquitoes that enter are killed. Furthermore, recent theoretical studies have shown that the success of ITNs or IRS is influenced by the extent of mosquito dispersal relative to the scale of intervention (Killeen et al. 2003) and the temporal or spatial heterogeneities in biting and transmission (Smith et al. 2007). Exploration of how these processes affect the deployment of biopesticides is needed.

We modelled the persistence of the fungus in the environment by assuming spores decayed at a constant rate. This simple assumption describes both spore death and also a reduction in transmission rate (lower F) over time. What we are currently unaware of is whether exposure of spores to the environment reduces their virulence (in the sense used here, the average length of time it takes to kill the host) after successful infection. For this to occur, more frequent spraying is likely to be necessary. A further simplification we have made is to assume that transmission rate and virulence are independent. Typically, successful infections are likely to be caused by contact with multiple spores and it is possible that the course of infection and ultimate outcome might be influenced by initial dose. Evidence from some insect–fungus systems indicates that virulence–dose relationships can be very shallow, with an order of magnitude change in dose leading to only small changes in average survival (e.g. Arthurs & Thomas 2001). However, these experiments were conducted under optimal conditions for fungal growth and dose may be more significant in less favourable circumstances. Recent biotechnological innovations have indicated the possibility of modifying fungi to increase pathogenicity to the point where fewer than five spores can represent a lethal dose (Wang & St Leger 2007). Models based on those developed here can help show when such strategies may be worthwhile.

We have focused primarily on the impact of the fungus on adult mortality, as this is known to have a very strong influence on malaria transmission rates (MacDonald 1957; Clements & Paterson 1981; McKenzie & Samba 2004; Styer et al. 2007). However, our investigation of other effects of biopesticides on mosquito life history has demonstrated that these can have an important impact on malaria transmission. A strong effect, such as reducing the ability of infectious mosquitoes to transmit malaria, has the potential to compensate for low virulence. Further exploration of the effects of fungal infection on mosquito life history and malaria transmission is needed. For example, the reduction in blood feeding rate and blood meal size caused by fungal infection could increase the length of the gonotrophic cycle and reduce the transmission efficiency (Koella & Agnew 1997; Blanford et al. 2005; Scholte et al. 2005). If used in conjunction with bed nets, feeding cycle length might be further increased due to mosquitoes spending longer time searching for unprotected hosts (Le Menach et al. 2007). The effective coverage of the fungal pathogen could also be improved as mosquitoes would be more likely to rest on an infected surface following deflection by the net. Impaired flight ability due to infection with the pathogen may compound these effects and further add to the pathogen-induced mortality (Scholte et al. 2005). An extension of the model framework to explicitly model the gonotrophic cycle would be needed to study the effects on the feeding cycle of fungal infection and its interaction with other control strategies such as bed nets.

The models developed here, in common with most mosquito–malaria models, assume that recruitment to the adult stage is independent of adult population size, clearly an approximation. Although models that explicitly incorporate juvenile mosquito stages have been studied (Hancock & Godfray 2007), their further development is hampered by a lack of understanding of how density dependence operates in the larval stage (Lyimo et al. 1992; Gimnig et al. 2002; Ahumada et al. 2004) and how to incorporate the effect of climate and spatial processes on juvenile life-history variables (Rosenberg et al. 1990; Gimnig et al. 2002; Gu et al. 2003; Depinay et al. 2004; Smith & McKenzie 2004). Entomopathogens can lower adult fecundity (Scholte et al. 2005) and may thus affect adult mosquito densities via recruitment as well as mortality. Developing models to include both the effects is challenging but important to assess the value of biopesticides and how they compare with alternative control strategies.

To conclude, the relatively simple models developed here, using our best current estimates of disease and vector dynamics, suggest that fungal biopesticides may significantly reduce infectious mosquito densities under realistic environmental scenarios. Modelling is no substitute for field trials, but our results are encouraging and argue for further investment in exploring this novel control strategy. The models also reveal how fungal pathogen application may be tailored to different vector–pathogen biologies and different environmental conditions by picking the appropriate combination of fungal strain and application strategy. By showing how the entomopathogen influences infectious mosquito density, comparison with other control strategies is facilitated, and the models can be extended to explore combinations of different control measures. Finally, our models can be used as a basis for developing more specific tactical tools to explore the optimum deployment of this technology within local epidemiological and socio-economic contexts.

Supplementary Material

Flow diagram showing model structure

Figure A. The model divides the mosquito population into six classes determined by their status of infection by the malaria parasite (susceptible, infected but not yet infectious, infectious) and by the fungus (uninfected, infected). Mosquitoes contract the Plasmodium at a rate abx (see table 1 for parameter definitions) if they are not infected with the fungus and a_Fbx if they are. When a mosquito has been infected by Plasmodium for TE days it becomes capable of transmitting the parasite and enters the infectious class. Mosquitoes are infected with the fungus at a rate F. All mosquito classes experience background mortality at a rate μ while if they are infected with the fungus they experience an additional mortality that depends on the time since they acquired the fungal infection, u. Mosquitoes are recruited to the susceptible adult class at a constant rate