Abstract
Individual and trophic efficiencies of size-structured communities are derived from mechanistically based principles at the individual level. The derivations are relevant for communities with a size-based trophic structure, i.e. where trophic level is strongly correlated with individual size as in many aquatic systems. The derivations are used to link Lindeman's trophic theory and trophic theory based on average individuals with explicit individual-level size spectrum theory. The trophic efficiency based on the transfer of mass between trophic levels through predator–prey interactions is demonstrated to be valid only when somatic growth can be ignored. Taking somatic growth into account yields an average individual growth efficiency that is smaller than the trophic efficiency.
Keywords: ecological efficiency, trophic efficiency, structured populations, trophic level, size spectrum
1. Introduction
Since Lindeman (1942), a trophic description of ecosystems has been a commonly employed abstraction. In this description, individual organisms are viewed as belonging to trophic levels, with each level acting as a transformer of energy as it ascends the trophic hierarchy. A central concept is the efficiency of the transfer of energy between trophic levels. This trophic efficiency has been related to the average growth efficiency of an individual and standard metabolism (Kerr 1974). A problem is that these efficiencies are hard to measure directly as they are abstract quantities and, as will be shown, depend on how they are defined. Furthermore, there exists a zoo of definitions of various efficiencies and there is no rigorous adherence to a specific nomenclature in the literature (Kozlovsky 1968). Here, it will be demonstrated how efficiencies at the level of a specific individual, an ‘average’ individual and a trophic level, can be derived from basic principles at the level of an individual organism only. Apart from providing rigorous definitions of these efficiencies, it will be demonstrated how the efficiencies provide a link between trophic and size-based community theories.
Community theories describe the broad patterns of communities observed over periods sufficiently long that fluctuations due to, for example, seasons or intra-generational cycles are averaged out. The theories can be used to infer the amount of production at higher trophic levels that primary production can support in a specific system (Sheldon et al. 1977) or on a global scale (Pauly & Christensen 1995; Jennings et al. 2008). The various community theories are constructed around assumptions based on either trophic arguments combined with size scalings (Kerr 1974; Sheldon et al. 1977) or arguments combining somatic growth and predation (Silvert & Platt 1980; Camacho & Solé 2001; Benoît & Rochet 2004). Even though the basic assumptions differ somewhat, one aim of this work is to show how these different theories are related by focusing on the shared significance of trophic or growth efficiency.
The trophic description by Lindeman can be formalized into a community theory linking the ratio of total productivity in adjacent trophic levels with the ratio of total biomasses (Bi+1/Bi) through the application of the trophic efficiency (Dickie 1976). Communities with a strong correlation between individual size and trophic level are called size-structured communities. This is the case for aquatic communities (Jennings et al. 2001), where most primary productivity is confined to the smallest organisms and trophic interactions are mainly driven by predation by larger organisms on smaller organisms. In such systems, trophic theory can be connected to the body mass mi of individuals in a trophic level i by how vital rates scales with body mass (e.g. Fenchel 1974). Using the scaling of population growth rate∝mn−1 with n≈3/4 and assuming that the scaling of population growth rates with mass reflects the scaling of per capita rates lead to , where ϵT is the trophic efficiency and β is the preferred predator–prey mass ratio (Kerr 1974; Sheldon et al. 1977).
Size-structured communities are also described by size-based community theory, which can be seen as a modern variant of the trophic theories, both static (Silvert & Platt 1980; Camacho & Solé 2001) and dynamical (Benoît & Rochet 2004; Maury et al. 2007; Law et al. in press). These theories formulate the growth and predation mortality of individuals based on the encounter with food consisting of smaller individuals. Somatic growth is calculated as consumed food multiplied by the growth efficiency of an average individual. Size-based community theory predicts that the density function Nc(m) of individuals of size m is a power law Nc(m)∝m−λ, where λ is the exponent, often referred to as the slope of the community size spectrum. This exponent depends mainly on the predator–prey mass ratio and a growth efficiency of individuals (Silvert & Platt 1980; Camacho & Solé 2001; Benoît & Rochet 2004).
Central to both trophic and size-based approaches is the reliance on a parameter describing the efficiency, either of trophic transfer of energy or of individual somatic growth, and the productivity of a system, e.g. fishing, can depend significantly on the value used (Baumann 1995). The trophic efficiency used in trophic theory has been linked to the somatic growth efficiency of an individual (Sheldon et al. 1977) or to a combination of assimilation efficiency and standard metabolism (Kerr 1974). This implies that the trophic efficiency should be the same as the average growth efficiency used in size-based theories. It will be demonstrated that these two efficiencies are not the same. Furthermore, the trophic efficiency cannot be linked to average growth efficiency but is determined by the structure of the ecosystem, specifically the predator–prey mass ratio. The growth efficiency used in size-based theory can be linked to individual assimilation efficiency, but only through a proper averaging of the distribution of different growth rates of individuals of a given size.
The efficiencies are calculated by a formal mathematical analysis using an individual-based framework, which predicts the structure of equilibrium size-based communities (Andersen & Beyer 2006). As this framework does not rely on a trophic or an average individual efficiency, it can be used to derive these efficiencies directly from principles at the level of the individual organism, namely the scaling of consumption and search rate with size, individual prey choice and individual assimilation efficiency.
2. Material and methods
The concept of efficiency comes from the analogy between the ecosystem and a thermodynamic engine. The engine uses energy to run and in turn delivers work as output. The efficiency is the ratio between output and input and is therefore always less than one due to the second law of thermodynamics.
Here, three different efficiencies are calculated: trophic efficiency ϵT; the efficiency of individual somatic growth, referred to as individual efficiency ϵI; and the somatic growth efficiency of an average individual, referred to as average growth efficiency The trophic efficiency is the efficiency at which mass (or energy) is transferred from one trophic level to the next through predation. The individual efficiency is the efficiency with which a typical individual turns its consumption into somatic growth. This efficiency is large for a juvenile, which invests most available energy into somatic growth, and decreases when the individual reaches its asymptotic (maximum) size and invests into reproduction. The average growth efficiency is the ϵI of individuals of a given size averaged over life histories with different asymptotic sizes.
The efficiencies are calculated through the use of equilibrium size spectrum theory (Andersen & Beyer 2006). In this framework, individuals are represented by their mass m and populations by their asymptotic mass M. The assumptions in size spectrum theory are the following: (i) the consumption of an individual of mass m is CI=hmn, where h is a constant and n is an exponent with a typical value of 0.75 and (ii) individuals eat smaller individuals with a preferred predator–prey mass ratio β and a volumetric search rate proportional to mq. These assumptions are used to derive the community size spectrum, which is the number of individuals in the size range [m,m+dm], as Nc(m)=m−λ (note that a constant prefactor is being ignored here and in the following, as it does not matter for the results). If the ecosystem is in equilibrium, that is, if every individual encounters sufficient food to meet its required consumption, no more and no less, the exponent of the community spectrum is λ=2+q−n (Andersen & Beyer 2006).
3. Results
(a) Lindeman's trophic efficiency
The original definition of trophic efficiency is due to Lindeman (1942) who defined it as the ratio between the total consumption (or production) of all individuals in two consecutive trophic levels: . Here, a trophic level is assumed to contain individuals of sizes mi to βmi, where β is the preferred predator–prey mass ratio. Either an arithmetic or a geometric mean can be used as a characteristic size of individuals in the trophic level, but as both estimates are proportional to mi, and as the constant of proportionality does not matter for the following, it will be ignored. The total consumption of a trophic level is , where Ni is the total number of individuals in the trophic level. Using mi+1=βmi and Bi=miNi in the definition of the trophic efficiency, the ratio between the total biomass in two trophic levels is (Kerr 1974; Sheldon et al. 1977). This result can be connected to size spectrum theory by using the community spectrum to calculate the total biomass in a trophic level . Using that expression in Bi+1/Bi leads to the trophic efficiency being expressed in terms of the exponent of the community size spectrum (Borgmann 1987):
| (3.1) |
where the result from equilibrium size spectrum theory λ=2+q−n has been used for the last equality. Using the values in table 1 leads to .
Table 1.
Parameters. The ranges are discussed in appendix B
| parameter | description | value (range) |
|---|---|---|
| n | exponent of consumption; Jobling (1994) | 0.75 (2/3–1) |
| β | predator–prey mass ratioa | 100 (10–1000) |
| q | exponent of search volume; Andersen & Beyer (2006) | 0.8 (0.62–1) |
A predator–prey mass ratio of 100 has been determined to be appropriate for fishes from analysis of stomach data (Ursin 1973) or stable isotopes (Jennings et al. 2002). The range should cover most reasonable estimates.
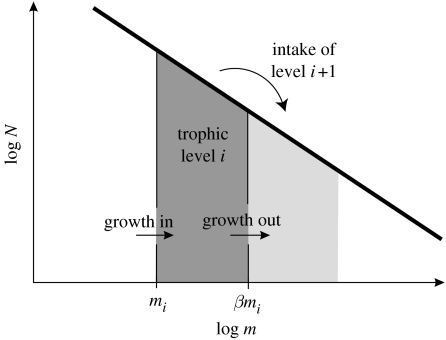
The trophic arguments developed above operate under the implicit assumption that the exchange of mass or energy between trophic levels is restricted to predator–prey interactions. In practice, most organisms exhibit somatic growth from offspring to adult, leading them to move between one or more trophic levels during their ontogeny. Apart from losses due to predation, losses of individuals growing out of a trophic level should therefore be taken into account, as well as the gains from those growing into the trophic level (figure 1). The loss from a trophic level through predation is the consumption by individuals on the next trophic level and can be derived using the community size spectrum by integrating over the consumption of individuals in trophic level i+1 over the mass range βmi to β2mi
| (3.2) |
The flux of mass into the trophic level is the average growth rate of individuals multiplied by their mass and the number of individuals. The average growth rate is the average individual growth efficiency ϵI multiplied by the individual consumption , so the flux becomes . The flux out can be derived analogously as . Equating the incoming flux with the outgoing flux plus losses Fi=Ci+1+Fi+1 and isolating the average individual efficiency leads to
| (3.3) |
The average individual efficiency is therefore smaller than the trophic efficiency by a factor , so . The average growth efficiency does not depend on the assimilation efficiency of an individual. This appears counter-intuitive as it means that the average growth efficiency of communities with individuals with low assimilation efficiency is the same as in communities where the assimilation efficiency is high. In the following, the average growth efficiency will be derived explicitly to illustrate why it is independent of the assimilation efficiency.
Figure 1.
Illustration of the mass balance used for the calculation of the growth-corrected trophic efficiency. m is the size (weight) of individuals and mi is the size of the smallest individuals in trophic level i. N is the abundance density of individuals at size m.
(b) Average growth efficiency
Individual growth is assumed to follow a von Bertalanffy type growth equation:
| (3.4) |
where M is the asymptotic size and α is the assimilation efficiency which is assumed to cover losses due to standard metabolism, egestion and metabolic losses due to digestion (specific dynamic action). The first term on the right-hand side (αhmn) is therefore the available energy after assimilation and standard metabolism. The last term (the catabolic term) covers activity and reproduction. The growth efficiency ϵI of an individual is the efficiency with which consumption hmn is turned into somatic growth. It is therefore
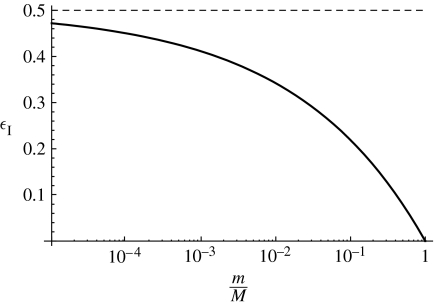
| (3.5) |
which is a decreasing function of size with a maximal value equal to the assimilation efficiency for small individuals, and a minimum value of zero as the size approaches the asymptotic size (figure 2).
Figure 2.
The efficiency ϵI of an individual as a function of size m divided by asymptotic size M. The dashed line is the assimilation efficiency, α=0.5.
Owing to indeterminate growth, most individuals of a given size m will be below their asymptotic size and their individual growth efficiency will vary within the range (0,α). The probability distribution of individual growth efficiency can be calculated if the distribution of asymptotic sizes is known (see appendix A)
| (3.6) |
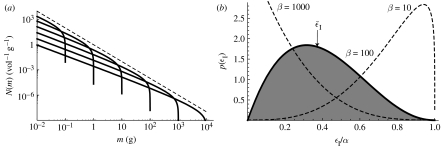
where is the physiological rate of predation (Andersen & Beyer 2006) and is a normalization constant. As the distribution of efficiencies depends on the predator–prey mass ratio through a, the average over the distribution depends on β (figure 3).
Figure 3.
(a) The abundance density N versus individual size m of a number of populations with varying asymptotic sizes given by equation (A 2) (solid lines) and the community spectrum (dashed line, elevated for clarity). (b) The distribution of individual growth efficiencies p(ϵI) for different values of the predator–prey mass ratio β. The x-axis is normalized with the assimilation efficiency α and the average growth efficiency is shown with the arrow for β=100.
So far, the numerical results of the various efficiencies have used the estimated values of the exponents n=0.75 and q=0.8 (table 1). An exploration of the reasonable upper and lower limits of the efficiencies when these exponents are varied is conducted in appendix B. Inevitably, the upper limit of the average individual growth efficiency is the assimilation efficiency. This is the case for small values of β, where the distribution of individual growth efficiency is skewed towards the assimilation efficiency (figure 3b).
4. Discussion
Individual and trophic efficiencies of size-structured communities have been derived from mechanistically based principles at the individual level. This is the first such derivation of ecological and trophic efficiencies (apart from the work of Economo et al. (2005) that admitted getting an unrealistically high predicted efficiency).
The trophic efficiency ϵT is shown to be related to the exponent of consumption with mass n together with the slope of the size spectrum λ or the exponent of the search rate q. The relation with λ is essentially the same as described earlier (Borgmann 1987; Brown & Gillooly 2003), but the relation to the scaling of the search rate is novel. The value of the trophic efficiency is predicted to be in the range of 13–50 per cent for a predator–prey mass ratio in the range of 1000–10, respectively, independent of size or trophic level. This is in accordance with empirical estimates based on measurements of the exponent of community size spectra giving trophic efficiencies in the range 22–26 per cent (Borgmann 1987). Direct estimates have given values ranging from 4–12 per cent (Jennings et al. (2002), 10 per cent (Humphreys 1979) to 25–50 per cent (Strayer 1991).
The trophic efficiency can theoretically have any value in the range [0 : 1], independently of the assimilation efficiency. Trophic theory only considers energy exchange between trophic levels due to predator–prey interactions, not due to somatic growth. Attempts to relate ϵT to individual growth are therefore only valid for communities where somatic growth can be ignored, e.g. communities with unicellular organisms reproducing by cell division. This does not invalidate trophic theory as such, but shows that in general ϵT is an abstract parameter not directly related to the growth efficiency of individuals.
Taking the trophic transfer of mass (or energy) due to somatic growth into account leads to the average growth efficiency . This efficiency is calculated by averaging over individuals of the same size but with different asymptotic sizes. Even though the efficiency of individual growth depends on the assimilation efficiency, the average growth efficiency does not. The assimilation efficiency only enters into the picture to form the theoretical upper limit for the average growth efficiency.
The calculations of both trophic and average individual efficiencies are performed under the assumption that the system is in equilibrium. This means that there are no sources of mortality other than predation mortality, i.e. all production is consumed. In reality, there is a small additional background mortality meaning that not all of the production of a trophic level is consumed. This can be taken into account by multiplying the trophic efficiency with a consumption efficiency stating how large a fraction of the production is actually consumed (e.g. Sheldon et al. 1977). The present estimates of trophic efficiency are therefore slightly overestimated. Most present-day marine ecosystems are heavily exploited, leading to a high rate of additional mortality from fishing and to an increase in the exponent of the community size spectrum (Rice & Gislason 1996). In these cases, predation mortality may not be the dominant source of mortality and the total trophic efficiency is therefore affected. The dependence of the trophic efficiency on the exponent of the size spectrum (3.1) shows that an increase in the slope of the spectrum leads to a decrease in the trophic efficiency. A measured trophic efficiency therefore represents a mix of the ‘ecological’ part of the trophic dynamics and that of the fishery, which is worth keeping in mind when estimated trophic efficiencies are compared between communities with different degrees of exploitation. This is a potentially important insight. If fishing, or any other process, distorts the community size spectrum, then not only are species abundances and species interactions altered (with a number of potential consequences for community dynamics and recovery), but also the trophic and average growth efficiency. The fact that these efficiencies are not constant, when the community is disturbed, is relevant for descriptions of how communities respond to nutrient enrichment, shifts in temperature regimes and the accumulation and sequestering of pollutants. The trophic efficiency estimated in this work is a purely ecological efficiency, and it is therefore in the upper range of the efficiencies that can be expected from exploited communities.
The use of a formalized framework proposed here not only makes it possible to derive individual and trophic efficiencies, but also to use these to connect traditional trophic theory with modern developments in size-based theories, i.e. making the link between trophic efficiency, predator–prey mass ratio and the exponents of consumption and search rate. The derivations demonstrate that it does not make sense to talk about ‘the’ efficiency of communities—one needs to be specific about exactly which efficiency is sought as the value depends on the definition. It also clearly shows the need to be specific about the level at which one is working, whether it is on the level of a typical individual, the average of individuals of a given size or a trophic level.
Acknowledgments
K.H.A. is supported by the Danish Research Council, grant no. 272-07-0485. P.L. is supported by grants from the Swedish Research Council.
Appendix A. Explicit derivation of the average growth efficiency
To find the average growth efficiency of individuals, the probability distribution of individual growth efficiencies p(ϵI) first needs to be established. To that end, the number of individuals with individual growth efficiencies in the range must be found. As the growth efficiency of an individual depends on the ratio of its size to its asymptotic size (figure 2), the distribution of efficiencies depends on the distribution of asymptotic sizes. The number of individuals in the range of asymptotic sizes [M,M+dM] is N(m,M)dM, and the number in the range can be found using the chain rule as
| (A1) |
where is a normalization constant ensuring that . From (3.5), it is found that and . The distribution N(m,M) of individuals with a given individual size m and asymptotic size M is given by equilibrium size spectrum theory as (Andersen & Beyer (2006); eqn (11))
| (A2) |
where is the physiological rate of predation. Substituting (A 2) into (A 1) gives
| (A3) |
where . The average efficiency can now be calculated as a straight forward but laborious integration
| (A4) |
An alternative derivation is to use the average somatic growth rate as calculated from equilibrium size spectrum theory (Andersen & Beyer 2006; eqn (16)) . Dividing by the consumption hmn and substituting gives the same result as (A 4) directly but without yielding the functional form of the distribution of efficiencies (figure 3b).
Appendix B. Parameter values and limits
Here, approximate values of the trophic and average growth efficiencies are estimated in a community in equilibrium, taking reasonable variations in the values of the parameters into account. Both efficiencies are functions of the predator–prey mass ratio β with an exponent 2n−q−1, i.e. depending on the exponents of consumption n and search rate q. Using n=0.75 and q=0.8 (table 1) leads to 2n−q−1=−0.3. Since this is negative, the efficiencies are decreasing functions of the predator–prey mass ratio.
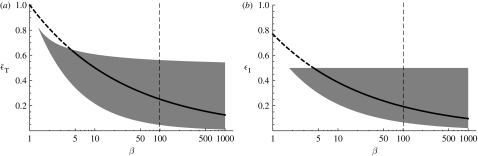
Consumption is classically thought of as being limited by the transfer of mass into a volume through the surface of the digestive tract, leading to an exponent n=2/3. In reality, the surface is fractal, leading to a somewhat higher exponent, so a reasonable lower limit is 2/3. The exponent of the search volume is made up of a search area multiplied by a search velocity. The search radius roughly scales with the length, so the search area scales with mass with an exponent 2/3. It is usually found that the foraging speed measured in body lengths per time is larger for small fish than for large ones, meaning that the exponent of the velocity is less than 1/3 (Peters 1983). The upper limit of q is therefore set to 1. Using these two limits leads to a lower value of both efficiencies as a function of predator–prey mass ratio, namely and .
The upper limit can be estimated in the same manner as above by finding an upper limit to the value of n and a lower one for q. However, in practice, another criterion turns to limit the efficiencies even further, namely that the exponent of a single-species spectrum , should be larger than the exponent of the community spectrum 2+q−n (Andersen & Beyer 2006). This leads to , which states that the average growth efficiency is smaller than the assimilation efficiency. The inequality can be used to give a lower limit of the exponent 2n−q−1 if solved numerically for this quantity (figure 4). Likewise, it can lead to a criterion for the lower limit of the value of q, which for β=100 and n=3/4 becomes q>0.62. The chosen value in table 1 of q=0.8 is therefore close to the average of the lower and the upper limits.
Figure 4.
(a) The trophic efficiency and (b) the average growth efficiency ϵI as functions of the predator–prey mass ratio β drawn using the values of the parameters from table 1 (thick lines). The grey areas are the valid ranges defined by the upper and lower limits of the exponents n and q. The upper limits are calculated using an assimilation efficiency of 0.5.The dashed vertical lines are drawn at the value of the predator–prey mass ratio β=100.
References
- Andersen K.H, Beyer J.E. Asymptotic size determines species abundance in the marine size spectrum. Am. Nat. 2006;168:54–61. doi: 10.1086/504849. doi:10.1086/504849 [DOI] [PubMed] [Google Scholar]
- Baumann M. A comment on transfer efficiencies. Fish. Oceanogr. 1995;4:264–266. doi:10.1111/j.1365-2419.1995.tb00150.x [Google Scholar]
- Benoît E, Rochet M.-J. A continous model of biomass size spectra governed by predation and the effects of fishing on them. J. Theor. Biol. 2004;226:9–21. doi: 10.1016/s0022-5193(03)00290-x. doi:10.1016/S0022-5193(03)00290-X [DOI] [PubMed] [Google Scholar]
- Borgmann U. Models on the slope of, and biomass flow up, the biomass size spectrum. Can. J. Fish. Aquat. Sci. 1987;44(Supp. 2):136–140. doi:10.1139/f87-316 [Google Scholar]
- Brown J.H, Gillooly J.F. Ecological food webs: high-quality data facilitate theoretical unification. Proc. Natl Acad. Sci. USA. 2003;100:1467–1468. doi: 10.1073/pnas.0630310100. doi:10.1073/pnas.0630310100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camacho J, Solé R.V. Scaling in ecological size spectra. Europhys. Lett. 2001;55:774–780. doi:10.1209/epl/i2001-00347-0 [Google Scholar]
- Dickie L.M. Predation, yield, and ecological efficiency in aquatic food chains. J. Fish. Res. Board. Can. 1976;33:313–316. [Google Scholar]
- Economo E.P, Kerkhoff A.J, Enquist B.J. Allometric growth, life-history invariants and population energetics. Ecol. Lett. 2005;8:353–360. doi:10.1111/j.1461-0248.2005.00737.x [Google Scholar]
- Fenchel T. Intrinsic rate of natural increase: the relationship with body size. Oecologia. 1974;14:317–326. doi: 10.1007/BF00384576. doi:10.1007/BF00384576 [DOI] [PubMed] [Google Scholar]
- Humphreys W.F. Production and respiration in animal populations. J. Anim. Ecol. 1979;48:427–453. doi:10.2307/4171 [Google Scholar]
- Jennings S, Pinnegar J.K, Polunin N.V.C, Boon T.W. Weak cross-species relationships between body size and trophic level belie powerful size-based trophic structuring in fish communities. J. Anim. Ecol. 2001;70:934–944. doi:10.1046/j.0021-8790.2001.00552.x [Google Scholar]
- Jennings S, Warr K.J, Mackinson S. Use of size-based production and stable isotope analyses to predict trophic transfer efficiencies and predator–prey body mass ratios in food webs. Mar. Ecol. Prog. Ser. 2002;240:11–20. doi:10.3354/meps240011 [Google Scholar]
- Jennings S, Mélin F, Blanchard J.L, Forster R.M, Dulvy N.K, Wilson R.W. Global-scale predictions of community and ecosystem properties from simple ecological theory. Proc. R. Soc. B. 2008;275:1375–1383. doi: 10.1098/rspb.2008.0192. doi:10.1098/rspb.2008.0192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jobling M. Fish and Fisheries Series 13. Chapman & Hall; London, UK: 1994. Fish bioenergetics. [Google Scholar]
- Kerr S.R. Theory of size distribution in ecological communities. J. Fish. Res. board. Can. 1974;31:1859–1862. [Google Scholar]
- Kozlovsky D.G. A critical evaluation of the trophic level concept. I. Ecological efficiencies. Ecology. 1968;49:48–60. doi:10.2307/1933560 [Google Scholar]
- Law, R., Plank, M. J., James, A. & Blanchard, J. In press. Food webs, size-dependent predation and oscillating size spectra. Ecology
- Lindeman R.L. The trophic aspect of ecology. Ecology. 1942;23:399–418. doi:10.2307/1930126 [Google Scholar]
- Maury O, Faugeras B, Shin Y.J, Poggiale J.C, Ari T.B, Marsac F. Modeling environmental effects on the size-structured energy flow through marine ecosystems. Part 1: the model. Prog. Oceanogr. 2007;74:479–499. doi:10.1016/j.pocean.2007.05.002 [Google Scholar]
- Pauly D, Christensen V. Primary production required to sustain global fisheries. Nature. 1995;374:255–257. doi:10.1038/374255a0 [Google Scholar]
- Peters R.H. Cambridge University Press; Cambridge, UK: 1983. The ecological implications of body size. [Google Scholar]
- Rice J, Gislason H. Patterns of change in the size spectra of numbers and diversity of the North Sea fish assemblages, as reflected in surveys and models. ICES J. Mar. Sci. 1996;53:1214–1225. doi:10.1006/jmsc.1996.0146 [Google Scholar]
- Sheldon R.W, Sutcliffe W.H, Jr., Paranjape M.A. Structure of pelagic food chain and relationship between plankton and fish production. J. Fish. Res. Board. Can. 1977;34:2344–2353. [Google Scholar]
- Silvert W, Platt T. Dynamic energy-flow model of the particle size distribution in pelagic ecosystems. In: Kerfoot W.C, editor. Evolution and ecology of zooplankton communities. Special symposium. vol. 3. University Press of New England; Hanover, NH: 1980. pp. 754–763. [Google Scholar]
- Strayer D. Notes on Lindeman's progressive efficiency. Ecology. 1991;72:348–350. doi:10.2307/1938928 [Google Scholar]
- Ursin E. On the prey size preferences of cod and dab. Meddelelser fra Danmarks Fiskeri- og Havundersøgelser. 1973;7:85–98. [Google Scholar]