Optimum Fuzzy Filters for Phase Contrast MRI Segmentation

Abstract

Purpose

To develop and validate a multi-dimensional segmentation and filtering methodology for accurate blood flow velocity field reconstruction from phase contrast magnetic resonance imaging (PC MRI).

Materials and Methods

The proposed technique consists of two steps: 1) the boundary of the vessel is automatically segmented using the active contour approach; 2) noise embedded within the segmented vector field is selectively removed using a novel fuzzy adaptive vector median filtering (FAVMF) technique. This two-step segmentation process is tested and validated on 111 synthetically generated PC MRI slices and on 10 patients with congenital heart disease.

Results

The active contour technique was effective for segmenting blood vessels having a sensitivity and specificity of 93.1 and 92.1 % using manual segmentation as a reference standard. FAVMF was the superior technique in filtering out noise vectors, when compared to other commonly used filters in PC MRI (p <0.05). The peak wall shear rate calculated from the PC MRI data (248 ± 39 s⁻¹), was significantly decreased to (146 ± 26 s⁻¹) after the filtering process.

Conclusion

The proposed two step segmentation and filtering methodology is more accurate compared to a single step segmentation process for post processing of PC MRI data.

INTRODUCTION

Phase contrast magnetic resonance imaging (PC MRI) is a widely used clinical imaging modality for visualizing and quantifying blood flow velocity fields in vivo. Besides the measurement of flow rates, it has been used to quantify wall shear stress (WSS)(1–5), pressure drops(2), and flow related phenomena like coherent structures and viscous dissipation energy losses(6). In addition, PC MRI has also been used to identify regions prone to atherosclerosis(7,8), aneurisms(9), and the patency of heart valves(10,11). However, an accurate post-processing methodology is crucial for quantifying these parameters.

One of the key post-processing steps is the segmentation of the velocity field within the blood vessel of interest. Typically, the segmentation process consists of the detection of the vessel boundary, and the velocity field inside this boundary is then used for quantifying the clinical parameters of interest. Most users employ manual outlining techniques for the purposes of segmentation, although they can be quite time consuming and tedious, especially in situations where large sets of data have to be processed. Automatic segmentation techniques that can significantly speed up the time taken to process and analyze these datasets are highly desirable. The most popular method in the literature for automatic PC MRI segmentation is active contours(12–15). Active contours, or snakes, are curves defined within an image domain that move under the influence of both external forces (based on image data) and internal forces (based on the contour itself). These forces are defined such that the snake will be attracted towards specific features within the image, and in most cases towards the edge of a vessel. Different formulations of the external force can be chosen. Options include gradient magnitude of phase images(15), velocity vector based forces (16,17), and statistical models(18), that are selected based on the desired segmentation application.

Active contours work well for detecting the morphology of the vessels. However, in situations when the vessel boundary is blurred there are no suitable edges for a contour to converge upon and hence only an approximation of the vessel boundary can be obtained. In such a scenario, vectors that are not part of the desired velocity field get incorporated into the segmentation (Figure 1). This effect is pronounced when the vessel is in close proximity to the lungs where the signal to noise ratio is significantly lower for pixels closer to the lungs s. Consequently, the presence of noise along the wall distorts the computation of quantities like wall shear stress, viscous dissipation, etc., that depend upon the spatial derivatives of the velocity field. Therefore filtering this noise is critical especially if PC MRI is to be used as a reliable technique for computing these parameters.

Figure 1.

Example of noise being embedded into the segmentation. Within this segmented vessel, noise vectors along the vessel walls are clearly evident as shown by the oval.

The most frequently cited technique for noise removal in PC MRI is the one proposed by Walker et al., which uses a standard deviation-based measure(19). This technique classifies regions of high standard deviation as noise, and regions of low standard deviations as flow. The technique is widely used because of its ease of implementation and effectiveness in removing noise. However, the primary drawback of this filter is that it is a scalar technique, and 3D PC MRI produces a vector field. When the Walker filter is applied to a vector field, there is a tendency of the filter to remove vectors that are actually part of the flow field. This is because the technique treats each component of the vector as an independent quantity, and does not factor in the local characteristics of the velocity field in the filtering process.

This paper proposes a novel PC MRI post processing strategy that tackles the issue of automatic vessel segmentation and noise filtering as two distinct steps. The morphology of the vessel is first segmented automatically using active contours and the segmented velocity field is filtered using a novel multi-dimensional fuzzy adaptive vector median filtering technique optimized for PC MRI. This two step process is validated using both in vivo and synthetically generated PC MRI datasets. The specific application targeted here is PC MRI data acquired on children born with single ventricle congenital heart defects. These children undergo a series of operations resulting in the connection of superior vena cava (SVC), inferior vena cava (IVC), left pulmonary artery (LPA), and the right pulmonary artery (RPA) in a configuration known as the total cavopulmonary connection (TCPC). The reason this application was chosen, is because blood flow fields within the TCPC are quite complex, and the ability to visualize and quantify these hemodynamics may help in identifying patients at risk for heart failure.

MATERIALS AND METHODS

Description of the Algorithm

Active Contour Segmentation

The original active contour model proposed by Kass et al.(20), minimizes the energy function

$$E=\underset{0}{\overset{1}{\int }}\frac{1}{2}[\alpha \mid C^{\prime }(s){\mid }^2+\beta \mid C^{″}(s){\mid }^2+E_{\mathit{ext}}(C(s))]ds$$ Equation 1

where C(s) is a contour described as a function of arc length, α controls the curvature of the contour, β controls the rigidity of the contour in the through-plane direction, C′(s) and C″(s) are the first and second derivatives of the contour with respect to arc length. The external energy E_ext (s) is derived from the image domain and can be regarded as a discrete potential field to guide the contour to the desired vessel. While there are many approaches in the literature to determine the choice of the external energy field, the gradient vector flow (GVF) implementation is chosen here because of its advantageous performance in segmenting a wide variety of shapes in the presence of neighboring anatomic structures(21). GVF fields are also less sensitive to noise and are more robust in segmenting complex shapes with boundary concavities (such as the TCPC).

Implementation of Active Contours

Once the external energy fields are estimated, the cine PC MRI data is first assembled as a 3D dataset (x, y, t) and the user is asked to select the vessel of interest by drawing a box around it in any one of the phases of the cardiac cycle (Figure 2a). The largest circle that fits within the box is then initialized and this circle serves as the initial contour (C(s)) for that phase. Equation 1 is then iteratively minimized, and after about 30–40 iterations the solution converges resulting in the segmentation of the vessel in the first cardiac phase (Figure 2b). This contour is then used as the initial contour in the subsequent cardiac phase, and the process is repeated until the vessel in all cardiac phases is successfully segmented (Figure 2c). The 2 constants, α, and β are set to be 0.2 and 0 respectively. β is set to 0 as the contour evolution is 2D (i.e. in the x-y image plane). The optimum value of α was determined based on an experimental study conducted on 50 datasets, where the segmentation error was evaluated for different values of α using a manually segmented dataset as a reference standard. Once the vessel is segmented, the enclosed vector field is used to evaluate a variety of clinically relevant parameters.

Figure 2.

Different steps in the automatic segmentation process. The user first selects the vessel by drawing a box around it -> The vessel is automatically segmented in that phase -> The vessel is segmented in all cardiac phases-> Parameters evaluated directly from the segmentation

Fuzzy Adaptive Vector Median Filters (FAVMF)

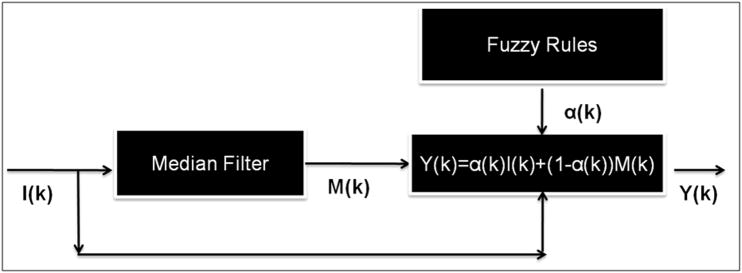
The proposed active contour algorithm works well when the vascular morphology is clearly defined. In situations when the vessel edge is blurred, it approximates the vessel shape, which results in random noise being incorporated into the segmentation. In order to filter this noise, two critical aspects to consider are: a) the detection of a noise pixel within the vector field (if any), and b) determining an appropriate value to replace this noise pixel. In order to tackle both (a) and (b), a new filter is proposed that is based on a hybrid multi-channel framework (Figure 3):

$$y(\overrightarrow{k})=\alpha (\overrightarrow{k})I(\overrightarrow{k})+(1-\alpha (\overrightarrow{k}))M(\overrightarrow{k})$$ Equation 2

where, k→ = (k1, k2) is the pixel co-ordinate vector, I(k→) is the input vector, α(k→) is a continuous fuzzy membership function that takes a value between 0 and 1 (this determines to what extent I(k→) is a flow pixel), and M(k→) is the chosen filter value for replacing the noisy component of the vector. If α(k→) equals or is close to one then I(k→) is classified as part of the flow field and is retained. If it is close to zero then I(k→) is considered random noise and is replaced by M(k→). Several choices for M(k→) are investigated including both scalar and vector based techniques. Since a segmented PC MRI dataset is a vector field with each data point having three components, a filter that is optimized for vector quantities is desirable. One such filtering technique is vector median filtering, which is the choice for M(k→) in this paper. The benefit of using vector median filtering will be demonstrated in the following sections.

Figure 3.

The hybrid multi-channel framework used in this study

Vector Median Filters (VMF)

A 3D PC MRI dataset can be thought of as a multi-channel image, where each component of the velocity field is a single channel of the image. To determine the filter output for the vector quantity I(k→), an interrogation window is selected around I(k→). Let this window be W={I_i: i = 1,2,…, w}, where w is the size of the window (w=9 for a 3×3 window, 25 for 5×5 window and so on) and I₁, I₂,…I_w is a set of vectors inside this window. Each component of the velocity vector is expressed as I_i1, I_i2, and I_i3. For each multi-channel image, I_i is associated with a distance measure:

$$D_i=\sum _{j=1}^w\mid \mid I_i-I_j\mid {\mid }_{\gamma }$$ Equation 3

where,

$$\mid \mid I_i-I_j\mid {\mid }_{\gamma }={(\sum _{k=1}^3\mid I_{ik}-I_{jk}{\mid }^{\gamma })}^{1/\gamma }$$

and γ is the chosen distance norm with a value greater than 1. This distance is computed for each vector in the window, and the values are ordered according to the criteria D₁<D₂..<D_w with D₁ being the smallest. If the same ordering is applied to the input set, then the ordered input sequence becomes I₁<I₂…<I_w. The sample I₁ associated with distance D₁ becomes the output of the vector median filter(22,23). Simply put, the output is the vector that has the smallest sum of vector distances to all of the other vectors in the interrogation window, or equivalently:

$$\sum _{i=1}^w\mid \mid I_{\mathit{VMF}}-Ii\mid {\mid }_{\gamma }\le \sum _{i=1}^w\mid \mid I_j-Ii\mid {\mid }_{\gamma }$$ Equation 4

Determination of Fuzzy Rules

The second component of the noise filtering algorithm is to determine a fuzzy membership function (α (k→)) for use in the hybrid multi-channel framework shown in Figure 3. A set of rules are employed for this purpose, which are established by studying the physical characteristics of flow and noise. The parameters used for establishing these rules as well as a description on how they are evaluated are discussed below.

Distance from vector median (DVM, U (k→))

Let I (k→) be the vector at the current location and M(k→) be the output of the median filter defined above for the interrogation window. The DVM is calculated as

$$U(\overrightarrow{k})=\mid \mid I(k)-M(k)\mid {\mid }_{\gamma }$$ Equation 5

where γ is the chosen distance norm for the VMF implementation. The larger the distance of the given pixel from the vector median within the interrogation window, the higher is the probability for the pixel to be a noise vector. The distances are normalized to be between 0 and 1.

Vector Direction Homogeneity (VDH, L (k→))

Since random noise has random direction, this property can be used to differentiate between noise and flow. Let u_i be the vector at location i, d_i(k→) the difference in orientation between u_k and u_i, where u_k is the vector that is in question, and L(k→) be the VDH metric for the interrogation window centered on k. Then the VDH metric can be evaluated as

$$L(\overrightarrow{k})=\sum _{j=1}^w{d}_i(j)$$

where

$$d_i(\overrightarrow{k})=\frac{\overrightarrow{u}(i)·\overrightarrow{u}(\overrightarrow{k})}{\mid \mid \overrightarrow{u}(i)\mid \mid ·\mid \mid \overrightarrow{u}(\overrightarrow{k})\mid \mid }$$ Equation 6

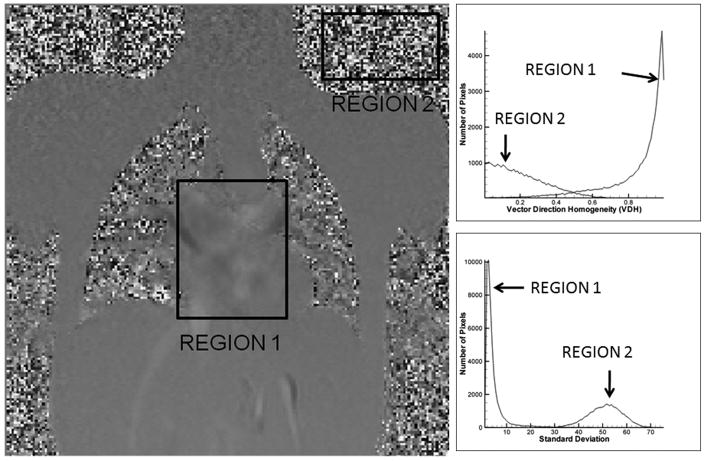
If the orientation of the directions within the interrogation window is random, then L(k→) tends to be 0, otherwise it has a high value. The histogram distribution for both random noise and flow regions within a 3 component PC MR image are shown as part of Figure 4. Notice the differences in VDH distribution for noise and flow.

Figure 4.

The properties of noise and flow in different regions of the PC MR image. The top right graph shows the histogram distribution of the vector direction homogeneity and the bottom right graph shows the histogram distribution of the standard deviation of the velocity field. Region1 is Flow and Region 2 is Noise

Vector Field Standard Deviation (SD, S (k→))

Another property that can be used to aid in noise detection is the standard deviation of the velocity field within the interrogation window. In this work, a standard deviation map S(k→) is evaluated for each component. This is accomplished as follows:

$$S(\overrightarrow{k})=\sqrt{\frac{{\displaystyle \sum _{j=1}^3}{(I(\overrightarrow{k},j)-\mu (j))}^2}{3}}$$ Equation 7

Here, μ (j) is the mean of the velocity component of each of the 3 vector components within the interrogation window W, and I (k→) is the vector that has to be filtered. The histogram distribution of the standard deviation map for both noise and flow pixels are shown in Figure 4. As can be observed, the distributions are markedly different, with noise having a higher standard deviation compared to flow.

Magnitude Image Intensity (MI, MI(k→))

Another aspect that can be used towards the filtering process is the intensity of the magnitude images. In the magnitude images, the regions of flow are white (having a value of 1), while the noise regions are typically black (0). Therefore, if a pixel has a magnitude image intensity closer to 1 it has a higher probability of being a flow pixel, while if it is closer to 0 then it is a noise pixel.

Based on the analysis and behavior of these four metrics in a PC MR Image, a set of general rules can be defined that can now characterize flow and noise. These are:

Rule #1: DVM is high for noise and low for flow

Rule #2: VDH is low for noise and high for flow

Rule #3: SD is high for noise and low for flow

Rule #4: MI is low for noise and high for flow.

A membership function α (k→) is then evaluated to determine the probability of a pixel being noise. This is accomplished using the Fuzzy C-Means Clustering technique(24).

Adaptive Fuzzy C-Means Clustering

The four parameters evaluated above can be stacked such that every pixel is characterized by a four-dimensional vector:

$$\overrightarrow{F}(\overrightarrow{k})=\left\{U(\overrightarrow{k}),L(\overrightarrow{k}),S(\overrightarrow{k}),MI(\overrightarrow{k})\right\}$$ Equation 11

Let C be the number of clusters of interest. In our case the two clusters are C1=flow and C2=noise. Therefore two membership functions will be simultaneously estimated: one for the degree of membership of a pixel to noise (α_C1(k→)), and a second for the degree of membership of a pixel to flow ((α_C2(k→)). According to fuzzy set theory:

$${\alpha }_{c1}(\overrightarrow{k})+{\alpha }_{c2}(\overrightarrow{k})=1$$ Equation 12

This effectively simplifies this process to estimating just a single function. Let C→_F(j) be the centroid vector associated with the cluster j. The corresponding membership functions α_C1(k→) and α_C2(k→), and the centroid vector C→_F(j) for each cluster can be simultaneously estimated by minimizing

$$J=\sum _{i=1}^{\mathit{MxN}}\sum _{j=1}^C{\alpha }_{ij}^2\mid \mid \overrightarrow{F}(i)-{\overrightarrow{C}}_F(j)\mid {\mid }^2$$ Equation 13

M×N is the size of the image, and C is the number of clusters. If the steepest descent algorithm is used, the corresponding update equations become

$$C_F(j)=\frac{{\displaystyle \sum _{i-1}^{\mathit{MxN}}}{\alpha }_{ij}\overrightarrow{F}(i)}{{\displaystyle \sum _{l=1}^{\mathit{MxN}}}{\alpha }_{ij}}$$ Equation 14

and

$${\alpha }_{ij}=\frac{1}{{\displaystyle \sum _{l=1}^C}{\left\{\frac{\mid \mid \overrightarrow{F}(i)-C_F(j)\mid \mid }{\mid \mid \overrightarrow{F}(i)-C_F(l)\mid \mid }\right\}}^2}$$ Equation 15

Iterations are continued until the value of a converges.

Algorithm Validation

Each step of the segmentation algorithm is quantitatively validated using synthetic PC MRI generated from computational fluid dynamic (CFD) simulations and in vivo PC MRI. The active contour segmentation methodology (step 1) is validated on in vivo datasets using a manually defined contour as the reference standard. The filtering algorithm (step 2) is validated using synthetic datasets generated from CFD simulations as well on in vivo datasets. The reference standard for the CFD simulations were the original velocity field themselves, while for the in vivo case, a manual filtering strategy was designed and implemented that served as the reference standard. The benefit of using the proposed FAVMF is demonstrated by comparing the velocity error/pixel, maximum wall velocities, maximum wall velocities/core velocities ratio, and wall shear rates with and without the filter.

Generation of Synthetic Datasets

To generate the synthetic datasets, a CFD simulation was conducted on a 3D patient specific TCPC model reconstructed from in vivo MRI(25,26). The TCPC model was first meshed using Gambit (FLUENT Inc.,) having 400,000 tetrahedral elements. The meshed geometry was then imported into the commercial CFD solver FLUENT, and the governing Navier-Stokes equations were solved to obtain a three dimensional vector field within the entire geometry of the TCPC. The CFD simulation was then sampled at 111 equally spaced planes (Figure 5a) to obtain 3 sets of phase images with velocity encoding in the anterior-posterior (AP), right-left (RL), and superior-inferior (SI) directions respectively (Figure 5b). The pixel size was 1 mm², the slice thickness was 1.2 mm, and the velocity encoding was 100 cm/s to obtain images having intensities ranging from 0–2¹⁶, which is the standard clinical dicom range. These images were noise free and served as the reference standard for comparing the performance of different noise filters (Figure 5b).

Figure 5.

The process of noise being embedded into the system. a) The CFD model is first sampled at 111 discrete locations. b) 4 images are acquired per location (Magnitude, and 3 phase images); c) Artificial noise is embedded into the phase images

In order to test the robustness of the filtering algorithm, artificial noise was embedded into the images (Figure 5c). An image (n (k→)) having random noise with values ranging between 0–2¹⁶ was generated for each image slice in the dataset. This image was then added to the original phase images according to the formula:

$$x(\overrightarrow{k})=(1-p_v)\ast o(\overrightarrow{k})+p_v\ast n(\overrightarrow{k})$$ Equation 16

where n(k→)is the noise pixel, p_v is the noise level, and o(k→)is the original value of the vector field. The value of p_v was uniformly varied from 0 to 0.5 at intervals of 0.1 and various filters were quantitatively compared using the normalized mean squared error (NMSE) metric:

$$\mathit{NMSE}=\frac{\sqrt{{\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{j=1}^N}{(o_{ap}(i,j)-{\widehat{o}}_{ap}(i,j))}^2+{(o_{fh}(i,j)-{\widehat{o}}_{fh}(i,j))}^2+{(o_{rl}(i,j)-{\widehat{o}}_{rl}(i,j))}^2}}{\sqrt{{\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{j=1}^N}{(o_{ap}(i,j))}^2+{(o_{fh}(i,j))}^2+{(o_{rl}(i,j))}^2}}$$ Equation 17

M and N are the image dimensions, o_ap, o_rl, and o_fh, are the original values without noise corruption (reference standard), and ô_ap, ô_rl, and ô_fh, are the filtered images. Noise was only embedded to within 5 pixels of the vessel for two reasons: a) to have noisy and noise-free regions within the same velocity field so that the impact of filtering on both the regions can be quantified; b) it was logical to embed noise into the system near the vessel border rather than anywhere else since most of the noise is observed along the vessel border in the presented application. However, it should be noted that the results of the algorithm are unaffected by the choice of pixels selected for noise addition. The NMSE of VMF is first compared to the filter proposed by Walker et al using the settings described in (19), and a standard Gaussian low pass filter with a kernel size of 15×15 and a standard deviation of 1.5. Then, the benefit of using VMF in a fuzzy framework is demonstrated by comparing the NMSE of VMF with FAVMF. In addition, maximum shear rates are computed for the original vector field as well as for the noisy, and the filtered datasets. The results obtained from FAVMF, low pass filter, and the Walker filter were then compared to the shear rates from the original vector field from CFD. Principal shear rates for the 3D vector field were calculated using the methodology outlined by Tambasco and Steinman (27).

In vivo PC MRI Acquisition Protocol

3D PC MR Images were acquired on 10 patients with single ventricle congenital heart disease. Each patient comprised a single dataset. A segmented k-space fast field echo sequence with 3 segments per acquisition was used to acquire images perpendicular to the four vessels of the TCPC, namely the SVC, IVC, LPA, and the RPA, as well as in the coronal orientation spanning the entire TCPC geometry, and the ascending aorta. All acquisitions were retrospectively gated with a typical R-R time interval of 750 ms, resulting in about 20 cardiac phases for each vessel. The TR and TE were set to be 50 and 3.8 ms respectively. A rectangular field of 66% was used resulting in a net field of view of 250 mm. The slice thickness was 6 mm with an average in-plane resolution of 1 × 1 mm². All images were acquired in the Children’s Hospital of Philadelphia using the Siemens 1.5T Avanto or Sonata scanners.

Manual Segmentation and Filtering Protocol

A manual segmentation protocol was designed and implemented to serve as a reference standard for evaluating the performance of the active contour methodology. To ensure the accuracy and reproducibility of this protocol, two independent users manually outlined the vessels of interest on 5 datasets. The protocol was refined until the reproducibility error of the segmentation overlap was less than 5%. Using this protocol, the vessels of interest in all the in vivo datasets were manually outlined by the trained user. The total time taken by the manual segmentation process for each dataset was about 30 minutes. The automatic active contour segmentation algorithm was quantitatively compared to the manually outlined contours by evaluating overlap, false positive (percentage of total area included in the automatic segmentation and not present in the manual segmentation), false negative (percentage of total area included in the manual segmentation and not present in the automatic segmentation), sensitivity {true positive/(true positive + false negative)}, and specificity {true negative/(true negative + false positive)} percentages respectively. True positive is the same as overlap, while true negative is the region excluded from the segmentation common to both the automatic and manual segmentations. The total time taken for the automatic segmentation process was significantly lesser than the manual process at less than 10 minutes for each dataset.

A manual filtering approach was adopted to provide a noise-free control for PC MRI filtering. The manual filtering protocol consisted of displaying the segmented velocities using a vector plot with colors varying from the lowest (blue) to the highest (red) velocities. Figure 1c shows an example of a typical vector plot. Color was used instead of grayscale because noise is more easily detected by the human visual system in color. The user was then asked to step through each phase of the cardiac cycle and click on the noise vectors. Due to the large number of noise vectors that are normally present, this process was independently conducted by two users to ensure that all noise was removed from the images. The operators of the manual filtering process were blinded to each other and to the results of the automatic filters used in the study to minimize any bias that may creep into the process. The identified noise pixels were then replaced with the vector median of the surrounding pixels. The presented approach has several benefits: a) Errant vectors that are not part of the flow structure can be easily removed as they clearly stand out in the color vector field; b) Pixel by pixel based error values can be calculated using the manually filtered dataset as the control. A student’s unpaired t test was used for comparing the performance of the proposed segmentation and filtering process.

RESULTS

Validation Based on Synthetic Datasets

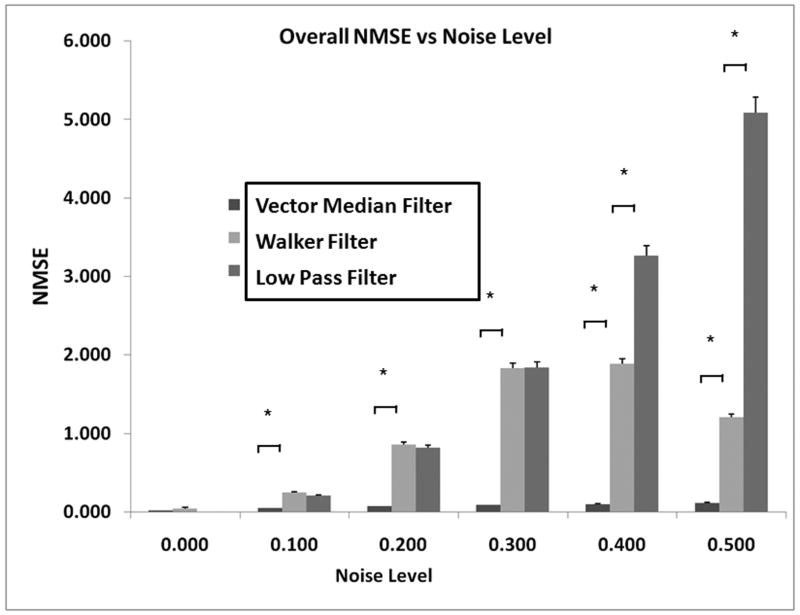
Figure 6 shows the error associated with using the VMF (without the fuzzy framework), Walker filter, and low pass filter as a function of increasing noise levels. As can be observed, NMSE with the VMF technique was significantly lower than the low pass filter and the Walker filter at all noise levels (p < 0.05). There were no significant differences between the Walker filter and low pass filter at low noise levels, but the difference at high noise levels was statistically significant (p<0.05). The increase in NMSE with increasing noise levels was quite small for the VMF, when compared to the other two techniques. This justified the use of VMF in the hybrid multi-channel FAVMF framework.

Figure 6.

Comparison of VMF with the Walker filter, and a standard low pass filter. VMF had the lowest error compared to the two other filters.

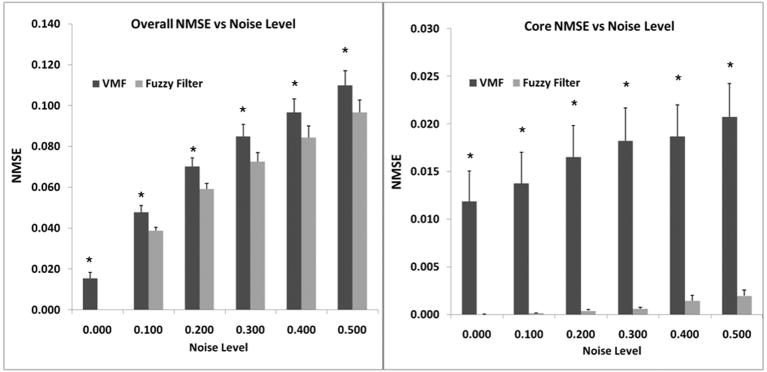
Figure 7 shows the overall benefit of using VMF in a fuzzy framework compared to VMF alone. There is a statistically significant drop in the overall NMSE at all levels of noise using the FAVMF technique (p < 0.05). The Fuzzy filter was also able to accurately differentiate between noise and flow as can be observed in Figure 7b, where the NMSE is compared between VMF and FAVMF in regions where there was no noise. FAVMF had extremely low error when compared to the VMF technique demonstrating that it had minimal impact on the true velocity field. In regions where noise was present, FAVMF performed as well as the VMF. This adaptive feature is highly desirable in applications which require quantification and visualization of complex flow patterns, especially where filtering artifacts can alter the measured velocity field. The maximum shear rates evaluated using the vector fields derived after FAVMF, Walker filtering, low pass filtering, and no filtering were 240 ± 40.3, 346 ± 11.6, 370 ± 15.9, and 453 ± 16 s⁻¹ respectively. Maximum shear rates derived from FAVMF were much closer to the true shear rate derived from CFD (176.1 ± 30.4) compared to the other filtering methodologies.

Figure 7.

a) Comparison of VMF with FAVMF; b) Comparison of VMF with FAVMF in regions where no noise is present. Using VMF in the fuzzy framework further reduced the error.

Validation based on in vivo datasets

Automatic Segmentation

Table 1a shows the numerical comparison of the manually and the automatically segmented datasets for the aorta, SVC, IVC, LPA, and RPA. Table 2 shows the net flow rates in L/Min evaluated using the manual and automatic segmentation techniques respectively. For the ascending aorta, 93 ± 4.6% of the automatically segmented region overlapped with the manually segmented region. The false positive rate was 6.9 ± 4.6 % and the false negative was 4.7 ± 3.6%. The percentage of the total flow through the overlapping, false positive and false negative regions were 98%, 2%, and 1% respectively. For both the IVC and SVC, the percentage of total flow through the overlapping, false positive and false negative regions were 98%, 2%, and 2% respectively. In the LPA and the RPA, the overlapping regions between the automatic and manual segmentation techniques were lower since the diameter of these vessels is much smaller than the IVC and the SVC. However, the net flow through the overlapping regions still remained at 98% for the LPA and the RPA. This showed that regions excluded from the automatic segmentation were generally characterized by low velocity flow. For each vessel the automatic and manual segmentation results (flow rates) were statistically identical with a type II (β) error < 0.05.

Table 1.

Comparison of manual and automated segmentation techniques

Vessel	Overlap (%)	False Positive (%)	False Negative (%)	Sensitivity (%)	Specificity (%)
AO	93 ± 4.6	6.9 ± 4.6	4.7 ± 3.6	95.4 ± 3.2	93.7 ± 3.9
IVC	93.3 ± 4.4	6.6 ± 4.4	7.7 ± 4.4	92.8 ± 3.4	94 ± 3.6
SVC	93.4 ± 4.3	6.5 ± 4.3	6.2 ± 4.4	94 ± 3.9	94 ± 3.7
LPA	87 ± 4.5	12.9 ± 4.5	7.49 ± 8.2	93 ± 7	89 ± 3.6
RPA	88 ± 8.6	11.8 ± 4.6	9.4 ± 4.6	91.1 ± 4.7	90.0 ± 6.5

Table 2.

Comparison of flows through the manually (MS) and automatically segmented (AS) regions (L/Min)

Vessel	AS Flow	MS Flow	Overlap Flow	False Positive Flow	False Negative Flow
AO	3.27 ± 1.57	3.27 ± 1.53	3.26 ± 1.55	0.00 ± 0.12	0.01 ± 0.07
IVC	1.88 ± 0.99	1.89 ± 1	1.85 ± 0.99	0.02 ± 0.02	0.04 ± 0.04
SVC	0.83 ± 0.45	0.88 ± 0.32	0.8 ± 0.44	0.02 ± 0.015	0.02 ± 0.02
LPA	1.22 ± 0.81	1.22 ± 0.78	1.19 ± 0.79	0.03 ± 0.05	0.02 ± 0.02
RPA	2.08 ± 0.76	2.12 ± 0.79	2 ± 0.76	0.07 ± 0.08	0.11 ± 0.10

Automatic Filtering

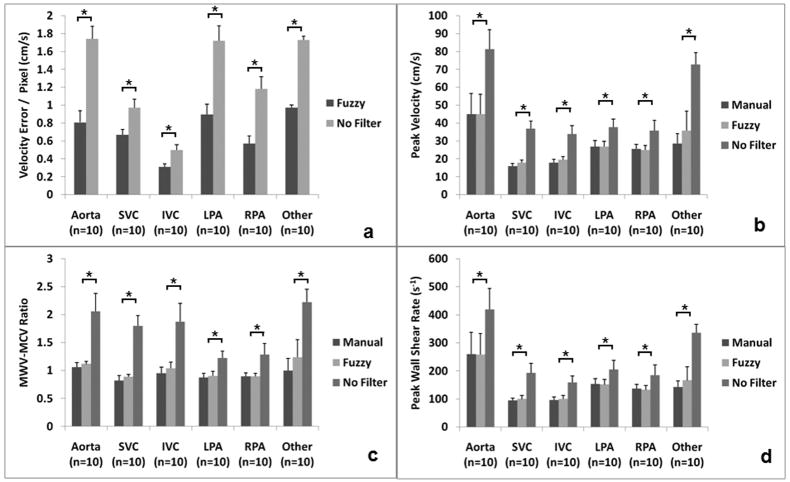
Figure 8a shows the drop in error that can be accomplished using the automated FAVMF technique when compared to the unfiltered dataset using the manually segmented dataset as reference. When no filtering was performed, the average error in the velocity measured was about 2cm/s/pixel. This error was reduced to < 1cm/s/pixel after the dataset was filtered using the FAVMF technique. Figure 8b shows the peak velocities in close proximity of the vessel wall for 3 different cases: a) Segmentation + No Filtering; b) Segmentation + Manual Filtering; c) Segmentation + FAVMF. Unrealistically high peak velocities were observed in the unfiltered dataset, which are not characteristic of the flows in the TCPC and the aorta. After filtering, the peak velocities significantly dropped to less than 50% of the original values (p<0.05). The peak velocities evaluated using the automatic filtering technique was statistically identical to the reference with a type II error <0.05. Figure 8c shows the ratio of the peak velocities along the vessel wall to those measured in the core of the vessel. This ratio should be between 0 (parabolic profile) and 1 (flat profile) for a physiological velocity field. For the unfiltered dataset, this ratio was about 2, which cannot be true, indicating that pixels giving such high values were noise pixels. This ratio dropped significantly to less than 1 once the filtering was performed (p<0.05). The performance of the automatic FAVMF technique was statistically identical to the reference with a type II error < 0.05.

Figure 8.

The benefit of filtering using the FAVMF approach. a) The reduction in error/pixel achieved after filtering with FAVMF compared to no filtering; b) Comparison of peak velocities close to the wall between manual filtering, FAVMF, and No Filtering; c) Comparison of mean peak wall velocity to mean peak core velocity (MWV-MCV) ratio between manual filtering, FAVMF, and No Filtering; d) Comparison of wall shear rates evaluated using manual filtering, FAVMF, and No Filtering.

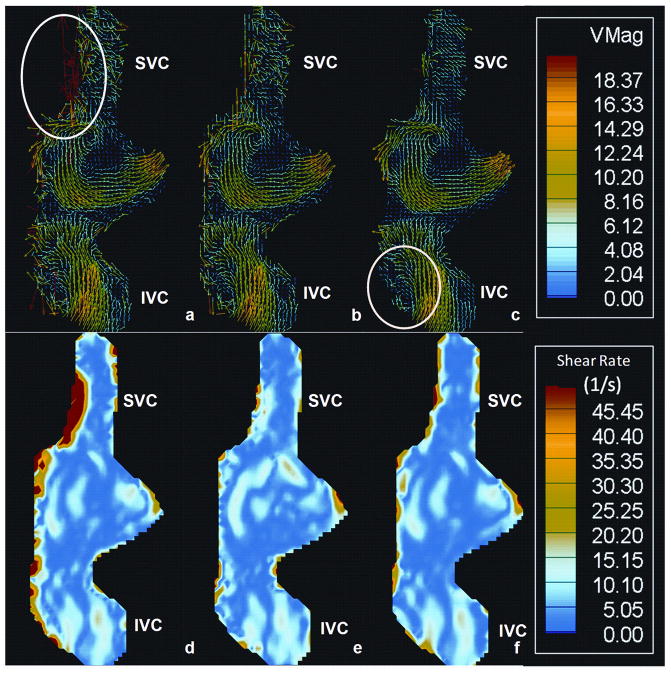
One important clinically relevant parameter that can be evaluated using PC MRI is wall shear stress. Wall shear stresses are evaluated by first computing the velocity shear rates along the wall. Figure 8d shows the peak wall shear rates computed for the 3 cases mentioned above. The peak wall shear rates in the unfiltered dataset were significantly higher compared to the filtered datasets (p=0.05). The peak wall shear rate for all the vessels dropped by about 50% after the filtering was performed. This mechanism is depicted in Figure 9 where the velocity fields (9 a–c) and the corresponding velocity shear rate contour plots (9 d–f) for the 3 cases are shown on a coronally acquired dataset. The noise present along the SVC resulted in an abnormally high shear region, which really doesn’t exist. Once the noise is filtered out using either the manual or the automatic technique, this region disappears. Overall, the two-step segmentation process produced much cleaner velocity fields, preserving key features of the flow field at the same time. For example, the recirculation region circled in Figure 9c is preserved, while the noise vectors circled in Figure 9a are removed. This demonstrates the benefit of using the FAVMF technique in conjunction with the segmentation process for velocity field quantification.

Figure 9.

a–c) The vector field of a TCPC reconstructed from a coronally acquired velocity field. a) Unfiltered dataset; b) Dataset manually filtered; c) Dataset filtered with FAVMF. Notice the vortex region is preserved while the noise is removed. d–e) The velocity shear rate map: d) Unfiltered dataset; b) Dataset manually filtered; e) Dataset filtered with FAVMF. Notice the reduction in wall shear rates along the SVC after the filtering is performed

DISCUSSION

With the growing application of 3D PC MRI for quantifying in vivo velocity fields, it is important that accurate post processing methodologies are developed and validated. Most of the current automated methodologies for PC MRI post processing, use a single step process for segmentation. This paper proposes a new two step segmentation and filtering process, where the vessel of interest is first segmented using the active contour technique, and the resulting velocity field is then automatically filtered using a novel Fuzzy Adaptive Vector Median Filter (FAVMF). This two-step approach produced velocity fields that are cleaner and more accurate for performing quantitative analysis, than the single step approach adopted by current methodologies. .

The automatic segmentation based on active contours for step 1 of the segmentation process, is not novel by itself. Kozerke et al, were the first to use active contours for automatic PC MRI segmentation. This paper improves the robustness of the active contour methodology by incorporating the gradient vector flow (GVF) for the external force field and a filtering process following it. The strength of this methodology is that vessels of arbitrary shapes can be segmented, and the resulting velocity field is clean and free of noise. The Fuzzy framework presented here is a significant improvement over both generic noise removal strategies from multi-dimensional image processing and current filtering methods popular for PC MRI. This framework requires no a priori knowledge for determination of the membership function and exploits differences between random noise and flow in the filtering process. It uses both velocity magnitude and direction information to achieve this objective. Techniques such as those proposed by Song et al, which use divergence as a parameter, cannot be applied to single velocity slices since one of the velocity derivatives is unavailable and hence the true divergence is unknown. The proposed Fuzzy filter is not subject to this limitation.

While the proposed methodology was tested here on 3D PC MRI slices, it can easily be adapted to 3D PC MRI volumes for newer sequences such as those proposed by Markl et al (28,29). The Fuzzy framework is robust enough, that the parameters in the filtering process can be easily evaluated for window sizes of 3×3×3. This may increase the total processing time, but will be negligible compared to the overall segmentation process. Besides flow applications, the framework can also be used in other situations where filtering can play a role on 3D data. For example, in displacement encoding using stimulated echo (DENSE)(30) and PC MRI of the myocardial wall(31), the presence of noise complicates the estimation of regional biomechanical parameters such as strains in the ventricle. The proposed filtering technique has significant potential in improving the quality of the vector fields acquired from any of these modalities if certain constraints on the quality of acquired images are met. Since this approach uses vector median filters with a minimum window size of 3 × 3, the resolution of the images should be high enough so that filtering can actually be performed within the region of interest; i.e. the number of pixels enclosed within should be much higher than 9. This is typically not a problem for a majority of PC MRI and DENSE acquisitions where large cardiac structures are being analyzed. Another requirement is that the signal to noise ratio and contrast to noise ratio should be sufficiently high, such that the bulk features of the flow field can be visualized. If these constraints are met, then the proposed FAVMF technique offers significant advantages for noise filtering over traditional scalar filters as it preserves the inherent characteristics of vector fields.

One case examined here was the total cavopulmonary connection, which is characterized by complex flow. Recirculation regions and vortex patterns are common in these geometries, and may be an indication of high energy losses within the system. The ability to accurately quantify such structures can tremendously improve clinical evaluation of the surgically altered connection. Hence the proposed Fuzzy filter plays a significant role as it offers an attractive solution for removing such noise vectors preserving flow features at the same time. While not all noise is filtered, performance is seldom worse than the manual technique, and usually better.

Although, there are several benefits of using the proposed two-step segmentation process for accurately quantifying flow from PC MRI data, certain limitations of the methodology are well acknowledged. Firstly, the performance of the filtering done during second stage is highly dependent upon the quality of the segmentation done in stage one. Therefore care should be taken that the vessel is not under segmented, i.e., all flow vectors are included in the segmentation. If there is a doubt that flow-vectors are being excluded during stage one of the segmentation process, then a dilation operation can be performed to include more vectors in the segmentation. If noise vectors get included in the process, then they can be removed during stage two. Secondly, there was a lack of true reference data for comparing the results of the filtering algorithm on in vivo datasets. A manual filtering algorithm was designed and developed to serve as a reference to get around this issue. However, data acquired from alternative computational and experimental fluid dynamic modalities may have served as better controls. Unfortunately, such data were not available for the patients used in this study. Finally, the proposed algorithm is ultimately dependent upon the quality of the MRI data acquired and is limited by SNR and CNR constraints. Although the algorithm works well with data having low SNR, the quality of the reconstructed velocity field goes down considerably as the noise components of the velocity field increase.

In conclusion, a two-step segmentation and filtering framework for multi-dimensional PC MRI is presented, which is more accurate compared to a single step process of segmentation alone. This is the first time a filtering technique based on fuzzy theory has been proposed and optimized for quantifying velocity fields from PC MRI. The framework is robust and easily extensible to other multi-dimensional MRI applications where noise is a significant problem.