Abstract
We tend to mentally organize numbers along a left-to-right oriented horizontal mental number line, with the smaller numbers occupying the more leftward positions. This mental number line has been shown to exert an influence on the visuo-spatial allocation of attention, with presentation of numbers from the low and high ends of the mental number line inducing covert shifts of spatial attention to the left and right side of visual space, respectively. However, the neural basis of this modulation is not known. Here we used transcranial magnetic stimulation (TMS) to study the role of the angular gyrus in shifts in visuospatial attention induced by the mental number line. We used a priming paradigm with a line bisection task to assess the bias in spatial allocation of visual attention induced by exposure to either small (16–24) or large (76–84) ends of the mental number line. In the small number prime condition, when attention is presumably biased to the left side of visual space, TMS applied over the right angular gyrus during the delay between the prime and the target line abolished the effect of number priming. In contrast, application of TMS over the left angular gyrus had no significant effect. In the large number prime condition (which shifted attention to the right side of visual space) both left and right TMS over the angular gyrus modulated the effect of number priming. This pattern of results reveals the involvement of the angular gyrus in the interaction between the mental number and visual spatial attention.
Keywords: line bisection, mental number line, priming, numerical cognition, transcranial magnetic stimulation, attention
Introduction
Humans tend to represent numbers as consecutively distributed along a horizontal left-to-right oriented mental number line, with small numbers lying on the left portion and large numbers on the right portion of the mental line (e.g., Dehaene et al., 1993; Hubbard et al., 2005; Longo and Laurenco, 2007). For example, subjects are usually faster to respond to small numbers with left-hand responses compared to right-hand responses, and faster to respond to large numbers with their right hand than with their left hand (the SNARC effect, Dehaene et al., 1993). Interestingly, the mental number line does not only influence overt spatial responses but it also exerts an effect on the allocation of spatial attention prior to any explicit response (although it is still subject to debate whether this effect is automatic or susceptible of top-down control, cf. Galfano et al., 2006; Ristic et al., 2006). For instance, Fischer et al. (2003) found that exposure to small numbers (1 or 2) preceding the presentation of the target stimulus in a simple visual detection task facilitated detection of target appearing in the left hemifield, while exposure to large numbers (8 or 9) facilitated target detection in the right hemifield (see also Stoianov et al., 2008).
The link between the mental number line and the representation of space raises the question of whether they share the same neural basis. Several neuroimaging findings indicate that the intraparietal sulcus (IPS) and the angular gyrus (ANG) in the posterior parietal cortex (PPC) are critically involved in numerical cognition (Cohen Kadosh et al., 2005; Pesenti et al., 2000; Pinel et al., 1999, 2001; Zago et al., 2001; for reviews, see Brannon, 2006; Dehaene, 2003; Rickard et al., 2000). Support for the role of these regions in numerical processing has also come from studies using transcranial magnetic stimulation (TMS) (Cappelletti et al., 2007; Göbel et al., 2001; Rusconi et al., 2005; Sandrini et al, 2004).
Interestingly, these same areas have also been implicated in functions involving the representation of visual space and the allocation of spatial attention. In particular, studies with stroke patients have shown that a lesion to the right parietal lobe can cause visual neglect, a deficit characterized by an impaired ability to detect stimuli presented on the side of space contralateral to the lesion (Mesulam, 1981). In the visual line bisection task (a paradigm often used to measure the allocation of visual attention in neglect patients) subjects are asked to judge the midpoint of a horizontal line. Typically patients with a right parietal lesion tend to mark the center of the line shifted to the right of the actual midpoint. One of the explanations of this deficit is that patients overestimate the extent of the right side of the line because their spatial attention is strongly biased to the right. This bias is a consequence of the right parietal lesion causing the left side of visual space to be underestimated relative to its actual size (Mesulam, 1981; Kinsbourne, 1982; see Driver and Mattingley, 1998, for review). These patients also show a systematic attentional bias towards larger numbers (i.e. the right side of the mental number line) when asked to bisect a numerical interval as if they were neglecting the left side of a mental number line in which small numbers are represented (Zorzi et al., 2002).
In neurologically normal observers neglect-like symptoms in the visual line bisection task have been produced by applying TMS over the angular gyrus within the inferior portion of the posterior parietal lobe (e.g., Bjoertomt et al., 2002; Fierro et al., 2000). Importantly, TMS applied over the right PPC also causes neglect-like symptoms in number bisection (Göbel et al., 2006). Also, TMS applied over the right PPC has been shown to correct leftward biases in number bisection (Oliveri et al., 2004). There is therefore evidence from both neglect patients as well as from normal subjects that the brain regions mediating the mental number line are similar to those involved in the representation of visual space and spatial allocation of attention.
Although the neural basis of the SNARC effect has been investigated previously (Rusconi et al., 2007), so far the neural basis of visuospatial priming by the mental number line has not been studied. Here we addressed this issue by investigating the role of the posterior parietal cortex in enabling the mental number line to influence the allocation of spatial attention. Subjects’ attentional bias, assessed using the line bisection task, was modulated by priming them to either the left or right side of the mental number line (by exposure to either small or large numbers). By applying TMS to transiently modify neural activity in the left or the right angular gyrus, we evaluated the causal role of these regions in enabling number priming to modulate the allocation of visual attention. In particular, here we applied TMS after number stimulus presentation to modulate its priming effect on attentional allocation.
Methods
Participants
9 subjects (7 males and 2 females, mean age of 26.25 years) took part in the experiment. All had normal or corrected to normal vision. 8 subjects were right-handed, 1 subject was left-handed. All subjects gave their written informed consent to the study, which had been approved by the Institutional Review Board at Beth Israel Deaconess Medical Center, and all were treated in accordance with the Declaration of Helsinki.
Line bisection task
The stimuli were presented on a 24 inch (1240 × 1024 pixels) monitor. Viewing distance was 57 cm. The stimuli were black, horizontal, transected lines presented on a white background. We used lines of three different lengths (37°, 38°, 39° of visual angle from a viewing distance of 57 cm) and the exposure duration on each trial was 200 msec. A short, black vertical line (2.2° long) indicated the point of transection of the horizontal lines. All lines were 0.1° thick. The target horizontal line was always presented such that the transection mark was at the sagittal midline of the subject and the horizontal line was at eye level. When the line transection was asymmetrical, the elongated line segment was 1° longer than the shorter line segment. A mask was presented after the target offset. This mask consisted of a thick horizontal line (thicker than the horizontal line of the stimulus) and a vertical line (with the same width as the transection mark and presented in the same position), and it covered the entire area of the previously displayed stimulus extending to the edges of the projected screen. The mask was displayed until the subject responded.
Each side of the target line was elongated in 50% of the trials. One block consisted of 90 trials. Each stimulus type, one of six types of lines (three left-elongated and three right-elongated), was presented an equal number of times (i.e. 15 times per block).
Number priming in the line bisection task
The target line was preceded by the presentation of number digits (see Fig 1a). Two ranges of numbers were used: from 16 to 24 (Small Prime condition) and from 76 to 84 (Large Prime condition). These priming conditions were tested in separate blocks of trials. On each trial, three numbers (height and width 0.5° per digit), randomly chosen, appeared from the given range either 3° above or below the fixation. The number primes appeared above or below fixation in order not to overlap with the location where the target line would appear. This was done to avoid any spatial priming effects. The numbers in a triplet were all consecutive (i.e. segments of the mental number line) but they could appear in all possible combinations (e.g., 16 17 18, 16 18 17, 17 16 18, 17 18 16, 18 16 17, 18 17 16).
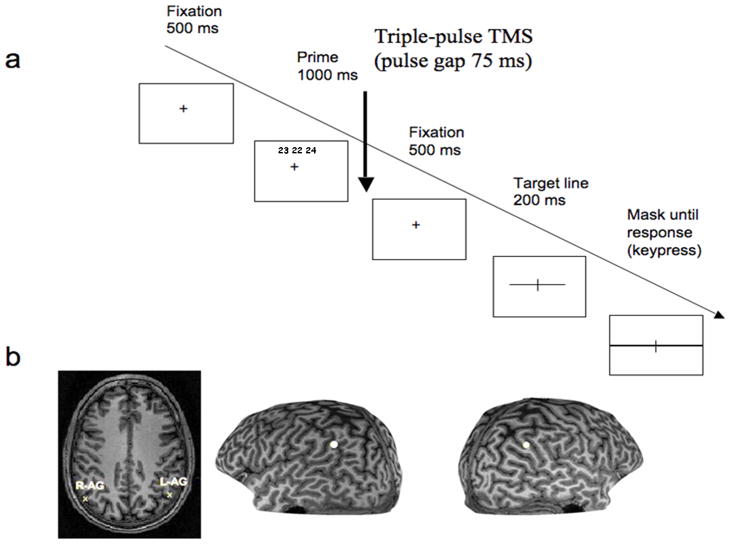
Figure 1.
a) The timeline of an experimental trial. Each trial began with a fixation cross appearing at the center of the screen (500 ms), at which the subjects were asked to fixate throughout the trial. The prime was then presented for 1000 ms (with the fixation cross also present), followed by another 500 ms of fixation. As in previous studies on visual priming (cf. Campana et al., 2002, 2006), TMS pulse was applied in the delay between the prime and the target line. A mask appeared 200 ms after the onset of the target stimulus. This mask, consisting of a thick horizontal line (thicker than the horizontal line of the stimulus) and a vertical line (with the same width as the transection mark) covered the entire area of the previously displayed stimulus and extended to the edges of the projected screen. The mask was displayed until the subject responded. b) Targeted anatomical locations for one representative naive subject. Left: transverse section showing the projected anatomical locations for the right (R-AG) and left (L-AG) angular gyrus respectively. Right: white dots indicating the stimulation sites shown on the left and right hemispheres on the 3-D reconstruction.
We also ran a control condition in which the number primes were replaced with six asterisks (two for each decimal number) presented at the same spatial location as the number primes. The primes were presented for 1000 ms, on the basis of a previous study by Fischer et al. (2003) who used a prime duration of 300 msec when presenting a single number prime followed by a detection task. A delay of 500 ms was introduced between the prime and the target stimulus presentation (cf. Campana et al., 2002, 2006) to prevent the occurrence of inhibitory attentional processes, possibly related to inhibition of return (cf. McKee et al., 2007).
Stimulation Parameters
The angular gyrus was localized in each subject on the basis of sulcal landmarks from individual MRI scans, and projected to the scalp surface using TMS/MR co-registration. Prior to testing, a T1-weighted MR scan was obtained from each participant using a 3 Tesla Philips MRI scanner. The ANG site was defined as the region directly adjacent to the dorsolateral projection of the superior temporal sulcus, which bifurcates the ANG. The stimulation sites were localized in slice and 3D-rendered brain scans using a frameless stereotaxy system (BrainSight, Rogue Research, Montreal, Canada); the same system was used to co-register the neuroanatomical sites with the scalp surface. A Polaris (Northern Digital, Ontario, Canada) infra-red tracking device was used to measure the position of the subject’s head. The TMS coil contained a tracking device that allowed online tracking of the stimulation site during the entire experiment. We also measured the Talairach coordinates of the projected cortical target of the angular gyrus in both hemispheres for all subjects (see Muggleton et al., 2006, for details). The mean Talairach coordinates of the angular gyrus were −41, −66, 38 (SD = 4.6, 4.1, 6.4) and 46, −64 and 34 (SD = 4.5, 3.3, 3.6) for the left and right hemisphere respectively (see Fig 1b). TMS was administered with a Magstim Super Rapid stimulator (Magstim Company, UK). The pulses were triggered remotely using a computer that controlled the stimulator, using E-Prime software. A 70 mm figure-of-eight coil was used. Similarly to other studies investigating the neural basis of visual priming (e.g., Campana et al., 2002, 2006), TMS was applied during the delay between the presentation of the prime and the target stimulus. Specifically, triple-pulse TMS (pulse gap 75 ms) was applied on each trial immediately after the presentation of the prime. A fixed TMS intensity of 65% was used on the basis of a number of previous successful TMS studies of the angular gyrus (e.g., Muggleton et al., 2006).
Procedure
At the beginning of the testing session, approximately 100 practice trials were presented to familiarize subjects with the bisection task. At the beginning of the experiment subjects were informed that the numbers ranged from 0 to 100 and they also had practice trials with both the small and large numbers. They were thus aware that the numbers ranging from 16–24 were small numbers and 76–84 were large numbers. 5 subjects were asked to report which side of the line was shorter, 4 subjects were asked to report which side was longer. Subjects were asked to maintain fixation on the center of the screen throughout each trial. Subjects were instructed that numbers ranging from 0 to 100 would have appeared on the screen on each trial. They were asked to pay attention to these numbers while maintaining fixation. Accuracy was emphasized but subjects were also encouraged to respond quickly. Subjects responded by pressing one of two buttons with the right index or middle finger for “left” or “right” responses.
Each combination of Priming Condition (Small Number Prime, Large Number Prime, Asterisk) and TMS condition (left ANG, right ANG and No TMS) was run in one block (see above). The order of blocks was randomized and counterbalanced across subjects.
Results
A 3 × 3 × 2 ANOVA performed on the mean accuracy with TMS site (No TMS, left ANG TMS, right ANG TMS), priming condition (Small Prime, Large Prime, Asterisk) and trial type (Right side is longer and Left side is longer) indicated a three-way significant interaction (F(2, 16)=5.87, MSE=1474.06; p=0.01). All the other effects were not significant. The overall mean accuracy was 66.50 (SD=5.03). Figures 2, 3 and 4 show subjects’ mean accuracies in the Small Number Prime, Large Number Prime and Asterisk conditions.
Figure 2.
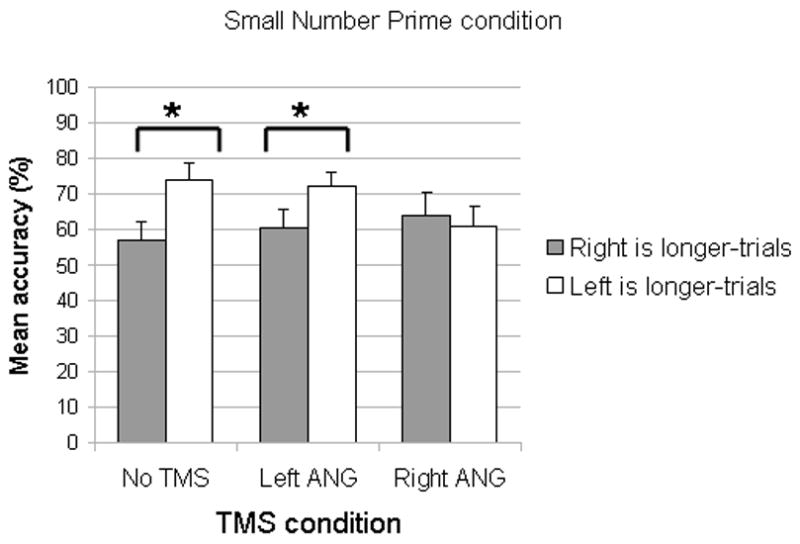
The mean (n=9) accuracy in the Small Number Prime condition (Error bars depict standard error of the means). Small numbers presumably shift attention to the left side of space and hence the left side of the line is overrepresented and it thus appears longer than it actually is. Because of this overrepresentation, the accuracy on trials on which the left side of the line is shorter should be lower than accuracy on trials on which the left side is longer. This pattern was observed in the No TMS Condition as well as in the Left ANG TMS condition. In contrast, this bias was abolished by right ANG TMS. Asterisks indicate statistically significant difference.
Figure 3.
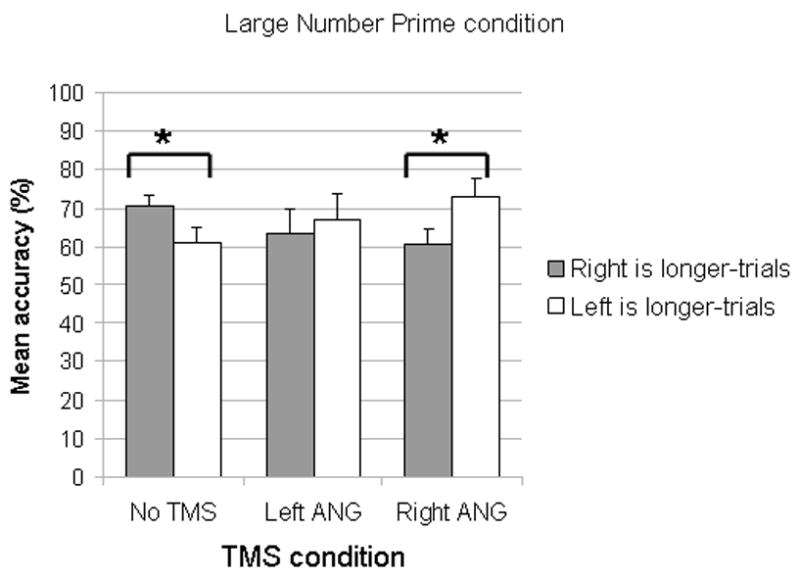
The mean (n=9) accuracy in the Large Number Prime condition (Error bars depict standard error of the means). Large numbers presumably shift attention to the right side of space and hence the right side of the line is overrepresented and it thus appears longer than it actually is. Because of this overrepresentation, the accuracy on trials on which the right side of the line is shorter should be lower than accuracy on trials on which the right side is longer. This pattern was observed in the No TMS Condition. In the Right ANG TMS condition, this pattern was reversed. In the Left ANG TMS condition, there was no significant statistical difference between the two types of trials. Asterisks indicate statistically significant difference.
Figure 4.
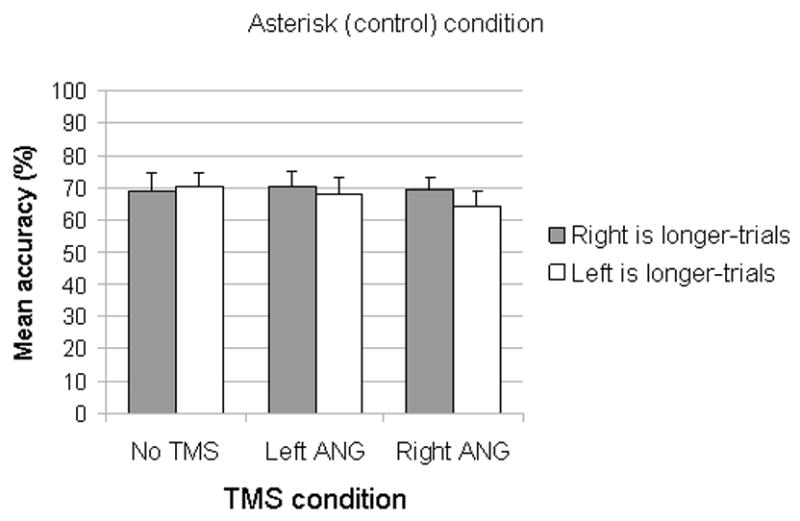
The mean (n=9) accuracy in the Asterisk condition (Error bars depict standard error of the means). In this condition, attention is not biased to either side of space; as a consequence, the level of accuracy is similar on both types of trials. Neither TMS on the Right ANG or on the Left ANG modulated performance compared to the No TMS condition, implying that the TMS effects in the present study are dependent on exposure to number primes.
In the Small Number Prime condition, successful priming is indicated by an accuracy which is higher for “Left side is longer”-trials than for “Right side is longer”-trials. This is because small numbers presumably shift attention to the left side of space and hence the left side of the line is overrepresented and thus appears longer than it actually is. Because of this overrepresentation, the accuracy on trials on which the right side of the line is longer should be lower than accuracy on trials on which the left side is longer. In the No TMS condition, this pattern of results was overall observed (in all but 2 subjects). Accuracy was significantly higher for “left side is longer” (mean=74.33, SD=14.34) compared to “right side is longer” (mean=59.67, SD=15.14), t(8)=2.726; p=0.026; this demonstrates that small numbers biased attention to the left side of space.
In the Large Number Prime condition, successful priming is indicated by an accuracy which is lower for “Left side is longer”-trials than for “Right side is longer”-trials. This is because large numbers presumably shift attention to the right side of space and hence the right side of the line is overrepresented and thus appears longer than it actually is. Because of this overrepresentation, the accuracy on trials on which the left side of the line is longer should be lower than accuracy on trials on which the right side is longer. In the No TMS condition, this effect was present (in all but 2 subjects) (mean accuracy for: “left side is longer”= 60.89, SD=12.64; “right side is longer”= 72.44, SD=8.11; t(8)=2.368, p=0.04) indicating that priming by large numbers successfully biased attention to the right side of space.
In the control priming condition (the asterisk condition), the target lines were preceded by asterisks instead of numbers. In this condition, there was no statistical difference between the two types of trials (mean accuracy for: “left side is longer”= 70.22, SD=13.04; “right side is longer”= 69.22, SD=15.61, t(8)=0.169; p=0.87).
The type of required response (i.e., select the shorter side vs. select the longer side) did not interfere with the effect of the priming (F(2, 14)= 0.59, p=0.57). These results show that the small and large numbers did induce the same attentional shift found by Fischer et al. (2003), demonstrating that our behavioural paradigm was valid and ruling out a possible role of inhibitory attentional effects in affecting performance (see also McKee et al., 2007).
The effect of TMS on Number Priming
Pairwise comparisons revealed that, for the Small Number Prime condition in the left ANG TMS condition, accuracy of “Left side is longer” trials (mean=73.56, SD=11.36) was significantly higher than on “Right side is longer” trials (mean=62.89, SD=15.98), t (8) = 2.712; p=0.027, indicating that left ANG TMS did not disrupt the effect of priming (6 subjects showed this pattern). In contrast, in the right ANG TMS condition the difference between the two types of trials was not significant (mean accuracy for: “left side is longer”= 62.56, SD=16.26; “right side is longer”= 63.00, SD=18.55; t (8) =0.055; p=0.96), indicating that right ANG TMS abolished the effect of priming (5 subjects were more accurate in saying ‘right is longer’).
In the Large Number Prime condition, both left ANG TMS and right ANG TMS modulated the effect of number priming. In the left ANG TMS condition, the difference in accuracy between the two types of trials was no longer significant (mean accuracy for: “left side is longer”= 69.56, SD=20.46; “right side is longer”= 64.89, SD=18.72; t(8)=0.666; p=0.53), indicating that left ANG TMS abolished the effect of priming (6 subjects were more accurate in saying ‘left is longer’). When TMS was delivered over the right ANG, the priming effect present in the No TMS condition was reversed (although the effect only approached significance), with accuracy on “Right side is longer”-trials (mean=62.11, SD=11.46) lower than on “Left side is longer” trials (mean=71.56, SD=13.83), t(8)=2.290; p=0.05 (8 subjects showed this pattern).
In the control priming condition (the asterisk condition), the target stimuli were preceded by asterisks instead of numbers. The lack of TMS effects in the asterisk condition would rule out any explanation of the results in terms of non-specific effects of TMS. TMS effects might be due to the presentation of any primes and not specific to number priming. There was no significant difference in the accuracy of Right side is longer-trials and Left side is longer-trials for both left ANG TMS (mean accuracy for: “left side is longer”= 68.00, SD=15.38; “right side is longer”= 70.33, SD=14.43; t(8)=0.411; p=0.69) and right ANG TMS (mean accuracy for: “left side is longer”= 64.44, SD=13.63; “right side is longer”= 69.44, SD=11.76; t (8)=0.364; p=0.36). The type of required response (i.e., select the shorter side vs. select the longer side) did not interact significantly with the TMS condition (F(1,77)=1.11, p=0.33).
Discussion
Our findings show that the angular gyrus plays a critical role in the allocation of visuospatial attention modulated by the mental number line. Confirming previous studies (Cattaneo, submitted; Fischer et al., 2003), our behavioral results (i.e. the No TMS condition) demonstrated that priming by small and large numbers shifts covert attention to the left and right sides of space, respectively. In the small number prime condition, the accuracy on trials on which the left side of the line was longer was significantly higher than the accuracy on trials on which the right side was longer. This suggests that attention was likely biased toward the left side of space, and as a consequence the left side of the line was perceived to be longer than it really was. This led to decreased accuracy on trials in which the right side was longer and increased accuracy on trials in which the left side was longer. Consistent with the findings of Fischer et al. (2003), the opposite pattern of results was observed in the large number prime condition where attention is presumably shifted to the right side of space.
In the small number prime condition, in which attention is presumably biased to the left side of visual space, TMS applied over the right ANG abolished the effect of number priming whereas application of TMS over the left ANG had no significant effect. In contrast, both left and right ANG TMS modulated the effect of priming by large numbers (which presumably shift attention to the right side of visual space). This pattern of results is mostly consistent with the established hemispheric asymmetry in attentional functions in humans according to which the right hemisphere processes information in both visual fields, whereas the left hemisphere in the right visual field only (e.g., Mesulam, 1981). Moreover, a stronger contralateral attentional bias of the left hemisphere (relative to the right hemisphere one) might have caused the effect of left ANG TMS to be selective for Large Number Prime only (cf. Kinsbourne, 1982; Reuter-Lorenz et al., 1990).
Although both left and right ANG TMS modulated the effect of priming by large numbers, this modulation was stronger with right ANG TMS; whereas left ANG TMS removed the effects of priming, right ANG TMS almost reversed these effects. In this case the effect of right ANG TMS is the opposite of what would be predicted by standard attentional accounts (cf. Mesulam, 1981). Assuming a contralateral neural organization of spatial attention (and competitive inhibitory interactions between the hemispheres), right ANG TMS should have disrupted contralateral (leftward) spatial orienting, strengthening the attentional orienting to the right driven by large numbers. Moreover, right ANG TMS by weakening the right ANG’s contralateral attentional vector should have released the left ANG from a source of competitive inhibition, thus further strengthening attentional orienting to the right (cf. Hilgetag et al 2001). Hence, the standard attentional framework would predict enhanced detection accuracy on ‘right is longer’ trials and reduced detection accuracy on ‘left is longer’ trials after right ANG TMS relative to no TMS. However the opposite pattern was observed. Although most of our findings can be explained by conventional attentional orienting accounts, this particular result is likely to reflect an additional mechanism, namely an interaction between the mental number line and processes that trigger attentional shifts. In fact, there is some evidence for a specialization of left and right hemispheres in the processing of large and small numbers. Using a number comparison paradigm, Göbel et al. (2001) found that stimulation of the left ANG tended to interfere more with large numbers (which are located on the right side of the mental number line). In contrast, right ANG TMS affected the processing of both small and large numbers (i.e. right ANG TMS affected both the left and right side of the mental number line). Consistent with this view, in our study left ANG TMS only affected number priming effects in the contralateral, right hemifield (induced by priming by large numbers). TMS over right ANG impaired number priming effects in left and right hemifield (induced by small and large number priming, respectively). Moreover, the finding that right ANG TMS reversed the effect of priming whereas in other conditions the effects of priming were just abolished is further evidence for the view that this particular effect cannot be explained by conventional attentional orienting accounts.
Our findings could thus be taken as evidence for the hemispheric asymmetry of the mental number line. However, TMS in the present study was unlikely to disrupt number processing per se, as TMS was applied not during number presentation but rather between the presentations of the number prime and the target. Therefore, it is more parsimonious to attribute the asymmetry found in the present study to that of attentional control.
Previous studies have also pointed to a stronger involvement of the right PPC in processes relying on the mental number line. For example, Göbel et al. (2006) found a stronger behavioral effect with TMS over right PPC than with over left PPC. Accordingly, a significant effect for rTMS over the right but not over the left PPC was found in number bisection (Oliveri et al., 2004). Some other studies found selective effect for left PPC TMS in comparing numerical magnitues (e.g., Göbel et al., 2001; Rusconi et al., 2005), and Rusconi et al. (2007) have recently observed that rTMS over both left and right PPC disrupted attentional orienting in number space. It is likely that the more a numerical task – such as number bisection – relies on spatial processes, the stronger is the involvement of the right hemisphere. Our task was essentially a spatial attentional task (no numerical operations were required), and our pattern of results fits well with what is known about the allocation of visuospatial attention in similar paradigms (cf. Fierro et al., 2000).
The finding that subjects’ performance in the Small Number Prime condition with left ANG TMS is not any different from their performance without TMS demonstrates that TMS did not induce nonspecific behavioral impairments or improvements. In fact, TMS over parietal regions has been found to cause both target detection impairment in the hemifield contralateral to TMS as well as enhanced stimulus detection in the visual field ipsilateral to TMS (Hilgetag et al., 2001; Walsh et al., 1999). This was not the case in our study. Furthermore, in the asterisk condition, TMS applied neither over the left nor over the right ANG influenced subjects’ performance, implying that the TMS effects in the present study were dependent on the presentation of numbers prior to application of TMS.
It is important to note that our findings cannot be due to the effect of TMS on the processing of the target line, as in the asterisk condition TMS did not modulate subjects’ performance. In a previous study (Bjoertomt et al., 2002), where ANG TMS modulated performance in the line bisection task, TMS was applied online (i.e. concurrently with the bisected line); here we applied TMS in the interval between the prime and the target (as has been done in other TMS studies investigating visual priming; e.g., Campana et al., 2002, 2006) in order to specifically modulate the activation state of the ANG prior to the arrival of information regarding the target line. It is unlikely that TMS disrupted the detection of the number primes because the primes were presented for 1000 msec and TMS was applied after their presentation; therefore, the numbers had been perceived by the subjects before the onset of the TMS. In other studies in which TMS has been used to disrupt number processing, TMS was applied simultaneously with the number stimulus (e.g., Rusconi et al., 2005; Sandrini et al., 2004). Therefore, it is likely that in our study TMS did not impair number processing per se; rather it abolished the effect of number processing on another visual function, namely the allocation of visuo-spatial attention. In this regard, it should be noticed that eye movements were not systematically controlled in this experiment, although participants were asked to keep their eyes on the centre of the screen. The short target exposure (200 ms) makes it unlikely that eye movements played a major role in this experiment, however the possibility that both attentional shifts and eye movements contributed to perceptual biases cannot be completely discarded.
What is the neural source of the modulation of the angular gyrus activity by the mental number line? One possibility is that the interaction between the mental number line and the allocation of visuospatial attention occurs within the angular gyrus. There is indeed evidence that angular gyrus is involved in both the numeric and visual versions of the bisection task (Bjoertomt et al., 2002; Göbel et al., 2006). An alternative possibility is that number priming initially activated another cortical region involved in numerical cognition, which then exerted a modulatory influence on the angular gyrus, thus causing shifts in the allocation of visuospatial attention. While the present study cannot distinguish between these possibilities, our results do show that the ANG is part of a network that mediates the impact of the mental number line on visuospatial representation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bjoertomt O, Cowey A, Walsh V. Spatial neglect in near and far space investigated by repetitive transcranial magnetic stimulation. Brain. 2002;125(Pt 9):2012–2022. doi: 10.1093/brain/awf211. [DOI] [PubMed] [Google Scholar]
- Brannon EM. The representation of numerical magnitude. Curr Opin Neurobiol. 2006;16(2):222–229. doi: 10.1016/j.conb.2006.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campana G, Cowey A, Walsh V. Priming of motion direction and area V5/MT: a test of perceptual memory. Cereb Cortex. 2002;12(6):663–669. doi: 10.1093/cercor/12.6.663. [DOI] [PubMed] [Google Scholar]
- Campana G, Cowey A, Walsh V. Visual area V5/MT remembers “what” but not “where”. Cereb Cortex. 2006;16(12):1766–1770. doi: 10.1093/cercor/bhj111. [DOI] [PubMed] [Google Scholar]
- Cappelletti M, Barth H, Fregni F, Spelke ES, Pascual-Leone A. rTMS over the intraparietal sulcus disrupts numerosity processing. Exp Brain Res. 2007;179(4):631–642. doi: 10.1007/s00221-006-0820-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattaneo Z, Silvanto J, Pascual-Leone A, Battelli L. Number priming modulates allocation of attention in a line bisection task. Cogn Neuropsych submitted. [Google Scholar]
- Cohen Kadosh R, Henik A, Rubinsten O, Mohr H, Dori H, van de Ven V, Zorzi M, Hendler T, Göbel R, Linden DE. Are numbers special? The comparison systems of the human brain investigated by fMRI. Neuropsychologia. 2005;43(9):1238–1248. doi: 10.1016/j.neuropsychologia.2004.12.017. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Bossini S, Giraux P. The mental representation of parity and number magnitude. J Exp Psych Gen. 1993;122:371–396. [Google Scholar]
- Dehaene S. The neural basis of the Weber-Fechner law: a logarithmic mental number line. Trends Cogn Sci. 2003;7(4):145–147. doi: 10.1016/s1364-6613(03)00055-x. [DOI] [PubMed] [Google Scholar]
- Driver J, Mattingley JB. Parietal neglect and visual awareness. Nat Neurosci. 1998;1(1):17–22. doi: 10.1038/217. [DOI] [PubMed] [Google Scholar]
- Fierro B, Brighina F, Oliveri M, Piazza A, La Bua V, Buffa D, Bisiach E. Contralateral neglect induced by right posterior parietal rTMS in healthy subjects. Neuroreport. 2000;11(7):1519–1521. [PubMed] [Google Scholar]
- Fischer MH, Castel AD, Dodd MD, Pratt J. Perceiving numbers causes spatial shifts of attention. Nat Neurosci. 2003;6(6):555–556. doi: 10.1038/nn1066. [DOI] [PubMed] [Google Scholar]
- Galfano G, Rusconi E, Umiltà C. Number magnitude orients attention, but not against one’s will. Psychon Bull Rev. 2006;13:869–874. doi: 10.3758/bf03194011. [DOI] [PubMed] [Google Scholar]
- Göbel S, Walsh V, Rushworth MF. The mental number line and the human angular gyrus. Neuroimage. 2001;14(6):1278–1289. doi: 10.1006/nimg.2001.0927. [DOI] [PubMed] [Google Scholar]
- Göbel SM, Calabria M, Farne A, Rossetti Y. Parietal rTMS distorts the mental number line: simulating ‘spatial’ neglect in healthy subjects. Neuropsychologia. 2006;44(6):860–8. doi: 10.1016/j.neuropsychologia.2005.09.007. [DOI] [PubMed] [Google Scholar]
- Hilgetag CC, Theoret H, Pascual-Leone A. Enhanced visual spatial attention ipsilateral to rTMS-induced ‘virtual lesions’ of human parietal cortex. Nat Neurosci. 2001;4:953–957. doi: 10.1038/nn0901-953. [DOI] [PubMed] [Google Scholar]
- Hubbard EM, Piazza M, Pinel P, Dehaene S. Interactions between number and space in parietal cortex. Nat Rev Neurosci. 2005;6:435–448. doi: 10.1038/nrn1684. [DOI] [PubMed] [Google Scholar]
- Jewell G, McCourt ME. Pseudoneglect: A review and metaanalysis of performance factors in line bisection tasks. Neuropsychologia. 2000;38:93–110. doi: 10.1016/s0028-3932(99)00045-7. [DOI] [PubMed] [Google Scholar]
- Kinsbourne M. Hemispheric specialization and the growth of human understanding. Am Psychol. 1982;37(4):411–420. doi: 10.1037//0003-066x.37.4.411. [DOI] [PubMed] [Google Scholar]
- Longo MR, Lourenco SF. Spatial attention and the mental number line: evidence for characteristic biases and compression. Neuropsychologia. 2007;45:1400–1407. doi: 10.1016/j.neuropsychologia.2006.11.002. [DOI] [PubMed] [Google Scholar]
- McKee D, Christie J, Klein R. On the uniqueness of attentional capture by uninformative gaze cues: facilitation interacts with the Simon effect and is rarely followed by IOR. Can J Exp Psychol. 2007;61:293–303. doi: 10.1037/cjep2007029. [DOI] [PubMed] [Google Scholar]
- Mesulam MM. A cortical network for directed attention and unilateral neglect. Ann Neurol. 1981;10(4):309–325. doi: 10.1002/ana.410100402. [DOI] [PubMed] [Google Scholar]
- Muggleton NG, Postma P, Moutsopoulou K, Nimmo-Smith I, Marcel A, Walsh V. TMS over right posterior parietal cortex induces neglect in a scene-based frame of reference. Neuropsychologia. 2006;44(7):1222–1229. doi: 10.1016/j.neuropsychologia.2005.10.004. [DOI] [PubMed] [Google Scholar]
- Oliveri M, Rausei V, Koch G, Torriero S, Turriziani P, Caltagirone C. Overestimation of numerical distance in the left side of space. Neurology. 2004;63:1994–1996. doi: 10.1212/01.wnl.0000145975.58478.6d. [DOI] [PubMed] [Google Scholar]
- Pesenti M, Thioux M, Seron X, De Volder A. Neuroanatomical substrates of arabic number processing, numerical comparison, and simple addition: a PET study. J Cogn Neurosci. 2000;12(3):461–479. doi: 10.1162/089892900562273. [DOI] [PubMed] [Google Scholar]
- Pinel P, Dehaene S, Riviere D, LeBihan D. Modulation of parietal activation by semantic distance in a number comparison task. Neuroimage. 2001;14(5):1013–1026. doi: 10.1006/nimg.2001.0913. [DOI] [PubMed] [Google Scholar]
- Pinel P, Le Clec HG, van de Moortele PF, Naccache L, Le Bihan D, Dehaene S. Event-related fMRI analysis of the cerebral circuit for number comparison. Neuroreport. 1999;10(7):1473–1479. doi: 10.1097/00001756-199905140-00015. [DOI] [PubMed] [Google Scholar]
- Reuter-Lorenz PA, Kinsbourne M, Moscovitch M. Hemispheric control of spatial attention. Brain Cogn. 1990;12(2):240–266. doi: 10.1016/0278-2626(90)90018-j. [DOI] [PubMed] [Google Scholar]
- Rickard TC, Romero SG, Basso G, Wharton C, Flitman S, Grafman J. The calculating brain: an fMRI study. Neuropsychologia. 2000;38(3):325–335. doi: 10.1016/s0028-3932(99)00068-8. [DOI] [PubMed] [Google Scholar]
- Ristic J, Wright A, Kingstone A. The number line effect reflects top-down control. Psychon Bull Rev. 2006;13:862–868. doi: 10.3758/bf03194010. [DOI] [PubMed] [Google Scholar]
- Rusconi E, Walsh V, Butterworth B. Dexterity with numbers: rTMS over left angular gyrus disrupts finger gnosis and number processing. Neuropsychologia. 2005;43(11):1609–1624. doi: 10.1016/j.neuropsychologia.2005.01.009. [DOI] [PubMed] [Google Scholar]
- Sandrini M, Rossini PM, Miniussi C. The differential involvement of inferior parietal lobule in number comparison: a rTMS study. Neuropsychologia. 2004;42(14):1902–1909. doi: 10.1016/j.neuropsychologia.2004.05.005. [DOI] [PubMed] [Google Scholar]
- Stoianov I, Kramer P, Umilta C, Zorzi M. Visuospatial priming of the mental number line. Cognition. 2008;106:770–779. doi: 10.1016/j.cognition.2007.04.013. [DOI] [PubMed] [Google Scholar]
- Walsh V. A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn Sci. 2003;7(11):483–488. doi: 10.1016/j.tics.2003.09.002. [DOI] [PubMed] [Google Scholar]
- Walsh V, Ellison A, Ashbridge E, Cowey A. The role of the parietal cortex in visual attention — hemispheric asymmetries and the effects of learning: a magnetic stimulation study. Neuropsychologia. 1999;37:245–251. doi: 10.1016/s0028-3932(98)00099-2. [DOI] [PubMed] [Google Scholar]
- Zago L, Pesenti M, Mellet E, Crivello F, Mazoyer B, Tzourio-Mazoyer N. Neural correlates of simple and complex mental calculation. Neuroimage. 2001;13(2):314–327. doi: 10.1006/nimg.2000.0697. [DOI] [PubMed] [Google Scholar]
- Zorzi M, Priftis K, Umilta C. Brain damage: neglect disrupts the mental number line. Nature. 2002;417:138–139. doi: 10.1038/417138a. [DOI] [PubMed] [Google Scholar]