Tracking butterfly movements with harmonic radar reveals an effect of population age on movement distance

Abstract

We used harmonic radar to track freely flying Glanville fritillary butterfly (Melitaea cinxia) females within an area of 30 ha. Butterflies originated from large and continuous populations in China and Estonia, and from newly established or old (> 5 years) small local populations in a highly fragmented landscape in Finland. Caterpillars were raised under common garden conditions and unmated females were tested soon after eclosion. The reconstructed flight paths for 66 individuals comprised a total distance of 51 km with high spatial resolution. Butterflies originating from large continuous populations and from old local populations in Finland exhibited similar movement behaviors, whereas butterflies originating from newly established local populations in the fragmented landscape in Finland moved significantly more than the others. There was no difference in the lengths of individual flight bouts, but the new-population females flew more frequently, resulting in longer daily movement tracks. The flight activity of all individuals was affected by environmental conditions, peaking at 19–23°C (depending on population type), in the early afternoon, and during calm weather. Butterflies from all population types showed a strong tendency to follow habitat edges between the open study area and the neighboring woodlands.

Dispersal capacity affects the survival of populations and species especially in fragmented landscapes in which habitat quality exhibits spatiotemporal variation. As with any other trait, dispersal behavior of an individual is affected by its genetic constitution, by its environment in the broad sense, and by the interaction between the two (1). From an evolutionary perspective, dispersal has the apparently opposing effects of swamping local adaptation but also supplying the genetic variation that is necessary for adaptation, leading to an intimate interaction between the effects of environmental conditions, ecological population dynamics, and evolution of dispersal and correlated life-history traits (2).

Theoretical work has shown that habitat fragmentation can select either for increased or decreased dispersal propensity (3–6). Increasing fragmentation makes it less likely that a dispersing individual will reach another habitat patch, hence selecting for decreased dispersal rate. But severe fragmentation of the habitat leaves many fragments unoccupied at any one time, thereby increasing the benefits gained from a successful dispersal event. Increasing fragmentation also influences other factors, such as the level of inbreeding and relatedness of individuals in local populations, which are likely to influence the evolution of dispersal (7).

Compared with many other life-history traits, dispersal is a complex trait that is difficult to define and measure. In terms of the movement ecology framework of Nathan et al. (1), the realized movement track of an individual is affected by the individual's motion capacity, by its navigation capacity, by its motivation to move, and by a number of external factors, such as the structure of the habitats in which the movements take place. Further, the evolutionary response to landscape structure can be masked by phenotypic plasticity (8, 9) and by interaction between genetic and environmental factors (10), making it challenging to arrive at a definite conclusion about the causes of any differences, or similarities, in the movements of conspecific populations living under different environmental conditions.

The most conclusive approach to resolve the independent effects of genetic composition, phenotypic plasticity and environment on dispersal is to conduct reciprocal transplant experiments. Such a study on the speckled wood butterfly (Pararge aegeria) showed that both the landscape of genetic origin and the landscape of individual development contributed substantially to variation in flight morphology (8). An experiment conducted in a population cage showed that in this species individuals originating from less fragmented habitat (woodlands) were more dispersive (covered longer distances and were more prone to cross habitat boundaries) than individuals originating from more fragmented habitat (agricultural landscapes) (11).

Theoretical and empirical studies conducted on the Glanville fritillary butterfly (Melitaea cinxia) have demonstrated that selection pressures on dispersal propensity may vary over small spatial scales, potentially leading to maintenance of genetic variation at the landscape level (4, 12, 13). The Glanville fritillary metapopulation in the Åland Islands in southwestern Finland persists in a balance between local extinctions and recolonizations (14). A common garden mark-recapture study showed that females from isolated new populations are more dispersive than females from old populations, suggesting that the most dispersive females are likely to colonize the more isolated habitat fragments (15). This conclusion has been supported by the finding of significant heritability for dispersal in the Glanville fritillary (16). However, dispersive individuals are likely to leave isolated fragments soon, which selects locally for reduced mobility. Therefore, the mean dispersal propensity in an isolated population decreases with population age (12, 13).

Field studies on the Glanville fritillary and countless numbers of other species have been conducted with the mark-recapture method. This method integrates the behavior of individuals over a long time span, and it therefore lacks the resolution to reveal the behavioral mechanisms involved in dispersal and, for example, the mechanistic causes of any differences between populations that may be detected. Here, we combine insect-tracking technology (17) with a common garden experiment to characterize the different components of movements in the Glanville fritillary butterflies originating from contrasting landscapes in terms of habitat fragmentation. Study populations in China and Estonia occur in large and relatively continuous expanses of habitat, whereas the previously much-studied metapopulation in the Åland Islands in Finland occurs in a highly fragmented landscape. In the latter case we further distinguish between butterflies originating from newly established versus old local populations.

Based on our previous work, we expected that butterflies from the newly established Finnish populations would move more than butterflies from the respective old populations. We hypothesized that butterflies originating from continuous habitats in China and Estonia would be least mobile. We had no prior expectation on exactly which component of movements (1) would differ among the populations. Hence, we examined possible differences in short-scale movements (the length, frequency, and speed of individual flight bouts), in navigation (the geometry of flight paths and the response to habitat edges), and in long-term movements integrated over the individual movement steps. Studies conducted to compare different butterfly species (18) as well as different populations within a species (19) have suggested that the optimal ambient temperatures for thermoregulation and maximal activity may depend on the environmental conditions under which the population has evolved. Hence, we hypothesized that the ambient temperature for maximal activity might be different for butterflies originating from Finland, China, and Estonia.

Results

Flight Paths Reconstructed with Harmonic Radar Data.

All larvae were reared under the same conditions from winter diapause onward. After eclosion, each butterfly was marked individually and a transponder was attached to its thorax. Butterflies were tracked in groups of 3–6 individuals by using the scanning harmonic radar (Fig. 1), usually in the second day after eclosion. Each butterfly experienced at least 2 h of environmental conditions favorable for flight. The total length of the reconstructed flight paths for 66 individuals was 50.7 km, including 4,821 measurements of spatial location. There was substantial variation among the individuals both in the overall level of activity and in flight behavior. The distribution of observed movement distances ranged from 9 to 5,490 m, with the median of 505 m (Fig. 2A).

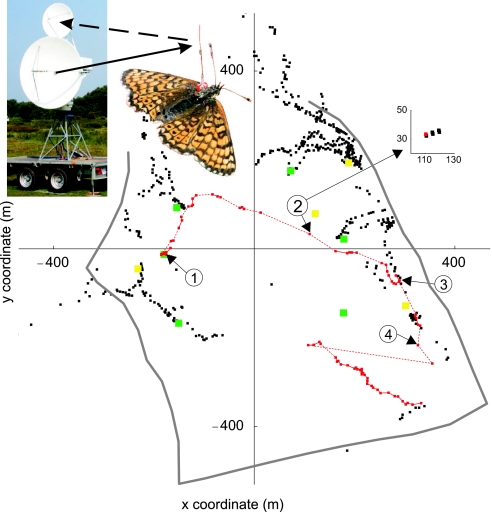
Fig. 1.

Tracking butterfly movements with harmonic radar. The signal emitted by the radar (continuous arrow) is modified by the transponder (visible in the picture) fitted to the butterfly, and the modified signal (dashed arrow) is picked up by the radar. The radar was located at the origin of the main picture, and it scanned over the area once every 3 s. The red dots correspond to locations associated with the focal butterfly; the black dots are locations of other butterflies during the same day. The focal individual was released at 13:19 h (location 1), recaptured to confirm identity at 13:59 h (location 3), after which it was followed until 14:50 h (location 4). (Inset) The sample points above the noise threshold on the radar Plan Position Indicator (PPI) corresponding to location 2. The black dots represent the raw data and the red dot represents the location identified by the algorithm “from hits to locations.” The continuous lines represent tracks (16 pieces) identified by the algorithm “from locations to tracks,” the dashed lines tracks joined manually (SI Text). Yellow dots show the locations of the four weather stations, green dots show the six locations used for the release of butterflies. Gray outline is the portion of East Wretham Heath visible to radar, which was bounded primarily by trees.

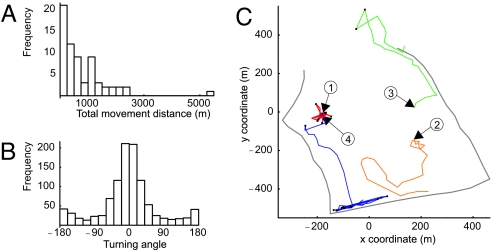
Fig. 2.

Characteristics of movement tracks. (A) Distribution of observed movement distances for the 66 individuals included in the experiment. (B) Distribution of turning angles (pooled data for all individuals). (C) Examples of contrasting flight paths. The numbered arrows show the starting locations for butterflies 1 (red), 2 (orange), 3 (green), and 4 (blue). The black dots indicate points classified as turning back (absolute value of turning angle >135°).

Fig. 2C depicts the flight paths of four individuals with roughly equal level of activity but dissimilar behaviors. Individual 1 remained within a small area because of a high frequency of turning back. Individual 2 flew in a directed manner over the heath, and individual 3 along the forest edge. Individual 4 first flew in a directed manner over the heath, then followed an edge with a high frequency of backtracking. The overall distribution of turning angles was bimodal (Fig. 2B), with the main peak at 0° (corresponding to straight flight) and the smaller peak at 180° (corresponding to turning back).

Maximal Distance Moved in Two Hours.

The total distance moved by an individual depends on day-to-day variation in weather conditions. Furthermore, some individuals were released before noon and others in the early afternoon, and some individuals emigrated earlier than the others from the study area scanned by the radar. To minimize the influence of these factors, we measured the long-term movement activity by the maximum distance during a period of 2 h.

The median maximal distance moved in 2 h was 488 m (minimum, 9 m; maximum, 3,730 m). Butterflies originating from the new populations in Finland moved longer distances than butterflies originating from the other population types (Fig. 3A, Tables 1 and 2). The maximal movement distance was achieved under warmer conditions by butterflies from the Finnish old populations than by the other butterflies. Wind speed, time of the day, or body mass (pupal weight) did not have statistically significant effects on the distance moved. Individuals tended to follow the wind, as illustrated by the excess in Fig. 3B in the class α < 45° (p₁ = 0.004, p₂ = 0.97; see Materials and Methods).

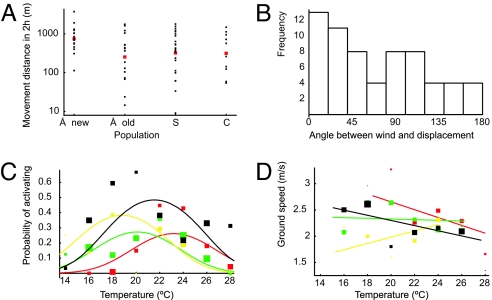
Fig. 3.

Population-level differences in movement statistics. (A) Maximal distance moved in two hours. The black dots correspond to individuals, the red dots to population means. The letters stand for Å(land), S(aaremaa), and C(hina). (B) The angle between displacement and the down wind direction for the maximal movement in two hours. (C) Probability of an inactive individual becoming active during a 5-min interval as a function of population type and temperature. The lines are based on the model (assuming the peak time 12:35 h), and the dots show binned raw data, dot size being proportional to the amount of data. The colors correspond to the Åland new (black), Åland old (red), Saaremaa (green), and Chinese (yellow) populations. (D) The dependence of ground speed on temperature, symbols as in C.

Table 1.

The statistical significance of variables included as fixed effects in different models of butterfly activity

Variable	Distance in 2 h, m	Probability of inactive to active	Probability of active to inactive	Distance in 5 min, m	Distance of flight bout, m	Speed of flight bout, m/s
Pop	F3,47 = 3.79	F3,60 = 1.97	—	F3,54 = 1.84	—	F3,53 = 5.35
	P = 0.016	P = 0.13		P = 0.15		P = 0.0027
Temp	F1,47=0.31	F1,1481 = 2.90	—	F1,393 = 21.8	F1,294 = 0.01	F1,494 = 1.72
	P = 0.58	P = 0.09		P < 0.0001	P = 0.93	P = 0.19
Pop*temp	F3,47=2.72	F3,1481 = 2.91	—	F3,393 = 5.14	—	F3,494 = 4.04
	P = 0.055	P = 0.03		P = 0.0017		P = 0.0074
Temp*temp	F1,47 = 13.35	F1,1481 = 19.6	—	F1,393 = 21.9	F1,294 = 17.0	—
	P = 0.0007	P < 0.0001		P < 0.0001	P < 0.0001
Time	—	F1,1481=1.49	—	F1,393 = 18.9	F1,294 = 6.66	F1,494 = 3.78
		P = 0.22		P < 0.0001	P = 0.01	P = 0.052
Time*time	—	F1,1481 = 11.7	—	F1,393 = 4.40	—	—
		P = 0.0006		P = 0.037
Wind	—	—	—	F1,393 = 5.14	F1,294 = 9.64	—
				P = 0.024	P = 0.0021
Weight	—	—	—	—	—	—

Nonsignificant variables that were dropped out from the model are indicated by —.

Table 2.

Model predicted activity at population-specific optimal temperature and the temperature at which the activity was maximized

Population	Distance in 2 h, m	Probability of inactive to active	Distance in 5 min, m
Åland new	1,850 (20.0°C)	0.48 (21.5°C)	77 (20.0°C)
Åland old	460 (22.6°C)	0.26 (23.2°C)	76 (25.0°C)
Saaremaa	700 (19.4°C)	0.27 (20.0°C)	71 (19.3°C)
China	514 (19.4°C)	0.38 (18.8°C)	66 (20.1°C)

If included in the model, time was set at 13:00 h and wind speed at 0 m/s. The model-predicted maximal distance of a flight bout was 36 m, maximized at 20.0°C, with no difference among populations (Table 1).

Activity Measured as Movements in 5-min Intervals.

To measure the frequency of movements and their dependence on environmental conditions, we split each day into 5-min intervals, and recorded for each interval whether a given butterfly was active (moved at least 5 m) or not. The mean probability of being active was 0.22. Butterflies switched from inactive to active with probability 0.12, and vice versa with probability 0.42. Flight activity started at 10:30 h at the earliest, and ended at 16:50 h at the latest, peaking at 12:40 h according to our model (Table 1). We did not have data for solar radiation, which is likely to be the causal factor explaining the effect of the time of the day.

In general, individuals from the Finnish new populations showed the highest probability of becoming active (Fig. 3C; Table 2). The probability of becoming active depended on temperature, and the optimal temperature, corresponding to the highest probability, depended on population type. The optimal temperature was highest for the Finnish old populations and lowest for the Chinese population. Wind speed or body mass did not have a statistically significant effect on the probability of becoming active. The probability of switching from active to inactive did not depend on any of the variables tested.

The distance moved in the active 5-min intervals depended on temperature. The optimal temperature was higher for butterflies originating from the Finnish old populations than for butterflies from the other three population types (Tables 1 and 2). The distance moved in the population-specific optimal temperature was similar among the population types (Table 2). Displacement directions in the 5-min intervals indicated that individuals tended to move downwind (p₁ = 0.04, p₂ = 0.94).

Speed and Length of Individual Flight Bouts.

Glanville fritillary butterflies do not fly continuously for a long time: short flight bouts are typically followed by times of rest, often on tops of plants. To examine whether individuals from the different population types differed in their ground speeds or in the lengths of individual flight bouts, we extracted from the flight paths the periods of continuous flight. Of the 354 flight bouts for which both the start and the end points could be reliably identified (see Materials and Methods), the lengths ranged from 7 to 415 m, with a mean of 32 m and median of 25 m. The flight bouts were longest in calm weather, at 20.0°C, and late in the afternoon (Table 1). The lengths of the flight bouts were not affected by population type or by body mass.

Ground speed decreased with increasing temperature for the Finnish new and old populations but increased with temperature for the Chinese population (Table 1, Fig. 3D). Ground speed was highest late in the afternoon, and it did not depend on wind speed or on body mass.

The length of individual flight bouts increased with ground speed (F_1,301 = 50.94, P < 0.0001), although the duration of the flight somewhat decreased with increasing ground speed (F_1,301 = 3.51, P = 0.06). The former could be an artifact, because we used a threshold speed to define the end of continuous flight. The data on individual flight bouts were too sparse to show a statistically significant relationship between displacement direction and wind direction (p₁ = 0.17, p₂ = 0.96).

Geometry of Flight Paths.

We split each movement path into segments by adding individual moves to the current segment until the distance measured along the movement track exceeded 200 m, after which a new segment was started. The largest distance between any two locations along a segment was used as a measure of path curvature (corrected for the number of observations; see Materials and Methods). Although the flight patterns of individual butterflies varied greatly (Fig. 2C), neither the path curvature (F_3,39 = 1.17, P = 0.33), the turning angle (F_3,48 = 0.12, P = 0.95), nor the probability of turning back (F_3,48 = 0.13, P = 0.94) depended on population type.

Butterflies showed a clear tendency to follow the edge between the heath and the surrounding woodland. Our data include 54 events of edge-following, comprising 23.0 km of movement tracks (45% of the total distance recorded). Typically an individual followed the edge for a few hundred meters (median, 310 m); the longest single edge-following event was 3,400 m. Edge-following was often characterized by the individual moving back and forth (Fig. 2C; individual 4), and indeed the probability of turning back was greater when the individual was located close to an edge (F_1,991 = 21.26, P < 0.0001). No differences in the lengths of edge-following events were observed between the population types (F_3,31 = 0.07, P = 0.97).

Discussion

Advances in global positioning system (GPS) tracking technology have generated a vast amount of high-resolution movement data for mammals and other large-bodied animals, changing our view on how these animals move as well as revolutionizing the kinds of questions that can be asked with movement data (1). In the case of small-bodied insects, the scanning harmonic radar provides one of the few technologies for acquiring high-resolution movement data for freely flying individuals in the field. In this article, we have shown that the availability of such data can make a real difference in answering many of the questions posed in movement ecology (1, 20), in particular, the decomposition of movement paths into their components down to individual flight bouts, the dependence of these different components on environmental conditions, and evolutionary responses to landscape structure.

Contrary to our expectations, we found no systematic differences in the 2-h movement distances between butterflies originating from the highly fragmented landscape in Finland and those from the relatively continuous habitats in Estonia and China. This is surprising, given the very different structure of these landscapes and the fact that the Chinese population has remained genetically isolated from the European populations since the last glacial maximum. However, a substantial and statistically significant part of the variation among individuals in Finland was attributed to the difference between butterflies originating from newly established (1 year old) versus old (>5 years) local populations, butterflies from the new populations being more mobile on average than butterflies from old populations. This difference is consistent with previous findings based on a mark-recapture study (15) and movements of butterflies in a population cage (12, 13). However, these previous studies lacked the resolution to disentangle exactly which components of the movement behavior might differ between the new and old populations.

Here we have shown that the distance moved within a 5-min period when the butterfly was active was nearly independent of population type, and there were no marked differences in the flight speed nor in the geometry of individual flight bouts. Butterflies from all populations showed an equally strong tendency to follow habitat edges. However, the maximal distance moved in 2 h was much longer for the new-population butterflies than for butterflies from the three other population types. The primary difference is thus simply in the frequency of flight bouts: females from new populations had roughly twice as high a probability of becoming active during a 5-min period than butterflies from old populations. Our findings point to population-level differences in internal state (motivation to move) or motion capacity, but not in navigation capacity (1). However, it should be noted that, as with any common garden experiments (in contrast to reciprocal transplant experiments), we cannot distinguish between genetic and plastic phenotypic responses, or interactions between genetic and environmental factors.

The habitat in which we conducted the experiment has nectar plants but not host plants for the Glanville fritillary butterfly, and it can therefore be considered to represent high-quality dispersal habitat. Because we could not take the risk of introducing a butterfly population in the study area, we were able to test the flight behavior for unmated females only. For this reason, the motivation of the butterflies to move remains partly unknown, and our observational data may include types of movements other than dispersive movements. But regardless of whether the movements represent dispersive or nondispersive movements, there was a predictable difference between the newly established and old populations from the fragmented landscape in Finland, suggesting that variation in motion capacity, which is necessary for any type of movements, explains a large part of the observed variation among individuals in their overall mobility.

The probability of becoming active from one 5-min period to another peaked at significantly different temperatures in different population types. Intriguingly, we found a difference not only among individuals originating from the three landscapes, but also within the Finnish metapopulation, such that females from new populations achieved their longest distances at lower temperatures than old-population females. Butterflies in the new versus old local populations in the Finnish metapopulation exhibit a syndrome of phenotypic life-history (12, 13, 15, 21) and genotypic differences (16), to which differences we can now add dissimilar temperature dependence of movement activity.

Activity peaked at the lowest temperature in the Chinese population. This population originates from an extremely continental climate in the Tian Shan Mountains with very hot summers. Field observations suggest that the butterflies have reduced activity in the middle of the day (R. Wang, personal communication), apparently having evolved to avoid the often detrimentally high noon temperatures. Butterflies from the Chinese population showed the second highest level of maximal activity in 5-min periods, but were classified as least mobile based on how far they moved in their most active 2-h period. This difference illustrates the difference between potential mobility, which was high at relatively low temperatures, and the mobility realized under the ambient environmental conditions (1).

In the Finnish metapopulation, the majority of individuals occur in large populations. As large populations tend to be relatively old, only a small fraction of all of the butterflies are likely to be as mobile as the new-population females tested in this study. However, the metapopulation shows a high rate of population turnover (14), and high-dispersal capacity is clearly advantageous in enhancing colonization rate. So what are the forces selecting for reduced mobility in old-population females?

In the Glanville fritillary, there is no trade-off between mobility and fecundity, rather there is a positive relationship between these two traits (21). Elevated mortality in the matrix seems to be an unlikely cost of high mobility, because the matrix habitats have nectar plants to allow feeding and we are not aware of any predators that would be more abundant in the matrix. However, mobile individuals with a high rate of emigration end up spending much time in the matrix, thereby losing time that could otherwise be used for locating mates and for ovipositing. For short-lived insects such a trade-off between dispersal rate and local habitat use can produce a substantial fitness cost for the most mobile individuals (12, 13).

High emigration rate of especially mobile individuals from small local populations implies a rapid change in the phenotypic composition of such populations. This expectation is supported by the contrast between the butterflies originating from the new versus old populations in this and previous studies (12, 13, 15, 21), because the “old” populations, in general, are not older than 6–10 years. Analogous rapid evolutionary changes have been observed in the context of range expansion induced by climate change. For instance, in two species of wing-dimorphic bush crickets (Orthoptera: Tettigoniidae), recently colonized populations at the range margin showed elevated frequencies of long-winged individuals, but this population-level increase in dispersal capacity was short-lived, because 5–10 years after colonization the frequency of long-winged individuals was at the average level (22).

The key challenge to movement ecology is to develop a mechanistic understanding from individual movement steps to distinct phases of movements all of the way to the lifetime movement track (1). There is no single method that could be used to investigate at all these spatial scales the roles of the internal state, motion, and navigation capacities of individuals and the role of the environment in affecting movements. To characterize the fitness consequences of lifetime movement tracks there is a need to integrate information from studies conducted at different spatial scales and with different methods (23). Harmonic radar and comparable technologies present promising opportunities to study the mechanisms and causes of movements at fine spatial scales.

Materials and Methods

Origin and Maintenance of Butterflies.

Butterflies used in this study originate from three regions: the Åland Islands in Finland, the island of Saaremaa in western Estonia (n = 24, 11 families), and the Tian Shan mountains in western China (n = 11, 3 families). Individuals from Åland originated either from newly established populations at sites known to have been unoccupied in the previous year (n = 15, 7 families), or from old populations at sites that had been occupied by a local breeding population for a minimum of 5 years (n = 16, 5 families). The Chinese butterflies were somewhat bigger (mean pupal weight, 216 mg) than the others (201–205 mg), but the overall difference in size among population types was not significant (F_3,60 = 2.45 P = 0.072). Larvae were reared under the same conditions from winter diapause onwards. Newly eclosed unmated females were marked individually and fitted with a transponder that enables real-time tracking with harmonic radar (24). For details on butterfly maintenance, see supporting information (SI) Text.

Field Procedures.

The tracking experiments were conducted in the open heath at East Wretham in Norfolk, United Kingdom (OS coordinates TL914878). The habitat is representative of open short grasslands typical for the Glanville fritillary, with nectar plants but no host plants. The harmonic radar was positioned in the center of the experimental arena to provide optimum coverage (Fig. 1). The transponders fitted to the butterflies pick up the transmitted radar signal, and immediately emit a signal at twice this frequency to which the radar receiver has been selectively tuned. When ready for release, the butterfly number and transponder number and color were noted, and insects were carefully placed on a patch of bare ground, and allowed to fly when ready.

Because the radar cannot distinguish among individuals, we released the butterflies in small groups of 3–6 individuals, one group in the morning (≈11:00 h) and the second one in the afternoon (≈14:00 h). Butterflies that did not disperse out of the experimental arena were retrieved after each experiment to avoid accumulating many butterflies that would interfere with tracking of the focal butterflies. For further details, see SI Text and Table S1.

Data Preparation and Data Quality.

In the raw data provided by the harmonic radar, the location of the transponder attached to a butterfly is represented by a cloud of some 5–20 sample points above the noise threshold; these points are displayed on the radar Plan Position Indicator (PPI) screen. Of these points, the one nearest to the radar can be considered to approximate the true spatial location of the target (Fig. 1 Inset). We developed computer algorithms to aid in the reconstruction of the flight paths based on the radar data (SI Text). The accuracy of the radar data were examined by keeping one transponder in a fixed position throughout the experiment, indicating that typical error in estimated locations is of the order of 2–3 m (SI Text).

For some of the analyses it was necessary to exclude periods during which an individual was visible to the radar but not moving. To do so, we subsampled the flight paths so that the minimum distance between any two observations was at least 3 or 20 m (depending on the analysis). Details on data selection and correction are given in SI Text.

Statistical Analyses.

The statistical analyses were performed with SAS 9.1.3 by using the macro Glimmix. We used backward model selection, in which we started with the full set of explanatory variables and removed the nonsignificant variables from the model (but retaining the main effect if an interaction was significant). We used type III to test for significance, with P = 0.05 as the cutoff level.

Activity based on maximal movement in two hours.

For each individual, we selected the 2-h period during which it moved the longest distance (data not subsampled). The movement distances were log transformed to obtain a roughly normally distributed variance. Our main interest was to test whether the movement distances depended on population type. We controlled in the model for the time of the day, the average temperature, and average wind speed during the flight period. We included a quadratic term for temperature, as we expected peak movements at an intermediate optimal temperature, and for the time, as we expected peak movements in the afternoon at time of maximal solar radiation. To examine whether individuals from different populations responded to temperature in dissimilar manner, we included in the model the interaction between population type and temperature. Day was included as a random factor.

We examined whether the angle between the 2-h displacement and the wind direction deviated from random by contrasting it with a uniform distribution in [−180°, 180°). Letting m₁ be the number of angles with absolute value <45°, m₂ the number of angles with absolute value >135°, and n the total number of angles, the random expectation is that m₁ = m₂ = n/4. We tested whether m₁ or m₂ exceeded the random expectation by calculating p_i = P(Bin(n,1/4) ≥ m_i) for i = 1, 2.

Activity based on movements in 5-min intervals.

To measure the frequency of movements and their dependence on environmental conditions, we split each day into 5-min intervals. For each time interval, we considered the individuals that were known to be in the study area based on an observation both before and after the focal period. For each such individual, we recorded a binary variable indicating whether the individual was active (observed to move at least 5 m), and in the case of active individuals also the distance moved and the direction of the observed displacement (data not subsampled).

For the individuals that were classified as active we modeled the log transformed distance moved by using population type, time (and its quadratic term), temperature (and its quadratic term and interaction with population type), and wind as explanatory variables. In the model we included the possibility of temporal autocorrelation by assuming the covariance structure Cov(ε_t, ε_t′) ∝ ρ^|t−t′| for the residual term, and used individual (nested within the population type) as a random effect. We tested for association between displacement and wind direction in the same way as for the maximal movement distance within 2 h (above).

We modeled separately the probabilities by which the individuals switched from active to inactive and from inactive to active. Both were modeled by using logistic regression, with the same explanatory variables as with move length. Modeling the two transition probabilities separately corresponds to viewing the activity state as a Markov process. Because the Markov process description already accounts for first-order temporal autocorrelation for the activity state, we did not include temporal autocorrelation for the models of transition probabilities.

Speed and length of individual flight bouts.

We considered flight continuous if the speed between observed locations (data not subsampled) remained over the threshold value of 1 m/s. Because of coverage problems with the radar, it was not always possible to determine whether the measured flight bout covered the entire track between resting points or whether it was part of a longer bout. For this reason, we included only flight bouts for which the distance between the starting point and the previous observation did not exceed 15 m, and for which the distance from the endpoint to the next observation was within 15 m. For each flight bout we calculated the distance moved and the average ground speed. We tested whether the ground speed and the log-transformed length of the flight bout depended on population type, controlling for possible effects of temperature (and its quadratic term and interaction with population type), time of the day (and its quadratic term), and wind speed during the flight bout. The temporal autocorrelation structure Cov(ε_t, ε_t′) ∝ ρ^|t−t′| was assumed for the residual term, and we used individual (nested within the population type) as a random effect.

We furthermore tested whether the log-transformed length or the log-transformed duration of the flight bout was associated with ground speed, controlling for the individual as a random factor. We tested for association of displacement direction with wind direction as in the analyses of maximal activity in 2h.

Edge-following.

The heath in which the experiment was conducted is bordered by woodland in several directions. Based on the raw data, it was apparent that butterflies tended to follow the edges between the heath and the woodland. We calculated for each location (data subsampled to 3 m) the distance to the nearest edge. For the individuals that approached the edge (distance to the edge 20 m or less), we calculated the distance along the flight path before the individual left the edge (distance to the edge 50 m or more). We tested whether the log-transformed distance moved along the edge depended on population type, controlling for the individual as a random effect.

Geometry of the flight paths.

To analyze whether the butterflies exhibited different geometries of their flight paths, we calculated two measures of path curvature. The first measure is based on the ratio between displacement and movement distance, whereas the second one relates to the distribution of turning angles. To calculate the first measure, we first split the flight path (data subsampled to 3 m) of each individual into segments of 200–220 m as measured along the flight path (because of discrete sampling it was not possible to split the track to segments of exactly the same length). As a measure of maximal displacement we calculated for each segment the largest distance between any two locations (not necessarily the first and last locations, for example, if the individual did a loop returning back close to the first location). Because the coverage of the radar varied across the study area, some regions produced a more dense set of locations than others. In a region with poor coverage, the reconstructed flight path is likely to be less detailed and hence less curved. To control for this, we regressed the displacement against the number of observed locations in the segment, and used the residual as a corrected measure of path curvature. We tested whether the path curvatures depend on population type, including the individual as a random effect.

To examine whether the turning angles depend on population type, we subsampled the data to 20 m and transformed the turning angles by taking the absolute of the cosine. We tested whether the probability to turn back (absolute value of turning angle >135°) depends on population type and a binary variable indicating if the individual is close to an edge (within 20 m). In these tests, the individual was included as a random effect.