Movement ecology of migration in turkey vultures

Abstract

We develop individual-based movement ecology models (MEM) to explore turkey vulture (Cathartes aura) migration decisions at both hourly and daily scales. Vulture movements in 10 migration events were recorded with satellite-reporting GPS sensors, and flight behavior was observed visually, aided by on-the-ground VHF radio-tracking. We used the North American Regional Reanalysis dataset to obtain values for wind speed, turbulent kinetic energy (TKE), and cloud height and used a digital elevation model for a measure of terrain ruggedness. A turkey vulture fitted with a heart-rate logger during 124 h of flight during 38 contiguous days showed only a small increase in mean heart rate as distance traveled per day increased, which suggests that, unlike flapping, soaring flight does not lead to greatly increased metabolic costs. Data from 10 migrations for 724 hourly segments and 152 daily segments showed that vultures depended heavily upon high levels of TKE in the atmospheric boundary layer to increase flight distances and maintain preferred bearings at both hourly and daily scales. We suggest how the MEM can be extended to other spatial and temporal scales of avian migration. Our success in relating model-derived atmospheric variables to migration indicates the potential of using regional reanalysis data, as here, and potentially other regional, higher-resolution, atmospheric models in predicting changing movement patterns of soaring birds under various scenarios of climate and land use change.

Traditionally, bird migration has been treated separately relative to other movements within an individual's life history (1–2). Although long-distance migration operates on different scales and produces different patterns than those of other movement types in a bird's life cycle, there are also many similarities (cf. ref. 3). As in other biotic movements, migration involves the assessment of internal state of the organism, external factors, and past behavior to make decisions about motion and navigation (4).

One significant challenge of migration research is measuring the extent to which migratory routes and schedules of individual migrants are influenced by external factors, including wind direction and speed (5–6), food availability and habitat (2), and the behavior of other migrants (1, 7). One important axis of variation among migratory birds is the extent to which environmental factors act as facilitators of, as opposed to barriers to, movement. Determining the effects of environmental factors is particularly important for soaring birds, whose movements rely upon environmental factors such as deflection updrafts and thermal convection as their principle means of propulsion, whereas those using primarily flapping flight are, in principal, not directly dependent on environmental forces for propulsion and lift. Although we recognize that this categorization can be overly simplistic (see, for example, ref. 8) and that other categorizations based on ecological function exist (9–10), the dichotomy of soaring versus flapping migration can play a useful role in understanding the internal costs of movement, flexibility of migration timing, and the ability to adopt new routes (refs. 1 and 2 and references therein).

Diurnal migrants are an excellent group in which to explore this issue, because they span the full range from soaring migrants [e.g., many raptors; ref. (1)] to flapping fliers [e.g., shorebirds (11)]. Some migrants, including swallows (12), raptors (1), and bee-eaters (N. Sapir, personal communication), switch between flapping and soaring flight modes based on atmospheric conditions. Turkey vultures are obligate soaring migrants (in the sense of 1). They rarely travel long distances without the aid of thermals and updrafts, and anthropogenic night-time thermals can increase their daily activity period (13). Because turkey vultures regularly perform long-distance movements within an ecological group that traditionally does not, we feel they can be used as a test case, against which future studies of this dichotomy in species that use both strategies can be compared.

Here, we set out a test case to assess the role of external factors and internal state on movement and navigation decisions. We seek to test the hypotheses that (i) specific route choices are determined to a large extent by wind, topography, and availability of turbulent uplift; (ii) the movement ecology framework can be used to formulate a movement equation that describes movement in terms of measurable proximal variables, including environmental variables and lagged distances and bearing deviations, and that this model can be fitted to the data using mixed and linear statistical models and autocorrelation functions; and (iii) that atmospheric regional-scale-modeling data can be effectively used to approximate the environmental conditions that affect migration flights. The movement ecology framework (4) guides the decomposition of complex movement phenomena into specific behavioral and environmental components. This provides a framework for the combination of meteorological and geographical data and direct observations of migrating birds to elucidate the proximate mechanisms driving vulture migration and, potentially, formulate hypotheses about evolutionary factors driving bird migration.

We focus on estimating the movement decision functions using external factors, internal state, and past behavior by fitting movement and navigation equations; we use weather data from a regional-scale observation-model reanalysis product and digital elevation model to estimate important components of the external factors, and measure heart rate to estimate internal state. Additionally, we evaluate how characteristics of present and preceding movements, such as previous distance, direction, altitude, speed, and autoregressive components of movement, influence subsequent movement.

Defining a movement ecology model (MEM) for migration requires that we “decompose” migration into different scales of movement: (i) A microscale (mm-meters, seconds-minutes), which represents the size of turbulent eddies around the bird and the instantaneous conditions that the bird perceives, and where many decisions about movement take place. Unfortunately, due to the chaotic nature of turbulent flows and the limitations of current computation and measurement ability, it is impossible to know the exact microscale conditions that determine a bird's movement. (ii) A coarser scale (tens of km and few hours), which provides a convenient source of information, because data from regional atmospheric models and miniature measurement devices are available at this regional scale. Some tactical decisions about migration movement are probably made at the coarser scale when perceived information is aggregated (e.g., 14–16). For convenience, we refer to this coarser scale as the “hourly scale,” and we use the hourly scale as a surrogate to the micromechanistic scale to determine how appropriate and useful information at this resolution can be to study migration movement. (iii) A daily scale, in which decisions about refueling, route choice, and distance to be traveled are set (for example, 17–19). (iv) An annual scale, in which birds (or other organisms) assess the success of previous migratory choices and decide on movements accordingly (20). (v) A life-history scale where broad decisions such as when and where (or if, in the case of facultative migrants) to migrate are set (for example 21). (vi) Finally, a long-term evolutionary scale in which natural selection on aspects of migration takes place (22). Understanding larger-scale phenomena requires mechanistic understanding at smaller scales. We focus on the hourly and daily scales where empirical data allow direct analysis.

The MEM framework provides an explicit guide to data analysis. Here, we parameterize, at two scales, the MEM controlling the migratory movements of turkey vultures. By fitting empirical data to the MEM, we set out explicitly to assess the relative roles of external-factor variables (turbulence, horizontal winds, and topography), internal state (heart rate), and the role of present state (altitude, speed) and past behavior (autoregressive components of movement) in determining the navigation and movement of a soaring migrant. Here, we assess navigation at two scales by looking for deviations from a local axis of movement (established based on the previous hours or days of movement); we infer that smaller deviations from a movement axis reflect a more direct route to local goals. Movement is assessed by looking at straight-line flight distances at two scales of movement, hourly and daily. We trapped 12 turkey vultures at carcasses in northeastern Pennsylvania and on nests in Saskatchewan, Canada, between August 2003 and November 2006. Of these, seven birds were fitted with GPS satellite tracking tags (Microwave Telemetry). A subset of the GPS birds was fitted with interperitoneal data loggers that recorded heart rate at 2-s intervals (Biometistics). GPS data on movements were collected at hourly intervals on all birds via the ARGOS satellite network. We were able to record hourly movements in 10 one-way migratory journeys in the seven GPS-fitted birds. These journeys totaled 724 hourly migratory movement segments that met our data quality criteria (described in Methods) and 152 daily movements. We used close proxies and representative variables to assess the effects of internal state, the role of past behavior, the initial state at each movement leg, and external factors. Mixed-effect linear models were used to fit these data to the MEM at both the hourly and daily scale of migration.

Results

We began with the general MEM (4) and adapted it to address external, internal, and temporal variables in a specific way (see Methods). Essentially, we assumed that a linear combination of the three classes of variables and their interactions would inform a movement decision function, and a navigation-decision function. We then tested these variables statistically.

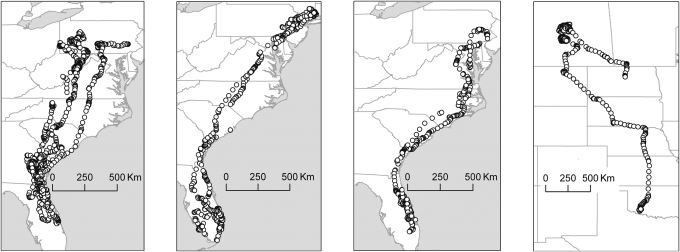
Ten migration events were successfully recorded in seven birds, including six southbound movements in fall and four northbound movements in spring. Turkey vultures caught in Pennsylvania migrated along the east coast of the U.S., principally to Florida and other areas of the southeast (Fig. 1). Two vultures caught in Saskatchewan, Canada did not complete migrations, but traveled through the central US before their accidental deaths. All birds were adults (≈3 years of age). For all seven birds, the longest straight-line distance traveled in a day was 327 km, and the longest straight-line hourly movement was 68 km. Birds did not migrate on 15 of the 152 days (10%). The straight-line distances between successive GPS observations grossly underestimate the total distances traveled, because visually tracked individuals revealed circuitous flight paths.

Fig. 1.

Maps of the migratory movements. At the far right are the two migratory tracks that originated in Saskatchewan, whereas the first three maps show the migrations of turkey vultures that were captured in Pennsylvania.

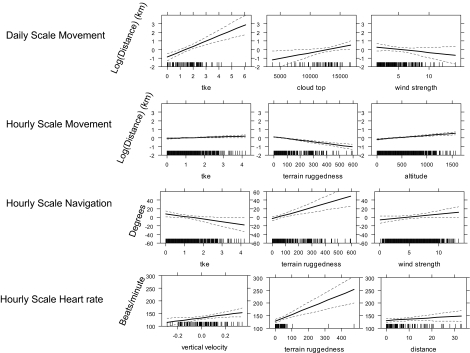
We measured field heart rate successfully in one bird during 38 days of southbound migration. An analysis of the heart rate (Fig. 2) showed it to be determined in only small part by distance; this suggests that, unlike flapping, soaring flight does not lead to greatly increasing metabolic costs with distance. Much more important in predicting heart rate were the vertical movements of air (as measured by the vertical movement of pressure levels in the model; VVEL) and the ruggedness of the terrain. As mentioned below, rugged terrain can change the spatial structure and consistency of thermals, which could lead to a less efficient use of atmospheric energy. We hypothesized that movement (both motion and navigation) is an autoregressive process: Across scales, distances and turning angles are likely to depend on previous movements. We fit the distances and bearing deviations at both the hourly and daily scale to autoregressive integrated moving average models to test the degree and magnitude of any autoregressive components in these time series (23). At all scales, movement vectors fit the ARIMA (1, 0, 0) class of models, which can be interpreted conceptually as a correlated random walk; distances and turning angles were influenced significantly only by the movement immediately preceding. Coefficients of autoregressivity are listed in supporting information (SI) Appendix. Future work, using higher-resolution data sources (e.g., 20), may improve the informatiom resulting from autoregressive integrated moving average approaches and bridge the gap between these simple approaches and other movement models, such as Lévy walks (24). In any event, we suggest that appropriate null distributions for the relation to previous states be evaluated as an important part of the analysis of movements.

Fig. 2.

Effects plots of the major findings in our statistical analysis. Effects of external factors on daily scale movement, hourly scale movement, hourly scale navigation, and hourly scale heart rate are shown. Plots were generated from the mixed effects linear models summarized in SI Appendix, Appendix 4.

Next, we set out to test the role of external factors (SI Appendix, Appendix 4) in determining the distance and turning angles of migration. We used turning angles as an indirect proxy for navigation, which we measured as an angular deviation from an axis of movement established by the previous 7 h (hourly scale) or week (daily scale) of movement. These two scales were chosen to assess the relative roles of scale in studying movement; the hourly scale is the smallest scale that was feasible for us to measure and record standardized data, whereas the daily scale is a common scale in studies of movement and especially migration. For some birds, we had more than one “migratory event,” which we defined as the collection of all daily and hourly movements in a given (fall or spring) migration season. Mixed effect models were run with random effects for individual movement events nested within migratory events, which were in turn nested within birds. There were no significant random effects for birds or migratory events at the scales we examined (P > 0.5).

Bearing deviations, our proxy for navigation decisions, were included as a variable in movement models, and movement (log distance) was included as a variable in navigation models. Bearing deviation had a negative association with distance traveled at an hourly scale and a positive association at the daily scale. This suggests that, hour to hour, birds are less likely to travel far if they are off-course. And at the daily scale, this result is likely due to the smaller distances and larger number of days traveled in a southeastern direction during the predominantly fall migratory events analyzed (Fig. 1).

Distance traveled was most strongly affected at both hourly and daily scales by turbulent kinetic energy (TKE), higher values of which were correlated with increased distance traveled (Fig. 2). Air movements represented as TKE result either from thermal convection or the shear of horizontal winds by the surface. In most situations, TKE generated by thermal convection results in larger, more structured air movements that are often used by soaring birds (cf. ref. 25); however, birds that migrate along mountain ridges are likely taking advantage of shear-generated TKE. At the daily scale, cloud top height, which indicates the strength of convective activity in the atmospheric boundary layer, had a strong positive effect on distance traveled. The role of this larger-scale atmospheric indicator is visible only at a larger scale of analysis, reinforcing the importance of scale in defining the scope of inference in studies such as this.

Terrain ruggedness had a negative effect on distance traveled, although this main effect was not as strong in magnitude as the positive effect of TKE. Terrain ruggedness had a very strong interaction, however, with TKE: ruggedness had large negative effects on distance traveled only at high values of TKE, suggesting that, on days with strong convective air-flow, ruggedness can act to decrease the spatiotemporal predictability of uplift and to decrease the coherent length scale of the spatial structure of thermal convection over rough terrain (e.g., ref. 26). The birds in this study primarily migrated along level ground where ruggedness is likely to disrupt otherwise predictable thermals, but other raptors that migrate along the Appalachian chain of mountains clearly benefit from the organizing effect of mountain ridges on wind-generated TKE (27) .

Wind speed had a negative effect on distance traveled at the daily scale. The negative effects of terrain ruggedness and horizontal winds together with the positive effect of TKE suggests that it is the thermal-convective component of TKE that most enables soaring and migratory movements in turkey vultures. As with distance, TKE had a strong effect on navigation (bearing deviation); high values of TKE strongly reduced the bearing deviation. This suggests that whenever uplift in the form of convectively generated TKE (i.e., thermals) is readily available, birds are able to fly in their preferred direction, whereas when there is less available uplift, deviations from the preferred direction of travel in search of useful energy are required to maintain passive flight. Strong winds increased bearing deviations; and cross winds are likely to cause wind-drift and blow the birds off their intended course, as in other raptors (1, 25). Terrain ruggedness also increased bearing deviations; a rugged landscape can disrupt the structure of convective cells, decreasing the availability of atmospheric energy in the preferred direction. Such landscapes interact with cross-winds to generate uplift along valley edges and topographic peaks, which may tempt vultures off their principal axis of movement.

At the hourly scale, but not at the daily scale, flight altitude and speed measured at the start of the movement vector had positive effects on the distance traveled: Birds that started a vector flying high and fast had more momentum and potential energy to travel farther. Thus, birds at this scale are more likely to fly long distances when they are headed in the preferred direction (i.e., the regional principal axis of migration). Full statistical models for all these results are presented in SI Appendix, Appendix 2 and Table 1.

Discussion

Migrants move and navigate in response to a host of external, internal, and temporal factors. Using a range of meteorological, geographical, and internal variables, we found support for the hypothesis that proximate route choices are affected by external meteorological and topographic factors. Increasing flight distances had a relatively small effect on measured heart rate. External factors, such as rugged terrain and the vertical movements of pressure levels in the atmosphere, had a relatively large effect on observed heart rate during migration (Fig. 2). Given the relatively small magnitude of variations in heart rate during flight, a detailed look at the effects of external factors on movements is appropriate.

In any study of movement, a detailed look at scales of movements and scopes of inference is critical. SI Appendix, Appendix 1 shows a series of possible scales in studies of migration and examples of literature working at these scales. We have focused on two scales: an hourly scale and a daily scale. The hourly scale represents the semistationary meteorological conditions, including wind and turbulence statistics, and it is the finest scale where meteorological data are currently available over large domains. In this study, it acts as a surrogate for the micromechanistic scale, whereas the daily scale is common in migration studies. Scale restrictions can have implicit drawbacks: The hourly scale, for example, grossly underestimates actual movement and thus becomes less appropriate for assessing tortuosity in studies of orientation.

Turkey vultures appear to depend on convectively generated TKE to supply the necessary vertical movement of air for their movements. The species exerts little additional energy during flight, and, as in albatrosses (28), long-distance movements do not strain the birds energetically more than do short-distance flights.

Several studies have looked at the relationship of soaring birds to convective and sheer turbulence, using direct observation, and found that use of thermals for soaring varies with species, body size, behavior, time of day, and thermal intensity (6, 14, 29, 30). The turkey vulture's ability to soar effectively in turbulent winds may be enhanced by its dihedral wing profile, which is inherently more stable than that of birds that soar with a horizontal wing profile (31) and may be particularly important in situations in turbulent conditions within the atmospheric boundary layer but close to the ground (32). Our findings of the role of horizontal winds contrast with those of Thorup et al. (5) on the effects of wind on migrating Ospreys (Pandion haliaetus) and Honey Buzzards (Pernis apivorus), which do not have a dihedral wing shape. These birds, adapted for more direct flight, engage in wind-drift compensation (5). We did not detect wind-drift compensation in the turkey vultures we followed. Rather, they showed increased deviation from the regional principal axis of migration (i.e., uncompensated wind drift) and traveled shorter distances in high winds irrespective of their direction. One likely explanation for this is that wind-drift compensation in vultures happens at a scale different from the scales explored here. Indeed, it is not likely that our analysis would detect responses to wind that happen at the micromechanistic scale, or at fairly large, strategic scales in the migration.

Our results show that TKE data generated by an open, regional-scale, meteorological dataset derived from the simulation results of a regional model, can serve as a surrogate measure for the intensity of thermals. This suggests a new avenue for studying use of turbulence in flying birds. The NARR meteorological dataset is a regional model product, forced by a large number of observations. Unlike direct meteorological observations, NARR is available over large domains in space and time. Even though the spatial and temporal resolution of the NARR model is much coarser than the physical size and turn-over time of eddies that generate TKE, the model parameterization appears to be sensitive enough, and the bird response strong enough, to show a significant correlation between the two. This indicates that data at a regional resolution of a few square kilometers and a few hours can be used as a substitute for high-resolution micromechanistic scale turbulence data, which to date has been impossible to obtain along a large portion of a migratory path. Customized runs of higher-resolution regional atmospheric models and large eddy simulations that resolve turbulent motion in the ABL (e.g., 33) and, together with more detailed physiological techniques, may also help confirm and extend these findings. This is important, because a major shortcoming of this study is that several of our major results are based on surrogates, including heart rate for energy expenditure, TKE for thermal convection, and terrain ruggedness for a “thermal-dissipating force.” Atmospheric models, which are a major tool in studying and predicting the effects of regional and global climate changes, the ecological effects of land-use changes (e.g., 34–36) and bird flight (5, 37–39) could be used to build on these equations of movement to test specific ecological and conservation-related hypotheses. By understanding movement-decision functions in the context of this class of models, we will come much closer to being able to predict future migration patterns and details of soaring flight under different future scenarios.

Our work with vultures suggests a way to understand the migration decisions that are being made and the integration of external factors that drives these decisions. This work also shows that the MEM can be approached empirically and that data can inform the relative strengths of linkages among factors and state variables. We think this MEM work can serve as the foundation for increased understanding of movements by focusing further empirical work on especially interesting systems and by serving as a basis for more strategic (i.e., adaptive) models of bird migration.

Methods

Tracking Vultures.

For information on the capture and tracking of vultures, please see SI Appendix, Appendix 3.

Assembly of Database.

We assembled hourly-movement vectors coded in radial coordinates from the GPS movement data. Radial coordinates have the advantage of (i) uncoupling the strong correlation of movements in the X and Y directions in both movement and wind speed, (ii) properly weighting large changes in direction on small movement days, and (iii) conceptually separating the ability to fly long distances with the direction of flight. In radial coordinates, it becomes necessary to establish a principal axis of movement and to measure angles (of both wind direction and movement) in terms of deviations from that axis of migration. In addition, the interaction of wind speed and direction becomes a critical measure for interpreting the appropriate effects of wind.

Because the migratory journeys examined consisted of multiple legs with different dominant bearings, we rejected the idea that we could choose a single axis of migration for all points along the migratory journey. Instead, for every movement vector, we used the bearings of the previous seven movement vectors to establish a direction of movement; we term this the local axis of migration. We then took the absolute value of bearing of the movement vector minus the local axis of migration; we termed this the bearing deviation. Wind directions were calculated in the same way, as a bearing minus the local axis of migration; we termed this the wind deviation. Thus, a wind deviation of zero would be considered a tailwind, whereas a wind deviation of 90° would be a considered a cross-wind. Following Oliveira et al. (40), we used bearing and wind deviations that were <90° to fit linear models. All angle calculations were done using the “Circular” package in R, Version 2.3.1 (41, 42), which uses a wrapped Cauchy distribution as the null distribution.

After discarding data from non-migratory birds (i.e., birds that did not show seasonal latitudinal shifts greater than summer latitudinal variance) and poorly performing transmitters, our dataset consisted of 10 migratory events from seven birds. To calculate latitudinal variance, we measured the maximum and minimum latitude in June and July. If birds did not exceed the minimum summer latitude and cover a latitudinal range greater than there summer range during the fall (October and November), we considered them nonmigratory. We adopted a conservative filter for hourly scale analysis that consisted of a movement of at least 4 km, during the months of October, November, April, and May, and during which both the beginning and end of each hour was successfully recorded by the GPS loggers (i.e., there are consecutive hourly measurements on the GPS that can bound an hour of movement). Months for filtering were selected by examining the timing of the beginnings and ends of migratory tracks visually within our data and determining the months of peak migration from counts at migration watchsites (43). The distance minimum was calculated by iterate plotting of the density function of mean bearing of movement using an increasing distance minimum. The break-point at which a normal distribution of bearings with a stable standard error emerged from the initially uniform distribution of bearings was found to be the 4-km distance minimum. For daily scale analysis, days were calculated as being from 0600 hours to the following 0600 hours in the local time zone. Points where the bird was within the above migratory months and between the beginning and end of latitudinal movements were included, except for those in which the beginning and end of the 24-hour period were not both measured successfully. A total of 154 daily movements fit these criteria.

We first examined spring and fall movements examined separately. Finding no difference between fall and spring movements (graphed distributions were visually indistinguishable, and t tests of logged distances, bearings shifted 180°, and total durations between spring and fall were all >0.5), spring bearings were shifted 180° and merged with fall movements. The month of data collection was retained as a main effect. Distance was log-transformed to satisfy assumptions of normality.

Equations of Motion.

We derived 2 equations from the MEM, using equations 2 and 3 of Nathan et al. (4), respectively, to describe the motion, Ω, and navigation, Φ, decision functions for turkey vultures. These structured our analyses. We used the straight line (i.e., loxodrome route) distances at two scales as a proxy for motion and bearing deviations as a proxy for navigation. We generated a series of independent variables that represented internal state, w, external factors, r, and temporal qualities, u_t, that might influence the bird's MEM decision. We used a statistical model to identify the relevant dependent variables at each scale and estimate their coefficients in a generalized equation structure, which represent a linear combination of all external, internal, and temporal terms, and interactions and autocorrelations, affecting the movement and navigation of a passive migrant:

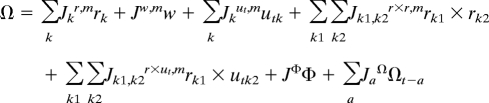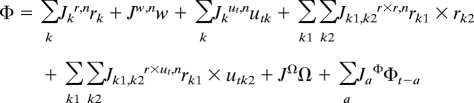Where subscripts k, k1, k2 are indexes over all of the variables in a categorical group. A subscript a is an index for time-lag (in integer units of hour or day). Interaction terms are marked with ×. J is the model coefficients for the variables, which we estimate statistically. A superscript for J marks the categorical group and the MEM variable (m, motion; n, navigation) it is associated with, and a subscript is a counter. We fit an autoregressive correlation structure to the dependent variable, which is represented by the final term in the equations; this accounts for the fact that all movement decisions must be viewed through the lens of previous movement. Because the vultures we tracked are strictly passive migrants, these equations represent the components within a single motion mode. They do not include the more complex model structure and decision parameters for switching between motion modes. While all of the following variables were considered, only the variables that had significant contributions were included in the final model.

Predictive Variables.

We calculated predictive variables in the following three categories: external, internal, and temporal.

External variables.

Meteorology.

Meteorological variable values were taken from the National Center for Environmental Prediction (NCEP) North American Regional Reanalysis (NARR) dataset. NARR (44) is a product of the ETA regional model (45) forced with a large set of satellite, surface and balloon observations. It consists of a 3D grid that covers all of North America with a horizontal resolution of 32 × 32 km², a vertical resolution defined along pressure levels, and a temporal resolution of 2 min. Snapshot and time averaged data are saved every 3 h.

The bird's longitude and latitude were matched with the nearest NARR grid-cell center. NARR data for that cell were interpolated linearly in time to the timestamp of the bird GPS data point. For 3D variables, we interpolated vertically between the NARR variable values for pressure levels height (HGT) closest to the GPS-determined altitude of the bird. Four meteorological variables were included: (i) Wind speed and wind direction, processed from the NARR variables for latitudinal and longitudinal wind velocities (UGRD and VGRD, respectively). Horizontal winds were translated into polar coordinates, and the angle was translated into a deviation from a local mean direction of movement. (ii) TKE, which is parameterized in NARR using empirical relationships between surface fluxes and the stability of the atmospheric boundary layer (ABL) (46). High TKE is typical for days with intermediate wind levels and strong convective heat flux from the ground (cloudless hot days) and indicates large thermals; conversely, days with very strong winds, neutral boundary layer conditions, and strong mechanical shear can also produce high values of TKE (referred to here as “shear” TKE; 47). (iii) Pressure vertical velocity (VVEL) is defined as the rate of change over time of the height of the pressure levels, which make up the vertical dimension of the grid. The vertical movement of pressure surfaces is associated with the daily cycle of ABL dynamics and mesoscale pressure fronts (4). Cloud top height, a two-dimensional model field, indicates the strength of parameterized convective activity in the ABL. To eliminate strongly cross-correlated variables (such as cloud base, cloud depth, and cloud top) from the model, we ran each variable separately in a mixed linear model including all weather components and no interactions, with ln(Distance) as the dependent variable. Cloud top height was found to be the variable with the best fit using AIC, BIC, and log-likelihood, and therefore, was included in the final model, whereas the other two, cloud base and cloud depth, were discarded.

Geography.

We used the GTOPO30 digital elevation model (DEM) available from the EROS database at the USGS, which has grid spacing of 30 arc seconds (≈1 km). We created a map of terrain ruggedness based on the variance in altitude of adjacent grid cells, using Manifold, Version 2.1. Terrain ruggedness was calculated according to the formula provided by Riley et al. (48) and provides a unitless index of variance in elevation.

Internal variables.

We modeled the role of internal state in migratory turkey vultures, using heart rate as a representation of the cost of movement. Six heart-rate loggers were deployed; three were recovered. One heart-rate logger worked successfully for a 38-day period, during which the vulture carrying it flew from northern Pennsylvania to southern North Carolina. This bird's behavior was monitored visually by Mandel, who followed the bird in a vehicle, and its positions were monitored by satellite tracked GPS harnessed to the back of the bird. Heart rate was averaged over 1-h periods that correspond to 1-h movement vectors recorded by the GPS. Because of the limited heart rate data, this internal effects model was run separately from external effects, using a simple linear model of heart rate vs. the log-transformed distance to estimate the cost of movement. Linear models of bearing deviation vs. heart rate were run to estimate the physiological cost, if any, of navigation decisions away from the local mean direction of movement. We also ran a linear model with heart rate as the dependent variable, against independent meteorological, geographical, and movement variables, in a similar fashion as the movement models.

Temporal variables.

Behavior at the beginning of a movement vector.

The speeds of travel and flight altitudes measured at the start of the movement vector represent the starting state of the migrating vulture at the beginning of any movement vector.

Past behavior estimated autoregressively.

We fit autoregressive integrated moving average (ARIMA) correlation matrices to all of the distance and bearing dataset separately to factor in the autoregressive components of movement. First, we modeled the 10 migratory journeys as random effects in a hierarchical, mixed model (see SI Appendix for full model summaries). Autoregressive integrated moving average models were fit to each dependent variable following the methodology outlined by Box and Jenkins (23), using autocorrelation, partial autocorrelation, and lag plots to assess the degree of autoregressivity and sampling noise. In all cases, the models consisted of a single autoregressive component. In short, at both temporal scales, movement was modeled as a correlated random walk.

Model simplification.

Statistical analyses of the variables above consisted of mixed linear models created using the “nlme” package in R (49). For each mixed model, an a priori correlation structure was specified using an autoregressive integrated moving average function. Correlated variables were tested independently against the log-transformed distance, and only the one with the most predictive power was kept. All models began with the inclusion of all main effects and all potentially relevant interactions. Backward selection, on interactions first, using maximum likelihood, was performed to determine the final model. Final models were compared with initial models, using ANOVA, and AIC was observed to decrease throughout model selection in all models. Parameter values were estimated using restricted maximum likelihood. The models were compared with identical models without random effects, to determine whether the random effects significantly changed the model. This was done by comparing the difference of −2×log-likelihoods with a χ² table at 1 degree of freedom.

Statistical Models.

Hourly Distance and Navigation Models.

The external effects on motion were modeled using the log-transformed distance as the dependent variable; for navigation, the deviation of bearing from a local mean was used. The variables for external effects and present state are listed in SI Appendix, Appendix 4.

Daily distance and navigation models.

We created vectors of daily movements for each vulture to determine the role of external effects on migratory movements at an intermediate temporal scale. We averaged wind and habitat variables in scaling our independent variables from hourly movements to daily movements. For TKE, pressure vertical velocity, and cloud top, which grow throughout the day and have a highly autoregressive daily structure, the maximum for each day was selected. For all variables, distributions of the reduced dataset were compared with the distributions of the original dataset to ensure that there was no loss of variability.

SI Appendix, Appendix 2 has further details on the models' run.