Individual movement behavior, matrix heterogeneity, and the dynamics of spatially structured populations

Abstract

The dynamics of spatially structured populations is characterized by within- and between-patch processes. The available theory describes the latter with simple distance-dependent functions that depend on landscape properties such as interpatch distance or patch size. Despite its potential role, we lack a good mechanistic understanding of how the movement of individuals between patches affects the dynamics of these populations. We used the theoretical framework provided by movement ecology to make a direct representation of the processes determining how individuals connect local populations in a spatially structured population of Iberian lynx. Interpatch processes depended on the heterogeneity of the matrix where patches are embedded and the parameters defining individual movement behavior. They were also very sensitive to the dynamic demographic variables limiting the time moving, the within-patch dynamics of available settlement sites (both spatiotemporally heterogeneous) and the response of individuals to the perceived risk while moving. These context-dependent dynamic factors are an inherent part of the movement process, producing connectivities and dispersal kernels whose variability is affected by other demographic processes. Mechanistic representations of interpatch movements, such as the one provided by the movement-ecology framework, permit the dynamic interaction of birth–death processes and individual movement behavior, thus improving our understanding of stochastic spatially structured populations.

Spatially structured populations (SSP) are composed of discrete patches of breeding habitat holding local populations that are connected by dispersing individuals. Their dynamics are characterized by local within-patch (birth and death rates) and global between-patch parameters (movement rates). There is an important core of theory characterizing some types of SSP, such as metapopulations and source-sink, by their different dynamic properties (1–3). Nonetheless, we still lack a more inclusive theory describing the continuous range of variability shown by SSP (4). The way to advance in our understanding of the processes involved is by focusing on the processes behind the variability shown by between-patch and within-patch properties (4–7). Only then, will we be able to make management and conservation predictions that can be linked directly to specific processes.

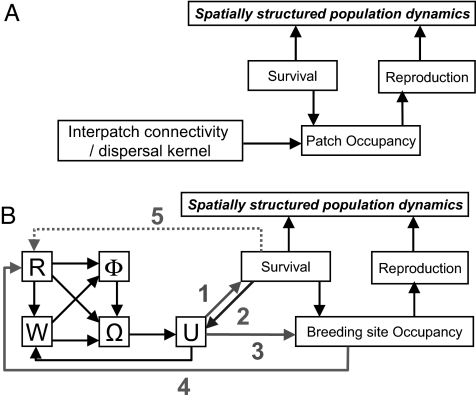
The dynamics of SSP are the result of processes at the level of individuals. Interactions with conspecifics and the environment generate demographic emergent properties that are described by processes at patch or at SSP levels. A basic description considers patch occupancy, reproduction, survival, and interpatch connectivities or distance kernels (Fig. 1A). Classically the pattern of patch occupancy is seen as the interplay between the mortality generating empty patches and the interpatch connectivities allowing their recolonization. Each patch can be characterized by its per capita birth B, death D, emigration E, and immigration I rates (4). The global dynamics of the system is described by a compensation axis reflecting the source-sink component of population structure with source populations exporting individuals (when B > D and E > I) and sinks and pseudosinks consuming them, and a mobility axis summarizing the involvement of local populations in between-patch processes, spanning from separate populations, when (E + I) ≈ 0, through metapopulations, when (E + I) < (B + D), to patchy populations, when (E + I) ≥ (B + D) (4).

Fig. 1.

Schematic representation of the processes involved in the dynamics of spatially structured populations. (A) Patch-centered view where survival and reproduction are considered as local processes. Between-patch processes (namely movement) are represented by a matrix of interpatch connectivities, commonly based on distance kernels (different survival regimes during interpatch processes act as modifiers of the complete kernel). (B) Individual centered representation, including the movement process of dispersing individuals in search of empty breeding sites (natal dispersal) as described within the movement-ecology framework. W, the internal state of the individuals motivating the movement; Ω, motion capacity; Φ, navigation capacity; R, external environmental conditions that can affect the internal state and the navigation and motion capacities; U, actual movement path followed by the individual. Numbered arrows represent the dynamic interaction of movement with demographic processes. Arrow 1, the actual path affects the survival (spatially heterogeneous, e.g., inside and outside a reserve); arrow 2, the actual survival of moving individuals affects the time moving and hence the length of the path; arrow 3, moving individuals settle in empty breeding sites, thus dynamically modifying the pattern of empty sites (which are dynamically generated); arrow 4, the pattern of empty sites is an external environmental modifier of the movement (potential targets); arrow 5, individuals perceive and respond to a differential risk of mortality associated with the presence of a fragmented matrix (the perceived risk depends on animal's position).

Much of the available theory describes between-patch processes with distance-dependent functions, implicitly assuming that the matrix between patches is homogeneous, not very relevant, or its heterogeneity is mostly random and hence can be spatiotemporally averaged (8–11). Nonetheless, there is considerable evidence showing that the matrix is important. Its heterogeneity can have profound effects on individual movement responses, on local population properties (E and I rates, distance kernels and connectivities), or on the actual dynamics of SSP (12–17). However, little is known about the mechanisms behind these effects at the level of individuals, with very few examples translating individual movement behavior to local population properties and then to the dynamics of the SSP. All this is probably a reflection of our lack of a clear mechanistic description of the movement process itself.

The movement-ecology framework provides a clear-cut mechanistic description of the basic processes involved in individual movement (18–19). Individuals are characterized by an internal state (W) directly related to the reasons behind the decision of the individual to move (goals), by a motion capacity (Ω) and by a navigation capacity (Φ, Fig. 1B). Navigation capacity is the ability of individuals to use information related to the goals, whereas motion capacity is the inherent ability to move with some properties. Individual motion capacity is modulated by the navigation capacity, affecting the movement path as a function of the information available to the individual. The dynamic interaction of these components with the environment (R) along time generates movement paths (U, Fig. 1B). Nevertheless, the movement ecology heuristic does not provide a connection with demography at the population level.

In this article, we aim to understand the role of individual-level movement processes and their interaction with survival and reproduction in generating the dynamics of a SSP in a highly heterogeneous matrix. We use the movement-ecology framework to characterize a model of movement of individuals from natal to breeding sites and link it with an individual-based spatially explicit demographic model. To achieve our aim, we first perform a traditional sensitivity analysis on the effect of model parameters on metapopulation growth rate, finding that the system is mostly sensitive to the survival of breeding animals. By evaluating the sensitivity on E and I, we find that that result does not mean that movement is not important because I strongly depends on the survival of breeding animals. Finally, we simulate different landscape scenarios, finding that matrix heterogeneity deeply affects the dynamics. The model is built and parameterized by using field data on the demography and individual movement behavior of Iberian lynxes (Lynx pardinus) living in a SSP.

Iberian Lynx in Doñana.

Doñana is a region of ≈2,500 km² in the southwest of Spain, at the heart of which there is a National Park (550 km²). Resident lynxes are territorial. The population is close to carrying capacity and has up to 14 potential territories. Territories are located in isolated patches of breeding habitat forming eight local populations (15, 20–24). Three of the patches are inside the National Park, where protection ensures high survival, whereas outside the mortality is high for all types of individuals. The system shows metapopulation properties and source-sink dynamics, with populations inside the park acting as sources and the ones outside as sinks (20–21). The matrix in which breeding habitat patches are embedded is used by animals during their interpatch movements. The matrix is composed by three types of habitat (22–24): barrier, which is never used; open, which is avoided but still used; and dispersal habitat, which lynxes use as available. Natal dispersal can last between a few weeks and more than a year.

We use an individual-based spatially explicit model to simulate the dynamics of the population (Fig. 1B). The model is composed of a demographic submodel [see The Demographic Submodel and The Movement Submodel in supporting information (SI) Appendix], which is briefly described below.

Individual Dispersal Movements.

Revilla et al. (15) described the dispersal movements of 30 lynxes at the temporal scale of periods of activity and used those data to construct and parameterize a simulation model to reproduce the movement of the same individuals. The model was able to replicate the field estimates of interpatch connectivities. Its performance and the relative importance of the different movement rules have been thoroughly analyzed (15). Virtual animals stochastically perform a sequence of movement steps in a landscape grid in which they can move to one of the surrounding eight cells or stay in their position. Time is modeled in steps of 1 day, within which individuals move sequentially. Here, we model population dynamics by adding survival and reproduction to that individual dispersal model within the conceptual framework of movement ecology (15, 18) see The Demographic Submodel and The Movement Submodel in SI Appendix).

Internal State.

We assume that for our spatiotemporal resolution, moving lynxes have two goals: finding unoccupied breeding habitat to settle and minimizing their risk of mortality. Empty territories can be located inside their own natal local population or somewhere else. Searching individuals minimize the time spent in open habitat or in areas with fragmented dispersal habitat.

Motion Capacity.

Lynxes have two default movement modes (18, 23, 25). The first is defined by the probability distributions of number of steps per day and the autocorrelation in turning angles when moving within unfragmented dispersal habitat. In the second movement mode, the autocorrelation of the path increases when animals move many steps per day (see The Movement Submodel in SI Appendix). Individuals use this second movement mode to leave their current local area, generating a path that resembles a Lèvy walk (27).

Navigation Capacity.

Lynxes can detect the type of habitat within their perceptual range (their eight-cell neighborhood), evaluating the existence of an empty territory whenever they detect a cell of breeding habitat. Open habitat strongly affects movement properties. Individuals avoid open habitat only in fragmented areas that have a reduced probability of use. At the same time, animals moving in fragmented areas increase the autocorrelation of their movement, resulting in faster moves per day. Lynxes explore the open habitat during their periods of activity but normally return to dispersal habitat as the period passes (exploration excursions; see The Movement Submodel in SI Appendix).

Survival and Settlement.

Dispersers move until they die or settle, suffering a higher mortality when outside the park (see Model Parameterization in SI Appendix). Additionally, we have some evidence that animals that spent more time on average in open habitat suffered an increased mortality (Cox proportional-hazard, P = 0.062). Therefore, we consider an additive increase of the risk of mortality when moving in open habitat (a linear increase in the daily mortality risk as a function of the proportion of time during each period of activity spent in open matrix; see The Movement Submodel in SI Appendix). The distribution and amount of breeding habitat determines the carrying capacity of each subpopulation (see The Demographic Submodel in SI Appendix). Females settle in empty breeding habitat, whereas males settle in areas where there is a lone resident female. Empty territories are generated on a daily basis by the mortality of residents.

Metapopulation Dynamics.

The system under the field-estimated parameterization has a high extinction probability. Dispersers move for an average of 111 days (SD = 152.6), with those finding a settlement site moving shorter periods than those dying (55 ± 107 vs. 175 ± 163 days). As expected from a typical metapopulation, local processes (B and D) are more important on a per capita basis than between population processes (E and I), with the local populations found inside the park acting as sources (B > D per capita), and net exporters (E > I, per capita, Fig. S1). On the other hand, the sinks outside the park are net importers (Fig. S1). All population units are below the compensation axis because of a high demographic stochasticity and, hence, the high extinction probability. The higher variability is observed in I values at source populations as well as E at sinks (Fig. S1). This variability is very important because it marks the rare events of empty source territories rescued by immigrants and sink populations having the chance of producing emigrants.

Metapopulation growth rate is strongly associated to parameters linked to the internal demography of source local populations: the survival of resident individuals explains almost half of the variance (Table S1). Only three movement parameters explained some variance of λ, two from the motion capacity (the number of steps moved per day and the strength of the autocorrelation in dispersal habitat) and one from the navigation capacity (the memory to return to dispersal habitat). The low variance explained by movement behavior parameters is reasonable, because the range of variability explored in the analyses is comparatively wider for survival and reproduction than for movement behavior parameters (Table S1). We wanted to explore only reasonable parameter values given field data, and not biologically implausible theoretical extremes. Nevertheless, if we look at the standardized parameter estimates of the statistical model, which can be compared between the blocks of reproduction-survival and movement behavior (Table S1), we observe the same results.

These results are typical for species with several breeding opportunities along their life, in which the most sensitive parameters determine how long breeding individuals can live (28–31). This might be the reason why the mechanistic understanding of individual movement has been neglected for such a long time in favor of birth–death processes and why recommendations for population management derived from sensitivity analyses tend to weigh in favor of birth–death parameters. This interpretation also holds here, but there are further effects that we cannot detect by looking only at λ, which is a very sensitive descriptor collapsing all of the effects of model structure and parameterization. As we show below, the survival of residents is not only a local-patch parameter, it is also an inherent part of the movement process.

E and I controls.

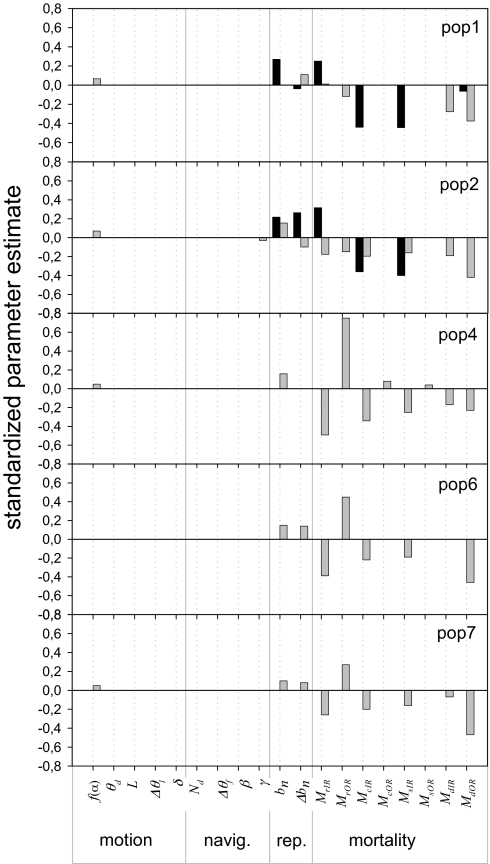
To understand the controls of E and I, we performed an analysis of sensitivity for each subpopulation (Fig. 2). E at source populations is positively controlled by reproductive rates and the mortality of residents inside the park and negatively controlled by the mortality of young and subadults inside the park (Fig. 2). The role of the mortality of residents inside the park is due to density dependence in reproduction, because a partially occupied source tends to produce more animals per capita (e.g., in population 1 B = 0.44 near carrying capacity, whereas B = 0.47 below it). In summary, E depends basically on the parameters controlling the number of animals available to start dispersal.

Fig. 2.

Sensitivity analysis of the effect of simulation parameters on yearly per capita emigration (E) and immigration (I) rates for each local population. Populations 1 and 2 (pop1 and pop2) are sources located inside a reserve; the rest are sinks. To compare the relative impact of the different simulation parameters on E and I, we obtained the standardized parameter estimates for E (black bars) and I (gray bars) from a statistical description using the parameters of the simulation model as independent variables. We excluded poor statistical models (adj r² < 0.4, corresponding with population 3, and E from sinks; for all of the plots 0.41〈adj r² < 0.75). We show only significant parameter estimates. Motion parameters: f(α), average number of steps per day; θ_d, autocorrelation in dispersal habitat; L, long-distance displacement threshold; Δθ_l, increase in autocorrelation in long-distance displacements; δ, bimodal distribution of turning angles. Navigation (Navig.): N_d, fragmentation threshold; Δθ_f, increase in autocorrelation in fragmented areas; β, avoidance of open habitat; γ, probability to return to dispersal habitat. Reproduction (Rep.): b_n, probability of reproduction; Δb_n, increase in reproduction probability. Mortality: M_rIR, mortality of residents inside the reserve; M_rOR, mortality of residents outside the reserve; M_cIR, mortality of cubs inside the reserve; M_cOR, mortality of cubs outside the reserve; M_sIR, mortality of subadults inside the reserve; M_sOR, mortality of subadults outside the reserve; M_dIR, mortality of dispersers inside the reserve; M_dOR, mortality of dispersers outside the reserve.

I at source populations is positively controlled by reproductive rates and negatively controlled by the mortality of residents both inside and outside, the mortality of young and subadults (except for the largest, population 1 in Fig. 2) and especially by the mortality of dispersers both inside and outside the park (Fig. 2). The same results hold for I at sink populations, except that the mortality of residents at sinks has a strong positive effect. Therefore, I rates depend on the number of animals available to emigrate, how long they can move and the dynamics of available settlement sites. The last also affects the time moving and shows a strong temporal heterogeneity. Note that survival during dispersal is spatially heterogeneous, and individuals can react to their perceived risk.

Parameters describing individual movement behavior show, at best, poor effects on both I and E (Fig. 2), indicating that, if the right model structure is identified, mechanistically rich models are probably more resilient to error propagation than previously thought (32–33). The use of the movement-ecology heuristic can be very helpful for this purpose, because it forces us to make explicit the behavioral processes involved, and the assumptions in case we simplify it. We tend to view behavioral parameters as the only responsibility of the movement process between populations. That is only half of the story. Within the movement-ecology framework, we immediately see that survival is an inherent part of the movement process, dynamically generating the patterns of available settlement sites, which is, in turn, an important part of the environmental dynamics of the landscape (arrow 4 in Fig. 1B), affecting the overall time dispersers can move (arrow 2 in Fig. 1B). Individual survival during dispersal is spatially heterogeneous because of the higher risk outside the park and in open habitat. Therefore, the actual path affects how long a disperser will move (arrow 1 in Fig. 1B). On the other hand, individuals can perceive some risk when moving, preferring safer areas and minimizing the time exposed to a higher risk, resulting in a longer dispersal event (arrow 5 in Fig. 1B).

These results are important for our understanding of the dynamics of SSP, because we tend to interpret interpatch connectivities as static, describing them with dispersal kernels or, at most, dependent on the behavior and matrix complexity. However, survival is an integrated dynamic modifier of the kernels, determining part of the environmental dynamics for the same matrix configuration. Different levels of survival while moving generate different E and I rates, whereas the spatiotemporal dynamics of the potential targets for moving individuals add stochasticity to the system, which is important, because it marks rescue events.

Additionally, our results are good news for the conservation of some types of SSP like ours. Theory predicts that asynchrony in the dynamics of local populations is important for long-term persistence (34–35) and that the high movement rates typical of highly mobile species will tend to couple the dynamics and increase extinction risk. This holds if individuals have a constant settlement rate. Conversely, we found that this is not necessarily the case, because it depends on the local dynamics of available sites, showing a strong density dependence. The system responds with flatter dispersal kernels at higher turnovers of settlement sites, with increased effective mobility only when far local populations need the immigrants. If the amount of breeding habitat is limiting and settlement is density dependent, then the coupling of the dynamics of different local populations will be buffered by the adjusted response of the realized kernels (36). Therefore connectivities and dispersal kernels are dynamic, context dependent and strongly linked to within patch dynamics.

Many works assume that the kernel of dispersal distances is an estimable function subject to selective pressures (e.g., 37). Nevertheless, the kernel we may estimate depends on the landscape and demographic context (where and when it was estimated) and the distribution is not stochastically “sampled” over the dynamics of the population because the tail occurs only under specific demographic conditions. For these reasons we need to focus on the movement processes when dealing with the evolution of dispersal distances (38).

Impact of Matrix Heterogeneity.

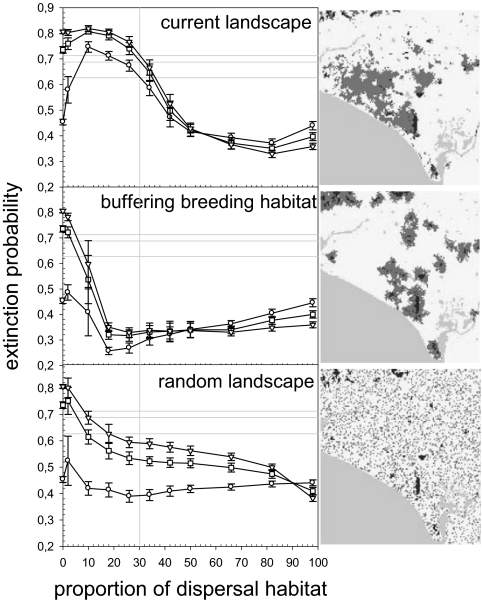
Previous work has shown that modifications of matrix heterogeneity can have important effects on connectivity and dispersal kernels (15, 39–41). More rarely, those effects have being translated to the dynamics and viability of SSP (12, 42). Here we explore the effect of changing matrix heterogeneity on the overall dynamics and on the actual E and I for each local population. We used the real configuration of the matrix in Doñana to which we added or removed dispersal habitat (in an autocorrelated way to keep the physiognomy) by changing the ratio of open to dispersal habitats. Additionally we considered a random distribution of dispersal habitat and a distribution buffering breeding habitat with dispersal habitat (Fig. 3).

Fig. 3.

Extinction probability in 100 years for landscapes with different levels of matrix heterogeneity. We considered the current landscape configuration (Top), a distribution of dispersal habitat buffering breeding habitat (Middle), and a random distribution of dispersal habitat (Bottom). In all cases, we only changed the proportion of dispersal/open habitats. The three maps show an example for each landscape configuration (dark gray represents breeding habitat, light gray barrier—the lower left corner is the Atlantic ocean—, intermediate gray dispersal habitat and white open habitat). We used three scenarios depending on the increase of risk of mortality during dispersal when individuals move in more fragmented areas (circles, no effect ρ = 0; squares, field estimate of the risk increase ρ = 5.8; triangles, ρ = 10; see The Movement Submodel and Model Parameterization in SI Appendix). In the three cases, the baseline mortality during dispersal was adjusted. The vertical gray line marks the proportion of dispersal habitat present in the current real landscape. Symbols are the average extinction probabilities for five landscape replicates (±SD). The three horizontal gray lines represent the extinction probabilities in the current landscape for the three risk scenarios.

For the real landscape, loosing dispersal habitat worsens the demographic status of the metapopulation, whereas adding it significantly reduces its extinction probability (Fig. 3). For the current proportion of dispersal habitat, random or buffering distributions are better than the actual physiognomy of the landscape. Buffering breeding habitat with dispersal habitat is the optimal configuration because it produces the lowest extinction probabilities for the lower proportions of dispersal habitat (Fig. 3). It builds bridges of dispersal habitat between close local populations, most importantly between sources, while constraining movements to the proximity of breeding habitat. That is why the best performance is obtained with a relatively low proportion of dispersal habitat, showing a behavior very similar to linear corridors, for which extinction probability goes down to 0.33. At the same time, it limits the movement of individuals to the proximity of breeding habitat, thus reducing the number of animals lost far from focal sites. On the contrary, random landscapes permit the use of stepping stones to move far from sources, hence their lower overall performance.

The consideration of different scenarios of risk of mortality in open habitat does not alter the overall behavior, with one exception. In random landscapes, where fragmentation is highest, if we do not consider any increase in risk of mortality (ρ = 0; see The Movement Submodel and Model Parameterization in SI Appendix) the overall extinction probability is lower, as occurs for the other two configurations at low proportions of dispersal habitat, when individuals have higher movement rates in fragmented areas (Fig. 3).

An important persistence condition for SSP is symmetry in connectivities, by permitting the recolonization of local populations by its own natives (6). Our system shows naturally a strongly asymmetric connectivity pattern, due to the landscape configuration between the two main source populations (15). Adding a corridor (either linear, buffering or stepping stones) between them removes the asymmetry, hence improving the demographic status.

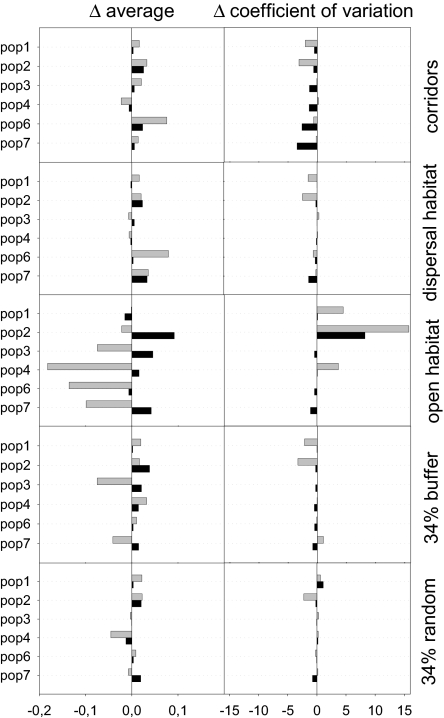
Changing matrix heterogeneity has a clear reflection on E, I and their CV in comparison with the real landscape (Fig. 4). The positive effect of corridors is due to a general increase of I and E (except for one sink population, which receives most of the emigrants from one source due to its specific spatial location and matrix composition, Fig. 4). Additionally, corridors strongly reduce the variability of I at sources and E from sinks, with sinks being occupied more often and showing more frequent rescue events. The same effects occur when the matrix is composed by only dispersal habitat, with buffering dispersal habitat, or with a random distribution. In this case we observe overall increases in I for the populations that are connected by bridges of dispersal habitat and reductions in variability as a function of the proportion of dispersal habitat. The strongest effects occur when the matrix is composed of only open habitat.

Fig. 4.

Variations in the yearly per capita emigration (E, black bars) and immigration (I, gray bars) rates for each local population (pop1 to pop7) in different matrix configurations. The bars represent the difference Δ between the average value (and coefficient of variation) of E and I for the current landscape (see Fig. S1) and the values estimated for each configuration. The configurations are Corridors: a linear corridor (4 cells of dispersal habitat wide) connecting each subpopulation to its closest neighbor; Dispersal habitat: all of the matrix (except for barriers) covered by dispersal habitat; Open habitat: all of the matrix (except for barriers) covered by open habitat; 34% buffer: 34% of the matrix composed by dispersal habitat located buffering breeding habitat (see Fig. 3); 34% random: 34% of the matrix composed by dispersal habitat located randomly (see Fig. 3).

It is interesting that when there is no dispersal habitat, the overall behavior of the metapopulation is not much different from the current situation (Fig. 3), but the effects on E and I are very strong (Fig. 4). The decrease in I and the increase of variability are compensated by an increase in the number of individuals staying in the proximity of their natal population forming a pool of floaters which in other conditions would be moving away. The higher E occurs because these individuals are counted as emigrants when they first leave the natal population in their daily excursions into the open matrix (if they do not find a place to move they return to their initial site). This fencing effect results in higher occupancy rates, because there are individuals around whenever a vacancy occurs, forcing the local recruitment. Here the system behaves as a patchy population.

We can identify two types of effects of modifying matrix heterogeneity with conservation implications. The first is the corridor effect, by which we can increase immigration rates among the connected populations and remove the asymmetry imposed by the spatial configuration of heterogeneity. For the Iberian lynx, corridors can be built by stepping stones of dispersal habitat separated as far as the distance they can cross overnight (up to 3 km). The second is the fencing effect, by which we can reduce the draining of individuals far from local populations, improving the probability of quickly rescuing empty sites, and reducing the mortality risk of dispersers. Both effects should guide a design of matrix heterogeneity that maximizes the persistence of lynx in Doñana.

Conclusions

Real dispersing lynxes perform a partially informed search of breeding habitat. They have information on matrix heterogeneity, on the proximity of breeding habitat, on risk of mortality in open habitat, and have memory on the position of the last visited dispersal habitat (15). We modeled their motion and navigation capacities with a set of behavioral functions and associated parameters which interact dynamically with the external environment and the internal state of the individual. The dynamic interaction between movement behavior and survival is an inherent part of the movement process, and the population dynamics are very sensitive to it. We identified this important role by applying the movement ecology framework at the level of individuals and evaluating the impact at local population and metapopulation levels.

As a result, E and I rates, and therefore connectivities and dispersal kernels, are dynamic values that depend on the actual demographic and landscape context. This context is determined by the structure of the landscape, the behavior of moving individuals, and also by the demographic variables associated with limiting the time moving, the dynamics of available settlement sites, and the individual response to the perceived risk. Nonetheless, one of the most pervasive concepts we find in spatial ecology is that dispersal kernels are estimable functions that depend only on landscape properties such as interpatch distance, patch size or matrix heterogeneity (8–11, 43). Researchers must focus on the processes, because the simple phenomenological description of the connectivities (or kernels) is not enough to understand the patterns we observe. The spatial and temporal structures go hand in hand (44) and cannot be decoupled without analyzing movement processes in detail. Our results show that the management of interpatch processes should deal with matrix design, making use of corridor and fencing effects, as well as with local dynamic variables.

Movement is more intricately linked with other demographic processes than we could think a priori. We must consider movement in an inclusive way, acknowledging that both behavioral and demographic mechanisms are nested, as recognized by the movement ecology framework, which helps not only at the level of individuals, but also at higher levels.

Methods

The model is individual-based and spatially explicit. It is composed by a demographic and a movement submodel [see The Demographic Submodel and The Movement Submodel in SI Appendix (15, 20–21)]. As initial condition for simulations we used the population size estimated in 2002 (including sex, age, status and spatial location) and the landscape map with the subpopulations known in that year. The parameterization of the model was done with field estimates for both demographic and movement behavior parameters [see Model Parameterization in SI Appendix (15, 20–21)].

In the analyses of sensitivity we distinguished between the mortality and reproduction parameters which might change in short periods of time and space, and other parameters whose values are more stable (e.g., litter size, maximum age). Instead of investigating the behavior of the model using a small percentage variation around the parameter estimates of survival and reproduction, we defined the range based on biologically plausible values (Table S1 and SI Appendix) (31). For movement behavior parameters we used the confidence intervals of the estimates (sampling them with a uniform probability distribution), which represent the biological plausibility of our knowledge (Table S1) (15). The statistical models (procedure REG in SAS) were fitted sequentially, entering a first block with all movement variables and then a second with all demographic variables (giving priority to movement parameters in the explanation of variance). The standardized statistical parameter estimates give information on the relative impact of each simulation parameter and can be compared between blocks. We considered only main effects. We measured metapopulation growth rate as the natural logarithm of the geometric mean of ΔN over the years simulated. E and I were estimated only when each subpopulation was occupied. Each parameterization was projected for 100 years and repeated 100 times. For the sensitivity analyses we generated 3000 parameterizations using a Latin Hypercube sampling procedure to ensure the full coverage of the n-dimensional parameter space.

The landscape is represented by a grid of barrier, open, dispersal and breeding habitats with a 0.5 km resolution (15). We generated the different landscape scenarios modifying the proportion between dispersal and open habitat without changing the amount and location of breeding, and barrier habitats. For the random landscapes, starting with a matrix with only open habitat, we added dispersal habitat randomly. For the scenarios with dispersal habitat buffering breeding habitat, starting with a matrix with only open habitat, we added dispersal habitat as a function of the amount of cells of breeding or dispersal habitat surrounding each matrix cell (the higher the number, the higher the probability to be converted into dispersal habitat). For the current landscape scenario, starting with the current amount and distribution of dispersal habitat, we added/removed dispersal habitat as a function of the amount of cells of dispersal habitat surrounding each matrix cell (the higher/lower the number, the higher/lower the probability to be converted into dispersal/open habitat). Corridors of dispersal habitat connected each local population to its closest neighbor. For each landscape combination we generated five map replicates in each of which we run 1000 simulations (each of 100 years).