Stress-driven buckling patterns in spheroidal core/shell structures

Abstract

Many natural fruits and vegetables adopt an approximately spheroidal shape and are characterized by their distinct undulating topologies. We demonstrate that various global pattern features can be reproduced by anisotropic stress-driven buckles on spheroidal core/shell systems, which implies that the relevant mechanical forces might provide a template underpinning the topological conformation in some fruits and plants. Three dimensionless parameters, the ratio of effective size/thickness, the ratio of equatorial/polar radii, and the ratio of core/shell moduli, primarily govern the initiation and formation of the patterns. A distinct morphological feature occurs only when these parameters fall within certain ranges: In a prolate spheroid, reticular buckles take over longitudinal ridged patterns when one or more parameters become large. Our results demonstrate that some universal features of fruit/vegetable patterns (e.g., those observed in Korean melons, silk gourds, ribbed pumpkins, striped cavern tomatoes, and cantaloupes, etc.) may be related to the spontaneous buckling from mechanical perspectives, although the more complex biological or biochemical processes are involved at deep levels.

Spontaneous buckling of thin films on compliant substrates can achieve numerous highly ordered patterns due to mismatched deformation (1–6), which can be manipulated in different ways (1, 7–9). Buckling may also play an important role in the morphogenesis of some plant parts, including phyllotactic pattern in compressed tunica (10, 11), primordium initiation in sunflower capitulum (12), and Fibonacci patterns resembling those in some flowering cactus and pine cones (2), among others, in a way that is similar to the energy-minimizing buckling of a compressed shell on an elastic foundation (10).

Many natural fruits and vegetables can be approximated as spheroidal stiff exocarp (shell)/compliant sarcocarp (core) systems, which exhibit intriguing buckle-like profiles. For example, the Korean melon (yellow melon) and ridged gourd (or silk gourd, luffa acutangula) are distinguishable by 10 equidistant longitudinal ridges that run from stem to tip. Small pumpkins, acorn squashes, and carnival squashes often have ∼10 uniformly spaced ribs, whereas the large pumpkins often have ∼20 or more ridges. Similar undulating morphologies found in varieties of cucumis melons, gourds, striped cavern tomatoes, bell peppers, and other fruits and vegetables underpin their distinctive appearances. Although pattern formation in plants usually involves various complex biological and biochemical processes (11, 13, 14), such distinctive yet simple features make one wonder whether there exist other relatively simpler mechanisms contributing to the morphogenesis at the macroscopic scale, and the possibility of stress-driven buckling is explored in this study.

Consider a model spheroidal core/shell system where the shell is characterized by (x² + y²)/a² + z²/b² = 1 with equatorial radius a, polar radius b, and thickness t (t ≪ a); the system remains closed and bonded together in the due course of buckling. Both film (shell) and substrate (core) are assumed to be homogeneous, isotropic and elastic, with their Young's moduli and Poisson's ratios denoted as E_f and v_f, and E_s and v_s, respectively (E_f > E_s). When the current model is applied to fruits and vegetables, the parameters (E_f, E_s, t) should be regarded as the “effective” (or nominal) variables because the true properties of fruit/vegetable components may be inhomogeneous, anisotropic, and gradient. We also neglect the boundary effect (e.g., the constraint imposed by the stem and the navel at a polar end) and assume no external constraint during the growth.* The simplified model system is used to reveal useful insights of the important parameters governing pattern formations.

The growth in plants can be analogously simulated (15) without any external guidance, and we assume that the unconstrained growth is isotropic and uniform within both film and substrate. Because the outer layer of plant meristems often expands faster than the inner one (12, 16), the growth expansion coefficient (rate) is larger in the shell than that of the core. The mismatch between the expansion of the stiff thin film and soft thick substrate causes the benign growth stress in the film compressive.

For a prolate spheroid (k = b/a > 1) or oblate spheroid (k < 1), the in-plane stress in the film is non-equi-biaxial (anisotropic) and increases with growth in the prebuckled state, where an interface pressure is acting on the film due to the expansion mismatch. Neglecting the shear stress at interface (9), the ratio between the prebuckling hoop (σ_h) and longitudinal (σ_l) growth stresses at any point in the spheroidal film is [see supporting information (SI) Text]

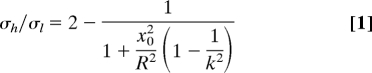where x₀ is the radius of latitudinal circle and R = a²/b is the radius of curvature at the pole. Apparently, σ_h/σ_l > 1 in a prolate spheroid, whereas σ_h/σ_l < 1 in an oblate system; the stress ratio also depends on the size of spheroid. Denote σ_f = Max(σ_h,σ_l), the film starts to buckle when σ_f = σ_c and σ_c is a critical stress—above such critical stress level, various buckle patterns emerge depending on the geometrical and material constraints, and the undulations tend to relax the higher stress component. The spontaneous buckles are simulated by using the finite element method (FEM) (see SI Text).

Results and Discussion

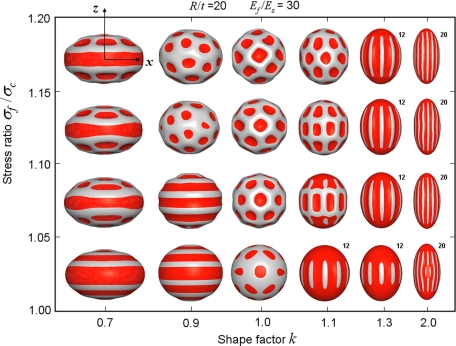
Four effective dimensionless parameters, the normalized size R/t = a²/bt, the shape factor k = b/a, the modulus ratio Ē_f/Ē_s = E_f(1 − ν_s²)/E_s (1 − ν_f²), and the normalized growth stress σ_f/σ_c, primarily affect the stress-driven buckling patterns. In Fig. 1, for representative values of R/t = 20 and Ē_f/Ē_s = 30, the buckled patterns vary with σ_f/σ_c and k (transition from oblate to prolate shape). When k = 1.0, according to Eq. 1, σ_h/σ_l = 1, and thus, reticular buckle patterns are formed on spherical core/shell system when R/t is not very large (17) and the buckle amplitude increases with σ_f/σ_c, as shown in Fig. 1. In spherical systems with large R/t, labyrinth undulations appear—the buckling mechanisms of spherical film/substrate systems have been studied in ref. 17.^† Note that the stress field is also isotropic (σ_h/σ_l = 1) if the substrate is planar without further manipulation of system properties (e.g., anisotropic growth), and the resulting buckling patterns have no directional preference; the principles of pattern formations on planar substrates (under both isotropic and anisotropic stresses) have been discussed extensively in earlier works, e.g., refs. 8, 9, and 18–20. In the present article with the spheroidal substrate, the stress is anisotropic when k ≠ 1, which leads to distinct buckling mechanisms and more variety of undulation morphologies than those on a spherical substrate (17), and they are explored in detail as well as their implications in fruit morphogenesis.

Fig. 1.

Deformation map of spheroid as both parameter k and film stress are varied (with R/t = 20 and Ē_f/Ē_s = 30). In all buckled morphologies in Figs. 1–3 and Figs. S1 and S2, the dark (red) areas mean that within such concave regions, the magnitude of the radial displacement is smaller than a certain value; all snapshots of the morphology are rescaled to fit into the map. For ridged morphology, the number of buckles is shown on the top corner of each simulated pattern.

In the case of slight deviation from spherical shape, e.g., setting k = 0.9 and 1.1, ordered latitudinal and pumpkin-like ribbed patterns are formed at the onset of buckling, respectively, which then transit to triangular patterns at higher stresses. With the more evidently oblate or prolate spheroids, the buckling pattern persists with film growth. In particular, when k is larger than ∼1.3, the hoop/longitudinal growth stress ratio σ_h/σ_l becomes increasingly ∼1 and reaches its maximum at the equator; consequently, equidistant longitudinal buckle ribs are first formed near the equator and extend to the poles as σ_f/σ_c is increased.

Because most fruits and vegetables with undulating morphology are prolate (in an approximate sense), in the following we focus on the buckling in prolate spheroids (especially those with k ≥ 1.3). With reference to Eq. 1, if R/t is very large, σ_h/σ_l decreases to approach the value of 1.0, consequently circumferential buckles may emerge (Fig. S1). At lower values of R/t (R/t ≤ 30), the stress anisotropy is higher and the ribbed morphology remains quite robust with continued moderate level of shell growth, which can be confirmed when both Ē_f/Ē_s and k are varied in a large range, Fig. S1 and Fig. S2 [if the growth strain is too large, the ridged morphology may become unstable (19)]. Owing to such a relative stability, we will explore subsequently how the initial buckle pattern (σ_f/σ_c ≈ 1.05) varies with the 3 dimensionless ratios (k, R/t, Ē_f/Ē_s).

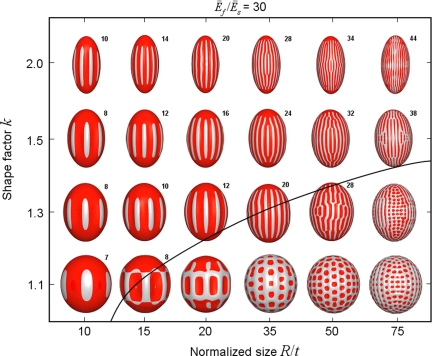
In the first buckling map (Fig. 2), Ē_f/Ē_s = 30 while k and R/t are varied. The solid line is a rough boundary to distinguish the geometrical parameter space of longitudinal ridged patterns from that of reticular ones. When k is fixed, with the increase of R/t (i.e., the larger a/t), the number of longitudinal ribs grows rapidly in accompany with the occurrence of circumferential waves, and the buckle finally transits to a reticular pattern at large R/t. Governed by the competition between k and R/t on growth stress (Eq. (1)), the longitudinal ridged buckle takes over at larger k and/or smaller R/t; otherwise the addition of circumferential waves makes the buckles reticular. At constant R/t, with the increase of k the ridged buckle dominates and the ridge number also increases primarily due to the increase of a/t. In such longitudinal ridged patterns the number of ribs is essentially only a function of a/t and Ē_f/Ē_s, as will be discussed below.

Fig. 2.

Deformation map of a prolate spheroid with varying k and R/t (with Ē_f/Ē_s = 30). The black solid line separates the ribbed and reticular patterns (same for Fig. 3). The initial buckle patterns (σ_f/σ_c ≈ 1.05) are shown.

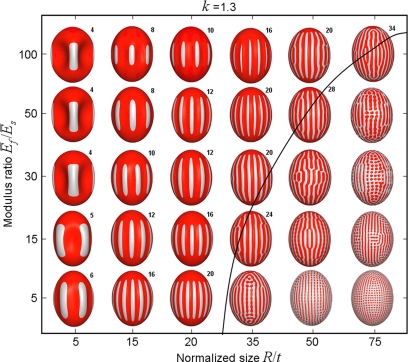
For a representative k = 1.3, the buckling map in Fig. 3 shows that at a fixed geometrical factor (R/t), the wave length of the buckled ridges increases with the elastic mismatch. At small Ē_f/Ē_s and large R/t, reticular pattern ensues; otherwise, ribs prevail which may extend to the polar regions as R/t increases. Near the boundary (solid line), one could identify the upper limits of the ribs in the stable longitudinal ridged configuration. When R/t is relatively small, the wave number appears to be quite stable against a large variation of Ē_f/Ē_s.

Fig. 3.

Deformation map of a prolate spheroid with varying Ē_f/Ē_s and R/t (with k = 1.3). The initial undulation patterns (σ_f/σ_c ≈1.05) are shown.

At large k, the prolate spheroid may be approximated as a long cylinder of radius a. The buckle wave number can be estimated as:

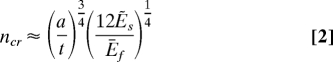where Ẽ_s = E_s/(1 + v_s)(1 − 2v_s) (see SI Text). Even at a relatively small k, k = 1.3 say, the wave number predicted by Eq. 2 is reasonably close to that obtained from FEM simulations of prolate spheroids (Fig. S3); the small difference is due to the geometrical constraints at capped poles and also to the system instability at large R/t. Hence, the characteristics of longitudinal ridged pattern is dominated by a/t (substrate curvature) and Ē_f/Ē_s (film/substrate modulus mismatch) and more ribs are possible with larger a/t and/or smaller Ē_f/Ē_s, as validated from Figs. 2–3.

Despite the complicated cellular processes involved during the growth of some fruits and plants, mechanical buckling may reproduce similar ribbed and reticular morphologies for prolate spheroidal core/shell structures (Fig. 4). The results demonstrate that a distinct profile is possible only when the 3 geometrical and material parameters fall within a certain range. For example, examination of the Korean melon shows that its effective R/t is ∼15–18, and k is ∼1.2–1.4, which may justify its 10 equidistant longitudinal ridges (see Fig. 2); in addition, to maintain such a profile, the effective Ē_f/Ē_s may vary between ∼20 and 40 (see Fig. 3). Similarly, if the distinct patterns are related to buckling, for ridged gourd whose k ≈ 5–6, its effective R/t and Ē_f/Ē_s should be ∼4–5 and 20–30, respectively; for striped cavern tomatoes with 4–6 ridged buckles, the effective R/t is ∼5; and for reticular patterns to prevail, cantaloupes (k ≈ 1.1–1.2) should have a large R/t and a low Ē_f/Ē_s. A resembler of pumpkins may be obtained by modifying the spheroid model (Fig. S4); because the wave number is related to the normalized equatorial radius (a/t), Fig. 4 shows that in a small pumpkin simulant, 10 ridges may emerge, and when a/t grows larger, 20 or more ribs are possible. In all cases, the ridged patterns are also robust when the effective mismatch Ē_f/Ē_s varies within a moderate range (Fig. 3); indeed, moderate variations of material properties are reasonable during fruit/vegetable growth (21) and despite the scatter of properties in individual fruits/vegetables, certain species (e.g., Korean melon) still exhibit a distinct topology.

Fig. 4.

Comparison between several fruits/vegetables and examples of corresponding simulated buckle shapes on model spheroids (see SI Text for more details).

There is no doubt that biological and biochemical processes also play a very important role in regulating the plant pattern formation. In leaf morphology for example, the mutation of CIN gene found in Antirrhinum exhibits excess growth in marginal regions (22), which makes the edges in compression and turns the normally flat leaves into wavy surfaces with buckled margins. Similar studies on Arabidopsis (23) and eggplant leaf (24) suggest a role for mechanical force in the regulation of plant morphology through its interaction with biological processes. The phenomenological study of stress-driven buckling in a spheroidal core/shell system may suggest a similar regulatory pathway: With the excessive growth of the shell-like exocarp (through certain biological processes), buckling occurs due to mechanical forces where the initiation locations and characteristics (e.g., the number of ribs) are roughly controlled by the aforementioned mechanical principles. Meanwhile, the effective material properties relevant to buckling modes are based on cellular properties of the exocarp and sarcocarp. During the buckling process, the mechanical forces may also confine and interact with certain biological processes such as cell growth and cell differentiation (11, 14) to help stabilize the global pattern features. In other words, the morphology of some plants/fruits may result from a concerted effort of the mechanical and biological processes.

We notice that the dehydration process or a fruit or vegetable can be free from the biological factors that could have been involved in its growth; therefore the surface pattern of a dehydrated fruit (or vegetable) is dominated by buckling. In a dried mini tomato (Fig. S5), the longitudinal ridges are analogous to that shown in Fig. 3 and the wave numbers are also associated with (k, R/t, and Ē_f/Ē_s) (the latter 2 factors are of more weight). In addition, experiments were carried out on a SiO₂ shell/Ag core microsystem, and the observed buckle patterns (Fig. S6) qualitatively agree with simulation (see SI Text); such results also demonstrate the potential applications in micro- and nanofabrications via controlled self-assembly on curved/closed substrate surfaces.

Conclusion

Although Charles Darwin remarked that the explanation of plant pattern formation could “drive the sanest man mad” (25), anisotropic stress-driven buckling in spheroidal core/shell system, as we have shown here, could, to some extent, resemble the global pattern features formed in the appearance of quite many kinds of fruits and vegetables, and each distinct pattern corresponds to certain ranges of the three dimensionless material and geometrical parameters. Mechanical buckling might have provided a template for the morphology development in some fruits/plants that may confine and interact with certain biological processes such as cell growth and cell differentiation. Note that we employ the simplest spheroid model, and such a model could be refined to include the end/boundary (stem) constraints, anisotropic growth, and more sophisticated material/structural details, among others. Nevertheless, the encouraging results obtained through the self-assembled patterns of the model system show that the initiation and macroscopic topological characteristics of these patterns may be connected to mechanical principles, and the morphology of plants/fruits may be manipulated by the interaction between mechanical forces and biological processes.

Materials and Methods

To establish the model system in Cartesian coordinates, the spheroidal surface (x² + y²)/a² + z²/b² = 1 is created by rotating the ellipse, x²/ a² + z²/b² = 1, about the z axis (vertical axis). The film thickness, t, is assumed to be much smaller than both a and b, and the film subtends a complete cover to the substrate. The film (in analogue to the fruit/vegetable shell) remains bonded to the substrate (core) throughout deformation. The growth is assumed to be isotropic within both film and substrate, but the unconstrained growth coefficient (expansion rate) is larger in the film. The mechanics of buckling is regulated by the minimization of system potential energy (because the film is bonded to the substrate, the substrate also deforms). Buckling simulation has been performed by using the finite element method (FEM). More details can be found in SI Text.