Comparison of successive transition states for folding reveals alternative early folding pathways of two homologous proteins

Abstract

The energy landscape theory provides a general framework for describing protein folding reactions. Because a large number of studies, however, have focused on two-state proteins with single well-defined folding pathways and without detectable intermediates, the extent to which free energy landscapes are shaped up by the native topology at the early stages of the folding process has not been fully characterized experimentally. To this end, we have investigated the folding mechanisms of two homologous three-state proteins, PTP-BL PDZ2 and PSD-95 PDZ3, and compared the early and late transition states on their folding pathways. Through a combination of Φ value analysis and molecular dynamics simulations we obtained atomic-level structures of the transition states of these homologous three-state proteins and found that the late transition states are much more structurally similar than the early ones. Our findings thus reveal that, while the native state topology defines essentially in a unique way the late stages of folding, it leaves significant freedom to the early events, a result that reflects the funneling of the free energy landscape toward the native state.

The description of the folding process of a protein in terms of pathways on a free energy landscape has provided much insight into the mechanism of the folding reaction (1–4). Free energy landscapes of many proteins appear to resemble the shape of a funnel that guides the folding process toward the native state (5–7). According to this view, folding is considered a stochastic process so that a protein reaches its native conformation through folding pathways made up by an ensemble of different trajectories (6, 8–10). It has been difficult, however, to establish experimentally the extent to which these trajectories can differ from each other, in particular in the wider region of the free energy funnel corresponding to the initial stages of the folding process, where a considerable heterogeneity may be expected. Many proteins exhibit single folding pathways composed of families of closely related trajectories, but parallel folding pathways have also been observed (11), as well as significant changes of pathways and transition state structures upon circular permutation (12, 13) or solvent conditions (14–16). In addition, different transition state structures were characterized in two homologous proteins with a highly symmetric native structure (17).

To obtain a glimpse of the width of the free energy landscape at the early stages of the folding reaction, we compared the folding pathways of two homologous three-state proteins. The study of homologous proteins represents a powerful approach to obtain insight into the process of protein folding (18–22), especially when combined with structural information on intermediate events (17, 23–25). The transition states of two-state proteins were compared in a series of studies (17, 23, 24, 26). Here we present a vivid illustration of the width of the upper regions of a free energy funnel by comparing the early and late transition states of two homologous three-state proteins, PSD-95 PDZ3 and PTP-BL PDZ2 (33% sequence identity, Fig. 1) (21, 27–29). The analysis was carried out by using the Φ value analysis, a powerful experimental method to obtain structural information about transition states (30). In this technique residue-specific structural information is inferred by comparing the kinetics of folding of the wild-type protein with those of a series of conservative single mutants (31, 32).

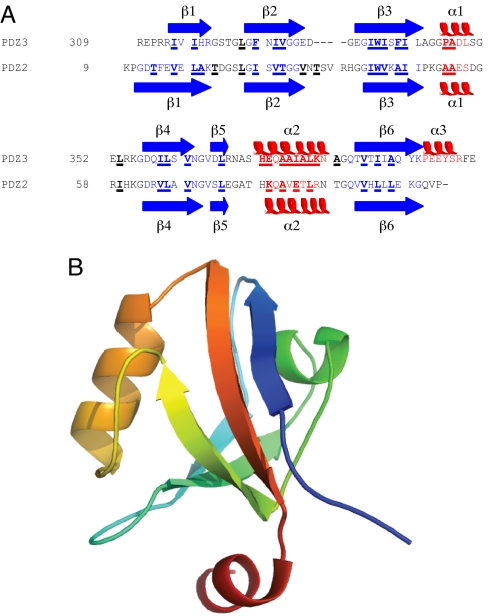
Fig. 1.

Sequence and structure of PSD-95 PDZ3. (A) Sequence alignment of PSD-95 PDZ3 and PTP-BL PDZ2. The secondary structure in the native state is also shown. Positions that were mutated in this study and in ref. 34 are underlined and in bold. (B) Native structure of PSD-95 PDZ3, rainbow colored from the N terminus (blue) to the C terminus (red).

Our results demonstrate that the late folding transition states (TS2s) for the PDZ proteins that we studied are more similar to each other than the early transition states (TS1s). Thus, taking two snapshots along each folding pathway illustrates the presence of a weak native bias at the early stages of the process, which results in alternative folding events. By contrast, in approaching the native conformation the folding pathway is essentially dictated by the native topology, as is generally the case for two-state proteins (33).

Results and Discussion

To test the dependence on sequence and topology of the protein folding free energy landscape, we performed an extensive Φ value analysis of the early and late transition states on the folding pathway of PSD-95 PDZ3 and compared the results with those from a previous analysis of PTP-BL PDZ2 (34).

Φ Value Analysis.

Thirty-five conservative mutations (35) at 30 positions of pseudo-wild-type PSD-95 PDZ3 (F337W) (21, 36, 37) were constructed (Table 1). Three of these mutants expressed poorly (L360A, L367A, and A390G) and could not be included in the analysis. The remaining 32 mutants were subjected to both equilibrium and kinetic folding experiments [supporting information (SI) Table S1] and Φ values could be calculated for 24 positions (Table 1). For 17 of these positions a direct comparison with Φ values reported for PTP-BL PDZ2 (34) was possible.

Table 1.

Experimental Φ values for PSD-95 PDZ3

Protein region	Mutant	ΔΔGD-N, kcal· mol−1	ΦTS1	ΦTS2
Mutation compared with wild type
β1	I314V	−0.44 ± 0.08*
β1	I316A	3.5 ± 0.2	0.28 ± 0.04	0.52 ± 0.03
Loop	L323A	1.87 ± 0.08	−0.20 ± 0.03	0.38 ± 0.05
β2	F325A	4.9 ± 1.0	0.36 ± 0.13	0.67 ± 0.07
β2	I327V	0.96 ± 0.07	0.25 ± 0.03	0.52 ± 0.09
β2	V328A	0.32 ± 0.08*
β3	I336V	0.45 ± 0.07*
β3	I336A	1.35 ± 0.08	0.01 ± 0.03	0.53 ± 0.06
β3	I338A	2.2 ± 0.1	0.15 ± 0.03	0.53 ± 0.04
β3	F340A	0.12 ± 0.08*
β3	I341V	−0.16 ± 0.08*
β3	I341A	1.57 ± 0.08	−0.08 ± 0.03	0.42 ± 0.05
α1	P346G	1.33 ± 0.07	−0.05 ± 0.03	0.27 ± 0.07
α1	A347G	1.32 ± 0.07	−0.05 ± 0.03	0.20 ± 0.07
Loop	L353A	2.24 ± 0.09	0.15 ± 0.02	0.50 ± 0.04
β4	I359V	0.94 ± 0.07	0.36 ± 0.04	0.60 ± 0.09
β4	V362A	1.68 ± 0.08	0.60 ± 0.02	0.87 ± 0.06
α2	H372A	−1.3 ± 0.1	0.87 ± 0.05	0.77 ± 0.09
α2	E373A	0.05 ± 0.08*
α2	E373G	0.65 ± 0.08	0.50 ± 0.06	0.62 ± 0.14
α2	A375G	0.98 ± 0.07	0.79 ± 0.05	1.04 ± 0.13
α2	A376G	1.35 ± 0.07	0.55 ± 0.03	0.84 ± 0.08
α2	I377A	0.00 ± 0.08*
α2	I377G	1.21 ± 0.07	0.58 ± 0.03	0.75 ± 0.08
α2	A378G	2.4 ± 0.1	0.34 ± 0.02	0.60 ± 0.04
α2	L379A	1.52 ± 0.07	0.59 ± 0.03	0.82 ± 0.07
α2	K380A	−0.58 ± 0.08	0.77 ± 0.09	0.69 ± 0.16
α2	K380G	0.53 ± 0.07	0.18 ± 0.07	0.75 ± 0.19
Turn	A382G	1.19 ± 0.08	0.38 ± 0.03	0.59 ± 0.07
β6	V386A	2.00 ± 0.07	0.16 ± 0.02	0.56 ± 0.04
β6	I388V	1.44 ± 0.07	0.35 ± 0.02	0.56 ± 0.06
β6	Y392A	1.51 ± 0.08	0.17 ± 0.03	0.96 ± 0.08
Val→Ala or Ala→Gly
β3	V336A	0.90 ± 0.08	0.00 ± 0.05	0.33 ± 0.10
β3	V341A	1.73 ± 0.08	−0.03 ± 0.03	0.45 ± 0.05
α2	A373G	0.60 ± 0.08	0.42 ± 0.06	0.51 ± 0.14
α2	A377G	1.21 ± 0.08	0.66 ± 0.04	0.78 ± 0.08
α2	A380G	1.11 ± 0.08	0.49 ± 0.03	0.72 ± 0.09

The standard errors of curve fitting for the kinetic parameters were similar to standard deviations, as determined from three independent kinetic measurements on the pseudo-wild-type PDZ3 (Fig. 2A). Therefore, fitting errors of k_f, k_u, and K_p were used to calculate the propagated errors in Φ and Δ Δ G_D-N as described (50).

*The ΔΔ G_D-N value is too low to calculate an accurate Φ value.

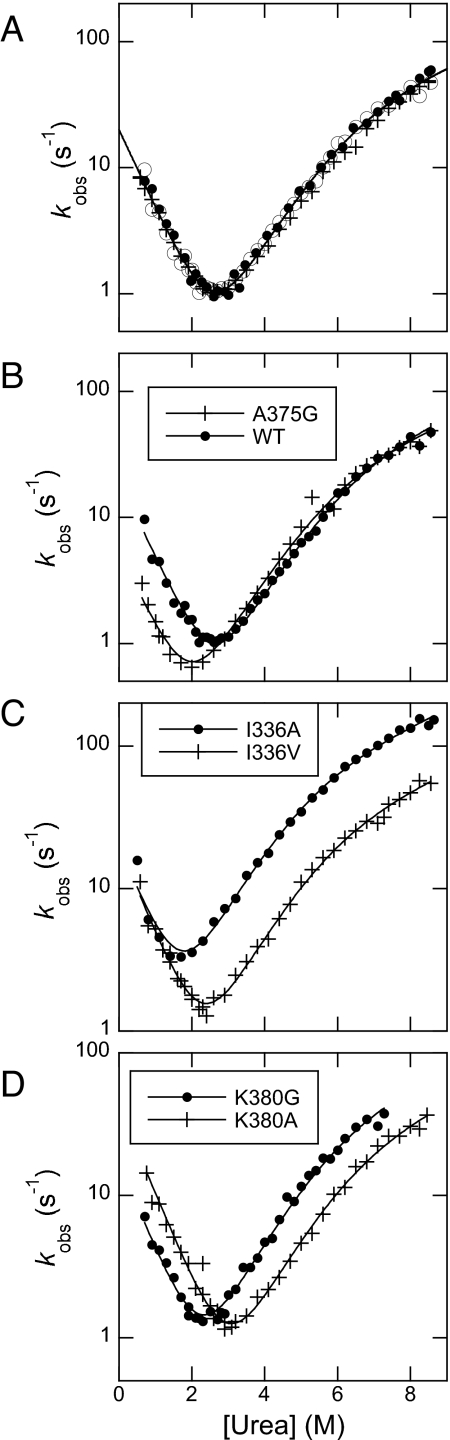
Kinetic folding experiments were performed by 11-fold dilution of protein buffer into urea buffer (unfolding) or protein buffer/urea into urea buffer solutions (refolding). Experimental traces were fitted to single-exponential time courses at all final denaturant concentrations, to obtain observed rate constants for folding. Analysis of kinetic amplitudes did not reveal the presence of any burst phase species in the experimental dead time (≈5 ms). Semilogarithmic plots of the observed unfolding and refolding rate constant versus denaturant concentration (chevron plots) for pseudo-wild-type PDZ3 and selected mutants are shown in Fig. 2. The chevron plots for all mutants were fitted globally to a three-state equation with shared m values (see Materials and Methods). The kinetic and equilibrium urea midpoint values correlated well (coefficient of correlation 0.99, R = 0.87) and the kinetic ΔΔG_D-N values were used in calculation of Φ values. Fitted parameters are shown in Table S1. The β_T values for the two transition states TS1 and TS2 were calculated to be 0.56 and 0.90, respectively, based on the global fit of all mutants. Φ values are reported in Table 1 (see Materials and Methods for definitions). To enable analysis of both transition states, the folding experiments of PSD-95 PDZ3 were performed at pH 2.85 (21). Five Φ values for TS1 (for positions I336A, V362A, A375G, A382G, and V386A) were repeated at pH 7.45 and found to be identical within error to those at pH 2.85, indicating that our choice of experimental condition did not affect the folding process (not shown).

Fig. 2.

Representative chevron plots. (A) Three chevrons of pseudo-wild-type PSD-95 PDZ3 (F337W). The solid line for the pseudo-wild-type in A is the average fit to the three independent experiments. (B–D) Examples of high (B), low (C), and average (D) Φ values. Only one chevron plot was measured for each mutant. The solid lines are obtained from a global fit of all kinetic data (all mutants and wild type), with shared m values (m_D-‡1 = 0.84 ± 0.01, m_N-‡1 = 0.66 ± 0.01, and m_p = 0.50 ± 0.01 kcal·mol⁻¹·M⁻¹; errors are from the global fitting).

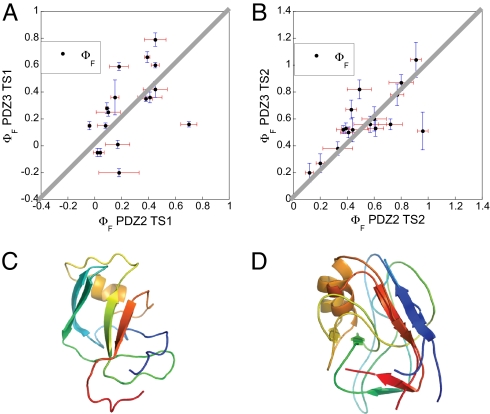
We compared the Φ values of PSD-95 PDZ3 with those of PTP-BL PDZ2 (Fig. 3 A and B), which were characterized in a previous study (34). Each point in Fig. 3 A and B represents a homologous position in the two proteins, for TS1 and TS2, respectively. It is clear that the correlation is rather weak for Φ_TS1 values (R value 0.50, Fig. 3A) but stronger for Φ_TS2 values, which lie almost perfectly along the line of unity slope (R value 0.72, Fig. 3B). Of the 17 structural positions where Φ_TS2 values could be directly compared, only three were found to lie significantly off this line: E373 (K79) and L379 (L85) in the N-terminal and C-terminal regions, respectively, of helix α2, and F325 (I27) in the strand β2. The first two Φ_TS2 values were based on similar mutations in PDZ3 and PDZ2 (Ala → Gly scanning and Leu → Ala, respectively). The Phe-325 → Ala mutation in PDZ3 is very destabilizing and less specific than the Ile → Val at the corresponding position in PDZ2. By contrast, several of the Φ_TS1 values were found to differ significantly between PDZ2 and PDZ3. In the region corresponding to α2 in the native state, which displayed the highest Φ_TS1 values for PDZ3, the differences were particularly clear: A375G (A81G), 0.79 vs. 0.45; I377A/G (E83A/G), 0.66 vs. 0.39; and L379A (L85A), 0.59 vs. 0.18. In addition, in the region of strand β6, which follows that of α2 along the sequence, the highest Φ_TS1 value for PDZ2 was found (0.70 for V92A), but the corresponding one for PDZ3 was as low as 0.16 (for V386A). In the case of PDZ2 the interactions between the regions corresponding to the native secondary elements β1–β6 and β4–β6 are key in stabilizing the structure of TS1 (34), whereas in the case of PDZ3 the early folding events are driven by the formation of α2, which is consolidated by interactions with the regions corresponding to β1 and β2 in the native state (see below).

Fig. 3.

Comparison of folding transition states for two PDZ domains. (A and B) Comparison of the 17 Φ values measured at corresponding positions in PSD-95 PDZ3 (present work) and PTP-BL PDZ2 (34) for the early (A) and late (B) transition state events, respectively. The solid gray lines correspond to the unitary slope. The mutants included were (with PTP-BL PDZ2 mutations in parentheses) I316A (L18A), L323A (L25A), F325A (I27V), I327V (V29A), I336A (I42V), I338A (V44A), P346G (A52G), A347G (A53G), L353A (I59V), I359V (V65A), V362A (V68A), [E]A373G ([K]A79G), A375G (A81G), ([I]A377G) ([E]A83G), L379A (L85A), V386A (V92A), and I388V (L94A). For the two positions where the Φ value was calculated from a second mutation (Ala → Gly scanning in helix 2) the wild-type residue is given in brackets, e.g., [E]A373G, where the Φ value was calculated from the A → G mutation (and not the E → G). (C) A representative structure of TS1 of PSD-95 PDZ3. (D) Alignment of representative structures of TS2 of PSD-95 PDZ3 and PTP-BL PDZ2. The TS1 structures of the two proteins were too different to be aligned.

In Fig. 3 C and D, we present representative structures of TS1 and TS2 (see below). These structures clearly indicate that TS1 is much less structured than TS2 and that it exhibits only sparse mainly nonobligatory elements of the native topology. In Fig. 3D, the TS2 structure of PSD-95 is aligned to that of PTP-BL PDZ2, showing their high degree of similarity.

Molecular Dynamics Simulations with Φ Value Restraints.

The structural information provided by the measurement of Φ values can be used to build models of the transition state structures (38). One strategy for obtaining this result is to use the Φ values as structural restraints in molecular dynamics simulations (34, 39, 40). In this approach, the trajectory generated by the integration of the equations of motions of a protein is biased toward the transition state region through the incorporation of the structural information provided by the Φ values in the force field. This approach is analogous to the use of interatomic distances obtained through nuclear Overhauser effects (NOEs) to determine native state structures (41, 42).

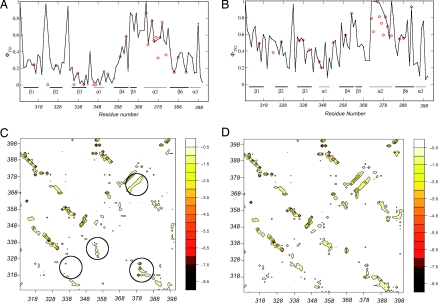
Here we used this approach to obtain two ensembles of structures representing TS1 and TS2, respectively (see Materials and Methods). The availability of structural models enables a prediction to be performed of the Φ values for all of the amino acids in a protein sequence, whether they have been measured or not (Fig. 4 A and B). These profiles indicate that the regions corresponding to the native secondary structure elements α2, β5, and β6 are relatively well structured in TS1, whereas the remainder of the protein is structurally rather heterogeneous. By contrast, in TS2 the native topology is well established, and essentially all of the secondary structure elements are substantially present and in their native mutual arrangement. A more quantitative assessment of the degree of formation of the native topology is provided by the energy maps (34, 39) (Fig. 4 C and D). In these maps the average interaction energy between residue pairs is reported for the structures making up the TS1 and TS2 ensembles. The results indicate that, whereas in TS2 essentially all of the secondary structure elements interact among each other in a native-like manner, in TS1 relatively stable native-like interactions are formed only between the regions corresponding to the native secondary elements α2, β1, and β2.

Fig. 4.

Characterization of the two transition state ensembles by molecular dynamics simulations with Φ value restraints. (A and B) Comparison of the experimental and calculated Φ values as a function of the position along the sequence for TS1 (A) and TS2 (B). (C and D) Energy maps of TS1 (C) and of TS2 (D); the native state is shown above the diagonal and the transition state below it. In C regions corresponding to the region corresponding to α2 in the native state and to its stabilizing contacts with the regions of β1 and β2 are encircled; also encircled are the areas of the interactions between the regions β2–β3 and β3–β4, which are very weak in TS1 but much stronger in TS2. The numbers on the energy scale in C and D are in kcal·mol⁻¹.

Conclusions

Our results suggest that the native bias is weak at early stages of the protein folding reaction of three-state proteins, allowing for alternative early folding events before reaching the intermediate for proteins within the same family. This situation is in pronounced contrast to what happens in the late stages of folding, or for two-state proteins, when the native topology essentially dictates the folding mechanism, at least from the transition state to the native state (33). This conclusion was reached by carrying out a Φ value analysis of PSD-95 PDZ3 and interpreting the results in terms of a three-state folding mechanism, which is consistent with observations made for other PDZ domains (21, 27). We then compared the structures of the early and late transition states of folding of PSD-95 PDZ3 with those of PTP-BL PDZ2 (27, 34), which have very similar native structures (43, 44). Our results revealed a stronger correlation between Φ values for corresponding positions in the amino acid sequence for PSD-95 PDZ3 and PTP-BL PDZ2 for the late transition states (R = 0.72) than those for the early transition states (R = 0.50) (Fig. 3 A and B). To obtain structural models of the early and late transition states of PSD-95 PDZ3, the Φ values measured experimentally were then used as restraints in molecular dynamics simulations. The analysis of the statistical properties of the resulting transition state ensembles in terms of energy maps has indicated that the native topology is fully established at the late transition state, as observed for the transition states of two-state proteins (45). In contrast, at the early transition state, although native contacts are established preferentially, they are not present simultaneously in numbers large enough to prompt the formation of the native topology, thus resulting in a wide range of conformations exhibiting largely nonobligatory native-like structural elements.

In summary, the comparison of the folding processes of PSD-95 PDZ3 and PTP-BL PDZ2 provides important insight into how the native state topology determines the folding mechanism. The native topology exerts a close control on the folding mechanism in the vicinity of the native state but leaves much more freedom away from it. Hence, homologous proteins may differ significantly in their folding processes at the early stages of folding, but their folding pathways converge at the late stages.

Materials and Methods

Mutagenesis, Expression, and Purification.

All mutants were made by PCR using Pfu Turbo polymerase (Stratagene) and the pseudo-wild-type PDZ3 F337W cDNA as template (21, 36). This construct codes for residues 309–401 of PSD-95 (compare Protein Data Bank file 1BFE; ref. 43) as well as a short His-tag, which does not influence the folding of PDZ3 (21). Expression and purification were as described earlier (37, 46). The purity was checked by SDS/PAGE and the identity, by MALDI-TOF mass spectrometry.

Equilibrium and Kinetic Experiments.

Equilibrium experiments were performed using an SLM 4800 spectrofluorimeter (SLM-Aminco). Excitation of the single engineered Trp residue (F337W) in PSD-95 PDZ3 was done at 280 nm and emission was monitored at 345 nm. Urea-induced equilibrium experiments of this pseudo-wild-type PDZ3 and its mutants were carried out in 100 mM potassium formate, pH 2.85, at 25°C. We observed a decrease in Trp emission upon denaturation, and the transition followed a two-state behavior. Data were fitted to the standard equation for solvent denaturation (30). All kinetic experiments were performed in an SX-17MV stopped-flow spectrometer obtained from Applied Photophysics in the same buffer as above or in 50 mM potassium phosphate, pH 7.45. The excitation wavelength was 280 nm, and the fluorescence emission was measured by using a 330-nm band-pass filter. We used a final concentration of the protein of 2–3 μM. Kinetic data displayed a roll-over in the unfolding limb of the chevron plot (21) and data were fitted to a three-state equation, as explained below.

Data Analysis.

Typically, the logarithms of the folding rate constants exhibit a linear dependence on urea concentration (30). The non-logarithmic versions of the equations for a two-state system are

and

The parameters m_D-‡ and m_‡-N are the slopes of the dependence of log k_f and log k_u, respectively, on urea concentration. The equation describing a simple two-state mechanism is the sum of Eqs. 1 and 2. When there is a change in rate-limiting step in either the refolding or unfolding arm data must be analyzed according to a three-state model. In the present case, the deviation from linearity was in the unfolding arm as described by Eq. 3. The folding reaction of PDZ domains can be explained by an on-pathway high-energy intermediate (21, 28). In water or low urea concentration, TS1 is rate limiting, and at high urea concentration, TS2 is rate limiting. Under such conditions, the intermediate is assumed to be a high-energy species, at steady state and at low (<1%) concentration (i.e., k_ID ≫ k_DI and k_IN ≫ k_NI). Observed rate constants over the urea concentration range studied are described by the sum of Eqs. 1 and 3 (47, 48).

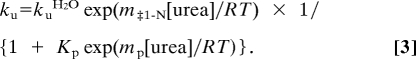In Eq. 3, K_p is the partitioning constant between the two transition states (i.e., the partitioning between the I → D and I → N reactions) and m_p is the associated m value. In the data fitting, all m values (m_D-‡1, m_‡1-N, and m_p) were shared among all mutants to increase the precision in the fitted kinetic/equilibrium parameters k_f^H2O, k_u^H2O, and K_p. The β_T values for the two transition states TS1 and TS2 were calculated according to:

and

For the early transition state, Φ values were calculated as

where ΔΔG_D-‡1 is the difference in free energy between the denatured state and TS1 upon mutation

and ΔΔG_D-N is the difference in free energy between the denatured and native states of unfolding upon mutation

For the late transition state, Φ values were calculated as

where

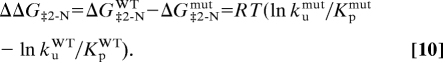Note that the presence of I does not affect the Φ value for unfolding Φ_U (31, 32), measured at high urea concentration. Φ_TS2 is defined as 1 − Φ_U in Eq. 9 and under such pseudo-two-state folding conditions the Φ_TS2 value reports on the transition D → TS2 and not I → TS2. Data analysis was performed by Prism (GraphPad Software) and Kaleidagraph (Synergy Software).

Molecular Dynamics Simulations with Φ Value Restraints.

Molecular dynamics simulations with structural restraints derived from Φ value measurements were carried out at 300 K to determine the structures of the two transition states for folding of PDZ3 (34, 39, 40). The CHARMM22 force field was used with an all-atom representation of the structure of the protein, the TIP3P water model and periodic boundary conditions (49).

To define the structural restraints, a Φ_i^sim value was calculated in the simulation for a residue i from the fraction of native contacts that it makes in a conformation C with all residues except for its nearest neighbors along the chain (39, 40).

The number of contacts n_i is defined as the number of side-chain heavy atoms within a cutoff distance of 5.5 Å. A reaction coordinate for the process, ρ(t), was defined as the mean square difference between the Φ_i^sim values and the experimentally determined Φ_i^exp values (39).

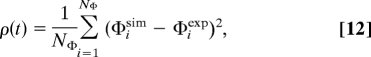where N_Φ is the number of Φ_i^exp values used in the calculations. The biasing pseudoenergy was defined as (39)

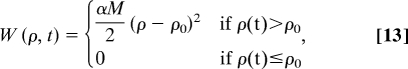where the parameter α controls the relative weight of the restraint term with respect to the force field, and ρ₀ is equal to the lowest value of the reaction coordinate reached by the system up to time t in the simulation.