Functional network reorganization during learning in a brain-computer interface paradigm

Abstract

Efforts to study the neural correlates of learning are hampered by the size of the network in which learning occurs. To understand the importance of learning-related changes in a network of neurons, it is necessary to understand how the network acts as a whole to generate behavior. Here we introduce a paradigm in which the output of a cortical network can be perturbed directly and the neural basis of the compensatory changes studied in detail. Using a brain-computer interface, dozens of simultaneously recorded neurons in the motor cortex of awake, behaving monkeys are used to control the movement of a cursor in a three-dimensional virtual-reality environment. This device creates a precise, well-defined mapping between the firing of the recorded neurons and an expressed behavior (cursor movement). In a series of experiments, we force the animal to relearn the association between neural firing and cursor movement in a subset of neurons and assess how the network changes to compensate. We find that changes in neural activity reflect not only an alteration of behavioral strategy but also the relative contributions of individual neurons to the population error signal.

A wealth of evidence associates learning with changes in neural activity (for reviews, see refs. 1–4). For example, the tuning functions of neurons in the motor cortex can change when monkeys adapt to perturbations that interfere with the execution (5–7) or visual feedback (8–10) of their movements. Although the observed changes in neural activity in these studies are closely associated with the behavioral manifestation of learning, it is difficult to interpret the behavioral significance of the neural changes because the precise relationship between neural activity and behavioral output is unknown. However, recent developments in brain-computer interface technology now make it possible to control the activity of a cursor in a three-dimensional (3D) virtual environment using the spiking activity of ensembles of simultaneously recorded motor cortical units (11–16). This “brain-control” paradigm is unique in that the behavior, cursor movement, is solely the result of neural activity in the population under study. Thus, any mismatches between desired cursor motion and decoded cursor motion can only be corrected by altering the activity of these recorded neurons.

The brain-computer interface also allows for a unique kind of perturbation that targets selective subsets of neurons. By altering the way that the firing activity of a subset of neurons is decoded and mapped into cursor movement, it is possible to test whether the tuning functions of the perturbed subset selectively change to compensate for the global error signal, or whether the entire population changes together.

To study the response to selective perturbations of this neural network, monkeys were trained to perform center-out movements to eight equally spaced targets in a 3D virtual environment under brain control, using the population vector (PV) algorithm (16–18). Once control had stabilized, the decoding algorithm was perturbed by rotating the tuning functions of a randomly chosen subset of units by 90° about a common axis, creating a global visuomotor rotation in decoded cursor movement. In addition to the expected global compensation for the resulting error in cursor movement, we found that the perturbed units underwent larger compensatory changes in tuning than the unperturbed units.

Results

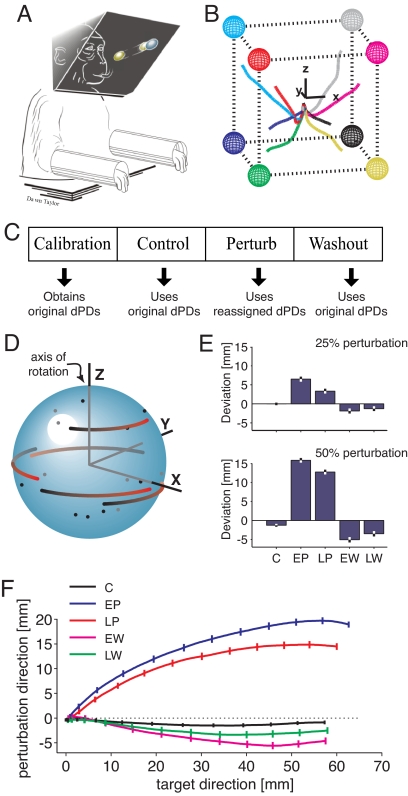
Monkeys implanted with arrays of chronic recording electrodes were trained to perform a 3D center-out task in virtual reality under brain control (Fig. 1 A and B). To establish a mapping from neural activity to cursor motion, each recorded unit was fitted with a cosine-tuning funtion (19–21) centered on its preferred direction (PD) of movement. Intended velocity was then estimated using the PV algorithm as the sum of each unit's PD weighted by its normalized firing rate. Each experiment consisted of the following sequence of four sessions (Fig. 1C): calibration, control, perturbation, and washout. The calibration session was used to estimate the tuning function of each recorded unit; on average, 40 units were used per session (range: 23–60). PDs obtained from the calibration session were fixed and subsequently used for decoding. (Henceforth, the PDs used for decoding will be called dPDs, to distinguish them from the PDs measured during other sessions.) In the control session, the center-out task was performed under brain control using the dPDs obtained from the calibration session. In the perturbation session, the dPDs of a randomly selected subset of units were reassigned, causing this subset of rotated units to contribute different directional components to the population vector than they did in the control session. For this subset, new dPDs were created by rotating the original dPDs by 90° about a common axis (Fig. 1D). The nonrotated units kept their original dPDs. In the washout session, the perturbation was removed and the original dPDs were reinstated. Two sets of experiments were performed, differing in the number of units randomly selected for perturbation. In the first set of experiments, 25% of the units were rotated during the perturbation session; in the second, 50% were rotated.*

Fig. 1.

Experimental design. (A) Schematic of the center-out brain-control paradigm. Monkeys were required to move a spherical cursor from the center of an imaginary cube in 3D virtual reality (VR) to a spherical target appearing at one of its eight corners. (B) Average trajectories to each target during one control session. Axes are inset for reference. (C) Timeline of recording session in one data set (left to right). (D) Schematic dPD rotation for a z-axis perturbation. The original dPDs (black dots) of a subset of units were rotated 90° to create the reassigned dPDs (red ends of comets). (E) Mean (± SE) of the cursor deviation in the direction of the perturbation, evaluated when the cursor moved half the distance to the target. Separate bars are shown for control (C), early perturbation (EP), late perturbation (LP), early washout (EW), and late washout (LW). The top panel shows the results from experiments in which 25% of the units were rotated; the bottom panel shows the results from experiments in which 50% were rotated. (F) Average trajectories from all experiments in which 50% of the units were rotated. To average trajectories from different targets, each trajectory was rotated into a common space, where the x-axis represents movement toward the target and the y-axis represents movement orthogonal to the target in the direction of the applied perturbation (20). Trajectories are collapsed along the z-axis, which represents movement orthogonal to both the target and the perturbation (noise). For information on movement times, see Table S1.

Average trajectories (Fig. 1 B, E and F) indicate that cursor movements were accurate during the control session, but deviated toward the applied perturbation immediately after the onset of the perturbation session.^† To analyze performance changes in the perturbation session, trials were divided into early and late sessions, consisting of the first and last five repetitions to each target, respectively. Early in the perturbation session, the average deviation in the perturbation direction was 6.5 ± 0.65 mm for experiments where 25% of the units were rotated (15.8 ± 0.60 mm for the 50% experiments^‡). In both cases, the deviation was significantly reduced in the late perturbation session (average deviation, 25% experiments: 3.3 ± 0.64 mm, P = 0.0006, paired t test; 50% experiments: 12.7 ± 0.64 mm, P = 0.0005). These trends reversed in the washout sessions: when the perturbation was removed, there was a clear after-effect in the cursor trajectory that decreased over time.

Three possible strategies that could be used to compensate for the errors caused by the perturbation are re-aiming, re-weighting, and re-mapping (Fig. 2). Re-aiming compensates for the applied perturbation by aiming for a virtual target located in the direction that offsets the visuomotor rotation (8–10). This is a global strategy, in that all units in the recorded population (both rotated and nonrotated) would have discharge rates that indicate the monkey's intended movement to a different, virtual target. This solution is suboptimal, however; the units active for a given target will, because of the perturbation, have dPDs that are highly dispersed (see Fig. 2C). This will tend to shorten the population vector, leading to a slower movement. Re-weighting minimizes error by suppressing the use of the rotated units: that is, by reducing their modulation depths so that they contribute less to the PV (see Fig. 2D). This is a local strategy, in that the brain must first identify these “noisy” units and then quiet them to remove their contribution to the PV. This may also be inefficient, as it leaves fewer units available to drive the cursor. The ideal solution is re-mapping: that is, selectively changing the directional tuning of the rotated units to match the way they are being used by the decoder (see Fig. 2E). We find elements of all three strategies in the neural responses.

Fig. 2.

Schematic of the influence of the perturbation on the population vector and of three possible compensation mechanisms. (A) Population vector before perturbation. When moving toward the target shown in blue, units with preferred directions pointing toward the target will fire above their baseline rates. The gray lines represent vectors pointing toward the dPD of each unit, with the length of the vector scaled by the neuron's normalized firing rate. The sum of these vectors is the population vector, shown in black. On average, this population vector will point straight toward the target. (B) After the perturbation, the same units shown in (A) will be recruited, but some will contribute differently to the population vector because of their rotated dPDs. Rotated units are shown in pink. The result is a population vector that does not point at the target. (C) Re-aiming. By aiming at the virtual target (dotted blue circle), a different set of neurons is recruited with PDs that point toward the virtual target. The net contribution of the rotated and nonrotated units will cause the population vector to move straight toward the actual target. Note that the length of the population vector is shorter than in (A) because the units that contribute to it have more dispersed dPDs. (D) Re-weighting. By selectively reducing the contribution of the rotated units (down-modulating their firing rates), the population vector straightens toward the target. (E) Re-mapping. By recruiting only unperturbed cells that point toward the target and perturbed cells that point 90° from the target, the population vector can be made to point directly at the target with its original length.

To differentiate among these possibilities, we fitted cosine tuning curves to the spike rate data collected during the control session and compared them to cosine tuning fits from spike rate data in the perturbation session. Firing rates were measured over the 200-ms interval ending when the cursor had moved half the distance to the target, in an attempt to give the monkey enough time to perceive the target direction and modulate its motor cortical unit activity according to its intended movement direction, but not enough time to re-aim the cursor to compensate for errors in its trajectory. To try to capture postlearning responses in the perturbation session, the first five movements to each target were removed from analysis.

To test for the use of a re-weighting strategy, we compared the modulation depths of the rotated and nonrotated sets of units across sessions.^§ We found that, on average, the modulation depths (m) of the rotated units showed a significant decrease from the control to the perturbation session (Δm = −0.84 ± 0.17 Hz, P < 10⁻⁶, weighted t test) (see the SI Appendix), whereas the nonrotated units did not (Δm = −0.19 ± 0.11 Hz; P = 0.10). The difference between the rotated and nonrotated Δm's was significant (P = 0.001, weighted paired t test). Thus, on average, the relative contribution of the rotated units to the cursor movement was smaller during the perturbation session than it was during the control session. The difference between the rotated and nonrotated units diminished to a nonsignificant level in the washout period (comparing control to washout, Δm_Non-Rotated − Δm_Rotated = 0.34 ± 0.20 sp/s, P = 0.09).

An analysis of the PD shifts revealed two results (Fig. 3). First, ignoring differences between rotated and nonrotated units, most points were shifted toward the applied perturbation, indicating that both rotated and nonrotated units shifted to accommodate the cursor deflection (25% experiments: ΔPD = 6.4 ± 0.48°; 50% experiments: ΔPD = 18.9 ± 0.89°; both were highly significant with P < 10⁻¹⁰, weighted t test). This is consistent with a global re-aiming strategy: if the monkeys had been aiming for a virtual target rotated in the opposite direction of the perturbation, regressing the spike rates against the direction of the actual targets would give PDs that point in the direction of the applied perturbation. The second result of this analysis is that the rotated units showed a greater shift toward the applied perturbation than the nonrotated units (see Fig. 3 A–D), which is consistent with a local re-mapping strategy (25% experiments: ΔPD = 4.61 ± 1.10°, P = 0.00003, weighted paired t test; 50% experiments: ΔPD = 5.59 ± 1.77°, P = 0.002).^¶ During the washout session (see Fig. 3 E and F), the difference between the rotated and nonrotated units disappeared (25% experiments: ΔPD = 0.09 ± 1.08°, P = 0.93, weighted paired t test; 50% experiments: ΔPD = −0.43 ± 1.36°, P = 0.75).

Fig. 3.

PDs shift during the perturbation session. (A and B) Shift in the PD measured during the perturbation session relative to the control session for all units in experiments where 25% (A) or 50% (B) of the units were rotated. Small dots represent the individual data points and large dots represent the means of the rotated (red) and nonrotated (blue) groups. The intensity of each point is proportional to the certainty of the estimate for that point (see SI Appendix). (C and D) Empirical cumulative distribution functions (CDFs) of the PD shift along the direction of applied perturbation. In each case, the CDF of the rotated group is shifted significantly to the right of the CDF of the nonrotated group. (E and F) Same as (A) and (B) for the washout session. The nonrotated group's mean is obscured by the rotated group's mean.

Although we found that the rotated units showed significant tuning changes relative to the nonrotated units, the differences were subtle. How much impact did these changes have on actual cursor movement? Because the population vector algorithm is linear, the movement of the cursor under brain control can be decomposed into a weighted sum of two trajectories: one from the rotated population and one from the nonrotated population (see the SI Appendix). This decomposition allows us to track the errors due to each subpopulation of units over time. Fig. 4 shows the perturbation-induced error of the trajectory components averaged over all experiments in which 50% of the units were rotated (see also Fig. 5). In the early trials (see Fig. 4A), error began to increase 125 ms after the target presentation, corresponding to the average reaction time. Between 125 ms and 400 ms, the rotated population caused the cursor to deviate away from the target while the nonrotated population did not contribute to error, indicating that the monkey was aiming directly for the target. The error attributable to the nonrotated population appeared 400 ms into the movement and was in the direction opposite that of the rotated units. We interpret this as evidence of a visual correction to the cursor deviation. After learning (see Fig. 4B), the nonrotated population responded immediately at the beginning of each movement, indicating that re-aiming had been incorporated as part of the motor plan.

Fig. 4.

Trajectory error contributions from the rotated and nonrotated populations of units as a function of time. The y-axis in each plot is the perturbation-induced error: that is, the deviation of the cursor from the ideal straight-line trajectory, in the direction of the applied perturbation. (A) Perturbation-induced error during the early part of the perturbation session. The black line denotes the actual cursor trajectory, the red line denotes the component of that trajectory arising from the rotated units, and the blue line denotes the component arising from the nonrotated units. Colored arrows indicate the time that the corresponding population first deviates significantly from baseline (according to a two-sided t test). (B) Same as (A), for trajectories recorded during the late part of the perturbation session. The early trajectories are shown as dotted lines for reference. (C) The difference in deviation from the early perturbation trials to the late perturbation trials for each population.

Fig. 5.

Comparison of trajectories between the early (dashed) and late (solid) perturbation sessions. To look at learning-related changes, we compared the trajectories from the nonrotated population (blue) to the trajectories that would have resulted from the rotated population if the perturbation had not been applied. (To compute this, we used the firing rates from the rotated population to construct a population vector with the decoding parameters from the control session.) In the early perturbation session, the nonrotated trajectory and the trajectory that the rotated population would have had, if not perturbed, overlap both in time (A) and in space (B). Late in the perturbation session, they overlap for the first 400 ms or so, and then they begin to diverge.

There was a difference in the learning profiles of the rotated and nonrotated units (see Fig. 4C). The nonrotated population showed the greatest learning effect in the middle of the movement; at the end of the movement, the magnitude of the deviation attributable to the nonrotated units was the same in the early perturbation session as in the late perturbation session. In contrast, the rotated population showed the greatest learning effect at the end of the movement (the average rotated-population trajectory deviation at the end of the movement in the early perturbation session was 59 ± 1.4 mm; in the late perturbation session it was 52 ± 1.6 mm; paired t test, P = 0.0004).

While it is difficult to precisely ascribe the amount of error correction to each of the compensation mechanisms outlined in Fig. 2, these temporal differences make it clear that the subtle re-weighting and re-mapping effects combined to have a real, functional impact on cursor trajectories. Further work will be required to elucidate exactly how each mechanism contributes to error compensation.

Discussion

Everyday behavior requires constant updating between intended and executed movements. For example, reaching for and lifting an object makes use of knowledge about its weight, center of mass, deformability, and surface characteristics. Interaction with the object then leads to an update of this knowledge (i.e., learning), which results in a change in the way the movement is performed. The very large number of cells participating in the network responsible for movement generation, and the huge number of interconnections between those cells, make it difficult to discover neural principles of learning. The brain-computer interface paradigm provides a fully observed neural network that, by experimental construction, drives the behavioral output in the context of a task with a straightforward learning objective.

In these experiments, we applied a unique type of perturbation by changing the way a subset of the recorded neurons mapped to cursor movement. The net result of this perturbation was a visuomotor rotation between the desired cursor movement and the decoded movement, and the dominant response was a global change in the activity level of all of the neurons, indicating that the monkey was re-aiming to counter the applied rotation.

On top of this global response was a local change specific to the perturbed subpopulation of neurons: the rotated subpopulation decreased their modulation depths and shifted their PDs more than the nonrotated subpopulation. Furthermore, the tuning of the two populations evolved in different ways as a function of time through the trial (see Figs. 4 and 5). How could the contributions of particular units to the population vector be recognized using only one global feedback signal, the movement of the cursor? One possibility is that learning occurs in a desired-movement space that has more dimensions than the three that identify direction (22–23). For example, it has been suggested that motor cortical neurons change their PDs in a posture-dependent manner (24). If this were true in our neurons, it is likely that the rotated and nonrotated populations would include different postural sensitivities, and learning to associate particular (imagined) arm postures with various directions of movement could result in differential changes between the two populations of neurons. Another possibility is that these neurons solve the “credit-assignment problem” described in the artificial intelligence literature (25–26). By using a form of Hebbian learning (27), each neuron could reduce its contribution to error independently of other neurons via noise-driven synaptic updating rules (28–30). Regardless of mechanism, this study suggests that the brain is capable of at least partial selectivity in its modification of neural activity when only a global feedback signal is available.

Methods

Behavioral Paradigm and Recording.

Three male Rhesus monkeys (Macaca mulatta), ≈3 to 4 years of age, were used in these experiments. For behavioral training, monkeys sat in a primate chair facing a mirror that reflects a 3D image from a stereoscopic computer monitor in a periscope-like design, allowing the space in front of the monkey to remain available for free arm movements. Before electrode implantation, the monkey was trained to move its hand, fitted with an optical marker, to proportionally move a spherical cursor from the center of an imaginary cube to targets appearing at one of its eight corners for a liquid reward (31). All procedures were performed in accordance with the guidelines of the Institutional Care and Use Committee of the University of Pittsburgh.

Once the monkeys became proficient at this 3D center-out reaching task, they were implanted with chronic recording arrays. Two of the monkeys (Monkeys O and P) were implanted with four or more 16-channel intracortical electrode arrays (50-μm Teflon-coated tungsten wires, arranged in 2 × 8 grids with 300-μm spacing), while the other (Monkey A) was implanted with one 96-channel array (Cyberkinetics Neurotechnology Systems, Inc.). All implantations were visually placed in the proximal arm area of primary motor or premotor cortex. Recordings were amplified, filtered, and sorted on-line with a 96-channel Plexon MAP system (Plexon Inc.).

Some of the units recorded were well-isolated single cells and some contained two or more cells that couldn't easily be isolated from one another, but which were nevertheless tuned to intended movement direction as a group. Once an adequate number of units were obtained, the monkey was trained to perform the center-out task, using “brain control” while both of its arms were restrained, moving the cursor by modulating the spiking activity of the recorded units as detailed in the next section, Decoding Algorithm for Brain Control. Once the monkeys became proficient (> 70% success rate) at the brain-control, center-out task with the final settings (diameter of cursor and target ≤2.5 cm, width of imaginary cube, 11 cm), they began participating in the experiments. On each recording day, a calibration brain-control session (4–10 cycle sets)^‖ was run to obtain each unit's original PD, baseline rate, and modulation depth. These original parameters were then fixed and subsequently used for decoding, as described in the next section. The control session (10–30 cycle sets) was run using the original dPDs (“decoding” PDs), the perturbation session (24–50 cycle sets) was run using the reassigned dPDs for the rotated subset of units, and the washout session (20 cycle sets, or until the monkey stopped working) was run with the original dPDs reinstated. A typical recording session lasted ≈3 hours.

Decoding Algorithm for Brain Control.

The PV algorithm used for brain control (12, 18) assumes that each unit is cosine-tuned with intended movement direction (17):

where f is the firing rate of a model unit, b₀ is its baseline firing rate, m is its modulation depth, and θ is the angle between the direction of intended movement and the unit's PD.

We adapted the PV algorithm described in refs. 12 and 18 as follows: The cosine tuning fit of each unit was calculated by regressing the firing rate of the unit to the target direction. The regression model was:

where Y_ki is the firing rate of unit i in the k^th trial, ε_ki is noise, d = (d_kx,d_ky,d_kz) is the unit-vector pointing in the direction of the target in the k^th trial, and the β's are the regression coefficients. The baseline firing rate b_0i was estimated as β_0i, the modulation depth m_i as the magnitude of the vector β→ = (β_xi,β_yi,β_zi), and the preferred direction p_i as β→/m_i.

Once the baseline firing rate, modulation depth, and preferred direction for decoding had been estimated for each unit, they were used to construct a movement estimate in real time as follows: Spike counts were measured at a regular rate (30 Hz for Monkeys O and P, 60 Hz for Monkey A) and converted to rates f_i(t) by dividing by the sampling interval. Normalized rates r_i(t) were computed through the equation

These normalized rates were then smoothed with a five-point boxcar filter. The filtered, normalized rates were converted to cursor velocity, v(t), as:

where n_D is the number of movement dimensions (in our case, 3) and N is the number of units being used for decoding. The speed factor, k_s, converts the magnitude of the PV from a normalized range to a physical speed in mm/s (typical values ranged from 75 to 200). Only units whose modulation depth exceeded a given cutoff (usually, 4–5 Hz) were used to construct cursor movements; this cutoff typically eliminates half to two-thirds of the units we record. Finally, cursor position, C_p, was updated every sampling interval as

Trajectories always started at the origin.

Trajectory Analysis.

To increase statistical power and help remove “drift” (bias caused by nonuniform distributions of dPDs, for example), trajectories to each target were first rotated into a common frame of reference where targets and errors were in similar directions. In this reference frame, x̂_r was defined to be the unit-vector pointing from the center of the cube toward the target, ŷ_r was defined as the unit-vector orthogonal to x̂_r pointing toward the direction of the applied perturbation, and the ẑ_r was defined as the cross product of x̂_r and ŷ_r, where the r subscript indicates values in the reference coordinate frame. To perform this rotation, every point p_r = (i,j,k) in the trajectory was multiplied by a rotation matrix R to form the new trajectory p_r = pR. R was created as the matrix whose columns were the new desired axes. Thus, for a target located at t = (t_x,t_y,t_z) and dPDs rotated clockwise by 90° about the z-axis:

where the prime symbol denotes the transpose operation and |a| denotes the norm of a.

In this new reference frame, movement along the x_r-axis represents movement toward the target, movement along the y_r-axis represents error in the direction of the applied perturbation, and movement along the z_r-axis represents error orthogonal to the applied perturbation.

Average cursor trajectories were obtained by smoothing and combining individual trajectories as follows: To combine trajectories of different durations, the time axis of each trajectory was uniformly scaled to the mean movement duration, τ_Avg. That is, the time samples for an individual movement t of duration τ were scaled by a gain factor α = τ_Avg/τ to create a new set of time samples t_s = tα. Each x, y, and z component of the trajectory was then independently resampled using spline interpolation to a common time axis consisting of 300 evenly sampled points (interp1 command in Matlab, The Mathworks). Finally, the mean and SE were calculated separately for each time point of the x, y, and z components.