The Stay/Switch Model of Concurrent Choice

Abstract

This experiment compared descriptions of concurrent choice by the stay/switch model, which says choice is a function of the reinforcers obtained for staying at and for switching from each alternative, and the generalized matching law, which says choice is a function of the total reinforcers obtained at each alternative. For the stay/switch model two schedules operate when at each alternative. One arranges reinforcers for staying there and the other arranges reinforcers for switching from there. Rats were exposed to eight or nine conditions that differed in the arrangement of the values of the stay and switch schedules. The generalized matching law described preferences when arrangements were similar to those found when using two concurrently running interval schedules. It did not, however, describe all preferences when using different arrangements. The stay/switch model described all preferences in one analysis. In addition, comparisons of selected conditions indicated that changing the ratio of obtained reinforcers was neither necessary nor sufficient for changing preference as measured by response ratios. Taken together these results provide support for the stay/switch model as a viable alternative to the generalized matching law and that the critical independent variable is allocation of stay and switch reinforcers.

Concurrent variable-interval (VI) VI schedules are used to analyze recurrent choice among two alternatives. In the standard model, subjects choose to respond at one alternative or the other (Herrnstein, 1961). Hence, the standard analysis of the resulting performance compares responding at the two alternatives using the generalized matching law. It says the ratio of the rates of responding at each alternative is a power function of the ratio of the rates of reinforcers obtained at each alternative (Baum, 1974). The rates of responding (and reinforcers) at each alternative are based on session duration, thus, each response (and reinforcer) rate is based on the same time. Consequently, time cancels in the both ratios. Thus, the generalized matching law may be expressed in logarithmic form as,

1

where B_n is the responses or time at alternative n, and R_n is the reinforcers obtained at alternative n. The two fitted parameters are s, which is the sensitivity to the ratio of reinforcers, and log b, which is the preference or bias towards one alternative that is not captured by the reinforcer ratio. Implicitly, the generalized matching law views each choice as starting from a neutral position and proceeding to a response on one of two alternatives (Sugrue, Corrado, & Newsome, 2004.

A different approach to understanding two-alternative concurrent choice starts by viewing choice not from a neutral position but from the alternative where responding is occurring. The choice is staying at the present alternative or switching from the present alternative. Thus, according to this view—the stay/switch model—concurrent choice consists of two independent sets of choices, one at each alternative (MacDonall, 2005; MacDonall, Goodell, & Juliano, 2006). Switching alternatives presents the other set of choices. The critical variables influencing choice are the events that occur during visits at each alternative: the reinforcers for staying and responding during visits and the reinforcers for ending visits by switching from that alternative. These reinforcers-per-visit control the behavior during visits, that is, the run lengths (the mean responses during visits) and the visit durations (the mean duration of visits).

According to the stay/switch model, run lengths and visit durations are functions of the ratio of the stay to switch reinforcers per visit (MacDonall, 1999, 2000, 2003) and the sum of the stay and switch reinforcers per visit (MacDonall, 2006). The reinforcers per visit for staying are the number of reinforcers obtained while pressing one lever, divided by the number of visits (i.e., changeovers from that lever). The reinforcers per visit for switching from a lever is the number of reinforcers obtained for switching by pressing the other lever divided by the number of visits (i.e., changeovers). Applying this model to concurrent choice, the equation with subscripts for one alternative is divided by the equation with subscripts for the other alternative. Formally the equation is (MacDonall et al., 2006):

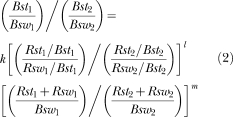2

Bst_n is the number of stay responses at Alternative n or the time spent staying at Alternative n. Bsw_n is the number of switches from Alternative n; 2Bsw_n equals, plus or minus 1, the total changeovers from both levers. Rst_n is the number of reinforcers obtained for staying at Alternative n, and Rsw_n is the number of reinforcers obtained for switching from Alternative n. Note the subscripts refer to the alternative changed from and the alternative where reinforces were arranged. The three fitted parameters are k, which is the bias towards an alternative that is not a function of the distribution of stay and switch reinforcers, l, which is the sensitivity to the ratio of the ratio of the stay and switch reinforcers and m, which is the sensitivity to the ratio of the sum of the stay and switch reinforcers (MacDonall et al., 2006). Because the number of switches from each alternative must be within 1 of each other, and provided the number of switches is large (≫ 100) they cancel. Expressing the resulting equation in logarithmic form produces:

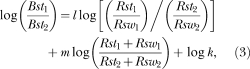3

which plots as a flat surface and can be fitted to the data using least-squares linear regression. This equation says that preference is a joint function of the ratio of the ratios of the reinforcers for staying and for switching (henceforth, the ratio of ratios) and the ratio of the sums of the reinforcers for staying and for switching (henceforth, the ratio of sums). Because response preference is measured using only stay responses, it is called the stay-response ratio.

Support for Equation 3 was provided by varying the ratio of the ratios as the ratio of the sums remained approximately constant (MacDonall, 2005). Rats were exposed to concurrent VI VI schedules composed of two pairs of stay and switch schedules. In one set of conditions the pair of schedules was arranged symmetrically, that is, the value of the stay schedule in each pair equaled the value of the switch schedule in the other pair. For example, a VI 36 s and a VI 320 s operated only while the subject was at Alternative 1. The VI 36 s arranged reinforcers for staying and responding at Alternative 1 while the VI 320 s arranged reinforcers for switching from Alternative 1. A VI 320 s and a VI 36 s operated only while the subject was at Alternative 2. The VI 320 s arranged reinforcers for staying and responding at Alternative 2 while the VI 36 s arranged reinforcers for switching from Alternative 2. Changing alternatives exchanged the pair of schedules operating. This procedure was equivalent to a standard concurrent VI 36 s VI 320 s schedule. Rats were exposed to four or five conditions that used symmetrical pairs of schedules and the resulting preferences were described by the generalized matching law (r² > .93).

In a second set of conditions, the influence of the ratio of the sums on preference was evident (MacDonall, 2005). In these conditions the values of the pairs of schedules were arranged asymmetrically, that is, the value of the stay schedule in each pair equaled the value of the switch schedule in the same pair. An asymmetrical arrangement based on the schedules in the above example produces a VI 36 s for staying at Alternative 1 and a VI 36 s for switching from Alternative 1 and a VI 320 s for staying at Alternative 2 and a VI 320 s for switching from Alternative 2. With an asymmetrical arrangement the sum of the scheduled reinforcers arranged per visit is greater at one alternative, in this case, Alternative 1; however, at both alternatives the ratio of the scheduled stay and switch reinforcers arranged per visit equals 1.0. The actual ratio of the ratios in each condition equaled approximately one and there were clear preferences, indicating that the ratio of the sums influenced preference. The response preferences maintained by the symmetrical conditions combined with the response preferences maintained by the asymmetrical conditions were not described by the generalized matching law (MacDonall, 2005, reproduced here in Table 6). A reanalysis of those data showed that Equation 3 described the combined data (.88 < r² < .96). Although these data support the stay/switch model, these two arrangements sampled a limited area in the two-dimensional space defined by the ratio of ratios and the ratio of sums.

Table 6.

The results of linear regression using the generalized matching law (Equation 5) and response data from all conditions of MacDonall (2005). Also shown is the result of the AIC analysis.

Rat	s	SE	log b	SE	r2	df	AIC
407	0.36	0.18	−0.03	0.08	.34	8	−16
408	0.52	0.18	0.01	0.09	.50	8	−18
409	0.66	0.10	0.02	0.04	.87	7	−32
410	0.45	0.09	0.03	0.04	.77	8	−34
411	0.19	0.11	−0.01	0.05	.28	7	−24
412	0.44	0.09	0.04	0.04	.79	7	−30

The primary purpose of the following experiment was to further assess the stay/switch model by exposing rats to other combinations of the ratio of ratios and ratio of sums. If the resulting data were described by the Equation 3 then the stay/switch model was further assessed by determining whether the behavior at each alternative was described by the stay/switch model. If the stay/switch model was supported by these data, a secondary purpose of this experiment was to assess the generalized matching law by seeing whether changing the ratio of obtained reinforcers was necessary or sufficient for changing preference when the magnitude, immediacy and quality of reinforcers remained unchanged.

In order to show that changing the ratio of obtained reinforcers is not necessary for changing preference, the ratio of obtained reinforcers must remain unchanged as preference changes. The ratio of obtained reinforcers was kept constant by using two pairs of schedules in which each switch schedule was programmed to produce 10% more reinforcers than its paired stay schedule. Previous research (MacDonall, 2005) showed that when the value of the stay and switch schedules were the same, about 10% more reinforcers were obtained for staying. This occurred because rats obtained stay reinforcers almost as soon as they were arranged, but obtained switch reinforcers after a delay when they switched alternatives, reducing the number obtained.

In order to show that changing the ratio of obtained reinforcers is not sufficient for changing preference, the ratio of the obtained reinforcers should change but preference should remain unchanged. One way to produce a constant preference is suggested by Equation 3; select values of random-interval (RI) schedules so that the ratio of the sums favor one alternative and the ratio of the ratios favor the other alternative. With appropriate schedule values these tendencies to favor opposite alternatives would then counteract each other, yielding no preference. The values of the schedules that will produce indifference cannot be determined a priori because the preferences produced by the each of these two ratios would be, in part, a function of the sensitivity to these ratios. Consequently, initial values were used and then modified depending on the resulting response preferences.

The symmetrical conditions were included to show that concurrent schedules implemented by using two pairs of stay and switch schedules produce data that are described by the generalized matching law. The values of the schedules in the asymmetrical conditions were selected to provide additional data for evaluating Equation 3. Generally, schedule values for the asymmetrical conditions were selected to try to produce to unique combinations of the ratio of ratios and the ratio of sums.

Method

Subjects

The subjects were 6 male naïve Sprague-Dawley rats (Hilltop Lab Animals, Scottdale, PA), and were approximately 120 days old when the experiment began. They were deprived to 85% of their just determined free-feeding weights and maintained at this weight throughout the experiment. They were housed individually in a temperature controlled colony room with a 14-hr light, 10-hr dark cycle beginning at 5 AM. Water was freely available in their home cages.

Apparatus

Six operant conditioning chambers were each located in a light- and sound-controlled enclosure. Four chambers were approximately 225 mm wide and 195 mm high; three of the chambers were 235 mm in length, whereas the fourth was 350 mm in length. A 50-mm square opening to the food cup was centered horizontally on one 225-mm × 195-mm wall, 20 mm above the floor. Two response levers (Model G6312, R. Gerbrands Co.), 45 mm long × 13 mm thick, protruded 15 mm into the chamber. The centers of the levers were 60 mm to the left or right from the center of the food cup and 50 mm above the floor. Each lever required a minimum force of approximately 0.3 N to operate. The other two chambers were 305 mm wide, 270 mm high and 245 mm long. On one 305-mm × 270-mm wall were three response levers (Model G6312, R. Gerbrands Co.) 90 mm above the floor. One lever was centered on the wall and the other two were 90 mm to the left or right of the center of the center lever. Only the two outside levers were used in this experiment. A 24-VDC stimulus light was centered approximately 75 mm above each lever. Centered horizontally on the opposite wall, 30 mm above the floor, was a 50-mm square opening to the food cup. The food cup was located on the opposite wall so that the food cup was approximately equidistant to each of the three levers. In each of the six chambers, a pellet dispenser, located behind the wall containing the food cup, dispensed 45-mg food pellets (Formula A/1, P. J. Noyes) which were 85% Purina rodent chow. Each chamber was illuminated during sessions by a pair of houselights mounted on the top center of the chamber. White noise was presented through a speaker centered between the houselights. An IBM-compatible computer and MED-PC® software and hardware (MED Associates Inc.) controlled the experimental events and recorded responses.

Procedure

Rats were placed in the chambers and every response on either lever was reinforced. After about 50 reinforced responses, RI 10-s schedules were in effect for all responses. Over several sessions the values of the RI schedules were increased to the values in the first condition. Rats were not explicitly magazine trained nor was lever pressing explicitly shaped. Rats usually pressed a lever within 30 min of the first session and usually pressed that lever exclusively. As the value of the RI schedules increased pressing of the other lever emerged.

Rats were trained on the same two-lever concurrent procedure (Herrnstein, 1961) throughout the experiment. At the beginning of each session no schedules operated. The first press at either lever started the associated pair of stay and switch schedules. Subsequently, the first press at the left lever started the stay and switch schedules associated with the left lever and stopped the stay and switch schedules associated with the right lever (unless this was the first response in the session). Similarly, the first press at the right lever started the stay and switch schedules associated with the right lever and stopped the schedules associated with the left lever (again, unless this was the first response in the session). When a stay or switch schedule arranged a reinforcer, that schedule stopped and resumed operating after the reinforcer was delivered. The first response at an alternative could only deliver a reinforcer if one was arranged by the schedule for switching from the other alternative. Subsequent responses at that alternative could only deliver a reinforcer if one was arranged by the schedule for staying at that alternative. If the rat switched alternatives, by pressing the other lever, before an arranged stay reinforcer was delivered, that stay reinforcer was held until the rat switched back to that alternative by responding at the associated lever, and the next response at that lever delivered that stay reinforcer. There was no change-over delay (COD).

Conditions differed according to the arrangement of stay and switch schedules at the alternatives. In the symmetrical conditions the value of the stay schedule that operated while at an alternative equaled the value of the switch schedule that operated while at the other alternative (see Table 1).

Table 1.

For each rat, the sequence of symmetrical (SY), necessary (N), sufficient (SU) and unsymmetrical (U) conditions, the values of the RI schedules in each condition and the number of session in each condition are shown. Also shown are the sums over the last five sessions of each condition of the left and right stay responses, the reinforcers obtained from the stay and switch schedule associated with each alternative, the time at each alternative and the changeovers from each alternative.

Condition	Sessions	RI schedule				Stay Responses
		Stay at Left	Switch from Left	Stay at Right	Switch from Right	Left (Bst1)	Right (Bst2)
Rat 758
SY	16	294	33	33	294	1410	22112
SY	19	33	294	294	33	16303	2098
N*	15	179	161	36	32	2160	14730
N	15	36	32	179	161	9164	3667
U*	26	50	10	83	417	4655	2051
SU	16	63	417	63	10	4868	5018
SU	15	63	10	50	417	4030	5905
SY	16	38	152	152	38	8850	4255
Rat 759
SY	28	294	33	33	294	598	21624
SY	16	33	294	294	33	25130	1661
N	20	179	161	36	32	1421	12504
N	16	36	32	179	161	19541	1619
SU*	15	83	8	28	500	4146	4538
U	17	28	500	83	8	11142	1916
SU	22	28	500	28	8	4017	5230
SY	17	38	152	152	38	11326	6859
Rat 760
SY	20	294	33	33	294	783	24665
SY	27	33	294	294	33	23201	2043
N	16	179	161	36	32	2664	18959
N	22	36	32	179	161	15293	3003
U*	23	63	8	29	500	4070	8351
U	16	42	500	63	8	9704	5236
SU	17	50	8	40	500	5668	6590
SU*	15	63	500	42	8	5979	7898
Rat 761
SY	16	294	33	33	294	258	17518
SY	25	33	294	294	33	19570	1648
SY	16	294	33	33	294	1707	23156
N	18	179	161	36	32	3986	16397
SU*	15	100	9	40	333	5874	6795
U	17	40	333	100	9	13013	2486
N	16	36	32	179	161	18280	2587
SU*	15	67	333	40	10	3197	5782
Rat 762
SY	42	294	33	33	294	1408	5523
SY	17	33	294	294	33	5921	1494
N	17	179	161	36	32	2010	8259
N	23	36	32	179	161	5592	2282
SU	19	83	8	40	333	2517	3009
U	15	40	333	83	8	2922	2769
SY	20	294	33	33	294	719	13064
SU	15	67	333	67	10	4220	1000
U	20	500	79	100	9	1866	4043
Rat 763
SY	27	294	33	33	294	2069	6183
SY	19	33	294	294	33	6878	2453
N	20	179	161	36	32	2119	14460
N	15	36	32	179	161	3495	9743
SU*	15	45	8	71	333	6708	3397
U	15	71	333	45	8	3970	4459
SY	18	294	33	33	294	4569	4415
U	26	25	23	250	227	2119	14460
SU	20	125	125	56	8	5316	2096

^*Several sessions that used other values of the RI schedules preceded this condition. See text for explanation.

Condition	Reinforcers obtained for				Time at (sec)		Switches from
	Stay at left (Rst1)	Switch from left (Rsw1)	Stay at Right (Rst2)	Switch from right (Rsw2)	Left (Bst1)	Right (Bst2)	Left (Bsw1)	Right (Bsw2)
Rat 758
SY	15	132	432	46	4816	15379	1617	1618
SY	441	47	12	126	15590	3470	1613	1610
N*	34	45	276	272	7212	10619	1941	1940
N	283	273	29	41	11228	6378	2611	2609
U*	103	451	60	11	5264	6221	2195	2198
SU	123	23	77	404	9263	5359	2435	2432
SU	73	401	138	13	5133	7748	2464	2466
SY	343	107	40	136	15588	6456	2711	2707
Rat 759
SY	8	106	452	60	3136	15968	1404	1405
SY	488	44	8	87	16872	2541	902	901
N	21	21	330	263	3360	11755	717	717
N	314	268	20	27	11008	4475	1211	1209
SU*	48	343	233	5	3918	6269	939	941
U	326	18	33	254	8831	2635	931	929
SU	155	16	132	323	4563	4197	703	699
SY	323	90	48	166	12542	6708	1693	1693
Rat 760
SY	12	90	403	45	3146	14635	2148	2146
SY	441	53	11	93	15445	3136	1906	1903
N	35	32	228	270	6700	8586	2995	2992
N	275	287	28	35	10493	5718	2045	2043
U*	42	352	222	10	3323	7036	1820	1822
U	180	20	60	365	8014	3761	2096	2093
SU	65	426	127	7	4328	5982	2270	2270
SU*	113	8	91	413	7749	4474	2621	2618
Rat 761
SY	8	91	477	50	3318	16620	1668	1669
SY	430	62	12	119	14821	3976	1557	1555
SY	6	86	478	52	3488	17602	1634	1632
N	48	24	269	283	7511	11562	2310	2309
SU*	31	390	185	19	4098	7912	1839	1842
U	186	18	48	374	9545	4056	1868	1866
N	272	284	37	34	9582	6264	2086	2085
SU*	54	13	124	435	4857	5681	2184	2181
Rat 762
SY	19	212	351	45	7286	13454	1607	1610
SY	457	55	13	101	17170	3843	1002	999
N	35	59	278	255	7585	11540	1115	1117
N	269	270	42	46	9775	6687	874	871
SU	49	376	169	32	4361	8420	1021	1022
U	223	32	42	332	9288	3973	835	830
SY	16	118	450	44	4271	18455	831	835
SU	88	24	90	424	7189	6969	919	919
U	14	84	65	462	7034	6502	1101	1102
Rat 763
SY	20	128	423	56	5064	22077	660	661
SY	443	57	9	118	21337	3323	959	957
N	54	65	268	240	9464	11135	1484	1485
N	245	283	42	58	11565	8907	1115	1116
SU*	89	377	131	29	5234	12449	1450	1453
U	135	34	74	341	17582	4914	1646	1647
SY	7	112	410	63	4732	24892	1396	1400
U	304	278	19	26	10848	5991	1096	1096
SU	88	107	67	364	15403	5645	1496	1494

^*Several sessions that used other values of the RI schedules preceded this condition. See text for explanation.

In the necessary conditions (conditions designed to determine if a change in the ratio of obtained reinforcers is necessary to produce a change in the response ratios), the ratio of sums favored one alternative and the ratio of ratios equaled 1.0. This was accomplished by using, at one alternative, RI 179 s as the stay schedule and RI 161 s as the switch schedule, and at the other alternative, RI 36 s as the stay schedule and RI 32 s as the switch schedule.

In the sufficient conditions (conditions designed to determine if a change in the ratio of obtained reinforcers is sufficient to produce a change in the response ratios), the ratio of sums favored one alternative and the ratio of ratios favored the other alternative. This was accomplished by using similar values of the RI schedules for staying at each alternative. The value of the switch schedule at one alternative was much longer than its associated stay schedule and the value of the switch schedule at the other alternative was much shorter than its associated stay schedule.

In the unsymmetrical conditions the combinations of ratios of ratios and ratios of sums were different from those used in other conditions. The operating of the schedules and the arranging of reinforcers was identical in all four arrangements of schedules.

For each RI schedule a probability generator was sampled every 0.5 s. If a signal occurred, then the next response associated with that schedule was reinforced. For each rat, Table 1 lists the sequence of conditions, the number of sessions that each condition was in effect, and the arrangement of schedules in each condition. All rats were first exposed to symmetrical conditions. Then they were exposed to two necessary conditions; the sum of the reinforcers was greater at the left alternative in one condition and greater at the right alternative in the other condition. For Rat 761, two sufficient conditions occurred between the two necessary conditions. Next, rats were exposed to two sufficient conditions. Across rats, after several sessions it was clear that for eight sufficient arrangements there was a preference for one alternative. Rather than continue using the values of these arrangements, the schedules were changed in order to produce indifference, because that was the aim of the sufficient condition. Data from these incomplete conditions are not reported. All other conditions remained in effect for at least 15 sessions and until visual inspection showed there were no apparent upward or downward trends in the logs of the ratios of the number of reinforcers, of responses, and of times for five consecutive sessions. Sessions were typically conducted 7 days a week and ended after the first changeover response following the 125th reinforcer. Fifteen to 30 min after each session rats were fed sufficient rat chow, usually 5 to 10 grams, to maintain their 85% weight.

Results

All results reported here are based on the sums of the data from the last five sessions of each condition. Table 1 presents these sums of responses for staying at the left and right alternatives, reinforcers obtained from the stay and switch schedules at each alternative, time spent at the left and right alternatives, and the changeovers (switches) from the left and right alternatives. The first press at an alternative (except for the first response in a session) was the response for switching from the other alternative (Bsw_i); subsequent presses, until the first press at the other alternative, were responses for staying at an alternative (Bst_i). Time spent at the alternative was the cumulative time from the first press at the alternative to the first press at the other alternative.

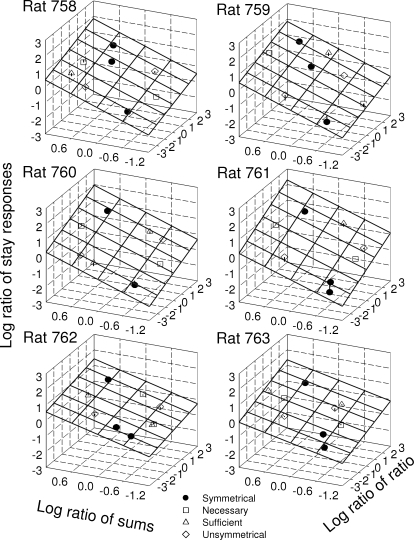
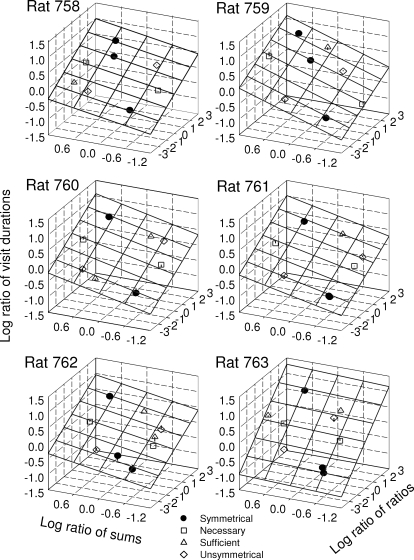
The stay/switch model described the results of each rat in this experiment. The logs of the stay-response ratios and the logs of the time ratios increased approximately linearly as a joint function of the logs of the ratios of the sums and the logs of the ratios of the ratios (with stay-response ratios shown in Figure 1 and time ratios shown in Figure 2). The results of least-squares linear regressions, presented in Table 2, show that Equation 3 described the stay-response ratios and time ratios for each rat (r² > .90 in every case). The best-fitting planes from the linear regressions are shown in the figures. The vertical line at each symbol indicates the residual—the amount the obtained datum deviated from the predicted datum. Often the residual is not visible because it is so small, or it is obscured by the filled symbol. This means, with few exceptions, the data points fall almost exactly on the plane. There was no consistent bias: the estimates of log k were usually within 2 SE of 0. For stay-response ratios, log k was at least 2 SE greater than 0 for Rat 758; log k was at least 2 SE less than 0 for Rat 762. For visit-duration ratios, log k was at least 2 SE greater than 0 for Rats 758 and 763. Both the ratio of the sums and the ratio of the ratios are necessary for the good descriptions. For stay-response ratios, estimates of both sensitivities, l and m, were more than 2 SE greater than 0 and they differed from each other by more than 2 SE, indicating they were not equal. For time ratios, estimates of these sensitivities were more than 2 SE greater than 0 for all rats, except m for Rat 763. For Rats 759, 761 and 763 the sensitivities differed from each other by more than 2 SE indicating they were different. Finally, the sensitivities to the ratios of the sums for stay-response ratios were always more than 2 SE greater than for ratios of visit durations. The sensitivity to the ratios of ratios for Rat 763 was more than 2 SE greater than for the ratios of the sums.

Fig 1.

The logs of the ratios of stay responses plotted as a joint function of the logs of the ratios of the sums of the stay and switch reinforcers obtained per visit and the logs of the ratios of the ratios of the stay and switch reinforcers obtained per visit. The plane shows the best-fitting plane, using the stay/switch model (Equation 3) and data from all conditions.

Fig 2.

The logs of the ratios of times plotted as a joint function of the logs of the ratios of the sums of the stay and switch reinforcers obtained per visit and the logs of the ratios of the ratios of the stay and switch reinforcers obtained per visit. The plane shows the best-fitting plane, using the stay/switch model (Equation 3) and data from all conditions.

Table 2.

The results of least-squares multiple linear regressions using the stay/switch model (Equation 3) and the data from all conditions. Also shown are the results of the F-test for each regression using time allocation.

Rat	l	SE	m	SE	log k	SE	r2	df	F
Ratio of run lengths
758	0.27	0.04	0.78	0.09	−0.15	0.06	0.96	5
759	0.23	0.07	0.98	0.17	−0.02	0.11	0.92	5
760	0.29	0.04	0.96	0.1	−0.08	0.07	0.96	5
761	0.36	0.07	0.92	0.17	0.1	0.12	0.93	5
762	0.15	0.04	0.71	0.1	0.14	0.06	0.93	6
763	0.25	0.05	0.61	0.1	−0.1	0.06	0.93	6
Ratio of visit durations
758	0.22	0.01	0.23	0.02	0.05	0.01	0.99	5	130.7*
759	0.18	0.03	0.45	0.06	0.01	0.04	0.96	5	42.47*
760	0.22	0.02	0.31	0.05	0.05	0.03	0.97	5	30.48*
761	0.22	0.01	0.3	0.03	0	0.02	0.99	5	96.82*
762	0.21	0.03	0.23	0.08	0.04	0.04	0.91	6	11.19*
763	0.38	0.02	0.06	0.04	0.08	0.02	0.99	6	3.47

^*p < .05

Because the stay/switch model described preference the following analysis assessed whether the stay/switch model described the performances at each alternative. The equation for applying the stay/switch model to behavior at Alternative 1 is,

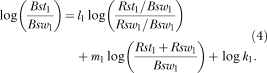4

The equation for performance at Alternative 2 is similar, with subscripts denoting Alternative 2. The results of linear regressions using Equation 4 for run lengths and visit durations at each alternative show that Equation 4 described the performances at each alternative (Table 3), although the goodness-of-fit, in terms of r², were usually smaller than the goodness-of-fit of the ratios of performances at both alternatives (Table 2). This difference in the goodness-of-fit may be because Equation 3 takes the ratio of the data from each alternative. In Equation 3, each ratio consists of a value plus error in the numerator and a value plus error in the denominator. Then, when dividing using logs, the errors subtract, which reduces the magnitude of error for the ratios. This results in a better goodness-of-fit (greater r²). With the exceptions of Rat 761 on Alternative 1 and Rat 763 on Alternative 2, the descriptions of run lengths were better than for visit durations.

Table 3.

The results of linear regressions using Equation 4, the stay/switch model applied to one alternative. Also shown are the differences between the l, m, and log k for the left and right alternatives and the SE of this difference.

Rat	Alternative 1				Alternative 2				l1-l2	SEl1-l2	m1-m2	SEm1-m2	log k1-log k2	SElog k1 – log k2
	l1	m1	log k1	r2	l2	m2	log k2	r2
Run lengths
758	0.33	0.69	0.97	0.97	0.21	0.84	1.25	0.86	0.12	0.09	−0.15	0.19	−0.29	0.2
759	0.29	1.04	1.3	0.9	0.15	0.71	1.12	0.75	0.14	0.15	0.33	0.33	0.19	0.24
760	0.36	0.96	1.33	0.95	0.21	0.74	1.2	0.83	0.16	0.09	0.22	0.23	0.12	0.23
761	0.4	0.98	1.4	0.8	0.35	0.71	1.07	0.9	0.05	0.16	0.27	0.35	0.33	0.36
762	0.2	0.7	0.93	0.92	0.13	0.65	0.75	0.86	0.07	0.07	0.05	0.17	0.18	0.11
763	0.23	0.69	0.82	0.93	0.26	0.59	0.86	0.85	−0.03	0.1	0.1	0.19	−0.04	0.15
Visit durations
758	0.25	0.11	0.69	0.75	0.19	0.37	0.89	0.81	0.07	0.09	−0.25	0.19	−0.19	0.18
759	0.19	0.35	0.98	0.84	0.15	0.36	0.98	0.68	0.04	0.1	−0.02	0.22	0	0.16
760	0.23	0.34	0.78	0.83	0.17	0.13	0.54	0.63	0.06	0.08	0.21	0.21	0.25	0.22
761	0.18	0.34	0.89	0.85	0.25	0.26	0.81	0.83	−0.07	0.08	0.09	0.18	0.07	0.17
762	0.21	0.13	0.99	0.83	0.21	0.31	1.07	0.8	0	0.07	−0.19	0.17	−0.08	0.11
763	0.31	0.15	1.06	0.79	0.4	0.19	1.03	0.86	−0.09	0.11	−0.04	0.21	0.03	0.16

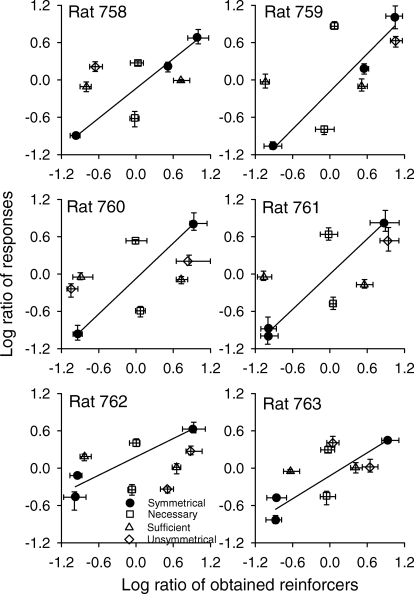
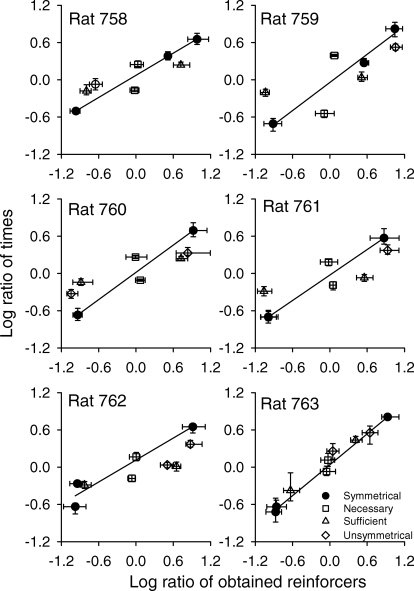
Response and time ratios from the symmetrical conditions increased with increases in obtained reinforcer ratios (Figures 3 and 4) and the generalized matching law described these data. Explicitly noting the stay and switch responses and the stay and switch reinforcers in the generalized matching law (Equation 1) produces

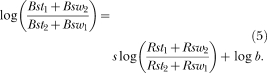5

It is important to note that the subscripts refer to the alternative switched from and the alternative where reinforcers were arranged. The symbols are the same as in previous equations. Reinforcer ratios were the sum of the stay reinforcers obtained at the left lever plus the switch reinforcers obtained by changing over from the right lever and pressing the left lever. This sum was divided by the sum of the stay reinforcers obtained at the right lever plus the switch reinforcers obtained by changing over from the left lever and pressing the right lever. This analysis is the standard application of the generalized matching law to concurrent choice, with stay and switch responses and reinforcers explicitly noted (MacDonall, 2000; MacDonall, 2005). Table 4, which shows the results of linear regressions using the data from symmetrical conditions, shows that although there were few data points (at most three), Equation 5 described response and time ratios for each rat (r² > .90 in every case). Excluding the rats with only two data points, the sensitivity, s, is within 2 SE of 1.0 for Rats 759 and 761, using response ratios. There was no consistent bias. The bias, log b, for response ratios for Rat 758 was at least 2 SE less than 0 and the bias for time ratios was at least 2 SE greater than 0. These results suggest that the generalized matching law described response and time ratios from the symmetrical conditions using the procedures in this experiment. Although there were only two or three control conditions in this experiment, the generalized matching law has also described data when rats were trained in the same procedure on four or five symmetrical conditions (MacDonall, 2005). Thus, any failure of the generalized matching law to describe data from all conditions cannot be attributed to this procedure.

Fig 3.

The logs of the ratios of responses plotted as a function of the logs of the ratios of obtained reinforcers. The solid line shows the best-fitting line, using the generalized matching law (Equation 5) and data from symmetrical conditions. The horizontal and vertical range bars show the range of the reinforcer ratios and the response ratios, respectively, during the 5 days of stable responding.

Fig 4.

The logs of the ratios of times plotted as a function of the logs of the ratios of obtained reinforcers. The solid line shows the best-fitting line, using the generalized matching law (Equation 5) and data from symmetrical conditions. The horizontal and vertical range bars show the range of the reinforcer ratios and the time ratios, respectively, during the 5 days of stable responding.

Table 4.

Results of the least-squares linear regressions using the generalized matching law, with stay and switch reinforcers noted (Equation 5), for response and time ratios from symmetrical conditions only.

Rat	s	SE	log b	SE	r2	df
Responses
758	0.80	0.05	−0.14	0.04	1.00	1
759	1.01	0.16	−0.19	0.14	.97	1
760	0.95	0.00	−0.07	0.00	1.00	0
761	0.94	0.06	0.00	0.06	1.00	1
762	0.49	0.15	0.18	0.14	.91	1
763	0.61	0.17	−0.12	0.15	.93	1
Times
758	0.60	0.00	0.07	0.00	1.00	1
759	0.76	0.09	−0.04	0.08	.99	1
760	0.73	0.00	0.02	0.00	1.00	0
761	0.68	0.00	−0.02	0.00	1.00	1
762	0.59	0.16	0.11	0.15	.93	1
763	0.83	0.03	0.04	0.03	1.00	1

The two necessary conditions produced response and time preferences first for one alternative and then for the other alternative. Figures 3 and 4 show these data (squares) are aligned approximately vertically over 0 on the x axis. There was a preference for the left alternative and then for the right alternative when the ratio of the obtained reinforcers did not change. The horizontal range bars show the reinforcer ratios overlapped during these two conditions; the vertical range bars show that the preferences did not overlap from one condition to the other.

In the two sufficient conditions no changes in preferences were found, when measured by response ratios. The data points (triangles) are approximately horizontally aligned near 0 on the y axis. The vertical range bars overlap for Rats 759, 760, 761 and 763. For Rats 758 and 762, the bars miss overlapping by 0.03 and 0.05, respectively; the horizontal range bars do not overlap, indicating that the ratio of obtained reinforcers was different in the two sufficient conditions. In these conditions, measuring preference in terms of time ratios shows that preferences did change. The data for Rat 763 lie on the matching line; however, the data for the other 5 rats show an attenuation of the preference compared to the expected preference based on each rat's generalized matching line. The vertical error bars generally were close but did not overlap, indicating the preference differed somewhat in the two conditions. The horizontal error bars did not come close to overlapping, indicating the ratio of obtained reinforcers was clearly different in the two conditions. The reason the preference for time ratios was attenuated but not eliminated, as it was for the response ratios, will be discussed later.

As suggested by Figures 3 and 4, the generalized matching law did not describe the combined data from all conditions. Table 5 shows the results of least-squares linear regressions using Equation 5, which did not describe response ratios well (r² < .53 in all cases). Equation 5 described the time ratios for Rat 763 very well(r²  =  .98), but not the time ratios for the other 5 rats (with r² ranging from .66 to .81).

Table 5.

Results of the least-squares linear regressions using the generalized matching law (Equation 5) for response and time ratios from all conditions.

Rat	s	S.E.	log b	S.E.	r2	df
Responses
758	0.43	0.22	−0.02	0.15	.38	6
759	0.62	0.28	0.00	0.22	.45	6
760	0.41	0.23	−0.03	0.18	.35	6
761	0.59	0.23	−0.02	0.18	.52	6
762	0.22	0.16	0.02	0.12	.22	7
763	0.47	0.18	−0.05	0.11	.50	7
Time
758	0.46	0.09	0.09	0.06	.81	6
759	0.54	0.16	−0.01	0.12	.66	6
760	0.45	0.10	0.05	0.08	.77	6
761	0.49	0.11	−0.06	0.09	.77	6
762	0.43	0.09	−0.02	0.07	.75	7
763	0.82	0.05	0.08	0.03	.98	7

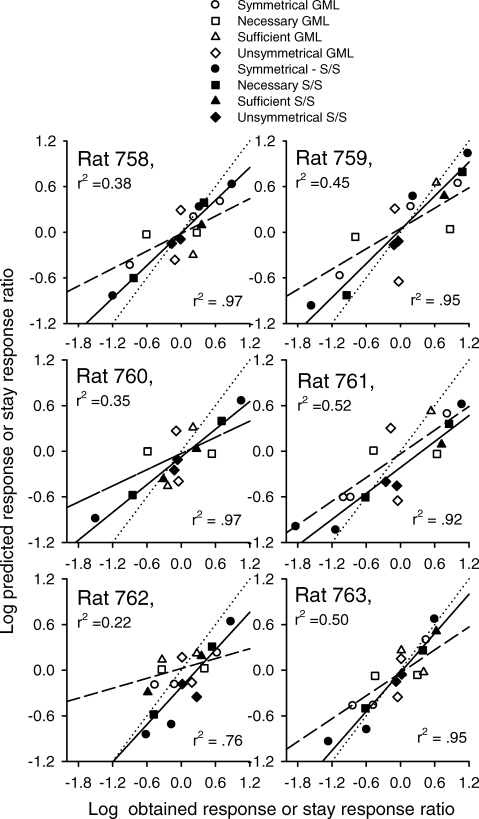
Equation 3, which has an additional fitted parameter, provided much better descriptions of time and response ratios, in terms of r², except for the time ratios of Rat 763, than did Equation 5. Because these equations differ in the number of fitted parameters, r² is not appropriate for comparing the descriptions. Because both models used time ratios, the variances are equal and the descriptions can be compared using an F test (Motulsky & Christopoulos, 2003, Ch. 21). The descriptions were significantly different for all except Rat 763 (Table 2). When measuring preference in terms of response ratios Equations 3 and 5 use different dependent variables, which means the variances are different, therefore the models cannot be compared using the F test. Instead, the predicted response (or stay-response) ratios using Equations 3 and 5, respectively, were plotted against the obtained ratios. Figure 5 shows that Equation 3 provided better descriptions. The r² for stay-response ratios (Equation 3) were at least .45 greater than the r² for response ratios (Equation 5). Additionally, the regression line for stay-response ratios was always closer to 1.0, perfect prediction, than the line for response ratios. Taken together, these comparisons indicate the stay/switch model (Equation 3) provided better descriptions of the response and time preferences than did the generalized matching law (Equation 5).

Fig 5.

The predicted (stay) response ratio plotted as a function of the obtained (stay) response ratio using the generalized matching law (GML, Equation 5) and the stay/switch model (S/S, Equation 3). The r² for descriptions by the generalized matching law is in the upper left-hand corner of each plot. The r² for descriptions by the stay-switch model is in the lower right-hand corner of each plot. The best-fitting line to the data using the stay/switch model is solid. The best-fitting line to the data using generalized matching law is dashed. The dotted line is the locus of perfect prediction.

Discussion

The generalized matching law has widespread empirical support. Consequently, caution should be used when comparing it to another model of choice, such as the stay/switch model. Nonetheless, the stay/switch model described the results of the present experiment when both the ratio of the ratios and the ratio of sums were varied and its description was generally better than that of the generalized matching law. The stay/switch model (Equation 3) described the time preferences from all conditions for each rat, and for 5 rats its descriptions (Table 2) were better than those of the generalized matching law (Table 5). The stay/switch model described the response data from all conditions of each rat and these descriptions were better than those of the generalized matching law. Because the stay/switch model is based on performances at the alternatives, it should also describe those performances. The stay/switch model applied to one alternative (Equation 4) described those performances (Table 3). Finally, the results in Figures 3 and 4 show that changing the ratio of obtained reinforcers, the predictor in the generalized matching law, was neither necessary nor sufficient for changing preference as measured using response allocations: Changing the ratio of obtained reinforcers was not necessary for changing preference as measured by time ratio. Changing the obtained reinforcer ratio, however, was sufficient for changing preference as measured by time ratios.

The reason the obtained reinforcer ratio was sufficient for changing time ratios but not for response ratios was the different sensitivities of stay-response ratios and time ratios to the ratios of sums. The sensitivities to the ratio of the sums was much greater for the stay-response ratio. Consequently, when selecting values for the stay and switch schedules at each alternative that would produce no preference in terms of response ratios, these ratios did produce a preference when measured using time ratios. With time ratios, the much lower sensitivity to the ratios of sums means, comparatively, the ratios of ratios had more influence on time ratios producing a preference. Presumably, one could select values of the schedules that would produce no preference in terms of time ratios, but which could produce a preference in terms of response ratios. It remains for future research to confirm this speculation.

Comparing The Generalized Matching Law and The Stay/Switch Model

The generalized matching law and the stay/switch model focus on different independent and different dependent variables. The generalized matching law focuses on total reinforcers obtained at each alternative and the stay/switch model focuses on stay and switch reinforcers obtained at each alternative. For the dependent variables, the generalized matching law focuses on the ratio of total behavior at each alternative while the stay/switch model focuses on the ratio of the stay responses (run lengths). They both focus on the ratio of time at each alternative. The ratio of visit durations is equivalent to the ratio of times because the switches from each alternative in the visit durations cancel.

Dependent Variables

Time ratios are the same in both models and the stay/switch model provided better descriptions of time allocations. Response measures, however, are different. In two-manipulanda procedures, such as used in the present experiment, the stay/switch model excludes the first response at the alternative, the switch response, from the ratio of stay responses at the alternative. The generalized matching law, on the other hand, includes these responses in the ratio of responses. Thus, although the stay/switch model was generally better, a comparison of the two models using the same dependent variables would be clearer. The difference in dependent variables disappear when using a switch-lever procedure (Findley, 1958), because identical response measures are used. In a switch-lever procedure responses at one lever (the main lever) earn and obtain reinforcers; responses at the other lever (the switch lever) change the alternative in effect. In this procedure the switch responses are the responses at the switch lever and stay responses are responses at the main lever. Consequently, the ratio of responses and the ratio of stay responses are, for both models, the responses at the main lever. Thus, using a switch-lever procedure allows a comparison of the two models with identical calculations of response ratios.

A previous experiment used a switch-lever procedure and varied the rates of earning stay and switch reinforcers at the alternatives (MacDonall, 2005). Table 6 shows the results of linear regressions using Equation 5 and response ratios. Table 7 shows the results of recalculating the linear regressions using Equation 3 and the same response ratios. The linear regressions are recalculated here because MacDonall (2005) did not use Equation 3. Because the same dependent measure was used, the Akaike Information Criterion (AIC, Akaike, 1974) was an appropriate statistic for comparing the models. AIC compares the residual sums-of-squares, considering the number of data points, after adding a penalty for extra fitted parameters. The absolute size of AIC is not meaningful. The difference in AIC is meaningful and the model with the lower AIC is the preferred model (Motulsky & Christopoulos, 2003, Ch. 21). For 5 rats, AIC was lower when using Equation 3 (Tables 6 and 7), meaning this equation was preferred. The AIC for Rat 409 favored Equation 5. This probably occurred because the ratio of the sums had no effect on response ratios; the value of 1 did not differ from 0. This variable did not affect response ratios and did not reduce the residuals. Consequently the penalty in AIC, for the extra parameter in the stay/switch model, increased AIC.

Table 7.

Results of linear regressions using the stay/switch model (Equation 3) and response data from all conditions in MacDonall (2005). Also shown are the results of the AIC analysis.

Rat	l	SE	m	SE	log k	SE	r2	df	AIC
407	0.07	0.04	0.39	0.06	−0.04	0.03	.89	7	−33
408	0.15	0.03	0.40	0.04	−0.01	0.03	.96	7	−37
409	0.28	0.06	0.07	0.07	0.03	0.04	.90	6	−27
410	0.16	0.03	0.16	0.04	0.03	0.02	.92	7	−39
411	0.05	0.03	0.20	0.03	−0.01	0.02	.88	6	−33
412	0.15	0.03	0.22	0.06	0.03	0.03	.92	6	−31

Independent Variables

The influence of switch reinforcers as used in the present experiment and previous experiments (MacDonall, 1999, 2000, 2003, 2005; MacDonall et al., 2006) is seen in the results reported by Vaughan, Kardish and Wilson (1982). They exposed pigeons to a concurrent VI 3 min VI 3 min and then added a VI 1 min to only one alternative, the varied alternative, that arranged reinforcers for switching from the varied alternative. These additional switch reinforcers were delivered by a response in the other (constant) alternative following a COD. Their procedure increased the switch reinforcers obtained in the constant alternative and they reported that preference shifted towards that alternative.

According to Equation 3 adding the VI 1-min schedule had two effects. First, the number of reinforcers obtained for switching to the constant alternative approximately quadrupled. This decreased the ratio of stay to switch reinforcers at the varied alternative to about 25% of its baseline value, which resulted in more switches to the constant alternative and shorter run lengths at the varied alternative. Second, because these switch reinforcers were delivered after a COD and one or more stay responses would occur during the COD, and because a stay response obtained the switch reinforcer, these switch reinforcers also had the effect of strengthening stay responses at the constant alternative, increasing run lengths at the constant alternative. These two effects, taken together, resulted in a shift in preference towards the constant alternative.

There are perhaps three reasons that the importance of stay-and-switch reinforcers in concurrent schedules was not recognized until now, and they result from the symmetrical arrangement of schedules in standard concurrent procedures. First, the value of the schedule for staying at an alternative is confounded with the value of the schedule for switching to that alternative. Second, sensitivity to the log of the ratio of the ratios, in the stay/switch model (Equation 3), equals half the sensitivity to the log of the ratio of obtained reinforcers in the generalized matching law (Equation 5; MacDonall, 1999). Third, the log of the ratio of the sums equals zero, thus it has no effect on preference. In effect, the stay/switch model is equivalent to the generalized matching law only when using symmetrical arrangements. In summary, I propose that the generalized matching law adequately described the data from concurrent choice procedures because they used symmetrical arrangements, even though obtaining reinforcers was not the critical variable.

Quantitative Descriptions of Preference

Equation 3, which describes a flat plane, provided good descriptions of the stay-response and time ratios from all rats. There were no more than nine data points for any rat, although these data covered a moderately wide range of each variable. The present experiment clearly showed that the generalized matching law did not describe these data, but Equation 3 described these data well. It remains for future research to fully evaluate Equation 3.

In the present experiment, the generalized matching law described the response ratios from the symmetrical conditions. This suggests that the generalized matching law might describe response ratios when the same rule, such as in the necessary conditions or sufficient conditions, is used to generate the schedule values. Figure 1 provides limited support for this idea. It appears data from each arrangement fall in a line going approximately through the origin. For each rat, however, visual inspection indicates the slopes for fits by the generalized matching law to the symmetrical, necessary, and sufficient conditions were very different. Although there are only two data points for each necessary and sufficient condition, similar results were obtained in previous experiments (MacDonall, 2005). Those experiments had more conditions per arrangement. One experiment compared symmetrical and asymmetrical arrangements, and the other compared symmetrical and weighted arrangements. Inspection of Figure 1 (MacDonall, 2005) suggests that the generalized matching law described the behavior from each arrangement, with a slope < 1 for symmetrical conditions and > 1 in the asymmetrical conditions. Inspection of Figure 3 (MacDonall, 2005) shows the generalized matching law described the data from each arrangement, with a different bias for each arrangement.

Although in the previous experiment (MacDonall, 2005) and the present experiment the generalized matching law can describe the results from each arrangement separately, the generalized matching law does not appear to provide a rationale for the changes in slopes or biases for each different arrangement. It appears that factors outside the generalized matching law, that is, the different arrangements, are the factors changing slopes and biases. Fitting the generalized matching law only to data obtained from conditions using the same arrangement of schedules means that data from each arrangement are fitted by the generalized matching law, each producing different bias and sensitivity parameters, one for each arrangement. A more parsimonious approach applies one model simultaneously to all the data from one experiment, regardless of the arrangements of schedules. This is the how the stay/switch model (Equation 3) was applied to the data from MacDonall (2005) and the present experiment. Thus, even though the generalized matching can describe data from each condition in isolation, the stay/switch model's approach is more parsimonious.

The stay/switch model may explain how changing the ratios of the sums changes slopes and biases. This provides additional support for the stay/switch model. The changes in slope and bias in descriptions by the generalized matching law result from the generalized matching law ignoring the ratio of the sums. That is, the changes in preference are caused by changes in the ratio of the sums, which is an independent variable not captured by the generalized matching law.

Summary

The stay/switch model has been presented as a viable alternative to the generalized matching law. It is more parsimonious in that it describes all the data in one analysis, whereas the generalized matching law may describe all the data but needs to apply the law to each different arrangement of schedule values. The stay/switch model explains why slope and bias change in the application of the generalized matching law to different arrangements. The obtained reinforcer ratio was found to be neither necessary nor sufficient for describing response ratios and not necessary for describing time ratios. This seems to imply that the generalized matching law does not identify the critical independent variable.

Although this and recent experiments (MacDonall, 2005, MacDonall et al., 2006) support the stay/switch model, additional experimental evidence is needed before concluding that it offers a better approach than the generalized matching law. First, and most importantly, it remains for sufficient data, covering a wide enough range of the ratio of ratios and ratio of sums, to conclude that a flat surface (Equation 3) describes the relation between reinforcer allocations and behavior. Second, the vast majority of choice experiments use a COD, but the stay/switch model has only been successfully applied using a COD with one pair of stay and switch schedules. Third, the generalized matching law describes choice when magnitudes, delays, and qualities of reinforcers differ. It remains to be demonstrated that the stay/switch model describes choice when varying these features of reinforcers. Fourth, the generalized matching law implies interactions among the two alternatives and the stay/switch model conceptualizes the two sets of choices, one set at each alternative, as independent of each other. Data related to whether or not the choices interact will clarify the stay/switch model. Fifth, in complex human behavior, choice is frequently between topographically different responses. Experiments extending the stay/switch model to choice among topographically different responses remain to be reported.