Delay, Probability, and Social Discounting in A Public Goods Game

Abstract

A human social discount function measures the value to a person of a reward to another person at a given social distance. Just as delay discounting is a hyperbolic function of delay, and probability discounting is a hyperbolic function of odds-against, social discounting is a hyperbolic function of social distance. Experiment 1 obtained individual social, delay, and probability discount functions for a hypothetical $75 reward; participants also indicated how much of an initial $100 endowment they would contribute to a common investment in a public good. Steepness of discounting correlated, across participants, among all three discount dimensions. However, only social and probability discounting were correlated with the public-good contribution; high public-good contributors were more altruistic and also less risk averse than low contributors. Experiment 2 obtained social discount functions with hypothetical $75 rewards and delay discount functions with hypothetical $1,000 rewards, as well as public-good contributions. The results replicated those of Experiment 1; steepness of the two forms of discounting correlated with each other across participants but only social discounting correlated with the public-good contribution. Most participants in Experiment 2 predicted that the average contribution would be lower than their own contribution.

The economist Julian Simon (1995) claimed that people allocate available resources on three dimensions: (a) current consumption by the person, (b) consumption by the same person at later times (delay discounting), and (c) consumption by other people (social discounting). Simon said: “Instead of a one-dimensional maximizing entity, or even the two-dimensional individual who allocates intertem 6 porally, this model envisages a three-dimensional surface with an interpersonal ‘distance’ dimension replacing the concept of altruism” (p. 367). Simon did not list probabilistic discounting as an additional form, perhaps because he considered expected value (probability times amount) to be an obvious rational adjustment to current consumption. However, in practice, probability discounting does not simply track expected value (Kahneman & Tversky, 1979). When probability (0 ≤ p ≤ 1) is converted to odds-against (θ  =  (1−p)/p) which, like delay, increases indefinitely from zero, human probability discounting takes the same hyperbolic form found by Mazur (1987) to describe delay discounting by pigeons (Rachlin, 1989; Rachlin, Logue, Gibbon, & Frankel, 1986).

Social discounting also takes this same hyperbolic form. Prior studies in our laboratory (Jones & Rachlin, 2006; Rachlin & Jones, 2008) have obtained social discount functions as follows. Participants were asked to imagine that they had made a list of the 100 people closest to them (but not to actually make the list). Order on the list (N, ranging from 1 to 100) was taken as a measure of social distance. Then participants were asked to choose hypothetically between a varying amount of money for themselves and a fixed amount for a person at a given social distance. For example, a participant might prefer $75 for himself to $75 for the 10^th person on his list (N  =  10) but prefer $75 for that person to $5 for himself. At some “crossover” amount (v) between $75 and $5 for himself, he must be indifferent between an amount for himself and a (usually) lesser amount for the 10^th person on his list. In our studies, as N increased, crossover amount decreased. In other words, as social distance increased, participants were willing to forgo less money for themselves in order to give a fixed amount to another person. The function thus obtained, relating social distance to amount of money forgone, is a social discount function.

In Rachlin and Jones's (2008) experiment the (hypothetical) alternatives were $75 for person-N and nothing for the participant versus a lesser amount for the participant and nothing for person-N (as in the example above). In Jones and Rachlin's (2006) experiment the hypothetical alternatives were an evenly shared $150 ($75 for the participant and $75 for person-N) versus an amount (between $75 and $150) for the participant and nothing for person-N. The social discount functions (median amounts of money forgone in the two experiments as functions of social distance) were virtually overlapping; they were well fitted by the following hyperbolic equation:

1

where v and V are discounted and undiscounted money amounts, N is social distance, and k_social is a constant that differed among individuals; the greater is k_social, the steeper is social discounting.

The present experiments measured social, delay, and probability discounting of participants who also played a public goods game (PGG) where they chose the fraction of an initial endowment to contribute to a common fund that would be doubled and distributed equally to all players. The PGG is a laboratory model of such real-world activities as contributing to charity or public television, voting, recycling, and other acts of social cooperation (Camerer, 2003). In a PGG each player has the option of contributing some fraction of an initial endowment to a common investment. The investment has a positive return and is distributed equally to all players regardless of the amount of their contribution. As an illustration, consider a PGG with 100 players, each of whom is given (a hypothetical) $100 endowment. A player may contribute any fraction of the $100. The total amount contributed is then doubled by the experimenter and distributed equally among the players regardless of their contribution. The amount earned by a player would then be the amount that player originally kept plus 1/50 of the total contributed.

The PGG is structurally the same as a prisoner's dilemma game (PDG: Rapoport, 1965). In the two-player version of the PDG, either player may “cooperate” or “defect.” If both players cooperate, both earn a moderately high reward; if both defect, both earn a moderately low reward; if one cooperates and one defects, the cooperator earns a very low reward while the defector earns a very high reward. As in the PGG, defection in the PDG maximizes the reward for the individual while cooperation increases reward for the group.

Since the PGG was played only once by participants in these experiments, and all choices were made simultaneously and anonymously, no player's contribution could have influenced that of any other player. With 100 players, each $1.00 contributed would earn a return of $0.02 for the contributor ($1.00 doubled and divided among 100 players) resulting in a loss of $0.98, for that dollar, regardless of others' contributions. But each dollar contributed would also result in a gain of $0.02 for each of the other 99 players. The net loss of $0.98 for the individual may be balanced by the total gain of $1.98 for the other players in the group. Thus there are structural similarities between the PGG and the social discounting task; in both, participants may forgo smaller rewards for themselves in exchange for larger rewards to other people. The main purpose of both experiments was to determine the extent to which behavior in one of these tasks predicts behavior in the other.

Like social discounting, delay and probability discounting are well described by hyperbolic functions in the form of Equation 1 (Green & Myerson, 2004). It has been speculated that one of these discounting processes is fundamental while another (or others) are derivable from it or that all three, or two of the three, depend on some common mechanism (Rachlin, 1989, 2002b). If this were the case, Simon's three dimensions of utility would not vary independently of each other; the steepness of the three discount functions would be expected to correlate across individuals and to vary together as discounting conditions vary.

Such common variation has not been consistently obtained with delay and probability discounting (Green & Myerson, 2004). Moreover, Rachlin and Jones (2008) found that, like probability discounting, but opposite to delay discounting, social discounting was steeper with higher undiscounted amounts (Vs). A second purpose of the experiments was to further examine relationships among the three forms of discounting as well as the relationship of each with performance in the PGG.

Experiment 1

Method

Participants

Participants were 103 Stony Brook University business school students (51 male, 47 female, 5 unreported, Mdn age  =  24), enrolled in two advanced undergraduate classes and one graduate class. They completed a pencil-and-paper PGG as well as social, delay, and probability discounting tests for partial course credit. Participants in each class completed the questionnaires at the same time in a lecture hall.

Materials and Procedures

The PGG instructions read as follows:

Imagine the following situation (purely hypothetical we regret to say):

1. The experimenter gives you $100.

2. A box is passed around to each person in this room.

3. Each person may put all or any part or none of the $100 into the box. No one else will know how much money anyone puts into the box.

4. After the box goes around the room, the experimenter doubles whatever is in the box and distributes it equally to each person in the room regardless of how much money they put into the box.

Each person will then go home with whatever they kept plus what they received from the box.

Note that you will maximize the money you receive by not putting any money in the box. Then you will take home the original $100 you kept plus what the experimenter distributes after doubling whatever money was in the box.

HOWEVER: If everybody kept all $100, nothing would be in the box and each person would take home $100.

Whereas, if everybody put all $100 in the box, each person would take home $200 after the money in the box was doubled and distributed.

Please indicate below how much of the $100, if any, you would put into the box. Please try to answer the question as if the money were real:

I would put the following amount into the box: $______

I would keep the following amount: $______

Sum must equal $100

Immediately after the PGG each participant completed social, delay, and probability discounting tests in a counterbalanced order. Each discounting test consisted of a page of instructions followed by five or six pages of questions.

For the delay discounting measure, five delays (D  =  1 day, 1 week, 1 month, 1 year, and 5 years) in 10 increments of money offered immediately were presented. Each delay was presented on its own page, with page order randomized with the following instructions:

Please choose which amount of money you would rather have for each line.

A. $75 for you right now. B. $75 for you after [D].

A. $70 for you right now. B. $75 for you after [D].

--------Down To-------

A. $5 for you right now. B. $75 for you after [D].

For the probability discount measure, five probabilities, expressed as percentages (p  =  90%, 70%, 50%, 30%, and 10%), were presented in 10 increments of money guaranteed. Each probability was presented on its own page, with page order randomized:

Please choose which amount of money you would rather have for each line:

A. $75 guaranteed or B. A [p]% chance of winning $75.

A. $70 guaranteed or B. A [p]% chance of winning $75.

-------Down To-------

A. $5 guaranteed or B. A [p]% chance of winning $75.

Social discounting instructions were as follows:

The following experiment asks you to imagine that you have made a list of the 100 people closest to you in the world ranging from your dearest friend or relative at position #1 to a mere acquaintance at #100. The person at number one would be someone you know well and is your closest friend or relative. The person at #100 might be someone you recognize and encounter but perhaps you may not even know their name.

You do not have to physically create the list- just imagine that you have done so.

Six social distances [N′s] were presented: #1, #5, #10, #20, #50, #100, each on its own page, with order of pages randomized. The amount of money to forgo in order to give $75 to another person was presented in 10 increments ranging from $85 to $0. Each page contained the following instructions:

Imagine you made a list of the 100 people closest to you in the world ranging from your dearest friend or relative at #1 to a mere acquaintance at #100.

Now imagine the following choices between an amount of money for you and an amount for the #[N] person on the list. Circle A or B to indicate which you would choose in EACH line.

A. $85 for you alone or B. $75 for the #[N] person on the list.

A. $75 for you alone or B. $75 for the #[N] person on the list.

-------Down To-------

A. $0 for you alone or B. $75 for the #[N] person on the list.

The maximum amount in Column-A was set at $85 rather than $75 because in previous research many participants preferred $75 for the 1^st or 2^nd person on their list to $75 for themselves (Jones & Rachlin, 2006).

For half of the discount tests the money amounts in Column A decreased (D) as shown above; for the other half, the amounts in Column A increased (I). The eight orders of increase and decrease across the three tests (III, IID, IDD, IDI, DDD, DDI, DII, DID) were counterbalanced across participants.

Data Analysis

The data of any participant who crossed over more than once on any page of a discount test were eliminated from all calculations involving that test. Also, the data of any participant whose PGG answers did not add to 100% of the total were eliminated from all calculations involving the PGG. A maximum of 11 participants were removed from the PGG analysis and a maximum of 10 participants were removed from the analyses comparing pairs of discounting measures. The number of participants removed for each analysis is reflected by the number of participants reported on each table in the results section.

The point (v) at which each of the remaining participants crossed over from preference for the Column-A amount to the Column-B amount (or vice versa) was determined at each social distance (N), delay (D) in days, and probability (p). Equations 1, 2, and 3 (see Rachlin, 2006 for discussion of this form of the equation) were fitted to the median crossover point at each social distance, delay, and probability. In addition, individual social, delay, and probability discount functions were determined for each participant by fitting individual crossover points (vs) to Equation 1, 2 or 3:

2

3

where D  =  delay in days; θ  =  (1−p)/p  =  odds against.

Results

Figure 1 shows median crossover points and crossover points of individual participants at the 20^th and 80^th percentiles for the three types of discounting. The exponent, s, represents sensitivity to the discounting variable (Green & Myerson, 2004). With social discounting (Equation 1), obtained values of s have not been significantly different from unity and were therefore set at unity in fitting Equation 1 to the median social crossover points. (But s was allowed to vary in fitting Equations 2 and 3 to the median delay and probability crossover points.) As in previous social-discounting tests, many participants preferred $75 for people at close social distances (N  =  1, 2) to $75 for themselves. Crossover points above $75 were obtained at these close social distances. The undiscounted value, V, was therefore allowed to vary in fitting Equation 1 to the median social crossover points. Parameters and fits of Equations 1, 2, and 3 to median crossover points are shown in the left side of Table 1. In addition, the three equations were fitted to individual participants' crossover points. For the individual fits, all parameters other than k were held constant. A k value was then determined for each participant for each of the three discount functions. The right side of Table 1 shows the mean of individual ks and mean of individual fits to Equations 1, 2, and 3.

Fig 1.

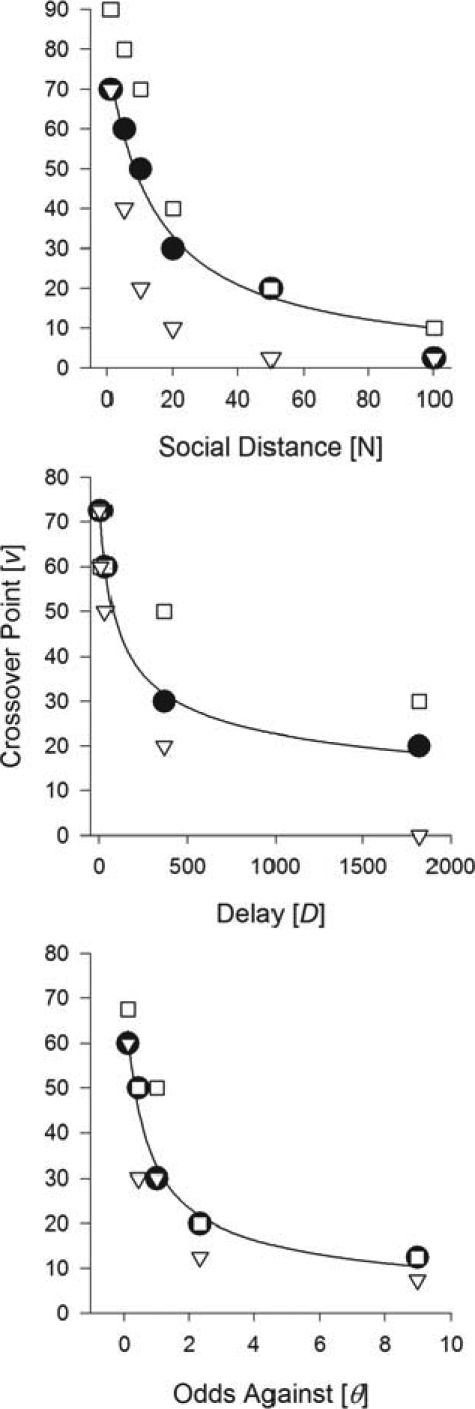
Upper graph: Social discount function: Amount of money for the participant equivalent to $75 for a person at a given social distance (N). The solid circles are median crossover points. The line is Equation 1 fit to the medians. Open squares are crossover points of the participant at the 80^th percentile (k  =  .04); open triangles are crossover points of the participant at the 20^th percentile (k  =  .27). Middle graph: Delay discount function: Amount of money now equivalent to $75 delayed by D days. The solid circles are median crossover points. The line is Equation 2 fit to the medians. Open squares are crossover points of the participant at the 80^th percentile (k  =  .01); open triangles are crossover points of the participant at the 20^th percentile (k  =  .09). Lower graph: Probability discount function: Amount of money for sure equivalent to $75 at a given odds against (θ  =  (1−p)/p). The solid circles are median crossover points. The line is Equation 3 fit to the medians. Open squares are crossover points of the participant at the 80^th percentile (k  =  2.8); open triangles are crossover points of the participant at the 20^th percentile (k  =  9.0).

Table 1.

Experiment 1. Best fit to median indifference points and mean of individual participant fits to Equations 1, 2 and 3.

Type of discounting	Best fitting Equation to median				Mean of fit to Equation for individuals
	V	k	s	R2	V	Mean k	SD	s	R2
Social (Eq. 1)	$77	0.067	1.00f	.97	$77f	0.081	0.272	1.00f	.80
Delay (Eq. 2)	$75f	0.029	0.35	.99	$75f	0.018	0.092	0.35f	.91
Probability (Eq. 3)	$75f	3.270	0.57	.97	$75f	4.570	2.949	0.57f	.89

^ffixed at this value.

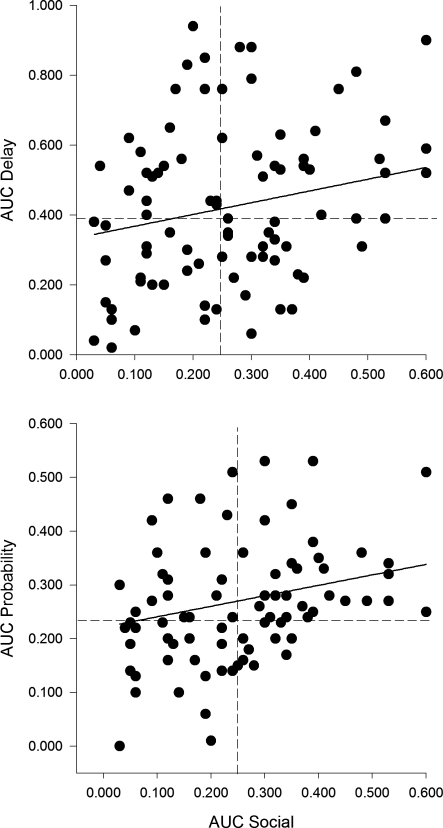
Area under the curve (0 ≤ AUC ≤ 1) is a single-parameter measure of discount rate that does not depend on functional form (Myerson, Green, & Warusawitharana, 2001). AUC is the sum of the areas of the trapezoids formed by adjacent crossover points and the abscissa (normalized with respect to the maximum). The closer the AUC is to unity, the shallower the discounting. Table 2 shows that participants with shallower social or probability discount functions (higher AUC) tended to contribute more in the PGG than did participants with steeper probability discount functions. However, there was no significant correlation between steepness of delay discounting and PGG contribution. Analyses reported in Tables 2 and 3 were performed using both AUC and log k. The significance of the results was the same for both measures. We report AUC because this measure involves no assumption of functional form. Figure 2 shows individual-participant delay AUC's (upper graph) and probability AUC's (lower graph), each plotted against individual-participant social AUC's.

Table 2.

Experiment 1. Best fit to median indifference points and Area Under the Curve (AUC) correlated with PGG contribution.

	Fit to Equation				AUC vs. PGG
Type of discounting	V	k	s	R2	AUC	r	p	n
Social (Eq. 1)	$77	0.067	1.00f	.97	.256	.245*	.016	96
Delay (Eq. 2)	$75f	0.029	0.35	.99	.391	.009	.935	92
Probability (Eq. 3)	$75f	3.270	0.57	.97	.248	.269**	.009	93

n: number of participants

^ffixed at this value.

^*p < .05.

^**p < .01.

Table 3.

Experiments 1 and 2: Correlations between AUCs for different forms of discounting.

	r	p	n
Social-Probability Experiment 1	.334**	.001	94
Probability-Delay Experiment 1	.205*	.048	94
Social-Delay Experiment 1	.282**	.006	93
Social-Delay Experiment 2	.249**	.001	160

n: number of participants.

^*p < .05.

^**p < .01.

Fig 2.

Upper graph: Social AUC versus delay AUC of individual participants. Lower graph: Social AUC versus probability AUC of individual participants. The different numbers of points in the two graphs at the same abscissa value are due to elimination from analysis of delay or probability data of participants who crossed over more than once on that measure. The solid lines are regression lines. The dotted lines are medians.

PGG contributions were not normally distributed across all participants. In order to account for non-normal distributions, we divided donations into those who contributed less than the median donation ($0–$25) and those who contributed more than the median ($26–$100) to create a binary variable. Four outliers of individual AUC social scores (all above .6) were removed from this analysis. Significances of all correlations did not change when the outliers were eliminated. The correlation between social discounting (AUC) and the binary PGG contribution was significant, r(90)  =  .222, p  =  .036. The correlation between AUC probability and the binary PGG contribution was also significant, r(92)  =  .371, p < .001. Table 3 shows that the AUC's of all three discount functions were significantly correlated with each other.

The average stated PGG contribution was $31. The distribution of contributions is shown in Figure 3 and will be discussed along with that of PGG contributions in Experiment 2.

Fig 3.

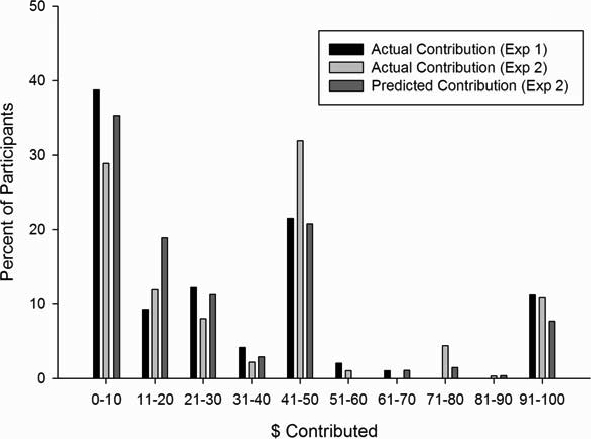
Distributions of stated PGG contributions in Experiment 1 and Experiment 2 and predictions of average contribution in Experiment 2.

Discussion

Participants who contributed higher percentages of their $100 endowment to the common good in the PGG were more generous to others at various social distances (shallower social discount functions) and were less risk-averse (shallower probability discount functions) than were participants who contributed less in the PGG. This is some evidence that social and probability discount functions may be meaningful measures of individual altruism and social cooperativeness.

However, no significant correlation was found between delay discounting and PGG contribution. That is, a participant's generosity to her future self, as measured by her individual delay discount function, did not predict her generosity to a group of fellow students, as measured by her PGG contribution. Steepness of delay discounting has been repeatedly found to correlate with failure of self-control or addiction in everyday life; individual delay discount functions have been obtained for alcoholics, cigarette smokers, gamblers, cocaine addicts, and heroin addicts; the delay discount functions of addicts were significantly greater than those of nonaddicts (Bickel & Marsch, 2001). Steepness of delay discounting has also been found to decrease with age of the discounter (Green, Fry, & Myerson, 1994). The high predictive power of the delay discounting measure in these cases together with the lack of correlation between delay discounting and social cooperation in the PGG in Experiment 1 is therefore evidence against Rachlin's (2002b) argument that self-control (as measured by delay discounting) on the one hand, and social cooperation (as measured by social discounting) on the other, are ultimately the same process.

In prior experiments, participants discounted higher delayed amounts (Vs) more than lower delayed amounts (the “amount effect”) but they discounted higher probabilistic and socially distant amounts less than lower probabilistic and socially distant amounts (the “reverse amount effect”). These effects are summarized for probability and delay by Green and Myerson (2004) and for social discounting by Rachlin and Jones (2008). Experiment 1 adds to the evidence that social and probability discounting share similar properties while delay discounting differs from both.

As Table 3 shows, despite the differing properties of social discounting together with probability discounting on the one hand and delay discounting on the other, all three discount functions correlated significantly with each other. The lack of transitivity (delay discounting uncorrelated with PGG contribution, social and probability discounting correlated with PGG contribution, but delay discounting correlated with both social and probability discounting) is possible due to the looseness of the correlations involved (significant r-values ranging from .22 to .32). For example, even though social and delay discounting correlated significantly, many participants differed strongly in steepness of social and delay discounting. Some had shallow delay discount functions but steep social discount functions (“Scrooges”) while some had shallow social discount functions but steep delay discount functions (“generous spendthrifts”). Intransitivities may occur when, as in this case, multiple factors underlie a given measure (Tversky, 1969).

It is conceivable that the three-way correlation found between the three discount measures is an artifact of the very similar choice procedures used to determine them (contrasted with the judgment procedure used to measure PGG contribution) but we believe this is unlikely. First, any tendency to cross over at the upper or lower parts of the answer sheet irrespective of the discounting variable would have been cancelled out by the counterbalanced up–down orders of the A-columns. Second, probabilistic alternatives were expressed in the answer sheets as percentages, whereas the AUC measures of probability were determined after conversion to odds-against. Odds-against ((1−p)/p) varies inversely with probability. If participants tended to cross over at high or low values of the variable being measured, probability AUC should have varied inversely, not directly with both social and delay AUCs.

However, it is possible that the long delays tested in Experiment 1 and typically used in delay discounting studies with humans (running to 5 years) dwarfed the $75 undiscounted reward and created a “peanuts” effect, wherein the delay discounting measure was somehow distorted. Or perhaps the similar undiscounted amounts of the discounting variables created an “atmosphere effect” wherein the two measures were confused. Another possibility is that the “sophisticated” business school seniors and graduate students of Experiment 1 were atypical. Accordingly, Experiment 2 repeated the PGG and the social and delay discounting tests (but not the probability test) of Experiment 1 with a higher undiscounted amount ($1,000) in the delay tests, with a larger number of participants, and with less sophisticated participants (mostly freshmen in an introductory psychology class).

Experiment 2

Method

Participants

Participants were 196 students (85 male, 111 female, Mdn age  =  19) enrolled in an undergraduate Stony Brook University psychology class. They completed a pencil-and-paper PGG, social discount, and delay discount tests simultaneously in a lecture hall.

Materials and Procedures

A single-page PGG was presented to each participant as in Experiment 1 with the addition of the following instructions:

How much do you think the average person in the class will put in? $______

Immediately after the PGG, each participant completed delay and social discount tests in a counterbalanced order. Each discount test consisted of a page of instructions followed by four pages. Four delays (1 day, 1 week, 1 month, 1 year) were tested in 11 increments ranging from $1,000 to $0. Participants were presented with a page for each delay in a randomized order that included the following instructions:

Please choose which amount of money you would rather have for each line.

A. $1,000 for you right now. B. $1,000 for you after [D].

A. $900 for you right now. B. $1,000 for you after [D].

A. $800 for you right now. B. $1,000 for you after [D].

------Down To------

A. $ 0 for you right now. B. $1,000 for you after [D].

Social discount instructions were identical to those of Experiment 1 except four social distances (1, 10, 50, and 100) were tested.

For half of the discount tests the money amounts in Column A decreased (D) as shown above; for the other half, the amounts in Column A increased (I). The four orders of increase and decrease for the two tests (II, ID, DD, DI) were counterbalanced across participants.

Results

The same participant elimination criteria were used in Experiment 2 as in Experiment 1; data from 36 participants were removed from analysis. Table 4 shows the fit of Equations 1 and 2 to the data. As in Experiment 1, both social and delay discounting were well described by hyperbolic functions. Table 5 shows the mean individual fits of social and delay data to Equations 1 and 2.

Table 4.

Experiment 2. Fits of data to Equations 1 and 2; Area Under Curve (AUC) correlated with PGG contribution.

		Fit to Equation			AUC vs. PGG
Type of discounting	V	k	s	R2	AUC	R	p	n
Social (Eq. 1)	$82	0.048	1.00f	0.97	0.369	.350**	0.001	160
Delay (Eq. 2)	$1,000f	0.005	0.37	0.96	0.755	0.117	0.139	160

n: number of participants.

^fparameter fixed at this value.

^*p < .05.

^**p < .01.

Table 5.

Experiment 2. Mean of individual participant fits to Equations 1 and 2.

		Fit to Equation
Type of Discounting	V	Mean k	SD	s	R2
Social (Eq. 1)	$82 f	0.119	.292	1.00f	.86
Delay (Eq. 2)	$1000f	0.002	.023	0.35 f	.72

^ffixed at this value

Again, as in Experiment 1, the correlation between social AUC and PGG contribution was statistically significant while the correlation between delay AUC and PGG contribution was not significant; again, as Table 3 shows, social and delay AUCs were significantly correlated with each other. Binary divisions of contributions into below median contribution ($0–$40) and above median contribution ($41–100) correlated with social AUC, r(196)  =  .29, p < .001. Correlations using individual-participant log ks corresponded to those obtained with individual-participant AUC's.

Figure 3 shows the distribution of PGG contributions in both experiments and the distribution of the participants' predictions for the average contributions in Experiment 2. As is typical of PGG contributions (Camerer, 2003), the distributions are not unimodal; there are large modes at $0 and $50, and a small one at $100. The mean and median PGG contributions were $40 and $38, respectively. The mean and median PGG predictions were $20 and $30. The mean difference across participants (contribution minus prediction) was $8, significantly greater than zero, t(285)  =  4.95, p < .001. That is, on average, participants claimed to be more generous than their classmates.

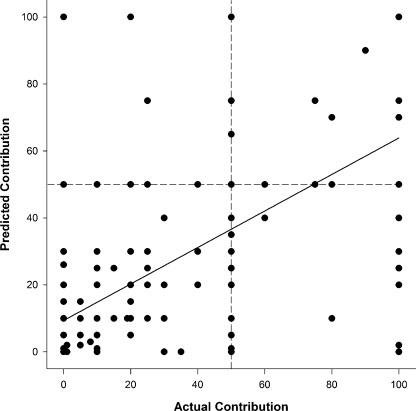
Figure 4 shows individual participants' predicted average contributions plotted against their own stated contributions. The solid line is the best-fitting straight line through the points, r(364)  =  .60, p < .001.

Fig 4.

The actual contribution versus predicted contribution in Experiment 2. The solid line is the best linear fit between contribution and prediction.

Discussion

The results of Experiment 2 followed the pattern of Experiment 1 with respect to social and delay discounting and the PGG. As in Experiment 1, in the social discounting test, participants who indicated that they would forgo more money for themselves in order to give $75 to other people also indicated in the PGG that they would contribute more to a common good. But, as in Experiment 1, the same did not hold for delay discounting; participants who indicated that they would forgo more money now in order to obtain $1,000 in the future contributed no more money in the PGG than did those who said they would forgo less money now in order to obtain $1,000 in the future. Despite this difference between social and delay discounting as regards the PGG, steepness of discounting was significantly correlated across the two measures—participants who sacrificed present good for the benefit of others also tended to sacrifice present good for the benefit of their future selves. But there were many exceptions; in both experiments some participants were Scrooge-like, with steep social and shallow delay discount functions, while others were generous spendthrifts, with steep delay and shallow social discount functions.

A notable difference between the results of this experiment and those of Experiment 1 was the much greater steepness of delay discounting in Experiment 1. The delay discount constant, k, for median crossover points, was 0.029 in Experiment 1 and 0.005 in this experiment—more than a fivefold difference. This is an example of the well established “amount effect” in delay discounting wherein larger amounts ($1,000 in this experiment) are discounted less than smaller amounts ($75 in Experiment 1; Raineri & Rachlin, 1993).

Unlike undiscounted delayed amounts, the undiscounted social amounts were set at the same value ($75) in the two experiments. Yet, the introductory psychology students in this experiment were (marginally) less selfish than the senior and graduate business-school students of Experiment 1. The mean PGG contribution was $31 in Experiment 1 and $38 in this experiment. The discount constant, k_social, for median crossover points, was 0.07 in Experiment 1 and 0.05 in the present experiment; in an independent samples t-test, t(294)  =  1.9, p  =  .05. The lower k_social of Experiment 2, implying shallower discounting, is typical of those obtained with introductory psychology students in prior experiments (Jones & Rachlin, 2006; Rachlin & Jones, 2008).

We cannot tell from these data whether the marginal differences in PGG contribution and steepness of social discounting in the two experiments were due to the slightly greater age of the participants in Experiment 1 or to the fact that they were business majors rather than psychology majors, or to both factors combined. If age turns out to be a significant factor, the age effect in social discounting would be opposite to that of delay discounting (as is the amount effect). Older people discount delayed rewards less than younger people do (Green, et al., 1994) whereas in these experiments (somewhat) older students discounted social rewards (somewhat) more than younger students did. In both delay and social cases, economists would consider the older participants' (more Scrooge-like) behavior to be more rational.

Figure 4 shows a wide divergence of predictions of average contribution as a function of participants' own stated contributions. Over most of the range, participants tended to predict that the average PGG player would contribute less than (but more than half as much as) they themselves would contribute. This tendency may reflect a rationalization of the participant's own predicted contribution. A contribution of $50 (of the $100 endowment) would have been relatively generous if the average contribution were $30, and still have returned $60 to the participant when $30 (times the number of participants) was doubled by the experimenter and distributed equally.

General Discussion

Prior experiments have found social discounting to be consistent in hyperbolic shape and in median k-value across different measures (Jones & Rachlin, 2006; Rachlin & Jones, 2008). The present experiments further validate hyperbolic social discounting, along with hyperbolic delay and probabilistic discounting, as dimensions of utility. Degrees of both social and probability discounting correlated significantly with contribution to a public good in both experiments. The relations found in these experiments, among laboratory measures using hypothetical rewards, do not come close in meaningfulness to the predictive power of delay discounting for real-world addiction (Bickel, & Marsch, 2001; Ross, Kincaid, Spurrett, & Collins, in press) but they are a step in that direction. The next step would be to study social discounting in contexts of real-world social cooperation.

As regards the relation among the three discounting dimensions, the present studies are ambiguous. A strong commonality is the fact that all three discount functions take the same hyperbolic form. However, although the steepness of each of them correlated significantly, across individuals, with that of both of the others, the correlations were low and contained many exceptions. Prior studies have found that the amount effects (how degree of discounting varies with undiscounted amount) of probability and social discounting, on the one hand, are opposite to that of delay discounting on the other. In the present experiments, both social and probability discounting were significantly correlated with PGG contribution, whereas delay discounting was not. Let us assume, for the sake of argument, that the three measures are valid; the shallowness of delay discount functions measures degree of self-control; the shallowness of probability discount functions measures willingness to take risks; the shallowness of social discount functions measures social cooperativeness. In what sense, then, might contributing in the PGG involve risk-taking and social cooperation but not self-control?

The PGG is clearly a social game. How might it also be a probabilistic game? In the PGG, the loss due to any given contribution ($.98 per $1.00 contributed assuming 100 players) is the same regardless of others' contributions. However, a player who contributes all $100 may well expect to regret the forgone $98 less if she earns $200 (all others contribute $100 as well) than if she earns $2 (all others contribute $0). That is, the subjective cost of contributing may be measured in relative, not absolute terms. As indicated in the discussion of Experiment 2, a $50 contributor would net $10 if contributions averaged $30. Contributing may therefore have been viewed by players as a gamble that other players' contributions would average more than half of their own contribution. Failure to contribute in the PGG may have been due to reluctance to take such a gamble (risk avoidance) just as much as (perhaps even more than) to a fundamental selfishness. Since steepness of the probability discount function is proportional to risk avoidance (Rachlin et al., 1986), the correlation found in Experiment 1 between PGG contribution and probability AUC (shallowness of the probability discount function) is some evidence for this possibility.

Although contributing in the PGG may be controlled by the same variables that control gambling (or investment), a PGG contribution is not a true gamble. In a true gamble, amount won or lost must be proportional to amount risked. In the PGG, however, amount contributed has only a negative effect on net earnings regardless of others' contributions.

Another possibility, in line with our conception of social discounting, is that donations to the general good, by increasing the welfare of others, will somehow redound to the good of the donator. For example, if the people we interact with are healthy we will be less likely to be infected by them; if they have leisure time to play games they will be more likely to play with us; if they are prosperous they will be more likely to trade with us. But in this scenario the probabilistic rewards for altruistic behavior would also be delayed, so the failure of delay discounting to predict the PGG contribution would seem to rule it out.

A concern about the methods of the present experiments is that the hypothetical rewards used may not have reflected real-world human behavior. This is a serious weakness, but the use of real monetary rewards would not solve the problem. From a behavioral viewpoint, a participant's stated hypothetical contribution in the PGG is essentially a prediction of what she would contribute if the money were real based on observation of her own past behavior. The difference between hypothetical and real rewards (aside from the larger amounts and varied situations possible with hypothetical rewards) lies in the context imposed by the two methods. With hypothetical rewards, if the instructions are carefully prepared and presented, the context is the real-world situation that the human participants are asked to imagine. With real rewards, the context is the immediate laboratory situation in which earnings are to be maximized.

Amounts of money typically offered in real-reward experiments in Western societies are typically much lower than those in real-life situations in those societies (Henrich et al., 2001); results with small real rewards may not be any more indicative of how people will behave in real-life situations, where motives and incentives are strong, than are results with larger, hypothetical rewards where participants imagine that the money is real. (See Rachlin, 2002a, for a behavioral analysis of imagination.) Moreover, where they have been compared, significant differences have not been found between delay discount functions for real and hypothetical rewards (e.g., Madden, Begotka, Raiff, & Kasten, 2003). As of now, the only studies where rewards have been both real and meaningful have been in non-Western societies, where other social factors and strong demand characteristics may overwhelm reward value (Henrich et al., 2001), or with nonhuman subjects.

The disparity between social and delay discounting remains surprising to us. Self-control (as measured by delay discounting) and social cooperation (as measured by social discounting) seem to share common properties. For example, organization of choices into patterns increases both self-control and social cooperation (Rachlin, 1995). You might expect that a person able to organize her behavior in patterns so as to maximize the benefit of her wider self extended in social space (i.e., to cooperate socially) to be also able to organize her behavior so as to maximize the benefit of her wider self extended in time (Rachlin, 2002b). On a less abstract level, despite the anonymity of a player's cooperation or defection in this particular laboratory game, cooperation in real-life social situations is often eventually rewarded. Rather than decide how to behave in each social situation on its own terms (and possibly be blinded by immediate, tempting alternatives), participants may obey a general rule to cooperate in social situations—because of the eventual reward often obtained thereby. Correlation between PGG contribution and degree of preference for larger–later rewards (shallowness of delay discounting) would have been some evidence for this possibility. Perhaps the anonymity of the PGG together with the very large number of participants in these experiments precluded expectation of delayed rewards. Further studies with non-anonymous social games, or social games with fewer participants, may resolve this issue.