The Probability of Small Schedule Values and Preference for Random-Interval Schedules

Abstract

Preference for working on variable schedules and temporal discrimination were simultaneously examined in two experiments using a discrete-trial, concurrent-chains arrangement with fixed interval (FI) and random interval (RI) terminal links. The random schedule was generated by first sampling a probability distribution after the programmed delay to reinforcement on the FI schedule had elapsed, and thus the RI never produced a component schedule value shorter than the FI and maintained a rate of reinforcement half that of the FI. Despite these features, the FI was not strongly preferred. The probability of obtaining the smallest programmed delay to reinforcement on the RI schedule was manipulated in Experiment 1, and the interaction of this probability and initial link length was examined in Experiment 2. As the probability of obtaining small values in the RI increased, preference for the schedule increased while the discriminated time of reinforcer availability in the terminal link decreased. Both of these effects were attenuated by lengthening the initial links. The results support the view that in addition to the delay to reinforcement, the probability of obtaining a short delay is an important choice-affecting variable that likely contributes to the robust preferences for variable, as opposed to fixed, schedules of reinforcement.

Identifying the relations between the various environmental factors that contribute to reinforcer value, and subsequently determine preference for a given situation, has become an important issue in the experimental analysis of behavior. Value is often understood to be determined by several factors, including the magnitude and delay to reinforcement, but overwhelmingly the relative rate of reinforcement has been the most extensively studied variable contributing to a reinforcement schedule's value. Traditionally, variable schedules have been specified by the arithmetic averages of the interreinforcer intervals (IRIs) that comprise the schedule. However, Herrnstein (1964) found that pigeons consistently prefer situations with variable delays to reinforcement (i.e., variable interval or VI schedules) when compared to situations that involve fixed delays (fixed interval or FI schedules) that have the same arithmetic mean. This finding has led to the conclusion that the value of a reinforcer in situations with variable outcomes is weighted differently than the value of a reinforcer in situations with fixed outcomes, and that in the context of preference for variable over fixed schedules the value of a variable schedule is not accurately predicted by the arithmetic mean of its component values, as is implicitly assumed by the convention of using that mean to specify the schedule.

Since the time that Herrnstein (1964) first questioned the arithmetic mean as an accurate predictor of preference for variable schedules of reinforcement, researchers in the experimental analysis of behavior have attempted to identify the determinants of preference for situations involving variable schedules. Studies by Fantino (1967), Killeen (1968), and Davison (1969) demonstrated that relative choice proportions are more accurately described by measures of central tendency that place heavier weight on the small intervals or ratios within the variable schedule's distribution. However, these studies each identified a different mathematical transformation of the data to best account for the observed preference for variable schedules. The difficulty in identifying a common transformation later led Navarick and Fantino (1972) to conclude that no simple invariance could be identified that could reliably and accurately predict this “preference for variability.”

Although the studies above did not converge on a single transformation to fit all of the data, they all retained the general feature, originally suggested by Pubols (1962) and by Herrnstein (1964), of weighting the smaller component values more heavily than the larger component values within the variable schedule's distribution. While it is clear from these studies that this is likely the operative variable responsible for the preference to work on variable schedules, the term “risk-proneness” has often been invoked to describe this phenomenon (e.g., Hamm & Shettleworth, 1987). Although that label may aptly characterize the non-optimizing aspects of the overall pattern of behavior, it may be a label that obscures the controlling variable. The available data suggest that it is not risk, nor even variability per se that affects preference, but rather the occasional quick payoff that overrides that payoff's infrequency.

To study preference for the variability of a situation irrespective of other variables (e.g., amount of reinforcement, occasional quick payoff, etc.), situations must be identified in which the variable alternative is often chosen even though it never provides an easier, quicker, or larger payoff than the fixed alternative. Under assumptions of optimization or maximization, it is predicted that in such situations the fixed alternative would always be preferred to the variable situation. This follows because the variable schedule never contains a quicker payoff than the fixed alternative, and all possible measures of central tendency are less favorable for the variable alternative. Despite this prediction, an arrangement has recently been identified in which subjects persistently chose the variable schedule even when it contained no component schedule value that was smaller than the fixed schedule. In a study by Andrzejewski, Cardinal, Field, Flannery, Johnson, Bailey, and Hineline (2005), pigeons were exposed to a discrete-trial procedure in which they were given repeated choices between working on FI versus random interval (RI) schedules of reinforcement. To eliminate the role of the occasional interreinforcement intervals (IRIs) in the RI schedule that were smaller than those available in the FI alternative, the programmed delays to reinforcer availability on the RI schedule were never shorter, and were often longer than on the fixed alternative. To arrange this feature, the rate of reinforcement on the RI was cut to half that of the FI (i.e., FI 30-s and RI 60-s terminal links). When the RI was chosen, the programmed delay to reinforcer availability on that particular trial was generated by sampling a probability gate at exact multiples of the FI schedule (every 30 s) with a probability of .50. Therefore, the average time to food availability on the RI was 60 s after the onset of the terminal link, averaging twice as long as the delay on the fixed alternative. From an assumption of maximization as well as from the previous findings that preference for variability is determined by occasional quick payoffs in the variable alternative, this procedure should have yielded virtually exclusive preference for the fixed situation; however, the results from this study as well as several others from our laboratory did not yield these preference patterns. The majority of the subjects—even after extended exposure (more than 5,000 trials and 100 experimental sessions)—chose the RI schedule in approximately one-third of the total trials in a given session. These results indicated that there may indeed be aspects of variable situations that are not confounded by other variables such as reinforcer magnitude or occasional quick payoffs that contribute to the previous findings of preference for variability or “risk-proneness”.

As has been pointed out by Kagel, Battalio, and Green (1995), the less-than-exclusive preference for working on an alternative that is not strongly favored by the usual determinants of choice is not unique to the study described here. However, the determinants of this phenomenon are often ignored, controlled for, or speculated on rather than investigated. From a global assumption of optimization it is tempting to account for or dismiss such findings by proposing an ad-hoc, phylogenic, intrinsic attraction to aperiodicity (e.g., Andrzejewski et al., 2005), or to appeal to the benefit of sampling all possible sources of a commodity in an environment prone to change (e.g., Baum, Schwendiman, & Bell, 1999). However, there are more relations to be explored that may systematically account for these data which are not accommodated by current behavioral models of choice. The pair of experiments presented here extends the analysis of preference for variability by manipulating and assessing the effects of not only the absolute value of the smallest component interval in the variable schedule, but also the probability of that interval's occurrence.

Additionally, in investigating the possible relation between the temporal distribution of events on the variable schedule of reinforcement and preference for working on that schedule, the present set of experiments incorporated an analysis designed specifically to examine temporal discrimination within the terminal-link schedules of a discrete-trial concurrent-chains procedure. In explaining preference behavior maintained on concurrent-chains schedules, it is generally assumed that initial-link responding is dependent upon terminal-link value. Some theories of choice, such as scalar expectancy theory (Gibbon, 1977; Gibbon, Church, Fairhurst, & Kacelnik, 1988), elevate temporally controlled behavior in the terminal links to the role of a fundamental determinant of choice, while other accounts, including the matching law, assume that performance in the initial links is determined by the conditioned reinforcement value of the discriminative stimuli present in the terminal links (Grace & Nevin, 1999). In light of these assertions, a peak procedure for studying the relation between preference and temporal discrimination within the terminal links of concurrent-chain schedules was developed by Grace and Nevin that allowed for the simultaneous but independent measurement of preference and temporal discrimination in various FI terminal links. Related to this procedure, and to investigate how the probability of obtaining the minimum schedule values affects both preference and temporal discrimination, the current set of experiments also utilized a modified post hoc peak procedure to examine temporal discrimination in both FI and RI terminal links and its relation to preference for those schedules.

Experiment 1

The current experiment retained a feature of the Andrzejewski et al. (2005) experiments in that the RI schedule never produced an interval shorter than the FI alternative. However, unlike that set of experiments, two distinct sampling intervals were used to create the RI on a given trial rather than sampling the probability gate at a constant interval. The first sampling of the probability gate occurred 30 s into the terminal link, but if this initial sampling did not make a reinforcer available, a second probability gate was sampled at an adjusted probability to maintain an overall reinforcement rate of one reinforcer per minute (an RI 60-s schedule). The purpose of this arrangement was to isolate the effect of the probability of obtaining the smallest possible RI value (here denoted as Pr[minRI]) while keeping the overall rate of reinforcement on both alternatives constant across all conditions.

Method

Subjects

Four white Carneau pigeons obtained from the Palmetto Pigeon Plant, Sumter, SC, served as subjects. They were maintained at approximately 80% of their free feeding body weights through an open feeding economy in which supplemental feedings were provided at the end of the each day and on weekends if needed. Water and grit were freely available in their home cages at all times. The 4 subjects, designated Jim, Jo, Jan, and Jules, had prior histories of responding on concurrent-chains schedules and choosing between FI and RI schedules, including participation in Experiment 3 of Andrzejewski et al. (2005). In those experiments, the duration of the smallest component interval on the RI was never shorter than the FI component interval duration.

Apparatus

Two identical Gerbrands pigeon operant chambers (Model G1705), measuring 30.5 cm high, 30.5 cm wide and 31 cm deep, were each equipped with three translucent response keys that were spaced evenly across the back wall of the chamber and positioned 22.5 cm above the floor. The two outside response keys were illuminated either yellow or red via 28-V DC lamps with translucent colored covers throughout the experimental session. The center key remained dark and inoperative at all times. The food hopper, accessible through a circular opening in the chamber wall that measured 5 cm in diameter, was positioned 10 cm directly below the center response key. The food hopper provided between 3 and 5 s of access to wheat grain, dependent upon the subject's weight, and during reinforcer deliveries all three response keys were dark and inoperative while the food hopper was illuminated by two 28-V DC lamps. A houselight was situated in the center of the ceiling of the chamber and was illuminated throughout each experimental session. Each operant chamber was enclosed in a sound-attenuating cabinet that contained a fan that served to ventilate the chamber and provide a masking noise during the sessions. All data were collected using a Med-PC® system for Windows® running on a Pentium-class personal computer that was housed in an adjacent room.

Design and Procedure

The pigeons had prior histories of free-operant and concurrent-chains exposure, and thus shaping of key pecking was not necessary. The pigeons were immediately placed on a protocol that involved daily experimental sessions involving a procedure that resembled a concurrent-chains schedule with FI 30-s and RI 60-s schedules serving as the terminal links. The daily experimental sessions were composed of 40 discrete trials with the terminal-link schedules correlated with key color, while the position of the schedules alternated randomly across right and left keys to eliminate position bias. A trial began with the initial link in which both response keys were illuminated and operating on a concurrent FI 3-s schedule such that the first peck after 3 s had elapsed produced entry into the terminal link. When a response on a particular key produced a transition to the terminal link, the key color remained unchanged while the other key was darkened and rendered inoperative until the completion of the terminal-link schedule produced access to wheat grain for 3 to 5 s depending on the subject's weight. Pecks on the darkened key during the terminal links had no programmed consequences. Following food delivery, a new trial began with the illumination of both keys and reentry into the initial link.

FI 3-s schedules were used in the initial links rather than the longer and more commonly used VI schedules in order to minimize the attenuation of preference for the dominant terminal-link schedule by the increases of initial-link length (Fantino, 1969). Furthermore, fixed-ratio 1 schedules were not used in the initial links because this schedule does not allow switching between alternatives and increases the likelihood that random pecks would complete the initial link and thus increase the probability of choosing the nonpreferred schedule in the terminal link.

The set of probabilities used to program the RI schedules in the terminal links served as the independent variable that changed across conditions. Across all phases of the experiment, upon entry into a yellow RI 60-s terminal link, a period of 30 s elapsed in which a reinforcer was never available. At 30 s into the RI terminal link, a probability gate was sampled and a reinforcer was set up with a probability of p. If a reinforcer was set up at 30 s into the terminal link, the next peck produced access to wheat grain. If a reinforcer was not set up at 30 s into the terminal link, the probability gate was sampled every second thereafter at a probability of q until a reinforcer was set up and the first peck thereafter produced access to wheat grain. The resulting RI schedules never had any component interval durations less than 30 s in length and held the overall mean interval value of 60 s constant while p and q varied according to condition. With the variation of p and q between the conditions, the proportion of trials that equaled 30 s and the trials greater than 30 s also varied across conditions, while the overall arithmetic mean of the RI schedule remained constant in that a reinforcer was delivered on average once every 60 s. The sequence of experimental conditions is displayed in Table 1.

Table 1.

Sequence of conditions for Experiment 1.

Phase	Probability of reinforcer availability at 30 s into RI terminal link (p)  =  Pr[minRI]	Probability of reinforcer availability every 1 s after 30 s into RI terminal link (q)
1	.50	.0167 (1/60)
2	.03	.03 (1/30)
3	.50	.0167 (1/60)
4	.25	.025 (1/40)
5	.75	.0083 (1/120)

Upon choice of the FI alternative, a reinforcer was always set up at 30 s after entry into the red FI terminal link, after which the first peck produced access to wheat grain. Therefore, across all phases, the minimum IRI of the RI schedule was equal to the IRI constantly available on the fixed alternative (i.e., 30 s), and the FI alternative held a rate of reinforcement twice that of the RI alternative across all conditions. Whereas the minimum IRI on the RI schedule was held constant across all conditions, the proportion of trials producing the minimum IRI on the RI varied across conditions.

Each subject was exposed to daily 40-trial sessions of this modified concurrent-chains procedure until stable preference patterns were established (i.e., the data failed to show any monotonic trends or excessive variability across daily preference ratios). Stability was assessed by visual examination of the graphical representation of the proportion of RI choices (defined as the proportion of entries into the RI terminal link in each daily experimental session).

Results

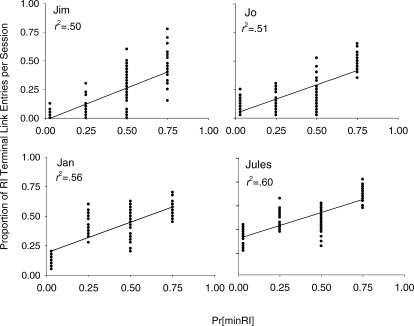
Although the overall rate of reinforcement and the absolute possible minimum RI value were not altered across conditions, shifts in preference were observed when the proportion of minimum-value RI trials was manipulated across the four conditions. The experimental conditions were composed of a range of 34 to 107 daily sessions depending on how quickly the data met the stability criteria. Each pigeon's data were aggregated across the last 20 sessions of each condition, and preference was measured by the proportion of RI terminal link entries in a given experimental session. Figure 1 shows that for each of the 4 pigeons, preference for the RI increased as the probability of obtaining the minimum RI interval (Pr[minRI]) increased; best-fit linear functions accounted for between .50 and .60 of the variance observed (mean r²  =  .54).

Fig 1.

The proportions of RI choices over the last 20 sessions in each condition are plotted against the probability of obtaining the minimum RI value (30 s) in the RI terminal link for 4 pigeons in Experiment 1.

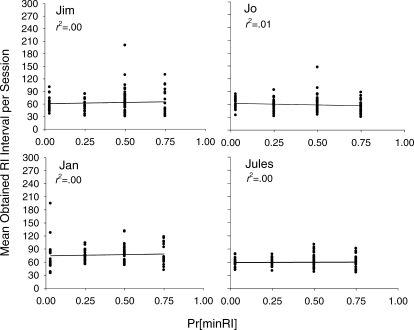
Figure 2 shows that, as planned, the mean obtained RI interval length remained constant over the four conditions in which the Pr[minRI] was manipulated. A best-fit linear regression revealed that virtually none of the variance observed in the mean obtained RI schedule values was accounted for by the Pr[minRI], demonstrating that the rate of reinforcement did not vary systematically with the Pr[minRI] and remained constant at approximately an RI 60-s schedule.

Fig 2.

The mean obtained schedule values for the RI terminal links per session over the last 20 days in each condition are plotted against the Pr[minRI] value for 4 pigeons in Experiment 1.

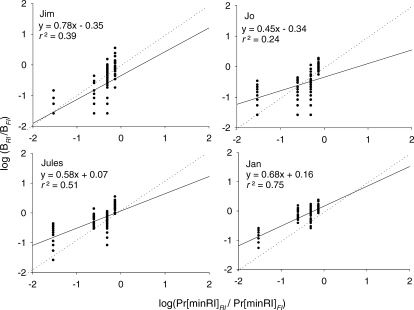
The preference data in the current experiment were also examined using an analysis based on the generalized matching equation (Baum, 1974). The logarithms (base 10) from two ratios were computed for the last 20 sessions of each condition: the proportion of entries into the RI terminal link relative to the proportion of entries into the FI terminal link (B_RI/B_FI), and the probability of obtaining a 30-s delay to reinforcer availability on the RI schedule to the probability of obtaining a 30-s delay to reinforcer availability on the FI schedule (Pr[minRI]_RI /Pr[minRI]_FI). The logarithms of these ratios were plotted on arithmetic coordinates for each bird, and the generalized matching equation was applied to each subject's data. A regression line was drawn for each subject's data, with goodness of fit assessed using r². Bias (log b, or the y-intercept) and sensitivity (a, or the slope) were determined from this regression line.

Figure 3 displays the results of the generalized matching analysis performed on the data from each subject. The solid line represents the regression line and the dotted line represents the locus of “strict matching” in which sensitivity (a) would equal 1 with the performance displaying no bias (b  =  0). The regression equation and r² are reported in the upper left corner for each bird. All 4 subjects' data display positive sensitivities, that is to say, the slopes of the regression lines were all greater than 0. Undermatching, or a sensitivity value less than 1, was observed in all 4 subjects' data, with a ranging between 0.45 and 0.78.

Fig 3.

Each point represents the logarithm of the proportion of entries into the RI terminal link to the proportion of entries into the FI terminal link (B_RI/B_FI) over the last 20 sessions of each condition plotted as a function of logarithm of the Pr[minRI] ratios (Pr[minRI]_RI /Pr[minRI]_FI) for each subject in Experiment 1. The solid lines indicate the best-fit regression line; the dotted lines indicate the line predicted by strict matching.

Temporal Discrimination Analysis

2Data from each of the last 20 sessions of each experimental condition were also analyzed to examine steady-state within-session behavior patterns using a post hoc peak analysis. In a standard peak procedure, behavior is first stabilized on a discrete-trial FI schedule of reinforcement, after which reinforcers are omitted on occasional, randomly dispersed trials that extend well past the FI value. When response patterns are analyzed on these “no-food” trials and response rate is viewed as a function of elapsed time within the trial, the result is typically a normal distribution in which the mode of the distribution (i.e., the “peak”) approximates the FI schedule value (Catania, 1970; Roberts, 1981). This procedure has been used to assess temporal discrimination in that the peak of the distribution has been interpreted as the behavioral estimate of the time to reinforcer delivery.

Recently, the peak procedure has been further integrated with concurrent-chains schedules with two FI terminal links to examine the relation between choice and temporal discrimination (see Grace, 2002; Grace & Nevin, 1999). In the current experiment, a traditional experimental peak procedure was not conducted, but the occasional RI trials that exceeded 90 s in length provided opportunities to analyze the data post hoc as though a peak procedure had been carried out within the RI terminal links. Trials in which the subject chose the RI schedule and in which the link's duration exceeded 90 s were selected and analyzed as simulated peak procedure trials. Response rates (responses per hour) from these selected trials that occurred within the first 90 s of the RI terminal link were placed in 1-s bins from the onset of the terminal link, and the bins were aggregated across the last 20 sessions in each experimental condition. The resulting sums were divided by 20 sessions to yield the distribution of mean response rates per session as a function of the time elapsed in the terminal link, providing a second-by-second overview of the temporally-based response patterning within the terminal link schedule. A similar binning analysis was conducted for all FI trials, but because these trials were truncated by the occurrence of a reinforcer around 30 s into the terminal link, the analysis was limited to the first 30 s of the terminal links. As a result, the FI trials did not require the selection of trials based on terminal link run length and all FI trials were included in the within-session peak analysis.

The primary measure used to assess temporal discrimination examined the time in the terminal link at which one-fourth of the total responses in the trial had been emitted. First proposed by Herrnstein and Morse (1957), this measure, referred to as quarter life, has often been used in the literature on temporal discrimination on FI schedules of reinforcement. The FI quarter life was identified as the second within the terminal link at which one-fourth of the total responses in first 30 s of the trial had been emitted, while the RI quarter life was identified as the second in the terminal link at which one-fourth of the total responses in the first 90 s of the RI terminal link had been emitted.

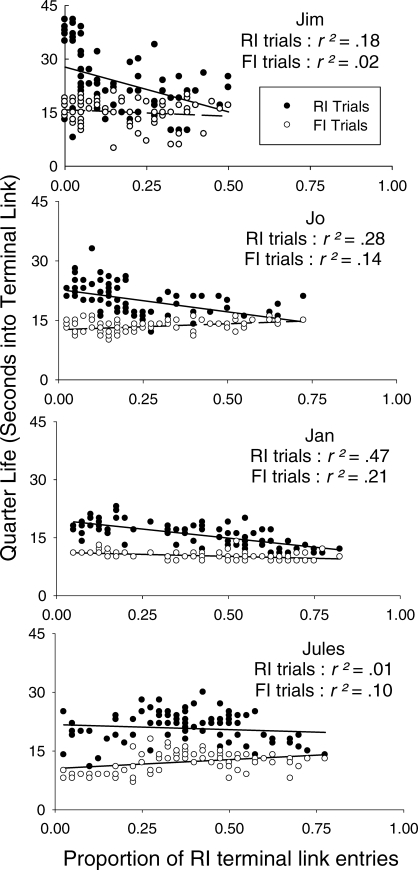
When the data were examined for each subject, the quarter life assessed in the RI trials decreased as Pr[minRI] increased for 3 birds such that between 36% and 59% of the variance in the RI quarter life was accounted for by the Pr[minRI] variable. For one of the birds (Jules), it was found that the RI quarter life was unaffected by the Pr[minRI] manipulations. For 3 birds, the quarter life assessed in the FI trials remained relatively stable or decreased slightly as Pr[minRI] increased such that only between 2% and 21% of the variance in the FI quarter life was accounted for by the Pr[minRI] variable. For the other subject (Jo), the FI quarter life increased as the Pr[minRI] value increased.

When the quarter life was examined as a function of the proportion of entries into the RI terminal link, there was a decrease in the quarter life with increasing preference for the RI terminal link (see Figure 4). For the FI terminal links, relatively little variance in the quarter life was accounted for by RI preference. However, for 2 subjects a small positive correlation was observed such that as the preference for the RI increased, so too did the FI quarter life.

Fig 4.

Quarter life measures for RI and FI trials plotted as a function of the proportion of entries into the RI terminal link for all 4 subjects in Experiment 1.

Discussion

Experiment 1 demonstrated that preference in a concurrent-chains procedure with FI and RI terminal links was sensitive to changes in the probability of obtaining the minimum-valued intervals embedded within the RI terminal links, even when those minimum values were never less than the fixed alternative. The preference data obtained in the current study replicated the earlier findings of Andrezejewski et al. (2005) in that the fixed schedule was rarely preferred exclusively over the random schedule, a finding that is counter to many predictions made by both molar- or momentary–maximizing theories of choice. Whether maximizing the rate of reinforcement as predicted by molar theories (i.e., the fixed schedule always produced reinforcers about twice as often as the random schedule on average), or minimizing the delay to individual reinforcers as predicted by molecular theories (i.e., the smallest interval in the RI distribution of possible intervals was never less than the interval always available on the FI schedule), both types of maximization-based theories predict strong if not exclusive preference for the fixed schedule in this particular experimental arrangement. Additionally, the peak analysis suggested that temporal discrimination was also affected by the Pr[minRI] variable in the RI terminal links such that reinforcer availability within the RI terminal links was discriminated as occurring sooner in the terminal link as the Pr[minRI] (and preference for the RI schedule) increased.

In Baum's (1974) original conception of the generalized matching law, sensitivity referred to the change in the allocation of behavior across two alternatives following a change in the relative rates of reinforcement for those two alternatives. In the present experiment, the absolute and relative rates of reinforcement remained unchanged across all conditions, and thus in the present analysis, sensitivity referred to the change in the proportion of RI terminal link entries following changes in the Pr[minRI] value. Positive sensitivities were found for each subject's data, indicating that as the relative probability of obtaining the smallest RI value increased, so too did the proportion of RI terminal link entries.

The finding that when the relative rates of reinforcement were held constant, the probability of obtaining the minimum value in the distribution of possible intervals in the RI terminal link (i.e., Pr[minRI]) served as a determinant of preference, suggests that this particular variable is relevant in many situations involving choice between probabilistic outcomes. Through these initial data, it appears that Pr[minRI] is a choice-affecting variable similar to rate of reinforcement, magnitude of reinforcement, and reinforcer immediacy, among others, that have all been found to predict behavior according to the generalized matching law. As first described by Baum and Rachlin (1969), response allocation between alternatives in a choice situation can often be predicted by the product of the ratios of all of the choice-affecting independent variables—including those variables that remain unknown. When all of these variables are included, this formula yields the concatenated generalized matching law:

1

where R is the rate of reinforcement, A is the amount of reinforcement, and I is the immediacy of reinforcement. Each of these choice-affecting independent variables has its own sensitivity term (i.e., a, b, and d respectively) and the bias multiplier c accounts for unknown ratios of independent variables that remain constant for variations in the three defined ratios. In the current investigation, the concatenated generalized matching law would be extended to encompass the Pr[minRI] value such that (assuming all other choice-affecting variables are held constant and equal):

2

The concatenated generalized matching law makes a theoretical assertion that there is no interaction among variables in their effects on behavior. Empirical support of this assertion has been obtained through the use of two-factor experimental designs in which two choice-affecting independent variable ratios are systematically varied such that a matching analysis can be carried out for each variable's effect on choice (e.g., Berg & Grace, 2004; Grace & Bragason, 2005; Kyonka, 2007; Kyonka & Grace, 2008). Further support for including Pr[minRI] in the concatenated matching law is dependent upon evidence from two-factor studies designed to examine this assertion in regard to the Pr[minRI] variable.

One of the most notable findings was that for 2 of the 4 subjects, the RI was preferred overall when the Pr[minRI]  =  .75. Even Mazur's hyperbolic decay function (1984), which takes the probability of encountering each interval into account, cannot fully account for this overall RI preference. The initial Pr[minRI]  =  .50 condition produced preference ratios that would be expected by the generalized matching law (i.e., choosing the RI schedule on about 33% of the trials), suggesting that a history effect may be responsible for the observed overall RI preference observed in the Pr[minRI]  =  .75 condition. Beginning at a baseline where the RI was chosen in about 33% of the trials, an increase in the Pr[minRI] was followed by an increase in RI preference that for 2 subjects resulted in the RI being chosen on over 50% of the trials. Therefore, it is possible that counterintuitive overall RI preference may have been partly determined by the Pr[minRI] value experienced early in the history of exposure to these types of arrangements.

The analysis of temporal discrimination used in this experiment is a relatively new technique in the study of preference within a concurrent-chains procedure. The quarter life measure provided evidence that temporal discrimination was affected by the Pr[minRI] variable in the RI terminal links, but there was little evidence that this variable affected response patterning in the FI terminal links. Reinforcer availability within the RI terminal links was generally discriminated as occurring sooner when the Pr[minRI] was relatively large; however, this effect was not observed for one of the subjects (Jules), despite the finding that this particular bird's preference patterns were sensitive to the Pr[minRI] manipulations. These findings suggest that the Pr[minRI] variable does affect response patterning in the terminal links, but that the presence of these temporally discriminated behavior patterns may not be necessary for preference to be sensitive to the Pr[minRI] variable. There are many elegant dissociations of a similar kind in the literature involving concurrent-chains schedules, most notably in the dissociation between elevated rates of responding in the terminal links and preference for a particular terminal link when those terminal links differ in rates of conditioned reinforcement (see Fantino & Romanowich, 2007, for a review). The findings of the current experiment extend this dissociation between performance in the initial and terminal links and gives limited support to the notion that temporally discriminated response patterns in the terminal link do not necessarily determine preference for a particular terminal link as measured by initial-link performance. Although the evidence is limited to only one subject in the current study, the dissociation in the response patterns suggests that temporal discrimination may not necessarily mediate preference for the RI schedule.

Experiment 2

Experiment 1 demonstrated that preference for RI schedules is sensitive to the probability of obtaining the minimum value within the random schedule's distribution of possible interval values. Despite the apparent robustness of this effect offered by the multiple single-subject replications reported in Experiment 1, it is possible that the sensitivity to the Pr[minRI] only occurs under certain conditions, thus limiting the generality of the findings of Experiment 1. As informed by Mazur (1984), the previous experiment used very short initial links (FI 3 s for both keys) to avoid influence of the initial-link effect, a robust finding that long initial links result in decreased control by the dominant alternative (Fantino, 1969). As this effect is commonly described, preference for a particular terminal-link schedule is more extreme when the initial links of a concurrent-chains schedule are short and equal to one another (Fantino, 1969; Wardlaw & Davison, 1974). Therefore, it is possible that the use of short initial links Experiment 1 favored extreme preference, creating a situation in which preference was sensitive to the Pr[minRI] variable and produced the counterintuitive overall preference for the RI schedule in the Pr[minRI]  =  .75 condition. Experiment 2 was aimed at further investigation of the determinants of the findings of Experiment 1, specifically through a systematic manipulation and comparison of initial-link length.

Method

Subjects

The 4 pigeons from Experiment 1 served as subjects. They were maintained under identical conditions described in the previous experiment, and training for the experiment commenced immediately after the completion of Experiment 1. Again, the pigeons were never exposed to component interval durations on the RI schedule that were shorter than the interval always available on the FI schedule.

Apparatus

The experimental chambers and controlling equipment were identical to those used in Experiment 1.

Design and Procedure

The pigeons were immediately placed on a protocol similar to the first experiment that involved daily experimental sessions of 40 discrete-trial choices between an FI 30-s schedule and an RI 60-s schedule whose minimum sampling interval was always equal to the FI (i.e., 30 s). The length of the initial link varied according to condition and served as one of the independent variables of the experiment (see Table 2). In the first three conditions of the experiment the initial link consisted of concurrent FI 3-s schedules, whereas in the final three conditions of the experiment the initial link consisted of concurrent RI 15-s RI 15-s.

Table 2.

Sequence of Conditions for Experiment 2.

Condition	Initial Link Schedule (seconds)	RI probability at 30 s; probability every 1 s after 30 s
1	FI 3 FI 3	p = .50; q =  .0167
2	FI 3 FI 3	p = .75; q = .0083
3	FI 3 FI 3	p = .50; q =  .0167
4	RI 15 RI 15	p = .50; q =  .0167
5	RI 15 RI 15	p = .75; q = .0083
6	RI 15 RI 15	p = .50; q =  .0167

The method used to program the RI 60-s schedules in the terminal links served as the second independent variable in this experiment. The technique used to generate the RI schedule was identical to that used in Experiment 1, but only two variations of the RI sampling method were used (Pr[minRI]  =  .50 and Pr[minRI]  =  .75).

Results

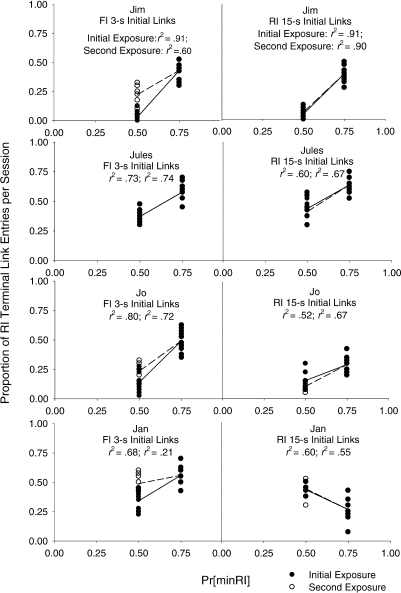
Figure 5 displays the proportion of RI choices made during the last 10 sessions of each condition presented as a function of Pr[minRI] for both the FI 3-s (left panel) and RI 15-s (right panel) initial-link conditions. The length of the experimental conditions in the current experiment ranged from 21 to 74 sessions depending upon how quickly the data met the stability criteria. For all of the subjects, preference for the RI increased as the Pr[minRI] increased in the FI 3-s initial-link condition, and for 3 subjects, preference for the RI increased as the Pr[minRI] increased in the RI 15-s initial-link condition. The increase in preference for the RI with an increase in Pr[minRI] was not as dramatic for 2 subjects (Jules and Jo) in the RI 15-s initial-link conditions as it had been in the FI 3-s initial-link conditions. For 1 subject (Jan), an inverse relation between the preference for the RI and the Pr[minRI] was observed in the RI 15-s initial-link conditions. Overall, similar increases in RI preference with increases in the Pr[minRI] were observed in the second exposure to the Pr[minRI]  =  .50 conditions in both the FI 3-s (Condition 3) and RI 15-s (Condition 6) initial links, as indicated by the open data points in Figure 5.

Fig 5.

The proportion of RI terminal link entries per session for last 10 sessions of the Pr[minRI]  =  .50 and Pr[minRI]  =  .75 conditions are plotted for each subject in Experiment 2 as a function of Pr[minRI]. The FI 3-s initial link conditions are displayed in the left hand panels and the RI-15 initial link conditions are displayed in the right hand panels. The closed data points indicate the initial exposure to the Pr[minRI]  = .50 conditions in each initial link length while the open data points indicate the second expsosure to the Pr[minRI]  =  .50 conditions.

Temporal Discrimination Analysis

Data from the last 10 sessions of each experimental condition were analyzed to examine steady-state within-session behavior patterns using the same modified post hoc peak analysis as that used in Experiment 1. The quarter life measures of the RI and FI terminal links were assessed for each subject for all experimental conditions.

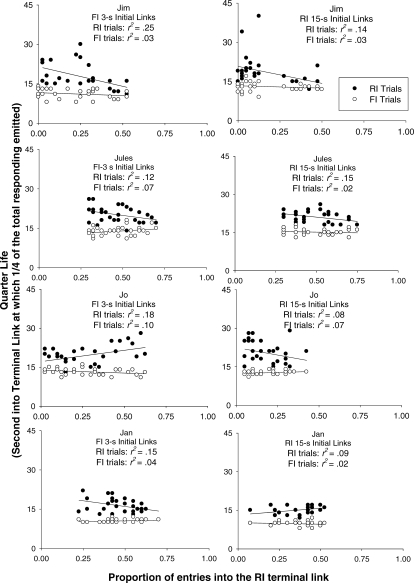
When the RI quarter life was examined separately for each bird, it was found that for 3 birds, the RI quarter life decreased as the Pr[minRI] increased under the FI 3-s initial links such that between 23% and 38% of the variance observed in the RI quarter life was accounted for by the Pr[minRI] variable. Under the long RI 15-s initial links, it was found that the RI quarter life decreased slightly for all 4 subjects such that between 12% and 22% of the variance in the RI quarter life was accounted for by variations in Pr[minRI]. When the FI quarter life was examined separately for each bird across all conditions it was found that quarter life did not vary with changes in the Pr[minRI].

The quarter life was also examined as a function of the proportion of entries into the RI terminal link (see Figure 6). For 3 of the 4 subjects, there was a decrease in the RI quarter life as preference for the RI alternative increased under short FI 3-s initial links. For 2 birds, FI quarter life increased slightly as RI preference increased under FI 3-s initial links. Under the RI 15-s initial links, three of the birds' FI quarter life measures decreased slightly with increases in RI preference. In addition, for 3 birds, the direction of the FI quarter life measures in relation to the RI preference in the RI 15-s initial links changed from that observed in the FI 3-s initial links.

Fig 6.

Quarter life measures for RI and FI trials plotted separately as a function of proportion of entries into the RI terminal link for all 4 subjects in Experiment 2. FI 3-s initial link conditions (left panels) are plotted separately from RI 15-s initial link conditions (right panels).

Discussion

The present experiment replicated the findings of Experiment 1 in that under relatively short initial links, when the probability of obtaining the minimum component schedule value on the RI schedule Pr[minRI] increased, so too did preference for the RI schedule. When the initial links were extended to a length that on average was five times longer than those used in Experiment 1, the Pr[minRI] variable continued to exert a similar type and degree of influence on preference for the RI alternative for 2 of the 4 subjects as it had in Experiment 1. For the other 2 subjects, the influence of the Pr[minRI] variable on preference was altered by lengthening the initial links.

The dependence of the effects of the terminal-link schedules on the duration of the initial-link choice period is well documented (Dunn & Fantino, 1982; Fantino, 1969; 1977; Wardlaw & Davison, 1974) and has resulted in difficulty developing a straightforward account of preference in the concurrent-chains preparation (Mazur, 1984). A variety of interpretations have been put forward to explain the initial-link effect, in which extension of the choice period results in decreased control by the terminal-link schedules and a regression towards indifferent preference patterns. At least one interpretation views this diminished control as an attenuation of the discrimination between the terminal-link alternatives, suggesting that concurrent-chains procedures have complex second-order features that complicate a straightforward discrimination of these alternatives (Gibbon et al., 1988).

As examined through measures of quarter life in the terminal links, overall the temporal discrimination in the RI terminal links changed as a function of the Pr[minRI] while the temporal discrimination in the FI terminal links remained relatively stable. These findings further support the results of Experiment 1 such that, under relatively short initial links, as Pr[minRI] increased, the time of peaked responding in the RI terminal link decreased. This suggests that the time of reinforcer availability was discriminated as occurring earlier into the RI terminal link as the probability of obtaining the minimum interval value on the RI schedule increased.

When the initial links were lengthened, the measure of temporal discrimination indicated that the relation between the Pr[minRI] variable and the time of peaked responding in the terminal links was weakened with increasing initial-link length. The percent of the variance in the temporal discrimination measures accounted for by the Pr[minRI] variable decreased for each subject in the RI terminal links and for all but one subject in the FI terminal links as initial-link length increased. This attenuation of the effects of the Pr[minRI] variable was more dramatic in the RI terminal-link measures of temporal discrimination.

Overall, the findings of the current experiment suggest that in a concurrent-chains arrangement, the effects of the Pr[minRI] variable are at least partly dependent upon the length of the initial-link choice period. The finding that the effects of various choice-affecting independent variables can be modified by the length of this choice period is a robust phenomenon, and the current experiment provides evidence that the Pr[minRI] variable operates much like other choice-affecting variables in this respect. Additionally, the relation between Pr[minRI] and temporal discrimination in the RI terminal links was also affected by initial-link length such that, as Pr[minRI] increased the discriminated time of reinforcer availability decreased, and this relation was also attenuated by increasing the initial-link length.

General Discussion

In addition to their implications for the understanding of preference for random schedules of reinforcement, the current experiments indicate the importance of simultaneously examining discrimination within the alternative situations while studying choices between those situations. The relation between preference for a situation and discrimination within that situation has only recently begun to be examined empirically (e.g., Grace & Nevin, 1999), despite the fact that assertions made about the necessity of this relation have been made in the experimental literature for decades (Gibbon, 1977). When the temporal discriminations were assessed in the terminal-link schedules of the two experiments presented, it was found that the Pr[minRI] variable affected the temporal discrimination in the RI terminal links systematically just as it had influenced the preference ratios, but there was also some limited evidence to suggest that this particular relation was not necessary to produce a change in preference for a particular RI schedule.

This particular finding suggests that, although the preference-affecting independent variables specified here can affect behavior on at least two levels of analysis, the interpretation that temporal discrimination mediates preference is not yet warranted. To be sure, the present evidence is limited to a few birds that displayed changes in preference ratios but not in temporal discrimination as a function of the independent variables investigated. A dissociation between preference and temporal discrimination, such as that found by Grace and Nevin (1999), presents a challenge to choice theories solely based on temporal discrimination or “timing” processes, including scalar expectancy theory (Gibbon, 1977).

The current experiments have important implications for the understanding of preference for variable schedules of reinforcement, in that the experiments identified an independent variable that has not been examined extensively in the study of choice and preference for variability. Furthermore, the use of a novel post hoc analysis provided an extension of the investigation to simultaneously examine the effect of these variables on temporal discrimination within the alternative terminal-link schedules. Whereas the study of this type of temporal discrimination in relation to preference is a relatively new area of interest, examining the effects of independent variables on multiple levels of analysis is important for gaining a more complete understanding of the relations between response patterning maintained on different reinforcement schedules and preference for those schedules in a choice situation.