Grid cell mechanisms and function: Contributions of entorhinal persistent spiking and phase resetting

Abstract

This article presents a model of grid cell firing based on the intrinsic persistent firing shown experimentally in neurons of entorhinal cortex. In this model, the mechanism of persistent firing allows individual neurons to hold a stable baseline firing frequency. Depolarizing input from speed modulated head direction cells transiently shifts the frequency of firing from baseline, resulting in a shift in spiking phase in proportion to the integral of velocity. The convergence of input from different persistent firing neurons causes spiking in a grid cell only when the persistent firing neurons are within similar phase ranges. This model effectively simulates the two-dimensional firing of grid cells in open field environments, as well as the properties of theta phase precession. This model provides an alternate implementation of oscillatory interference models. The persistent firing could also interact on a circuit level with rhythmic inhibition and neurons showing membrane potential oscillations to code position with spiking phase. These mechanisms could operate in parallel with computation of position from visual angle and distance of stimuli. In addition to simulating two-dimensional grid patterns, models of phase interference can account for context-dependent firing in other tasks. In network simulations of entorhinal cortex, hippocampus and postsubiculum, the reset of phase effectively replicates context-dependent firing by entorhinal and hippocampal neurons during performance of a continuous spatial alternation task, a delayed spatial alternation task with running in a wheel during the delay period, and a hairpin maze task.

The experimental properties of grid cell firing in medial entorhinal cortex demonstrate systematic regularities that could give insight into the functional principles of entorhinal circuits. As a rat forages in an open field, a single medial entorhinal grid cell spikes in an array of locations making up a grid of equilateral triangles (Hafting et al., 2005; Sargolini et al., 2006; Moser and Moser, 2008). The firing of a single neuron can be quantified by three parameters: 1.) spatial periodicity, 2.) spatial phase, and 3.) orientation. Within a local anatomical region, grid cells show the same spacing and orientation, but a range of spatial phases. In contrast, at different positions along the dorsal to ventral axis of medial entorhinal cortex, grid cells show a change in spatial periodicity; with an increase in spacing and field size for grid cells recorded in more ventral regions of medial entorhinal cortex (Hafting et al., 2005; Sargolini et al., 2006; Solstad et al., 2007; Brun et al., 2008; Moser and Moser, 2008).

This paper presents a new model of grid cells based on the mechanism of intrinsic persistent spiking shown in entorhinal neurons. This model provides an alternate implementation of the oscillatory interference model (Burgess et al., 2005; Burgess et al., 2007; Burgess, 2008) that is compared to the implementation using membrane potential oscillations (Giocomo et al., 2007; Hasselmo et al., 2007; Giocomo and Hasselmo, 2008).

In standard slice preparations, most cortical neurons generate spikes during depolarizing input, but will not continue firing after stimulation ends. However, in the presence of cholinergic or metabotropic glutamate agonists, pyramidal cells in medial entorhinal cortex commonly show persistent firing (Klink and Alonso, 1997; Egorov et al., 2002; Fransén et al., 2006; Tahvildari et al., 2007; Yoshida et al., 2007) even when all synaptic input is blocked. As shown in Figure 1A, layer V pyramidal neurons of medial entorhinal cortex continue firing at stable frequencies for an extended period after termination of current injection or synaptic stimulation. For layer V pyramidal cells, the stable persistent firing frequency of neurons is determined by the integral of previous input (Egorov et al., 2002; Fransén et al., 2006), whereas in layer III of lateral entorhinal cortex individual pyramidal cells show persistent firing at cell-specific frequencies (Tahvildari et al., 2007). Stable persistent firing has also been shown in layer III pyramidal cells of medial entorhinal cortex (Yoshida et al., 2007), whereas layer II cells tend to show persistent firing that turns off and on over extended periods (Klink and Alonso, 1997). The currents underlying persistent spiking appear to be calcium-sensitive non-specific cation currents regulated by cholinergic or muscarinic activation (Shalinsky et al., 2002; Fransén et al., 2006; Yoshida et al., 2007). Persistent spiking is activated by 5 micromolar concentrations of cholinergic agonists (Egorov et al., 2002) consistent with acetylcholine concentrations measured during behaviour (Parikh et al., 2007). The mechanisms of intrinsic persistent firing in single neurons could contribute to persistent spiking shown with unit recording during the delay period of delayed matching to sample tasks in awake, behaving rats (Young et al., 1997) and monkeys (Suzuki et al., 1997). Persistent spiking could also underlie persistent fMRI activation appearing during delay periods in human memory tasks, which can be reduced by muscarinic cholinergic blockade (Schon et al., 2004; Schon et al., 2005; Hasselmo and Stern, 2006).

Figure 1.

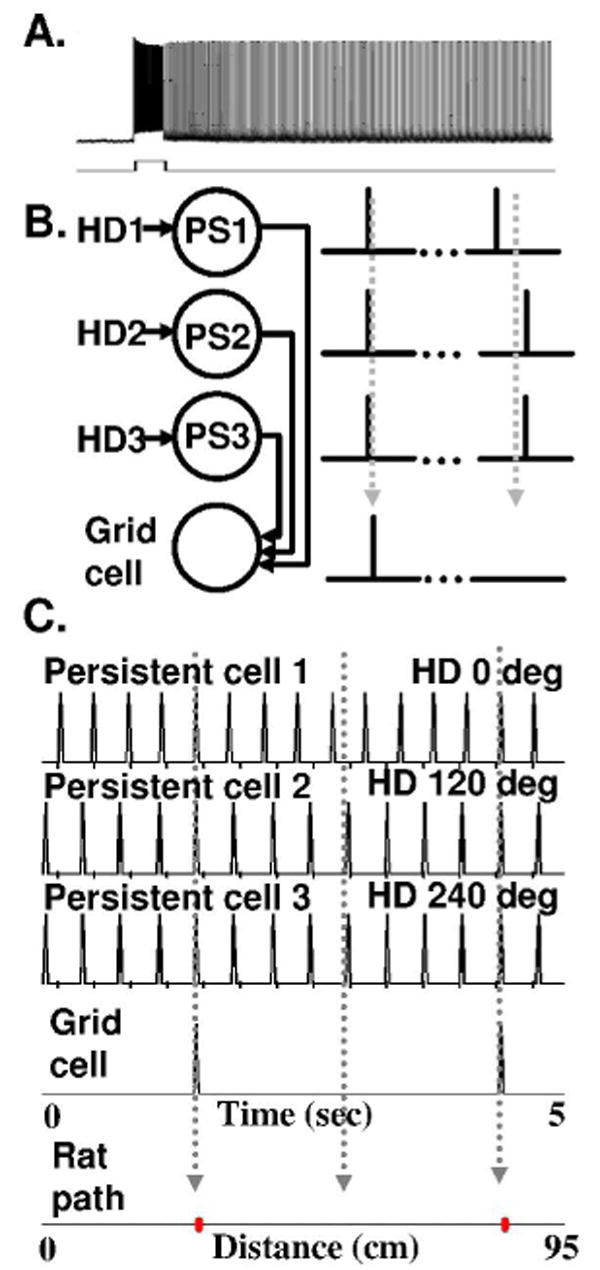
A. Example of persistent firing in a layer V pyramidal cell reprinted from (Egorov et al., 2002). B. Schematic of circuit involved in generating grid cells from persistent firing cells. Individual persistent firing cells (PS1, PS2, PS3) receive input from different head direction cells (HD1, HD2, HD3). When spiking of persistent firing cells is synchronous, it causes spiking in a grid cell via convergent synaptic input. C. Simulation of three interacting persistent firing cells. The top cell (persistent cell 1) receives depolarizing input from a speed modulated head direction cell with preference angle zero (HD zero). This causes spiking at a slightly higher frequency than baseline, while persistent cells 2 and 3 are pushed to lower frequencies by input from HD cells with preference angles of 120 and 240 degrees. (Tick marks below x axis indicate baseline frequency of 3 Hz). Cell 1 spiking starts out in phase with the other cells, then shifts out of phase, then back into phase, resulting in grid cell firing at regular locations in space (red dots).

Previous modeling showed that membrane potential oscillations in entorhinal neurons might also contribute to grid cell firing (Burgess et al., 2005; Giocomo et al., 2007; Burgess et al., 2007; Hasselmo et al., 2007; Giocomo and Hasselmo, 2008a). Entorhinal layer II stellate cells show subthreshold membrane potential oscillations when depolarized near firing threshold (Alonso and Llinas, 1989; Alonso and Klink, 1993; Giocomo et al., 2007). These subthreshold oscillations can influence the timing of action potentials (Fransen et al., 2004) and network oscillations (Alonso and Garcia-Austt, 1987; Acker et al., 2003). The frequency of membrane potential oscillations differs systematically along the dorsal to ventral axis of the medial entorhinal cortex (Giocomo et al., 2007; Giocomo and Hasselmo, 2008a). Previous modeling showed how these differences in membrane potential oscillation frequency could underlie differences in grid cell spatial periodicity along the dorsal to ventral axis (Burgess et al., 2005; Giocomo et al., 2007; Burgess et al., 2007; Hasselmo et al., 2007; Giocomo and Hasselmo, 2008a). The oscillations appear to be due to a hyperpolarization activated cation current known as the h-current (Dickson et al., 2000), that differs in time constant along the dorsal to ventral axis (Giocomo and Hasselmo, 2008b). In contrast to stellate cells, membrane potential oscillations do not usually appear in layer II and III pyramidal cells (Alonso and Klink, 1993), but are observed in layer V pyramidal cells, where they may be caused by M-current (Yoshida and Alonso, 2007; Giocomo and Hasselmo, 2008a). Membrane potential oscillations do not appear in neurons of the lateral entorhinal cortex (Tahvildari and Alonso, 2005), and grid cells do not appear in lateral entorhinal cortex (Hargreaves et al., 2005).

This paper will start with presentation of a model using a new mechanism for grid cell firing based on input from persistent spiking neurons. The persistent spiking model provides a new implementation of the oscillatory interference model of grid cells (Burgess et al., 2005; Burgess et al., 2007; Burgess, 2008), that could be complementary to the implementation using membrane potential oscillations (Giocomo et al., 2007; Burgess et al., 2007; Hasselmo et al., 2007; Giocomo and Hasselmo, 2008a). The interaction of head direction cell input and visual input will be discussed with regard to sensory influences on grid cell firing. In addition to simulating two-dimensional grid patterns in open fields, these models can replicate context-dependent firing of entorhinal and hippocampal neurons in other tasks, as shown here using phase reset in large scale simulations of the interaction of entorhinal cortex, hippocampus and postsubiculum.

Persistent spiking model of grid cells

The model of grid cell firing based on persistent firing neurons requires separate populations of neurons showing persistent firing at the same stable baseline frequency that remains constant in the absence of input. Figure 1A shows an example of 20 seconds of stable persistent firing in a layer V pyramidal cell from medial entorhinal cortex after induction with a 2 second current injection (from Figure 3a in (Egorov et al., 2002)). Stable persistent firing has been observed in layer V neurons at a single frequency for over 13 minutes (Egorov et al., 2002). A plot of cumulative interspike interval in data from one cell shows little variation in frequency over a 7.5 minute period (see Figure 1C2 in (Fransén et al., 2006)). In the model, the stable frequency must be the same across the persistent firing cells providing input to a given grid cell, consistent with evidence that some neurons consistently return to a characteristic persistent spiking frequency (Tahvildari et al., 2007).

In the model, different persistent firing cells all send convergent synaptic input to individual grid cells (Figure 1B). As shown in Figure 1C and Figure 2, an individual grid cell will be brought over threshold and will spike when there is near simultaneous spiking across the persistent firing cell populations, that is when the persistent firing cells are firing in phase with each other.

Figure 2.

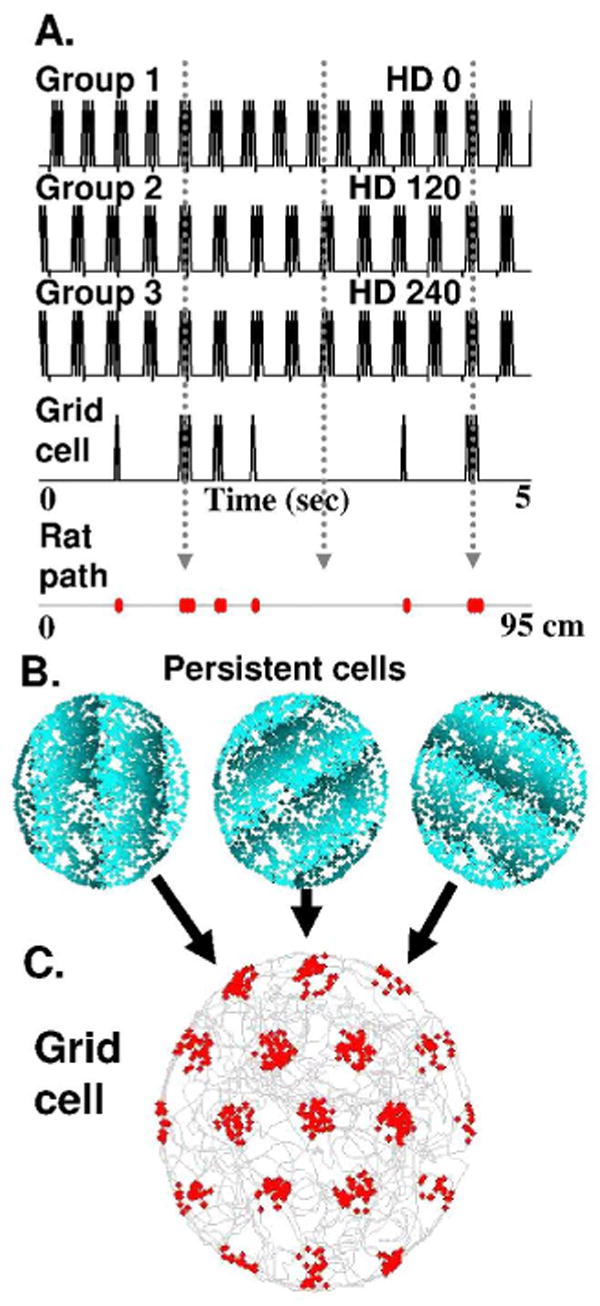
Mechanism for interaction of persistent firing cells to cause grid cell firing. A. Spiking activity over time of three different groups of persistent firing neurons. Here, each group consists of three persistent spiking cells firing with a baseline frequency of 3 Hz with different phases. Cells receive input from head direction (HD) cells with 0 degree preferred angle for Group 1, 120 degree angle for Group 2, and 240 degree angle for Group 3. Grid cell firing arises from the convergent spiking of the three groups of persistent firing neurons. When all three persistent firing groups fire in synchrony, the grid cell will fire (red dots). B. Persistent firing cells with 4 Hz baseline frequency in a two-dimensional circular environment. Dots indicate location of virtual rat during each spike, showing no spatial specificity. In contrast, phase of spiking depends on location. Dot color (light to dark blue) indicates phase of spike relative to a single reference oscillation. C. Grid cell spiking (red dots) occurs only when all of the persistent firing neurons fire at the same phase, resulting in a typical grid cell firing pattern. Gray line indicates rat trajectory from experimental data (Hafting et al., 2005).

In the model, the phase of the persistent firing cells is influenced by synaptic input coding speed and head direction, as in the oscillatory interference model (Burgess et al., 2007). The speed-modulated head direction signal could come from head direction cells in the postsubiculum (dorsal presubiculum) (Taube et al., 1990; Blair and Sharp, 1995; Muller et al., 1996; Sharp, 1996; Taube, 1998; Boccara et al., 2008), or in deep layers of the medial entorhinal cortex (Sargolini et al., 2006) or indirectly from head direction cells in other areas such as anterior thalamus (Knierim et al., 1998; Taube, 1998; Yu et al., 2006). The velocity dependent depolarization causes a temporary and transient change in frequency, but does not shift the neuron into a different stable frequency of spiking (the stable equilibrium point remains the same). In the simple form presented here, this model does not use the capacity for shifting to multiple different graded frequencies of persistent spiking that has been shown in data and models of layer V neurons (Egorov et al., 2002; Fransén et al., 2006).

In the model, the phase of persistent spiking depends on the integral of velocity, due to transient shifts in the frequency of persistent spiking. The simulation of distributed firing fields of grid cells requires input from persistent firing cells in populations with spiking covering a range of different phases (Figure 2), but still being restricted to only part of the theta cycle. For each persistent firing population, firing frequency is transiently increased by synaptic input from a population of head direction cells with a particular preference angle, and decreased by synaptic input from a population of head direction cells with the opposite angle of preference. (Alternately, two populations receiving separate head direction input could converge to neurons providing input to the grid cell.)

A simple example is shown in Figures 1C and 2A for persistent spiking cells with baseline frequency of 3 Hz. If a rat moves with heading 0 degrees, then the speed-modulated head direction cells with preference for 0 degrees will increase the firing frequency of one population of persistent firing cells, while speed-modulated head direction cells with preference for 120 or 240 degrees will decrease firing frequency in two other populations. These transient changes in frequency will cause the populations to shift in phase relative to each other. If the persistent firing cells start out synchronized in phase with each other, then the shift will move them out of phase with each other and the grid cell receiving input will stop firing for a period of time until the shift is sufficient to bring the cells back into phase with each other to cause grid cell spiking (Figures 1C and 2A). The strong rhythmicity of neural firing in this model is consistent with experimental data on theta rhythmicity of neural spiking in entorhinal cortex (Stewart et al., 1992; Hafting et al., 2008).

With at least two populations of persistent firing cells receiving input from head direction cells with differences in preference angle at multiples of 60 degrees, the input from these persistent firing cells will cause the grid cell to fire in a hexagonal array of locations (Burgess et al., 2005; Burgess et al., 2007; Hasselmo et al., 2007; Burgess, 2008). Figure 2C shows spiking of a simulated grid cell based on simulated persistent spiking cells as a rat runs a foraging trajectory in a circular open field of about 185 cm diameter using data from (Hafting et al., 2005). As shown in Figure 2C, the grid cell shows a pattern of firing similar to experimental data on grid cells. In contrast, the persistent firing cells themselves fire throughout the environment with an absence of spatial specificity, as shown in Figure 2B. However, the phase of the persistent firing cells shifts in different locations as shown by the change in color (light to dark) of dots in Figure 2B. Persistent firing is desynchronized outside of the grid cell firing fields, and synchronized within the grid cell firing fields.

Equations for persistent spiking grid cell model

The persistent spiking model of grid cells can be summarized with the following equation:

$$g(t)=\prod _i[\text{cos}2\pi (ft+P(z)\underset{0}{\overset{t}{\int }}{h}_i(\tau )d\tau )+{\varphi }_i(0){]}_H$$ (1)

Where g(t) is the firing of the grid cell over time. The equation takes the product Π of input to a single modelled grid cell from multiple persistent firing neurons i characterized by a single stable baseline frequency f. The repetitive spiking of individual persistent firing neurons is represented by a thresholded Heaviside step function []_H of a cosine function. The persistent spiking neurons have different initial phases represented by the initial phase vector φ_i(0) and they receive input from different speed modulated head direction cells h_i with different preference angles indexed by i. The frequency of each persistent firing neuron is transiently perturbed from baseline by depolarization in proportion to speed modulated head direction, scaled by the parameter P(z).

In the simplest form of the model, speed modulated head direction input h_i is obtained by multiplying the rat velocity vector v(t)=[Δx(t), Δy(t)] by each row i of the head direction transformation matrix H consisting of unit vectors corresponding to each preferred head direction:

$$h_i=H_{i}v=\left[\begin{array}{cc}\text{cos}({\theta }_b+{\theta }_i)& \text{cos}({\theta }_b+{\theta }_i)\\ ⋮\hfill & ⋮\hfill \end{array}\right]\left[\begin{array}{c}\Delta x(t)\\ \Delta y(t)\end{array}\right]$$ (2)

Where θ_b is the baseline head direction preference angle (set to zero in most simulations) and θ_i represents the relative preference angle of other head direction cells (at multiples of π/3). The phase of the spiking across each population of persistent spiking cells (indexed by i) changes at each time step according to the input from speed modulated head direction input plus the baseline frequency. Thus, the change in phase across the population is represented by:

$$\Delta {\varphi }_i(t)=2\pi (f+P(z)H_i\stackrel{\rightharpoonup }{v}(t))\Delta t$$ (3)

The phase of spiking is obtained by integrating this phase equation over time to yield the t phase representation in equation 1: ${\varphi }_i(t)=2\pi (\text{ft}+P(z)\underset{0}{\overset{t}{\int }}{H}_i\stackrel{\rightharpoonup }{v}(\tau )d\tau )+{\varphi }_i(0)$ Note that this mechanism performs path integration, integrating velocity to make phase proportional to location because $\underset{0}{\overset{t}{\int }}{H}_{i}v(\tau )d\tau =H_{i}x(t)$. The grid cell model in equation 1 results in grid cell firing with orientation determined by the baseline head direction angle θ_b, spatial phase determined by the initial phase vector φ_i(0) and spacing G = 2/3P(z) for 120 degree differences in head direction preference (θ_i = ±2π/3) and G = 2/P(z) for 60 degree differences in head direction preference (θ_i = ±π/3). In Figures 1C and 2A, the speed-modulated head direction input shifts frequency according to the parameter P(z)=0.0116 cycles/cm, causing phase in group 1 to shift by 360 degrees relative to baseline frequency over about 1/P(z)=86 cm (note shift of spiking relative to tick marks, which represent the 3 Hz baseline frequency f). In this model, the spacing G between the grid cell firing fields is smaller than the spatial periodicity of the phase of persistent spiking by a factor of 2/3, giving a grid cell spacing of about 57 cm in Figs. 1C and 2A. In Figures 2B and 2C, the parameter takes the value P(z)=0.0154, causing phase shifts of persistent spiking over about 65 cm and spacing G between grid cell firing fields of about 43 cm. Baseline frequency f is 4 Hz in Figures 2B and 2C.

A range of frequencies and spatial phases are used in the larger scale simulations used for Figures 5-7. Note that the spatial phase of firing (that is, the relative location of grid cell firing fields) can also be determined by the initial location x₀ and the initial phase can be scaled to a location shift x_S as follows: φ_i(0) = f 2πBH (x⃑_S). Note also that this model can account for differences in spacing G at different positions z along the dorsal to ventral axis by changing the frequency response to depolarization P(z). Thus, the parameter P(z) is analogous to the parameter B(z) in the model based on membrane potential oscillations (Giocomo et al., 2007; Burgess et al., 2007; Giocomo and Hasselmo, 2008a; Burgess, 2008).

The equations presented above use head direction cell input that goes positive and negative, but in simulations the model was adapted to use inputs from head direction cells with rectified cosine tuning. This represents a persistent spiking neuron receiving excitatory input from a rectified cosine head direction cell (e.g. a preference angle of zero) and receiving inhibitory input from a rectified cosine head direction cell with the opposite preference angle (e.g. a preference angle of 180 degrees).

Theta phase precession properties

Both hippocampal place cells (O'Keefe and Recce, 1993; Skaggs et al., 1996) and entorhinal grid cells (Hafting et al., 2008) exhibit theta phase precession, in which spiking activity shifts from late to early phases of theta oscillations in the local field potential as a rat traverses the firing field of a neuron. Similar to the oscillatory interference model (Burgess et al., 2007), the model of grid cell firing based on persistent firing at stable frequencies can account for theta phase precession, as shown in Figure 3, replicating the theta phase precession of grid cells in entorhinal cortex layer II (Hafting et al., 2008). As shown in Figure 3B, the persistent spiking model can also account for precession in the very large grid fields in ventral entorhinal cortex (Solstad et al., 2007; Brun et al., 2008). If one assumes that the theta rhythm oscillations in the entorhinal cortex are determined by the synaptic input arising from the full population, then the stable baseline frequency of the population without any shifts can be assumed to be the reference theta phase. The figure shows that the phase of firing of the convergent input to a grid cell from a population of persistent spiking neurons (green trace) shifts relative to the phase of the baseline spiking frequency (blue), as shown by the timing of the spiking raster plot (blue vertical lines) relative to the gray vertical lines indicating phase zero of the baseline spiking frequency. The absence of theta phase precession in many grid cells in entorhinal cortex layer III (Hafting et al., 2008) presents a difficulty for the model, but these layer III neurons could be driven by network interactions with other grid cells. The absence of theta phase precession in many layer III neurons also argues against entorhinal cortex driving theta phase precession in hippocampal region CA1, but hippocampal theta phase precession could arise separately from frequency differences between layer III and hippocampal region CA1.

Figure 3.

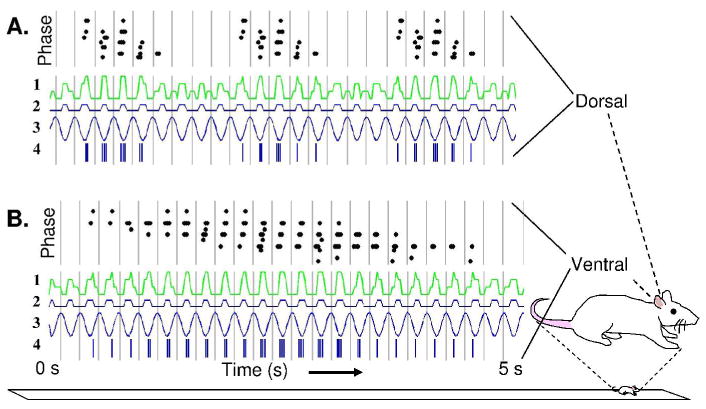
Theta phase precession using the persistent spiking neuron model with 5 Hz baseline frequency. A. Dorsal entorhinal cortex is simulated with parameter P(z)=0.0193, resulting in a larger shift in persistent firing frequency (and faster shift in phase) for a given velocity. Black dots at top show phase of spiking versus location during multiple passes through firing fields. Line 1 (green) shows the summed activity of all three populations of persistent spiking neurons, resulting in grid cell spiking in Line 4. Line 2 shows the baseline persistent spiking frequency. Line 3 depicts the EEG oscillation that might be expected from rhythmic spiking (with a downward deflection during strongest excitatory input). Note that the grid cell spiking (Line 4) shifts in phase relative to the peak of the EEG oscillation shown by vertical gray lines. B. Simulation of a more ventral entorhinal neuron using a smaller value for parameter P(z)=0.0048. This results in a smaller shift in persistent spiking frequency (and slower shift in phase) for a given velocity, and results in a larger grid field and a slower shift in firing phase relative to background theta, consistent with experimental data (Brun et al., 2008; Hafting et al., 2008).

Biophysical implementation of persistent spiking model

A detailed conductance-based biophysical simulation of persistent spiking in single entorhinal layer V neurons (Fransén et al., 2006) has recently been used to test the persistent spiking model of grid cells. The conductance based model shows the capability of shifting the phase of persistent firing due to depolarizing head direction input to cause systematic changes in the synchronization of different populations (Fransen and Hasselmo, 2008). Thus, the biophysical simulation demonstrates the basic cellular properties necessary for this model of grid cells. A paragraph describing the persistent spiking model was previously presented (Hasselmo and Brandon, 2008) for comparison with a separate model of grid cells based on the cyclical persistent firing present in layer II of entorhinal cortex.

Mechanism using rhythmic inhibition

Note that the crucial feature of this model is the shift in relative phase of rhythmic spiking. This function could also be obtained via mechanisms that do not require persistent spiking mechanisms. For example, experimental data shows that inhibitory interneurons demonstrate theta rhythmic spiking in the hippocampus (Fox et al., 1986; Klausberger et al., 2003) and in the entorhinal cortex (Frank et al., 2001). Rhythmic spiking of interneurons could cause rhythmic inhibition in groups of excitatory cells, restricting spiking activity to a specific range of phases, similar to mechanisms proposed for hippocampal theta (Stewart and Fox, 1990; Buzsaki, 2002). If different populations of inhibitory interneurons are driven by head direction input to exhibit different phases of spiking, then they can create phase specific firing of excitatory neurons similar to Figure 2. Thus, a network involving different populations of inhibitory interneurons firing at different phases due to feedback interactions is mathematically similar to the persistent spiking model described here. Alternately, the rhythmic firing modulated by head direction could arise from a local circuit that includes excitatory neurons with persistent spiking or membrane potential oscillations that interact with feedback inihibition.

Relationship to oscillatory interference model

In the simplified mathematical representation presented here, the model of grid cells based on persistent firing strongly resembles the previously presented model of grid cells based on oscillatory interference (Burgess et al., 2007; Burgess, 2008). The role of oscillation frequency in the previous model is taken over by the stable baseline firing frequency of persistent spiking cells in the new model (Egorov et al., 2002; Fransén et al., 2006). The initial model description included possible spiking implementations (Burgess et al., 2007), but initial data supporting the model came from data and simulations of the interference of membrane potential oscillations (Giocomo et al., 2007; Hasselmo et al., 2007; Giocomo and Hasselmo, 2008a).

The mathematical representation of the persistent spiking model presented here differs from the original oscillatory interference model in two features: 1. The persistent spiking model puts the threshold function inside the product or summation sign, and 2. The persistent spiking model utilizes direct interaction of the spiking frequencies in three populations. Thus, it does not contain the interaction of soma and dendritic oscillations that appears in the original oscillatory interference model (Burgess et al., 2007). This results in the different relationship for the scale of grid field spacing, which is G = 2/3P(z) in the persistent firing model (see Figure 2) versus $G=2/\sqrt{3}B(z)$ in the oscillatory interference model. Note that the use of rectified cosine head direction inputs is similar to the oscillatory inteference model that also requires paired inputs of opposite preference angle (Giocomo et al., 2007; Burgess et al., 2007; Hasselmo et al., 2007). The crucial similarity of these models is the integration of velocity by phase, and the read-out of this phase by interference between different phases, so these models will be referred to collectively as phase interference models.

These phase interference models resemble the model of grid cells based on Moire interference of higher spatial frequency grids (Blair et al., 2007; Blair et al., 2008). The initial Moire interference model did not use the integration of speed-modulated head direction to map from temporal oscillations to spatial periodicity. However, a new version of this model has been presented with an alternate mechanism that updates frequency of subcortical oscillators based on running velocity (Blair et al., 2008).

Biophysical differences from membrane potential oscillation model

Though the simplified mathematical representation of the persistent spiking model described above strongly resembles the mathematical representation used in the membrane potential oscillation model, the functional mechanism for the persistent spiking differs completely from the mechanisms of membrane potential oscillations, both in terms of channels and dynamical properties. Rhythmic persistent spiking arises from a tonic non-specific cation current (Fransén et al., 2006) that does not change in response to small changes in frequency or depolarization (See Fig. 6 in (Fransén et al., 2006)), but sets the equilibrium state of activation that determines the baseline frequency of spiking. This channel is not voltage sensitive, but responds transiently to small perturbations of calcium concentration. After transient changes in spiking frequency, neurons will return to the baseline spiking frequency determined by the stable fixed point attractor. Spiking is required to maintain the phase representation.

In contrast, membrane potential oscillations involve cyclical changes in two voltage-sensitive currents (Dickson et al., 2000; Fransen et al., 2004): 1. the persistent sodium current, I(NaP), and 2. the hyperpolarization activated cation current I(h). These currents cause subthreshold membrane potential oscillations that can influence spike timing, but they are changing constantly with voltage and do not provide an equilibrium state. Therefore, neurons showing membrane potential oscillations do not have a stable fixed point attractor. Generation of spikes will perturb the representation of phase, and the cell does not have a stable baseline firing frequency. When simulating the models with cosine functions, the implementations look similar, but if the actual underlying biophysical dynamics are represented more directly, then the persistent spiking model and membrane potential oscillation model differ categorically. These different molecular mechanism could allow testing of these hypotheses using recordings of grid cells in mice (Fyhn et al., 2008) with genetic knockout of different channels.

Circuits with combined mechanisms

A full implementation of the phase interference model for grid cells could require multiple different cell types, including the persistent spiking cells and inhibitory interneurons described here, as well as cells showing membrane potential oscillations. Biophysical implementations using membrane potential oscillations within a single neuron suffer the problem that membrane potential oscillations tend to synchronize within a single neuron (Eriksson et al., 2004; Remme et al., 2007; Heys et al., 2008). This indicates the need to utilize interactions of spiking neurons. However, it is difficult to use membrane potential oscillations within single neurons to regulate a stable baseline spiking frequency. One might think that rhythmic spiking could be generated by membrane potential oscillations, but neurons with membrane potential oscillations only show a small perturbation of their f-I curves at their oscillation frequency that is not sufficient to sustain a stable spiking frequency (Giocomo and Hasselmo, 2008a; Heys et al., 2008). Thus, stable spiking frequencies dependent upon membrane potential oscillations can only be obtained with a network of interacting neurons.

This presents a problem for modeling the direction-dependent grid cells known as conjunctive cells (Sargolini et al., 2006). Conjunctive cells have been modelled with directional voltage-controlled oscillators that maintain phase everywhere but spike only when receiving specific head direction input (Burgess, 2008). However, it may be unrealistic to assume that such oscillators will fire at the correct phase when given a separate suprathreshold input, as cells with membrane potential oscillations that are pushed over threshold usually fire at frequencies higher than their oscillation frequency (Giocomo and Hasselmo, 2008a). In contrast, persistent spiking mechanisms result in stable baseline spiking frequencies, but these cells must keep spiking in order to maintain phase.

As a solution for conjunctive firing, input from persistent spiking neurons combined with head direction input may be required to cause spiking that has the correct phase but fires only for specific heading directions. As shown in Figure 4A and 4B, a cell that only spikes with convergent input from both persistent spiking cells and head direction cells can show conjunctive firing properties similar to data (Sargolini et al., 2006). This model could be used to address the data that many conjunctive cells become pure head direction cells when the hippocampus is inactivated. The grid cell model using just persistent spiking input does not show head direction selectivity, as shown in Figure 4C and 4D.

Figure 4.

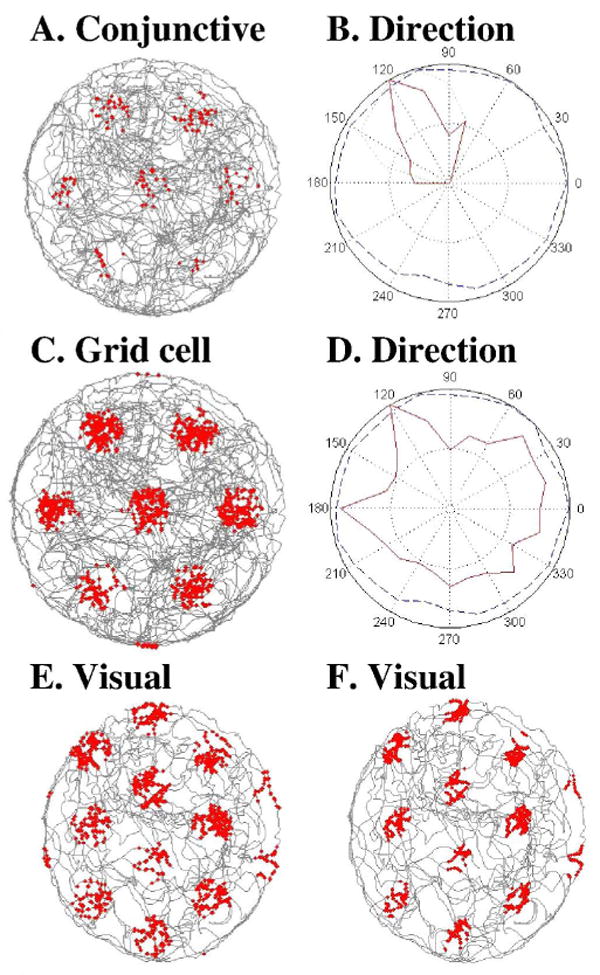
A. Conjunctive grid cell with spiking determined by persistent spiking cells combined with input from a single head direction cell. B. Head direction specificity of the conjunctive cell spiking shown in red demonstrates strong directional selectivity of this conjunctive cell. Blue dashed line shows total dwell time at different head directions. C. Grid cell generated with persistent firing input without additional direct head direction input. D. Red line shows lack of head direction specificity for grid cell generated with persistent spiking cells input alone. E. Simulation of grid cell firing based on phase determined by the angle and distance of 3 visual stimuli. F. Grid cell simulation with phase determined by visual stimulus viewed from two eyes with 120 degree difference in visual angle.

The full implementation of the phase interference model will probably require a combination of neurons showing persistent spiking with other neurons showing strong membrane potential oscillations as well as inhibitory interneurons. Local circuits of these neurons can show rhythmic firing properties that would provide the type of rhythmic spiking activity on a group level as shown in Figure 2. Network interactions would allow the persistent firing model to be influenced by the differences in frequency of membrane potential oscillations along the dorsal to ventral axis (Giocomo et al., 2007; Giocomo and Hasselmo, 2008a).

General Properties of Grid Cell Models

A general model of grid cells could represent grid cell firing as a function: g(t) = g(x(t), x′(t), θ(t), θ′(t), R(t), φ(t), φ′(t)) dependent on the location x, the velocity x′, the head direction θ, the angular velocity θ′, the angle to visual stimuli φ, and the pattern of reward R(t). A simplified mathematical description of the experimental data on grid cells has been used in a number of publications (Fuhs and Touretzky, 2006; Solstad et al., 2006; Molter and Yamaguchi, 2007; Hayman and Jeffery, 2008). This equation is not as general, but allows discussion of different possible models:

$$g(t)=[\prod _{\theta }\text{cos}(\omega H\stackrel{\rightharpoonup }{x}(t)+\varphi ){]}_{+}$$ (4)

This description combines one dimensional waves characterized by the parameters of orientation θ, spatial phase φ and spacing between fields determined by the angular frequency ω. H is the orientation transformation matrix described above. These waves are combined by using a product Π or sum Σ.

A number of models can be expanded from the basic description of the experimental data in equation 4. The dimensions of this expansion correspond to different components of the equation. Three dimensions considered here are 1.) The stimulus used for computing the changing location vector x(t), 2.) The mechanism for converting the stimulus into location, and 3.) The locus of thresholding within the model.

Location from velocity

One class of models integrates rat velocity to code location. Velocity could be obtained from head direction cells modulated by running speed. This class of model includes the phase interference models described above (Burgess et al., 2007; Hasselmo et al., 2007). Possible methods of integration include changes in phase of membrane potential oscillations, phase of inhibitory neuron spiking, and phase of persistent spiking, as well as rate of persistent spiking driving phase relative to network oscillations. These models differ mathematically primarily by whether thresholding is applied before or after multiplication of the oscillations. In a further variant, differential head direction firing could be obtained by integration of angular velocity and speed could be obtained by integration of acceleration.

The above models use temporal codes for integration. As an alternative, a rate code for integration could be provided by the tendency of layer II pyramidal cells to show cyclical persistent firing. If the mechanism of cyclical persistent firing is directly advanced by excitatory input currents and retarded by inhibitory input currents, the velocity input could be directly integrated by firing rate rather than by firing phase (Hasselmo and Brandon, 2008).

Location from visual stimuli

The location vector can also be obtained by computing current location based on the distance and angle to reference stimuli in the environment. In a familiar environment, the initial oscillation phase can be computed from the distance and angle to a particular stimulus. The location vector x⃑ can be determined from the distance D and absolute angle θ_A of a visual stimulus x⃑ = D cos(θ_A), D sin(θ_A). The absolute angle can be determined by subtracting the visual angle θ_R (retinal eccentricity) from the current head direction θ_H as follows x⃑ = D cos(θ_H − θ_R), D sin(θ_H − θ_R). Note that θ_H is actual head direction, not preferred head direction. The location vector x⃑ determined by this mechanism can then be used to determine the phase vector in the model as follows φ = f 2πBHx⃑.

This provides a potential alternate mechanism for the hexagonal pattern of grid cell firing. The head direction cells coding θ_H respond to the heading of the rat, but the visual angle θ_R for each eye is at an approximate 60 degree offset from this heading (120 degrees relative to each other). Thus, the phase of persistent firing neurons could be updated by the absolute angle computed computed with visual input from each eye $\varphi (t)=f2\pi B\text{cos}\left[\begin{array}{c}{\theta }_A(t)+\pi /3\\ {\theta }_A(t)-\pi /3\end{array}\right]$. The 120 degree difference in angle of visual input from each eye could therefore cause the hexagonal grid cell firing patterns. This effect is shown in a simulation of grid cell based on the update of position by visual angle and position as shown in Figure 4E and 4F.

As an alternative to direct computation of phase from the distance and angle to visual stimuli, the rat could compute its velocity within the environment based on optic flow. In particular, rats might compute their movement toward a boundary wall based on the optic flow of the upper edge of the wall, or the flow of the border between the wall and the floor. Optic flow is complex, but has features that could relate to the rather narrow tuning of head direction cells relative to a cosine function. In particular, the 90 degree range of tuning with a triangular shape in most head direction cells could relate to optic flow at different angles relative to movement. In the center of the visual field, directly in front of the rat, optic flow will be zero. Flow increases almost linearly for objects at greater eccentricity, up to 45 degrees, and then decreases. Thus, head direction tuning might rescale optic flow at different points along a horizontal line across the center of the visual field. Alternately, head direction tuning might be scaled in proportion to optic flow on the ground in front of the rat. Features at a 45 degree vertical angle from the rat heading to the ground directly below will have the greatest optic flow, and features at a greater angle show optic flow that falls off almost linearly over angles up to 45 degrees lateral to rat movement.

The framework for updating grid cells based on visual stimuli suggests a potential use of conjunctive cells. Because updating based on visual stimuli requires an interaction of head direction and visual angle, this might require conjunctive cells that respond selectively when the rat is facing in a specific head direction, as seen in layers III, V and VI of medial entorhinal cortex (Sargolini et al., 2006). In fact, this might reflect the visibility of specific visual stimuli. The conjunctive grid-by-direction cells resemble the theta-modulated place-by-direction cells observed in the post- and parasubiculum, which respond only when then the rat faces a preferred direction while occupying a single location (Cacucci et al., 2004).

Phase Reset and Context-Dependent Firing

Entorhinal cells do not always fire as grid cells, and hippocampal cells do not always fire as place cells. A number of studies have shown that the context of recent behaviour has a strong influence on spiking activity in the entorhinal cortex (Frank et al., 2000; Derdikman et al., 2006; Lipton et al., 2007) and hippocampus (Markus et al., 1995; Gothard et al., 1996; Wood et al., 2000; Lee et al., 2006; Griffin et al., 2007; Pastalkova et al., 2008). This data potentially counters the view of grid cells as providing a spatial map, as the context dependence suggests that neurons do not only respond to the two-dimensional location in the environment. These data present a broad range of phenomena that must be accounted for by models of grid cell mechanisms. The grid cell models based on phase interference (Burgess et al., 2007; Hasselmo et al., 2007; Burgess, 2008) can easily account for both context-dependent firing and regular grid cell firing in the open field. The simulations presented here demonstrate how context-dependence could arise from resetting the phase of persistent spiking at specific locations (e.g. stopping locations, reward locations or turning locations), either by shifting the phase of one population, or turning off the current population and turning on a new population of persistent spiking neurons. These context-dependent responses would also need to be addressed by network models of grid cells (McNaughton et al., 2006; Fuhs and Touretzky, 2006; Kropff and Treves, 2008).

The possibility of reset was mentioned in the original oscillatory interference model presentation (Burgess et al., 2007), but there is a further division of models based on the mechanism of phase update (Hasselmo, 2007). In the original Euclidian model, a two-dimensional representation of space results from phase integration of input from speed-modulated head direction cells. Without reset these models show spiking dependent on two-dimensional location. Reset results in separate two-dimensional maps for different phases of a task. In an alternative model, referred to here as the Arc-length model, the phase of spiking or oscillation can be shifted by running speed alone, independent of head direction (Hasselmo, 2007). In this case, the integration of speed by phase results in firing dependent upon the one-dimensional arc length of a trajectory (Hasselmo, 2007). In the arc length model, reset results in firing dependent on arc length from the last reset location. The arc length model generates different predictions, such as the absence of mapping to a hexagonal array of firing fields, and the mirror symmetry of firing for different directions of running along a linear track with reward at both ends. In a final model, referred to here as the Time Interval model, the phase is not shifted by any external input and interference depends on time interval alone. Reset results in firing dependent on the time interval since the last reset location.

Resetting of phase can be represented in the equation by changing phase according to a reset function R(x) that could reflect stopping at reward locations, but could also reflect sensory input such as a strong angular velocity signal or change in visual features at a hairpin turn. In the first two simulations presented below, phase is reset to a zero vector each time reward is received. Note that though the reward is presented at different locations, the phase is reset to the same zero vector. In contrast to a previous paper about the arc-length model (Hasselmo, 2007), these simulations use input from speed-modulated head direction cells (the Euclidian model) rather than using one dimensional speed input. Also, the simulations presented here include separate populations of entorhinal neurons and hippocampal neurons and address two additional tasks: spatial alternation with running in a wheel during delay (Pastalkova and Buzsaki, 2007; Pastalkova et al., 2008), and the hairpin maze task (Derdikman et al., 2006).

In these simulations, the activity of entorhinal neurons was determined by the older oscillatory interference model using simple non-thresholded cosine functions. These simulations used interacting populations of 75 entorhinal cells and 400 hippocampal cells, as in a recent model of temporally structured replay (Hasselmo, 2008). The population of 75 entorhinal neurons was modelled as three groups of 25 neurons with different baseline oscillation frequencies of 2, 4 and 6 Hz. In each group of 25 entorhinal neurons, a full range of spatial phases were selected by choosing appropriate values of φ_i at 5 different initial phases in two dimensions. The whole population shared the same orientation θ_b=0.

The activity of individual cells within a population of 400 hippocampal cells was simulated by randomly selecting groups of three entorhinal grid cells and plotting spiking that would occur based upon simultaneous spiking in all three entorhinal cells (Hasselmo, 2008). The population of hippocampal cells was selected at the start of the simulation based on the variance of spiking location falling below a numerical limit. After selection of each hippocampal cell, Hebbian modification strengthened synapses from the three selected entorhinal cells to the selected hippocampal cell. This created a matrix of synaptic connectivity W_EH allowing the 75 entorhinal cells with activity g(t) to cause spiking in 400 hippocampal cells with activity p(t) as follows: p(t) = W_EHg(t). Many other papers have explored how convergent input from grid cells causes place cell activity (O'Keefe and Burgess, 2005; Solstad et al., 2006; Blair et al., 2007; Franzius et al., 2007; Blair et al., 2008; Hayman and Jeffery, 2008).

Without resetting, entorhinal cells fired as grid cells and hippocampal neurons fired as place cells. Resetting shifted the spatial phase of the entire entorhinal population, and thereby shifted the spatial phase of the hippocampal cell firing, so that both populations showed strong context-dependency caused by reset (Figures 5-7).

Figure 5.

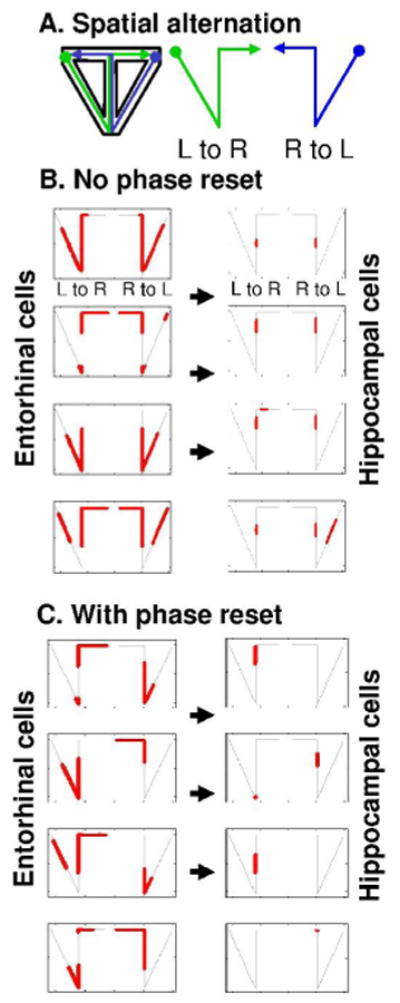
Simulated spiking activity during continuous spatial alternation. A. In the task, rats alternate between running from left reward, up stem to right reward (L to R) and running from right reward, up stem to left reward (R to L). B. With no phase reset, 4 example entorhinal cells show firing dependent upon where the linear task intersects with a grid. Input from the 75 entorhinal cells results in hippocampal cells that fire as place cells. In the stem of the maze, 4 example hippocampal cells fire the same for L to R and R to L trajectories, with no dependence on past or future location. C. With phase reset of entorhinal neurons at reward locations, examples of 4 of the 75 entorhinal neurons show context-dependent firing that differs between L to R and R to L trajectories, resulting in differential firing patterns on the stem of the maze. Input from the 75 entorhinal cells results in hippocampal cells that show context-dependent firing. 4 example cells show different patterns of firing on the stem during L to R and R to L trajectories.

Continuous spatial alternation

The first simulations shown here moved the virtual rat through a continuous spatial alternation task and replicated data in this task on firing of entorhinal cells (Lipton et al., 2007) and hippocampal cells (Wood et al., 2000; Lee et al., 2006). Without resetting, the network shows spatially consistent firing, with entorhinal cells firing in locations on the linear track that fall within the firing fields of a grid cell, as shown in Figure 5A (left), and hippocampal neurons showing the spatially consistent firing of place cells, as shown in Figure 5A (right). In particular, cells respond in the same location in the stem for both left to right and right to left trajectories. In contrast, with reset of phase at reward locations, simulated entorhinal neurons show context-dependent firing on the stem that differs between the left-to-right trajectory and the right-to-left trajectory, as shown in Figure 5B (left). This is consistent with physiological recordings showing context dependent entorhinal activity during this task (Lipton et al., 2007; Eichenbaum and Lipton, 2008). The input from these entorhinal neurons results in context-dependent firing of hippocampal neurons on different trajectories, as shown in Figure 5B (right). This is most evident on the stem of the maze, where reset results in different firing on left-to-right versus right-to-left trajectories, consistent with previous recording of context-dependent hippocampal spiking on the stem during spatial alternation (Wood et al., 2000; Lee et al., 2006). The Euclidian model reset resembles previous simulations using arc length coding with reset (Hasselmo, 2007). This model could be used to simulate the differential firing of place cells when an open field foraging task is replaced with repetitive running between different goal locations (Markus et al., 1995).

Spiking in running wheel during delay

An exciting prediction of these interference models is that they can show firing dependent on running alone, thereby decoupling neuronal firing from shifts in actual spatial location. Because the phase of these models integrates velocity input, the phase will continue to be updated when a rat runs in a running wheel, as long as the perception of velocity is based on proprioceptive feedback rather than visual input. Thus, with simulation of a rat running in a wheel, the model generates spiking at specific reproducible intervals from the start of running, replicating recent experimental data using such a task (Pastalkova and Buzsaki, 2007; Pastalkova et al., 2008). The structure of the task is illustrated in Figures 6A and 6B. During each trial, the simulated rat runs the left side of a spatial alternation task, then runs in the running wheel at a constant speed for a fixed time period (straight lines on left side of each plot), then runs the right side of the spatial alternation task, then runs in the running wheel at a constant speed for a fixed time period (straight line plots on right side). The figure shows activity of 4 representative cells out of the 75 cells in entorhinal cortex and 4 representative cells out of the 400 cells in hippocampus. With phase resetting at reward location, the model shows differential firing in the running wheel after left versus right side runs. In addition, the firing appears at specific time points during wheel running that are consistent across the 7 trials shown in Figure 6C (corresponding to the perceived distance or arc length of the wheel run). The hippocampal neuron at the top of Fig. 6C shows firing only during the middle period of wheel running after the left side of the track. The third hippocampal neuron in Fig. 6C shows firing only during the middle period of wheel running after the right side of the track.

Figure 6.

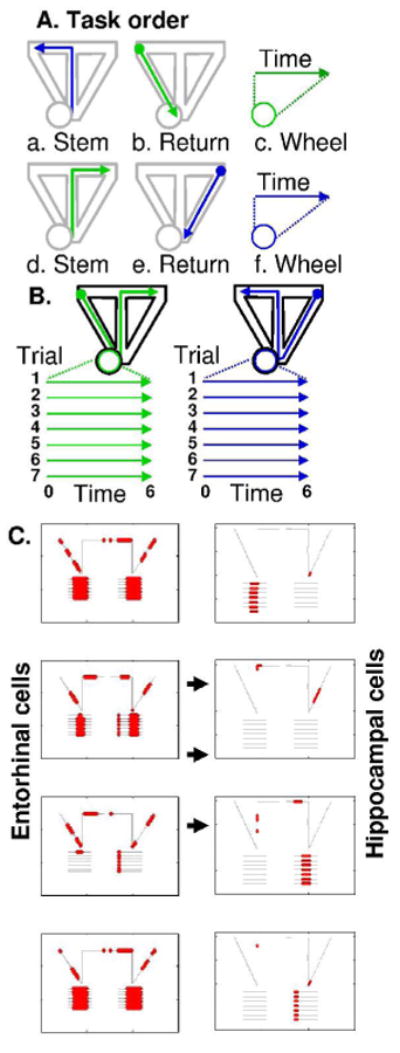
Simulated spiking activity in delayed spatial alternation task with wheel running during the delay period. A. Order of behaviour in the task. Rat runs up stem into left arm (a), then down left return arm (b), then runs in wheel during delay (c), then runs up stem into right arm (d), then down right return arm (e), then runs in wheel during delay (f). B. Spiking is plotted spatially for left to right trials (green). Between left return and right reward, running in wheel spiking is plotted in lines on left depicting time during each trial. Similarly, spiking is plotted spatially for right to left trials (blue), and relative to time during wheel running in each trial. C. With reset at reward location, the simulation generates context-dependent spiking activity during wheel running in the delay period. Typical examples of four (out of 75) entorhinal neurons plotted in left column show spiking in many locations and during long time segments in running wheel. Typical examples of four hippocampal neurons plotted in right column show spiking in discrete spatial locations and at brief restricted time points during wheel running after just one type of trajectory. This replicates experimental data in the same task (Pastalkova and Buzsaki, 2007; Pastalkova et al., 2008).

This simulation matches experimental data showing similarly reproducible time-locked firing in the running wheel during the delay period of a spatial alternation task (Pastalkova and Buzsaki, 2007; Pastalkova et al., 2008). This task provides another potential test for comparing the two-dimensional Euclidian model, which predicts differences in firing for running wheels oriented at different angles, versus the one-dimensional arc length model (Hasselmo, 2007) which predicts that firing in the running wheel will not depend upon the orientation of the running wheel, but will depend on running speed, and the Time Interval model which predicts firing independent of orientation or running speed. The data shows evidence for changes in firing with different directions of running (Pastalkova and Buzsaki, 2007; Pastalkova et al., 2008), supporting the Euclidian model. Neural firing in the running wheel is not as selective when the rat runs in its home cage, outside of the task. This indicates that activity in the running wheel might partly be determined by training-dependent strengthening of associations between the current grid and place cell activity and the associated speed-modulated head direction activity that shifts firing. Thus, mechanisms used in a recent model of temporally structured replay (Hasselmo, 2008) could be active during waking to contribute to these differences in firing. The presence of these associations could drive shifts in entorhinal and hippocampal firing during wheel running, and thereby allow selective time-dependent firing.

Hairpin task

The simulation has also been used to address data from running of a hairpin maze. This was motivated by data from cells that show grid cell firing properties in an open field but shift their pattern of firing in a hairpin maze in the same environment (Derdikman et al., 2006). Rather than firing in locations corresponding to the two-dimensional location of a grid cell firing field, the neurons fire at regular intervals relative to the starting point of each segment of the hairpin maze. This pattern can be obtained in the simulation by resetting the phase of the oscillations at each turning point, as shown in Figure 7B, in contrast to the grid cell pattern that appears without reset (Figure 7A). This model accounts for the pattern of firing of both entorhinal cells and hippocampal cells, which show firing dependent upon distance from turns in this task (Derdikman et al., 2006). This simulation also accounts for the pattern of firing observed in entorhinal cortex in earlier studies in a U maze and W maze (Frank et al., 2000). These data provide an important opportunity for testing reset of the one-dimensional Arc-length model based on running speed alone versus the two-dimensional Euclidian model based on speed and head direction. As noted above, the one-dimensional model could generate mirror-image symmetry of firing for trajectories going from left to right versus right to left. The two-dimensional model would not generate the same type of mirror symmetry.

Figure 7.

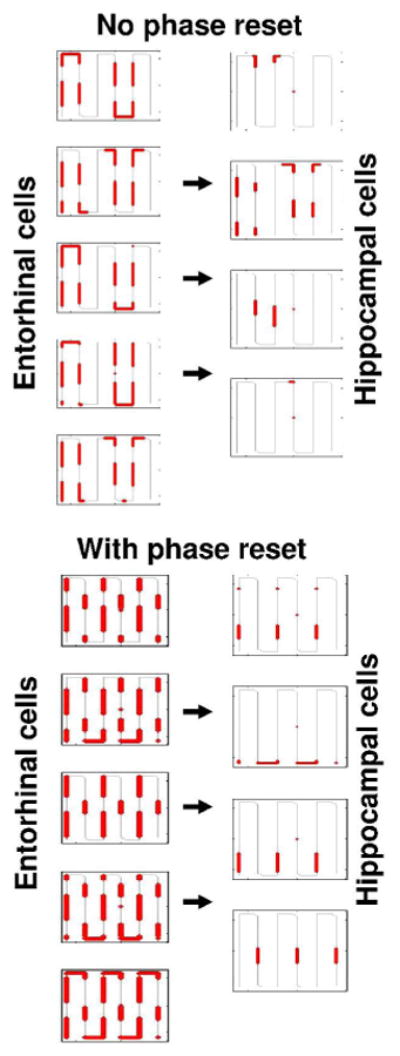
Simulated spiking activity during running on a long linear track with multiple hairpin turns. A. No reset of phase results in firing that depends upon the two-dimensional location in the environment. Firing of 5 entorhinal neurons appears in multiple grid cell firing fields and examples of firing in 4 hippocampal neurons shows multiple place fields that match spatially adjacent segments. B. Resetting of phase at each hairpin turn results in firing fields that occur at specific distances from the turning points in both entorhinal neurons (firing of 5 neurons on left) and hippocampal neurons (4 neurons on right). This firing dependent on distance from turns is consistent with experimental recordings of entorhinal neurons and hippocampal neurons (Frank et al., 2000; Derdikman et al., 2006).

The reset at turning points that induces this pattern of firing could be due to the strong drop in running speed at the turning point, to other cues such as the increase in angular velocity at turns, or to the abrupt change in visual stimuli before and after the turn. This could also reflect the creation of intermittent goal representations for guiding sequential behaviour in the maze, which could guide behaviour at each point based on a goal vector created by integration of movement between each reset location (Hasselmo and Brandon, 2008). The loss of grid cell firing could result from the barriers on each segment shutting off forward retrieval (or planning) based on any action other than along the one-dimensional trajectory of the task. In contrast, the grid firing in open fields might result from retrieval (or planning) of multiple possible directions of movement.

The forward retrieval (or planning) mechanism could involve the representation of location by phase in grid cells, which provides a continuous representation of location appropriate for trajectory encoding and retrieval. A recent model encodes trajectories by strengthening synaptic connections between place cells and head direction cells during encoding (Hasselmo, 2008). During retrieval, place cells drive persistent spiking in head direction cells that update the phase of grid cells, causing the internal state to advance along the previously experienced trajectory. Persistent spiking has recently been shown in the postsubiculum (Yoshida and Hasselmo, 2008), where head direction cells are commonly recorded. A model of this circuit allows simulation of activity during REM sleep that shows temporally structured replay of place cell activity that occurred during previous waking periods (Hasselmo and Brandon, 2008; Hasselmo, 2008). This model predicts replay of head direction activity during REM sleep which has been shown experimentally (Brandon et al., 2008).

Discussion

The model presented here effectively simulates the firing properties of grid cells based on intrinsic persistent spiking of entorhinal neurons (Figures 1-4). The model can be simulated with compartmental biophysical simulations of persistent firing (Fransen and Hasselmo, 2008), avoiding the issue of synchronization within a single neuron that affects the grid cell model based on membrane potential oscillations (Giocomo et al., 2007; Hasselmo et al., 2007). The persistent spiking and membrane potential oscillation models could be combined at the circuit level. As shown in Figures 5-7, models using phase interference have an advantage over network models because, with addition of reset, they can account for context dependent firing properties of entorhinal and hippocampal neurons observed in a range of different tasks.

The discussion below will evaluate some of the strengths and weaknesses of different types of grid cell models. Though the models are contrasted here, the evidence strongly suggests that the correct model of grid cell firing properties will depend upon a combination of phase interference mechanisms and network attractor dynamics. The important question is how the network properties interact with the interference properties.

This section will focus on the oscillatory interference model, and compare it with the persistent spiking model that shares many features, as well as recurrent attractor models.

Strengths of phase interference models

1. Simplicity

The oscillatory interference model has the advantage of simplicity, as it can be described with a single equation (Burgess et al., 2005; Burgess et al., 2007; Giocomo and Hasselmo, 2008a; Burgess, 2008). A single simulated neuron with three head direction inputs effectively simulates the pattern of spiking observed during unit recording from awake behaving animals. The persistent spiking model presented here uses four neurons, but the equation is similar (see Equation 1). These phase interference models have only three parameters: A. Spatial frequency, which can be directly scaled to intracellular membrane potential oscillation frequency or persistent spiking frequency, B. spatial phase, which relates to initial phase of oscillations or spiking, and C. orientation, which can be linked to head direction cell orientation.

2. Theta phase precession

The oscillatory interference model of grid cells (Burgess et al., 2007) arose naturally out of models simulating the theta phase precession of hippocampal place cells (O'Keefe and Recce, 1993; Lengyel et al., 2003; O'Keefe and Burgess, 2005; Burgess et al., 2005; Burgess et al., 2007), and effectively models theta phase precession in entorhinal cortical neurons (Burgess et al., 2007; Hasselmo and Brandon, 2008; Burgess, 2008). In fact, these place cell precession models automatically generated multiple firing fields, and had to be modified to prevent multiple fields. As shown in Figure 3, the persistent spiking model also generates precession. In contrast, recurrent attractor models of grid cells do not require theta rhythm and published attractor models do not yet simulate theta phase precession.

3. Prediction of spatial scaling mechanism supported

The oscillatory interference model already generated a prediction that differences in spatial scaling of grid cells along the dorsal to ventral axis of entorhinal cortex arises from differences in intrinsic oscillation frequency (O'Keefe and Burgess, 2005; Burgess et al., 2007). This explicit prediction has been supported by experimental data showing differences in membrane potential oscillation frequency along the dorsal to ventral axis of entorhinal cortex (Giocomo et al., 2007; Hasselmo et al., 2007; Giocomo and Hasselmo, 2008a). As shown in (Giocomo and Hasselmo, 2008a), oscillation data fits the additive version of the model (Burgess et al., 2007; Giocomo andHasselmo, 2008a) and provides the parameter B(z) that accounts for both the scaling of field size and spacing along the dorsal to ventral axis (Giocomo and Hasselmo, 2008a). Simulations of the model (Giocomo and Hasselmo, 2008a) also effectively account for the very large grid cell scale in very ventral regions of medial entorhinal cortex (Solstad et al., 2007; Brun et al., 2008). The simulation of both field size and spacing with the same parameter differs from recurrent attractor models of grid cells that model grid field size with the pattern of synaptic connectivity, but model spacing with the gain of velocity input. As an alternate mechanism, the biophysical time scale of adaptation has been shown to account for differences in grid cell spatial scaling (Kropff and Treves, 2008).

4. Prediction of grid cell firing frequency

The oscillatory interference model (Burgess et al., 2007; Burgess, 2008) predicted dorsal to ventral differences of in-field firing frequency of grid cells and scaling of in-field frequency with running speed. Both of these predictions are supported by experimental data (Jeewajee et al., 2008b; Jeewajee et al., 2008a). The model also accounts for the change in network theta rhythm frequency correlated with running speed (Maurer et al., 2005; Hasselmo et al., 2007; Jeewajee et al., 2008a).

5. Expansion in novel environments

The model (Burgess et al., 2007) predicted that the expansion of grid fields in novel environments (Barry et al., 2008) should be accompanied by a reduction in network theta rhythm frequency, as supported by experimental data (Jeewajee et al., 2008c).

6. Path integration

The same mechanism that produces the pattern of grid cell firing in the model also performs path integration (Burgess et al., 2007; Hasselmo and Brandon, 2008; Burgess, 2008). This contrasts with recurrent attractor models in which the pattern of firing is created by the pattern of excitatory recurrent connectivity (McNaughton et al., 2006; Fuhs and Touretzky, 2006), and the network mechanism of path integration is a separate velocity dependent shift in representation that works just as well with a place cell representation (Samsonovich and McNaughton, 1997).

Weaknesses of phase interference models

1. Synchronization of oscillations within single neurons

The single cell version of the oscillatory interference model has not yet been successfully simulated in compartmental biophysical models of entorhinal stellate cells. Simulations demonstrate that membrane potential oscillations within a single neuron have a strong tendency toward synchronization of phase and frequency (Eriksson et al., 2004; Remme et al., 2007; Heys et al., 2008). This suggests that the influence of membrane potential oscillations requires network interactions between cells, such as those in the persistent spiking model of grid cells presented here.

2. Sensitivity to noise

All phase interference models are sensitive to noise, including both noise in the phase and noise in the speed modulated head direction input. Experimental data on membrane potential oscillations shows high variance that can disrupt the model grid pattern (Giocomo and Hasselmo, 2008a). Spiking will disrupt phase in the membrane potential oscillation model, but not in the persistent spiking model. Whole cell patch recordings of persistent spiking show variation of spike interval (Yoshida et al., 2007), but sharp electrode recordings of persistent spiking show remarkable stability of interspike intervals over many minutes (Fransén et al., 2006; Tahvildari et al., 2007).

3. Requirements for initial phase and phase reset

The sensitivity to noise in the oscillatory interference model can be counteracted by resetting of phase based on current place cell activity (Burgess et al., 2005; Burgess et al., 2007; Burgess, 2008). However, the oscillatory interference model requires specific phase relationships in the initial phase. A grid cell model starting with all phases at zero will not show the same grid cell pattern if all phases are shifted by 180 degrees (Burgess et al., 2005; Hasselmo et al., 2007). This problem is avoided if the soma reference phase is not used, as in the persistent spiking model presented here, or if phase is only reset at specific locations where all phases are zero. It may be simpler to reset phase in the persistent spiking model with a single strong input.

Phase reset may be a strength of the interference models (Figures 5-7), as phase reset allows simulation of the context dependent firing properties of grid cells (Frank et al., 2000; Derdikman et al., 2006; Lipton et al., 2007) and place cells (Markus et al., 1995; Wood et al., 2000; Lee et al., 2006; Griffin et al., 2007). Phase reset could also provide a mechanism for changes in grid fields associated with changes in the size of the environment including expansion (Barry et al., 2007) or remapping (Savelli et al., 2008).

4. Head direction preference intervals

To obtain the hexagonal pattern of grid fields, the oscillatory interference models requires that head direction inputs have preference angles at 60 degree intervals (Burgess et al., 2007; Hasselmo et al., 2007) or 120 degree intervals in the persistent spiking model in equation 1. Though this could arise from self-organization, physiological or anatomical data has not demonstrated this selective pattern of connectivity dependent on preference angle. As noted here, the preference angle could arise from the eyes having a visual angle offset by 60 degrees from head direction. The assumption of head direction input angle applies to both the persistent spiking model presented here and the membrane potential oscillation implementation of the oscillatory interference model. This problem specifically does not apply to the recurrent attractor models of grid cells, which obtain hexagonal firing patterns from circularly symmetric excitatory connectivity.

5. Requires cosine function of head direction tuning

Effective path integration requires that head direction cells fire at a rate determined by a cosine (or sine) function of actual head direction (covering 180 degrees). However, most actual head direction cells have much narrower tuning with a triangle shape covering about 90 degrees (Taube et al., 1990; Taube and Bassett, 2003). In addition, head direction cells lack the negative component of the cosine function. Head direction cells commonly do not show strong tuning to speed, though other neurons in the same region (Sharp, 1996) or connected regions (O'Keefe et al., 1998; Sharp et al., 2006) do show sensitivity to speed. These data suggest that an alternate representation might utilize head direction and angle of visual stimuli as a state instead of the allocentric location, and this suggests that updating of state might utilize angular head velocity and the shift in viewing angle of visual stimuli.

Both oscillatory interference models and recurrent attractor models require cosine tuning of the head direction input. The problem of the negative component of firing has partly been solved by using a rectified cosine function, but this requires coupling pairs of head direction inputs that are tuned at 180 degree differences. This modification allows simulation of theta phase precession that shows the correct phase shift (from late to early) regardless of the direction that the rat runs through the place field (Burgess et al., 2007; Hasselmo and Brandon, 2008; Burgess, 2008). Otherwise, the model shows a phase shift from early to late. However, this version requires even more selective connectivity in the form of pairs of inputs to individual neurons, and does not avoid the need for cosine tuning of head direction cells.

Strengths and weakenesses of attractor models

Some network models obtain grid cell firing through attractor dynamics of recurrent connectivity (Burak and Fiete, 2006; McNaughton et al., 2006; Fuhs and Touretzky, 2006; Welinder and Fiete, 2008; Fiete et al., 2008). These attractor network models have certain strengths that support the idea of combining the interference models and the attractor models. In particular, the network models are less sensitive to noise. Inclusion of network interactions within a population could enhance the stability of phase responses in an interference model. In addition, the network models provide a mechanism to ensure an even distribution of different spatial phases within a single region, as single neuron models cannot directly account for this. Because network models do not use oscillations, they do not have the requirements for specific phase relationships among oscillations that the interference models have. The hexagonal pattern of firing in network models appears due to the pattern of recurrent excitation and inhibition (McNaughton et al., 2006; Fuhs and Touretzky, 2006). This avoids the problem of head direction input with specific preference angle relationships, but replaces it with the requirement of specific synaptic connectivity. An alternate network model avoids the need for specific recurrent connectivity by obtaining hexagonal patterns of synaptic input by self-organization of afferent input regulated by the time course of neuronal adaptation (Kropff and Treves, 2008).

The network models suffer disadvantages relative to the single cell models. In particular, the network models do not use theta rhythm oscillations, and it is likely that incorporation of oscillations will interfere with attractor dynamics, rather than enhancing them. This means that the published attractor network models of grid cells (McNaughton et al., 2006; Fuhs and Touretzky, 2006; Welinder and Fiete, 2008) do not yet simulate theta phase precession of grid cells (Hafting et al., 2008), though ongoing research is addressing this point. Network models also do not yet account for the modulation of theta rhythm frequency by running speed. In contrast to interference models, the mechanism of path integration is a separate process superimposed on the network dynamics for grid firing (Burak and Fiete, 2006; McNaughton et al., 2006; Fuhs and Touretzky, 2006; Welinder and Fiete, 2008). In addition, because the grid pattern in network models requires particular patterns of synaptic connectivity, this might prevent these models from being flexible in different tasks. These models do not yet account for the immediate shift to context dependent firing of entorhinal neurons shown in linear tasks such as the hairpin maze (Derdikman et al., 2006) or the spatial alternation task (Lipton et al., 2007), relative to the firing in the open field. In contrast, as shown in Figures 5-7, interference models can easily account for context-dependent firing in linear tasks with only minor modification in the form of phase reset.