The Time Course of Transmitter at Glycinergic Synapses onto Motoneurons

Abstract

The concentration of transmitter in the synaptic cleft and its clearance time are one of the main determinants of synaptic strength. We estimated the time course of glycine at rat lumbar motoneurons synapses in spinal cord slices by recording synaptic currents in the presence of a low-affinity competitive antagonist at glycine receptors [2-(3-carboxypropyl)-3-amino-6-(4-methoxyphenyl)pyridazinium (SR-95531)]. Data were analyzed by using the established activation mechanism for glycine receptors and our measurements of SR-95531 binding rates. We show that this technique alone is not sufficient to determine simultaneously the peak concentration of transmitter and its clearance time. However, we found that block of the glial glycine transporter prolongs the glycine transient. This observation puts additional constraints on the range of possible values of the time course of glycine, indicating that glycine reaches a peak concentration of 2.2–3.5 mm and is cleared from the cleft with a time constant of 0.6–0.9 ms.

Introduction

During synaptic transmission, postsynaptic receptors are exposed to a fast transient of high concentration of agonist. Knowledge of the time course of neurotransmitter after release is essential in understanding synaptic function and modulation because it can indicate whether postsynaptic receptors are saturated or not and therefore whether they are susceptible of modulation by to presynaptic factors affecting release.

Estimates of the neurotransmitter concentration and its time course in the cleft refer mostly to glutamatergic synapses and indicate that glutamate reaches concentrations of 1–3 mm and it is cleared from the cleft in <1 ms. Two approaches have been used so far to determine the time course of transmitter in the cleft. One is the mathematical modeling of the diffusion process, making use of realistic data on the geometry and ultrastructure of the synapse (Barbour et al., 1994; Barbour and Häusser, 1997; Rusakov and Kullmann, 1998a,b; Savtchenko and Rusakov, 2007). The other approach is pharmacological and involves measuring the inhibition of synaptic currents by a fast dissociating competitive antagonist (Clements et al., 1992; Diamond and Jahr, 1997; Overstreet et al., 2003).

Most of these studies were performed on glutamatergic synapses because of the vast amount of anatomical data on hand and the availability of low-affinity competitive antagonists with dissociation rates fast enough to be comparable with the residence of transmitter in the cleft on the other.

To date, there are no available estimates of the time course of glycine in the cleft and there is also little evidence on whether glycine receptors (GlyRs) are saturated or not.

In this study, we determined the time course of glycine at inhibitory synapses onto lumbar motoneurons. Motoneurons receive from Renshaw cells powerful inhibitory input that is mostly mediated by glycine (Eccles et al., 1954; Curtis et al., 1976); this inhibitory feedback circuit contributes to motor coordination.

We took advantage of the recent characterization of 2-(3-carboxypropyl)-3-amino-6-(4-methoxyphenyl)pyridazinium (SR-95531) (a potent and selective GABA_A antagonist) as a fast dissociating competitive antagonist at GlyRs (Wang and Slaughter, 2005; Beato et al., 2007) and of the detailed knowledge of the scheme of activation of GlyRs (Burzomato et al., 2004).

In the present study, we confirm that SR-95531 is a competitive antagonist at native GlyRs and that the time course of its unbinding is comparable with the lifetime of transmitter in the cleft. It is shown that data from steady-state inhibition induced by a low-affinity competitive antagonist alone are compatible with a wide range of transmitter concentrations and clearance times. However, the use of a blocker of the glial glycine transporter combined with the fast competitive antagonist shows that postsynaptic GlyRs at motoneurons are not saturated and this allows much narrower estimates for the time course of glycine in the cleft.

Materials and Methods

Slice preparation.

Rats [postnatal day 12 (P12) to P13] were anesthetized with urethane (1.8 g/kg, i.p. injection of 10% w/v solution; Sigma-Aldrich) and decapitated in accordance with United Kingdom Home Office regulations. A ventral laminectomy was performed in ice-cold solutions and midthoracic to lumbar segments of the cord were glued to an agar block with tissue glue (Vetbond; WPI Scientific Instruments). The block was fixed vertically on the platform of a Leica VT100 vibratome, and transverse slices were cut at a thickness of 350 μm from the lower lumbar region (L2–L5 segments). The slicing solution was kept ice-cold and contained the following (in mm): 130 K-gluconate, 15 KCl, 0.05 EGTA, 20 HEPES, and 25 glucose, pH adjusted to 7.4 with NaOH. This solution mimics the intracellular medium and improves motoneuron survival, possibly by preventing entry of extracellular ions through neurites cut during slicing (Dugué et al., 2005). Kynurenic acid (3 mm) was added to the slicing solution to protect the tissue from glutamate excitotoxicity.

The extracellular solution for recordings contained the following (in mm): 124 NaCl, 3 KCl, 25 NaHCO₃, 1 NaH₂PO₄, 2 CaCl₂, 2 MgCl₂, 11 d-glucose, pH 7.4, continuously bubbled with 95/5% O₂/CO₂ mixture. Slices were fixed to the bottom of the chamber with a nylon threaded mesh mounted on a platinum wire and were continuously superfused (10–12 ml/min).

Whole-cell patch-clamp recordings and stimulation.

Recordings were performed in the whole-cell or outside-out voltage-clamp configuration with an Axopatch 200B amplifier (Molecular Devices), filtered at 5 kHz with an eight-pole Bessel filter, and digitized at 50 kHz. Electrodes were pulled on a Flaming-Brown horizontal puller (P-97; Sutter Instrument) from thick-walled borosilicate glass (GC150F; Harvard Apparatus) to a resistance of ∼0.5 MΩ. The tips were fire polished to a final resistance of 1–1.5 MΩ and filled with an internal solution composed of the following (in mm): 140 CsCl, 4 NaCl, 1 Mg₂Cl, 0.5 CaCl₂, 5 EGTA, 10 HEPES, 2 Mg-ATP, 3 mm QX-314 (lidocaine N-ethyl bromide), pH 7.3 with CsOH.

Cells were visualized using infrared–differential interference contrast (DIC) optics on a Nikon Eclipse E600FN microscope with a 40× water-immersion objective.

Recordings were performed from motoneurons, identified by their position in the lateral motor column and soma diameter of at least 20 μm (Takahashi, 1992; Thurbon et al., 1998).

In whole-cell experiments, motoneurons were clamped at −70 mV, the series resistance was between 4 and 10 MΩ (monitored throughout the recording), and it was compensated by 60–80%. The experiment was abandoned if series resistance increased by >20%. Given the typical motoneuron whole-cell capacitance of ∼200 pF, this corresponds to a corner frequency between 0.2 and 0.8 kHz.

The stimulating electrode was a patch pipette filled with external solution and connected to a constant current stimulator (DS-3; Digitimer). After establishing the whole-cell configuration, the stimulating electrode was placed in the ventral part of Rexed's lamina VII, in which Renshaw cell density is highest (Fyffe, 1990; Geiman et al., 2000; Gonzalez-Forero et al., 2005). This region is distinct from the rest of lamina VII because it contains myelinated axon collaterals from motoneurons, and therefore it appears darker under DIC optics.

The slice was continuously perfused with 3 mm kynurenic acid or a combination of 40 μm AP5 and 10 μm CNQX to block fast glutamatergic transmission. SR-95531 was initially added at a concentration of 3 μm, which is sufficient to block fast GABAergic transmission (Chéry and de Koninck, 1999; Lindquist et al., 2005) but has no effect on glycinergic currents. The mix of antagonists allowed isolation of glycinergic responses evoked by electrical stimulations, but prevented the detection of possible glycine and GABA corelease in some of the recordings (Jonas et al., 1998). The glycinergic nature of the synaptic response was confirmed at the end of the experiment by complete block of the IPSCs after application of 0.5 μm strychnine (data not shown). N-Methyl-N-[3-[4-trifluoromethyl)phenoxy]-3-phenylpropyl]glycine (ORG-24598) (10 μm) was diluted from a stock solution. The concentrations of SR-95531 used for the dose–inhibition curve were obtained by dilution of 1 mm stock (in extracellular solution) prepared on the day of experiment and sonicated for 10–20 min to ensure complete dilution.

To evoke a postsynaptic potential, the stimulation intensity was gradually increased until an evoked IPSC (eIPSC) could be detected on the recorded motoneuron (typical latency, 1.5–2 ms). The stimulation strength was fixed at 1.5 times threshold (typically 3–5 μA), which resulted in stable amplitudes of the eIPSCs. An additional increase of the stimulation intensity did not change the size of the IPSC up to values of three to four times threshold, when additional fibers were probably recruited (detected as an increase in the amplitude as well as in the rise time of the response) (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). If additional fibers were recruited with an increase of less than three times threshold, the stimulating electrode was moved to another location. Stimuli were delivered every 5–10 s.

Outside-out patches.

Pipette resistance for outside-out experiments was between 6 and 8 MΩ (same internal solution as whole-cell experiments). After excision, the patch was brought in proximity of a theta tube (14-072-01; Hilgenberg) with tip diameter of ∼150 μm driven by a piezo-stepper (Burleigh Instruments). Glycine or SR-95531 was applied through the double-barrel system. At the end of the experiment, the patch was ruptured and the exchange time measured by applying a diluted extracellular solution (100–200 μs, 10–90% rise time).

Glycine was applied every 7 s for short (200 ms) pulses and every 50 s for long ones. For the analysis of outside-out experiments, 10–40 sweeps were averaged. The rate constants corresponding to the desensitization states in the scheme of Figure 1H and the binding and unbinding rates of SR-95531 were determined using ChanneLab software (Synaptosoft) by optimizing the rate constant with a Simplex algorithm. The open tip potential (appropriately scaled) was used as an input for the concentration profile of both agonist and antagonist.

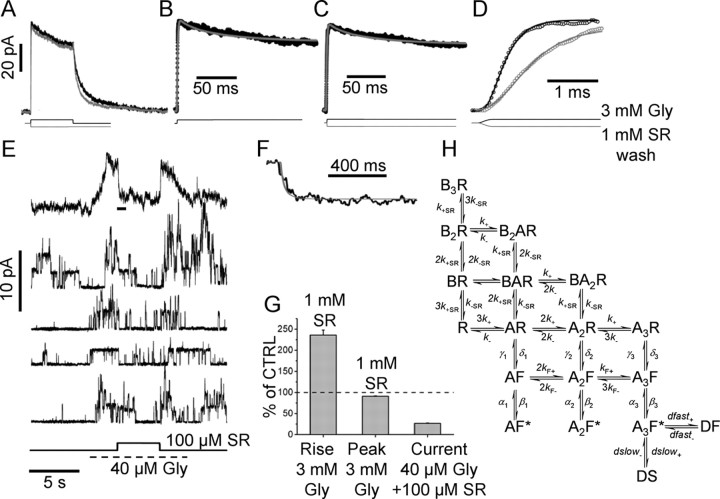
Figure 1.

The determination of binding rates for SR-95531 from patches excised from motoneurons. A, The response to a 3 mm, 200 ms glycine application (black trace; average of 15 sweeps) is shown superimposed to the response to the same glycine pulse, but after preequilibration with 1 mm SR-95531. B–D show current responses overlapped with fits. B, The current responses were fitted to the model of H that extends the scheme by Burzomato et al. (2004) to include two desensitized states and the binding of a competitive antagonist (B). The desensitization rates from states DF and DS were free variables [all the other rates were fixed to the values determined in the study by Burzomato et al. (2004)]: α₁ = 3400, β₁ = 4200, α₂ = 2100, β₂ = 28,000, α₃ = 7000, β₃ = 129,000, γ₁ = 29,000, δ₁ = 180, γ₂ = 18,000, δ₂ = 6800, γ₃ = 900, δ₃ = 20,900, k₋ = 300, k₊ = 0.59 × 10⁶, k_F− = 1200, k_F+ = 150 × 10⁶ (all in s⁻¹ or m⁻¹s⁻¹, where appropriate). B, The continuous gray line shows the fit to the data (black dots) in control obtained by optimizing the four desensitization rates. The same desensitization rates give a good description of the current trace after wash of SR-95531 (C). D, Expanded timescale of the rising phase of the response in control (black dots) and after preincubation and wash of SR-95531 (gray dots). The response after wash of the antagonist is slowed down. The rising phase of the control response was fitted using the k₊ for glycine as a free parameter (black continuous line). Once k₊ was determined, all rates were fixed and the two traces were simultaneously fitted using k_−SR as the only free parameter (continuous gray line). E, The four individual sweeps (bottom traces) show single-channel activity in the presence of 40 μm glycine and the effect of jumping into 100 μm SR-95531 (indicated by the step below the current traces). SR-95531 at 100 μm reduces the frequency and duration of the single-channel activation. Note that glycine was applied by simply switching on the perfusion line within the double barrel of the theta tube, and therefore some variability in the timing of the application results in channels opening well before the application of the antagonist (see, for example, the first individual sweep). The top trace in E is the average of 26 individual sweeps. The timescale expansion of the part of the averaged trace indicated by the horizontal bar is shown in F (black line) superimposed to a fit obtained by keeping all the rate constants fixed to the average values determined previously and using only k_+SR as a free parameter. The bar plot in G shows the increase in rise time and decrease in peak current induced by preincubation with 1 mm SR-95531 (expressed as percentage of control) and the 27% residual current in the presence of 40 μm glycine and 100 μm SR-95531. Error bars indicate SDM.

Data analysis and fitting.

The time course of evoked IPSCs was fitted from 20% of rise time with an empirical function with an exponential rise and a single exponential decay of the following form:

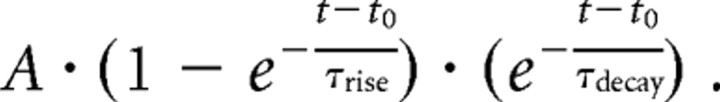The mean amplitude was calculated as the average of individual events (excluding failures when present). Evoked events with amplitude less than five times the SD of the baseline noise were considered failures. Rise times (20–80%) of individual events were measured in each recording condition, and their averages were compared. Miniature events were recorded in the presence of 0.5 μm tetrodotoxin (TTX) and analyzed using Mini-Analysis software (Synaptosoft).

The fit that determines the values of Gly_peak and τ was performed with a fitting routine written in Interactive Data Language (IDL) (from ITT Visual Information Solutions). The time course of glycine in the cleft was described by the following function:

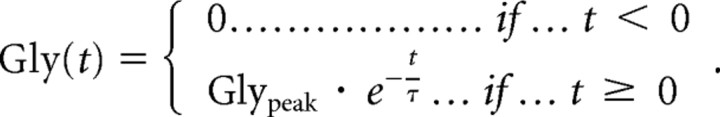The Q matrix (Colquhoun and Hawkes, 1982) corresponding to the model of Figure 1H was used to solve the differential equation that describes the current time course (Colquhoun et al., 1997) as follows:

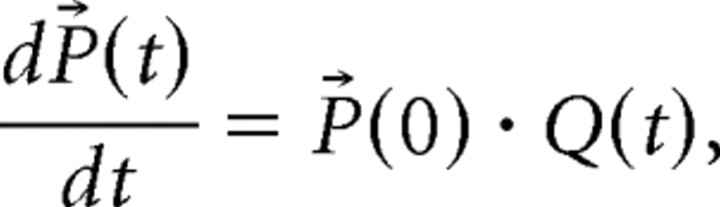where P⃗(t) is the row vector of occupancies of each of the 18 states of the model. The current amplitude was calculated as the sum of the occupancies of the three open states. Because Q(t) depends on time (through the time dependence of the glycine concentration), the solution is not a simple exponential of the Q matrix and therefore it was evaluated numerically using an adaptive Runge–Kutta integration (RK5). For each concentration of SR-95531, the amount of inhibition was calculated, and Gly_peak and τ were optimized using a Levenberg–Marquardt algorithm to minimize the sum of squared deviation (SSD) from the data points. The errors on parameter estimates were calculated as the square root of the diagonal element of the information matrix (the inverse of the Hessian matrix of second derivatives of the SSD with respect to the free parameters). The correlation coefficient was determined as the covariance divided by the square root of the product of the individual variances. Because of the high correlation coefficient (r = −0.999) (see Results), we expressed the uncertainty on parameter estimates by determining a confidence region as the region in which SSD < SSD_min + t², where t = 2.57 is the value of Student's t statistic for five degrees of freedom (t² is used instead of χ² because the errors are estimated from the data) (Colquhoun, 1971). The search in the parameter space was limited to values of Gly_peak between 0.1 and 100 mm and τ between 0.1 and 10 ms. When the values of inhibition by SR-95531 were calculated over the parameters space (see Fig. 7; supplemental material, available at www.jneurosci.org), the above ranges for Gly_peak and τ were divided into 30 equally spaced points on a logarithmic scale and the amount of inhibition was calculated over the resulting 30 × 30 grid.

Figure 7.

The effect of block of the glial glycine transporter on the evoked IPSCs. A, Evoked IPSC in control were inhibited by 35%. After wash, ORG-24598 was applied. This resulted in an increase in the amplitude of eIPSCs. Subsequent application of 50 μm SR-95531 resulted in a reduced inhibition of the eIPSC (14% of its value with ORG-24598 alone). The overall effect of ORG-24598 on the amplitude of eIPSC with and without 50 μm SR-95531 is shown in B. Block of the glycine glial transporter strongly reduces the inhibition induced by 50 μm SR-95531, indicating that the transporter has a role in determining the time course of glycine in the cleft. Error bars indicate SDM. C, The average eIPSC in the presence of ORG-24598 (superimposed to the scaled eIPSC in control) has a prolonged decay time that is fitted with a single exponential with time constant of 5.7 ms. D, Application of 50 μm SR-95531 failed to change the decay time in all the cells tested. E, The eIPSCs rise time increased in the presence of ORG-24598 (compare black and dark gray lines) but did not change when 50 μm SR-95531 and ORG-24598 were subsequently applied (G, light gray line). F, Pooled cumulative distribution of rise times for 10 cells (F) and individual values in each experiment (G).

Calculated IPSCs were generated by solving the above equation using the values of Gly_peak and τ indicated in the text. Rise and decay times of calculated IPSCs were measured after applying a digital low-pass filter with a cutoff frequency of 0.5 kHz (similar to that imposed by the recording system).

Data are expressed as mean ± SD of the mean (SDM), with the exception of rate constants, which are expressed as mean ± coefficient of variation of the mean (CVM).

Results

Measurement of binding rates for SR-95531

On recombinant α1β glycine receptors, SR-95531 acts as a competitive antagonist with an extremely fast unbinding rate (k_−SR ∼ 3000 s⁻¹) (Beato et al., 2007). To use SR-95531 as a tool to determine the time course of glycine in the synaptic cleft, it is first necessary to determine its binding rates onto native GlyRs. Both somatic and synaptic channels in juvenile motoneurons are mostly α1β heteromeric receptors (Malosio et al., 1991; Takahashi and Momiyama, 1991; Momiyama and Takahashi, 1993). The scheme of activation for α1β GlyRs has been described for recombinant receptors (Burzomato et al., 2004), and its validity for native GlyRs has been confirmed with single-channel experiments performed from spinal motoneurons taken from animals of the same age range as those used in this study (Beato and Sivilotti, 2007). We used kinetic modeling of currents evoked by fast glycine concentration jumps on outside-out patches excised from motoneurons to determine the binding and unbinding rates of SR-95531.

The first step was to estimate desensitization. Responses to a long (200 ms) jump to a saturating glycine concentration (3 mm) (Fig. 1A, black trace) had a desensitized phase that was best described by two exponential components with time constants 8 ± 3 and 140 ± 24 ms (13 ± 7 and 87 ± 7%, respectively; n = 5). The same experiment was repeated after preequilibration with 1 mm SR-95531 (Fig. 1A, gray trace), which was removed simultaneously with glycine application. The responses were similar to those observed in control condition, with a double exponential decaying phase of time constants 7 ± 3 and 130 ± 30 ms (11 ± 6 and 89 ± 6%, respectively). The peak current was only slightly reduced (91 ± 1% of control) (Fig. 1G), indicating that receptors that were bound to the antagonist become available on a timescale of milliseconds.

Because the mechanism fitted to single-channel data does not contain information about desensitization rates, it was first necessary to add extra shut states (i.e., desensitized states) to the scheme of Burzomato et al. (2004) to describe the attenuation of current in the continuous presence of glycine.

Therefore, we used the minimal model that can predict a biexponential decay of the response in the continuous presence of glycine. The model and its rates are taken from Burzomato et al. (2004), but two extra desensitized states are connected to the fully bound state (Fig. 1H). This is only a partial description of the desensitization process because it does not take into account the possibility of more desensitized states from single and doubly liganded states, nor the additional reduction in current observed with longer pulses (Singer and Berger, 1999). However, the purpose is not to obtain a full description of the desensitization process over all the timescales and concentration ranges, but to correct for desensitization only for the protocols used, on a timescale similar to what is expected for the time course of glycine at the synapse.

The control response (Fig. 1B, black dots) was fitted from the onset to the end of the glycine pulse with the four desensitization rates and the binding rate for glycine used as free parameters. All remaining rates were fixed to the values in the study by Burzomato et al. (2004), their Figure 1. The rates for entry and exit into the fast desensitized state (DF) were averaged across patches (n = 5) and were as follows: dfast₊ = 100 s⁻¹ ± 50% (CVM) and dfast₋ = 300 s⁻¹ ± 34% and those for the slow desensitized state (DS) were dslow₊ = 15 s⁻¹ ± 40% and dslow₋ = 22 s⁻¹ ± 28%. Once a satisfactory fit of the desensitization phase was obtained for each patch (Fig. 1B, gray line), the four desensitization rates were fixed and the initial phase of the response in control was fitted using only the binding rate for glycine (k₊) as a free parameter (Fig. 1D, black line in the timescale expansion). The resulting average k₊ was 0.9 × 10⁻⁶ s⁻¹m⁻¹ (31% CVM), in good agreement with the previous single-channel estimate (0.6 × 10⁻⁶ s⁻¹m ⁻¹).

Preincubation with 1 mm SR-95531 significantly slowed down the 20–80% rise time of the current response from a control value of 0.5 ± 0.1 to 1.1 ± 0.2 ms (paired t test, p = 16 × 10⁻⁴) (Fig. 1D, histogram; G) (n = 5). In this protocol, the increase in rise time is a measure of how fast the antagonist unbinds from the channels and was used to estimate k_−SR. The rising phases of responses in control and after agonist preincubation were simultaneously fitted using only k_−SR as a free parameter. The fitted curve described well the slower rise time caused by unbinding of the antagonist (Fig. 1D, continuous line) and gave a value of k_−SR = 2050 s⁻¹ ± 13% (CVM; n = 5). This fit was insensitive to the exact value of the antagonist binding rate, and this was fixed to the value previously determined for recombinant receptors (k_+SR = 1.8 × 10⁻⁷ s⁻¹m⁻¹). The value of k_+SR was also independently estimated from the onset of inhibition induced by 100 μm SR-95531 on the steady-state current produced by 40 μm glycine (Fig. 1E). Because of the very low density of somatic GlyRs (Beato and Sivilotti, 2007), it was always possible to detect single-channel openings after application of glycine. Events were reduced in duration and frequency during wash-in of SR-95531 (Fig. 1E, individual sweeps). Averaging these responses (n = 26 sweeps) resulted in a smoother response that declined to 27 ± 1% (n = 5) of its control value (Fig. 1E, top trace; G, bar plot). The onset of the effect of SR-95531 was fitted to estimate the value of k_+SR leaving all other rates fixed at previously determined values. The timescale expansion of Figure 1F shows the fitted curve (gray line) superimposed to the experimental data; the average value for k_+SR was 1.8 × 10⁻⁷ s⁻¹m⁻¹ ± 9% (CVM; n = 5). The fitted values of k_−SR and for k_+SR give a K_B equilibrium constant of ∼120 μm.

The effect of SR-95531 on evoked synaptic currents

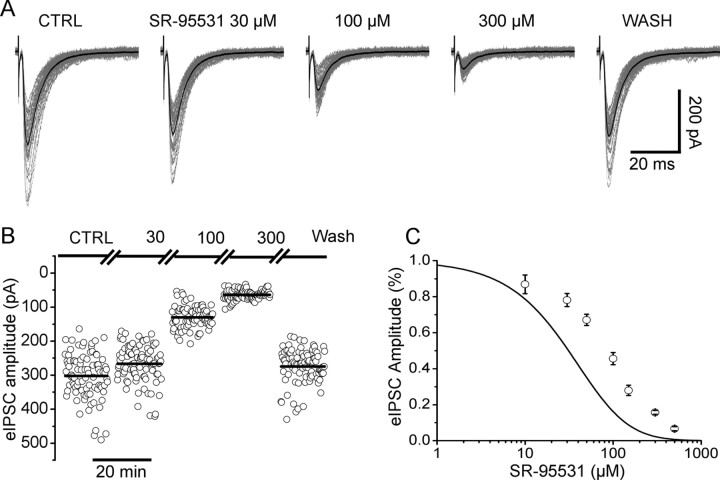
The effect of increasing concentrations of SR-95531 (typically two or three concentrations per cell tested) was studied on evoked IPSCs recorded from lumbar motoneurons. Figure 2A shows that SR-95531 at 30 μm reduced the amplitude of the evoked synaptic current to 88% of its control value. Increasing the concentration to 100 and 300 μm reduced the average eIPSC to 43 and 18% of control, respectively. Amplitudes of individual responses are shown in Figure 2B (80–100 responses; 0.1 Hz). The amplitude remained stable during SR-95531 application and the IPSCs were characterized by a high coefficient of variation (30–40% in the example shown) as also shown previously in similar recording conditions (Takahashi, 1992). SR-95531 was applied to different cells at concentrations ranging from 10 to 500 μm, and a dose–inhibition curve was obtained by pooling values of percentage inhibition with respect to control for each concentration tested (6–20 cells per concentration) (Fig. 2C). Figure 2C also shows for comparison the dose–inhibition curve predicted from the equilibrium K_B (120 μm) obtained from the rates determined from the concentration jump experiments of Figure 1. This curve is calculated assuming that there is no antagonist unbinding. At all concentrations tested, the amount of inhibition observed was much less than this prediction, confirming that unbinding of SR-95531 has a timescale comparable with the lifetime of glycine in the cleft; therefore, a significant amount of antagonist unbinds during the glycine pulse and is replaced by neurotransmitter.

Figure 2.

The effect of SR-95531 on evoked glycinergic IPSCs. A shows the evoked responses in control (left) and in the presence of increasing concentrations of SR-95531. Individual sweeps (>50) are shown in gray, superimposed to the average IPSC (in black). The amplitude of individual responses is shown in B for the three concentrations of SR-95531 tested in this cell. Complete wash of the antagonist was achieved after 5 min. C shows the experimental dose–inhibition curve obtained pooling data from 45 cells. The continuous line is the dose inhibition calculated from the equilibrium constant (K_B = 120 μm). The discrepancy between the equilibrium curve and the observed data indicates that significant unbinding of the antagonist occurs during the pulse of synaptically released glycine. Error bars indicate SDM.

The effect of SR-95531 on the time course of the eIPSCs

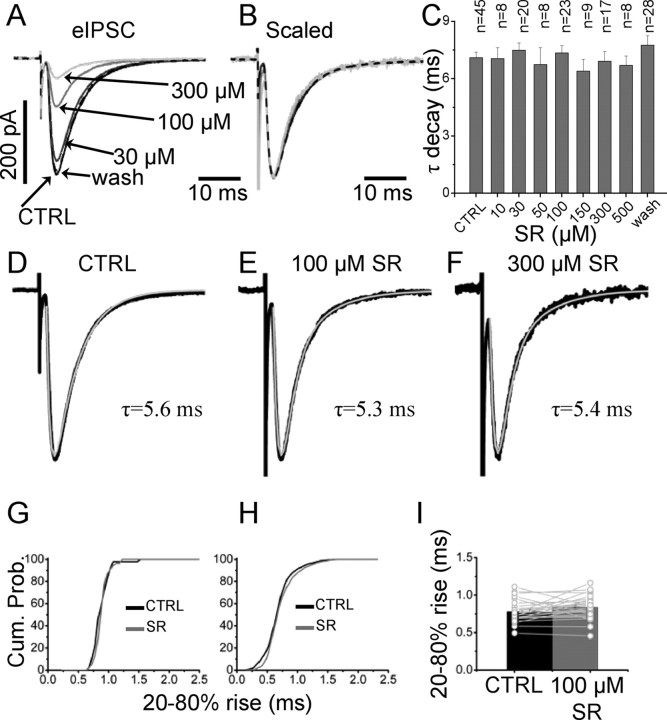
Analysis of the decay time of eIPSC in control conditions and in the presence of increasing concentrations of SR-95531 revealed no significant differences. Figure 3A shows average eIPSCs in control and with three different concentrations of SR-95531. The scaled traces overlap during the decay and the rising phase (Fig. 3B). In all cells, the rise and decay phases were simultaneously fitted with an empirical exponential function (see Materials and Methods) and a single exponential adequately fitted the decay of the eIPSC in control and at all concentration of antagonist (Fig. 3D–F). When a second exponential component was fitted to the control data, the quality of the fit was significantly improved in only 5 of 45 cells in which the relative area of the slow component (12–22 ms) was always <10%. The average value for the decay time constant in control (7.1 ± 0.3 ms; n = 45) and in the presence of SR-95531 is shown in the bar chart of Figure 3C. All differences in decay time in control and in the presence of SR-95531 were not significant (paired t test, p values ranging from 0.3 to 0.9).

Figure 3.

SR-95531 does not alter the time course of eIPSCs. A, Average eIPSCs in control and in the presence of three concentrations of SR-95531 are shown in A. B, C, Overlap of the scaled traces (B) shows that there is no difference in the decay time of the evoked IPSC at different antagonist concentrations (summarized in the bar plot in C for all the concentrations tested; error bars indicate SDM). D–F, The fit of the evoked responses to an exponential pulse function with a single exponential decay and rise (see Materials and Methods). Cumulative distribution of the individual rise times in control (black line) and in the presence of 100 μm SR-95531 (gray line) are shown in G. H, No significant differences in rise times were observed when the cumulative distributions of each cell were pooled together (n = 23). Cum. Prob., Cumulative probability. I, Summary of the average of individual rise times for each experiment in the presence of 100 μm SR-95531. The black and gray bars are the average of 23 experiments in control and with 100 μm SR-95531, respectively.

The rise times of individual evoked events were used to compute the cumulative distribution in each cell. An example for the cell of Figure 3 is shown in Figure 3G, in which no significant difference was found between the rise times in control and in the presence of 100 μm SR-95531 (0.89 ± 0.02 and 0.90 ± 0.02 ms, respectively; p = 0.57, Mann–Whitney unpaired test). Cumulative distributions for 23 cells are combined in Figure 3H, giving an average rise time of 0.79 ± 0.02 ms in control and 0.84 ± 0.03 with 100 μm SR-95531, but this difference was not significant (paired t test, p = 0.08) (individual values are shown in Fig. 3I).

In concentration jump experiments, SR-95531 strongly increased the rise time of the responses (see above) (Beato et al., 2007), and therefore a slowing down of the rise of the eIPSC would be expected. We have no evidence of the location of the recorded synapses and the slow observed rise times could be attributable to electrotonic filtering and also to the intrinsic low-pass filtering of the recording apparatus (see Materials and Methods). These two factors could make subtle variations in the rise times of the eIPSC hard to detect. Alternatively, the observed rise time could be partly determined by release asynchrony at different release sites and/or by simultaneous release of more than one vesicle at the same site. In these conditions, the rise time of eIPSC would be little affected by changes in the rise time of events at individual release sites (Diamond and Jahr, 1995).

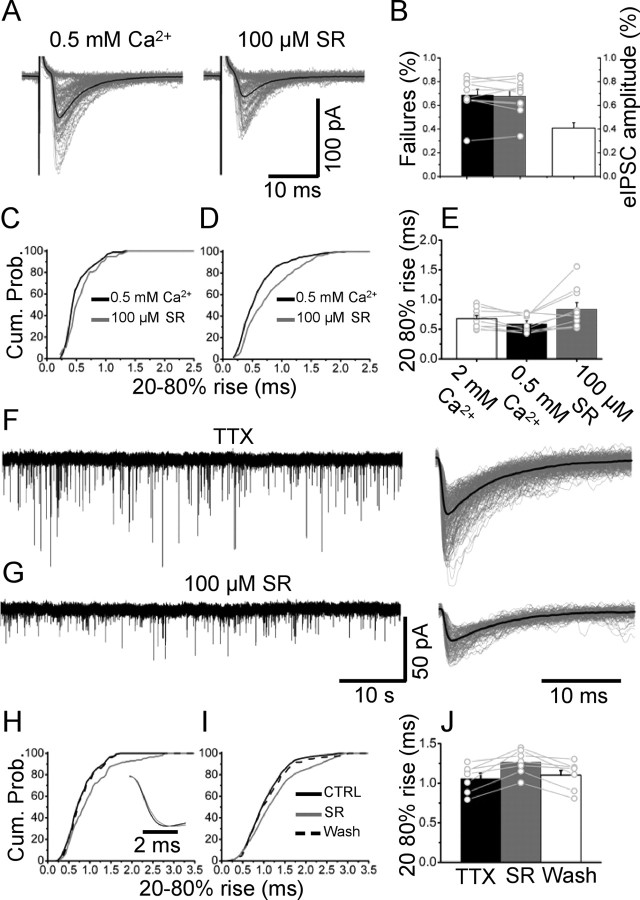
If the latter hypothesis was true, a change in the rise time would be expected if SR-95531 is applied in conditions of very low release probability (in which the release of more than one vesicle is unlikely) and in the rise time of spontaneous quantal events. When eIPSCs were evoked in the presence of 0.5 mm Ca²⁺/3.5 mm Mg²⁺, the average failure rate was 69 ± 5% (n = 10), a value that did not change in the presence of 100 μm SR-95531 (68 ± 5%) (Fig. 4B). Individual sweeps in Figure 4A include 70–90 successful events and 20 representative failures. The rise time of evoked events in low Ca²⁺ solution decreased significantly from 0.68 ± 0.05 to 0.54 ± 0.05 ms (p = 0.015, paired t test; n = 10) (Fig. 4E), suggesting that in normal Ca²⁺ release asynchrony among different release sites plays an important role in determining the rise time of evoked events. The amount of inhibition induced by 100 μm SR-95531 (42 ± 7%) was similar to that observed in normal Ca²⁺ (Fig. 4B). However, the cumulative distribution of individual rise times showed a significant shift to the right (Fig. 4C) in the presence of SR-95531. Within-cell significance (p < 0.05) was observed in 7 of 10 cells, and the overall effect is shown in the combined cumulative plot of Figure 4D, in which all 10 cells are pooled together. The averaged rise time significantly changed from 0.54 ± 0.05 ms in 0.5 mm Ca²⁺ to 0.78 ± 0.12 ms with 100 μm SR-95531 (p = 0.012, paired t test; n = 10), whereas the decay time showed only a small change (from 4.9 ± 0.5 to 4.5 ± 0.6 ms; p = 0.07, paired t test; n = 10). This observation was confirmed in recordings of miniature IPSCs (mIPSCs) (in the presence of 0.5 μm TTX). Spontaneous miniature events in control are shown in Figure 4F. Application of 100 μm SR-95531 (Fig. 4G) reduced the amplitude of mIPSC (48 ± 9% of control; n = 7). The corresponding cumulative distribution of individual rise times shows that SR-95531 slows down the rise time of quantal events (Fig. 4H) and this effect is apparent in the average mIPSCs (aligned over their rising phase) shown in Figure 4H, inset, black and gray traces for control and 100 μm SR-95531, respectively. Washout of SR-95531 (Fig. 4H, dashed line) restored the mIPSC rise times to control values. When data from n = 7 cells were combined (Fig. 4I,J), this effect was highly significant (from 1.06 ± 0.06 to 1.27 ± 0.06 ms; p = 0.004, paired t test), despite the broad distribution of rise times attributable to different locations of release sites. These observations indicate that, in conditions of normal release probability, the rise time of evoked events is determined more by the asynchronous release of vesicles at different release sites than by the kinetic of postsynaptic GlyRs. Therefore, the effect of SR-95531 on the IPSCs rise time can be unmasked only when a single or few vesicles are released, as is the case for mIPSC and eIPSCs in low Ca²⁺, respectively.

Figure 4.

The effect of SR-95531 on eIPSCs at low release probability. A, IPSC were evoked with a reduced (0.5 mm) concentration of Ca²⁺ in control (left) and in the presence of 100 μm SR-95531 (right). B, In these conditions, the failure rate was typically ∼60% and was not affected by application 100 μm SR-95531 (black and gray bars). The amplitude of the evoked events was reduced by the same amount as in control conditions (white bar). Lowering Ca²⁺ decreased the rise time of evoked events (E, white and black bars). Application of 100 μm SR-95531 in conditions of lowered release probability increased the rise time of individual events, as shown by the cumulative distribution in C. This effect was significant across cells (pooled distribution of rise times in D and individual and average values in E, black and gray bars; n = 10). F, G, Continuous recording of quantal events before (F) and after (G) application of 100 μm SR-95531 (individual sweeps and their average are shown on the right of each trace). The rise time of individual events is prolonged by the antagonist, as shown for one cell in H. Cum. Prob., Cumulative probability. The pooled distributions in seven cells and their individual and average values of rise time are reported in I and J, respectively. Error bars indicate SDM.

Presynaptic effects of SR-95531

It is possible that high concentrations of SR-95531 have nonspecific effects on the probability of release. This possibility was investigated by analyzing the paired-pulse facilitation of a train of four eIPSCs (30 ms interval) in control (Fig. 5A, black trace) and in the presence of 100 μm SR-95531 (Fig. 5D, gray trace). As shown in the scaled average (Fig. 5A, right), the facilitated pulses are inhibited less than the first one, and as a consequence the paired pulse ratio for the four consecutive eIPSCs increases in the presence of SR-95531. The second pulse was inhibited less than the first one only in three of eight cells, and in fact the overall average amplitude reductions were not significantly different for the first and second pulses in a train (Fig. 5B) (44 ± 9 and 47 ± 9% of control, respectively; p = 0.35, paired t test; n = 8). However, a significant difference was observed for the third and fourth pulses, which were reduced to 56 ± 9 and 65 ± 10% of control, giving rise to a significant increase in paired-pulse facilitation (Fig. 5C) (p = 0.05 for both pulses, paired t test; n = 8). This could be attributable either to an unspecific effect of SR-95531 on the release probability or to the occurrence of multivesicular release in conditions of high probability of release (as occurs during repetitive trains of stimulations), which exposes the synapses to a higher glycine concentration. To test this, we repeated the trains of stimuli in a low Ca²⁺ solution (1 mm Ca²⁺/3 mm Mg²⁺) (Fig. 5D) (average of >100 sweeps). In these conditions, all four pulses in the train were inhibited by the same amount (between 42 and 46%) (Fig. 5E) and the paired-pulse ratio did not increase in the presence of 100 μm SR-95531 for any of the pulses in the train (Fig. 5F). Therefore, in normal Ca²⁺ solution, the decreased effectiveness of SR-95531 in blocking the later pulses in a train can be attributed to a higher concentration of glycine in the cleft when the release probability is increased by repetitive stimulation.

Figure 5.

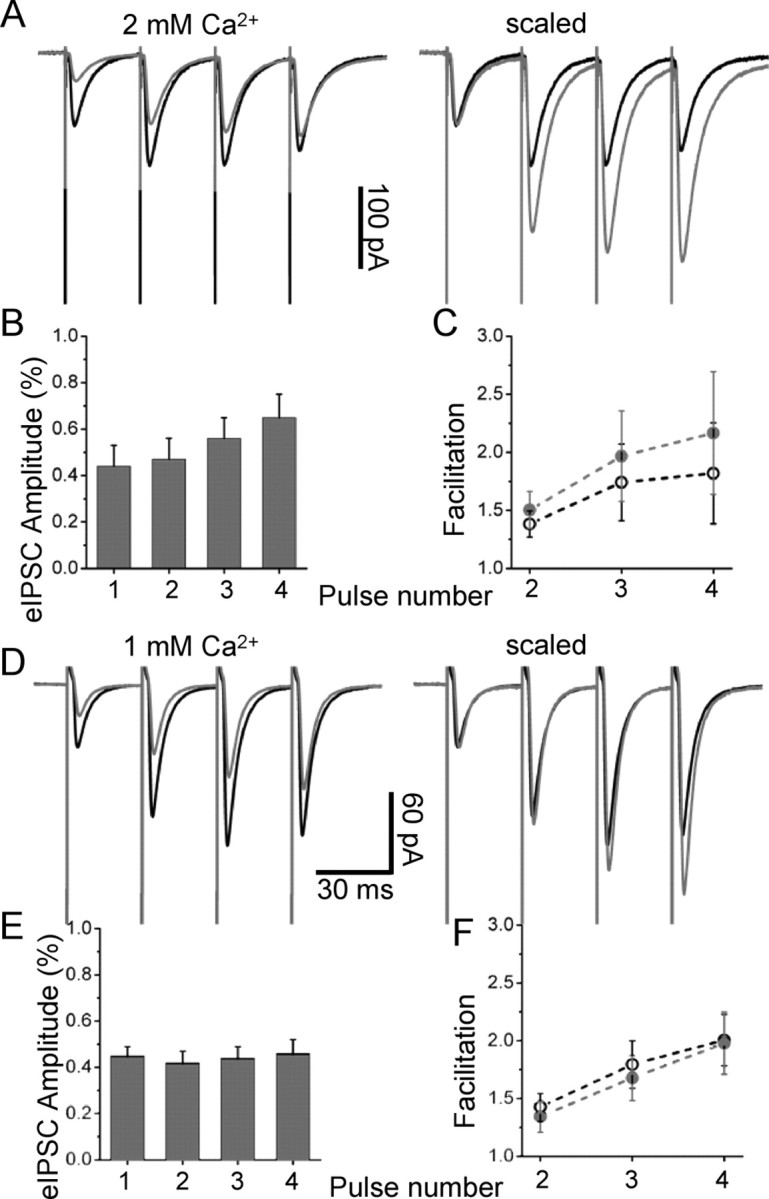
SR-95531 does not have presynaptic effects. A shows paired-pulse facilitation over four stimulations (every 30 ms) in control (black trace; average of 64 sweeps) and in the presence of 100 μm SR-95531 (gray trace; average of 96 sweeps). B, C, As shown in the scaled average (right) and in the bar chart (B), the facilitated pulses are inhibited less than the first one, and as a consequence the paired-pulse ratio for the four consecutive eIPSCs increases in the presence of SR-95531 (C). The paired-pulse ratios in control (black circle) and in the presence of SR-95531 (gray circles) were significantly different for the third and fourth pulses in the train. D–F, In conditions of low release probability (1 mm Ca²⁺/3 mm Mg²⁺), the increase in paired-pulse facilitation was abolished (D) (average of >100 sweeps) for all the pulses in the train (F, plot), and each pulse in the train was inhibited by the same amount (E), suggesting that, in conditions in which multivesicular release is less likely, SR-95531 does not increase the probability of release. Error bars indicate SDM.

If multivesicular release occurred also after a single stimulus (or at the first stimulus in a train), it could affect our estimate of glycine concentration because if more than one vesicle is released at the same site the postsynaptic GlyRs would be transiently exposed to higher glycine concentrations. However, we observed the same amount of inhibition induced by SR-95531 in normal and 1 mm Ca²⁺ (a condition in which multivesicular release does not occur even during the last pulse in a train) and on quantal IPSC recorded in the presence of TTX (see above). This indicates that, at least after single pulses, multivesicular release is unlikely to occur frequently also in normal Ca²⁺ solution.

This was further confirmed by experiments performed with 0.5 mm Ca²⁺, in which the failure rate was ∼60%. In these conditions, single eIPSCs were reduced to 42 ± 7% of control (Fig. 4B), not different from the reduction observed with 1 or 2 mm Ca²⁺.

We also checked the failure rates in different Ca²⁺ solutions, to rule out the hypothesis of a contribution of a reduced release probability to the reduction in amplitude of the IPSCs induced by SR-95531.

In normal Ca²⁺, glycinergic synapses on motoneurons have a very low failure rate (Takahashi, 1992), and in fact in most cells (34 of 45) no failures were observed in control conditions or in the presence of 10–500 μm SR-95531. In the minority of experiments in which failures were observed in control, the failure rate was increased by SR-95531 application (from 9 ± 5 to 11 ± 4% in seven cells treated with 300 μm SR-95531 and from 5 ± 2 to 6 ± 3% in four cells treated with 500 μm SR-95531), but this increase was not statistically significant (p = 0.1 and 0.5, respectively). When experiments were repeated in the presence of low (1 mm) Ca²⁺ solution, the failure rate did not increase significantly (from 0.38 ± 0.10 in control to 0.42 ± 0.10 with 100 μm SR-95531; p = 0.09, paired t test; n = 11) (data not shown). Similarly, 100 μm SR-95531 failed to increase significantly the failure rate in the presence of 0.5 mm Ca²⁺ (Fig. 4B), indicating that the antagonist has no major effect on the release probability.

Estimating the time course of glycine in the cleft

Having determined the dose–inhibition curve of eIPSC and knowing all the necessary parameters that describe the activation of GlyRs and the binding and unbinding rates for SR-95531, these data were used to estimate the time course of glycine in the synaptic cleft. The glycine pulse was modeled with an instantaneous rise and a single exponential decay; it was therefore determined by two parameters, the peak glycine concentration (Gly_peak) and the time constant describing its clearance from the cleft (τ).

A simple exponential probably does not describe the actual concentration profile to which postsynaptic receptors are exposed, because the solution to the diffusion equations (even in a simplified geometry) is not an exponential (Barbour and Häusser, 1997). However, the resolution of the competitive antagonist method used in this study would not allow us to distinguish between different functional forms describing the concentration profile. Furthermore, the use of a simple exponential allows a direct comparison with previous results obtained from glutamate synapses (Clements et al., 1992; Diamond and Jahr, 1997).

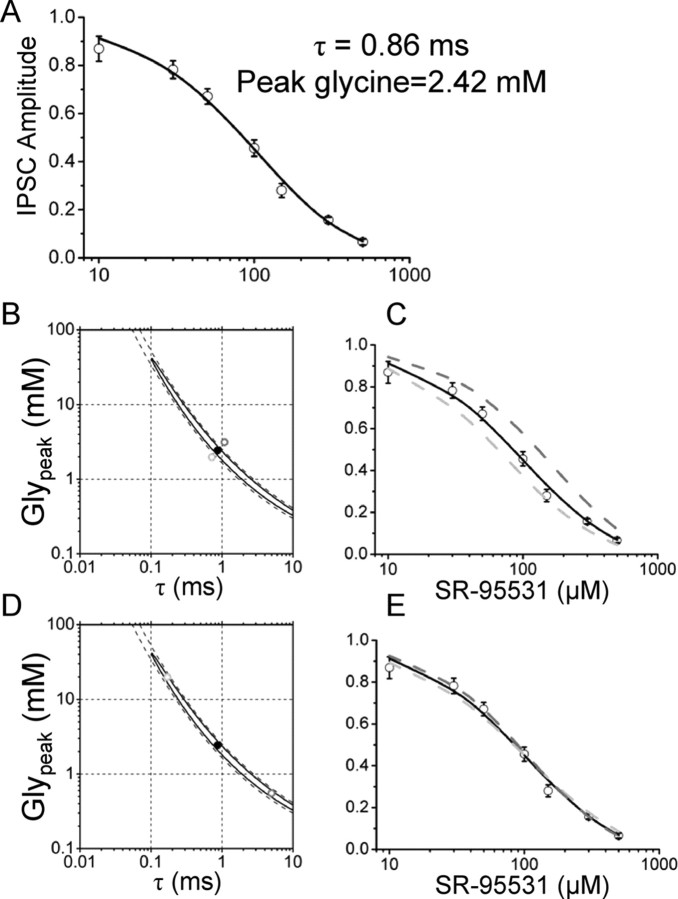
The model of Figure 1H was used to solve the set of differential equations whose solution is the response to a pulse of glycine in control and after equilibration with different concentrations of SR-95531. Gly_peak and τ were systematically varied to minimize the weighted SSD between the observed data and the calculated dose–inhibition curve. The resulting best fit is shown in Figure 6A: the continuous line is the calculated dose–inhibition curve for the optimized parameters that are Gly_peak = 2.4 mm and τ = 0.86 ms. These values provide a good fit of the experimental data with a SSD of 4.3 (better than a least-squares fit with a Hill equation; SSD = 7.2) (data not shown) and are similar to what has been calculated for the glutamate transient at NMDA (Clements et al., 1992) and AMPA (Diamond and Jahr, 1997) receptors. The estimates are very robust to changes in the initial guesses, because changes of three orders of magnitude in the starting values did not affect the final estimates of the two parameters (supplemental Fig. 2, available at www.jneurosci.org as supplemental material).

Figure 6.

Fitting the dose–inhibition curve of eIPSC does not determine the values of Gly_peak and τ. The dose inhibition of Figure 2C was fitted by solving the equations for the scheme of activation of GlyRs using as free parameters the values of Gly_peak and τ that determine the concentration and clearance time of glycine in the cleft. A, Values of Gly_peak = 2.4 mm and τ = 0.86 ms provide a satisfactory fit of the data points. B shows the 95% (continuous line) and 99% (dashed line) confidence interval for the estimate of the two free parameters. The region of confidence extends over two orders of magnitude for both Gly_peak and τ. The calculated dose–inhibition curve corresponding to the best fit is shown again in C as a black line, superimposed to the calculated curves for values of Gly_peak and τ slightly above (B, dark gray dot; C, dark gray dashed line) or below (light gray dot and curve in B and C, respectively) the confidence region. As shown, even a small variation outside the confidence region produces a poor fit of the experimental data. However, when values of Gly_peak and τ were chosen within the confidence region but very far from the estimated values (D, light and dark gray dots), the calculated dose–inhibition curves (E, in light and dark gray) were not significantly different from the one corresponding to the best estimate for Gly_peak and τ. Error bars indicate SDM.

Despite the robustness and goodness of the fit, the joint errors on the parameter estimates calculated from the diagonal elements of the information matrix (see Materials and Methods) gave a very high SD. The calculated values were Gly_peak = 2.4 ± 2.0 mm and τ = 0.86 ± 0.69 ms, leaving Gly_peak and τ undetermined. Such large errors were not attributable to a wide flat region of the SSD surface around the minimum because the individual SD of Gly_peak and τ (calculated as the inverse of the square root of the second derivative of the SSD evaluated at the point of minimum) were 0.1 mm and 0.03 ms, respectively, indicating that along each coordinate the SSD profile is very steep. The reason for the large error was instead a very high correlation coefficient between Gly_peak and τ (r = −0.999), indicating that the data do not contain information that allows independent estimation of the two parameters. In cases like this, in which there is a high correlation, the joint errors reported above have little or no meaning and it is necessary to calculate joint confidence regions instead. This is shown in Figure 6B in which the 95% (continuous line) and 99% (dashed line) confidence regions are shown as a contour plot of the SSD, together with the values of Gly_peak and τ (solid circle) that give the best fit.

Very small changes in the Gly_peak and τ values can produce large, detectable changes in the predicted IPSC inhibition, but only if these changes take Gly_peak and τ outside the confidence region (Fig. 6B,C). Conversely, large changes within the confidence region (Fig. 6D, gray circles) generate a dose–inhibition curve almost identical with the one corresponding to the best estimate of Gly_peak and τ.

This indeterminacy can be intuitively explained by the general observation that an antagonist with a fast k_off can inhibit by the same amount the synaptic response to a long low concentration pulse or to a short high concentration pulse (Diamond, 2001) (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). Therefore, the decrease in eIPSC amplitude alone cannot indicate univocally the time course of transmitter and this causes the high correlation in the estimates of Gly_peak and τ.

Block of glial glycine transporter prolongs the glycine synaptic pulse

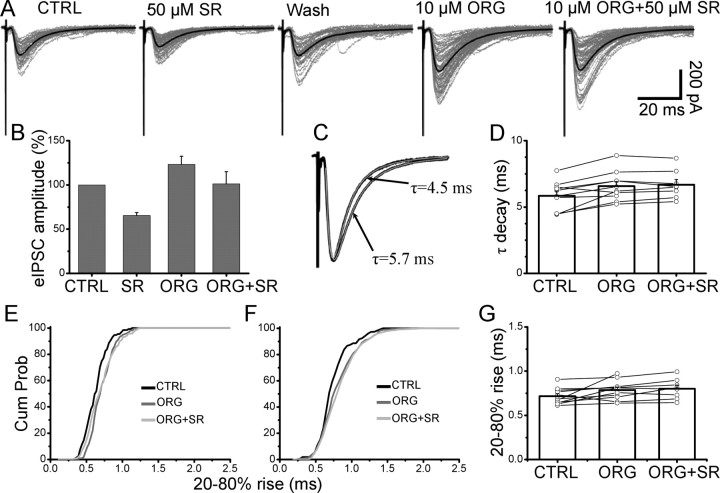
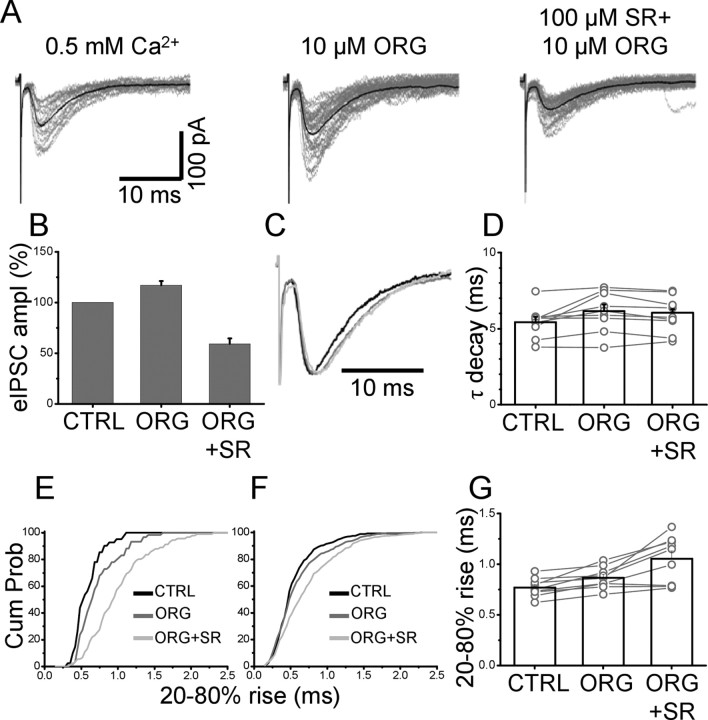
To restrict the range of our estimates, we performed experiments to alter the transmitter concentration in the cleft. It has been shown previously that block of the glial glycine transporter (GlyT-1) changes the time course of spontaneous and evoked IPSCs in lamina X interneurons without affecting their mean amplitude (Bradaia et al., 2004). Therefore, we studied the effect of ORG-24598, a selective blocker of GlyT-1 (Brown et al., 2001), on eIPSCs in lumbar motoneurons.

Figure 7 shows the effect of ORG-24598 on the eIPSCs before and after application of 50 μm SR-95531. In control solution, SR-95531 reduced the amplitude of the eIPSCs to 65% of control. After wash of SR-95531 and full recovery of the eIPSC amplitude, 10 μm ORG-24598 was bath-applied and caused an increase in the amplitude of the eIPSC. Subsequent application of 50 μm SR-95531 resulted in only a slight reduction of the IPSC amplitude (in this cell, 86% of the value observed in ORG-24598 alone). On average blocking, the GlyT-1 transporters increased the eIPSC amplitude to 123 ± 9% of control (Fig. 7B) (n = 10). After application of 50 μm SR-95531 in the continuous presence of ORG-24598, the eIPSC amplitude was 102 ± 13% (n = 7) of its control value (Fig. 7B). This indicates that, in the presence of ORG-24598, SR-95531 is less potent at inhibiting the eIPSCs than in control solution: the eIPSC amplitude is in fact reduced by only 22 ± 5% (ORG-24598 vs ORG-24598 and 50 μm SR-95531), compared with 35 ± 3% (control solution vs 50 μm SR-95531 alone).

Block of the glial transporter slowed the eIPSC monoexponential decay (increasing its τ from 5.8 ± 0.3 to 6.6 ± 0.3 ms; p = 0.001; n = 10) (Fig. 7C). The decay time constant was not affected by subsequent application of 50 μm SR-95531 (6.7 ± 0.4; n = 8; p = 0.7, paired t test) (Fig. 7D).

In the presence of ORG-24598, the value of individual rise times was also increased: an example from an individual cell is shown in Figure 7E, in which the cumulative distribution of individual 20–80% rise times in control (black line) is compared with that observed in the presence of ORG-24598 alone (dark gray) or in combination with 50 μm SR-95531 (light gray). Block of the glial transporter significantly increased the rise times of evoked events in 8 of 10 cells (p < 0.05, Mann–Whitney unpaired test). However, subsequent application of 50 μm SR-95531 failed to further prolong the rise times (p values ranging from 0.1 to 0.8 in eight cells). This was confirmed by pooling the cumulative distribution of all the cells tested (Fig. 6F). The average values of rise times in control and ORG-24598 were 0.72 ± 0.03 and 0.79 ± 0.03 ms, respectively (p = 0.04; n = 10; paired t test). This value was not significantly increased by application of 50 μm SR-95531 (0.80 ± 0.11 ms; p = 0.08; n = 8; paired t test), similar to what was observed in control conditions.

Because the effects of SR-95531 on the rise times were revealed only in conditions of low probability of release, the experiments on block of the glial glycine transporter were repeated in low Ca²⁺ (0.5 mm Ca²⁺/3.5 mm Mg²⁺) extracellular solution. Responses to single stimulation exhibited a very high failure rate (up to 80%). As shown in Figure 8A, in these experimental conditions the effects of ORG-24598 were similar to those observed in normal Ca²⁺: the amplitude of eIPSPs was enhanced to 117 ± 4% of control (n = 9), whereas in the presence of 100 μm SR-95531 it was 59 ± 5% of its value with ORG-24598 (Fig. 8B). The effect of SR-95531 in the presence of ORG-24598 was not compared with its effect in control conditions in the same cells, because, as a result of the high failure rate, typically at least 200–300 sweeps had to be collected for each experimental condition. However, the decrease in amplitude induced by SR-95531 after block of the glial transporter was much smaller than that observed in control conditions in the previous experiments (46 ± 3% of control; n = 23; p = 0.04, unpaired t test). Similar to what observed in normal Ca²⁺ solution, ORG-245978 prolonged the decay time of the eIPSCs as shown from the average traces in Figure 8C. The mean decay time was increased from 5.4 ± 0.3 to 6.1 ± 0.4 ms (n = 9; p = 0.03, paired t test), whereas application of SR-95531 failed to change the decay time (98 ± 2% of its value in the presence of ORG-24598) (Fig. 8D).

Figure 8.

The eIPSC rise times are increased by both ORG-24598 and SR-95531 in conditions of low release probability. A, Individual eIPSCs (with their average superimposed and failures omitted) in 0.5 mm Ca²⁺ and after perfusion with ORG-24598 (middle) and 100 μm SR-95531 (right). B, ORG-24598 enhances the response, which is inhibited by 100 μm SR-95531 less than in control conditions (bar chart). Error bars indicate SDM. C, D, Overlap of average traces (C) shows that the decay time is prolonged by application of ORG-24598 (dark gray) and is not changed by SR-95531 (light gray; individual values in D). E, The eIPSC rise time is prolonged by ORG-24598 (dark gray) and further prolonged by 100 μm SR-95531 (light gray). This is summarized in the pooled distributions from nine cells (F) and the individual values in G.

In this set of experiments, the rise time in normal Ca²⁺ was 0.85 ± 0.05 ms and was significantly accelerated to 0.77 ± 0.03 ms when the external Ca²⁺ concentration was reduced to 0.5 mm (n = 9; p = 0.04, paired t test). Application of ORG-24598 in low-Ca²⁺ solution slowed down the rise time to 0.87 ± 0.04 ms (n = 9; p = 0.003, paired t test), but, in contrast to what was observed in normal Ca²⁺, the effect on the rise time of SR-95531 was strongly enhanced, with an average rise time of 1.00 ± 0.08 ms (n = 9; p = 0.008, paired t test). Within-cell significance (Mann–Whitney unpaired test) was achieved in six of nine cells (ORG-24598 vs control) and seven of nine cells (SR-95531 with ORG-24598 vs ORG-24598 alone). An example of cumulative distributions of rise times in the three experimental conditions is shown in Figure 7E for the cell shown in Figure 7A. The effect of rise times was highly significant when all nine cells were combined (p = 0.008, paired t test) (cumulative plots are shown in Fig. 7E; individual values and averages are shown in Fig. 7G).

These data show that postsynaptic GlyRs are not saturated by evoked release. Without a precise knowledge of the geometry of the synaptic cleft and of the density, location, and binding rates of the glycine transporter, it is difficult to predict how the glycine transient is affected by the block of GlyT-1. The most detailed calculation of diffusion within the cleft (Rusakov and Kullmann, 1998a) is based on measured geometric parameters of glutamatergic synapses in the hippocampus. The authors showed the peak concentration of agonist at the postsynaptic membrane is not affected by the concentration of glutamate transporter. However, transporters could accelerate the clearance of glutamate in the first few hundreds of microseconds, a result confirmed by using blockers of glutamate transporters in cultured hippocampal cells (Diamond and Jahr, 1997). In our conditions as well, it is likely that the main effect of ORG-24598 is to prolong the glycine transient, without affecting the peak concentration because an increase in peak concentration would have accelerated the rise time. On the contrary, we observed a slowing of the rise time with both high and low release probability (see above).

The range of Gly_peak and τ compatible with the experimental dose–response curve is extremely wide. However, the above observations of the effect of block of GlyT-1 allow us to narrow the range of concentration profiles compatible with the data.

The real rise time of the IPSCs at a single synaptic site may be different from our observed value because of the possibility of asynchronous release from multiple sites, the filtering of the recording system, and electrotonic filtering of signals coming from distal synapses. All of these factors, whose relative contribution may change from cell to cell, would only make the IPSC rise time we record slower than that at the synapse. Hence the real rise time has to be 1 ms at most.

The rise times of the current responses (filtered at 500 Hz to account for the average bandwidth of the recordings) were calculated over a grid of Gly_peak and τ and the part of the 95% confidence region of Figure 6B that corresponds to values of the rise time >1 ms was excluded (Fig. 9A, bottom dotted curve). This is a very conservative limit, because the actual unfiltered rise time of the eIPSCs would be certainly faster than observed, but it excludes concentrations lower than ∼1.8 mm and consequently τ >1.1 ms.

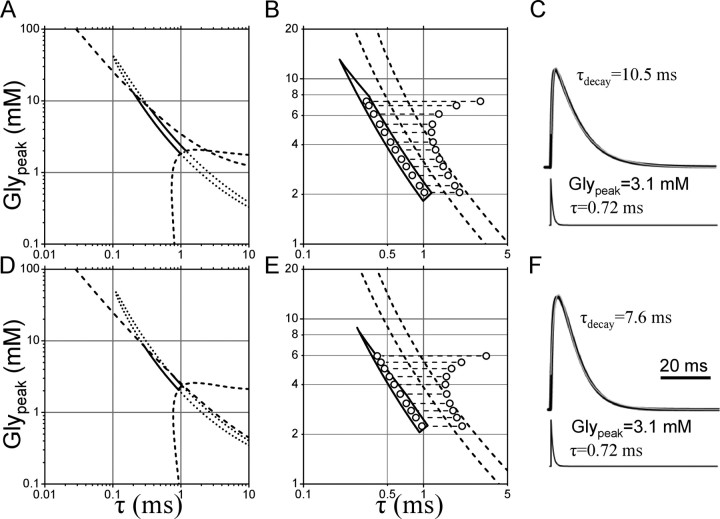
Figure 9.

The values of Gly_peak and τ can be determined by combining the experimental dose–inhibition curve with the observation of the increase in amplitude induced by block of the glial glycine transporter. The continuous line in A represents the 95% confidence limits in the estimate of Gly_peak and τ. The dashed line in the bottom corner of the plot delimits the area below which the rise time of the calculated IPSC would be >1 ms, therefore limiting the acceptable values of Gly_peak and τ to the region above the dashed line. The dashed line at the top of the plot indicates the region in which the amplitude of the calculated current is >80% of its maximum value. The intersection of this line with the 95% confidence region restricts the permitted value of Gly_peak and τ to points below the dashed line to account for the observed >20% increase in amplitude of eIPSC induced by the block of the glycine transporter. B shows the resulting confidence region on an expanded scale. The increase in τ needed to increase the calculated peak current by 23% is shown by the length of the dashed lines joining the dots taken within the confidence region for Gly_peak and τ. To account for the experimental results, the rightmost dots should give rise to calculated IPSCs that are 22 ± 5% inhibited by 50 μm SR-95531 (corresponding to the region delimited by the two dashed lines in B). C shows the time course of an IPSC calculated from the concentration profile of glycine shown at the bottom of the trace and the rates of the model in Figure 1H. The calculated IPSC is filtered at 500 Hz and fitted with a single exponential pulse function. The same analysis was performed using the model of Figure 1H without the extra desensitized states. The 95% confidence region comprises an area similar to the one shown above (compare D with A). Only the line delimiting the region corresponding to amplitude values <80% of the maximum is slightly shifted with respect to the one calculated in A. However, this does not affect the shape and boundaries of the remaining confidence region (shown on an expanded scale in E). Only values of Gly_peak < 3.5 mm and τ > 0.6 ms can predict the 23% increase in amplitude observed with ORG-24598 together with the 22% inhibition observed with 50 μm SR-95531. F, Same as in C, but with desensitized states omitted.

We can further restrict the possible values of Gly_peak and τ because of the observed increase in the amplitude of eIPSCs after block of GlyT-1. The peak amplitude (expressed as the occupancy of all the open states) was calculated over all values of Gly_peak and τ. The values above the transversal dashed line in Figure 9A correspond to occupancies >80% of the maximum and therefore incompatible with the 23% increase in peak amplitude observed in the presence of ORG-24598. This second constraint excludes values of Gly_peak >13 mm, because they would produce a response that is too close to saturation. Following the shape of the 95% confidence interval, this corresponds to τ values >0.2 ms. Even so, the revised interval (Fig. 9B, closed contour) are still wide, ranging from 1.8 to 12 mm for Gly_peak and from 0.2 to 1.1 ms for τ.

If we assume that block of GlyT-1 only prolongs the clearance time of transmitter, we can add a third constraint (Fig. 9B) by calculating the increase in τ needed to produce the observed 23% increase in the synaptic response. These longer τ values have to be compatible with the 22 ± 5% decrease in eIPSC amplitude produced by SR-95531 in the presence of ORG-24598. The increment in τ is shown by dashed horizontal lines joining the open circles in Figure 9B, calculated for sample responses generated by a discrete set of Gly_peak and τ values (indicated by circles in Fig. 9B) included in the confidence region. The two oblique dashed lines delimit the region compatible with the observed effects of SR-95531.

This excludes all concentrations >4 mm because above that level the increase in τ necessary to achieve a 20% enhancement of the response would produce a current that is less inhibited by 50 μm SR-95531 than what was observed. It follows that, to describe the data, the peak glycine concentration must be within the 2–4 mm range. As shown by the confidence limits of Figure 9B, this corresponds to values of τ between 1 and 0.5 ms.

These estimates for the time course of the glycine concentration at the synapse predict an IPSC decay time constant of 10 ms (Fig. 9C). This is somewhat slower than both the experimental value (7.1 ± 0.3) and the value of 7 ms predicted from the model and rates determined from single-channel experiments (Burzomato et al., 2004). The discrepancy with the prediction from the single-channel model is attributable to the fact that the mechanism used in the present study incorporates two additional desensitized states, the faster of which is expected to slow the current decay. These desensitized states and their entry and exit rates could only be characterized in excised patches, by analyzing concentration jumps. Nevertheless, the kinetics of GlyRs is known to be different in excised patches from that in the cell-attached configuration (Fucile et al., 2000) (S. J. Pitt, L. G. Sivilotti, and M. Beato, unpublished observations), and it is impossible to determine whether the desensitization properties of synaptic receptors resembles that of receptors in excised or cell-attached recordings.

Therefore, we repeated our determination of the confidence region omitting the desensitized states from the model. From the fit of the dose–inhibition curve, we obtained estimates of Gly_peak = 3.3 mm and τ = 0.64 ms. Again, the shape of the confidence region showed correlation between the two parameters and it stretched to include values over an order of magnitude around the best estimate (Fig. 9D). The dotted lines in Figure 9D indicate the regions that were excluded on the basis of the observed rise time and from the requirement for the postsynaptic channels to be far enough from saturation to account for the 23% increase observed in the presence of ORG-24598.

In Figure 9E, the increase in τ necessary to produce a 23% enhancement of the eIPSC is calculated and superimposed to the region of values of Gly_peak and τ that predict a 78 ± 5% inhibition in the presence of 50 μm SR-95531 (as observed experimentally).

If desensitization is not included in the model, the range of acceptable values for Gly_peak is approximately between 2.2 and 3.5 mm (with corresponding values of τ between 0.9 and 0.6 ms). This is not very different from the estimates obtained from a model that includes desensitization and confirms that the average concentration pulse seen by GlyRs has a fast clearance time (<1 ms) and the Gly_peak is close to a value of ∼3 mm.

When desensitization is not included in the model, the time course of the calculated synaptic responses is in better agreement with the observations, with a monoexponential decay ranging from 7.3 to 7.7 ms (as Gly_peak increases, see the calculated sample trace in Fig. 9F). The increase in decay time in the presence of ORG-24598 is also well predicted and ranges from 8.3 to 9.8 (∼10% more than control, as observed). The model of Figure 1H also predicts a small decrease in decay time in the presence of SR-95531 (from 7.6 to 7.2 ms in the presence of 100 μm SR-95531 for the time course calculated in Fig. 9F). This could account for the small difference in decay observed in the experiments with 0.5 mm Ca²⁺ (see above), but was not detected in normal Ca²⁺, possibly because of release asynchrony affecting the time course of eIPSCs.

Because the gating rates for glycine are very fast, the conclusions above are insensitive to the exact values of the opening and shutting rates. However, we investigated the sensitivity of our conclusions to the exact values of the binding rates for glycine and for SR-95531. The k₊ for glycine previously determined from single-channel experiments was adjusted to 0.9 × 10⁻⁶ s⁻¹m⁻¹ in the present study to account for the observed rise time in concentration jumps. Changes to this value within the experimental error (30%) did not produce any change in the calculated confidence region and only a minor shift in the calculated rise time. This had the effect of changing the lower limit on Gly_peak from 1.8 to 1.6 mm (decreasing k₊) or to 1.9 mm (increasing k₊), a difference that does not affect the above conclusions. Whereas the binding rate of SR-95531 was found to be identical with what has been estimated from recombinant GlyRs, the unbinding rate was 30% slower (Beato et al. 2007). Repeating the calculation of the confidence region using the previously determined value for k_−SR (∼3000 s⁻¹) produced a parallel shift in the confidence limit of ∼320 μm in the curve shown in Figure 9. Similarly, a 20% change in k_+SR (the experimental error in the present experiments) produced only a parallel shift in the confidence limits that was always within 200 μm (in either direction) of the curves of Figure 9. Therefore, the present estimates are robust with respect to changes of individual rate constants within the experimental errors.

Discussion

We have shown that concentrations of SR-95531 higher than those normally used to block GABA_A receptors can antagonize the glycinergic currents recorded in outside-out patches or as eIPSCs on motoneurons. Following the method first used by Clements et al. (1992), we have fitted the experimental dose–inhibition curve for the eIPSCs using a detailed activation scheme for GlyRs and the measured binding rates for SR-95531, leaving as the only free parameters the peak glycine concentration and its clearance time course. This approach revealed degeneracy in the parameter space, with highly correlated estimates of Gly_peak and τ; therefore, only broad confidence intervals could be defined for the two fitted parameters. This is in agreement with the observation by Diamond (2001), who showed that the degree of inhibition of a competitive antagonist alone is not sufficient to determine simultaneously the peak concentration of transmitter and its time course. A major refinement of the estimates for Gly_peak and τ can be derived from the knowledge of the activation mechanism of postsynaptic glycine receptors, combined with an experimental manipulation (block of glycine transporter) that affects the clearance time of glycine in the cleft. We have shown here that Gly_peak is between 2.2 and 3.5 mm and that glycine is cleared from the cleft with a time constant between 0.9 and 0.6 ms. The present data suggest that the peak concentration of glycine produced by synaptic release is higher than that of glutamate at NMDA postsynaptic channels in hippocampal cultured neurons (in which only data from the dose–inhibition curve were used). However, our estimate is closer to that of Diamond and Jahr (1997) for glutamate at AMPA synapses in the same preparation, in which the fast competitive antagonist technique was used together with data obtained with glutamate transporter block. The values of 3 mm and 0.7 ms for the transmitter concentration and its clearance time are compatible with realistic modeling of diffusion at glutamatergic synapses (Trommershäuser et al., 1999). However, the lack of modeling studies of diffusion with realistic geometric constraints on glycinergic synapses onto motoneurons does not allow an independent test of our estimates of Gly_peak and τ.

In this study, we applied the oversimplification of describing the transmitter pulse with an instantaneous rise and a single exponential decay. Given the unbinding rates of the SR-95531, very few molecules would dissociate in the first 100 μs of the pulse, and therefore using a fast rising function for the initial phase of the transmitter pulse would have no effect on the calculated responses. Our choice of a single exponential decay to model the time course of glycine contrasts with the double exponential waveform proposed for glutamatergic synapses (Clements, 1996; Diamond and Jahr, 1997; Diamond, 2001). A double exponential shape for the decay phase of the time course of transmitter could reflect either a spillover component originating from neighboring synapses or diffusion of transmitter (at lower concentration) to distal receptors located in the perisynaptic region. In either case, SR-95531 should inhibit more efficiently the low concentration component, and therefore we should have observed a faster deactivation of the synaptic response [as shown by Diamond (2001)]. In contrast, in our experiments the deactivation time in the presence of any concentration of antagonist was not different from control, indicating that a monoexponential glycine pulse is a good description of the average behavior of the synapses. This is further supported by the observation that, even in conditions in which spillover could be potentially enhanced (i.e., after block of GlyT-1), equilibration with the antagonist does not affect the decay time of the eIPSCs. It is also important to add that, given the degeneracy of the two parameters used, a fit with more parameters could not have given any meaningful result.

The estimate of the glycine time course in the cleft relies on how accurately our model and rates describe GlyRs activation. Model and rates were obtained from single-channel analysis of recombinant α1β GlyRs (Burzomato et al., 2004). These rates were confirmed with single-channel experiments on somatic GlyRs of lumbar motoneurons (Beato and Sivilotti, 2007), but there is no guarantee that the properties of somatic receptors are the same as those of synaptic ones. This could be attributable to different subunit composition, density of channels (Legendre et al., 2002), phosphorylation states (Gentet and Clements, 2002), or the interaction with anchoring proteins at the synapse (Zita et al., 2007). However, both somatic and synaptic GlyRs are known to be composed of α1β heteromers in juvenile animals (Malosio et al., 1991; Takahashi and Momiyama, 1991), and the rates used in this study accurately predict the observed time course of the IPSCs (Burzomato et al., 2004), suggesting that modulatory factors are not essential in shaping the synaptic current.

In our experimental conditions, the role of desensitization is more difficult to assess: using the model of Figure 1H and omitting the desensitized states, the decay time of the calculated IPSC was in agreement with the experimental observations. Including the two desensitized states that are needed to fit the outside-out concentration jumps experiment did not change the estimates for Gly_peak and τ, but gave rise to a calculated IPSC with a decay time longer than observed (∼10 ms instead of 7 ms). It is known that currents evoked by short pulses of glycine (1 ms) applied to outside-out patches from neurons (Singer and Berger, 1999) or recombinant GlyRs (Beato et al., 2007) deactivate with time constants of 20–40 ms. This is probably attributable to intrinsic differences in the gating behavior of the channel after excision of the patch (Fucile et al., 2000) (Pitt, Sivilotti, and Beato, unpublished observation). It is therefore possible that the desensitization rates estimated in the present study from outside-out recordings, do not reflect the behavior of GlyRs in an intact cell, which are better described by the rates obtained in the cell-attached mode, as shown by the agreement between the calculated and observed decay time of the IPSC. An additional complication arises from the observation that at some synapses GABA is coreleased with glycine (Jonas et al., 1998; Chéry and de Koninck, 1999): although this would not affect our estimate of the glycine time course, it may affect the time course of synaptic currents, as recently shown by Lu et al. (2008).

The estimates for the glycine time course have to be regarded as averages across many different synapses, because data from different cells were pooled together. Despite careful placement of the stimulating electrode in the region in which the density of Renshaw cells is maximal, we cannot be sure that the stimulation came from a uniform population of presynaptic cells. However, the relatively small variation in the amount of inhibition observed in different cells suggests that the concentration profiles to which postsynaptic GlyRs from motoneurons are exposed do not vary over a wide range.