Contextual analysis of fluid intelligence

Abstract

The nature of fluid intelligence was investigated by identifying variables that were, and were not, significantly related to this construct. Relevant information was obtained from three sources: re-analyses of data from previous studies, a study in which 791 adults performed storage-plus-processing working memory tasks, and a study in which 236 adults performed a variety of working memory, updating, and cognitive control tasks. The results suggest that fluid intelligence represents a broad individual difference dimension contributing to diverse types of controlled or effortful processing. The analyses also revealed that very few of the age-related effects on the target variables were statistically independent of effects on established cognitive abilities, which suggests most of the age-related influences on a wide variety of cognitive control variables overlap with age-related influences on cognitive abilities such as fluid intelligence, episodic memory, and perceptual speed.

The finding that nearly all cognitive variables are positively related to one another has been described as one of the most replicated results in psychology (cf. Deary, 2000), and one of the most replicated results in research on aging and cognition is that a very large number of cognitive variables are negatively related to adult age (e.g., Salthouse, 2001a; 2004; Salthouse, Atkinson & Berish, 2003; Salthouse & Davis, 2006; Salthouse & Ferrer-Caja, 2003). Interestingly, these two sets of results are linked because the degree to which a given cognitive variable is related to other cognitive variables (as reflected by the variable’s loading on the first principal component in a principal components analysis) has been found to predict the magnitude of the age correlation on the variable (e.g., Salthouse, 2001a,b, c). To illustrate, in an analysis of 30 different data sets, Salthouse (2001a) found a median rank-order correlation of .80 between a variable’s loading on the first principal component and the absolute magnitude of the variable’s correlation with age. Another intriguing outcome of these analyses was that the variables with the strongest associations with other variables and the strongest associations with age were frequently measures of reasoning or fluid intelligence (Gf).

Relations among cognitive variables are often represented in terms of an organizational structure based on the patterns of correlations. There is considerable agreement that a particularly meaningful correlation-based organization is a hierarchical structure, with observed variables at the lowest level, various cognitive abilities at intermediate levels, and a g factor at the highest level (e.g., Carroll, 1993; Gustafsson, 1988; Jensen, 1998). A consistent finding of analyses investigating where in the hierarchical structure age-related influences operate is the discovery of significant negative relations of age on the highest-order factor in the structure (e.g., Salthouse, 2004; 2005a; Salthouse & Ferrer-Caja, 2003). Moreover, these and other analyses (e.g., Gustafsson, 1988) have found a very strong relation between the higher-order factor and a Gf factor.

These two sets of results suggest that a key to understanding age-related influences on many different cognitive variables may be understanding the nature of individual differences in Gf. Although the term fluid intelligence is sometimes used to refer to any cognitive variable that is negatively related to age, Cattell (1943), the originator of the term, defined it as the ability to discriminate relations, and it is often conceptualized as influencing the quality of reasoning, novel problem solving, and adaptation to new situations. Publishers of cognitive test batteries that include tests of this construct have provided similar definitions:

“… Gf is a broad ability to reason. … This capacity is manifested in drawing inferences and comprehending implications. Gf is best measured with tasks that are novel – i.e., those that require one to discover the essential relations of the task for the first time and draw inferences that could not have been worked out before. Tasks intended to measure Gf should not depend heavily on previously acquired knowledge or earlier-learned problem-solving procedures (Woodcock & Mather, 1990, p. 13).”

“ … Gf … is the ability to solve new problems, specifically the type that are not made easier by extended education or intensive acculturation. ‥‥ Fluid tasks must involve stimuli and concepts that are about equally available to virtually anyone in a culture (Kaufman & Kaufman, 1993, p. 11).”

These definitions are useful in distinguishing Gf from other ability constructs, but they are not very helpful in specifying the precise nature of Gf. A primary goal of the current project was to apply a recently proposed analytical method to attempt to understand the nature of Gf, and its relations to age differences in different types of cognitive variables.

The analytical method used in the current project is termed contextual analysis because the meaning of target variables, and the age-related influences on them, are interpreted in the context of established cognitive abilities (Salthouse, 2005b; Salthouse, Siedlecki & Krueger, 2006). Each reference cognitive ability is represented in the analyses as a latent construct defined by the variance common to between 3 and 6 measured variables. When a target variable is regressed on these reference cognitive ability constructs, the magnitudes of the standardized regression coefficients predicting the target variable from the cognitive abilities can be interpreted as reflections of the extent to which the target variable is uniquely related to each cognitive ability. Because several cognitive abilities are used as simultaneous predictors of the target variable, the analytical procedure is equivalent to a set of multiple regression equations, one for each target variable. However, in order to allow the cognitive abilities to be represented as latent constructs, the analyses were conducted with a structural equation modeling program rather than as simple regression analyses. This contextual analysis method has some resemblance to Dwyer’s (1937) extension analysis, and is closely related to a procedure described in Salthouse and Ferrer-Caja (2003; also see Salthouse, 2001a).

Among the advantages of this analytical method are that several reference abilities can be examined simultaneously to determine the unique influences of each ability on the target variable, each reference ability is represented as a latent construct that is theoretically free of measurement error, and when the age variable is included in the analyses, age-related effects on the target variable can be decomposed into effects shared with other cognitive abilities and effects that are statistically independent of other abilities. Simultaneous analyses of multiple abilities is important because the magnitudes of the relations on the target variable could be overestimated if several constructs are not included in the analyses. That is, influences shared with other constructs cannot be distinguished from influences that are unique to a given construct when only one construct in considered. Conceptualizing abilities as latent constructs is also important because the magnitudes of the relations may be underestimated if the reference abilities are represented by single variables in which the presence of measurement error may attenuate observed correlations. Finally, because a very large number of cognitive variables has been found to be related to age, cumulative progress can be ensured by establishing that age-related effects on a target variable represent something different from what is already known. That is, when researchers study isolated variables there is no way to determine whether the age-related influences on those variables are distinct from the age-related influences on other variables. Unique effects associated with age in a contextual analysis are particularly informative in this respect because, by definition, they are statistically independent of age-related influences on other variables and constructs included in the analyses.

The reference cognitive ability variables used in earlier contextual analyses have been found to have good internal consistency reliability (e.g., Salthouse, 2005b; Salthouse, Atkinson & Berish, 2003; Salthouse, Berish & Siedlecki, 2004; Salthouse, et al., 2006), and to have parallel factor structures across studies. Evidence relevant to the robustness of the structures is summarized in Table 1, where it can be seen that the patterns of construct-variable and construct-construct relations were similar in four independent data sets. Because of the differing sample sizes, the chi-square values varied considerably across data sets, but the CFI and RMSEA fit statistics were between .91 and .93 and between .08 and .09, respectively. The fits of the data to the model could be improved by specifying correlated residuals (e.g., between the Pattern Comparison and Letter Comparison variables), and allowing variables to load on more than one factor (e.g., Shipley Abstraction and Logical Memory on the Vocabulary factor). Sample-specific modifications such as these would increase the precision with which the model fit a particular set of data, but it is important to note that the fit of this simple model was moderately good in each set. Furthermore, the primary purpose of the measurement model in these analyses was to derive latent constructs that represent distinct cognitive abilities, and assessment of these constructs would not necessarily improve by adding complexity to the model to increase the fit to a specific set of data. Although not reported in the table, nearly identical patterns have also been obtained in analyses of aggregate data reported in Salthouse (2004; 2005a) based on 6,832 individuals across 33 studies. Qualitatively similar results have also been found when the contextual analysis method was applied with different combinations of reference variables and constructs (e.g., Salthouse & Davis, 2006).

Table 1.

Relations of cognitive variables to reference constructs in prior studies and the current studies

Source	1	2,3	4,5	6	Study 1	Study 2
Sample Size	261	330	328	327	791	236
Relation between reference constructs and indicator variables
Vocab →WAIS Vocabulary	.85	.86	.89	.88	.84	.87
Vocab → WJ-R Picture Vocabulary	.82	.80	.80	.82	.80	.66
Vocab → Synonym Vocabulary	.90	.91	.87	.89	.88	.89
Vocab →Antonym Vocabulary	.88	.89	.81	.83	.83	.87
Gf → Ravens	.81	.86	.84	.85	.88	.87
Gf → Letter Sets	.71	.70	.71	.72	.71	.76
Gf → Shipley Abstraction	NA	NA	.80	.82	.81	.84
Gf → Spatial Relations	.83	.83	.82	.80	.79	.76
Gf → Paper Folding	.80	.83	.79	.81	.79	.70
Gf → Form Boards	.70	.73	.69	.77	.71	.70
Memory → Word Recall	.73	.80	.74	.78	.76	.79
Memory → Logical Memory	.65	.72	.64	.65	.68	.62
Memory → Paired Associates	.65	.71	.77	.77	.76	.79
Speed → Digit Symbol	.82	.85	.81	.77	.82	.87
Speed → Letter Comparison	.78	.71	.81	.66	.78	.77
Speed → Pattern Comparison	.74	.73	.85	.85	.79	.75
Relations between reference constructs
Vocab ← → Gf	.39	.33	.52	.48	.38	.44
Vocab ← → Memory	.37	.44	.39	.38	.33	.38
Vocab ← → Speed	.18	.09	.22	.07	.05	.12
Gf ← → Memory	.69	.64	.64	.67	.74	.78
Gf ← → Speed	.66	.72	.67	.66	.70	.71
Memory ← → Speed	.64	.62	.56	.49	.58	.63
Age → Vocabulary	.36	.31	.26	.30	.30	.40
Age → Gf	−.46	−.60	−.49	−.51	−.56	−.48
Age → Memory	−.47	−.47	−.44	−.48	−.49	−.40
Age → Speed	−.58	−.69	−.66	−.72	−.65	−.62

1 - Salthouse, Atkinson & Berish (2003)

2 - Salthouse, Berish & Siedlecki (2004)

3 - Siedlecki, Salthouse & Berish (2005)

4 - Salthouse, Siedlecki & Krueger (2006)

5 - Salthouse (2004)

6 - Salthouse & Siedlecki (2007)

Note: NA indicates that the variable was not available in the study.

The rationale underlying the current project is that not only can contextual analysis be informative about the meaning of target variables, but by examining a variety of different types of target variables with the same reference constructs, it may also be informative about the nature of the reference constructs. The focus in the current project is the Gf construct, and therefore target variables that might help elucidate the nature of that construct are of particular interest. A key assumption of our approach is that it should be possible to learn something about a hypothesized causal factor by examining the breadth of variables that it influences.¹ The dominant approach to understanding Gf has been to postulate that some variable is a critical determinant, or cause, of Gf, and then treat evidence of a relation between Gf and the variable as support for that interpretation. This approach can be considered somewhat analogous to research in cognitive neuroscience in which a specific cognitive task is found to activate a particular brain region, and then that region is inferred to be responsible for the processes involved in that task. An alternative perspective, which is more similar to our approach, is to focus on a brain region and examine a variety of tasks that might be associated with activation in that region to infer the range of functions affected, or controlled, by that region. The two approaches are complementary, although a motivation for our research is the belief that exclusive reliance on the dominant approach of focusing on a single variable to predict Gf could result in a narrowly defined Gf construct that neglects many of its important aspects.

Any variable found to have a significant relation to Gf could be inferred to be influenced by Gf, but information of this type may be of limited value by itself because most variables are likely to have numerous influences. A second type of comparison involving pairs of variables from two closely related tasks is potentially more informative because when there is a unique Gf influence on one of two similar variables, the dimension(s) along which the variables differ can be inferred to reflect something about the nature of Gf.

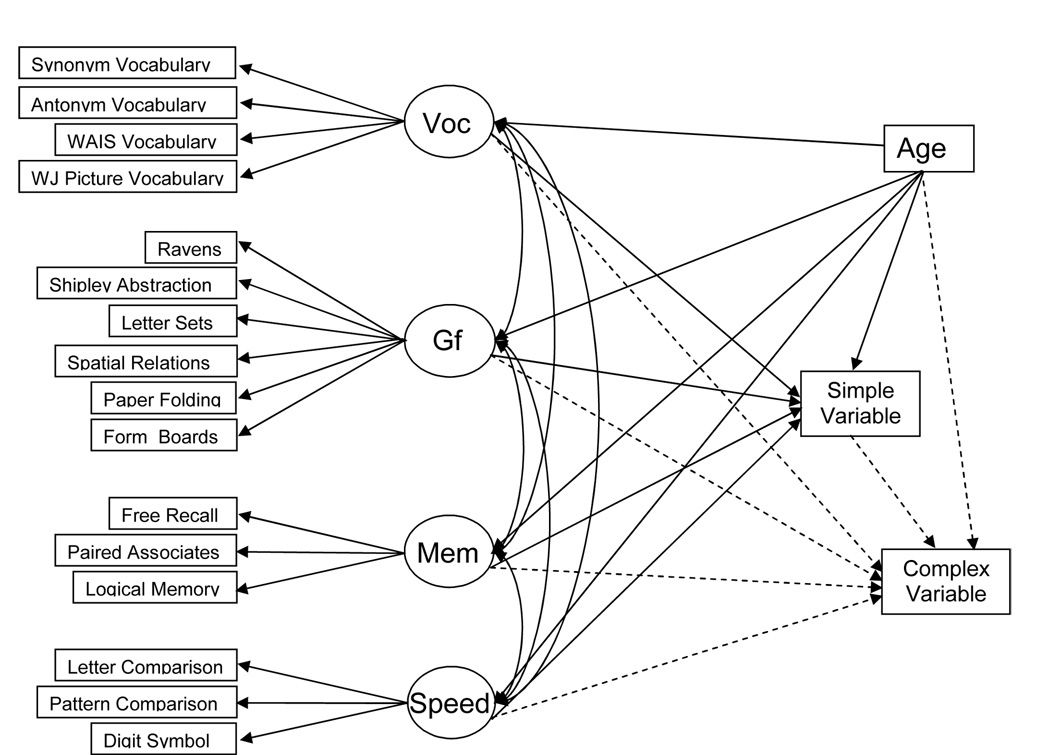
The model in Figure 1, which is an extension of the contextual analysis model used in previous studies, can be used to investigate influences of reference cognitive ability constructs and age on a second variable after controlling the influences on a first variable. The two target variables are designated simple and complex because the first variable often has a higher level of performance, and seems intuitively simpler, than the second variable, but the complexity categorization should be considered tentative because no independent assessment of complexity is currently available. If neither variable is found to have a Gf influence, then it is reasonable to infer that none of the aspects of processing involved in either of the tasks reflect Gf. However, the model in Figure 1 controls for effects on the complex variable that are mediated through the simple variable, and thus a discovery of significant effects of Gf on the complex variable would signify that there is a unique, or incremental, influence of Gf on the complex variable, above and beyond that on the simple variable.

Figure 1.

Contextual analysis model to investigate unique influences of age and established cognitive abilities on a simple and a complex target variable. See text for details.

The same cognitive ability reference constructs listed in Table 1 and portrayed in Figure 1 have been used to investigate the convergent and discriminant validity of latent constructs postulated to reflect executive functioning (Salthouse, Atkinson & Berish, 2003; Salthouse, Berish & Siedlecki, 2004; Salthouse & Davis, 2006), inhibition, updating, and time-sharing (Salthouse, et al., 2003), source memory (Siedlecki, Salthouse & Berish, 2005) and prospective memory (Salthouse, et al., 2004). However, there were two reasons for focusing on observed variables rather than latent constructs as the target variables in the current project. First, if the target variables were to be grouped into hypothesized constructs, then determinants of individual variables not shared with other variables in that group would be difficult to detect. That is, a primary goal was to investigate the breadth of the Gf construct by examining the pattern of Gf influences across a variety of different types of cognitive variables, and some of those influences might be obscured if the variables were aggregated prior to the analyses. And second, in some cases it was the contrast between two specific variables that was of greatest interest, and the critical difference between the variables might be lost if constructs were formed by aggregating variables from different pairs of variables. For example, separate constructs created to represent the simple and complex versions of pairs of variables would reflect what is common across all of the simple or all of the complex variables, but not necessarily what distinguishes the complex from the simple version in any given pair of variables.

Results of contextual analyses for a variety of variables from previous studies conducted by Salthouse and colleagues are summarized in Table 2 for single variables, and in Table 3 for pairs of related variables based on the model in Figure 1. The first variable in each pair in Table 3 is considered the simple variable, and the second variable is considered the complex variable. The entries in each row (or pairs of rows in Table 3) are based on a separate analysis, with the same reference constructs but with the designated variable as the target variable. Notice that there was no Gf relation for variables representing recognition or recall of words, pictures, faces, category-exemplar pairs, or color-location pairs (Table 2), or for the speed of responding to congruent or incongruent items in a Stroop task, speed of normal reading or reading with distraction, or for the rapid generation of exemplars from single or alternating categories in a fluency task (Table 3). In contrast, strong Gf relations were apparent on several variables, including old/new recognition of dot patterns, free recall of line drawings and spatial locations, and measures of memory for the source of recently presented information.

Table 2.

Contextual analysis results with variables from earlier studies

	Age		Reference Constructs
Variable	Total	Unique	Gf	Mem	Speed	Voc	%Var
Siedlecki, Salthouse & Berish (2005)
Word Recall	−.51*	−.21	−.05	.72*	−.01	−.01	62.8
Color of Word	−.24*	.09	.35*	.37*	−.19	−.23	16.2
Picture Recognition	−.32*	.01	−.01	.48*	.05	−.20	21.7
Location of Picture	−.50*	−.12	.33*	.18	.06	−.19	33.0
Fact Recognition	−.15*	.04	.18	.52*	−.20	.07	31.2
Voice of Fact	−.26*	−.13	.17	.47*	−.20	.18	39.2
Command Recognition	−.55*	−.10	.27*	.50*	−.04	−.23	47.2
Source of Command	−.58*	−.13	.34*	.47*	−.10	−.28*	48.8
Salthouse, Siedlecki & Krueger (2006)
Word Recall	−.39*	−.20	−.09	.42*	.14	.17	41.0
Picture Recall	−.29*	.17	.07	.48*	.27*	−.14	33.2
Cat.-Exemplar (P) Assoc.	−.17*	−.08	.01	.34*	−03	.18	20.2
Cat.-Exemplar (NP) Assoc.	−.09	.03	−.08	.41*	.02	.15	19.6
Location-Color Trls-to-Learn	.30*	.12	−.15	−.32*	.02	.08	26.3
Location-Color (P) Recog.	−.36*	−.14	.15	.47*	−.06	−.02	36.9
Location-Color (NP) Recog.	−.28*	−.12	−.01	.49*	.01	.10	34.7
Salthouse & Siedlecki (2007)
Word Recognition, Study 1	−.02	.17	−.04	.40*	.10	.13	21.7
Word Recognition, Study 2	−.12	.30	.03	.39*	.29	−.03	20.1
Faces Recognition	−.24*	−.06	.25	.04	.05	.00	12.3
Dot Pattern Recognition	−.30*	.14	.72*	−.08	.13	−.07	44.2
Siedlecki (2007)
Word Recognition	−.06	.37*	.22	.30*	.15	−.21	10.4
Word Cued Recall	−.27*	.24	.06	.52*	.24	−.21	26.3
Word Recall	−.40*	.02	−.15	.65*	.23	−.07	43.8
Figure Recognition	−.08	−.05	−.01	.03	−.01	−.09	1.3
Figure Cued Recall	−.23*	−.09	.15	.07	.01	−.10	6.2
Figure Recall	−.48*	−.11	.46*	.16	.02	−.17	37.8
Spatial Recognition	−.27*	−.07	.21	−.02	.13	−.02	11.7
Spatial Cued Recall	−.43*	.16	.73*	.08	.18	−.22	53.4
Spatial Recall	−.40*	.05	.67*	−.06	.16	−.09	47.2

^*Note: p<.01. The values in the “Total” column are simple correlation coefficients and those in the other columns are standardized regression coefficients predicting the target variable from age and the reference constructs. The “%Var.” column contains the percentage of variance in the target variable accounted for by age and the four reference constructs. See cited articles for details on the variables.

Table 3.

Contextual analysis of sequential variables with the model in Figure 1 applied to variables from earlier studies

	Age			Reference Constructs
Variable	Total	Unique	Simple	Gf	Mem	Speed	Voc	%Var
Salthouse, Atkinson & Berish (2003)
Stroop Time
Congruent	.23*	−.06	--	.14	.07	−.66*	−.00	27.0
Incongruent	.51*	.10	.15*	−.13	−.06	−.50*	.01	60.1
Reading Time
Normal	.19*	.29*	--	.38*	−.01	−.47*	−.55*	39.0
With Distraction	.18*	.06	.26*	−.05	.03	−.29*	−.29*	42.3
Matrix Monitoring
One Matrix	−.16*	.12	--	.28	.03	.18	−.11	12.1
Two Matrices	−.26*	.17	.32*	.46*	.07	.17	−.12	47.2
NBack Errors
1 Back	.39*	−.03	--	−.18	−.22	−.33	.12	34.8
2 Back	.40*	−.09	.28*	−.54*	−.04	−.10	.15	54.2
NBack Errors
Alone	.46*	−.02	--	−.33*	−.18	−.34*	.13	50.3
With Driving	.41*	−.10	.62*	−.27*	−.11	.01	.14	65.2
Paired Associates1
Alone	−.35*	−.14	--	.13	.43*	−.02	.09	39.0
With Tracking	−.49*	−.12	.52*	.27*	.19	−.07	−.06	69.4
Salthouse, Berish & Siedlecki (2004)
Fluency
Category	−.19*	.07	--	−.02	.21	.36*	.26*	36.5
Alternating Cat.	−.18*	.17	.40*	−.15	.18	.42*	.00	43.4
Salthouse & Siedlecki (2007)
Mazes (Time)
Trace	.28*	−.14	--	−.03	−.26*	−.39*	.15	22.1
Solve	.52*	.11	.21*	−.33*	.08	−.26*	.22	41.3
Salthouse, Siedlecki & Krueger (2006)
Brown Peterson
List 1 (& 4)	−.31*	−.02	--	.05	.49*	.13	.13	46.0
List 3 (& 6)	−.27*	.13	.35*	.28*	.24*	−.01	−.21	35.7

^*Note: p<.01. The values in the “Total” column are simple correlation coefficients and those in the other columns are standardized regression coefficients predicting the target variable from age and the reference constructs. The column labeled “Simple” contains the standardized regression coefficients for the path from the simple to the complex variable in Figure 1.

¹The paired associates variable was omitted from the reference memory construct for this analysis. The “%Var.” column contains the percentage of variance in the target variable accounted for by age and the four reference constructs.

Results in Table 3 are derived from contextual analyses using the model portrayed in Figure 1 with pairs of related target variables. Note that some variable pairs had cognitive ability influences only on the simple variables in the pair. For example, there was an influence of speed on errors in the NBack 1 condition, an influence of memory on the paired associates variable, and an influence of vocabulary on the category fluency variable. In these cases, effects of the cognitive abilities on the complex variable can be inferred to be completely mediated through effects on the simple variable. Of greatest interest in Table 3 are the pairs of variables in which there was an influence of Gf on the complex variable after taking into consideration influences on the simple variable. This pattern was evident when monitoring changing positions in two matrices compared to one, when reporting items two back in a sequence compared to reporting items one back, when performing the paired associates and NBack tasks with a concurrent perceptual motor task (i.e., manual tracking with paired associates and simulated driving with NBack) compared to performing them alone, when solving rather than merely tracing mazes, and when recalling words from a category after attempting to recall several prior lists of words from the same category. These results are intriguing because they suggest that even though the Gf construct is typically conceptualized as involving reasoning and novel problem solving, it appears to capture nearly the same dimension of individual differences as measures of performance on a collection of tasks that can be broadly characterized as requiring aspects of cognitive control. That is, trying to remember difficult-to-verbalize information, monitoring complex sequences of information, and dividing one’s attention between two concurrent activities, are all situations that seem to involve substantial amounts of deliberate or controlled cognitive processing.

One category of cognitive control that has been the focus of considerable recent research is the construct of working memory (WM). A major reason for this interest is that numerous studies have reported moderate to strong correlations between measures of Gf and measures hypothesized to assess WM. Some early research of this type was reported by Salthouse and colleagues where significant correlations were found between computation span, reading span or listening span measures of WM and various measures of reasoning or Gf (e.g., Salthouse, 1991; 1992a, b, c; 1993; Salthouse, Hancock, Meinz & Hambrick, 1996; Salthouse & Mitchell, 1989; Salthouse, Mitchell, Skovronek & Babcock, 1989). For example, after controlling for influences of age and of perceptual speed, Salthouse (1991) found standardized regression coefficients between a composite WM measure and a composite measure of accuracy from several different cognitive tasks of .35, .42, and .56 in three separate studies. Furthermore, correlations between a WM composite and score on the Raven’s Advanced Progressive Matrices test, which is often considered a prototypical Gf test, were .69, .59, and .61 in three studies reported in Salthouse (1993a).

Significant correlations with individual WM measures and Raven’s Progressive Matrices have also been reported in more recent studies involving only young adult participants. For example, correlations ranging from .15 to .47 have been reported by Conway, Cowan, Bunting, Therriault and Minkoff (2002), Conway, Kane, Bunting, Hambrick, Wilhelm and Engle (2005), Engle, Tuholski, Laughlin and Conway (1999), Kane, Hambrick, Tuholski, Wilhelm, Payne and Engle (2004), and Unsworth, Heitz, Schrock and Engle (2005). After adjusting for unreliability, Ackerman, Beier and Boyle (2004) found a meta-analytic estimate for the Gf-WM correlation of .63. The Gf-WM correlations are generally higher when the relations are examined at the level of factor scores, composite scores, or latent variables. To illustrate, correlations ranging from .59 to .89 have been reported in studies by Ackerman, Beier and Boyle (2002), Colom, Abad, Rebollo and Shih (2005), Colom, Flores-Mendoza and Rebollo (2003), Colom, Rebollo, Palacios, Juan-Espinosa and Kyllonen (2004), Colom and Shih (2004), Conway, et al. (2002), Conway, Kane and Engle (2003), Kyllonen and Christal (1990), Suss, Oberaurer, Wittmann, Wilhelm and Schulze (2002), Unsworth, et al. (2005), and Wilhelm and Oberaurer (2006), and Kane, Hambrick and Conway (2005) reported a median correlation of .72 across 14 different data sets.

There is still some controversy about the exact magnitude of the Gf-WM relation, and how it should be interpreted (e.g., Ackerman, et al., 2004; Beier & Ackerman, 2005; Blair, 2006; Kane, et al., 2005; Oberauer, Schulze, Wilhelm & Suss, 2005), but there is also considerable agreement that the correlation is moderately high. The sizeable correlations have led a number of researchers to speculate that the Gf (or g) and WM constructs may even be identical:

Kyllonen (2002), p. 433 – “…we have our answer to the question of what g is. It is working memory capacity.”

Conway, et al. (2002), p. 178 – “…WMC might be a ‘primary determinant’ of Spearman’s g”

Engle (2002), p. 22 – the WM construct “…is at least related to, and maybe isomorphic to, general fluid intelligence,” and p. 23 - “WM capacity … appears to be an important mechanism underlying fluid intelligence.”

Kane and Engle (2002), p. 638, “… we view WM capacity … as the psychological core of the statistical construct of general fluid intelligence, or psychometric Gf.”

It should be pointed out that some of these claims were subsequently qualified, as indicated by the following quotations:

Conway, et al., (2003), p. 547 – “Early investigations of working memory capacity (WMC) and reasoning ability suggested that WMC might be the basis of Spearman’s g. However, ‥‥ A review of the recent research reveals that WMC and g are indeed highly related, but not identical.”

Kane, et al. (2004), p. 210 – “… it is probably unwise to claim WMC to be the cognitive mechanism of Gf.”

Kane, et al. (2005), p. 66 – “…WMC is not equivalent to g, Gf, or reasoning ability.”

Despite the vacillation of opinions, it is fair to say that in recent years WM has been assumed to be a central concept in cognition, and it has been argued to be more “theoretically tractable” (Kane, et al., 2004), or less “conceptually opaque” (Oberaurer, et al., 2005) than Gf. Oberaurer and colleagues (2005) were so convinced of the importance of the working memory construct that they suggested that “… investigating WMC, and its relationships with intelligence, is psychology’s best hope to date to understand intelligence (p. 64).” Although one can question whether the WM construct deserves this lofty status, its relation to Gf clearly warrants further examination. The current studies were therefore designed to apply the contextual analysis procedure to storage and processing measures from popular tasks used to assess WM, and to variables from other tasks hypothesized to represent conceptually related aspects of cognitive control.

Three key requirements for contextual analyses are moderately large samples to have sufficient power to detect theoretically interesting differences in the magnitudes of the relations, a relatively wide range of ability among the participants in the sample to avoid attenuation of relations due to restriction of range, and reliable assessment of all variables at the level of the individual. A number of previous studies investigating Gf-WM relations have been based on samples of 150 or fewer individuals, which is associated with relatively low power to detect differences that might be theoretically important. College students have served as the research participants in many studies, which could lead to attenuation of the observed relations relative to the true relations because in some colleges the students are selected on the basis of high levels of cognitive ability. A sample with a broader range of cognitive ability levels can be obtained by recruiting participants across a wide age range, which also has the advantage of allowing age-related influences on the variables of interest to be examined. Finally, reliability is important because relations with other variables are limited by the relation that a variable has with itself, which is one way of conceptualizing reliability. The problem of weak reliability was evident in a recent report that examined variables hypothesized to represent efficiency of memory control. Although the major phenomena were replicated at the group level, the critical variables had very low reliability, which precluded meaningful analyses of individual differences (Salthouse, et al., 2006).

The current article describes two studies in which the contextual analysis procedure was applied to variables hypothesized to be informative about the nature of Gf. In the first study a relatively large sample of participants performed two storage and processing tasks frequently used to assess WM, and a variant of a trail-making task in which the position in one sequence had to be maintained while the participant selected and moved to the next element in the other sequence. In addition, performance on pre- and post-interference trials in a multiple-trial free-recall task was examined to investigate the possibility that Gf is related to the ability to resist interference, in which case one might expect an influence of Gf on post-interference recall. The second study involved a smaller sample of participants, but a wider variety of cognitive control measures, including an additional storage-plus-processing task, several tasks hypothesized to reflect updating of continuously changing information, items used to assess mental control from standardized test batteries, and new tests of Gf.

Study 1

The storage-plus-processing WM tasks used in the first study were developed by Engle and his colleagues (e.g., Conway, et al., 2005; Kane, et al., 2004). One of the tasks, Operation Span, involves the participant attempting to remember a sequence of letters while evaluating the accuracy of arithmetic problems, and the other task, Symmetry Span, involves the participant attempting to remember positions of dots in a matrix while deciding whether spatial patterns were symmetrical. These two tasks were selected because they have a similar format but involve different types of to-be-remembered information and processing requirements, the measures have been reported to have good reliability (e.g., Kane, et al., 2005; Kane, et al., 2004), and the authors have developed computer-administered versions of the tasks that have been made available for use by other researchers.

Method

Participants

Participants in Study 1 consisted of 791 adults ranging from 18 to 98 years of age. They were recruited through newspaper advertisements, flyers, and referrals from other participants. Approximately 30% (i.e., 67) of the adults in the 18-to-39 age group were college students.

Table 4 summarizes demographic characteristics of the participants. It can be seen that increased age was associated with a slightly lower self rating of health, but with somewhat more years of education. One way to characterize the representativeness of the sample is in terms of scores on standardized tests that have been normed in nationally representative samples. The Wechsler batteries (Wechsler, 1997a; 1997b) are very useful for this purpose because they contain many variables expressed in scaled scores units separately for different age groups. These age-adjusted scaled scores have a mean of 10 and a standard deviation of 3 in the normative sample, and thus the individuals in the current sample can be inferred to be functioning above average relative to the nationally representative normative sample. However, it is important to note that there is little relation of the scaled scores to age, and hence there is no evidence that participants of different ages vary in the degree to which they differ from their age peers in the normative sample.

Table 4.

Descriptive characteristics of the participants, arbitrarily divided into three groups.

Age Group
	18–39	40–59	60–98	All	Age r
Study 1
Number	222	294	275	791
Age	26.5 (6.5)	50.7 (5.5)	70.6 (7.5)	5.8 (18.6)
Prop. Females	.64	.75	.62	.67	−.03
Health	1.6 (.9)	1.7 (1.0)	1.8 (1.0)	1.7 (1.0)	.13*
Years Education	15.0 (2.3)	15.7 (2.4)	16.2 (3.2)	15.7 (2.7)	.19*
Age-Adjusted Scaled Scores
Vocabulary	13.2 (3.0)	12.5 (2.9)	13.6 (2.5)	13.1 (2.8)	.06
Digit Symbol	11.4 (2.7)	11.6 (2.8)	12.0 (2.8)	11.7 (2.8)	.11*
Word Recall	12.1 (3.0)	12.8 (3.3)	12.6 (3.4)	12.5 (3.3)	.02
Logical Memory	11.8 (2.8)	12.0 (2.8)	12.4 (2.7)	12.0 (2.8)	.08
Study 2
Number	73	91	72	236
Age	27.7 (5.7)	5.6 (5.5)	71.1 (8.2)	49.8 (18.2)
Prop. Females	.60	.62	.69	.64	.05
Health	2.0 (.9)	2.2 (1.0)	2.2 (.8)	2.1 (.9)	.08
Years Education	14.9 (2.9)	15.2 (2.5)	16.5 (2.6)	15.5 (2.7)	.23*
Age-Adjusted Scaled Scores
Vocabulary	12.1 (3.2)	11.6 (2.8)	13.3 (2.2)	12.3 (2.8)	.14
Digit Symbol	10.9 (2.8)	10.5 (2.8)	11.8 (2.7)	11.0 (2.8)	.12
Word Recall	12.2 (3.2)	12.0 (3.4)	12.4 (3.4)	12.2 (3.3)	.03
Logical Memory	10.6 (3.0)	11.2 (3.1)	12.3 (2.8)	11.3 (3.1)	.23*

^*p<.01

Procedure

Each participant was tested individually in three 2-hour sessions, with the Connections and Symmetry Span tasks performed in the second session and the Operation Span task performed in the third session. The reference cognitive ability tasks were all performed in the first session, and other tasks unrelated to the current project were performed in the remaining time in the other sessions.

The reference battery of 16 cognitive tests has been described in several articles (Salthouse, 2004; 2005b; Salthouse, et al., 2003; 2004), and the tests are listed, together with their sources, in the appendix. This combination of tests was originally selected to represent five different cognitive abilities, but the reasoning and spatial visualization abilities are highly correlated (e.g., .93 in Study 1, and .87 in Study 2), and thus they were combined to form a fluid intelligence (Gf) ability construct.

Appendix.

Description of reference variables and sources of tasks

Variable	Description	Source
WAIS Vocabulary	Provide definitions of words	Wechsler (1997a)
Picture Vocabulary	Name the pictured object	Woodcock & Johnson (1990)
Antonym Vocabulary	Select the best antonym of the target word	Salthouse (1993b)
Synonym Vocabulary	Select the best synonym of the target word	Salthouse (1993b)
Matrix Reasoning	Determine which pattern best completes the missing cell in a matrix	Raven (1962)
Shipley Abstraction	Determine the words or numbers that are the best continuation of a sequence	Zachary (1986)
Letter Sets	Identify which of five groups of letters Is different from the others	Ekstrom, et al., (1976)
Spatial Relations	Determine the correspondence between a 3-D figure and alternative 2-D figures	Bennett, et al. (1997)
Paper Folding	Determine the pattern of holes that would result from a sequence of folds and a punch through folded paper	Ekstrom, et al. (1976)
Form Boards	Determine which combinations of shapes are needed to fill a larger shape	Ekstrom, et al., (1976)
Logical Memory	Number of idea units recalled across three stories	Wechsler (1997b)
Free Recall	Number of words recalled across trials 1 to 4 of a word list	Wechsler (1997b)
Paired Associates	Number of response terms recalled when presented with a stimulus term	Salthouse, et al. (1996)
Digit Symbol	Use a code table to write the correct symbol below each digit	Wechsler (1997a)
Letter Comparison	Same/different comparison of pairs of letter strings	Salthouse & Babcock (1991)
Pattern Comparison	Same/different comparison of pairs of line patterns	Salthouse & Babcock (1991)

The two storage-plus-processing tasks have been described in Conway, et al. (2005), Kane, et al. (2004), and Unsworth, et al. (2005), and were obtained from http://psychology.gatech.edu/renglelab. Both tasks involve the performance of a processing component while simultaneously remembering a series of items. The processing and storage components are initially performed separately to familiarize the participants with each aspect of the task. The number of to-be-remembered items (i.e., set size) in the combined storage-plus-processing phase varied randomly across trials for different participants such that, on average, there was no correlation between set size and trial number. Measures of performance in each WM task were the total number of to-be-remembered items recalled in the correct sequence across all trials and at each set size, and the number of decision errors in the processing component.

In the Operation Span task the storage component consisted of a sequence of three to seven letters, and the processing component involved verification of arithmetic operations (e.g., [8/2] + 3 = 6?). The storage component in the Symmetry Span task consisted of a sequence of two to five positions of dots in a matrix, and the processing component involved judgments about whether patterns of filled cells in an 8×8 grid were symmetrical along the vertical axis.

The Connections task was described in Salthouse, Toth, Daniels, Parks, Pak, Wolbrette and Hocking (2000). It consists of eight pages that each contain 49 circles. Two pages contain only numbers within the circles, two contain only letters in the circles, two contain numbers or letters with a number as the first item, and two contain numbers or letters with a letter as the first item. In each case, the task for the participants is to connect circles in numeric, alphabetic, or alternating numeric and alphabetic sequence as rapidly as possible. Because errors were infrequent, the average number of same sequence or alternating sequence connections correctly completed in 20 seconds served as the measure of performance.

Two variables from the Wechsler Memory Scale (Wechsler, 1997b) Word Recall Test were also used in the contextual analyses. These were the scores on Trial 4 and on Trial 5 of the same list of 12 words. The trials differed in that the list of to-be-remembered words was presented prior to the recall attempt in Trial 4 but not in Trial 5, and another list of words, List B, was administered for recall between the two lists.

Results and Discussion²

Table 5 contains means, standard deviations, estimated reliabilities, and age correlations for the reference cognitive ability variables. It can be seen that the internal consistency estimates of reliability were all above .71, and that the age correlations were positive for the vocabulary variables, but negative for the remaining variables.

Table 5.

Summary statistics for reference cognitive variables in Studies 1 and 2

Variable	Mean	SD	Alpha	Age corr.
WAIS Vocabulary	52.3 / 49.6	9.6 / 10.1	.90 / .90	.12* / .20*
WJ-R Picture Vocabulary	18.5 / 17.4	5.2 / 6.4	.87 / .89	.33* / .33*
Antonym Vocabulary	6.6 / 6.4	2.8 / 3.0	.79 / .81	.21* / .38*
Synonym Vocabulary	7.2 / 6.9	2.7 / 2.9	.82 / .83	.32* / .43*
Raven’s	7.9 / 7.4	3.6 / 3.7	.84 / .87	−.54* /−.47*
Letter Sets	11.4 / 11.3	2.7 / 2.7	.73 / .78	−.33* /−.21*
Shipley Abstraction	13.6 / 13.4	3.4 / 3.5	.83 / .83	−.45* /−.36*
Spatial Relations	9.0 / 8.6	5.1 / 5.2	.90 / .91	−.32* /−.28*
Paper Folding	6.2 / 6.0	2.7 / 2.6	.73 / .71	−.44* /−.38*
Form Boards	7.3 / 7.3	4.6 / 4.3	.88 / .85	−.33* /−.50*
Word Recall	35.3 / 34.9	6.3 / 6.4	.89 / .89	−.41* /−.43*
Logical Memory	44.8 / 42.7	9.9 / 10.5	.85 / .89	−.27* /−.08
Paired Associates	3.1 / 3.0	1.8 / 1.8	.83 / .81	−.37* /−.29*
Digit Symbol	74.3 / 70.8	17.8 / 17.2	.581 / .611	−.54* /−.56*
Letter Comparison	10.6 / 10.3	2.5 / 2.5	.86 / .84	−.48* /−.44*
Pattern Comparison	15.8 / 15.7	3.6 / 3.5	.83 / .83	−.53* /−.49*

^*Note: p < .01. The first number in each cell is the value from Study 1 and the second number is the value from Study 2. Alpha refers to coefficient alpha, which is an internal consistency measure of reliability.

¹Reliability estimated from multiple R² in a regression equation with the other reference variables as predictors.

Standardized coefficients for the measurement model with the four reference cognitive abilities are reported in column 6 of Table 1, where it is apparent that the pattern is very consistent with the patterns from earlier studies. Although not reported here, the results were also very similar when the analyses were repeated after partialling age from all variables, and when the sample was divided into groups with narrow age ranges.

Age relations

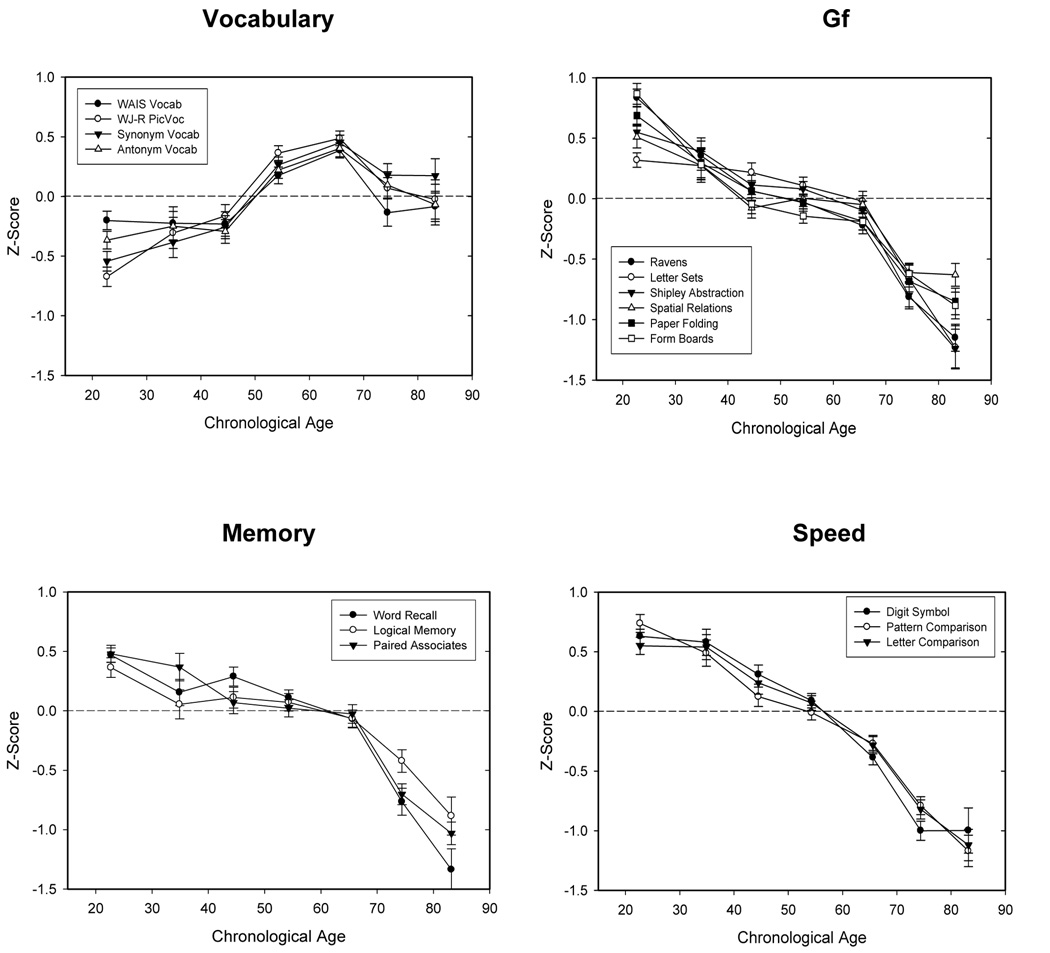
Figure 2 portrays the mean levels of the reference cognitive variables as a function of age. In order to express all variables in a common scale, they have been converted into standard deviation units based on the entire distribution of participants. Notice that there were similar age relations for the variables representing the same reference ability, and that for most of the variables increased age was associated with a nearly monotonic decrease in performance. The exceptions are the four vocabulary variables, which increased until about age 65 followed by a modest decrease. Although some of the variables in Figure 2 had non-linear age trends, quadratic and cubic trends accounted for small proportions of the variance compared to the linear term (also see Salthouse, 2004). Only linear age relations were therefore modeled in the analyses, which could result in an underestimation of the absolute magnitude of some of the age-related influences.

Figure 2.

Means and standard errors of z-scores for each reference cognitive variable as a function of decade in Study 1. The data points for the oldest decade are based on between 30 and 40 individuals but all of the other points are based on at least 90 individuals.

The results summarized in Table1 and Table 5 and portrayed in Figure 2 are well-established, and can be considered to represent the context within which new variables should be interpreted, both in terms of their relations with established abilities and the degree to which the age-related influences on the new variables are statistically independent of age-related influences on established abilities.

Contextual Analyses

Means, standard deviations, estimated reliabilities, and age correlations for the target variables in the contextual analysis are reported in the top panel of Table 6. For some of the variables reliability estimates are reported both in terms of coefficient alpha and multiple R². The two values represent different aspects of reliability because the former is a measure of internal consistency and reflects the degree to which different parts of the test correlate with one another. Because it corresponds to the proportion of variance in the variable that is predicted by other variables, multiple R² should be considered a lower-bound estimate of reliability.

Table 6.

Summary statistics for contextual analysis target variables

Variable	Mean	SD	Alpha / R2	Age corr.
Study 1
Operation Span Storage	51.2	18.2	NA / .37	−.33*
Operation Span Processing	6.3	6.1	NA / .31	.23*
Symmetry Span Storage	19.4	9.3	NA / .51	−.50*
Symmetry Span Processing	4.1	4.9	NA / .33	.21*
Connections Same	25.1	9.5	.93 / .73	−.59*
Connections Alternate	13.3	5.1	.75 / .69	−.48*
Word List Trial 4	10.3	1.7	NA / .72	−.37*
Word List Trial 5	8.3	2.6	NA / .55	−.41*
Study 2
Analysis Synthesis	16.6	4.4	.86 / .61	−.23*
Concept Formation	13.1	4.2	.78 / .46	−.10
Mystery Codes	30.1	8.9	.88 / .73	−.56*
Logical Steps	10.1	3.8	.84 / .73	−.29*
Keeping Track	21.0	4.0	.50 / .35	−.15*
Color Counters 2	9.4	4.7	.88 / .73	−.28*
Color Counters 3	8.2	4.4	.86 / .78	−.30*
Matrix Monitoring 1	15.0	2.1	.83 / .63	−.11
Matrix Monitoring 2	11.9	2.5	.47 / .51	−.21*
Running Memory Letters	39.3	17.6	.92 / .61	−.17*
Running Memory Positions	31.8	19.7	.94 / .65	−.35*
Operation Span Storage	50.0	19.2	NA / .70	−.32*
Operation Span Processing	6.8	6.8	NA / .53	.18*
Symmetry Span Storage	19.9	9.3	NA / .68	−.60*
Symmetry Span Processing	4.5	4.9	NA / .56	.18*
Reading Span Storage	46.5	17.1	NA / .71	−.22*
Reading Span Processing	2.9	3.0	NA / .47	.05
Connections Same	25.6	8.6	.94 / .75	−.56*
Connections Alternate	13.4	5.6	.84 / .76	−.41*
Word List Trial 4	10.2	1.7	NA / .78	−.36*
Word List Trial 5	8.2	2.5	NA / .72	−.40*
Simple Search	49.2	14.0	.93 / .65	−.38*
Complex Search	18.6	8.3	.84 / .74	−.43*
Number Arithmetic	28.8	7.2	.91 / .69	−.28*
Alphabet Arithmetic	11.8	4.1	.92 / .73	−.17*
Days Forward (Sec)	2.5	0.9	NA / .43	.22*
Days Backward (Sec)	3.6	1.2	NA / .41	.20*
Months Forward (Sec)	4.7	1.3	NA / .50	.13
Months Backward (Sec)	11.8	7.8	NA / .42	−.06
Curve Letters (Num)	10.3	1.4	NA / .41	.01
Curve Letters (Sec)	18.9	9.4	NA / .46	.04
Rhyme with Key	7.1	2.9	NA / .42	−.01

^*Note: p<.01. Reliability estimates are coefficient alpha and multiple R² with all other variables in the study as predictors. NA indicates that an estimate was not available because the tasks did not have multiple parts with separate scores.

Although some of the estimated reliabilities were low, each of the variables was significantly related to age. Furthermore, the storage (total number of items correctly recalled) and processing (number of errors in the arithmetic or symmetry judgments) measures within each storage-and-processing task were significantly correlated with each other (i.e., −.33 for Operation Span, and −.37 for Symmetry Span). This indicates that the two aspects of the tasks were not independent with respect to individual differences, and thus implies that both aspects should be considered when evaluating performance on these tasks.

The initial contextual analyses were conducted with the storage measures and the processing measures from the Operation Span and Symmetry Span tasks. These analyses are based on the original version of the contextual analysis procedure with a single target variable. Results of the analyses are presented in Table 7, where it can be seen that there were no unique age relations on any of the storage or processing variables after taking into consideration age-related influences on the reference cognitive abilities. The Operation Span storage variable was positively related to speed ability, indicating somewhat higher recall of letters in the correct order among individuals with faster speed. The negative relation of vocabulary with arithmetic errors in the Operation Span task indicates that there were fewer errors among people with higher levels of vocabulary. Vocabulary level was also negatively related to Symmetry Span storage score, indicating that when other influences are controlled, individuals with higher vocabulary had somewhat lower accuracy in recall of the dot positions in correct order.

Table 7.

Contextual analysis results on variables from storage-and-processing tasks, Study 1.

	Age		Reference Constructs
Variable	Total	Unique	Gf	Mem	Speed	Voc	%Var
Operation Span Storage	−.33*	.03	.40*	.07	.20*	.03	36.3
Operation Span Processing	.23*	.08	−.37*	−.11	.04	−.19*	31.9
Symmetry Span Storage	−.50*	−.10	.71*	−.05	.01	−.13*	51.1
Symmetry Span Processing	.21*	−.01	−.69*	.08	.15	−.06	32.5
Age 18–39
Operation Span Storage	.09	−.05	.37*	.02	.19	−.03	25.1
Operation Span Processing	−.13	.06	−.17	−.14	−.13	−.19	25.5
Symmetry Span Storage	−.26*	−.14	.61*	−.10	.14	−.10	39.3
Symmetry Span Processing	.08	.01	−.56*	.08	.06	−.05	27.1
Age 40–59
Operation Span Storage	.03	.00	.33*	.08	.11	.15	30.2
Operation Span Processing	−.07	−.04	−.52*	−.09	.21	.01	25.1
Symmetry Span Storage	−.07	−.06	.68*	−.10	−.04	−.02	35.9
Symmetry Span Processing	.05	.10	−.60*	.08	.14	−.11	32.4
Age 60–98
Operation Span Storage	−.28*	.03	.41*	.06	.20	−.05	32.9
Operation Span Processing	.31*	.06	−.35*	−.06	.07	−.34*	43.3
Symmetry Span Storage	−.24*	.10	.69*	.11	.04	−.23*	38.5
Symmetry Span Processing	.21*	−.03	−.73*	.11	.15	−.06	34.6
Age-Partialled
Operation Span Storage	--	--	.32*	.06	.16*	.03	36.2
Operation Span Processing	--	--	−.30*	−.11	.03	−.18*	31.9
Symmetry Span Storage	--	--	.58*	−.04	.01	−.11	50.8
Symmetry Span Processing	--	--	−.57*	.06	.11	−.06	32.4

^*Note: p<.01. The values in the “Total” column are simple correlation coefficients and those in the other columns are standardized regression coefficients predicting the target variable from age and the reference constructs. The “%Var.” column contains the percentage of variance in the target variable accounted for by age and the four reference constructs.

Although some other influences were identified, the contextual analyses revealed that the dominant influence on the storage and processing measures used to assess WM was from the Gf construct. Furthermore, when the variation in Gf and other cognitive abilities was controlled, there were no longer significant relations of age on any of the WM variables. The lower panels of Table 7 contain results of the analyses in subsamples with narrower age ranges, and in the complete sample after partialling the influence of age from all variables. Inspection of the entries reveals that the results, particularly the strong influences of Gf on the target variables, were similar in each analysis. These findings indicate that the results in the complete sample are not distorted by the relations that each variable had with age.

Table 8 contains results of the analyses on pairs of related variables with the contextual analysis model in Figure 1. The variables in these analyses were selected to represent different levels of complexity, such as connecting elements in the same (simple) or alternating (complex) sequences, or performing WM tasks with small (simple) or large (complex) set sizes. Although the total effects of age, corresponding to the simple correlation of the variable with age, were significant for every variable, none of the unique age relations were significantly different from zero. The absence of a unique speed influence on the alternating sequence variable in the Connections task suggests that all of the speed influences on the same and alternating sequence variables were shared. Unique influences of Gf were evident on the alternating sequence variable, and on the higher set sizes in the Operation Span and Symmetry Span tasks, which suggests that Gf may be related to the ability to preserve information during processing. However, the lack of a relation of Gf with the post-interference recall variable implies that Gf is apparently not involved in the maintenance of information during the presentation and recall of another list of words.

Table 8.

Contextual analysis results with the model in Figure 1, Study 1

	Age			Reference Constructs
Variable	Total	Unique	Simple	Gf	Mem	Speed	Voc	%Var
Connections
Same Seq.	−.59*	−.02	--	.34*	.03	.55*	−.05	71.5
Alternating Seq.	−.48*	.07	.51*	.36*	.06	.04	.00	71.4
Operation Span
Set Size 3	−.29*	.07	--	.30*	.14	.18*	−.04	25.6
Set Size 7	−.33*	−.04	.48*	.24*	.03	.02	.03	47.4
Symmetry Span
Set Size 2	−.36*	−.01	--	.54*	.04	.03	−.05	34.3
Set Size 5	−.45*	−.12	.26*	.52*	−.12	−.05	−.13*	41.3
Word List1
Trial 4	−.37*	.13	--	−.15	.98*	.06	−.29*	56.2
Trial 5	−.41*	.06	.34*	−.13	.67*	.06	−.20	65.0

^*Note: p<.01. The values in the “Total” column are simple correlation coefficients and those in the other columns are standardized regression coefficients predicting the target variable from age and the reference constructs. The column labeled “Simple” contains the standardized regression coefficients for the path from the simple to the complex variable in Figure 1. The “%Var.” column contains the percentage of variance in the target variable accounted for by age and the four reference constructs.

¹The word recall measure was omitted from the reference memory construct for this analysis.

Study 2

The goal of Study 2 was to extend the investigation of Study 1 by including an additional storage-plus-processing task of working memory, and a broader range of cognitive control variables. Storage-plus-processing tasks are based on a conceptualization of WM in which the individual must remember some information while processing other information. However, a somewhat different conceptualization of WM views it as responsible for accurate updating of the status of continuously changing information. Several measures assumed to reflect updating were therefore included in Study 2 to determine if they would exhibit the same patterns of influences from cognitive abilities and from age as the storage-plus-processing measures.

Because the measure of performance in the alternating sequences condition of the Connections task had a unique Gf influence, two new speeded tasks with both simple and complex versions were included. One was a visual search task with simple targets consisting of a single letter or digit, and complex targets defined by a rule such as an odd digit paired with a vowel. The other speeded task consisted of arithmetic with either two numbers (e.g., 3 + 2 = ?), or with a letter as the first element and a number as the second element (e.g., C + 2 = ?). In the latter case the instructions were to move forward or backwards in the alphabetical sequence by the designated number of letters to determine the identity of the target letter.

Several items from standardized test batteries that have been postulated to assess efficiency of controlling mental operations were also included. Some of the items are intuitively plausible as measures of mental control, such as the additional time needed to say the days of the week in reverse as compared to forward order. However, there has apparently been little empirical research with these items, and thus we had no specific predictions regarding the patterns of cognitive ability influences on these variables.

Finally, new measures hypothesized to represent Gf were included to provide baseline contextual analysis results with variables assumed to be alternative indicators of the same reference construct. If the relations of the reference cognitive abilities on the target variables are very similar to those on these alternative indicators of what is assumed to be the same construct, then it may be reasonable to infer that they are all manifestations of the same dimension of individual differences.

Method

Participants

Characteristics of the sample are summarized in the bottom of Table 4. The participants were recruited with the same methods as in Study 1, and they had similar characteristics. Twenty-one percent of the participants in the youngest group were students. Compared to the other age groups, the oldest group had more years of education, and a higher average scaled score on the Logical Memory test, and thus these individuals can be inferred to be somewhat higher functioning relative to their age peers than the members of the other age groups.

Procedure

The participants performed 32 different tasks across the three two-hour sessions. The 16 reference ability tests were all performed in Session 1 in the same order as in Study 1. Tasks performed in the second session were Analysis-Synthesis, Reading Span, Mystery Codes, Visual Search, Symmetry Span, Keeping Track, Running Memory - Positions, and Connections. The Session 3 tasks were Mental Control, Color Counters, Logical Steps, Operation Span, Alphabet Arithmetic, Running Memory - Letters, Matrix Monitoring, and Concept Formation.

The Reading Span task was described in Conway, et al. (2005) and Kane, et al. (2004), and was obtained from the same web site as the Operation Span and Symmetry Span tasks. It was nearly identical to the Operation Span task except that the processing component consisted of making decisions about whether sentences were meaningful or nonsensical instead of making decisions about the validity of arithmetic operations. The to-be-remembered items were letters with set sizes, which varied randomly across trials, from three to seven letters.

Four new tasks hypothesized by the test publishers to assess fluid intelligence, but which had little superficial resemblance to the Gf tests in the reference battery, were adapted for computer administration. Two tests, Analysis-Synthesis and Concept Formation, were modified from tests of the same name in the Woodcock-Johnson Revised Psycho-Educational Battery, where they were described in the following manner:

“Analysis-Synthesis is designed to measure the ability to analyze the presented components of an incomplete logic puzzle and to determine the missing components … Concept Formation measures the ability to identify the rules for concepts when shown illustrations of both instances of the concept and non-instances of the concept (Woodcock & Mather, 1990, p. 22).”

Stimuli in the Analysis-Synthesis test consisted of colored boxes which were related according to specified rules (e.g., Blue + Yellow = Red). The task for the participant was to determine the color of a blank box based on the presented colors and rules. A total of 24 trials was presented, and the measure of performance was the number of items answered correctly within the allotted time of 12 minutes.

The Concept Formation stimuli consisted of drawings of objects varying in size, shape, color, and number. A trial consisted of the presentation of several objects, with a rectangle enclosing some of them to indicate that they were grouped together. The task for the participant was to designate what dimension(s) distinguished the enclosed objects from the non-enclosed objects. The two sets of objects could differ from one another in a single dimension, or by a conjunction (AND) or disjunction (OR) of two or more dimensions. A time limit of 15 minutes was imposed for the participants to complete 23 trials, and the measure of performance was the number of items answered correctly.

The Logical Steps and Mystery Codes tests were adapted from the Kaufman Adult Intelligence Test, where they were described as follows:

“Logical Steps. Examinees attend to logical premises … and then respond to a question by making use of the logical premises. …

Mystery Codes. Examinees study the identifying codes associated with a set of pictorial stimuli and then figure out the code for a novel pictorial stimulus (Kaufman & Kaufman, 1993, p. 6).”

The Logical Steps task consisted of three types of problems involving positions of items on a staircase, in a horse race, or at a dinner table. A set of premises described items in certain positions along with a set of constraints, and the task was to specify the position of a test item. For example, a staircase problem might consist of stating the position of item B given that it is two positions ahead of item C and one position behind item A, and item C is on step 3. Fifteen minutes were allowed for the participants to complete 15 trials, and the measure of performance was the number of items answered correctly.

In the Mystery Codes task the stimuli consisted of line drawings of objects differing in several dimensions such as pattern, shading, and orientation, and a series of codes. The task for the participant was to determine the code corresponding to a test stimulus. There were a total of 18 trials for which the participant was allowed 15 minutes, and the measure of performance was the number of dimensions identified correctly out of a maximum of 72 (i.e., 4 for each of the 18 trials).

The remaining tasks were added to investigate a broader range of cognitive control functions. The Keeping Track task was identical to that used in Salthouse, et al. (2003). It consisted of a succession of words, presented at a rate of 1 second per word, from different semantic categories and occasional probes of a category name and a word. On the probe trials the participant was asked to decide whether the target word was the most recently presented exemplar from that category, and performance was represented by the number of items answered correctly. There were a total of 32 probes, 50% with the most recently presented exemplar and 50% with an earlier-presented exemplar.

The Matrix Monitoring 1 and 2 tasks were the same as those used in Salthouse, et al. (2003). The sequence of events on a trial in the version of the task with one matrix consisted of a display, for 2.5 seconds, of a dot in one cell of a 4×4 matrix, followed by two successive arrows, for 1 second each, indicating that the dot position should move one cell in the direction of the arrow. The probe consisted of a dot in a cell of the matrix, with the participant instructed to press one key if it was in the correct final position given the initial position and sequence of arrows, and to press a different key if it was not in the correct position. There were two versions of the task, one with a single matrix and another with two independently varying matrices, but in each case the test probe consisted of a cell in only one matrix. After a short set of practice trials the participants performed blocks of 16 trials each with 1, 2, 2, and 1 matrices. The measure of performance with each number of matrices was the average number of probes answered correctly across the two blocks of trials.

The Color Counters task was adapted from Larson and Saccuzzo (1989). It consisted of an initial presentation of either two or three colored bars for 2.5 seconds each, followed by a sequence of squares displayed, for 1.5 seconds each, either above or below one of the bars. The task was to monitor the value of each bar (counter) by adding one for every square above the bar and subtracting one for every square below the bar. After a sequence of eight operations, which varied randomly across counters and plus or minus operations, the value of one of the counters was to be reported. Practice trials were administered with one and with two counters, followed by 16 trials with two counters and 15 trials with three counters. The measure of performance in each condition was the number of trials with the correct counter number.

Two versions of a Running Memory task (e.g., Talland, 1968) were performed, one with letter stimuli and one with dot position stimuli. Trials in each version consisted of displays of between 4 and 12 successive items at a rate of 1 second each, with instructions to report the last 4 items in the order in which they were presented. There were a total of 18 trials with each version, consisting of two trials with each sequence length from 4 to 12, presented in random order. The stimuli consisted of the letters from A through L, or dots in cells of a 4×4 matrix, with the items on a given trial sampled without replacement from the pool of 16. The recall test consisted of the presentation of a matrix of either letters or blank cells, with the participant using a mouse to select the last 4 letters or the last 4 matrix positions in their original order of presentation. The measure of performance in each version of the task was the number of items in the correct order across the 18 trials, with one point awarded for each item recalled in the correct order (i.e., a maximum of 72 across the 18 trials).

The Visual Search task was adapted from one described in Salthouse (2001). The test stimuli consisted of eight pages that each contained 75 letter-digit pairs. Four pages had 16 simple targets (e.g., H, or 6), and four had 16 complex targets (e.g., a digit 6 or greater preceded by a digit less than 4, or a letter between A and D paired with an even digit). Pages with simple and complex targets were presented in counterbalanced order (i.e., Simple-Complex-Complex-Simple-Simple-Complex-Complex-Simple). The task for the participant was to draw a line through as many targets as possible in 30 seconds, and the measure of performance was the average number of targets minus the number of false alarms across the four trials of each type.

The Alphabet Arithmetic task was adapted from Salthouse and Kersten (1993). It consisted of two pages with simple addition or subtraction of the number 1 or 2 from a number between 1 and 8, and two pages with a letter from A to H and subtraction or addition of 1 or 2. In the alphabet condition the answer was the letter corresponding to the designated number of positions in the alphabetical sequence before (−) or after (+) the original letter. To illustrate, the answer for (F − 2) was D. Each page contained 40 problems, and the pages were presented in counterbalanced order (i.e., Number-Alphabet-Alphabet-Number). The measures of performance were the average number of correct answers in 30 seconds across the two number arithmetic pages, and across the two alphabet arithmetic pages.

Several items from the Mental Control subtests in the Wechsler Memory Scale – III (Wechsler, 1997b) and the Kaplan Baycrest Neurocognitive Assessment (Leach, Kaplan, Rewilak, Richards & Proulx, 2000) were also administered. Four items consisted of rapid naming of days of the week or months of the year in forward and in backwards sequence, another item involved naming all capital letters that have curves, and the final item consisted of naming as many words as possible that rhymed with “key”. The time to respond was the primary dependent measure except for the “key” rhyme item in which the measure of performance was the number of appropriate words spoken in 30 seconds. However, because people varied in the number of curved letters reported, both the number of correct letters reported and the time to report them were used as dependent variables for this item.

Results and Discussion

Summary statistics for the reference variables are presented in Table 5, and results of the measurement model for the reference constructs are presented in column 7 of Table 1. Inspection of these entries reveals that in both cases the results closely resembled those from Study 1. The target variable summary statistics are presented in the bottom of Table 6. It can be seen that most of the variables were at least moderately reliable, and had significant negative correlations with age. Furthermore, the values for the variables common to Study 1 were quite similar across the two studies.

Examination of Table 6 reveals that accuracy was lower with more counters in the Color Counters task, and with more matrices in the Matrix Monitoring task. Fewer items were completed with alternating compared to single sequences in the Connections task, with complex compared to simple targets in the Visual Search task, and with alphabet problems compared to numeric problems in the Arithmetic test. The time to name days or months was also longer when the items were to be spoken in backwards order compared to forward order. These results are all consistent with the assumption that the second variable in each pair required more, or different, processing than the first variable. Although the mean levels of performance differed across members of the pairs, it is noteworthy that there was no systematic increase in the age correlations from the simple to the more complex versions of the tasks.

Contextual Analyses

Results of the contextual analyses for single target variables are presented in Table 9. The values in the second column indicate that many of the variables were significantly correlated with age, but the values in the third column indicate that none of the age relations on the target variables were statistically independent of effects on the reference cognitive abilities. All of the age-related influences on the target variables can therefore be inferred to be shared with influences on the reference cognitive abilities.

Table 9.

Contextual analysis results applied to measures from tasks assumed to reflect aspects of cognitive control, Study 2

	Age		Reference Constructs
Variable	Total	Unique	Gf	Mem	Speed	Voc	%Var
Additional Gf variables
Analysis Synthesis	−.23*	.02	.83*	−.04	−.14	.09	55.8
Concept Formation	−.10	.11	.51*	.17	−.13	.04	30.0
Mystery Codes	−.56*	−.21	.73*	−.09	.05	−.02	66.4
Logical Steps	−.29*	.08	.82*	.10	−.08	.02	67.3
Storage-plus-processing WM variables
Operation Span Storage	−.32*	−.01	.57*	.14	−.07	−.06	38.7
Operation Span Processing	.18*	−.20	−.74*	−.02	.06	.14	32.4
Symmetry Span Storage	−.60*	−.11	.65*	−.04	.14	−.27*	56.5
Symmetry Span Processing	.18*	.03	−.57*	−.13	.25	−.05	32.3
Reading Span Storage	−.22*	−.12	.40*	.05	−.03	.21	34.0
Reading Span Processing	.05	.22	.05	−.25	.10	−.45*	27.0
Updating WM variables
Keeping Track	−.15*	.08	.55*	.15	−.20	−.09	23.3
Running Memory Letters	−.17*	.24	.78*	−.03	.02	−.12	38.4
Running Memory Positions	−.35*	.15	.81*	.04	.03	−.19	51.4
Mental control variables
Curve Letters (Num)	.01	.03	.44*	−.09	−.17	.15	14.7
Curve Letters (Sec)	.04	−.24	−.30	−.11	−.19	−.08	25.7
Rhyme with Key	−.01	−.26	−.35	.30	.01	.53*	23.6

^*Note: p<.01. The values in the “Total” column are simple correlation coefficients and those in the other columns are standardized regression coefficients predicting the target variable from age and the reference constructs. The “%Var.” column contains the percentage of variance in the target variable accounted for by age and the four reference constructs.

As expected, the new Gf variables, Analysis-Synthesis, Concept Formation, Logical Steps, and Mystery Codes, had strong influences of Gf. The Gf and age relations were relatively weak for the Concept Formation variable, but the reasons are not obvious because the estimated reliability of this variable was in the same range as those for the other Gf variables (cf. Table 7).

The pattern with the Operation Span and Symmetry Span variables closely resembled that in Study 1, with strong Gf influences and no unique age relations. Individuals with high levels of vocabulary made fewer processing errors in the Reading Span task, which may reflect an influence of verbal ability on reading comprehension. High vocabulary was also associated with lower accuracy in reproducing dot positions in the Symmetry Span task after controlling influences of other abilities. This relation was also evident in Study 1, and therefore it is apparently consistent, but we have no simple explanation for why this would be the case.

Both running memory variables had Gf influences that were as high as those on the alternative indicators of Gf. The requirement of having to continuously update the most recently presented four items in a list of unpredictable length therefore seems to make demands on a similar individual difference dimension as that involved in successful reasoning and novel problem solving.

Only weak relations of age and cognitive abilities were evident on the variables from the mental control subtests of standardized test batteries, possibly because they were individual items with relatively low levels of reliability. More curved letters were named by individuals with higher Gf, which may reflect requirements of sequencing through the alphabet while visualizing each letter. There were no relations of any reference cognitive abilities on the time to name the curved letters. The fluency measure of the number of words that rhymed with “key” was only related to vocabulary, with more words generated by individuals with a higher level of vocabulary.

Results from the analyses with pairs of related variables based on the model in Figure 1 are summarized in Table 10. The pattern with the Connections variables closely resembled that in Study 1 with influences of speed and Gf on the same sequence (simple) variable, and no significant speed influence but a strong Gf influence on the alternating sequence (complex) variable. The results with the Visual Search and Alphabet Arithmetic tasks were very similar to those with the Connections task. In both cases there were strong speed influences on the simple variable, but weak speed and strong Gf influences on the complex variable. Even though the three tasks differed in the nature of the additional processing required in the complex variable compared to the simple variable, they all exhibited unique Gf influences on the complex variable. This finding raises the possibility that amount of processing may be more important as a determinant of Gf influences than the specific type of processing.

Table 10.

Contextual analysis results with the model in Figure 1, Study 2

	Age			Reference Constructs
Variable	Total	Unique	Simple	Gf	Mem	Speed	Voc	%Var
Connections
Same Seq.	−.56*	−.04	--	.47*	−.06	.43*	−.14	61.7
Alternating Seq.	−.41*	.14	.55*	.58*	−.06	−.09	−.11	69.0
Visual Search
Simple Target	−.38*	.25	--	.12	.15	.67*	−.22	47.3
Complex Target	−.43*	.03	.40*	.52*	−.04	.06	−.07	62.3
Arithmetic
Number	−.28*	.37*	--	.25	−.06	.84*	−.10	59.7
Alphabet	−.17*	.20	.37*	.34*	−.02	.23	.08	60.3
Operation Span
Set Size 3	−.20*	.11	--	.43*	.13	−00	−.12	19.6
Set Size 7	−.35*	−.13	.42*	.38*	.02	−.09	−00	48.7
Symmetry Span
Set Size 2	−.38*	.12	--	.53*	.06	.13	−.35*	29.1
Set Size 5	−.51*	−.20	.17*	.46*	−.14	.05	−.13	38.8
Reading Span
Set Size 3	−.19*	−.01	--	.23	.16	.04	.06	18.7
Set Size 7	−.22*	-0.16	.36*	.28	−.04	−.09	.15	33.3
Word List1
Trial 4	−.36*	.27	--	.04	.92*	.17	−.58*	57.6
Trial 5	−.40*	.05	.25	−.05	.67*	.14	−.31	61.5
Matrix Monitoring
One Matrix	−.11	.10	--	.62*	−.05	−.06	.07	30.4
Two Matrices	−.21*	.13	.23*	.52*	−.01	.07	−.10	38.2
Color Counters
Two Counters	−.28*	.13	--	.45*	.19	.13	−.10	36.0
Three Counters	−.30*	.02	.65*	.27	−.04	.06	.01	69.4
Days of Week (seconds)
Forward	.22*	.23	--	.04	−.03	−.07	−.11	6.5
Backward	.20*	−.13	.28*	−.26	.11	−.25	.06	21.0
Months of the Year (seconds)
Forward	.13	.06	--	.31	−.21	−.32	−.16	11.6
Backward	−.06	−.42*	.03	−.19	−.08	−.35*	.02	20.5

^*Note: p<.01. The values in the “Total” column are simple correlation coefficients and those in the other columns are standardized regression coefficients predicting the target variable from age and the reference constructs. The column labeled “Simple” contains the standardized regression coefficients for the path from the simple to the complex variable in Figure 1. The “%Var.” column contains the percentage of variance in the target variable accounted for by age and the four reference constructs.

¹The word recall measure was omitted from the reference memory construct for this analysis.

The age relations were reversed on the number arithmetic variable after controlling influences through the cognitive abilities. This finding indicates that after removing the influence of other abilities, and particularly, perceptual speed, increased age in this sample was associated with better performance in simple arithmetic.

As in Study 1, there were unique influences of Gf on larger set sizes in the Operation Span and Symmetry Span tasks, but surprisingly, not for the Reading Span task. Also like Study 1, there was no influence of Gf on the post-interference recall trial after controlling the influences on the pre-interference recall trial. The matrix monitoring results were similar to those in Table 3 with a unique Gf influence when two matrices were monitored compared to when only one matrix was monitored. However, in contrast to expectation, the relation of Gf on the more complex three-counter version of the Color Counters task was not significant after controlling effects on the simpler two-counter version. The only unique influences on the backwards versions of naming days of the week or months of the year were on the months backward measure. Increased age was associated with slower performance on this task, but individuals with higher perceptual speed were faster at naming the months in reverse order.

General Discussion

The current research was motivated by the assumption that a key to understanding the relations that many cognitive variables have to one another, and to adult age, may be understanding Gf. The research was therefore designed to investigate the nature of Gf by determining the cognitive variables that were related to, and were potentially manifestations of, Gf. The results revealed that a large number of apparently diverse cognitive variables have very strong relations to Gf.

Not surprisingly, the strongest relations of Gf were with its own indicator variables, which had standardized coefficients ranging from .69 to .88 in Table 1. New variables postulated to assess Gf had comparable relations, ranging from .73 to .83, with the puzzling exception of the Concept Formation variable which had a standardized coefficient on Gf of only .51 (cf. Table 9).

Despite a lack of obvious novel problem solving or reasoning requirements, a variety of other variables were also found to have very strong Gf relations. For example, performance in the running memory tasks with letter or dot position stimuli had standardized relations of .78 and .81, which are in the same range as those for the conventional indicators of Gf. Both the measures of the number of items recalled and of the number of processing errors committed in the Operation Span and Symmetry Span WM tasks had high Gf relations. However, high Gf relations are not restricted to measures from storage-plus-processing or updating tasks hypothesized to assess WM because strong Gf influences were also apparent on measures of source memory, dot pattern recognition, and free recall of line patterns and spatial locations (cf. Table 2).

The contrasts of Gf influences on pairs of closely related variables with the model in Figure 1 were designed to be particularly informative in elucidating the nature of Gf. That is, because the model contains a path from the simple variable to the complex variable, any direct influences on the complex variable can be inferred to be specific to the characteristic(s) that differ between the two variables. The results in Table 3, Table 8, and Table 10 indicate that unique Gf relations were evident when monitoring two matrices compared to monitoring only one, when reporting items that occurred two back in a sequence compared to those that occurred one back in the sequence, when performing a memory task concurrently with a perceptual motor task compared to performing the memory task alone, when recalling items from larger compared to smaller set sizes in tasks requiring simultaneous storage and processing, when connecting elements from alternating sequences compared to single sequences, when searching for complex targets compared to simple targets, when performing arithmetic that required an alphabet transformation compared to arithmetic without a required transformation, when solving mazes as opposed to merely tracing mazes, and when recalling a third list of words from a given semantic category compared to recalling an initial list of words from that category. This pattern of results suggests that Gf may be involved whenever substantial amounts of controlled or effortful processing are required, almost regardless of the particular type of stimuli or the specific processing requirements.

An advantage of examining a broad variety of variables with the same analytical procedures is that it allows the range of Gf influences to be investigated. When only a limited set of variables are considered, such as measures hypothesized to represent storage-plus-processing conceptualizations of working memory, there is a tendency to view those particular variables as having unique relationships to Gf. However, the results of this project reveal that Gf is related to many different types of variables, including measures of monitoring the status of changing sequences of information, measures of memory for non-verbal information, and measures from a variety of simple tasks when some type of additional processing is required. Because these measures are quite diverse, it may not be reasonable to assume that one particular subset of them necessarily represents the core or essence of Gf without explaining the relations of Gf to the other measures.

The idea that Gf encompasses a broad spectrum of controlled processing is consistent with earlier research which found strong relations between the Gf construct and the variance common to different variables hypothesized to reflect the neuropsychological construct of executive functioning (e.g., Salthouse, 2005b; Salthouse, et al., 2003; Salthouse & Davis, 2006; Salthouse, et al., 2005). Although motivated from different research traditions and usually studied separately, the results of this and other recent studies suggest that research with cognitive, psychometric, and neuropsychological variables may have been characterizing essentially the same dimension of individual differences among normal healthy adults. Whether this dimension is labeled Gf, working memory, executive processing, or some form of cognitive control may reflect the research tradition of the investigator more than any fundamental differences among the concepts because it appears that individuals would be ordered in nearly the same way with variables from each of these perspectives. A major challenge for future research is to go beyond labels and classifications to explain why certain types of processing must be controlled, what distinguishes controlled from non-controlled processing, and how the efficiency of this type of processing declines with increased age. These questions cannot be answered in the current studies, but because a broad variety of variables was examined, the results are valuable in specifying the scope of what will, and will not, need to be explained in this manner.

For example, although Gf clearly has broad influences, it is important to recognize that neither in the earlier nor in the current studies was Gf related to all cognitive variables, or even to all of variables that had significant negative correlations with age. Many variables that were significantly related to age were predominantly influenced by the memory or speed constructs and not Gf. As suggested by Salthouse (2004) and Salthouse and Ferrer-Caja (2003), there is evidence for at least three statistically independent influences of age on cognitive functioning, one on g, one on episodic memory, and one on speed.

It is also noteworthy that some variables that might be hypothesized to involve aspects of cognitive control, such as the time to respond to incongruent items in the Stroop Color-Word test, or the number of words recalled after an interference list, were not related to Gf. These findings indicate that the current analytical method is capable of distinguishing among different types of cognitive processing because the Gf construct apparently does not affect conflict monitoring of the type involved in the Stroop test, or maintenance of information in the presence of distraction as operationalized in the contrast of pre- and post-interference recall.

Two sets of results concerning the age variable are particularly noteworthy. One is the finding in Table 7 that the relations between the reference construct abilities and the storage-plus-processing measures from the tasks hypothesized to assess WM were similar in samples with narrow age ranges, and when the influence of age was partialled from all variables. Because the relations in the complete sample were not distorted by the relations of the variables to age, studies with age-heterogeneous samples can be inferred to address the same phenomena, but with potentially greater generalizability, as studies with age-homogeneous samples.

The second interesting result with respect to age concerned the age relations on the cognitive variables. Lower levels of performance with increased age were evident in most of the variables in Table 2, Table 3, Table 5, and Table 6, and in Figure 2. If these variables were to be considered separately, each might be “explained” with a different age-related mechanism. However, the contextual analyses revealed that very few of the age-related influences on the variables were independent of the age-related influences on established cognitive abilities. In other words, when the reference cognitive abilities are viewed as mediators of the age-related influences, there were very few direct, or unique, effects of age on the target variables. These findings imply that an explanation for the influence of age on certain cognitive abilities, and particularly Gf, will be sufficient to account for the age relations on a wide variety of variables that have been hypothesized to reflect aspects of cognitive control.

The analytical method used in these studies relies on patterns of relations among variables to infer how people differ from one another. That is, variables that covary together are assumed to represent a similar dimension of individual differences, and variables that do not covary together are assumed to represent different dimensions of individual differerences. Because a very high degree of covariation exists among Gf variables and variables assumed to reflect aspects of working memory and cognitive control, the results of these studies suggest that, at least with respect to individual differences and age-related influences, these variables may have common underlying mechanisms.

However, it is important to emphasize that different levels of analyses need not have perfect correspondence with respect to how variables are categorized. That is, a discovery of a high degree of covariation of variables across individuals does not necessarily imply that all of the variables involve identical cognitive processes, or share the same neuroanatomical substrates. It is quite possible that a different level of analysis, perhaps focusing on the susceptibility of variables to particular manipulations, or on patterns of neuroimaging activation within specific brain regions, might result in different groupings of variables. Nevertheless, if the primary interest is in determining how people differ, and identifying the number of distinct explanations that might be needed to account for age-related differences in cognitive functioning, the type of individual difference level of analysis used in these studies appears to be particularly valuable.