An exploratory algorithm to identify intra-host recombinant viral sequences

Abstract

Since recombination leads to the generation of mosaic genomes that violate the assumption of traditional phylogenetic methods that sequence evolution can be accurately described by a single tree, results and conclusions based on phylogenetic analysis of data sets including recombinant sequences can be severely misleading. Many methods are able to adequately detect recombination between diverse sequences, for example between different HIV-1 subtypes. More problematic is the identification of recombinants among closely related sequences such as a viral population within a host. We describe a simple algorithmic procedure that enables detection of intra-host recombinants based on split-decomposition networks and a robust statistical test for recombination. By applying this algorithm to several published HIV-1 datasets we conclude that intra-host recombination was significantly underestimated in previous studies and that up to one-third of the env sequences longitudinally sampled from a given subject can be of recombinant origin. The results show that our procedure can be a valuable exploratory tool for detection of recombinant sequences before phylogenetic analysis, and also suggest that HIV-1 recombination in vivo is far more frequent and significant than previously thought.

1. Introduction

Evolutionary inferences based on phylogenetic analyses that include recombinants sequences can be severely misleading (Schierup and Hein, 2000). Because recombination is known to occur at a high rate in quickly evolving organisms such as RNA viruses (e.g. Levy, 2004), the identification and removal of recombinants is priority for phylogenetic analyses. Many general methods and software packages have been developed to investigate the presence of recombination, either directly through sequence comparison or indirectly through phylogenetic means (Posada and Crandall, 2001) including Geneconv (Sawyer, 1989), MaxChi (Smith, 1992), RDP (Martin and Rybicki, 2000), Phypro (Weiller, 1998), RecPars (Hein, 1990), and neighbor similarity score (Jakobsen and Easteal, 1996). It is relatively easy to detect recombination between highly divergent sequences, e.g. viruses of different subtypes, with such methods (Kiwelu et al., 2005; Koulinska et al., 2001; McCutchan, 2000; Posada, 2002; Wiuf et al., 2001) which do not require assumptions about sample history (Bruen et al., 2006b). On the other hand, intra-host recombination, such as viral population belonging to the same subtype, is more difficult to assess. Tests for recombination among closely related sequences are usually based on assumptions about population and demographic history, recombination rate, or mutation rate of the aligned sequences under investigation and may not be appropriate for all data sets (Bruen et al., 2006b). Moreover, even when such tests can accurately assess the presence of recombination within the data, the detection of specific recombinant sequences typically requires the prior identification of putative parental sequences for comparison.

Phylogeny-based methods, such as the widely used bootscanning, infer phylogenetic trees along a sliding window scanning a set of aligned sequences which include a query sequence (the putative recombinant) and putative parental sequences (Salminen, 2003). Since recombination leads to the creation of mosaic genomes originating from different ancestors, a recombination event can be detected by the “jumping” of the query sequence between highly supported phylogenetic clades in trees obtained from different genomic regions (Salminen, 2003). It has been shown that this method is not very powerful, especially when sequences are closely related (Posada and Crandall, 2001; Salminen, 2003). Improved bootscanning methods have been introduced that either do not require prior identification of parental sequences and incorporate distance measures as well (Martin et al., 2005) or that can incorporate serially sampled sequences into the analysis (Buendia and Narasimhan, 2007), both of which are more powerful methods than the original bootscanning implementation. An alternative approach is to use phylogenetic networks to investigate data sets that are suspected to contain recombinants (Huson and Bryant, 2006). The key difference between networks and trees is that a network allows cycles, i.e. paths that begin and end at the same node, through which conflicting phylogenetic histories (trees) can be simultaneously represented (Posada and Crandall, 2001; Moulton, 2003). However, conflicting phylogenetic signals in a network can be due to recombination or to convergent substitution and, in general, it is not possible to distinguish between these two alternatives by examining the network alone (Wain-Hobson et al., 2003). Genetic algorithms that allow accurate testing for the presence of recombination in a set of aligned sequences have also been developed (Kosakovsky Pond et al., 2006b). Although such methods are quite powerful, they are computationally intensive, making it difficult to analyze large data sets (Kosakovsky Pond et al., 2006a).

Bruen et al. (2006) recently described a simple and robust statistical method, the PHI test, able to detect the presence of recombination in a set of aligned sequences. Extensive simulation studies and comparison with other available methods have shown that the PHI test is extremely powerful in detecting recombination. Moreover, the test produces the lowest number of false positives even in the presence of strong rate heterogeneity across sites when compared to other well-known test statistics (Bruen et al., 2006a). Finally, the PHI test can be used easily for very large data sets because of its computational efficiency (it does not require the computation of phylogenies), and performs well regardless of the population history, demographic history, recombination rate, or mutation rate underlying the evolutionary history of the data (Bruen et al., 2006a).

By using phylogenetic networks in conjunction with the PHI test, we describe a simple algorithmic procedure that enables detection of intra-host recombinants. We implemented this algorithm to investigate human immunodeficiency virus type 1 (HIV-1) data because of the potential for multiple intra-host recombinants within a population containing limited diversity and mutational hotspots (Fang et al., 2004; Taylor et al, 2005; Piantadosi et al, 2007; Rousseau et al, 2007). Intra-host evolution of HIV-1 is characterized by the ability of the virus to generate an extensive sequence diversity due to reverse transcriptase high mutation rate (Mansky and Temin, 1995), rapid viral turnover (Ho et al., 1995; Rodrigo et al., 1999), a large number of infected cells (Chun et al., 1997), and recombination (Jung et al., 2002; Morris et al., 1999; Shriner et al., 2004). HIV-1 recombination in vivo can be explained by the diploid nature of the retroviral genome and the ability of the nascent viral strand to switch RNA templates during reverse transcription (Coffin, 1979). It has been shown that recombination between two HIV-1 genomes during reverse transcription can occur as many as three to nine times per round of replication (Levy et al., 2004; Zhuang et al., 2002). The major genome rearrangements that can be caused by recombination play an important role in the generation and diversification of the viral population and have been associated with rapid spread of drug resistance (Kellam and Larder, 1995) and accelerated progression to AIDS (Liu et al., 2002).

2. Materials and Methods

2.1. Representing conflicting phylogenetic signals by split-decomposition networks

The standard way to represent evolutionary relationships between a given set of aligned sequences is to use a phylogenetic tree, in which internal nodes represent ancestral sequences and the branch tips are labeled by present-day sequences. A tree presumes that the underlying evolutionary processes are bifurcating (or, at best, multifurcating if more than two leaves are allowed to descend from the same common ancestor). Therefore, a tree implicitly assumes that once two lineages are created they subsequently never interact with one another, an assumption that is obviously violated in case of recombination. In such a case, evolutionary relationships among DNA sequences are better represented by a network, i.e. a graph, allowing cycles that begin and end at the same node (Moulton, 2003). A network represents incompatible and ambiguous signals in a data set originating via either recombination or homoplasy (Huson and Bryant, 2006). Conflicting phylogenetic signals in each data set were investigated using split-decomposition networks inferred with the Neighbor Net (NNet) algorithm (Bryant and Moulton, 2004) using SplitsTree version 4.8 (Huson and Bryant, 2006).

2.2. PHI test of recombination

The presence of recombination signal in a data set of aligned DNA or amino acid sequences can specifically be tested with the PHI statistic (Bruen et al., 2006a). The test is based on the idea of refined incompatibility score, which represents the minimum number of homoplasies that have occurred in the history of the aligned sequences between two sites. In the absence of recombination the score represents the minimum number of homoplasies that have occurred in the history of the aligned sequences between two sites. In the absence of homoplasy the score represents the minimum number of recombination events that have occurred between two sites. Given a set of aligned sequences, the PHI test calculates the pairwise homoplasy index (PHI) as the mean of the refined incompatibility scores obtained for nearby nucleotide sites along the sequences (Bruen et al., 2006a). Significance of the PHI statistic for the presence of recombination is assessed with the normal approximation of a permutation test where, under the null hypothesis of no recombination, sites along the alignment are randomly permuted to obtain the null distribution of PHI: p-values < 0.05 indicate significant presence of recombination (Bruen et al., 2006a). For the current analysis, PHI tests were carried out on each dataset using the version of the test implemented in SplitsTree v4.8 (Huson and Bryant, 2006).

2.3. Data sets

Two different kinds of previously published datasets were used: HIV-1 longitudinal sequences from peripheral blood mononuclear cells (PBMCs) and HIV-1 sequences collected at a single time point from different tissues. Four data sets included longitudinal sequences of the V1-V3 domain of the env gene sampled from PBMCs (7 to 10 viral clones at each time point) of four male subjects (Mild et al., 2007); the other two datasets contained V1-V3 env sequences collected at a single time point from plasma and cervicovaginal lavage (CVL) of two female subjects (Philpott et al., 2005). Details on the data sets are summarized in the first four columns of Table 1.

Table 1.

Non-parametric test of HIV-1 intra-patient subpopulation structure.

Study	Patient ID	No.sequences	No.separate samples	Population 1a	Population 2a	Pb
Mild et al (2007)	1865	40 (V1-V3)	4	M49 (1381)	M55 (1874)	< 10-10
				M55 (1874)	M61 (2337)	< 10-10
				M61 (2337)	M70 (3305)	< 10-10
Mild et al (2007)	2239	48 (V1-V3)	5	M25 (670)	M45 (1945)	< 10-10
				M45 (1945)	M68 (4032)	< 10-10
				M68 (4032)	M79 (5011)	0.0001
				M79 (5011)	M88 (5827)	< 10-10
Mild et al (2007)	2242	94 (V1-V3)	6	M18 (80)	M45 (1886)	< 10-10
				M45 (1886)	M56 (2919)	< 10-10
				M56 (2919)	M63/M63c (3560, 3596, 3707)	< 10-10
				M63/M64c (3560, 3596, 3707)	M76 (4874)	< 10-10
				M76 (4874)	M84/M84c (5598, 5632, 5681)	< 10-10
Mild et al (2007)	2282	72 (V1-V3)	5	M10 (615)	M21 (1251)	< 10-10
				M21 (1251)	M24 (1495)	0.9997
				M21/M24d (1251, 1495)	M41 (2974)	< 10-10
				M41 (2974)	M47 (3603)	< 10-10
				M47 (3603)	M62/M62c (5070, 5163)	0.0004
				M62/M62 (5070, 5163)	M70 (5696)	0.0375
Philpott et al(2005)	WC10	19 (V1-V3)	2	CVL	Plasma	0.0003
Philpott et al(2005)	WC14	16 (V1-V3)	2	CVL	Plasma	0.0001

^aMxx indicates the sampling time in months after seroconversion for the PBMCs longitudinal data (Mild et al. 2007) data. The identification number for sequences collected at a given time point within each one of the sets is given in parenthesis. CVL indicates cervicovaginal lavage (Philpott et al., 2005).

^bA p-value < 0.01 indicates that the null hypothesis of no structure between population 1 and 2 is rejected and the two subpopulations can be considered significantly different.

^cSamples were combined because of the close proximity in time of sampling (< 1 month).

^dSamples from the two populations were combined because the probably of panmixia (no structure) was > 0.01.

2.4. HIV-1 metapopulation structure

The algorithm described below aims at the detection of recombinant sequences in data sets that may also exhibit metapopulation structure. In case of sequences sampled from distinct subpopulations, the goal is to identify both intra-and inter-population recombinants. Therefore, before proceeding with the analysis, viral sequences from different time points and/or different tissues should be tested to confirm that they belong to statistically different viral subpopulations rather than freely intermixing. We explored the data sets with a test for population subdivision originally developed by Hudson, Boos and Kaplan (1992) and adapted to study HIV population by Achaz et al. (2004). The method calculates a matrix of pair-wise sequence differences from an aligned dataset including DNA or amino acid sequences from two putative subpopulations and two additional matrices for each subpopulation separately. The rationale is to detect patterns of genetic structure in which pair-wise differences within a subpopulation tend to be smaller than pair-wise differences between different subpopulations. Extensive simulations have shown that such a test is robust even in the presence of recombination (Achaz et al., 2004). If the p value is less than the nominal level of significance (1%), the null hypothesis of no structure is rejected and the two subpopulations can be considered significantly different. A web-based interface to carry out the population subdivision test is available at http://wwwabi.snv.jussieu.fr/~achaz/hudsontest.html.

2.5. Detecting Recombinant Sequences using a PHI-NNet algorithm

Different sub-alignments are generated for each discrete subpopulation as determined by the test described above (for example genetically distinct sequences from brain and from PBMCs, from different time points, etc.). Putative recombinant sequences are then progressively removed from each intra-population alignment until the PHI test for the remaining sequences is no longer significant (p > 0.05). Without any a priori information, any sequence in a given set could be a potential recombinant. An exhaustive algorithm would require removing in turn each sequence, and each possible combination of sequences to detect exactly which ones contribute the most to the recombination signal (i.e. low p-value in the PHI test). Due to combinatorial complexity, even for small datasets such a procedure would be unfeasible. Rather than blindly removing a sequence/combination of sequences in turn, NNets can be used to detect sequences of possible recombinant origin, as they typically are located at the vertices of large splits. This approach reduces considerably the number of possible combinations (although it can still be large for large data sets represented by complex networks). An increase in the p-value (i.e. lower signal for recombination) indicates that the excluded sequences are indeed potential recombinants. Otherwise, the sequences are included back in the data set and a new sequence (or group of sequences) is removed. The procedure continues until subsets of non-recombinant sequences (PHI test p-value > 0.05) for each intra-population alignment are found. Finally, all datasets from discrete populations are pooled together and the procedure is repeated to detect possible inter-population recombinants. A detailed description of the procedure is given in the Appendix.

2.6. Recombination analysis by Bootscanning and Genetic Algorithms

To locate possible recombination breakpoints, selected recombinants and their putative parental sequences detected by the PHI-NNet algorithm were also evaluated by bootscanning using the Simplot program (Lole et al., 1999), and by a genetic algorithm for recombination detection (GARD) developed by Kosakovsky Pond et al. (2006a). The GARD method was designed to screen multiple sequence alignments in search for evidence of segment-specific phylogenies. The algorithm searches for the location of all possible recombination breakpoints B (the best B is also inferred by the algorithm) and computes the phylogenies for each non-recombinant fragment. The goodness of fit of the model assuming B recombination breakpoints is then assessed with the Akaike Information Criterion (AIC_c). Therefore, GARD can test simultaneously for the presence of recombination and infer putative recombination breakpoints along the sequences. GARD analyses were carried out with the web-based version of GARD available at www.datamonkey.org (Kosakovsky Pond et al., 2006b).

3. Results

3.1. HIV-1 subpopulation structure

Each subset of sequences collected at a given time point (from subjects 1865, 2239, 2242, and 2282) or obtained from a specific tissue (plasma or CVL from subjects WC10 and WC14) was considered a potential subpopulation. The last three columns of Table 1 show the result of the subpopulation structure test comparing subpopulation pairs within each patient. In general, HIV-1 sequences obtained at different time points belonged to significantly different subpopulations (p < 0.01). Only two exceptions were found for patient 2282. Viral sequences obtained at month 21 (sequences id: 1251) and 24 (sequences id: 1495) post seroconversion were not significantly different (p = 0.9997) and they were pooled together as a single population in the following analysis. Similarly, sequences obtained from the same patient at month 62 (sequences id: 5070, 5163) and 70 (sequences id: 5596) did not show significant subpopulation structure (p = 0.037). The subpopulation test of HIV-1 sequences from CVL and plasma also indicated the presence of significantly different viral subpopulations within patient WC10 (p = 0.0003) and WC14 (p = 0.001), i.e. compartmentalization between the two tissues in both subjects, in agreement with the conclusions of the previous study (Philpott et al., 2005).

3.2. Detecting recombinant sequences by PHI test and phylogenetic networks (PHI-NNet)

Figure 1 shows the split decomposition graphs obtained with the NNet algorithm for each data set. NNets from PBMC longitudinal data sets (Mild et al., 2007) display a large number of splits indicating the presence of several conflicting phylogenetic signals (Figure 1A-D). In contrast, NNets for single time point HIV-1 sequences from CVL and plasma (Philpott et al., 2005), appear to be more tree-like with relatively fewer splits (Figure 1E-F). In each NNet, sequences detected as recombinants in the previous studies were highlighted in blue, while the additional recombinants detected by our analysis are shown in red. As expected, all the recombinant sequences were located at the vertices of large splits, although not every sequence at a vertex was found to be a recombinant. Table 2 shows in detail the recombination analysis using the PHI test for the combined datasets. Each dataset displayed strong evidence of recombination with p-values ranging from 10^-4 to 10^-99. Interestingly, the test detected significant recombination signal not only within the aligned HIV-1 V1-V3 sequences from subject 2239 (p < 10^-99), 2242 (p= 9.2 10^-9), and 2282 (p < 10^-99), but also from subject 1865 (p = 2.6 10^-5), WC10 (p = 2.5 10^-4), and WC14 (p = 5.5 10^-5) for which no recombinants were identified in the previous studies (Mild et al., 2007; Philpott et al., 2005). Except for sequence 4032.1 from subject 2239, which was found to be non-recombinant by our method (details are given in the next section), removal of sequences previously identified as recombinants from subjects 2239, 2242, and 2282 led to a decrease in the p-value by several orders of magnitude (Table 2). However, a strong recombination signal was still detected within each data set (p = 3.3 10^-13, 3.8 10^-4, and 1.08 10^-5, for subject 2239, 2242, and 2282, respectively), which disappeared only after further removal of previously undetected recombinant sequences. The percentage of recombinant sequences found in the different data sets ranged from 5% to 28%.

Figure 1. Phylogenetic networks for different HIV-1 data sets.

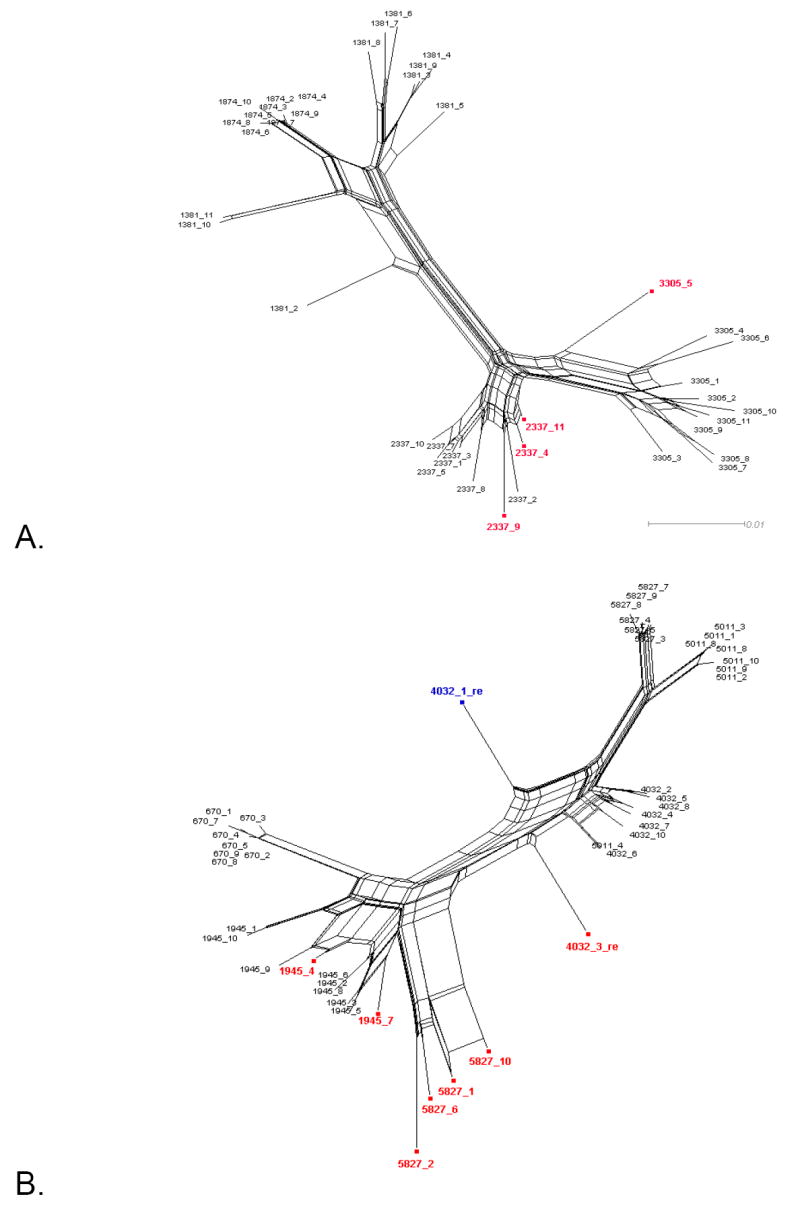
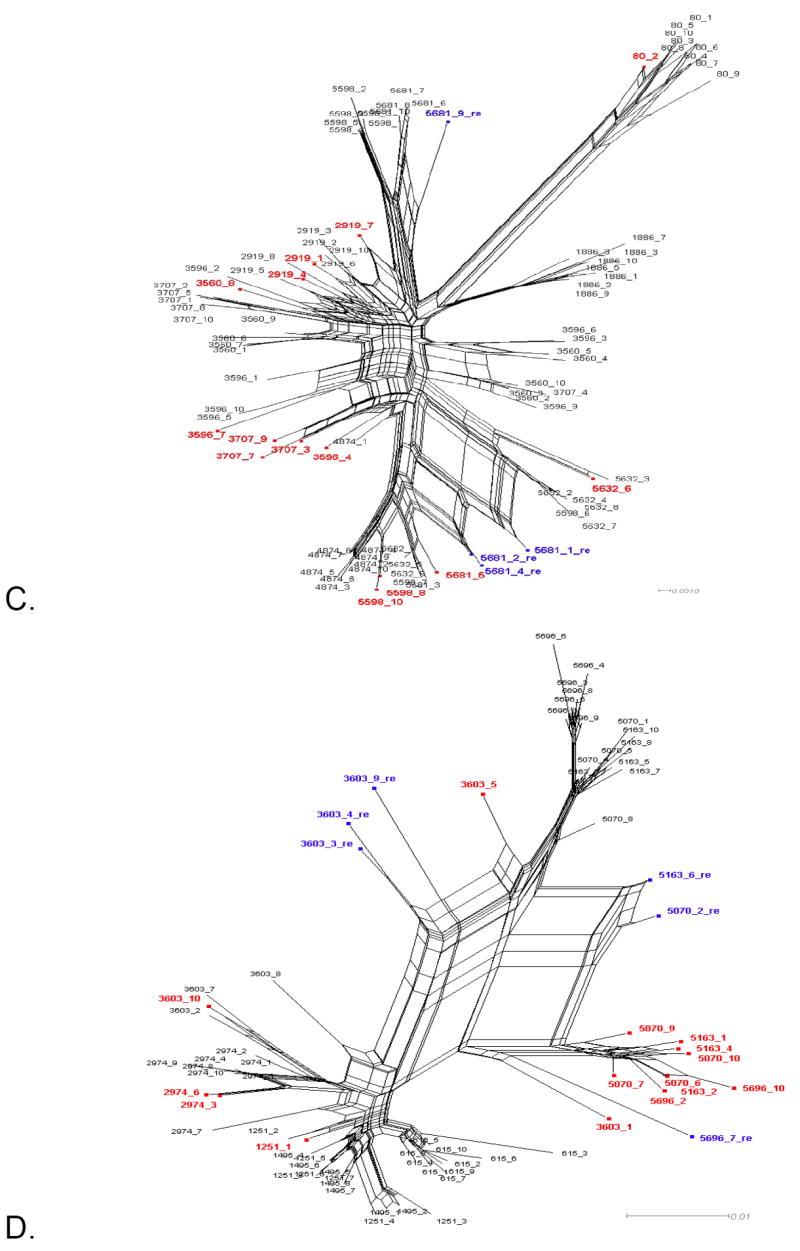
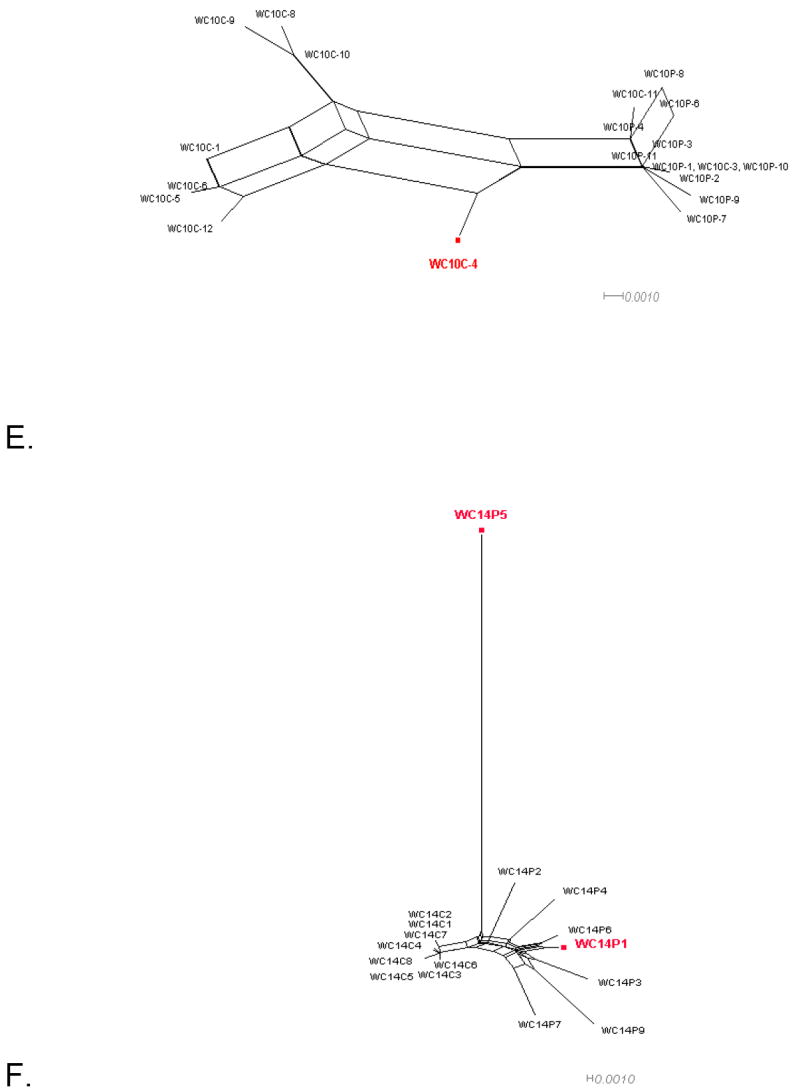
Neighbor-Nets (NNets) obtained with the split-decomposition method and uncorrected p-distances for different HIV-1 intra-patient data sets. Branch lengths are drawn to scale with the bar at the bottom indicating 0.01 nucleotide substitutions per site. Panels A-D include data sets from Mild et al. (2007). Panels E-F data sets from Philpott et al. (2005). Sequences identified as recombinant in the previous study are shown in blue; sequences identified as additional recombinants in this study in red. A. Patient 1865. B. Patient 2239. C. Patient 2242. D. Patient 2282. E. Patient WC10 F. Patient WC14.

Table 2.

PHI test of recombination for different HIV-1 intra-patient data sets

Patient ID	Previously identified recombinants	Recombinants detected by PHI-NNet		P-value (1)	P-value (2)	P-value (3)
1865	-	2337.4	2337.11	2.641 10-5	-	0.056 (10%)
		2337.9	3305.5
2239	4032.1*	1945.4	5827.2	< 10-99	3.302 10-13	0.111 (15%)
	4032.3*	1945.7	5827.6
		4032.3*	5827.10
		5827.1
2242	5681.1*	80.2	4874.1	9.242 10-9	3.844 10-4	0.072 (20%)
	5681.2*	2919.1	5632.6
	5681.4*	2919.4	5598.8
	5681.9*	2919.7	5598.10
		3560.8	5681.1*
		3596.4	5681.2*
		3596.7	5681.4*
		3707.3	5681.5
		3707.7	5681.9*
		3707.9
2282	3603.3*	1251.1	5070.7	< 10-99	1.085 10-5	0.111 (28%)
	3603.4*	2974.3	5070.9
	3603.9*	2974.6	5070.10
	5070.2*	3603.1	5163.1
	5163.6*	3603.3*	5163.2
	5696.7*	3603.4*	5163.4
		3603.5	5163.6*
		3603.9*	5696.2
		5070.2*	5696.7*
		5070.6	5696.10
WC10	-	C4		2.506 10-4	-	0.187 (5%)
WC14	-	P1 P5		5.509 10-5	-	0.305 (12%)

Sequences in bold were not identified as recombinant when analyzed by time point.

Sequences identified by the previous studies are indicated by an asterisk.

(1) PHI test p-value: All sequences

(2) PHI test p-value: Recombinants identified in the previous study removed

(3) PHI test p-value: All recombinants detected using the new algorithm removed. The percentage of recombinant sequences in the data set is given in parenthesis.

Table 3 shows the results of the PHI test for each subpopulation separately. In general, sequences from earlier time points did not show significant signal for recombination (p > 0.05), and only one sequence from CVL and two from plasma were detected as recombinants in subject WC10 and WC14, respectively. A comparison of Table 1 and Table 3 shows that 20% to 75% of the recombinant sequences in the longitudinal data sets (subject 1865, 2239, 2242, and 2282) could only be detected after pooling sequences from different time points together. The finding suggests that ancestral sequences originated at different time points were still circulating in the blood at the time of recombination. On the other hand, no inter-tissue (CVL/plasma) recombinants were found by our analysis.

Table 3.

PHI test of recombination (by subpopulation) for different HIV-1 intra-patient data sets.

Patient ID	Month/Compartment	Sequences ID	p-value (all sequences)*	Sequences Removed		p-value (recombinants removed)
1865	49	1381	0.630	-		-
	55	1874	NI	-		-
	61	2337	0.001	2337.4		0.080
	70	3305	0.063	-		-
2239	25	670	NI	-		-
	45	1945	0.000	1945.4	1945.7	0.669
	68	4032	0.217	-		-
	79	5011	NI	-		-
	88	5827	0.035	5827.2	5827.10	0.209
2242	18	80	0.003	80.2		0.084
	45	1886	0.240	-		-
	56	2919	0.052	-		-
	63, 63 64	3560, 3596, 3707	8.815 10-7	3596.4 3596.7 3707.3	3707.7 3070.9 3560.8	0.080
	76	4874	NI	-		-
	84, 85 :1, 85:2	5598, 5632, 5681	<10-99	5681.1 5681.2 5681.4 5681.5 5681.9	5598.8 5598.10 5632.6	0.011
2282	10	615	1.0	-		-
	21, 24	1251, 1495	0.026	1251.1		0.122
	41	2974	0.002	2974.3	2974.6	1.0
	47	3603	5.673 10-14	3603.5	3603.9	0.211
	62, 63, 70	5070, 5163, 5696	2.063 10-8	5696.7 5070.9 5163.6		0.058
WC10	CVL	WC10-C	5.264 10-4	10C4		0.427
	Plasma	WC10-P	1.0	-		-
WC14	CVL	WC14-C	NI	-		-
	Plasma	WC14-P	0.006	14P1	14P5	0.559

^*NI = not informative (not enough sequences and/or nucleotide substitutions to carry out the PHI test

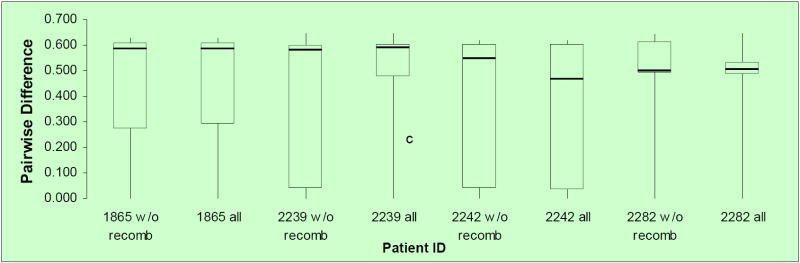
Removing recombinant sequences from our datasets may have significantly reduced genetic diversity diminishing the statistical power of the PHI test. To test this possibility, we obtained box-plots of pair-wise p-distances for each of the longitudinal PBMC datasets analyzed either before (including all sequences) or after (including only non-recombinant sequences) the recombinants were removed. As shown in Figure 2, removing the recombinants did not significantly lower the genetic diversity of any of the data sets studied indicating the reliability of our results.

Figure 2. Box-plots of pair-wise p-distances among HIV-1 DNA sequences from different subjects.

Pair-wise distances were obtained for each HIV-1 PBMC longitudinal dataset from Mild et al. (2007). Patient ID and whether recombinants were excluded (w/o) or including (all) are indicated along the x-axis. The distribution of p-distances, reported along the y-axis, is depicted as boxes, with the lower and upper limits of the box delineating the 25th and 75th percentiles and the bars indicating the 10th and 90th percentiles, respectively.

3.3. In-depth recombination analysis and breakpoints detection

In order to locate putative recombination breakpoints, programs such as bootscanning or GARD can be used to analyze recombinant sequences identified by the PHI-NNet algorithm. As an example, we will discuss in detail the analysis of the data set from subject 2239. Two recombinants were detected within this data set by the previous study: sequence 4032.1 and 4032.3 (Mild et al., 2007). Our final analysis identified 4032.3 and six additional sequences as recombinants (Table 2).

Four sequences (1945.4, 1945.7, 5827.2, and 5827.10) were initially determined to be recombinant when individual time points were analyzed (Table 3), and were removed from the dataset. However, the PHI test was still significant for the remaining sequences when analyzed together (p = 1.37 10^-10), and remained significant even after removal of sequence 4032.3 (p = 3.85 10^-5), previously detected as recombinant (Mild et al., 2007), thus indicating the presence of other inter-time point recombinants. The inferred NNet displayed four major splits indicated by a, b, and c and d in Figure 3A. The p-value was no longer significant for recombination only after removing the sequences within group a (p = 0.11), although a few splits were still visible in the new inferred NNet (Figure 3B). These splits are most likely the result of homoplastic mutations and do not represent undetected recombinant sequences. In contrast, including sequences from group a and excluding sequences from group b, c, d, or sequence 4031.1 in turn, always generated higher recombination signal within the data set (p = 4.78 10^-7, 0.003, 1.85 10^-4, 1.99 10^-4, after removing group b, c, d, or sequence 4031.1, respectively). Two breakpoints, at nucleotide position 300 and 430 (HXB2 nucleotide position 6860 and 6990), were visible in the bootscanning with group a sequences as query (Figure 3C), suggesting that their mosaic genomes originated from two recombination events between lineage 4032 and lineage 1945. Notice, however, that the bootstrap support clustering the query sequences with lineage 4032 after the first breakpoint, and again with lineage 1945 after the second one is relatively low (between 30% and 70%, with only one peak > 70%). In fact, the analysis using GARD (Figure 3D) only found one significant recombination peak at position 311 (HXB2 position 6871), which was very close to the first recombination breakpoint inferred by bootscanning. Finally, the bootscanning obtained using sequence 4032.1 as query (Figure 3E) displayed several peaks of extremely low bootstrap values (15% to 60%), while no recombination breakpoints were inferred by GARD (data not shown). Therefore, although the bootscanning seems to imply that sequence 4032.1 has mosaic genome originated from multiple recombination events, such a conclusion is at best ambiguous. A more conservative interpretation would suggest that 4032.1 is a divergent lineage displaying, in agreement with the PHI test, no significant signal for recombination.

Figure 3. Schematic illustration of recombination breakpoints analysis exemplified by clones from patient 2239.

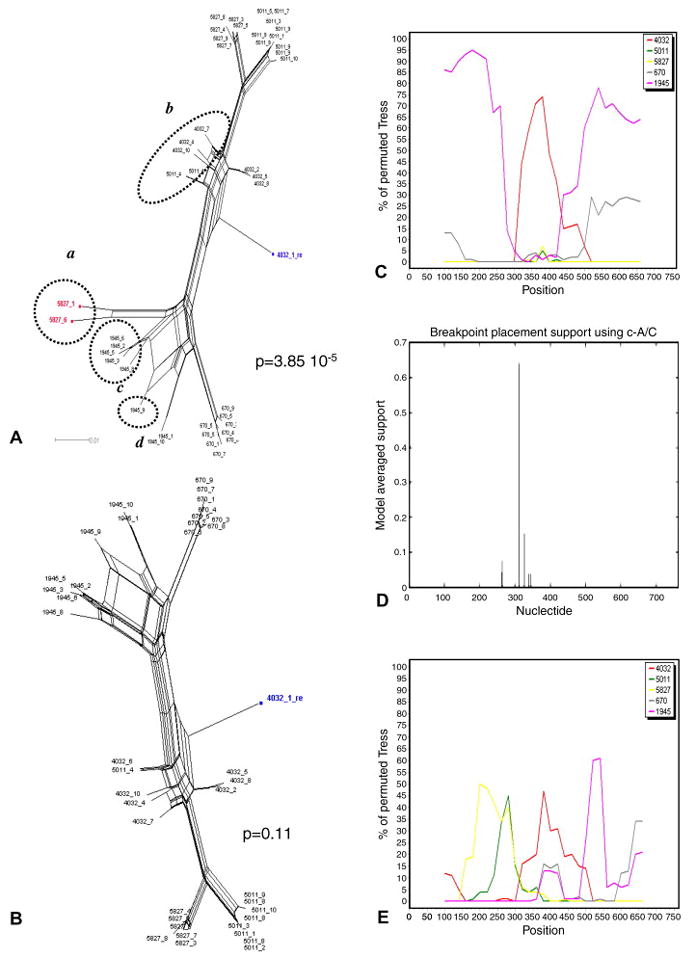
A. Neighbor-Nets (NNets) obtained with the split-decomposition method and uncorrected p-distances using sequences from patient 2239. The p-value of the PHI test is also indicated. Recombinant sequences are highlighted in red. A putative recombinant sequence identified in the previous study (Mild et al., 2007) is highlighted in blue. Dotted circles include potential recombinant sequences belonging to other major splits. B. NNet and PHI test p-value after removing the recombinant sequences highlighted in red in the previous panel. C. Bootscanning using recombinant sequences highlighted in red in panel A as query. Putative parental sequences were chosen using the NNet in panel A as a guidance, and are indicated by different colors according to the legend in the box on the right. The bootstrap support is shown on the y-axis. D. Recombination breakpoints analysis including all sequences in panel A using GARD. E. Bootscanning using the putative recombinant sequence 4032.1, highlighted in blue in panel A, as query.

4. Discussion

We described an exploratory algorithm developed to detect recombination among closely related sequences, for example intra-host recombination within viral population, based on the well established PHI statistic in conjunction with split-decomposition networks. Since recombination violates the basic assumption of a bifurcating evolutionary process, the inclusion of recombinants in phylogenetic analysis can easily lead to serious mistakes in the interpretation of the results. Our approach offers three advantages over traditional techniques such as bootscanning. First, it is based on the PHI test for recombination which has been shown through extensive simulation studies to be reliable regardless of population history, recombination rate, mutation rate, and rate heterogeneity across sites underlying the data (Bruen et al., 2006a). Second, it does not require the previous knowledge of putative parental sequences in order to detect recombination. Third, although large splits in networks do not necessarily imply recombination, split decomposition networks in conjunction with the PHI test can easily detect which sequences in a given data set contribute the most to the recombination signal.

Our analysis of published data sets, which were already investigated for the presence of HIV-1 intra-host recombinants, confirmed all but one of the previously identified recombinant sequences. However, the PHI test showed that even after the exclusion of such sequences, each subset still displayed a strong statistical signal for recombination. By progressively removing sequences at the vertices of large splits in the phylogenetic networks obtained from each alignment, our algorithm detected several recombinants missed by previous analyses. The detection of recombinant sequences in such studies was based on the estimation of separate phylogenetic trees for different genomic regions (for example the V1-V2 and V3 regions of the env gene) and/or on the bootscanning method (Mild et al., 2007; Philpott et al., 2005). In both methods, a given sequence is considered recombinant if it clusters with different groups of sequences separated by significant (>90%) bootstrap value in two (or more) trees inferred from different genomic regions. It has been demonstrated that such a strategy is not very powerful in detecting recombination, especially in cases of low sequence diversity (Posada and Crandall, 2001). First, the strategy relies on the estimation of phylogenetic trees based on short alignments (usually 200-600 nucleotides). Such trees often lack resolution because of low phylogenetic signal, especially when closely related sequences are investigated. Second, tree-building algorithms can be biased severely by the presence of homoplasy making it difficult to distinguish between true homology (clustering due to common ancestry) and convergent evolution (Felsenstein, 2004). Third, bootstrapping as a measure of support for a specific cluster can be misleading (Felsenstein and Kishino, 1993; Hillis and Bull, 1993). For example, if the tree construction method makes a bad estimate of the phylogeny due to systematic errors, which are caused by incorrect assumptions in the tree construction method, or if the sequence data are not representative of the underlying distribution, the resulting confidence intervals obtained by the bootstrap are not meaningful (Van de Peer, 2003). Therefore, it is not surprising that most recombinant sequences were missed by the previous studies.

This algorithm should be considered as an exploratory tool to investigate both the overall degree of recombination in a dataset as well as putative recombinant sequences. It is possible that the minimization criteria may result in the removal of parental sequences if the recombinant offspring are more numerous in the dataset, and additional methods could be used to confirm that the removed sequences are in fact recombinants. However, because of the high degree of recombination in HIV-1, the majority of sequences over time could be of recombinant origin, but they may also contain valuable phylogenetic signal if they have been evolving via point mutations after the early recombination event. Thus identifying the original “true” parental sequences if they are not sampled remains a major computational challenge.”

Our algorithm identified sequences significantly contributing to the recombination signal within HIV-1 intra-patient strains collected at both multiple time points from PBMCs and at the same time point from different tissues. The finding that up to one third of the sequences from the PBMC longitudinal data sets were of recombinant origin strongly suggests that the extent of HIV-1 intra-patient recombination may have been largely underestimated by previous studies employing phylogeny-based methods. Caution may be advised in interpreting inter-timepoint recombinants because, in general, methods not based on a phylogeny may not be able to appropriately incorporate rate and lineage information which thus may affect recombinant identification. Methods designed specifically for longitudinal datasets (e.g. Buendia and Narasimhan, 2007) could be used to confirm these recombinants. However, our analysis recovered far more recombinants within a single timepoint than the previous studies, which supports our overall conclusion. Since our algorithm tests for the presence of both intra-and inter-population recombinants, it could be an extremely useful tool to investigate HIV-1 subpopulation structure. However, its application is quite general and can be used to investigate the presence of recombinants in any alignment of closely related nucleotide or amino acid sequences for which traditional methods may lack sufficient power.

Appendix – Detailed protocol of the PHI-NNet algorithm

1. Protocol to detect intra-population recombinants:

   1. Infer a NNet and test for recombination.
   2. If p > 0.05, go to step VIII
   3. If p < 0.05, use the NNet to locate sequences on the network displaying ambiguous phylogenetic signals (possible recombinant sequences)
   4. Remove a possible recombinant sequence based on its position at the vertex of splits in the graph unless that sequence was already unsuccessfully removed [if a monophyletic clade appears to be of recombinant origin, like sequence 2 and 3 in Figure 3C, remove all the sequences in that clade simultaneously]
   5. Infer a NNet and test for recombination.
   6. If p increases by at least 0.1, consider the excluded sequence(s) as possible recombinant(s) and go back to II
   7. Otherwise, the sequences have been removed unsuccessfully: include the sequences back in the data set and go back to I
   8. If no sequences were identified as recombinants, stop. Otherwise, go to IX
   9. If some sequences were excluded (possible recombinants), each sequence (group of sequences) identified as possible recombinant(s) should be put back into the data set in turn to determine if the p-value remains > 0.05. The fewest number of sequences required to obtain the highest non-significant p-value should be used [If an equal number of different sequences give a p-value >0.05, the sequence(s) that give the largest p-value should be chosen as the recombinants].
2. Detecting inter-population recombinants:

   1. Combine the non-recombinant sequences from each intra-population dataset found after implementing protocol A
   2. Use protocol A to detect the possible presence of recombinant sequences within the inter-population dataset.