Intron positions correlate with module boundaries in ancient proteins

Abstract

We analyze the three-dimensional structure of proteins by a computer program that finds regions of sequence that contain module boundaries, defining a module as a segment of polypeptide chain bounded in space by a specific given distance. The program defines a set of “linker regions” that have the property that if an intron were to be placed into each linker region, the protein would be dissected into a set of modules all less than the specified diameter. We test a set of 32 proteins, all of ancient origin, and a corresponding set of 570 intron positions, to ask if there is a statistically significant excess of intron positions within the linker regions. For 28-Å modules, a standard size used historically, we find such an excess, with P < 0.003. This correlation is neither due to a compositional or sequence bias in the linker regions nor to a surface bias in intron positions. Furthermore, a subset of 20 introns, which can be putatively identified as old, lies even more explicitly within the linker regions, with P < 0.0003. Thus, there is a strong correlation between intron positions and three-dimensional structural elements of ancient proteins as expected by the introns-early approach. We then study a range of module diameters and show that, as the diameter varies, significant peaks of correlation appear for module diameters centered at 21.7, 27.6, and 32.9 Å. These preferred module diameters roughly correspond to predicted exon sizes of 15, 22, and 30 residues. Thus, there are significant correlations between introns, modules, and a quantized pattern of the lengths of polypeptide chains, which is the prediction of the “Exon Theory of Genes.”

Do introns delineate elements of protein tertiary structure? This issue is crucial to the debate about the role and origin of introns (1–8): did introns appear at the beginning of evolution, creating the first genes by exon shuffling, or did they arise during evolution by the insertion of adventitious elements into genes? The “introns-early” view predicts that the exons should represent functional or folding elements of protein structure (1–4), whereas the “introns-late” view (5–8) expects that the insertion of introns might respect DNA sequence but should be uncorrelated with protein structure.

The Exon Theory of Genes (1), an expansion of the introns-early approach, hypothesizes that the first protein coding genomes had an intron–exon structure in which the introns served as hotspots of recombination to shuffle exons to create the first genes. The products of the original coding elements, the first exons, were short polypeptides 15–20 amino acids long that served as elements of folding or function. This theory holds that over time small exons were fused together by reverse transcriptase-mediated retroposition to make more complicated exons to be shuffled in turn. [A complete example of the creation of complex exons by retrotransposition has been worked out for the gene Jingwei in Drosophila (9)]. Two or three fusions on average would be needed to lead to today’s exon distribution peaked at 35–40 residues (10).

The Exon Theory of Genes holds that the basic processes of gene evolution were exon shuffling, the sliding and drift of introns at exon boundaries, and the creation of complicated exons by the loss of introns. Intron loss is hypothesized to be very easy and to occur down all lines that specialize for rapid replication, such as the bacteria or Saccharomyces cerevisiae (11).

The critical prediction of the Exon Theory of Genes is that proteins will turn out to be assembled from small folding elements, modules in the sense of Mitiko Gō (regions of the polypeptide chain that are compact in space), which will be related to the products of exons. Although a variety of arguments for early introns have been advanced, some of which include the use of the module hypothesis to predict the existence of certain introns (12–14) while others involve the coincidence of intron positions in genes separated by great evolutionary distances (13), arguments for the introns-late view have recently appeared.

Stoltzfus and collaborators (6) attacked the general notion that exons were related to elements of protein structure by showing that introns were not correlated with the ends of protein secondary structure elements (α-helices and β-sheets) and challenged all efforts to show a connection between exons and modules. Palmer and coworkers (5) argued that introns arose late in evolution, based on the broad phylogenetic distribution of introns (lacking in bacteria and many protists present in higher eukaryotes), as well as on the specific distribution of novel introns in triosephosphate isomerase (8). These defenders of the introns-late view challenge all notions of intron sliding or drift (15) and assert that introns very close in position in homologous genes represent separate acts of addition. That novel introns can arise in general is supported by the finding of introns in the U6 RNA in fungal species (16–18), which clearly have arisen recently by reverse splicing followed by reverse transcription and gene conversion. However, some introns arising late does not prove that all introns were late. The problem is to detect whether or not some introns arose early. This paper introduces a statistical test to demonstrate that introns correlate with module boundaries in ancient proteins and shows that this correlation is neither due to a composition or sequence bias in the module boundaries nor to a surface bias in intron position. We argue that this correlation strongly suggests that there was exon shuffling in the progenote.

MATERIALS AND METHODS

Sample.

The data (Table 1) consists of 32 ancient conserved proteins, which have homologs without introns in prokaryotes and with introns in eukaryotes, and their intron positions. Intron positions were defined by aligning the homologous sequences to the Protein Data Bank (PDB) reference sequence with clustal v and counting each position and phase separately to yield 570 instances. These proteins represent all the full-length ancient proteins with known coordinates that appear in an intron data base of ancient proteins. The PDB files occasionally have missing residues, for which coordinates were not determined. For such missing residues, we supplied dummy coordinates for the α-carbon positions by linear interpolation. The intron data base, based on GenBank 90, is an updated version of a similar data base based on GenBank 84 and previously described (10).

Table 1.

The sample of 32 proteins

Protein	Abbreviation	PDB
Acid amylase	ACIDAMY	2AAA
Acyl-CoA dehydrogenase	ACYL	3MDD
Aldolase	ALDOL	1ALD
Aldose reductase	ALREDUC	1DLA
Alcohol dehydrogenase	ADH	1ADB
Alkaline phosphatase	ALK	1AJA
Amylase	AMY	1PPI
Aspartate aminotransferase	AAT	1AMA
Catalase	CAT	8CAT
Citrate synthase	CSYN	1CTS
Cu-superoxide dismutase	CUSOD	1SDY
Cytochrome c	CYT	1CCR
Dihydrofolate reductase	DHFR	1DHF
Elongation factor TU	EFTU	1EFT
Enolase	ENOL	1EBG
Glucose-6-phosphate dehydrogenase	G6PD	1DPG
Gluthatione S-transferase	GST	1GSS
Glyceraldehyde 3-phosphate dehydrogenase	GAPDH	3GPD
Glycogen phosphorylase	GLYPHOS	1GPA
Heat-shock protein 70	HSP70	1ATR
Hemoglobin	HEMO	2DHB
High pI amylase	HIAMY	1AMY
Lactate dehydrogenase	LDH	2LDX
Lysozyme	LYS	1LAA
Malate dehydrogenase	MDH	4MDH
Mn-superoxide dismutase	MNSOD	1MSD
Phosphoglycerate kinase	PGK	3PGK
Phosphofructokinase	PFK	3PFK
Phosphoglycerate mutase	PGM	3PGM
Pyruvate kinase	PK	From author
Triosephosphate isomerase	TPI	1TIM
Xylanase	XYLA	1CLX

The last column lists the PDB entry that yielded the coordinates. Where the PDB files were missing a few coordinates the α-carbon positions were filled-in by linear interpolation. Pyruvate kinase coordinates were supplied by H. Muirhead (University of Bristol, United Kingdom). 

Algorithm.

inter-module is written in ansi c and compiled with a Sun C compiler in SunOS 4.1 (on a Sun SPARCstation 10). The source code will be available in our web site (http://golgi.harvard.edu/gilbert.html).

RESULTS

Modules and Linker Regions.

We define a module as a continuous region of polypeptide chain all of whose α-carbons lie less than a defined distance apart, the module “diameter.” Such a region lies inside a geometric volume of constant diameter called a “Reuleaux Form.” For a given diameter d, the Reuleaux Form of largest volume is a sphere of diameter d. In general, a Reuleaux Form in three dimensions can be circumscribed by a sphere of diameter ≤ 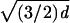. If the polypeptide chain fills the Reuleaux Form, the module would represent a compact element along the chain. On a triangular Gō plot (12) of the distances between each pair of α-carbons in a three-dimensional structure, if all distances greater than the defining size are shaded black, then any right triangle drawn along the diagonal that does not contain black regions will define a module. The longest-chain modules correspond to those triangles whose size is limited by touching black regions on both sides. Fig. 1 shows such a Gō plot: the five large triangles define the set of longest chain modules at 28 Å.

Figure 1.

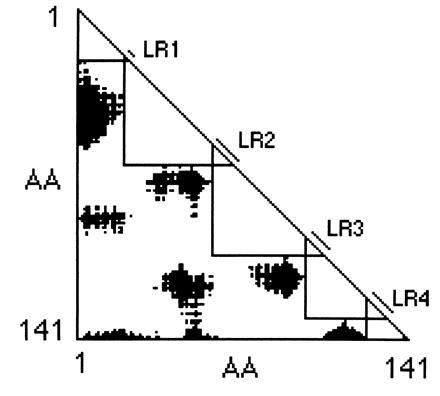
Gō plot for hemoglobin. The black regions represent pairs of α-carbons that are separated by 28 Å or more in horse hemoglobin (2DHB). Five modules are identified by large triangles along the diagonal, whose size is limited by touching the black regions. The linker regions (LR) are defined as the region of overlap of those triangles.

Although this definition enabled one to hypothesize the relationship between exons and modules and to predict the existence of certain introns (12–14), it does not provide an obvious way to predict specific boundaries for each module.

The problem is essentially that the longest chains at 28 Å (Fig. 1) overlap, and so, if one is to draw smaller triangles for non-overlapping modules, the Gō plot offers no guidance as to where to mark the boundaries. We turn this problem around by defining the overlaps between the longest modules as “linker regions” (Fig. 1). If an intron were to be placed in each linker region, the protein would be dissected into a set of modules each less than 28 Å in diameter.

This notion of linker regions immediately defines a simple statistical test, a χ² test, for the correlation of intron positions and module boundaries. If the introns were correlated with modules, one expects an excess of intron positions to fall within linker regions. If the introns have been added to previously existing DNA sequences, one expects the intron positions to be arranged randomly, and there should be no significant excess in the linker regions.

To define the linker regions objectively, we have written a computer program, inter-module, which first takes a Brookhaven Protein Databank file of coordinates, constructs a Gō plot of distances between α-carbons, and then, for a specified distance criterion, defines the set of linker regions. Where the triangles overlap nicely, as in Fig. 1, the definition of linker regions is straightforward. In general, the program begins with the longest chain N-terminal module and then, at that module’s C-terminal residue, constructs the largest module (right triangle) possible by first extending its C-terminal boundary until that line touches a black area and then increasing its size until its N-terminal boundary touches a black area. The program then repeats for the next module. The overlaps of these modules define the linker regions.

Tests at a 28-Å Module Size.

Is there a statistically significant excess of intron positions within the linker regions? We first examine 28-Å modules, since modules of this size were defined by Mitiko Gō for her analysis of hemoglobin and her prediction of a novel intron (12) and were used again for the prediction of introns in triosephosphate isomerase (13, 14). Table 2 shows that 216 of the 570 introns lie in the 28-Å linker regions, almost 34 more than expected on a random basis. This distribution has χ² = 9.0; P < 0.003. We can reject the null hypothesis that introns are located randomly in genes; rather they show a preference for the boundaries of 28-Å modules in the protein products.

Table 2.

Intron positions in linker regions

Protein	Fraction	No. introns	E	O	O-E	P
AAT	0.24	30	7.3	10	+2.7	0.27
ACIDAMY	0.31	9	2.8	3	+0.2	0.99
ACYL	0.43	15	6.5	5	−1.5	0.43
ADH	0.22	38	8.5	9	+0.5	0.99
ALDOL	0.31	17	5.2	8	+2.8	0.14
ALK	0.30	10	2.9	1	−1.9	0.18
ALREDUC	0.30	16	4.8	7	+2.2	0.22
AMY	0.34	17	5.7	6	+0.3	0.99
CAT	0.29	20	5.9	7	+1.1	0.65
CSYN	0.26	4	1.0	1	0.0	1.0
CUSOD	0.35	23	8.1	4	−4.1	0.07
CYT	0.31	7	2.2	4	+1.8	0.14
DHFR	0.42	13	5.5	10	+4.5	0.01
EFTU	0.42	10	4.2	5	+0.8	0.68
ENOL	0.35	28	9.8	10	+0.2	0.99
G6PD	0.28	19	5.4	6	+0.6	0.75
GAPDH	0.40	46	18.6	24	+5.4	0.1
GLYPHOS	0.28	20	5.6	8	+2.4	0.22
GST	0.25	28	7.0	6	−1.0	0.70
HEMO	0.23	15	3.4	8	+4.6	0.005
HIAMY	0.36	4	1.4	1	−0.4	0.68
HSP70	0.36	31	11.1	16	+4.9	0.07
LDH	0.27	11	3.0	3	0.0	1.0
LYS	0.32	4	1.3	1	−0.3	0.99
MDH	0.22	23	5.1	3	−2.1	0.28
MNSOD	0.26	12	3.1	3	−0.1	0.99
PFK	0.26	26	7.5	14	+6.5	0.006
PGK	0.41	20	8.2	9	+0.8	0.75
PGM	0.35	5	1.8	2	+0.2	0.99
PK	0.44	16	7.0	6	−1.0	0.65
TPI	0.36	21	7.6	9	+1.4	0.52
XYLA	0.35	12	4.2	7	+2.8	0.09
Total		570	182.5	216

A listing for each protein of the fraction of the sequence that lies in the linker regions, the total number of intron positions, the expected (E) and observed (O) number of intron positions within the linker regions, and the excess of observed over expected (O–E). The χ² value for the overall sum of E and O values, using a two-way test for excess inside and depletion outside, appears at the bottom: χ² = 9.0, P < 0.003. 

If the excess of introns in the linker regions is due to a signal from ancient introns, seen above a background of added or moved introns, then in a subset of clearly “old” introns that excess should be greater. Table 3 lists 20 “old” introns: introns conserved in position between at least three of the groups of vertebrates, invertebrates, plants, and fungi. (This identification of conserved introns accepts a small amount of sliding, up to four codons). Fourteen of the 20 introns are located within the linker regions, rather than the 6.4 expected; P < 0.0003. This sharply higher significance argues that the intron/module correlation is a consequence of the age of the intron.

Table 3.

Old introns

Protein	Intron position	Status
TPI	38	In
TPI	79	Out
TPI	108	Out
TPI	152	In
TPI	181/4	In
TPI	210	In
GST	148/51	In
HEMO	30	Out
HEMO	100	In
ALDOL	266/9	In
PFK	264/6	In
GAPDH	9	In
GAPDH	43	In
GAPDH	75/8/9	In
GAPDH	146/7	Out
PGK	22	In
PGK	91/2/3	In
CUSOD	23/4	Out
HSP70	69	In
ENOL	60/4	Out

A listing of 20 “ancient” introns identified as having matching positions in three out of four groups of vertebrates, invertebrates, plants, or fungi. Introns were considered homologous if they had slid up to four codons. The status column defines their character with respect to the linker regions for 28-Å modules (using the average position for slid introns). Fourteen of the 20 intron positions are within the linker regions rather than the 6.4 expected: χ² = 13.3, P < 0.0003.  

Tests of Insertional Models.

Could this excess of intron positions within linker regions be explained by some biased addition model? Such a model might hypothesize that there is a bias in DNA composition or sequence in the linker regions, possibly caused by an amino acid bias, that would serve to target an excess of intron additions to these regions. One such model would follow from the hypothesis of Craik et al. (19) that intron positions lie on the surface of proteins. If it were true that introns entered more frequently into codons for surface residues and if module boundaries were to lie on the surface of proteins, then intron positions and module boundaries would be correlated, but not in a causal fashion.

We find no support for such insertional models. The linker regions for the set of 32 proteins show no significant variation from the global average in amino acid or DNA composition. The frequency of hypothesized “proto-splice sites,” such as AGGT or AGG (20), show no preference for linker regions (0.42% in linker regions vs. 0.44% in general for AGGT or 1.60% in linker regions vs. 1.89% for AGG). Furthermore, neither the linker regions nor the intron positions are unusually located on the protein surface. Using the program naccess (21) to calculate the relative accessibility [the percent accessibility of each residue in the protein compared with its solvent accessibility in an Ala-X-Ala tripeptide (22)], we find that the relative accessibility of the average residue is 26 ± 26%, of the linker region 20 ± 19%, and of the introns, 25 ± 24% (±SD). Fig. 2 shows the detailed distribution of relative accessibility values for residues of these three classes. The hypothesis of Craik et al. (19) that intron insertions are restricted to the surface of proteins is not supported by these data.

Figure 2.

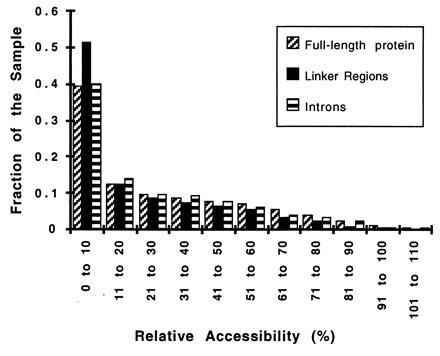
Distribution of relative accessibility values for introns. A histogram of the relative accessibility as defined by naccess (ratio of solvent accessibility in the structure to that in the tripeptide Ala-X-Ala) for residues in general in the 32 proteins, residues in the linker regions, and residues that contain introns or that flank phase 0 introns.

General Test at All Module Sizes.

Since inter-module will predict linker regions for any module diameter, one is not restricted to a 28-Å criterion. Fig. 3A shows the excess of intron positions inside the linker regions for the range of module diameters from 6 to 50 Å. Fig. 3B plots the corresponding χ² values. There are three major peaks in both excess introns and statistical significance at module diameters centered at 21.7, 27.6, and 32.9 Å, all with P values around 0.001. The peak near 28 Å corresponds to the traditional module size.

Figure 3.

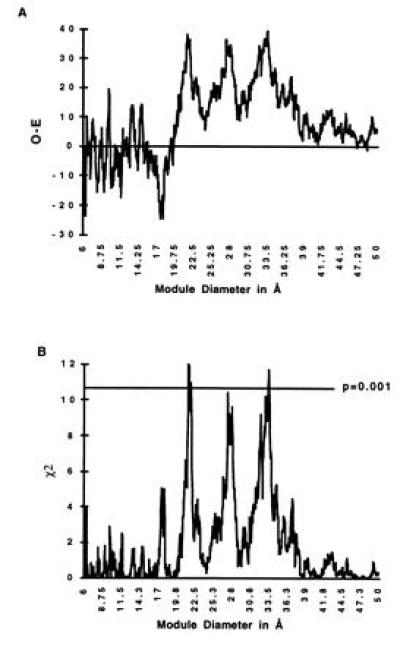
Excess intron positions in linker regions as a function of module diameter. (A) The excess (Observed-Expected, O-E) values for each module diameter ranging from 6 to 50 Å in intervals of 0.05 Å. (B) The χ² values for the excess. There are peaks of significance. The peaks centered at 21.7, 27.6, and 32.9 Å have P values around 0.001. The peak values are at 21.4, 27.4, and 33.5 Å, with χ² = 12.0, 10.4, and 11.7, respectively.

How are these significant module diameters to be understood? In predicting linker regions, inter-module is effectively predicting a set of exons for each three-dimensional structure. We calculated the average internal exon length (and standard deviation), assuming “exons” to be defined as lying between the midpoints of the linker regions, for each of these peaks. Fig. 4 shows that the three peaks correspond to exon sets that are roughly 15, 22, and 30 amino acid residues in length (15 ± 5, 22 ± 9, and 30 ± 14).

Figure 4.

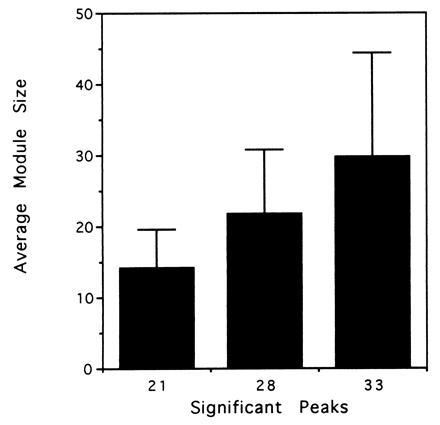
Lengths of predicted exons for each of the peaks of significance. inter-module predicts the length of internal exons (defined between the mid-points of the linker regions) for the module diameters corresponding to the peaks of significance centered at 21.7, 27.6, and 32.9 Å. The plot shows the average and standard deviation of the internal exons. The three peaks correspond to distributions centered around 15, 22, and 30 amino acids.

DISCUSSION

This finding of a correlation of intron positions with the boundaries of modules, corresponding to exon sizes of 15, 22, and 30 amino acid residues, fulfills the prediction of the Exon Theory of Genes and suggests that we are seeing a residual signal of the ur-exons that combined to make the present exons.

Is this statistical signal what one would expect if these ancient protein genes had been assembled by exon shuffling in the progenote? Any signal of correlation would have been weakened over time by very easy intron loss (2, 3), by intron sliding or slipping (15), or by intron addition (16–18). Furthermore, any agreement between the three-dimensional structure of the original exons and that of their descendants would be weakened through changes in the protein shape arising by mutation and selection after assembly. Thus, one expects only a small fraction of the current introns and module boundaries to match. Nonetheless, the statistical signal itself is very strong.

Are there alternative explanations for this correlation of introns with three-dimensional structure other than the one of original introns? The introns-late school might argue that introns insert into specific nucleic acid sequences and these sequences, pre-intron targets (20), might be tied to specific amino acid patterns, and those patterns again tied, in some to-be-defined way, to the three-dimensional structure. One variant of this idea is the argument that introns “add” to sequences of biased composition, which might be associated with amino acids that lie on the surface of proteins.

We have shown that the linker regions are not biased in amino acid composition, in DNA composition, or in proto-splice sequences. Furthermore, the linker regions do not lie on the surface of the proteins, nor do the intron positions in our set show a surface bias.

Still another type of intron-insertion argument suggests that a bias might have arisen through natural selection. One assumes that introns entered genes randomly, but that only those organisms were selected within which the introns had inserted in such a way as to permit a useful module to be shuffled out of an ancient protein and used elsewhere as a target of natural selection. This model, however, does not work. The issue is one of the fixation of mutations. The selection that fixes the exon-based module in some novel protein does not fix the appropriate donor form of the gene in the population. If one argues that it is selection that has fixed the exon in the ancient gene itself, that statement corresponds to exon shuffling in the progenote, which is the introns-early conclusion.

The strongest argument against a biased insertion model is that the subset of putatively old introns shows enhanced localization, since on an insertion model for introns any subset should not behave differently. However, in defining ancient introns, we have accepted some use of sliding. We emphasize that our full intron correlation studies do not assume intron sliding and treat each intron position as a separate object.

How strong is the statistical argument? The argument for a correlation with 28-Å modules is straightforward. The module size was chosen in advance, by previous work, and the χ² value has a straightforward interpretation. However, when we vary the module size in the graph of Fig. 3B, we are doing almost a thousand calculations, and if these were only random fluctuations, one might still expect one of the points to vary out to P = 0.001. However, Fig. 3A shows that the excess of intron positions in the linker regions is robust, showing general peaks in that excess centered at 21.7, 27.6, and 32.9 Å in module diameter. The χ² plot shows that these peaks are broadly significant.

Why have other groups failed to find a correlation between exons and modules? Beyond the specific definition of modules, a further problem is that of sample size. Only 6% of the intron positions in our sample were involved in the excess at 28 Å. One needs a sufficiently large number of introns to see such an excess with high significance. Previously, Stoltzfus and coworkers (6) tested just four proteins and found indeed that exons in general coded for 28-Å modules, but that this correlation lacked significance. Logsdon and coworkers (8) tested only triosephosphate isomerase to find no correlation. However, Gō and Noguti (23), using the same four protein sample used by Stoltzfus et al. (6), claimed to reach statistical significance when they tested the position of introns in relation to the type of module boundaries defined by their analysis.

What is the significance of the “exon sizes”? We speculate that the sizes around 15 residues correspond to α-helices and α-helices with turns. Specific small peptides of these size ranges have such structures in solution (24–28). The longer sets would then be more complicated structures, involving turns to make the modules compact, and may represent the fusion of simpler elements. Preliminary analysis of the three-dimensional structures of 21-Å modules shows that many correspond to two secondary structure elements (such as helix/helix, helix/strand, strand/strand, and strand/helix) interconnected by a turn.

CONCLUSION

This paper demonstrates that intron positions are strongly correlated with the boundaries of modules around 22, 28, and 33 Å in diameter in the three-dimensional structure of current proteins. These sizes would correspond to a hypothetical exon pattern with exons about 15, 22, and 30 residues long, which supports the idea that short exons were used to assemble the ancient conserved proteins. A second argument that some introns are very old is the intron-phase correlation in ancient genes (10). The excess of phase symmetric exons, exon-pairs, and exon-triples in genes that came into existence in the progenote is also an argument for exon shuffling in the common ancestor. The Exon Theory of Genes, which holds that some introns are very old and were used to assemble genes in the common ancestor of all life, is now supported by two strong, independent statistical arguments that detect a signal of ancient introns over any possible background of loss and addition.