Frequency of migrants and migratory activity are genetically correlated in a bird population: Evolutionary implications

Abstract

Most migratory bird populations are composed of individuals that migrate and individuals that remain resident. While the role of ecological factors in maintaining this behavioral dimorphism has received much attention, the importance of genetic constraints on the evolution of avian migration has not yet been considered. Drawing on the recorded migratory activities of 775 blackcaps (Sylvia atricapilla) from a partially migratory population in southern France, we tested two alternative genetic models about the relationship between incidence and amount of migratory activity. The amount of migratory activity could be the continuous variable “underlying” the phenotypic expression of migratory urge, or, alternatively, the expression of both traits could be controlled by two separate genetic systems. The distributions of migratory activities in five different cohorts and the inheritance pattern derived from selective breeding experiments both indicate that incidence and amount of migratory activity are two aspects of one trait. Thus, all birds without measurable activity have activity levels at the low end of a continuous distribution, below the limit of expression or detection. The phenotypic dichotomy “migrant–nonmigrant” is caused by a threshold which may not be fixed but influenced both genetically and environmentally. This finding has profound implications for the evolution of migration: the transition from migratoriness to residency should not only be driven by selection favoring resident birds but also by selection for lower migratory activity. This potential for selection on two aspects, residency and migration distance, of the same trait may enable extremely rapid evolutionary changes to occur in migratory behavior.

Migratory bird species have developed a sequence of migration strategies ranging from regular biannual long-distance migration to facultative eruptive movements. Obligate partial migration is the name given to the situation in which a fraction of the population migrates some distance every year while the rest of the population remains on the breeding grounds (1). Obligate partial migration is most probably the prevalent migratory habit in birds, and has been proposed as the crucial transitional stage in the evolution from migratoriness to residency, or from residency to migratoriness (2, 3). This behavioral dimorphism is under endogenous control and to a large extent inherited both in birds (4–6) and in a variety of other organisms (7). However, social and environmental factors may be influential modifiers of the innate migration program (e.g., refs. 8 and 9).

While different hypotheses on how ecological and social factors determine avian migration habits have been proposed (for reviews, see refs. 10–14), little attention has been given to genetic constraints, imposed, for example, by genetic variances and covariances, on possible evolutionary trajectories (but see refs. 15 and 16 for avian migration models considering the influence of genetic variables). Recently, genetic constraints have been discussed as major determinants of evolutionary trajectories (e.g., refs. 17 and 18), and the consideration of genetic correlations has led to accurate predictions of microevolutionary changes (19). Moreover, it has been demonstrated that migratory traits in insects form coadapted migratory syndromes (7). Thus, we have reason to expect genetic correlations between migratory traits in birds.

In the last 20 years, the blackcap (Sylvia atricapilla) has become a model organism for studying the control of microevolutionary changes in migratory behavior. Breeding and common garden experiments have revealed that population-specific migratory habits have an endogenous basis and are polygenically inherited (reviewed in refs. 3, 14, and 20). In an artificial selection experiment with blackcaps from a partially migratory population of southern France, it was demonstrated that there is a large amount of additive genetic variance for the incidence of migratory activity, and that this trait could be changed rapidly by artificial selection (5, 21). Moreover, the responses to selection suggested that the threshold model of quantitative genetics (22–24) holds for this binary trait (5, 25). This model assumes that there is an unknown continuously distributed variable (= liability) underlying the dichotomous trait. The all-or-none response is caused by a threshold which divides individuals into those above and below the threshold value (Fig. 1A; see refs. 22–24). Selection could either shift the populational mean of liability (22, 23) or could change the position of the individual threshold (26).

Figure 1.

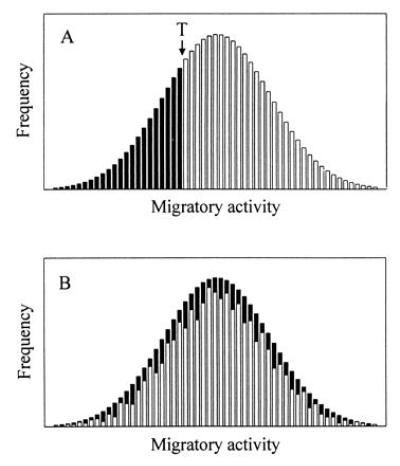
Models for the relationship between incidence and amount of migratory activity. In the “one-trait model” (A), nonmigrants (in black) are individuals on the left tail of a continuous distribution, with activities below a threshold value T. In the “two-trait model” (B), nonmigrants are randomly distributed over all activity classes; their activities are switched off by genes uncorrelated to the genes controlling the expression of migratory activity.

Here we analyze the relationship between the incidence and the amount of migratory activity in the blackcap with the aim of predicting evolutionary trajectories imposed by the genetic architecture of these traits. This is particularly important in view of the dramatic changes in avian migratory behavior to be expected in response to global warming (15, 27). We will test two alternative hypotheses on the inheritance of migratory activity and migratory urge (Fig. 1) using the data of blackcaps from the partially migratory population of southern France. The first hypothesis considers these behaviors to be different aspects of the same trait. It assumes that the two aspects of migratory behavior are controlled by the same genes. This “one-trait model” (Fig. 1A) is equivalent to the threshold model if the amount of migratory activity is the variable underlying the expression of migratory urge. As the classification migrant–nonmigrant and the amount of migratory activity is based on the same measurement (i.e., migratory restlessness), nonmigrants could simply be the censored observations at the left tail of a continuous normal distribution. Therefore, we would expect to find a type I censored normal distribution (for a definition and description of this distribution, see ref. 28) to fit the migratory activities in partially migratory populations (Fig. 1A). A second prediction derived from this model is that the genetic correlation between both measurements, which would represent two aspects of the same trait (i.e., migratoriness), should be one (23).

Alternatively, the “two-trait hypothesis” assumes that frequency of migrants and amount of migratory activity are different traits controlled by two separate polygenic systems. One, controlling the amount of activity, working like a “rheostat,” thus generating a continuous distribution of activities. A second genetic system, working like a switch (via a threshold), determines whether a bird is migratory or not. Contrary to the one-trait model, the two-trait model predicts that if nonmigrants are disregarded, an uncensored normal distribution should fit the distribution of activities. In this model, both traits are assumed to be uncorrelated; hence, nonmigrants are randomly distributed over all activity classes (Fig. 1B). In fact, the genetic correlation between the two traits could lie between −1 and +1. However, if the correlation approaches +1, this model will be practically indistinguishable from the one-trait model. Thus, under the two-trait model we should expect the genetic correlation between incidence and amount of activity to be lower than 1 (in Fig. 1B, it is zero).

MATERIALS AND METHODS

In 1976, 1980, 1982, 1984, and 1991, a total of 299 blackcaps from 81 nests (see Table 1) was collected at an age of about 6 days in southern France near Arles (about 43.30° N, 04.30 E). Nestlings were transported to our institute in Radolfzell, Germany (47.46° N, 09.00° E), hand-raised, and kept under identical controlled conditions (see ref. 29 for a description of the population, and refs. 5 and 21 for rearing procedures). Night activity was recorded for each bird in registration cages during its first migratory season (from September 14 through December 31; in 1980 until December 4). Activity was measured on the scale of half-hour intervals with activity—i.e. with more than one registered hop. This behavioral trait, known as zugunruhe or nocturnal restlessness, is normally distributed (15) and highly correlated with timing and intensity of migratory activity, and as a consequence with migration distance, in the wild (reviewed in refs. 3 and 14). A nonmigrant is defined as an individual with zero half-hours of nocturnal activity. The proportion of inactive birds corresponds to the proportion of resident birds in nature (29). In principle, it is not known to what extent these birds do not express any activity or whether the activity is below the detection limit of our equipment.

Table 1.

Incidence, amount, and variance of migratory activities in migrants, and adjusted estimates of the mean activity and variance for the total population (assuming a censored normal distribution) in different years

Cohort	n	% nm	mam	s2	δ1	% nmadj	mamadj	s2adj	δ1
1976	25	20.0	426	61,018	0.173	18.3	304	112,857	0.135
1980	77	27.3	301	37,464	0.126**	27.5	158	70,537	0.088
1982	51	23.5	392	65,479	0.136*	23.4	252	120,413	0.087
1984	66	19.7	398	67,575	0.146**	20.1	283	113,582	0.105*
1991	80	12.5	347	35,936	0.092	11.1	289	56,055	0.086

Mean activity in migrants (mam) is given in half hours with night activity. Frequency of nonmigrants (% nm) was measured in percent of individuals with zero activity (n = number of individuals studied). Adjusted estimates of the mean (mam_adj) and the variance (s²_adj) for the total sample were calculated using the method developed by Cohen (30, 31). % nm_adj gives the frequency of nonmigrants expected for the fitted distribution. Goodness-of-fit between the observed and the fitted distributions were tested using the δ-corrected Kolmogorov–Smirnov statistics with δ = 1 (32). ∗, P < 0.05; ∗∗, P < 0.001. 

For assessing genetic correlations we reanalyzed migratory activities of 427 individuals from two lines which had been selected for higher and lower frequency of migrants (see refs. 5 and 21 for sample sizes and details of the experiment). Here we consider individuals of generations 1–3 of the upward line, and generations 1–4 of the downward line. In addition, 49 birds from 20 migratory parents of the 1991 cohort were bred. In total, migratory activities of 775 individuals were used for this analysis.

We computed adjusted estimators of the mean and variance from the distribution of migratory activities assuming a left-censored normal distribution—considering individuals with zero activity as the censored sample—using the auxiliary estimation function λ (30). Values of λ for each cohort were obtained by interpolation from table 2 in Cohen (31). The goodness-of-fit of the distributions of migratory activities in migrants against censored (including nonmigrants) and uncensored (excluding nonmigrants) normal distributions was assessed using the δ-modified Kolmogorov–Smirnov statistic adapted for estimated parameters by Khamis (32). This test with δ = 1 proved to be markedly more powerful than the classical Kolmogorov–Smirnov statistics or a Kolmogorov–Smirnov statistic modified for censored samples (33), which did not detect any deviation in any cohort (results not shown).

In all statistical testing we used square-root transformed migratory activities to achieve homoscedasity. Arcsine-transformation of the frequencies of nonmigrants improved the fit of this variable to the normal distribution. We tested the influence of parental migratory activity on the migratory status of the offspring (migrant or nonmigrant) with the aid of logistic regression analysis using a maximum likelihood loss function and a logit link (34). By building a subject-specific model we would have achieved the largest statistical power. This approach, however, is biased as migration status of nestlings within a family is not independent. We therefore chose to account for this bias by using a more conservative approach based on the migration status of the family. Families with at least one nonmigrant were classified as having migration status one. Families without nonmigrants were coded as zero. We built two different regression models for predicting the probability that migratory parents have nonmigratory offspring. In the first model, only offspring produced by birds taken from the wild are considered. In the second model, all offspring produced in three generations of breeding migrants with migrants (see the above-mentioned selection experiment) are taken into account. Here, the effect of selection on the parameters of the logistic model is tested.

We estimated the realized genetic correlation (r_a) between the incidence (x) and the amount (y) of migratory activity from the regression (b_[x.y]) of the correlated response of migratory activity (CR_[y] = cumulative correlated response in standard deviation units) on the standardized selection differential for the proportion of migratory offspring (I_[x] = cumulative selection intensity) by the equation:

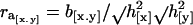where

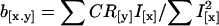A bootstrap confidence interval (35) for this estimate was obtained by randomly taking a sample (with replacement) of the size of the original sample from each of the seven generations of the selection experiment. In this way, we generated 1000 bootstrap samples. For each of these samples we estimated the slope of the regression of cumulative response on cumulative selection differential, thus obtaining the bootstrap distribution of b_[x.y], and r_a[x,y]³. The 95% confidence interval (CI_95%) is defined as the central 950 values of this distribution [percentile method (35)]. We accounted for the complexity of the breeding scheme (see ref. 21), for the heterogeneity of the frequencies of nonmigrants and for the heterogeneity in the means and variances of activities in migrants across cohorts (see Table 1) and generations, by weighting selection intensities and responses by the number of offspring each parent contributes to the next generation (23); the arithmetic mean and standard deviation of the respective parental cohort was taken as reference. Selection responses and intensities for each generation of selection were estimated as the arithmetic means of individual values.

RESULTS

Among the 299 studied birds from the wild, we found 61 individuals (20.4%) with no migratory activity. Although the frequency of nonmigrants varied between cohorts (Table 1), we found no heterogeneity in the distribution of nonmigrants across cohorts (χ² = 5.644; df = 4; P = 0.227). Also, there was no significant effect of the cohort on the total variance of migratory activity in migrants (one-way ANOVA: F = 1.880; df = 4, 233; P = 0.115). The overall mean activity of migrants over the five cohorts was 361 half-hours with activity (SD = 226; n = 238).

In all cohorts the distribution of migratory activities was better described by a censored normal distribution, than by an uncensored normal distribution fitted to the activities of migrants only (Table 1). In the 1984 cohort, however, neither the censored nor the uncensored normal distribution fitted the actual distribution. This discrepancy is most probably due to the large variance in family size in 1984. Furthermore, the proportion of nonmigrants (number of censored observations) was accurately predicted from the mean and the variance of the fitted censored distribution. In any cohort the proportion of nonmigrants estimated by the fitted distribution deviated by no more than 1.7% from the actual frequency.

Considering only families with parents hatched in the wild (n = 32) the most influential variable for predicting the probability that at least one nestling is a nonmigrant is the mean migratory activity (MMA) of the parents (Table 2). On the basis of this variable alone, 78% of the families can be assigned to the correct migratory status (with or without nonmigrants). The coefficients in the complete regression equation (MMA, b = −0.226; SE = 0.112; constant = 3.72; SE = 2.30) indicate that the probability of having nonmigratory offspring increases if migratory activity in the parents is low.

Table 2.

Logistic regression model predicting the probability of migratory parents having nonmigratory offspring

Explanatory variable	Offspring generation 1			All offspring generations
	df	χ2 (1)	χ2 (2)	df	χ2 (3)	χ2 (4)
Midparental migratory activity (MMA)	1	6.152*	—	1	0.801	2.014
Difference between parental activities (DPA)	1	2.564	2.003	1	0.039	0.579
Nonmigrants in parental families (NPF)	1	0.318	0.058	1	2.074	1.303
Parental birth year (PBY)	2	0.689	0.541	7	10.016*	1.280
Offspring birth year (OBY)	5	2.134	1.254	6	8.605	2.111
DPA × OBY	5	8.993	4.548	6	12.961*	5.712
Offspring generation (GE)	—	—	—	2	9.522**	—
MMA × GE	—	—	—	2	6.973*	5.562
DPA × GE	—	—	—	2	8.721*	1.335
NPF × GE	—	—	—	2	7.183*	1.303

DPA is the absolute difference between the square-root transformed migratory activities of the parents. NPF is the mean of the arcsine-transformed frequencies of nonmigrants in the parental broods. χ² (1) and χ² (3) give the change in deviance if the single variable is entered into the model; χ² (2) gives the change in deviance if the variable is entered into a model including MMA; χ² (4) gives the change in deviance if the variable is added into a model including GE. For offspring generation one the number of families studied is 32. In all offspring generations, n = 59. Only interaction terms with significant changes in deviance are given. ∗, P < 0.05; ∗∗, P < 0.01. 

If all generations with migratory parents are considered (n = 59), the variable offspring generation (GE) is the best predictor of migration status (χ² = 9.52; df = 2, P = 0.009; Table 2). However, although the model including the variable GE classifies all families without nonmigrants correctly (n = 46), none of the families with nonmigrants (n = 13) were assigned to the right class. In this second approach, the model with the highest goodness-of-fit (χ² = 6.08; df = 1; P = 0.014) includes MMA and the interaction GE × DPA (χ² = 13.14; df = 2; P = 0.001). This regression model (χ² = 14.8; df = 3; P = 0.002) classifies 50 out of 59 (85%) families correctly. Again, the regression coefficients [MMA, b = −0.190; SE = 0.0907; GE × DPA (1): b = 1.574; SE = 0.070; GE × DPA (2); b = 0.090; SE = 0.062] indicate that the probability of having nonmigratory offspring is higher the lower the activity of the parents.

Bidirectional selection for the frequency of migratory offspring not only changed the proportions of migrants and nonmigrants (5, 21) but also significantly changed the mean migratory activity of migrants (Fig. 2). In four generations of selection for residency, the mean migratory activity of migrants decreased from 380 to 77 half-hours with activity. In three generations of selection for a higher proportion of migratory offspring, the activity of migrants increased from 348 to 379. In both lines, a decrease of the variance in the course of selection was observed (which we took into account when estimating selection intensities and responses). Considering both selection lines, the cumulative selection response of migratory activity increased on average 0.472 times (bootstrap 95% confidence limits: 0.272; 0.658) the cumulative selection intensity for the frequency of migrants. If we divide this regression coefficient by the product of the square-root of the heritabilites of both traits [0.6 for the incidence of migratory activity (5) and 0.3–0.4 for the amount of migratory activity (ref. 15 and F.P. and P.B., unpublished data)], we obtain estimates for the genetic correlation between 0.964 (CI_95% = 0.554 < r_a < 1.344) and 1.112 (CI_95% = 0.640 < r_a < 1.552).

Figure 2.

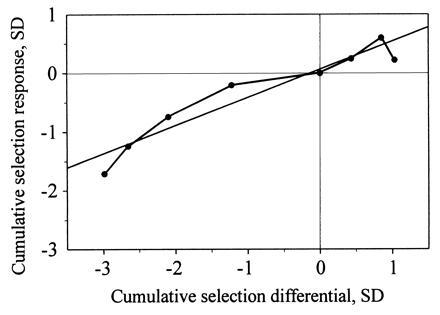
Correlated response of migratory activity to four generations of selection for lower proportion of migrants and three generations of selection for higher frequency of migrants (see ref. 21). Correlated selection responses (CR) and selection intensities (I) are given in standard deviations of the populational mean of the respective parental generation. Points give single generation cumulative selection responses and intensities. A linear regresssion line was fitted to all single generation cumulative selection responses and intensities (CR = 0.472 I + 0.042).

DISCUSSION

Both predictions made by the one-trait model were confirmed by the data on migratory activity in southern French blackcaps. (i) In all cohorts a censored normal distribution gave a better fit to the actual distribution of migratory activities and to the frequency of nonmigrants than an uncensored normal distribution fitted to the activity of migrants. This result shows that the distribution of migrants and nonmigrants is not independent of the distribution of migratory activities. Consequently, if we know the mean and variance of the activity in migrants, we can determine the proportion of nonmigrants in the population. (ii) As predicted by the one-trait model, we found a significant genetic correlation between both traits. This correlation could be demonstrated in two ways. First, we found (in spite of the low power of the statistical approach) that the activity of migratory parents significantly influences the frequency of nonmigratory progeny, providing evidence that by selecting for lower activity we could rapidly change the proportion of nonmigrants. Second, we demonstrate that in a bidirectional selection experiment for higher and lower frequency of migrants, the amount of activity in migrants was significantly changed. As predicted, the estimate of the realized genetic correlation is very close to one. Although we did not have replicate lines to control for genetic drift and for differences in pleiotropic effects (36), and the estimates of genetic correlations have large sampling errors, the results of the logistic regression analysis and of the selection experiment both indicate that there is a high genetic correlation between the incidence and the amount of migratory activity. These results suggest that the incidence of migratory activity is indeed a threshold trait and that the amount of migratory activity is the continuous variable “underlying” the binary classification into migrants or nonmigrants (Fig. 1A). Therefore, it seems justified to use the threshold model of quantitative genetics to estimate variance components of the incidence of migratory activity (5, 25).

Although our study strongly supports the one-trait model, we cannot distinguish this model from a two-trait model with high genetic correlation between the amount of migratory restlessness and the variable underlying the incidence of migration. While the main conclusion—i.e., that in partially migratory populations the incidence and amount of migratory activity will evolve together—holds for both models, there are differences between the models in the evolutionary trajectories predicted for completely migratory (or sedentary) populations. According to the one-trait model, no alleles for residency (or migratoriness) are to be expected but only an accumulation of allelic contributions to migratory activity. Consequently, under directional selection for lower or higher migratory activity any completely migratory population could evolve residency, and any sedentary population could evolve migratoriness without introducing new alleles. If, however, the two-trait model holds, this transition from complete migratoriness or complete residency to partial migration would not be accomplished without the introduction of alleles for “residency” or “migratoriness” into the population. We are currently running a selection experiment to exclude one of these alternative models.

Furthermore, we cannot exclude other factors (besides migratory activity) that may influence the incidence of migratory behavior in the blackcap or in other bird species. The logistic regression analysis based on the data of the selection experiment indicates that “generation” (selection) has a significant influence on offspring migratory status within families. Besides, it is remarkable that although the frequencies of nonmigrants in three artificial partially migratory populations vary considerably: 6% in a Madeira × Southern German cross (H. Bletz and P.B., unpublished data), 63% in a Cape Verde × Southern Germany cross (37), and 45% in a Canary Islands × Southern German cross (38), the mean migratory activity in migrants is almost identical (499, 521, and 583 half hours, respectively). Consequently, the distribution of migratory activities of the parents cannot be the only determinant of whether an individual will become a migrant or not. These results suggest that the position of the threshold may not be fixed but might be changed by selection—i.e., that there is additive genetic variance for this trait (24). Moreover, it is very likely that the position of the threshold for migratory activity is influenced by environmental factors as has been suggested by several authors (e.g., refs. 8–10; see ref. 26 for a threshold model based on this assumption). Alternatively, a single “knock-out” mutation at an enzyme locus crucial to migratory metabolism could switch off all activity (39) without changes in the genes regulating the amount of activity (which is equivalent to the two-trait model in Fig. 1B). In this fashion, migratory activity would become a quasi-monogenic trait uncorrelated to the amount of activity. Such an inborn enzymatic error causing residency should be reflected in Mendelian ratios in the migration status of the offspring, which we did not find in southern French blackcaps. Therefore, it seems unlikely that this process is a significant cause of residency in this partially migratory population. In completely resident populations, however, the “knocking-out” of enzymes crucial to migratory metabolism could be an important mechanism underlying residency (39). It should be further investigated to what extent these different mechanisms are responsible for the evolution of residency in birds.

Our finding that the amount and the incidence of migratory activity are genetically correlated and most probably two different aspects of one single trait has important implications for the evolution of migratory behavior. It allows us to make predictions about the distribution of migration distances and their changes in natural bird populations. One prediction is that in partially migratory populations the distribution of migratory distances in migrants, from the most distant wintering area to the breeding area, should be continuous. On average, migrants should migrate only moderate distances. This is indeed what we find in nature: individuals from partially migratory populations are short or middle distance migrants, and the distribution of migration distances as derived from banding recoveries is continuous. Possible exceptions to this predicted pattern [for example, the discontinuity of migration distances in British song thrushes, Turdus philomelus (40)] can generally be refuted under closer examination. For example, species with discontinuous distribution of migration distances turn out to be either facultative migrants (like the song thrush), or have very divergent population-specific wintering sites [like, for example, the central European gray wagtail, Motacilla cinerea (41)]. Other possible sources of spurious discontinuity in migration distances are the discontinuity of recovery sites and heterogeneity of recovery probabilities (e.g., ref. 42).

Another prediction derived from the one-trait model is that selection for residency will always be accompanied by decreasing migration distances, and that selection for migratoriness will result in increasing migration distances. In a wild bird species, the house finch (Carpodacus mexicanus), which recently evolved into a migrant, we found the latter prediction confirmed. In 1941 the first house finch was introduced to the North American East Coast, most probably as a consequence of a release by a bird trader on Long Island, NY (43). This species, native to western North America, is largely sedentary in its original range. After its introduction, the eastern house finch has been steadily expanding its range. Concomitantly, migratory activity has evolved in this population, and an increase in migratory distance with time has been observed (see figure 2 in ref. 44). Thus, the proportion of migrants and migration distances have apparently evolved together. However, it has not yet been investigated to what extent migratory behavior in the house finch is obligate—i.e., endogenously controlled.

An important consequence of the genetic correlation found is that selection favoring birds overwintering in areas closer to the breeding sites (i.e., having shorter migration distances) and selection favoring nonmigratory individuals [both consequences to be expected under global warming (27)] will jointly increase the number of residents. This may have caused the marked increase of nonmigratory great crested grebes, Podiceps cristatus, in The Netherlands over the last decades (45). As the selection response in both traits is the sum of both selection differentials (46), the potential for rapid evolutionary change to complete residency or migratoriness should be larger in partially migratory than in completely migratory populations (where there are no resident individuals to select). In completely migratory populations, evolution to residency can only be achieved by gradually decreasing mean migration distance. Consequently, short-distance migrants should achieve residency (assuming equal direction and similar intensity of selection) much faster than long distance migrants. The genetic correlation between both traits thus provides a plausible mechanistic explanation for the observation that changes in migratory behavior of long-distance migrants are much slower than in short-distance migrants (see ref. 14). On the other hand, if selection differentials for both traits are of opposite sign, the evolutionary response could be retarded or completely prevented. For example, if wintering sites located between the breeding area and the current overwintering areas are unsuitable, selection acting against shorter migration distances would counteract possible selection favoring residency. In the Palearctic–Afrotropical migration system, this may be an important constraint for trans-saharan migrants to evolve residency by gradually decreasing migration distances.

In conclusion, we have shown the importance of the genetic architecture of migratory traits for predicting evolutionary change in avian migratory behavior. Thus, whether incidence and amount of migratory activity are genetically correlated or not can result in a substantial difference in evolutionary trajectory. Although phenotypic models can give us an idea about the direction and intensity of natural selection on migratory behavior (e.g., ref. 47), the predicted outcomes can be significantly favored or constrained by the genetics of traits. To predict evolutionary change, we need both insight into the expression of genetic variation and knowledge of the intensity and direction of selection (e.g., ref. 48).

Our study has demonstrated that the frequency of migrants and migratory activity are two different aspects of one trait, migratoriness. Indeed, we expect to find migrants and nonmigrants in all bird populations (or species), although frequencies may be unmeasurably low in populations considered as nonmigratory or completely migratory. Thus, all bird populations are, in fact, partially migratory, with varying proportions of migrants (14). Therefore, we should abandon the migrant–nonmigrant dichotomy and focus future research in this field on the environmental and genetic mechanisms that regulate migratory activities and determine the threshold of expression (see ref. 40, p. 146). This knowledge will be crucial for accurately predicting the adaptability of migratory birds to environmental changes, and will have to be incorporated into models on the evolutionary consequences of global warming for migratory behavior in birds (15, 27).