Abstract
Changes in the configurational entropies of molecules make important contributions to free energies of reaction for processes such as protein-folding, noncovalent association, and conformational change. However, obtaining entropy from molecular simulations represents a long-standing computational challenge. Here, two recently introduced approaches, the nearest-neighbor (NN) method and the mutual-information expansion (MIE), are combined to furnish an efficient and accurate method of extracting the configurational entropy from a molecular simulation to a given order of correlations among the internal degrees of freedom. The resulting method takes advantage of the strengths of each approach. The NN method is entirely nonparametric (i.e., it makes no assumptions about the underlying probability distribution), its estimates are asymptotically unbiased and consistent, and it makes optimum use of a limited number of available data samples. The MIE, a systematic expansion of entropy in mutual information terms of increasing order, provides a well-characterized approximation for lowering the dimensionality of the numerical problem of calculating the entropy of a high-dimensional system. The combination of these two methods enables obtaining well-converged estimations of the configurational entropy that capture many-body correlations of higher order than is possible with the simple histogramming that was used in the MIE method originally. The combined method is tested here on two simple systems: an idealized system represented by an analytical distribution of 6 circular variables, where the full joint entropy and all the MIE terms are exactly known; and the R,S stereoisomer of tartaric acid, a molecule with 7 internal-rotation degrees of freedom for which the full entropy of internal rotation has been already estimated by the NN method. For these two systems, all the expansion terms of the full MIE of the entropy are estimated by the NN method and, for comparison, the MIE approximations up to 3rd order are also estimated by simple histogramming. The results indicate that the truncation of the MIE at the 2-body level can be an accurate, computationally non-demanding approximation to the configurational entropy of anharmonic internal degrees of freedom. If needed, higher-order correlations can be estimated reliably by the NN method without excessive demands on the molecular-simulation sample size and computing time.
Keywords: configurational entropy, nearest neighbor, mutual information, dimension reduction, molecular simulations, many-body correlations
Introduction
Changes in the configurational entropy of molecules are believed to contribute importantly to the free energies of conformational change and binding. A reliable method of computing configurational entropy could provide valuable insights into the mechanism of such processes, and could also offer important assistance in problems of molecular design. However, calculating entropy is traditionally a highly challenging problem, especially for complex molecules. One long-standing approach is the quasi-harmonic approximation,1,2 which approximates the probability density function (PDF) of a molecule's internal coordinates as a multivariate Gaussian distribution. However, this simple Gaussian model does not yield accurate estimates of entropy when the true multivariate distribution of the spatial fluctuations in a molecule differs significantly from the Gaussian distribution, especially when the PDF is multimodal.3,4 Recently, two novel methods of estimating configurational entropy from molecular simulation data, which do not rely on any specific model of the probability distribution of molecular coordinates, have been introduced.
One is the nonparametric nearest-neighbor (NN) method of Hnizdo et al.,4 which utilizes k-th NN estimators of entropy. These estimators have been shown to be asymptotically unbiased and also asymptotically consistent (i.e., having asymptotically vanishing variance),5,6 thus guaranteeing accuracy for any probability distribution when sufficiently large samples of molecular simulation data and adequate computer power for their processing are available. The NN method makes excellent use of the available simulation data, and thus enables accurate estimations of entropies for fairly high-dimensional systems. However, it is not exempt from “the curse of dimensionality,” 7 as the convergence and computational complexity of the calculations eventually become intractable as the dimensionality increases.
The second method, of Killian et al.,8 is based on the mutual-information expansion (MIE),9 which is a systematic expansion of the entropy of a multidimensional system in mutual-information terms of increasing order m that capture the m-body correlations among the molecular coordinates. A truncation of the MIE is thus an approximation to the full joint entropy of a multidimensional system that is well-characterized in the sense that it includes correlations up to the specified order. Killian et al. implemented the MIE with a histogram method of computing the mutual-information terms from molecular simulation data, and demonstrated good agreement with a reference method for molecular systems having multiple energy wells and hence multimodal PDFs.8
The histogram method used by Killian et al. is computationally fast, but requires very large data sets to achieve convergence at or beyond third order (m = 3). This is because the available data points become more and more sparsely distributed as the dimensionality, and hence the number of histogram bins, increases. Increasing sparseness results in most bins containing either 0 or 1 sample points and thus the histogram providing almost no useful information about the probability density function it is intended to capture. The NN method addresses this problem by employing what can be loosely described as adaptive bin widths, where “bins” are sample-point-centered hyperspheres that contain k nearest sample points. The resolution of such a “histogram” adapts in this way to the sample points growing sparse with increasing dimensionality. On the other hand, determining the radius of the hypersphere that contains k nearest points in a given sample is computationally time-consuming. Overall, then, for a given number of sample points, the NN method typically requires more computer time than the histogram method, but it yields a more accurate estimate of the entropy. Based upon these considerations, there appears to be potential for strong synergy between the NN and MIE methods.
The present study for the first time combines the systematic dimension-reduction approximations of the MIE with the power of the NN method, using the latter to estimate the individual MIE terms. This combined approach is tested on two model systems: an idealized system represented by an analytical distribution of 6 pairwise-correlated circular variables, where the full joint entropy and all its MIE terms are exactly known; and the RS stereoisomer of tartaric acid, a molecule with 7 internal-rotation degrees of freedom, where the full-dimensional configurational entropy of internal rotation has been estimated accurately by the NN method.4 For both model systems, the NN method is used to estimate all the terms of the MIE, and the performance of the combined method is compared with that of the original histogram method of Killian et al.,8 applied to these systems up to the third-order terms.
The Theory section of this article surveys the formalisms pertaining to the MIE of entropy and the NN method, respectively. In the Methods section, the test systems used and some computational details are described. The Results section describes the numerical performance and CPU timings, and the last section summarizes the results and discusses their implications.
Theory
The Mutual-Information Expansion of Entropy
Information theory uses the quantity of mutual information to express dependence, or correlation, between two systems. The mutual information I(i, j) of systems i and j is defined as10
| (1) |
where S(i), S(j), and S(i, j) are respectively the Shannon entropies of systems i, j, and the joint system {i, j}. (Note that the present notation differs somewhat from that of Killian et al.8). In general, the Shannon entropy S(1, . . . , s) of a joint system {1, . . . , s} of s systems, characterized by a joint probability distribution f(q1, . . . , qs), where q1, . . . , qs are (continuous) random variables describing the systems, is given by
| (2) |
where the integration extends over the whole s-dimensional space that is accessible to the joint system. In the present application, each qi will represent one torsional (dihedral-angle) coordinate; when multiplied by the gas constant (or Boltzmann's constant), the Shannon entropy becomes a physical entropy associated with the given probability distribution. For simplicity, we shall suppress the gas constant and report all entropic results as unitless quantities. A reduced system, say {1, . . . , i−1, i+1, . . . , s}, is characterized by a reduced, or marginal, probability distribution
| (3) |
and its Shannon entropy S(1, . . . , i−1, i+1, . . . , s) is defined in terms of the marginal distribution as in (2).
Mutual information I(i, j) can be generalized to express higher than two-body correlations. The m-body correlation among systems 1, . . . , m is expressed by the mth-order mutual information Im(1, . . . , m), which is defined as9
| (4) |
where the second sum runs over all the distinct combinations {i1, . . . , il} ε {1, . . . , m}. According to definition (4), the 1st-order mutual information I1(i) is the entropy S(i) of a single individual system i, the 2nd-order mutual information I2(i, j) is the pairwise mutual information I(i, j), the 3rd-order mutual information among systems i, j, and k is
| (5) |
etc. Recursion relations can be derived that express mutual information of a given order m in terms of mutual information functions of orders lower than m.8,9
Given the definition of the mutual-information functions (4), the joint entropy S(1, . . . , s) can be expanded as8,9
| (6) |
where
| (7) |
This is the MIE of entropy. An MIE term Tm(1, . . . , s) is the sum of all the mutual-information functions Im pertaining to the joint system {1, . . . , s}, capturing the m-body correlations in that system. The lowest-order term, T1, is the sum of the “marginal” entropies S(i) of the individual systems, and as such it equals the full joint entropy when the systems are independent, i.e., when there are no correlations and the joint probability distribution factorizes into a product of independent probability distributions of each system. Expansion (6) is constructed so that it equals the joint entropy S(1, . . . , s) when all the terms Tm, m = 1, . . . , s are included.
The truncation of the MIE at an order mt < s,
| (8) |
is an approximation of the joint entropy S(1, . . . , s) that neglects correlations of order higher than mt. Such an approximation is good when the neglected higher-order correlations are unimportant, and it may also be necessary to make on practical grounds since the difficulty of accurately estimating the MIE terms Tm increases rapidly as their order m increases. Killian et al.8 implemented the MIE method using a straightforward histogramming technique to evaluate the individual mutual-information terms. Good results were obtained to second order, but convergence became difficult at third order, and was intractable thereafter. The following subsection describes a powerful alternative to simple histogramming for the calculation of high-order mutual information terms, the NN method.
The Nearest-Neighbor Method
The entropy S(1, . . . , s) of a general probability distribution f(q1, . . . , qs) can be estimated from a random sample of n observations, xi = (x1;i, . . . , xs;i), i = 1, . . . , n, of the random vector q = (q1, . . . , qs) in terms of NN distances of the sample points without any assumption about the functional form of the distribution f(q1, . . . , qs). An asymptotically unbiased and consistent estimator of the entropy is given by5,6
| (9) |
where γ = 0.5772 · · · is Euler's constant, and
| (10) |
is the Euclidean distance between a sample point xi and its k-th nearest (in the Euclidean distance sense) neighbor xik in the sample.
The k-th NN estimator of entropy can be viewed as an estimate based on a sample-point-centered “histogram” with bin sizes equaling the distances to the k-th nearest neighbors in the sample, adjusted for an asymptotic bias Lk−1 − ln k − γ that such “histogramming” entails.4 Apart from being entirely nonparametric, the NN estimator has the highly desirable properties of being adaptive, data efficient and, at a given finite sample size n, having minimal bias,11 in any given number of dimensions s. Nonetheless, the computational complexity of NN searching algorithms increases markedly with the dimensionality. Approximations based on a reduction of the dimensionality of the problem are thus desirable.
Hnizdo et al.4 proposed grouping the molecular coordinates into non-overlapping clusters of manageable dimensionality so that the dependence between variables from different clusters is minimized. For this purpose, they introduced a general coefficient of association, based on the pairwise mutual information I(i, j). The same measure of correlation of molecular degrees of freedom was also proposed by Lange and Grubmüller.12 The sum of the estimates of entropies of the clusters is then an estimate of an upper bound on the full joint entropy. However, available algorithms13 provide only guidance to a clustering of this kind; there is no guarantee that any specific non-overlapping clustering provides the closest upper bound on the full entropy at a given maximum dimensionality of the clusters. In contrast, the MIE systematically accounts at each cluster size m for all possible clusters, including those that overlap, and thus fully captures the m-body correlations at each expansion order m. The MIE therefore promises to be a more suitable approximation scheme for joint entropy than standard clustering methods.
Methods
Model System I: Analytical Distribution of Circular Variables
The feasibility of reliable estimation by the NN method of MIE terms of increasing order can be investigated rigorously only by using random samples from a nontrivial multivariate distribution for which the full joint entropy and all its MIE terms are known exactly. Circular variables are particularly relevant for molecular systems because the torsional degrees of freedom, which are the chief determinants of molecular conformation, are circular in nature. Analytical distributions with exactly calculable entropic attributes do not seem available for more than two correlated circular variables, but one may construct a distribution of higher dimensionality by taking the product of a suitable number of bivariate distributions. Since such a distribution cannot describe many-body correlations of order higher than 2, all the terms Tm with m ≥ 3 in the MIE of its entropy will vanish. Monte Carlo samples can be drawn from such a distribution, and the practicality of a reliable estimation of the vanishing higher-order MIE terms by the NN method can be investigated.
We constructed an analytical 6-dimensional distribution of circular variables as a product of three bivariate von Mises distributions. The bivariate von Mises distribution14 is a circular analogue of the bivariate normal (Gaussian) distribution; it is defined as
| (11) |
where
| (12) |
is the normalization constant, and Ik(·) is the modified Bessel function I of order k. The parameter λ controls the statistical dependence between the circular variables φ1 and φ2, and l1 and l2 are positive integers that allow for multiple modes in the marginal distributions. The Shannon entropy of the distribution (11) is given by
| (13) |
where
| (14) |
| (15) |
The marginal distributions are
| (16) |
and their entropies are given as
| (17) |
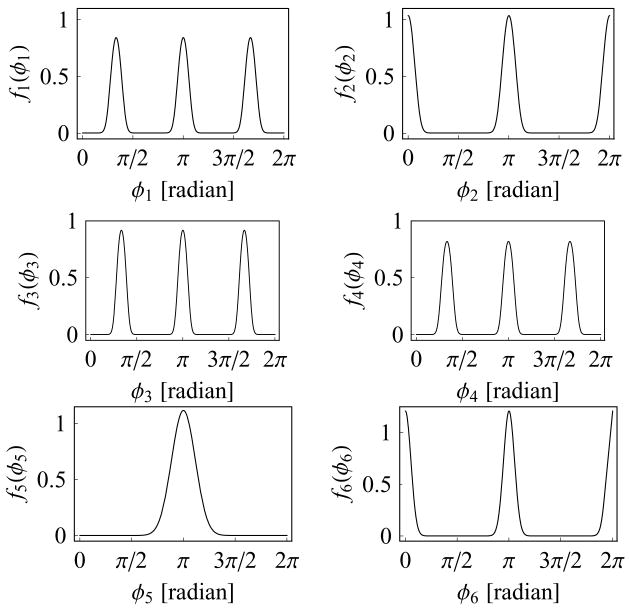
The joint entropy of eq. (13) and the marginal entropies of eq. (17) can be easily evaluated, as they are given in terms of rapidly converging series and one-dimensional integrals. The entropy S(i1, . . . , il), l ≤ 6 of any cluster of variables from a product of three bivariate distributions is then given very easily in terms of bivariate entropies and marginal entropies. For example, the full joint entropy S(1, . . . , 6) = S(1, 2) + S(3, 4) + S(5, 6), where S(i, j) are the bivariate entropies of eq. (13), or S(1, 2, 3, 5) = S(1, 2) + S(3) + S(5), where S(i) are the marginal entropies of eq. (17). The parameters of the three bivariate von Mises distributions we chose, and the corresponding joint and marginal entropies, and general coefficients of association,4 are given in Table I. Plots of the six marginal distributions are in Figure 1. Monte Carlo samples of the six circular variables were drawn from this analytical distribution, using the Fortran double-precision version of the random number generator RANARRAY of Knuth.15
TABLE I.
Parameters and entropies of the bivariate von Mises distributions used to construct Model System I, a 6-dimensional distribution of circular variables.
| k1 | k2 | λ | μ1 | μ2 | l1 | l2 | S(1) | S(2) | S(1,2) | rIa |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 15 | 10 | π | π | 3 | 2 | 0.6158 | 0.4133 | 0.6803 | 0.7087 |
| 15 | 12 | 12 | π | π | 3 | 3 | 0.4958 | 0.6054 | 0.6628 | 0.7641 |
| 12 | 14 | −8 | π | π | 1 | 2 | 0.3809 | 0.3021 | 0.4902 | 0.5656 |
General coefficient of association, .
FIG. 1.
Marginal distributions fi(φi), i = 1, . . . , 6 of the analytical distribution given as a product of three bivariate von Mises distributions.
It is worth noting that this long-period random number generator is well suited for use with the NN method of entropy estimation, which does not tolerate so-called ties. Ties are sample points that happen to be the same to the given accuracy of recording; they lead to vanishing NN distances Ri;k and thus to diverging contributions ln Ri;k in the NN estimator of eq. (9). It seems that little attention has been paid so far to the tie aspect of random number generation. For example, the widely used, single-precision, long-period random number generator ran2 (ref. 18) — whose authors have promised a reward of $1000 to the first user to convince them that the generator fails a statistical test in a nontrivial way — produces on average 267.7 ± 0.4, 521.8 ± 0.7, and 5002 ± 2 (mean ± std. error) pairs of ties in samples of n = 105 random numbers 0 < r < 1 when they are recorded in fixed-point format to d = 8, 7, and 6 decimal places, respectively, while the correct expectation values are , 500, and 5000, respectively. The double-precision generator RANARRAY appears to produce the expected number of ties in samples of size up to n = 107 and recording accuracy up to d = 16. For example, no ties were observed in several samples of n = 107 and d = 16, for which the expected number of ties is 0.005.
Model System II: Dihedral Angles of Tartaric Acid
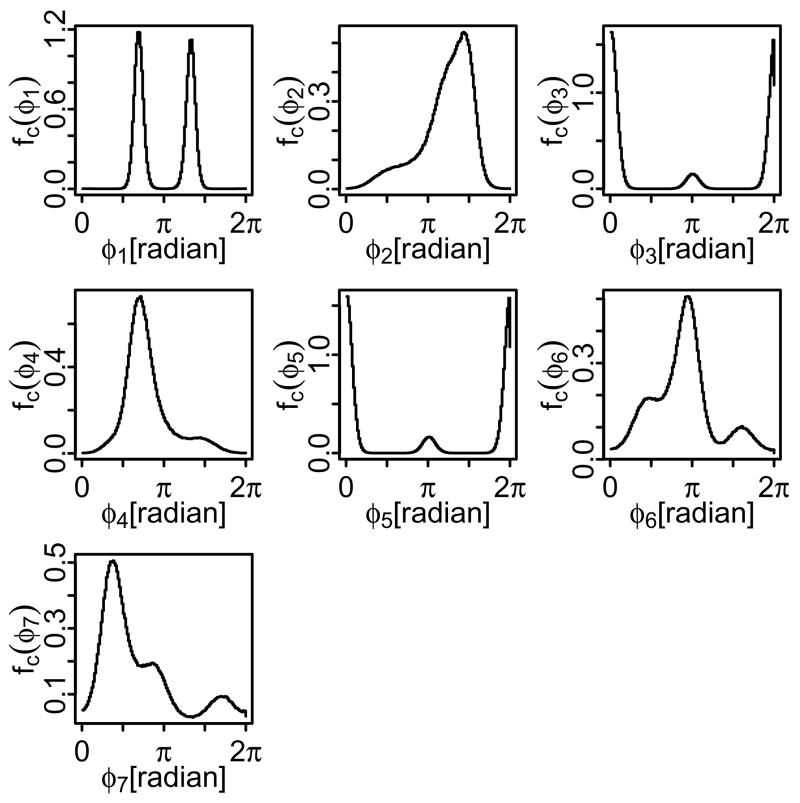
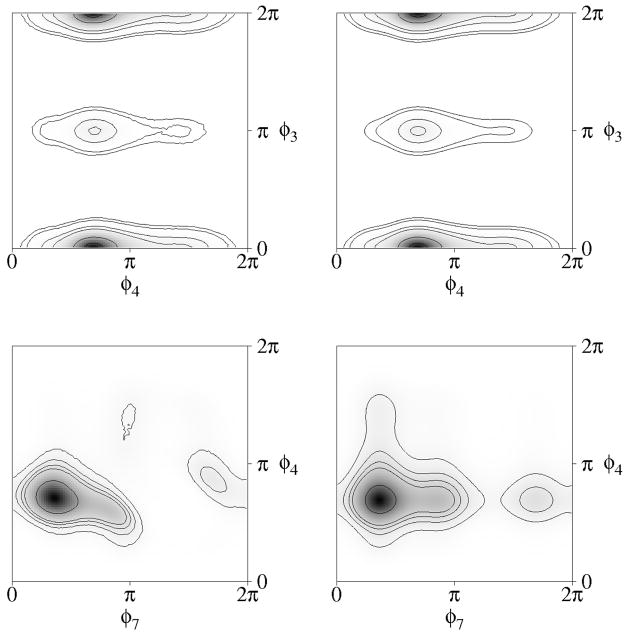
Samples were drawn from up to 14.4 million “observations” of the dihedral angles of the R,S stereoisomer of tartaric acid, a molecule with 7 internal-rotation degrees of freedom, obtained from molecular-dynamics trajectories of this molecule by Hnizdo et al.4 The simulations used a box of 72 molecules in the NVT ensemble at 485 K; the details are given in ref. 4. The resulting marginal distributions of the seven dihedral angles of R,S-tartaric acid are displayed in Figure 2 as smoothed histograms. Correlations among some pairs of dihedral angles are illustrated in Figure 3 by two-dimensional contour plots.
FIG. 2.
Marginal distributions of the dihedral angles φi, i = 1, . . . , 7 of R,S-tartaric acid obtained (as smoothed histograms) by molecular dynamics simulations.
FIG. 3.
Sample two-dimensional distributions of the dihedral angles of R,S-tartaric acid. (a) Dihedral angles φ3 and φ4, which have a low estimated coefficient of association, rI = [1 − e−2I(3,4)]1/2 = 0.0657; (b) dihedral angles φ3 and φ4 plotted as just a product of their marginal distributions; (c) dihedral angles φ4 and φ7, which have a relatively high estimated coefficient of association, rI = 0.5491; (d) dihedral angles φ4 and φ7 plotted as just a product of their marginal distributions. Shading ranges from white (zero probability density) to black (maximum probability density).
To minimize correlations between different “observations,” the molecular-dynamics trajectory was 20 ns long, and only snapshots separated by 100 fs were utilized, each snapshot being that of 72 independent molecules. The time ordering of the full 14.4 million set of the seven dihedral angles of tartaric acid obtained in this way was then randomly shu²ed, so that the convergence behavior of entropy estimates as a function of (pseudo-)random-sample size n, as opposed to the trajectory length in time, could be investigated.
Entropy Computations
Histogram estimates of the entropies were obtained with the computer code ACCENT-MM.8 For the analysis of the bivariate von Mises distributions (Model System I), 200 bins were used for each dimension in the case of 1- and 2-dimensional histograms, and 100 bins were used for each dimension in the case of 3-dimensional histograms. The distributions for R,S-tartaric acid (Model System II) tend to be broader than for Model System I, and thus fewer bins were required: 160 bins for the 1- and 2-dimensional histograms, and 80 bins for the 3-dimensional histograms. The analysis of R,S-tartaric acid was repeated 10 times; in each analysis, the full set of 14.4 × 106 data points was randomly shu²ed. This was done to smooth the convergence plots of the entropy approximations as functions of the number of data points analyzed. The convergence plot for the von Mises data was sufficiently smooth so that only the analysis at n = 1 × 106 data points was repeated to obtain statistics.
The NN estimates [eq. (9)] of the entropies S(i1, . . . , il) of all the l-dimensional coordinate clusters, l = 1, . . . , s were calculated. For the analytical distribution (Model System I, s = 6), simulation samples of sizes n = 5 × 104 − 1 × 107 were used; for tartaric acid (Model System II, s = 7), the samples had sizes n = 5 × 104 − 14.4 × 106. The numbers of distinct l-dimensional clusters of the variables of the analytical distribution are , 15, 20, 15, 6, 1 for l = 1, . . . , 6, respectively, and the numbers of such clusters for tartaric acid are , 21, 35, 35, 21, 7, 1 for l = 1, . . . , 7, respectively. The estimates of S(i1, . . . , il) were used to calculate the mutual information functions Im(1, . . . , m), m = 1, . . . , s [eq. (4)], which were then used to calculate all the MIE terms Tm(1, . . . , s), m = 1, . . . , s according to eq. (7). Finally, estimates of the values Smt(1, . . . , s) of the MIE truncations at orders mt = 1, . . . , s were obtained [eq. (8)]. In the NN method, the NN distances were determined with the k-d tree sorting algorithm16 implemented in the code ANN,17 with the maximum-error parameter set to zero.
Results
Model System I: Analytical Distribution
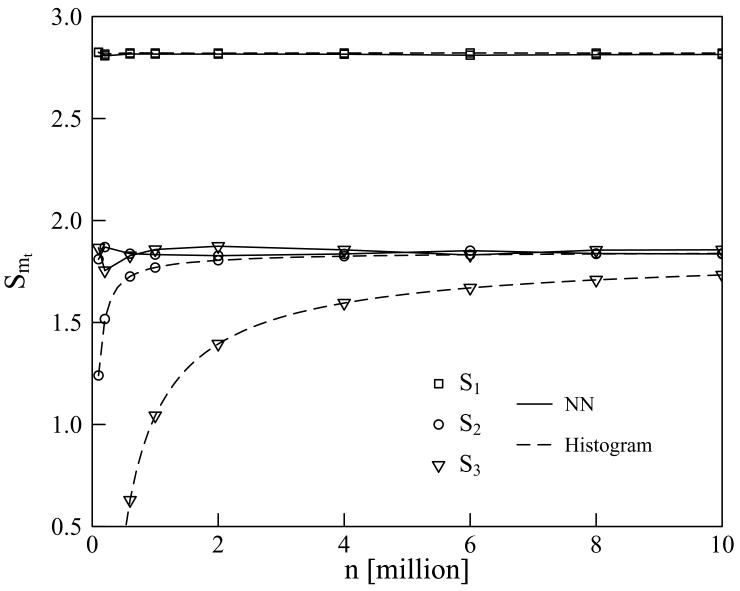
The numerical performance of the NN and histogram methods for the analytical distribution of circular variables is compared in Tables II and III, and in Figure 4. Table II lists the NN estimates of all the MIE terms Tm(1, . . . , 6), m = 1, . . . , 6 for various sample sizes n, and the corresponding histogram data up to third order; the higher-order histogram did not converge well enough to merit analysis. Table III presents analogous results for the values Smt(1, . . . , 6) of the MIE truncated at orders mt = 1, . . . , 6. In both tables, the statistical fluctuations of the estimates are indicated by providing means and standard deviations for 10 independent samples of n = 106. The two tables also give the analytic values of Tm and Smt, respectively, calculated as described in the previous section.
FIG. 4.
Nearest-neighbor and histogram estimates of the mutual-information expansion truncations S1 (□), S2 (○), and S3 (▽) for the analytic distribution of 6 circular variables, as functions of sample size n. The trendlines for the nearest neighbor (—) and the histogram (– –) data are included as a guide for the eye.
TABLE II.
Nearest-neighbor and histogram estimates of the mutual information expansion terms Tm(1, . . . , 6) for Model System I, the analytical distribution of 6 circular variables. Sample sizes, n, are in millions. Analytic values in last row are given to 4 decimals or are identically zero.
| Nearest Neighbor
|
Histogram
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| n × 10−6 | T1 | T2 | T3 | T4 | T5 | T6 | T1 | T2 | T3 |
| 0.05 | 2.8345 | 1.1269 | 0.3271 | 0.3674 | 0.4509 | 0.1058 | 2.8243 | 2.0844 | −7.1889 |
| 0.10 | 2.8252 | 1.0148 | 0.0554 | 0.0318 | 0.1349 | 0.0124 | 2.8238 | 1.5832 | −4.3817 |
| 0.20 | 2.8074 | 0.9375 | −0.1155 | −0.1718 | −0.0212 | −0.0180 | 2.8158 | 1.2984 | −2.5952 |
| 0.40 | 2.8199 | 1.0108 | 0.0739 | 0.0705 | 0.0806 | −0.0006 | 2.8196 | 1.1479 | −1.5137 |
| 0.60 | 2.8165 | 0.9790 | −0.0098 | −0.0156 | 0.0420 | 0.0016 | 2.8214 | 1.0955 | −1.0969 |
| 0.80 | 2.8201 | 1.0046 | 0.0601 | 0.0600 | 0.0611 | −0.0026 | 2.8217 | 1.0691 | −0.8700 |
| 1.00 meana | 2.816 | 0.983 | 0.025 | 0.032 | 0.044 | −0.004 | 2.820 | 1.057 | −0.774 |
| 1.00 sdb | 0.004 | 0.022 | 0.055 | 0.069 | 0.045 | 0.012 | 0.002 | 0.002 | 0.010 |
| 2.00 | 2.8159 | 0.9882 | 0.0463 | 0.0562 | 0.0461 | −0.0008 | 2.8208 | 1.0156 | −0.4103 |
| 4.00 | 2.8153 | 0.9792 | 0.0200 | 0.0189 | 0.0114 | −0.0083 | 2.8210 | 0.9958 | −0.2299 |
| 6.00 | 2.8105 | 0.9583 | −0.0212 | −0.0324 | −0.0225 | −0.0132 | 2.8214 | 0.9888 | −0.1631 |
| 8.00 | 2.8130 | 0.9747 | 0.0166 | 0.0104 | −0.0014 | −0.0093 | 2.8208 | 0.9845 | −0.1276 |
| 10.00 | 2.8141 | 0.9781 | 0.0203 | 0.0125 | 0.0010 | −0.0068 | 2.8207 | 0.9821 | −0.1055 |
|
| |||||||||
| Analytic | 2.8134 | 0.9800 | 0 | 0 | 0 | 0 | 2.8134 | 0.9800 | 0 |
Data provided are means for 10 independent samples of n = 106.
Data provided are standard deviations for 10 independent samples of n = 106.
TABLE III.
Nearest-neighbor and histogram estimates of the mutual information expansions truncations Smt (1, . . . , 6) for Model System I, the analytical distribution of 6 circular variables. Sample sizes, n, are in millions. Analytic values in last row are given to 4 decimals.
| Nearest-Neighbor
|
Histogram
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| n × 10−6 | S1 | S2 | S3 | S4 | S5 | S6 | S1 | S2 | S3 |
| 0.05 | 2.8345 | 1.7076 | 2.0346 | 1.6672 | 2.1181 | 2.0123 | 2.8243 | 0.7400 | −6.4489 |
| 0.10 | 2.8252 | 1.8104 | 1.8657 | 1.8339 | 1.9688 | 1.9564 | 2.8238 | 1.2406 | −3.1411 |
| 0.20 | 2.8074 | 1.8699 | 1.7545 | 1.9263 | 1.9050 | 1.9231 | 2.8158 | 1.5174 | −1.0779 |
| 0.40 | 2.8199 | 1.8091 | 1.8830 | 1.8124 | 1.8930 | 1.8936 | 2.8196 | 1.6717 | 0.1580 |
| 0.60 | 2.8165 | 1.8375 | 1.8277 | 1.8433 | 1.8853 | 1.8870 | 2.8214 | 1.7259 | 0.6290 |
| 0.80 | 2.8201 | 1.8156 | 1.8757 | 1.8157 | 1.8768 | 1.8793 | 2.8217 | 1.7526 | 0.8826 |
| 1.00 meana | 2.816 | 1.833 | 1.858 | 1.826 | 1.870 | 1.874 | 2.820 | 1.764 | 0.989 |
| 1.00 sdb | 0.004 | 0.018 | 0.037 | 0.032 | 0.013 | 0.002 | 0.002 | 0.001 | 0.011 |
| 2.00 | 2.8159 | 1.8277 | 1.8740 | 1.8178 | 1.8639 | 1.8647 | 2.8208 | 1.8052 | 1.3949 |
| 4.00 | 2.8153 | 1.8362 | 1.8561 | 1.8372 | 1.8486 | 1.8570 | 2.8210 | 1.8252 | 1.5954 |
| 6.00 | 2.8105 | 1.8522 | 1.8310 | 1.8633 | 1.8409 | 1.8540 | 2.8214 | 1.8326 | 1.6695 |
| 8.00 | 2.8130 | 1.8383 | 1.8549 | 1.8445 | 1.8431 | 1.8524 | 2.8208 | 1.8364 | 1.7088 |
| 10.00 | 2.8141 | 1.8361 | 1.8564 | 1.8439 | 1.8449 | 1.8517 | 2.8207 | 1.8387 | 1.7331 |
|
| |||||||||
| Analytic | 2.8134 | 1.8334 | 1.8334 | 1.8334 | 1.8334 | 1.8334 | 2.8134 | 1.8334 | 1.8334 |
Data provided are means for 10 independent samples of n = 106.
Data provided are standard deviations for 10 independent samples of n = 106.
It is evident from Table II that, at sample sizes n ≳ 106, the NN estimates of T1 and T2 converge to within second decimal place of their exact values, while the estimates of the terms Tm, m ≥ 3, whose exact values vanish, fluctuate at small values of order 0.01. The standard deviations of the estimates, given for n = 106, indicate that the statistical uncertainty of the estimates of T1 and T2 is significantly smaller than that of the estimates of Tm, m = 2, . . . , 5, which reflects the fact that the evaluation of the former requires a smaller number of statistically fluctuating terms than the evaluation of the latter [see eqs. (4) and (7)]. The results in Table III show that the NN estimates of S1 converge to within the second decimal place of the exact values at sample sizes n ≳ 106, while the convergence of S2, which is subject to greater statistical fluctuations, is only slightly worse. In this idealized model system, the truncation S2, together with all the higher-order truncations Sm, m ≥ 3, equals the full entropy S(1, . . . , 6) because of the absence of correlations of order m ≥ 3. For sample sizes n ≳ 106, the estimates of Sm with m = 3, 4, 5 fluctuate within the second decimal place of the exact value of the ful entropy S(1, . . . , 6), but the estimates of S6, which by definition equal the full 6-dimensional NN estimates, display a trend of slow monotonic decrease with n; at n = 106 and 107, the estimates of S6 are approximately 1.87 and 1.85, respectively, while the exact value is 1.8334. Assuming that the NN estimate of S6 depends upon large n according to the phenomenological form4 S(1, . . . , 6) + a=np, and using the exact value S(1, . . . , 6) = 1.8334, along with the the values a = 1.79 and p = 0.285 that fit best the estimates of S6 at 4 ≤ n=106 ≤ 10, one may estimate that a sample size n ≳ 8 × 107 would be needed to generate a 6-dimensional NN estimate with a bias smaller than 0.01. This is a large sample, but arguably still modest given the high dimensionality of the problem.
The histogram estimates of MIE terms up to second order (T1, T2, S1, S2) in Tables II and III closely approach the nearly-converged NN estimates, as well as the analytic results, at sample sizes n ≳ 106. However, the histogram estimates of the truncation S3 converge far more slowly than the NN estimates. The slow convergence of the histogram results is particularly striking given that the 3rd-order MIE term T3 is identically zero, so that S3 = S2, for this artificial model system. Graphing the data for S1, S2 and S3 of Table III as functions of sample size highlights the strength of the NN method for the higher-order terms (Figure 4). On the other hand, the analytic result for S3 can be approached closely with the histogram method via extrapolation of the third-order entropy estimates as a function of the number of data points, using the same phenomenological form as given in the previous paragraph. One finds a = −31, 406 and p = 0.760, and the resulting third-order approximation to the entropy is S3 = 1.8922, which is within 0.06 of the analytic value. Also, the NN estimates require greater computing time, as discussed in the last subsection.
These results indicate that the first- and second-order MIE terms (T1 and T2, respectively) can be reliably estimated by the NN method already with random samples of size n ~ 106. Samples of such size should be also sufficient for an estimation of the importance of MIE terms Tm of orders m ≥ 3, as such sample sizes yielded good estimates of the vanishing higher-order MIE terms.
Model System II: Tartaric Acid
The numerical performance of the NN and histogram methods for the tartaric acid simulation is compared in Tables IV and V, and in Figure 5, as done for Model System I. In this system, for which analytic results cannot be available, the entries S7 equal by definition the full 7-dimensional NN estimates of the entropy of the entropy of internal rotation from the given samples of sizes n. As in Tables II and III, the entries for n = 106 include means and standard deviations for 10 independent samples.
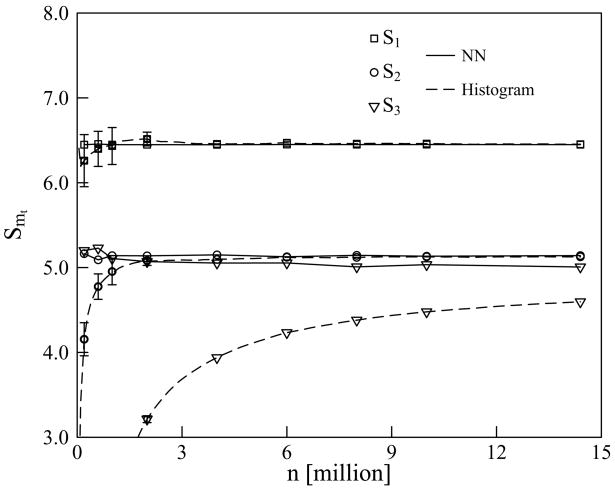
FIG. 5.
Nearest-neighbor and histogram estimates of the mutual-information expansion truncations S1 (□), S2 (○), and S3 (▽) for R,S tartaric acid, as functions of sample size n. The trendlines for the nearest-neighbor (—) and the histogram (– –) data are included as a guide for the eye. Histogram data are the averages and standard deviations for 10 analyses, as described in the Methods section; only standard deviations that are greater than the data symbols are shown, as error bars.
The NN estimates of the MIE terms T1 and T2 at sample sizes n > 2 × 105 display fluctuations only in the 2nd decimal place, indicating near-convergence. This is understandable because the entropies of only one- and two-dimensional coordinate clusters are involved in the definitions of T1 and T2. The NN estimates of the MIE terms Tm with m ≥ 3 fluctuate more with n, but the magnitudes of these estimates are much smaller than those for both T1 and T2. This indicates that many-body correlations of orders m ≥ 3 in R,S-tartaric acid are much weaker than two-body correlations. Table V expresses these results in terms of the MIE truncations Smt : the values of the estimates of S1 and S2 fluctuate only at the 2nd decimal place while the estimates of Smt with mt ≥ 3 differ relatively little from those of S2. The approximation S2, which retains only the two-body correlations, yields an estimate for the configurational entropy of internal rotation of R,S-tartaric acid, using a sample size of 1 million only. This is consistent with the upper bound obtained by Hnizdo et al.4 by grouping the seven unique dihedral angles of this molecule into two non-overlapping clusters of dimensions 3 and 4, the convergence of the entropy estimates of which required samples of considerably larger size. The n → ∞ extrapolation of ref. 4, which included correlations of all orders, yielded , in reasonable agreement with the present results. However, that extrapolation required evaluation of the full 7-dimensional estimates , k = 1, . . . , 5 at several sample sizes n in a range 10 million { 14.4 million.
TABLE V.
Nearest-neighbor and histogram estimates of the mutual information expansion truncations Sm(1, . . . , 7) for Model System II, R,S-tartaric acid. Sample sizes, n, are in millions.
| Nearest Neighbor
|
Histogram
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n × 10−6 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S1 | S2 | S3 |
| 0.05 | 6.4537 | 5.1252 | 5.2428 | 5.4943 | 5.4034 | 5.4657 | 5.4408 | 6.4061 | 2.3402 | −16.6412 |
| 0.10 | 6.4496 | 5.1970 | 5.0692 | 5.5097 | 5.3005 | 5.3824 | 5.3699 | 6.1944 | 3.4141 | −9.2524 |
| 0.20 | 6.4485 | 5.1642 | 5.2006 | 5.1525 | 5.4578 | 5.2749 | 5.3119 | 6.2605 | 4.1557 | −4.3927 |
| 0.40 | 6.4601 | 5.1263 | 5.1840 | 5.2117 | 5.2318 | 5.2674 | 5.2540 | 6.3444 | 4.5980 | −0.9626 |
| 0.60 | 6.4559 | 5.0918 | 5.2295 | 5.1041 | 5.2672 | 5.2332 | 5.2290 | 6.3992 | 4.7761 | 0.5356 |
| 0.80 | 6.4597 | 5.1100 | 5.1761 | 5.1676 | 5.2121 | 5.2265 | 5.2167 | 6.4270 | 4.8705 | 1.3798 |
| 1.00 meana | 6.449 | 5.141 | 5.107 | 5.208 | 5.178 | 5.218 | 5.205 | 6.433 | 4.954 | 1.932 |
| 1.00 sdb | 0.004 | 0.016 | 0.035 | 0.040 | 0.032 | 0.012 | 0.004 | 0.218 | 0.156 | 0.053 |
| 2.00 | 6.4485 | 5.1389 | 5.0709 | 5.2032 | 5.1250 | 5.1887 | 5.1728 | 6.5151 | 5.0823 | 3.2141 |
| 4.00 | 6.4480 | 5.1501 | 5.0537 | 5.1707 | 5.1290 | 5.1595 | 5.1488 | 6.4571 | 5.0953 | 3.9383 |
| 6.00 | 6.4506 | 5.1276 | 5.0548 | 5.1730 | 5.0950 | 5.1472 | 5.1373 | 6.4707 | 5.1218 | 4.2335 |
| 8.00 | 6.4495 | 5.1447 | 5.0087 | 5.2164 | 5.0595 | 5.1439 | 5.1291 | 6.4594 | 5.1205 | 4.3803 |
| 10.00 | 6.4502 | 5.1341 | 5.0345 | 5.1580 | 5.0998 | 5.1238 | 5.1239 | 6.4611 | 5.1271 | 4.4788 |
| 14.40 | 6.4489 | 5.1413 | 5.0074 | 5.1755 | 5.0753 | 5.1206 | 5.1154 | 6.4536 | 5.1272 | 4.5970 |
Data provided are means for 10 independent samples of n = 106.
Data provided are standard deviations for 10 independent samples of n = 106.
As for Model System I, the histogram results of up to second order approach closely the corresponding NN estimates for tartaric acid at sample sizes n ≳ 106, while the histogram estimates of the third-order terms converge very slowly, remaining unconverged even at n ~ 1.4 × 107. In contrast, the NN estimates of S3 display near-convergence already at n ≳ 2 × 106. However, the extrapolated histogramming value of the third-order approximation is S3 = 5.3183, obtained with fitting parameter values a = −19, 098 and p = 0.624; this extrapolated value is within 0.3 of the 7-dimensional result 5.04 ± 0.01 of ref. 4 for .
CPU Timing Data
The greater accuracy of the NN method for a given sample size comes at a computational cost, relative to the simpler histogram method. A histogram estimate of S3 for tartaric acid at n = 1.44 × 107, with the binwidth parameters as described in Section IIC above, took about 5.25 min of CPU time on a system with an AMD Opteron 248 processor (2.2 GHz) and 2 GB of RAM. The corresponding NN estimate took about 17.3 h on a Macintosh PowerMac G5 with a dual-core 2.3 GHz processor and 4 GB of RAM. This computer was used for all the NN estimates. However, much less time, 45.5 min, was required for an NN estimate of S3 with n = 106, which proved to be accurate to within about 2% of the fully converged result. NN estimation of all the truncations Sm, m = 1, . . . , 7 at n = 1 × 106 took about 2.45 h. With the present k-d sorting of ANN, the CPU time for the NN calculations scales approximately as n log n, while the time for the present histogram method (with the same binning at changing n) scales approximately linearly with n.
Discussion and Conclusions
The present study indicates that the NN method of entropy estimation combines with the MIE to provide a powerful technique for extracting configurational entropy from molecular simulations. Truncating the MIE of entropy at order mt < s, where s is the number of dimensions of a given molecular system, provides for a systematic dimension-reduction approximation to the system's joint entropy in terms of the entropies of all the subsystems of dimensions 1 ≤ l ≤ mt. Physically, such a truncation amounts to neglecting all the system's m-body correlations of orders m > mt. The NN method is complementary to the MIE in making excellent use of the available simulation data for estimating the mutual information terms of orders m ≤ mt. In particular, for a given conformational sample, the NN method provides more accurate results than the histogram approach originally combined with the MIE.
A full comparison of the histogram and NN methods requires discussion of the bias of an entropy estimate, a quantity which is distinct from the standard deviation of the entropy estimate. The bias is the difference S − 〈Ŝ(n)〉, where S and 〈Ŝ(n)〉 are, respectively, the true entropy value and the statistical mean of its estimates from independent samples of size n. An entropy estimate is an average, and, as expected for an average, its standard deviation decreases approximately as with increasing n. However, the entropy is unlike a standard average in that it can have nonzero bias at a finite n. For example, the histogram estimate of S3 for Model System II is 1.93, quite different from the correct value of about 5.0, yet the standard deviation of the estimate is only 0.05. (See Table V.) Therefore, the convergence of an entropy estimate is determined by the bias as a function of the sample size n, rather than by the standard deviation of the estimate.
The present study indicates that, although the histogram method requires less computer time than the NN method to extract an entropy estimate from a given data sample, its estimate has greater bias. Thus, to provide an entropy estimate of a desired accuracy, the histogram method requires a longer molecular simulation but less post-processing time. As a consequence, which method is faster, histogram or NN, will depend upon the details of the molecular system and the parameters of the entropy calculation. It is perhaps worth noting as well that, whereas the NN method converges to the correct result as n goes to ∞, the histogram method at least formally does so only as the bin width also goes to 0.
It is of interest to consider the application of these methods to larger systems, such as proteins. For systems in which correlations above second order are not thought to be important, the original histogram implementation of the MIE may be suitable, particularly if more than 5 × 106 data points are available. This possibility is supported by the present observation that that the second-order MIE truncation yields an excellent estimate of the full configurational entropy of internal rotation of tartaric acid, in agreement with prior observations for other molecular systems.8. However, as previously noted,8,19 higher order correlations are likely to play a significant role in other cases, and the combined MIE-NN method should be particularly valuable for exploring the importance of such correlations, since three-body and higher MIE terms can be estimated reliably by the NN method with samples that need not be of excessive size. In addition, the MIE-NN calculations can be trivially parallelized because the MIE breaks the calculation into entirely independent calculations for the various coordinate clusters. Thus, the combined MIE-NN method should find fruitful applications in important chemical and biomolecular problems, such as protein folding and protein-ligand association.
TABLE IV.
Nearest-neighbor and histogram estimates of the mutual information expansion terms Tm(1, . . . , 7) for Model System II, R,S-tartaric acid. Sample sizes, n, are in millions.
| Nearest Neighbor
|
Histogram
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n × 10−6 | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T1 | T2 | T3 |
| 0.05 | 6.4537 | 1.3285 | 0.1176 | −0.2515 | −0.0908 | −0.0623 | −0.0250 | 6.4061 | 4.0659 | −18.9814 |
| 0.10 | 6.4496 | 1.2527 | −0.1278 | −0.4406 | −0.2092 | −0.0819 | −0.0126 | 6.1944 | 3.3185 | −16.6484 |
| 0.20 | 6.4485 | 1.2843 | 0.0364 | 0.0482 | 0.3054 | 0.1829 | 0.0370 | 6.2605 | 2.4891 | −10.4825 |
| 0.40 | 6.4601 | 1.3338 | 0.0578 | −0.0277 | 0.0201 | −0.0356 | −0.0134 | 6.3444 | 1.9817 | −6.2903 |
| 0.60 | 6.4559 | 1.3641 | 0.1377 | 0.1254 | 0.1632 | 0.0340 | −0.0043 | 6.3992 | 1.8102 | −4.6288 |
| 0.80 | 6.4597 | 1.3498 | 0.0661 | 0.0084 | 0.0445 | −0.0143 | −0.0098 | 6.4270 | 1.6959 | −3.7330 |
| 1.00 meana | 6.449 | 1.308 | −0.034 | −0.100 | −0.030 | −0.040 | −0.012 | 6.433 | 1.511 | −2.977 |
| 1.00 sdb | 0.004 | 0.018 | 0.050 | 0.074 | 0.068 | 0.042 | 0.012 | 0.218 | 0.069 | 0.124 |
| 2.00 | 6.4485 | 1.3095 | −0.0681 | −0.1324 | −0.0782 | −0.0637 | −0.0159 | 6.5151 | 1.4723 | −1.9095 |
| 4.00 | 6.4480 | 1.2978 | −0.0964 | −0.1170 | −0.0417 | −0.0305 | −0.0107 | 6.4571 | 1.3593 | −1.1442 |
| 6.00 | 6.4506 | 1.3230 | −0.0728 | −0.1182 | −0.0780 | −0.0522 | −0.0100 | 6.4707 | 1.3266 | −0.8785 |
| 8.00 | 6.4495 | 1.3048 | −0.1360 | −0.2077 | −0.1568 | −0.0844 | −0.0148 | 6.4594 | 1.3211 | −0.7329 |
| 10.00 | 6.4502 | 1.3161 | −0.0995 | −0.1234 | −0.0581 | −0.0239 | 0.0001 | 6.4611 | 1.3329 | −0.6469 |
| 14.40 | 6.4489 | 1.3077 | −0.1339 | −0.1681 | −0.1002 | −0.0453 | −0.0053 | 6.4536 | 1.3264 | −0.5302 |
Data provided are means for 10 independent samples of n = 106.
Data provided are standard deviations for 10 independent samples of n = 106.
Acknowledgments
The authors thank Drs. Dan S. Sharp, E. James Harner and Robert Mantsakanov for many helpful discussions. This work was supported by grant no. GM61300 from the National Institute of General Medical Sciences of the National Institutes of Health to MKG, and by contract no. 212-2006-M-16936 from the National Institute of Occupational Safety and Health to West Virginia University (JT). The findings of this report are solely those of the authors and do not necessarily represent the views of the National Institute for Occupational Safety and Health or the National Institutes of Health.
Contributor Information
Vladimir Hnizdo, Health Effects Laboratory Division, National Institute for Occupational Safety and Health, Morgantown, West Virginia 26505.
Jun Tan, Department of Statistics, West Virginia University, Morgantown, West Virginia 26506.
Benjamin J. Killian, Center for Advanced Research in Biotechnology, University of Maryland Biotechnology Institute, Rockville, Maryland 20850
Michael K. Gilson, Center for Advanced Research in Biotechnology, University of Maryland Biotechnology Institute, Rockville, Maryland 20850.
References
- 1.Karplus M, Kushick JN. Macromolecules. 1981;14:325. [Google Scholar]
- 2.Levy RM, Karplus M, Kushick J, Perahia D. Macromolecules. 1984;17:1370. [Google Scholar]
- 3.Chang CE, Chen W, Gilson MK. J Chem Theory Comput. 2005;1:1017. doi: 10.1021/ct0500904. [DOI] [PubMed] [Google Scholar]
- 4.Hnizdo V, Darian E, Fedorowicz A, Demchuk E, Li S, Singh H. J Comput Chem. 2007;28:655. doi: 10.1002/jcc.20589. [DOI] [PubMed] [Google Scholar]
- 5.Singh H, Misra N, Hnizdo V, Fedorowicz A, Demchuk E. Am J Math Manag Sci. 2003;23:301. [Google Scholar]
- 6.Goria MN, Leonenko NN, Mergel VV, Novi Inveradi PL. J Nonparametr Stat. 2005;17:277. [Google Scholar]
- 7.Scott DW. Multivariate Density Estimation: Theory, Practice, and Visualization. John Wiley and Sons; New York: 1992. [Google Scholar]
- 8.Killian BJ, Kravitz JY, Gilson MK. J Chem Phys. 2007;127:024107. doi: 10.1063/1.2746329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Matsuda H. Phys Rev E. 2000;62:3096. doi: 10.1103/physreve.62.3096. [DOI] [PubMed] [Google Scholar]
- 10.Cover TM, Thomas JA. Elements of Information Theory. John Wiley; New York: 1991. [Google Scholar]
- 11.Kraskov A, Stögbauer H, Grassberger P. Phys Rev E. 2004;69:066138. doi: 10.1103/PhysRevE.69.066138. [DOI] [PubMed] [Google Scholar]
- 12.Lange OF, Grubmüller H. Proteins. 2006;62:1053. doi: 10.1002/prot.20784. [DOI] [PubMed] [Google Scholar]
- 13.Hartigan JA. Clustering Algorithms. John Wiley; New York: 1975. [Google Scholar]
- 14.Singh H, Hnizdo V, Demchuk E. Biometrika. 2002;89:719. [Google Scholar]
- 15.Knuth DE. The Art of Computer Programming. 3. Addison-Wesley; New York: 2004. http://www-cs-faculty.stanford.edu/~knuth/programs.html. [Google Scholar]
- 16.Friedman JH, Bentley JL, Finkel RA. ACM Transactions on Mathematical Software. 1977;3:209. [Google Scholar]
- 17.Arya S, Mount DM. Approximate nearest neighbor searching. Proceedings of the Fourth Annual ACM{SIAM Symposium on Discrete Algorithms; 1993. p. 271. http://www.cs.umd.edu/~mount/ANN/ [Google Scholar]
- 18.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in Fortran. 2. Cambridge University Press; New York: 1992. [Google Scholar]
- 19.Mountain RD, Raveché HJ. J Phys Chem. 1971;55:2250. [Google Scholar]