Afferent Responses During Experimentally Induced Semicircular Canalithiasis

Abstract

Benign paroxysmal positional vertigo (BPPV) is a common vestibular disorder that results in brief periods of vertigo and nystagmus, when the head is tipped relative to gravity. Symptoms are commonly attributed to the pathological presence of heavy calcium carbonate particles within the lumen of the semicircular canal(s)—a condition termed canalithiasis. In the present work, we induced canalithiasis in an animal model (oyster toadfish, Opsanus tau) by introducing heavy glass microbeads into the lumen of the lateral semicircular canal. Bead movement under the action of gravity and canal afferent nerve discharge were recorded in vivo. When the head was oriented nose-down, beads moved toward the nose and the lateral canal afferent discharge rate increased. Afferents that normally encoded angular velocity during oscillatory head rotations responded with tonic increases in the discharge rate during gravity-dependent bead movement. Other afferents, such as the units that rapidly adapt to a step increase in angular head velocity, responded with an initial increase in discharge rate followed by a period of adaptation. Afferent responses occurred in the complete absence of head movement and quantify the pathological inputs to the brain that arise from canalithiasis. The magnitude and time course of the responses reported here are sufficient to explain the symptoms of BPPV.

INTRODUCTION

First described by Bárány (1921) in the early 1920s, benign paroxysmal positional vertigo (BPPV) is the most common vestibular disorder leading to vertigo (Froehling et al. 1991; Mizukoshi et al. 1988). Patients suffering from BPPV experience debilitating symptoms of impaired vision, dizziness, and imbalance. These vestibular symptoms are precipitated when the orientation of the head is changed relative to gravity. Posterior semicircular canal positional vertigo (PC-BPPV) is the most commonly occurring form of the disorder. Although not as common, positional vertigo can afflict the lateral canal (LC) and/or anterior canal (AC) as well (Baloh et al. 1993; Honrubia et al. 1999; McClure 1985). In PC-BPPV, vestibular symptoms are provoked when the head is tipped back relative to gravity—for example, when a subject looks up to view an object on a high shelf or when the head is tipped back as the result of lying down. Dix and Hallpike (1952) identified the semicircular canals as the origin of gravity-sensitive afferent neural inputs to the brain during BPPV and introduced the most widely used clinical test popularly referred to as the Dix-Hallpike maneuver. The test involves a reorientation of the head to align the posterior canal (at its entrance to the ampulla) with the direction of gravity. This test stimulus is effective in provoking the symptoms in subjects suffering from archetypal PC-BPPV.

Two distinct pathological conditions were previously identified as possible causes of the symptoms: cupulolithiasis (Schuknecht 1962) and canalithiasis (Brandt and Steddin 1993; Epley 1992; Hall et al. 1979). Cupulolithiasis describes a condition where otoconial debris adheres to a semicircular canal cupula rendering it “heavy” relative to the surrounding endolymphatic fluid. When the head is reoriented relative to gravity, the cupula is weighted down by the dense particles, thereby inducing an immediate and maintained excitation (or inhibition) of semicircular canal afferents. It is well established that afferent inputs from the semicircular canals are reflected in the slow-phase eye movements (Suzuki et al. 1969; Wilson and Jones 1979) and, as a result, pathological afferent inputs arising from cupulolithiasis would be expected to generate short-latency and tonic nystagmus. Rapid-onset tonic nystagmus indeed has been observed in a small subset of subjects suffering from BPPV (Smouha and Roussos 1995), observations that are consistent with pathological cupulolithiasis in these subjects. Unlike cupulolithiasis, in most cases the nystagmus decreases over time and typically reverses direction when the head is returned to its original position. The symptoms begin after the head has been reoriented with an onset latency of ≥ 1 s and the eye movements are phasic with a duration ranging from 5 s to more than 1 min (Brandt and Daroff 1980; Epley 1980; Herdman 1990). These long-latency phasic eye movements are consistent with a canalithiasis diagnosis—a condition characterized by the presence of free-moving dense particles (e.g., otoconial debris) within the lumen of the afflicted semicircular canal. Free-moving particles have indeed been directly observed in the lumen of the semicircular canal in patients suffering from BPPV (Parnes and McClure 1992).

To provide orientation, Fig. 1 illustrates canalithiasis of the human posterior canal (Rajguru et al. 2004, 2005). The orientation of head and the vestibular labyrinth in the initial upright position (Fig. 1A) and in the supine head-hanging Dix-Hallpike position (Fig. 1B) commonly used to provoke PC-BPPV symptoms are shown (see movie, online Supplement 1, showing dynamic movement of particles).¹ The head-hanging position causes dense particles to fall from the PC ampulla (Fig. 1A), under the action of gravity, in the direction indicated by the dotted arrow. In human canalithiasis, the dense particles are suspected to be displaced otoconia calcium carbonate crystals (Parnes and McClure 1992) with a density of about 2.7 g/cm³ (Carmichael 1984; Lim 1984). Because the endolymph density is near that of water (1.0 g/cm³) (Steer et al. 1967), dense particles would sink in the endolymph and move along the long arm of the canal. A portion of the drag force acting between the moving particles and the endolymph would be transmitted by fluid pressure to the semicircular canal cupula (Rajguru et al. 2004, 2005; Squires et al. 2004). This pressure would deflect the cupula and hair bundles and ultimately lead to modulation of afferent spike trains and pathological signals sent to the brain that underlie symptoms of the disorder.

FIG. 1.

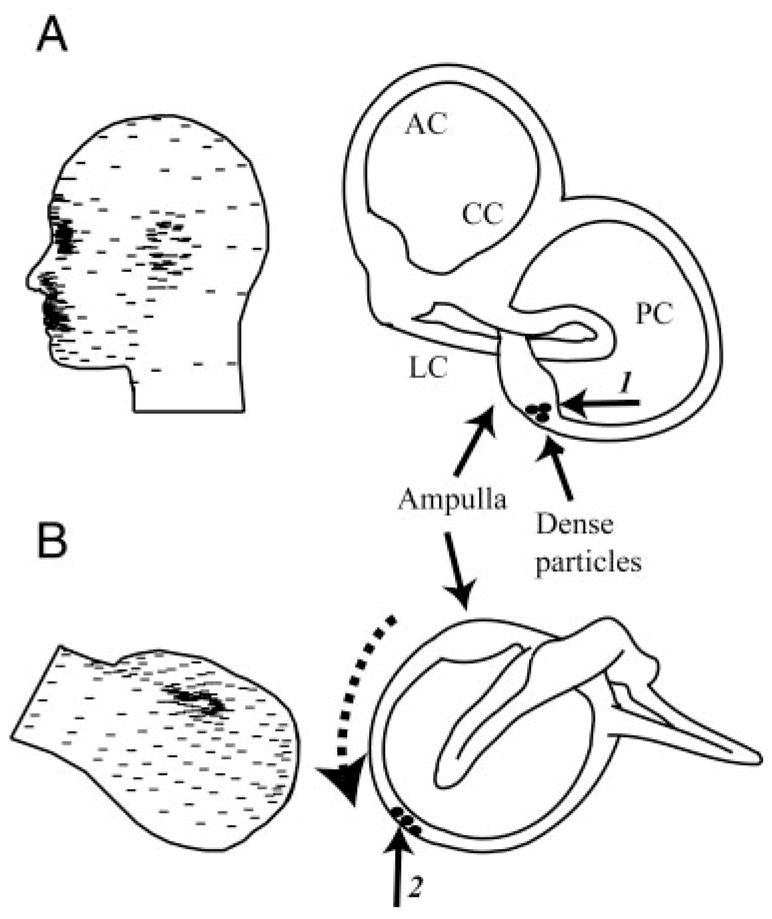
Canalithiasis mechanism of posterior canal (PC) benign paroxysmal positional vertigo (BPPV). A: dense debris (presumably loose otoconia, not to scale) initially located in the PC ampulla (arrow 1) when the subject is standing. B: in the provocative head-hanging Dix-Hallpike position, gravity causes the dense debris to fall “downhill” (dotted arrow) into the slender lumen as the canal (arrow 2). Debris movement leads to a pathological pressure across the PC-cupula, modulates afferent nerve discharge, and results in BPPV nystagmus. LC, lateral canal; PC, posterior canal; AC, anterior canal; CC, common crus.

Hypothesizing that the dense particles lead to the symptoms of canalithiasis, Epley (1992) introduced a treatment for PC-BPPV designed to reposition particles from the canal lumen to the utricular vestibule through a series of timed head rotations. Once within the large cross-sectional area of the vestibule, the free-moving particles would no longer be expected to evoke vestibular symptoms (Rajguru et al. 2004). Canalith repositioning procedures (CRPs) are now routinely applied in the clinic and have good efficacy for treatment of PC-BPPV.

Theoretical investigations of the etiology of BPPV focused on the biofluid mechanics of canalithiasis and generally support the hypothesis that free-moving dense particles could account for the symptoms of BPPV (House and Honrubia 2003; Rajguru et al. 2004, 2005; Squires et al. 2004). Experimental investigations have thus far focused on changes in whole nerve compound action potentials during canalithiasis (Inagaki et al. 2006; Suzuki et al. 1996a,b). These studies indeed confirm that gravity-driven particle movements within the lumen of the canal can evoke significant afferent responses. In the present work, we induced canalithiasis in an animal model in vivo and recorded afferent nerve responses to explicitly define the relationship between canalithiasis and the equivalent (pathological) angular velocity inputs to the brain. Afferent responses were calibrated using mechanical stimuli and recorded during gravity-driven particle movements to estimate the equivalent head velocity that would be present in BPPV. Results quantify the neural sensory signals evoked by canalithiasis and show that these afferent signals account for the common symptoms of BPPV.

METHODS

Canalithiasis BPPV was induced experimentally in the oyster toadfish, Opsanus tau (n = 5). The use of adult toadfish of either sex, approximately 500 g, obtained from Marine Biological Laboratory (Woods Hole, MA) was approved by the Institutional Animal Care and Use Committee at the University of Utah. The toadfish was selected because its membranous canal morphology is similar to that of humans (Ghanem et al. 1998; Rajguru et al. 2004) and because the cartilaginous anatomy facilitated simultaneous recordings of canal afferent discharge and particle movements in vivo (Rabbitt et al. 2005). It is also a well-established animal model for the vestibular semicircular canal system (Boyle and Highstein 1990; Highstein et al. 1996; Rabbitt et al. 1995). Physiological preparation followed methods described previously (Boyle and Highstein 1990). Briefly, fish were anesthetized with MS222 (25 mg/mL in seawater, 3-aminobenzoic acid ethyl ester, Sigma), partially immobilized through intramuscular injection of pancuronium bromide (0.05 mg/kg) in the tail, and secured in an experimental tank with two thirds of its body and gills immersed in bubbled seawater (Instant Ocean, at 10–15°C). The eyes and remainder of the body were covered with moist tissue papers. A small craniotomy (3–4 mm in diameter) was performed lateral to the dorsal course of the anterior canal and rostral to the common crus (CC) to expose the LC and nerve. This surgical approach allowed direct access to the LC nerve without disturbing the membranous labyrinth structures. During surgery, the perilymph within the upper region of the cavity was replaced with fluorocarbon (FC-75, 3M) to improve optical access to the nerve and canal structures and provide a water-immiscible encapsulation of the section of the labyrinth under study.

Canalithiasis was induced by surgical introduction of glass microbeads (density about 2.5 g/cm³; diameters between 15 and 25 μm) into the canal lumen. The glass beads mimic the mammalian otoconia because they have a similar density and fall within the size range between 0.1 and 30 μm (Lim 1984). To facilitate introduction of microbeads, a small endolymphatic fenestra was made by brief delivery of 4- to 8-W cutting waveform by a 76-μm-diameter tungsten electrode (SSE4, Valleylab). This allowed access to the endolymph from a 25- to 75-μm-diameter hole in the membranous wall (Fig. 2A, arrow a). The use of electrically insulating fluorocarbon covering the membranous duct was key to success of the electrosurgical fenestration technique. Fluorocarbon is immiscible with endolymph and thereby prevented any fluid or ionic movement through the hole. It is important to note that the pressure required to overcome the fluorocarbon/water interface surface tension (about 0.015 N/m) and push endolymph though a 50-μm-diameter fenestration in the membranous labyrinth is about 600 Pa, a value that exceeds the endolymph pressure known to be generated during indentation by three orders of magnitude (Yamauchi et al. 2001). Because of this, normal fluid mechanics of the canal is maintained even after fenestration. In addition to preventing translabyrinthine pressure loss, the fluorocarbon also prevented tissue dehydration during the experimental procedure. Neural responses to calibrated mechanical indentation (see following text) were recorded for the same units both before and after generation of the fenestration to ensure that the procedure did not disrupt normal function. An endolymph-filled pressure-balanced micropipette containing beads was inserted into the fenestration, allowing the beads to fall out of the pipette tip and into the lumen of the canal under the action of gravity. The animal was oriented with the plane of the canal tilted roughly 21° relative to the horizontal, such that the slippery beads introduced into the canal moved under the action of gravity, down the canal lumen, and toward the ampulla (Fig. 2B, dotted arrow).

FIG. 2.

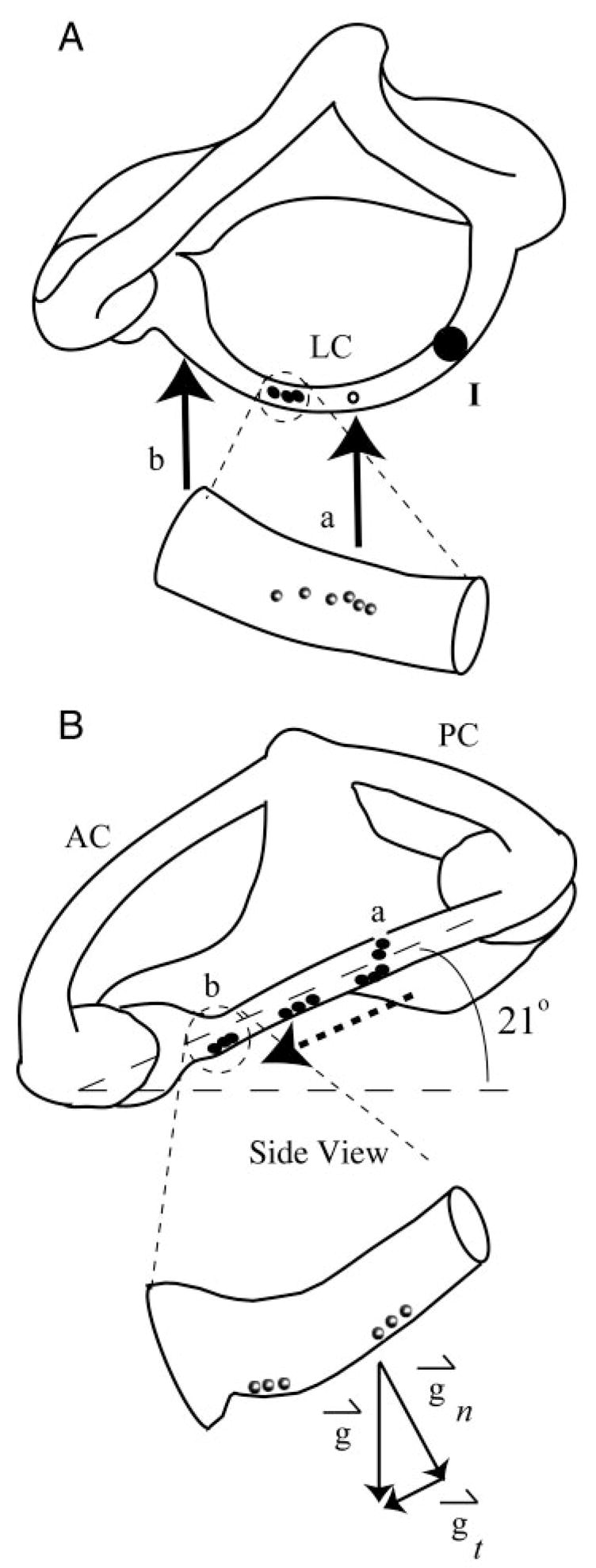
Experimentally induced canalithiasis: A and B: orthographic projections (A, dorsal view; B, lateral view) of the right vestibular labyrinth in toadfish. Glass beads (black dots and inset spheres) were introduced through a fenestration (arrow a) made in the LC wall. Plane of LC was tilted 21° nose-down relative to horizontal such that, under the effect of gravity (g→_t component of gravity tangent to canal), beads fell in a single line along the bottom wall of LC toward the ampulla. Enlarged views of a small section of the canal illustrate the beads within the lumen. At the end of each experiment, most of the beads congregated near the entrance of the ampulla (arrow b), whereas some fell into the relatively large cross section of the ampulla. Mechanical indentation was used (point I) to simulate angular rotation (Rabbitt et al. 1995), a stimulus used to characterize sensitivity and discharge properties of canal afferents and confirm physiological functioning before and after introduction of beads.

Motion of the beads was viewed from a dorsal vantage point (Fig. 2A) through a surgical microscope (Zeiss, OPNI), and bead positions were recorded in real time using a digital camera (Hamamatsu Photonics). Canal afferent responses were recorded for the duration of each experiment. We also determined angular motion sensitivities of afferents both before and after bead movement using a calibrated mechanical indentation stimulus that mimics head rotation and induces equivalent afferent responses (applied at point I, Fig. 2A) (Dickman and Correia 1989; Rabbitt et al. 1995). Afferent responses to indentation and rotation were within the range reported previously in this species (Rabbitt et al. 1995), thus providing experimental evidence that the surgical approach and introduction of beads did not significantly alter canal responses to angular rotation. Knowing the afferent responses for angular rotation stimuli also allowed us to estimate the equivalent head velocity that would reproduce the pathological afferent discharge observed during canalithiasis while the head was stationary. This equivalent head velocity is the pathological signal that was transmitted to the brain during experimentally induced canalithiasis BPPV.

Preparation of glass beads

The glass microbead (Mo-Sci) surfaces were cleaned with piranha solution (70% H₂SO₄:30% H₂O₂) for 15 min and subsequently rinsed thoroughly with deionized water. After drying in a vacuum dessicator, the surfaces were cleaned further with oxygen plasma (PLASMOD, Tegal) for 2 min. To obtain hydrophobic surfaces, the beads were soaked for 10 min in 10 vol % dimethyldichlorosilane (DMDCS, Sigma) in dry toluene (EM Science) (Lowe et al. 1986). The soak was followed by three rinses in absolute ethanol, one rinse in glass-distilled water, and a final ethanol rinse. The surfaces were then air-dried and cured in an 80°C oven with nitrogen flow for 3 h and stored in an airtight container. Beads were then soaked in bovine serum albumin solution (Sigma) in deionized water for 1 h. This treatment made the beads slippery and prevented adhesion of the beads to macromolecules in the endolymphatic space as well as adhesion to the membranous wall.

Afferent recording

Extracellular action potentials were recorded using saline-filled glass suction electrodes (tip diameter ≃ 50 μm) that were brought in contact with the outside surface of the LC nerve near the ampulla. A small suction was applied until extracellular potentials were observed and maintained over the duration of the experiment. In most cases, individual single units could be identified using a simple window threshold (example Fig. 5). The extracellular potentials were conventionally amplified, filtered at 5 kHz, digitized at 10 kHz (National Instruments), and stored for subsequent analysis. Afferent responses were characterized in each animal using sinusoidal mechanical indentation (simulating head rotation) before, during, and after introduction of beads (Rabbitt et al. 1995).

FIG. 5.

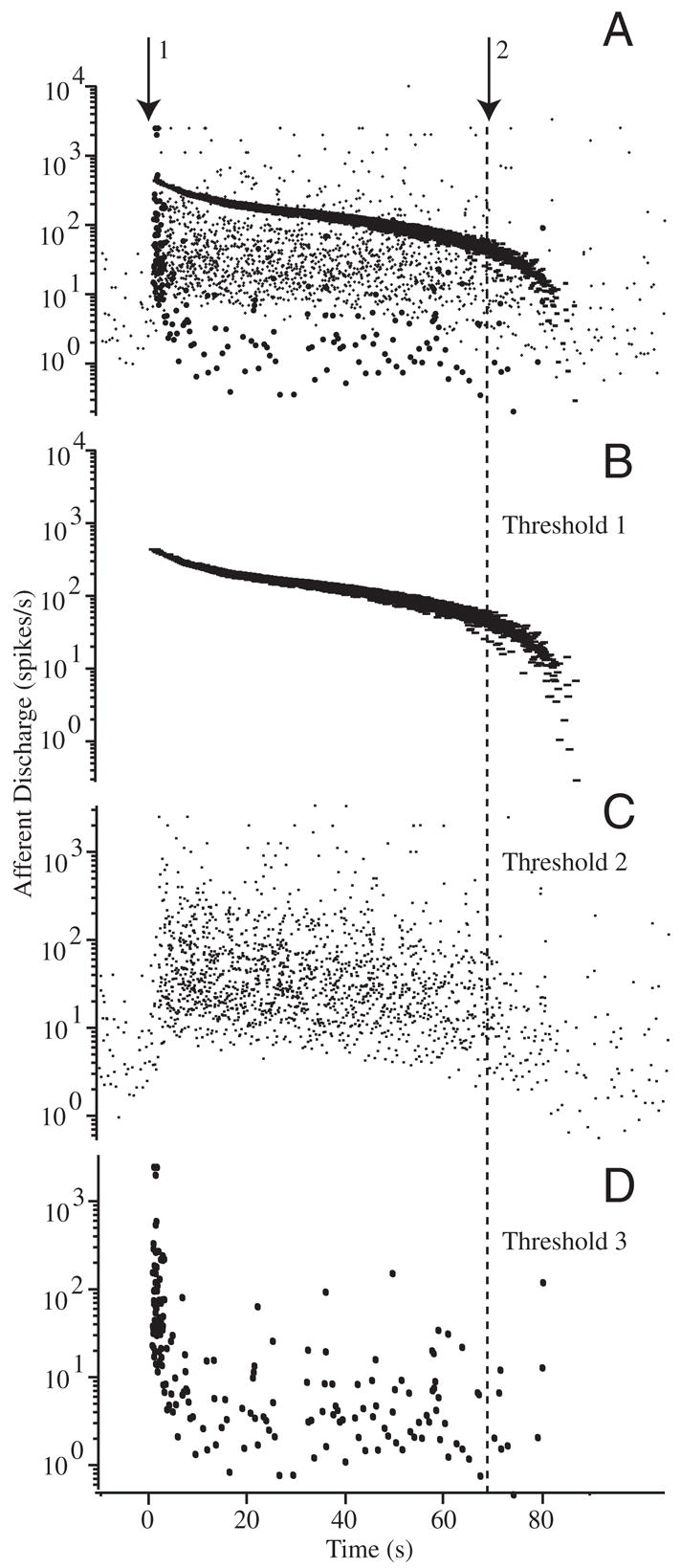
Raw afferent responses to canalithiasis: example raw data illustrating the diversity of afferent responses to canalithiasis bead movement. Afferent discharge patterns shown were recorded simultaneously in response to a single epoch of bead movement in an example animal. A: extracellular action potentials recorded using glass suction electrode attached to the side of the lateral canal nerve branch. Arrow 1 indicates the instance when beads were introduced into the LC and arrow 2 indicates when the beads stopped moving. Window discrimination was applied to associate voltage spikes with individual afferent units. B and C: examples of 2 different afferent units exhibiting tonic increases in discharge over the entire duration of bead movement. Discharge rate returned to the prestimulus background rate only after the beads completely stopped moving (lasting >60 s). D: example of a third afferent exhibiting and initial increase in discharge rate followed by a period of adaptation that returned the discharge to the prestimulus rate before the beads stopped moving.

Analysis

The afferent discharge modulations recorded in response to the sinusoidal stimuli allowed calculations of gain (spikes/s per deg/sec · s⁻¹ of head rotation) and phase shift (degrees relative to the peak stimulus). The gain and phase were computed based on ≥10 consecutive sinusoidal stimulus cycles by manually selecting portions of the record. Using the zero crossing of the sinusoidal mechanical stimulus, response phase histograms of 25 bins per cycle were generated. Histograms were normalized by the number of cycles and displayed in the form of spike frequency (spikes/s). Histograms were fit with a sine wave to determine the magnitude and phase of the afferent response modulation. Bins containing no data were ignored and did not influ­ence the curve fit. The phase was expressed as the difference in degrees between the peak amplitude of afferent response and the peak stimulus. The gain (sensitivity) was defined as the amplitude of sinusoidal afferent modulation over the amplitude of mechanical stimulus (spikes · s⁻¹ · μm⁻¹) and converted to the equivalent head rotation (spike/s per deg/s) by noting that a l-μm LC indentation corresponds to about 4°/s of head angular velocity at the frequencies used (Rabbitt et al. 1995).

Afferent responses recorded during sinusoidal stimuli were used as a calibration to estimate the angular head velocity that would generate the same afferent discharge modulation as observed during pathological canalithiasis. For this, it was necessary to use a model of afferent discharge that was able to account for afferent discharge adaptation to maintained cupula displacements (Rabbitt et al. 2005) and capture gain and phase for sinusoidal stimui (Holstein et al. 2004). A fractional-order model was used because of its ability to fit both gain and phase of afferent discharge during sinusoidal stimuli and fit multi-time-constant adaptation to step stimuli. Responses for sinusoidal stimuli were first characterized using a simple fractional-order model of the form: S – S̄ = G_α(d^αH/dt^α). Here S (spikes/s) is the afferent discharge rate as a function of time, S̄ (spikes/s) is the background discharge rate in the absence of a stimulus, H (deg/s) is the angular head velocity, t (s) is time, and G_α [spikes/s per deg/s (s^α)⁻¹] is the fractional afferent gain. For sinusoidal stimuli, the fractional derivative power α is related to the phase advance θ of afferent discharge relative to the stimulus by θ = α × 90° (0 ≤ α ≤ 1). The fractional order (α) and gain (G_α) were determined using responses to low-frequency sinusoidal stimuli by curve fitting the fractional-order model to bin histograms of the afferent modulation using least squares (Igor Pro, WaveMetrics, Lake Oswego, OR). We then used these same model parameters to estimate the equivalent head velocity that would need to occur to reproduce the afferent discharge patterns observed during BPPV when the head was stationary. This quantifies the pathological angular velocity signal transmitted to the brain. One complicating factor in the experiments was that introduction of the beads, because of their volume in the canal, caused excitation of the canal nerve even in the absence of gravity-driven bead movement. Afferent modulation caused by bead introduction followed the dynamic S_t = G_t(e^−t/τ₁ – e^−t/τ₂), where G_t is the gain (spikes/s), τ₁ is the recovery time constant, and τ₂ is the rise time constant. These parameters were determined using untreated sticky beads that entered the canal but stuck to the wall and did not move under the action of gravity. Knowing the transient caused by introducing the beads S_t and the background discharge S̄, we integrated the raw spike rate data S using the equation S – S_t – S̄ = G_α(d^αH/dt^α) numerically (Podlubny 1999) to estimate the equivalent head rotation H that would reproduce the same afferent discharge modulation observed experimentally during BPPV bead movement. Smoothing splines were used to interpolate the discharge rates to a continuous functions before numerical integration. In some cases, the background discharge rate at the end of the experiment differed slightly (up or down) from the rate before introducing beads. To account for this slow drift we used a straight-line interpolation of the background discharge S̄ from the pre- to the postbead data.

RESULTS

Figure 3 shows transient excitatory afferent responses that occurred when sticky beads were dropped from the pipette into the LC, fell across the lumen, and subsequently stuck to the opposite side of the membranous duct wall. This was expected based on previous work showing increases in afferent discharge simply resulting from small-volume injections into the lumen of the lateral canal (Rabbitt et al. 1995). The sticky beads did not move under the action of gravity toward the ampulla. Both adapting and nonadapting afferents (Rabbitt et al. 2005) responded with short-transient increases in discharge followed by a period of recovery to their resting discharge. Excitation occurred because the endolymph was displaced as the beads fell into the canal lumen. Part of the endolymph was directed toward the ampulla and this generated a transient excitatory response of afferents. In some cases (not shown), a small volume of endolymph was pulled out of the canal using the pipette, a manipulation that caused transient decreases in afferent discharge opposite of that caused by the introduction of beads. The small volume increase on introduction of the beads and the corresponding transient afferent response would not be present in human canalithiasis because the dense particles are already in the canal and are not suddenly introduced. Because of this, we focused our attention on experimental results obtained 1–4 s after the initial transient caused by introduction of the beads—a period when the dense particles were moving with nearly constant velocity toward the ampulla.

FIG. 3.

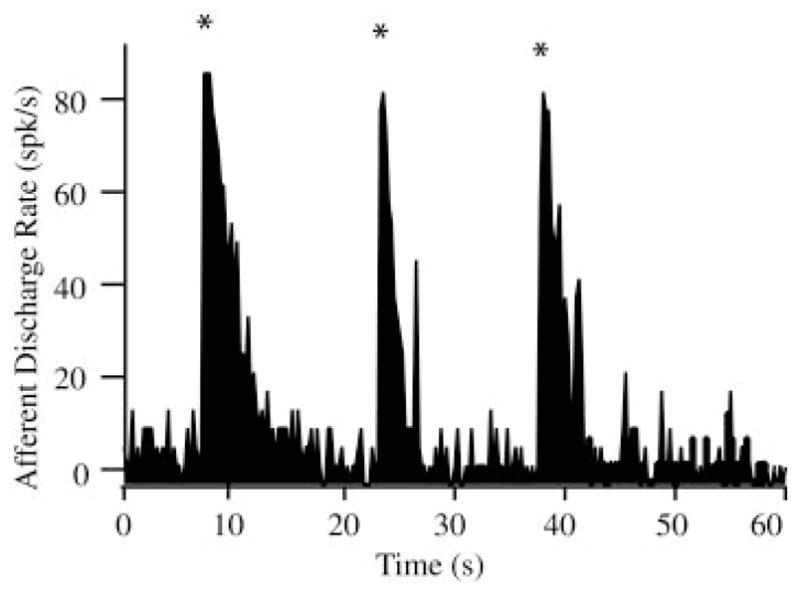
Transient afferent discharge evoked by bead introduction: Excitatory discharge activities lasting between 1 and 4 s were observed with the introduction of the beads into the canal lumen (n = 5 animals). Discharge patterns shown here are for “sticky” beads that fell into the lumen of the canal, dropped across the cross section, and then adhered to the bottom wall of the canal. These transient increases (*) were the result of bead introduction (analogous to canal indentation) and are not the result of bead movement along the canal.

On introduction into the canal lumen, the “slippery” beads fell to the bottom inside surface of the canal lumen and subsequently began to move downhill toward the ampulla. In most case, beads were introduced in groups of about eight to 20. The beads self-separated into a single-file line, spaced about 20–50 μm apart, and moved uniformly under the action of gravity toward the ampulla. Occasionally two or three beads moved together as a group, but in a vast majority of cases beads formed a single-file line as they moved along the canal (see online supplemental movie). Figure 4 shows the velocity of the beads recorded in a representative experiment. Because of the curved geometry of the canal, the beads reached a peak velocity of about 81 μm/s at a distance of about 5 mm from the ampulla and came to rest just before entering the ampulla after about 62–65 s of movement (see movie, online Supplement 2). In some animals, three to five beads fell into the ampulla, but in most cases the beads stopped moving just before entering the ampulla because of the presence of a small ledge in the anatomy adjacent to the ampulla (Fig. 1). The shaded region in Fig. 4 indicates the time range where afferent responses were dominated by transients associated with the introduction of the beads into the canal lumen (Fig. 3); after this initial period afferent responses observed were the result of bead movement along the canal lumen (see following text).

FIG. 4.

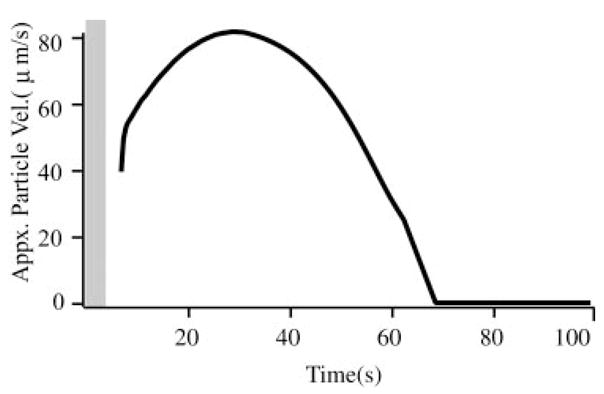
Bead velocity: typical particle velocities (μm/s) over the duration of the gravity-driven bead movement determined from a time sequence of digital images. Beads moved along the canal bottom wall with a velocity of about 80/μm/s in this animal (population average 81 ± 25/μm/s, n = 5 animals). Shaded vertical bar indicates the average duration of transient responses associated with the introduction of beads (cf. Fig. 3).

Figure 5 shows multiunit afferent responses recorded using a single electrode in an example experiment. Simple voltage thresholding was used to separate the afferent nerve recording into three “units” shown separately in Fig. 5, B, C, and D (superimposed in A). The time course corresponds to the bead movement in Fig. 4. Beads were introduced at time 0 s (arrow 1), moved along the canal lumen according to the velocity shown in Fig. 4, and eventually can to rest after about 70 s (arrow 2). Note that the units shown in B and C exhibited tonic responses that lasted during the entire duration of bead movement, whereas the unit shown in D had a rapidly adapting component followed by a mild tonic response. It is important to note that all of these responses were recorded simultaneously during the same bead movement. Thus differences arose from interafferent response dynamics and not from the mechanical stimuli caused by canalithiasis. Figure 6 shows the average increase in afferent discharge rate during bead movement recorded in three fish reported as three groups—A: units with tonic increases in discharge rate during bead movement; B: units that responded vigorously during the first 15s but then adapted by nearly 10-fold after 55 s; and C: units that responded vigorously during the first 15 s but then adapted by nearly 100-fold after 55 s. Error bars denote the SE based on the number of spikes within the time window and averaged over units and should be interpreted as the SE of the average unit. For the tonic units (A) and the modestly adapting units (B), the increase in discharge during bead movement was significantly different from zero over the entire period of bead movement (paired t-test, P ≪ 0.01). However, for the highly adapting units (C) the increase in discharge rate 40–50 s after the introduction of the beads was not statistically significant (P > 0.8).

FIG. 6.

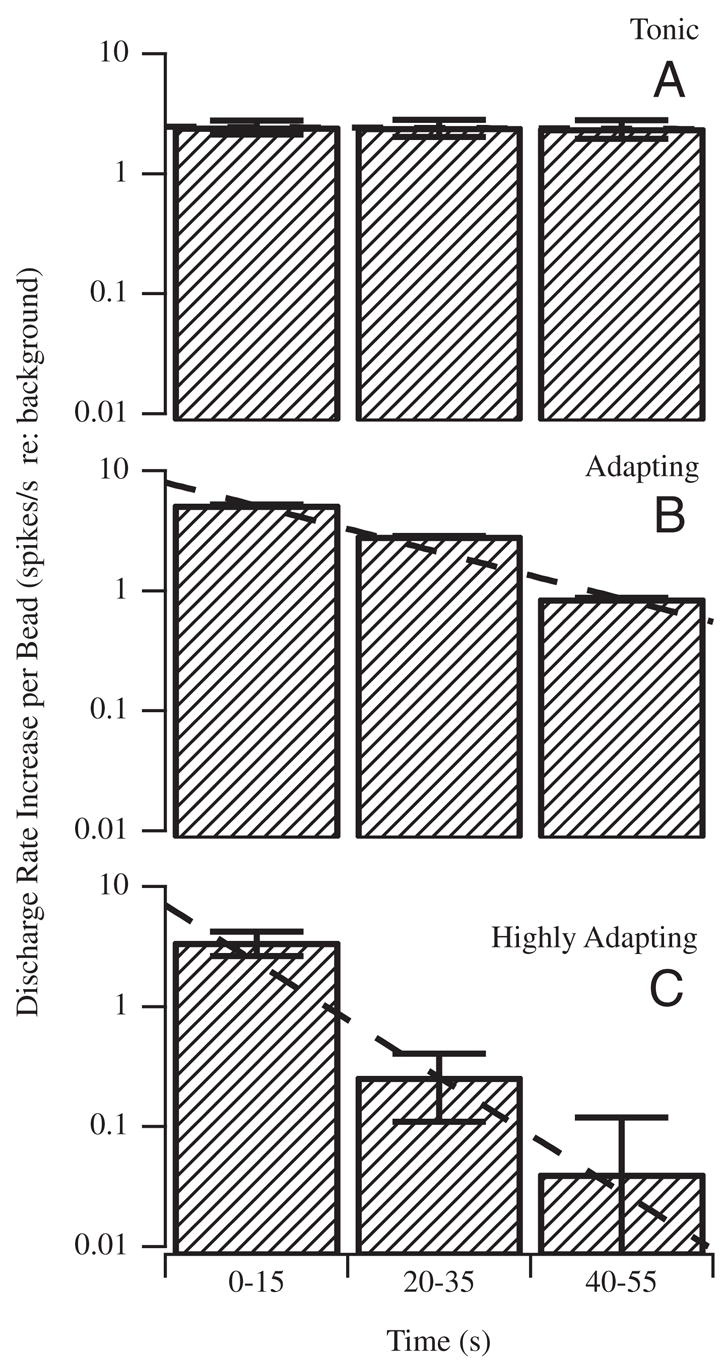
Afferent response types evoked by canalithiasis: canal afferents were divided into 3 groups according to their tonic (A) or adapting (B, C) discharge (spikes/s) responses evoked during bead movement (n = 7). Shaded bars report the average increase in discharge rate over each time interval, with the error bars denoting the SE within each time interval. Increases are shown per bead and relative to the prestimulus background discharge rate, such that “zero” would denote no increase evoked by bead movement. Large diversity of adaptation (A–C) to maintained bead movement is consistent with the diversity reported previously for adaptation to maintained cupula displacement (Rabbitt et al. 2005). Adaptation to bead movement (B, C) was not a macromechanical effect, but rather reflected hair-cell/afferent adaptation.

As a control and calibration, we recorded modulation of all afferent units in response to 0.1- to 2-Hz sinusoidal mechanical stimuli both before introduction of the beads, during bead movement, and after the beads came to rest. Figure 7 shows raw data for a typical unit in response to a sinusoidal mechanical stimulus at 2 Hz superimposed on a canalithiasis bead movement (bead movement epoch starting at t = 0). Before bead introduction this afferent had a gain (sensitivity) of 0.88 spikes/s per deg/sec and no phase lead relative to the 2-Hz sinusoidal stimulus. This gain was maintained nearly unchanged during the entire bead movement period and beyond. This held for all afferents, both adapting and nonadapting types. Figure 8 shows example responses of two additional afferent units for 2-Hz stimuli (C) both before bead introduction (A) and after (B) bead movement. The important point to note is that the magnitude and the phase of afferent modulations to sinusoidal mechanical stimuli were virtually unchanged by the introduction of beads (Figs. 7, A and B and 8, A and B). Although some units did show slight changes, there were no consistent trends across units and statistical significance of the difference (pre vs. post) was very poor. Therefore we concluded that temporal response dynamics of afferents was not altered in any significant way by the introduction of beads. Changes in afferent discharge arose only from bead movement and not from bead presence. There were also some changes in background discharge of afferents over the long time course of the experiments, but again these changes were relatively small and were not consistent between units (e.g., Fig. 7, lower discharge on left vs. right). It is likely that the small background discharge changes resulted from uncontrolled factors such as temperature or slow regulatory mechanisms.

FIG. 7.

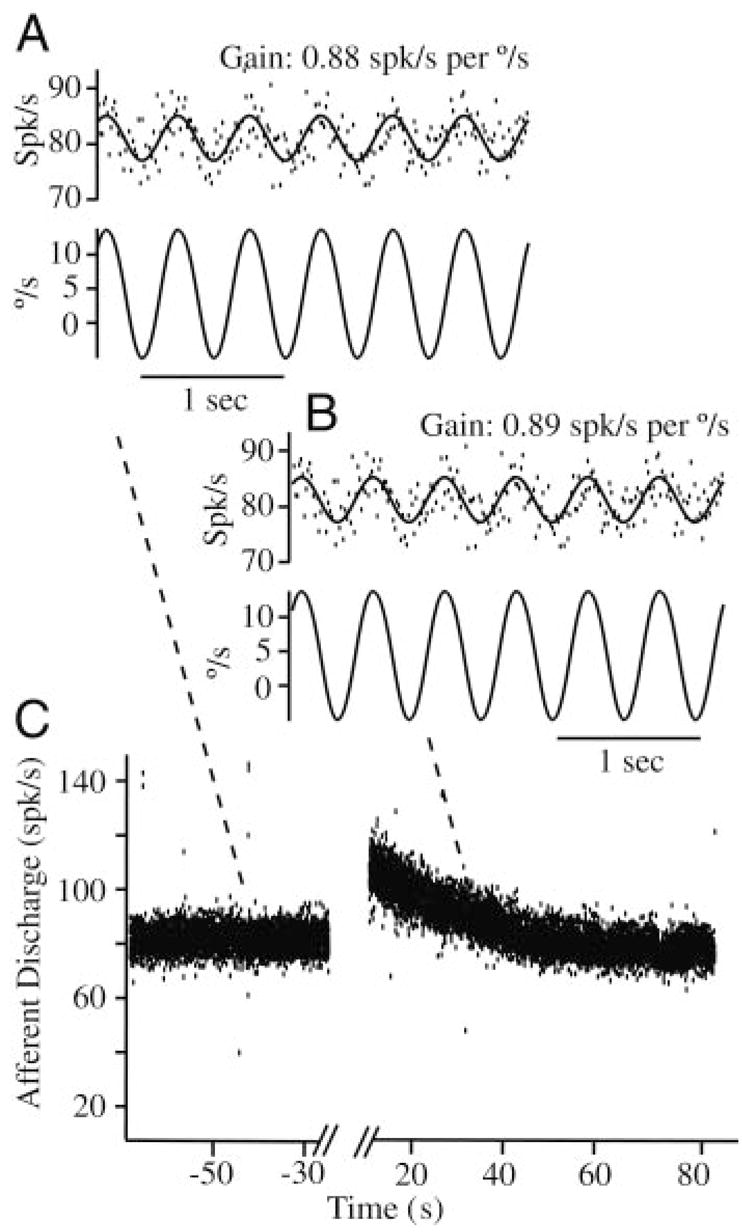
Afferent responses to sinusoidal stimuli during canalithiasis: example single-unit discharge rate in response to a nearly 40°/s sinusoidal mechanical stimulus at 2 Hz before introduction of the glass beads (e.g., A, gain 0.88 spikes/s per deg/sec), during bead movement (e.g., B, gain 0.89 spikes/s per deg/sec), and after the beads came to rest (not shown). Responses to sinusoidal stimuli were used to verify normal physiological function of the labyrinth and calibrate the afferent modulation using sinusoidal stimuli. Calibration was then used to convert afferent discharge evoked by bead movement (e.g., C, large exponential modulation) to the equivalent angular head velocity (see Fig. 9). Note that afferent responses to sinusoidal stimuli did not change significantly as a result of bead introduction and simply superimposed on top of the slow canalithiasis modulation.

FIG. 8.

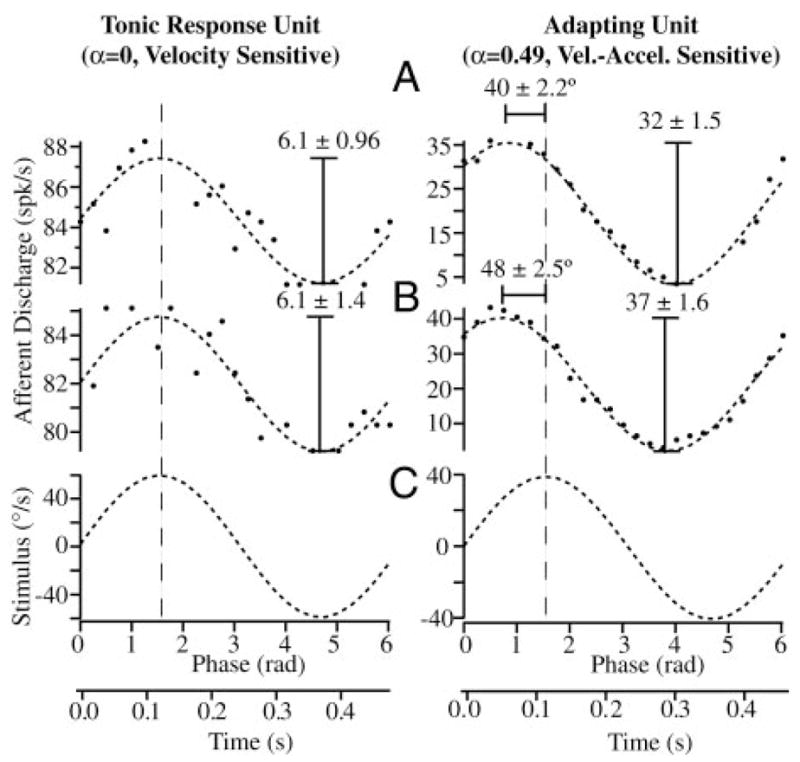
Calibration using sinusoidal stimuli: example afferent discharge rates of tonic (left, velocity sensitive) and adapting (right, velocity-acceleration sensitive) afferent units in response to 2-Hz sinusoidal stimuli (C) are shown in the control condition before introduction of beads (A) and after the beads came to rest (B). Gain (spikes/s per deg/sec) and phase of the peak response relative to the peak stimulus did not change significantly after introduction of the beads (A vs. B). Unit on the left is a typical velocity-coding afferent that modulated its firing rate in phase with the mechanical stimulus and had a gain that was constant with stimulus frequency (fractional order of α ≃ 0 at 2 Hz). Unit on the right had a phase advance of roughly 44° relative to the stimulus and a gain that increased with stimulus frequency, typical of a unit coding a mixture of angular velocity and acceleration (fractional order of α ≃ 0.49 at 2 Hz). Responses to sinusoidal stimuli were used to calibrate each afferent, thereby allowing us to convert discharge patterns observed during canalithiasis to the equivalent angular head velocity that would generate the same afferent responses (see Fig. 9).

After establishing a calibration using sinusoidal stimuli, we used the discharge pattern recorded during bead movement to estimate the equivalent angular head velocity that would elicit the same afferent discharge as observed bead movement (see METHODS). This quantifies the equivalent pathological angular velocity signal that is transmitted to the brain. The pathological velocity (deg/s per bead) was determined as a function of time for each bead movement epoch based on calibrated individual afferent responses. Figure 9A provides the equivalent angular head velocity (dashed curve) determined for one bead movement epoch using the calibrated afferent response. The pathological signal derived from our afferent data had a distinct period of maintained angular velocity. The bottom panel in Fig. 9B is a summary of the equivalent angular head velocity per bead averaged over three animals. Error bars denote the SE between animals. For the first 15 s the afferent responses transmit a signal of about 120°/s per bead to the brain even though the head is stationary. This reduces to nearly 75/s per bead during after 40–55 s of bead movement. The reduction seen here does not arise from afferent adaptation—afferent adaptation is accounted for by modeling the afferent using a fractional operator (see METHODS). Instead, the reduction in the angular velocity signal arises from the curved morphology of the canal and slowing of the beads over time as reported in Fig. 4.

FIG. 9.

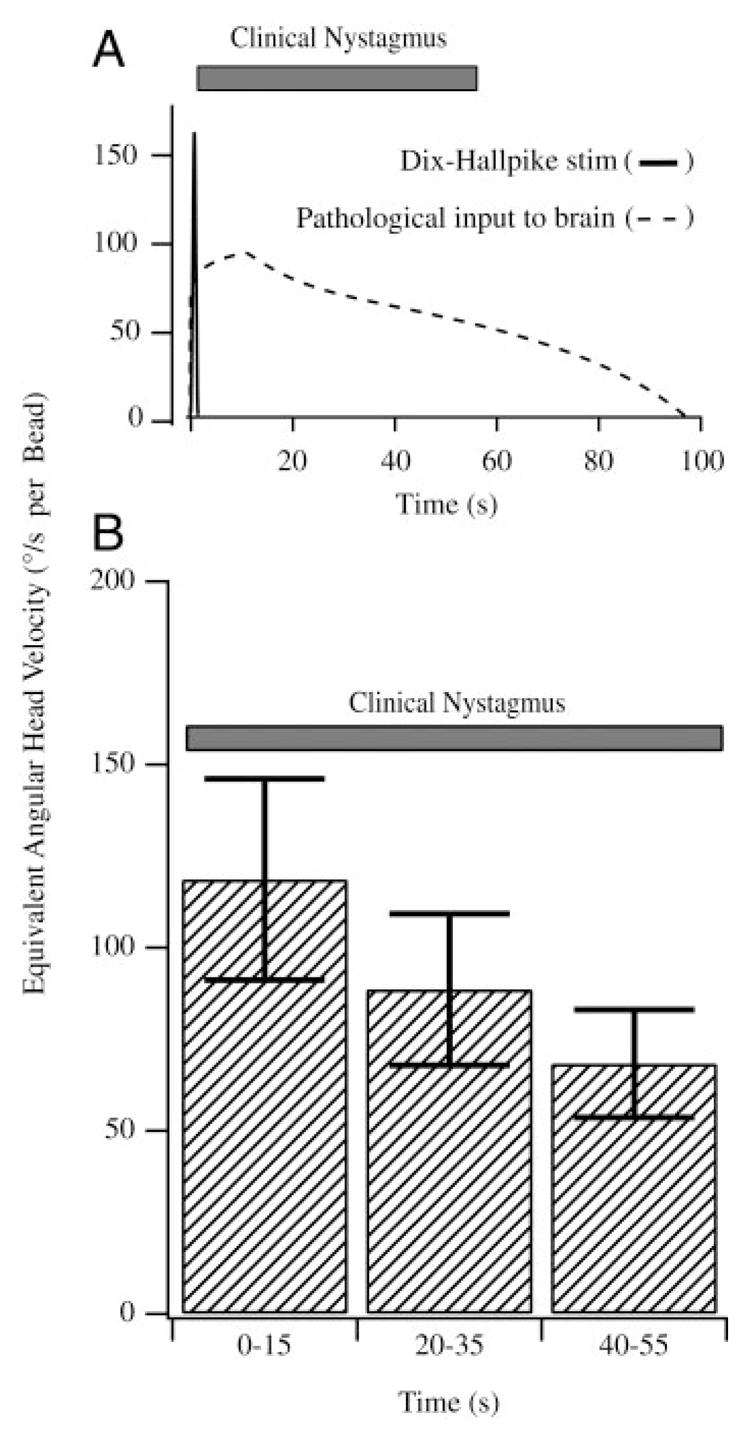
Equivalent angular head velocity: afferent responses to canalithiasis bead movement were converted to the equivalent angular head velocity based on responses of the same afferents recorded for sinusoidal stimuli (Figs. 7 and 8). A, top: equivalent angular head velocity (dashed curve) that would be transmitted to the brain by a representative afferent during bead movement. Note the initial acceleration phase and a long duration of the pathological angular velocity input to the brain (>60-s duration). A summary of the equivalent head velocity based on all afferents is provided in the bottom panel (B, n = 7). Error bars denote SE based on all afferents tested. Results are reported per bead, such that 10 beads would increase the response 10-fold. For comparison, the average duration of nystagmus observed in human BPPV subjects is also shown (solid bars).

Figure 9 also shows the angular head velocity (solid curve) applied in the clinic during the Dix-Hallpike maneuver to evoke the symptoms of BPPV. Note that the Dix-Hallpike angular velocity stimulus is very brief (<2 s, solid curve) relative to the long-term afferent responses evoked by canalithiasis bead movement. The clinically observed nystagmus evoked by the Dix-Hallpike maneuver in human subjects suffering from BPPV occurs after an onset latency and has a long duration as indicated by the solid bar in Fig. 8, A and B (Aw et al. 2005; Honrubia and House 2001), with onset and duration consistent with the signals transmitted to the brain by afferents in the present experimental study.

DISCUSSION

Present results confirm that small dense particles moving within the lumen of the semicircular canal duct elicit afferent responses consistent with the magnitude and duration of archetypical BPPV. Specifically, a single slippery glass bead with a diameter of about 20 μm and moving at nearly 80 μm/s within the lumen of the canal elicited pathological afferent inputs to the brain equivalent to an angular head velocity stimulus of about 100°/s. Each particle thus evokes relatively large inputs to the brain that would inappropriately activate compensatory vestibular responses such as the vestibuloocular reflex. The anomalous afferent inputs to the direct vestibular pathway and conflicting sensory inputs from the proprioceptive and visual systems presumably underlie the debilitating vestibular symptoms evoked by canalithiasis.

The afferent responses evoked by canalithiasis arise because the falling beads induce cupula deflection. Once a bead reaches its terminal velocity of falling, its acceleration is zero and the entire bead weight is taken up by the fluid surrounding the bead. If the bead is in the exact center of the canal, all of the weight is transferred to the cupula, thereby deflecting the cupula and leading to the observed afferent responses. The terminal velocity of a 15-μm-diameter spherical bead (2.8 specific gravity) sedimenting along the centerline of a perfectly vertical canal is predicted by Stokes flow to be 245 μm/s. In our experiments, the canal was oriented at an angle of nearly 21° and thus the component of the gravitational acceleration acting in the direction of bead movement was only 3.51 m/s² (vs. 9.8). For this angle, the terminal velocity of a 15-μm-diameter settling otoconia predicted by Stokes equation would be about 88 μm/s—a figure that compares well with the present experimental observation of 81 (±25) μm/s.

Interestingly, once introduced into the canal, the beads self-separated and moved in a single-file line toward the ampulla along the bottom inside surface of the canal. The fact that the beads were moving along the wall rather than along the centerline of the duct lumen would cause part of the bead weight to be lost to viscous interaction with the wall instead of being transferred to the cupula. This effect would reduce the cupula deflection for beads moving along the wall versus beads moving along the centerline. It was shown previously (Bungay and Brenner 1973) that the influence of a cylindrical tube wall on the pressure caused by a spherical particle moving in a tube the size of the canal duct is small for large particles (> 1 μm), but becomes large for small particles (≪1 μm; e.g., zero-diameter Stokeslet limit). Particles in the present experiments were relatively large (about 15–20 μm), but still much smaller than the lumen. As expected from the work of Bungay and Brenner (1973) for straight tubes, experimental results in this study were consistent with an analysis of larger beads (Rajguru et al. 2004, 2005), but inconsistent with the zero-diameter Stokeslets moving along the duct wall (Squires et al. 2004). The Stokeslet limit might be appropriate for very small particles (≪ 1 μm), but such small particles would not generate large symptoms once moving along the wall because of the dominant viscous interaction with the duct wall. This implies that archetypical canalithiasis BPPV most likely involves larger particles on the order of 5–20 μm in diameter. The present experiments did not investigate the amplifying effect that occurs when particles move from the relatively large cross-sectional area ampulla into the smaller canal lumen—an effect that is likely to be a major contributor to the onset latency in posterior canal BPPV and is a direct result of the hydrodynamics (House and Honrubia 2003; Rajguru et al. 2004, 2005; Squires et al. 2004).

Because endolymph fluid mechanics is linear, it is possible to extrapolate present results to otoconia and to a different number of particles and to particles with larger or smaller Stokes diameters. Otoconia, although not completely spherical (Lira 1984), have an effective Stokes radius that allows the present results to be applied to otoconial particles. The magnitude of the afferent response reported here simply scales with the number of particles—doubling the number of particles will double the magnitude. Changing the diameter of the particles is more complex because it changes the latency to the peak response, the terminal velocity of the particles, and the magnitude of the response. For example, the Stokes terminal velocity increases as the square of the diameter, so doubling the diameter will quadruple the terminal velocity and will reduce the latency to peak response. At the same time, the weight will increase as the cube of the diameter, thus predicting a much larger cupula displacement at steady state. Offsetting this is the somewhat slow response of the cupula. If the particles are large and move too fast, the cupula will not have sufficient time to come to a steady-state deflection and the magnitude of the neural response will not reach the level expected from the full weight of the particle(s). In addition, the complex geometry and curvature of the labyrinth are also important. These mechanical factors are discussed in more detail by Rajguru et al. (2004) in the framework of a morphologically descriptive biomechanical model of canalithiasis.

The present work is focused on afferent responses to canalithiasis. It is important to note that not all semicircular canal afferents respond equally in response to step excitatory cupula displacements—some afferents respond with tonic increases in discharge rate whereas other afferents initially increase their discharge rate and then adapt back to prestimulus levels over time (Rabbitt et al. 2005). The same diversity was observed during canalithiasis bead movement (Figs. 5 and 6). Afferents with tonic increases in discharge during bead movements were identified as classic velocity-sensitive afferents that modulate their discharge rate in direct proportion to head angular velocity over a broad bandwidth. These are the well-studied velocity-sensitive units in the toadfish (Boyle and Highstein 1990) and are analogous to the regular-discharging units in mammals (Fernández and Goldberg 1971; Goldberg and Fernández 1971). Velocity-sensitive afferents are also known to be non-adapting (or very slowly adapting) for maintained stimuli (Goldberg and Fernández 1971; Rabbitt et al. 2005). Other afferents exhibited an initial increase in the discharge rate followed by a period of adaptation during the bead movement. The most rapidly adapting were representative of phasic acceleration-sensitive afferents in the toadfish (Boyle and Highstein 1990)—units that are also known to adapt to maintained cupula deflection (Rabbitt et al. 2005). Adapting afferents in the fish have some response characteristics similar to the irregularly discharging units in mammals (Fernández and Goldberg 1971; Goldberg and Fernández 1971). Within this broad diversity of afferent responses and adaptation times, it is known that the velocity-sensitive (Fig. 6A, very slowly adapting regularly discharging units in mammals) are the most critical to the low-frequency vestibuloocular reflex (Minor and Goldberg 1991) and therefore would be expected to be the most important afferent inputs to the brain underlying nystagmus of patients suffering from canalithiasis BPPV. With this understanding, present results show that canalithiasis indeed generates significant and long-lasting pathological inputs to the brain stem that are sufficient to explain the symptoms of archetypical BPPV.