Visual short-term memory operates more efficiently on boundary features than on surface features

Abstract

A change detection task was used to estimate the visual short-term memory storage capacity for either the orientation or the size of objects. On each trial, several objects were briefly presented, followed by a blank interval and then by a second display of objects that either was identical to the first display or had a single object that was different (the object changed either orientation or size, in separate experiments). The task was to indicate whether the two displays were the same or different, and the number of objects remembered was estimated from the percent correct on this task. Storage capacity for a feature was nearly twice as large when that feature was defined by the object boundary, rather than by the surface texture of the object. This dramatic difference in storage capacity suggests that a particular feature (e.g., right tilted or small) is not stored in memory with an invariant abstract code. Instead, there appear to be different codes for the boundary and surface features of objects, and memory operates on boundary features more efficiently than it operates on surface features.

The short-term storage of visual information is a critical component of visual information processing. It enables incoming stimuli to be tracked and compared with current percepts and with other information already in short-term storage or in long-term storage. Early work on visual memory by Phillips (1974) revealed that there are two separate storage systems for visual information: One is a high-capacity sensory store, and the other is a short-term store with a relatively limited capacity, referred to here as visual short-term memory. Recent work has shown that the upper limit on the number of objects that can be stored in visual short-term memory is quite small, on the order of about four or five simple objects (Luck & Vogel, 1997). The number that can be stored is limited both by an upper limit on the number of objects that can be stored and by the total amount of visual information that can be stored in memory. Thus, increasing the amount of information stored per object reduces the number of objects that can be stored (Alvarez & Cavanagh, 2004).

The question addressed in the present article is whether the same abstract code, such as right-tilted or small, is stored regardless of the format in which that information was initially presented. It is easy to imagine abstract codes for verbal memory. For example, if asked to store the uppercase letters A, P, Q, T in verbal memory, there would be no difficulty in recognizing the lowercase letters a, p, q, t as the same, despite the change in physical appearance, presumably because the information has been encoded in an abstract form. Similarly, work on visual memory suggests that letter shape can be encoded with a somewhat abstract structural description, so that memory for conjunctions of color and shape is insensitive to font changes that preserve letter structure (e.g., A vs. A), whereas large impairments occur with changes that alter letter structure (e.g., A vs. a; Walker & Hinkley, 2003). Thus, it appears that, in some cases, visual memory stores complex shape information with an abstract structural code.

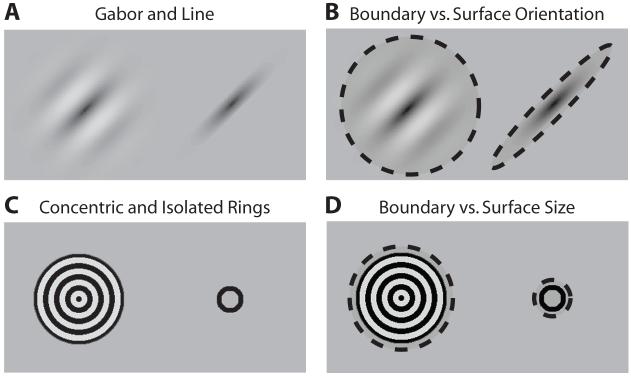
In the present study, we explored whether boundary and surface features of objects are treated equally by visual short-term memory, as would be expected if visual short-term memory operates over abstract codes. Figure 1 illustrates the difference between boundary and surface orientation and between boundary and surface size. In Figure 1A two different objects with identical orientations are presented. On the left is a Gabor patch (a sine wave grating with contrast vignetted by a Gaussian envelope), and on the right is a single bar of the Gabor patch. Figure 1B highlights the boundary of each object. The boundary of the Gabor has no clear orientation, whereas the boundary of the bar has a strong rightward tilt. In contrast, within the boundary, the Gabor surface texture has a clear right-ward tilt, whereas the bar texture (homogeneous black) has no orientation information. Thus, some features—in this case, orientation—can be carried by either the boundary or the surface texture of an object. Figures 1C and 1D illustrate this point for the dimension of size.

Figure 1.

The distinction between boundary and surface features. (A) On the left is a Gabor patch (a sine wave grating with contrast modulated by a Gaussian envelope), and on the right is a single isolated bar of a Gabor patch. (B) The boundary of each object is highlighted with a dashed line. The Gabor boundary has no dominant axis of orientation, but the striped texture within the boundary has a strong orientation. The bar has a strong boundary orientation but no surface orientation (its surface texture is a homogenous, unoriented color). (C) On the left is a radial grating (set of concentric rings), and on the right is a single isolated ring of the radial grating. (D) The boundary size of each object is highlighted with a dashed line. The radial grating has two size features: the size of the outer boundary and the spacing of the rings within that boundary. The isolated ring, on the other hand, has only a boundary size (the diameter of the disk). Within the boundary, its surface is homogenous and carries no size information.

Although the boundary and surface features can be clearly perceived in these stimuli, (e.g., the rightward tilt of both the Gabors and the bars is easily perceived and visually salient), it is unknown whether the boundary and surface features are treated equivalently at different stages of processing and, in particular, whether visual short-term memory encodes and stores them equally efficiently. If the same abstract code is stored for both types of features, then after this abstract visual label is encoded, there should be no consequence of the different presentation formats for the storage capacity of visual short-term memory. For example, the ability to remember right tilted or small should be the same whether those features were present in the boundary or within the surface texture of an object.

The distinction we are making here between boundary and the surface features is motivated by strong evidence that there are separate boundary and surface systems in the human visual system. Work on object individuation in infants has shown that shape and boundary features are used to segment objects at a younger age than are surface features, such as color or texture. For example, Needham (1999) has shown that at the age of 4 months, differences in shape lead infants to interpret a pair of adjacent objects as separate individuals (leading to surprise when the objects move together as if attached), whereas differences in color do not result in such segmentation (leading to surprise when the objects move separately). By the age of 12 months, infants use both shape information and color to individuate objects (Tremoulet, Leslie, & Hall, 2000). However, after objects are occluded, infants at this age notice changes in the specific shape identities of the objects, but not the specific color identities of objects. Thus, it appears that infants’ use of boundary information precedes the use of surface information in the development of several different types of processing, including object individuation (determining which regions of an image correspond to separate objects) and identification (remembering which objects had which particular features).

The most extensive research on the distinction between boundary and surface features in adult vision has been the perceptual and physiological models proposed by Cohen and Grossberg (1984) and Grossberg and Mingolla (1985a). Grossberg and his colleagues have proposed a model in which there are two parallel systems in visual processing: (1) a boundary contour system that is sensitive to the orientation and amount of contrast at an edge but is not concerned with the direction of contrast, and (2) a feature contour system that is sensitive to both the direction and the amount of contrast, but not the orientation of contrast. Critically, these two systems interact, so that the boundary system forms a barrier to the diffuse “filling-in” of surface luminance and color that is triggered by feature contours. This model has been applied to explain a broad range of perceptual phenomena, including several aspects of brightness perception (e.g., the Cornsweet illusion; Cohen & Grossberg, 1984), perceptual grouping (Grossberg & Mingolla, 1985a), and neon color spreading (Grossberg & Mingolla, 1985b), to name a few.¹

Note that each of these lines of evidence suggests not only that there are separate boundary and surface systems in vision, but also that the boundary system is, in some sense, primary. In infant development, the boundary system comes “online” for various types of processing earlier than the surface system. In adult perception, the boundary system operates more quickly than the surface system, and in the perceptual and neural model of Grossberg and colleagues (Cohen & Grossberg, 1984; Grossberg & Mingolla, 1985a), the boundaries form a barrier within which surface information is filled in. According to these models, boundary features are necessarily processed more quickly in order to restrict the filling in of surface features (Dresp & Grossberg, 1999). Here, we seek to determine whether this primacy of boundary features extends to the operation of visual short-term memory.

To anticipate our results, in the following series of experiments, we find that the memory storage capacity for bar orientations is nearly double the storage capacity for Gabor orientations (Experiment 1). The critical difference between the bars and the Gabors in Experiment 1 appears to be the shape of the object boundary (Experiments 2 and 3). The more salient the orientation of the object boundary appears to be, the greater the visual short-term memory capacity for both Gabors and bars. In fact, if the saliency of the object boundary orientation is matched, there is no difference in storage capacity for Gabors and bars. We also demonstrate that the greater memory capacity for boundary features, relative to surface features, is not limited to orientation but is also found for size (Experiment 4). Finally, we present a number of control experiments that demonstrate that the advantage for remembering boundary orientation over surface orientation is not accounted for by differences in the ability to accurately perceive the orientation of these stimuli (Experiment 1), the time needed to encode items into memory (Experiment 5), decision stage limitations (Experiments 6 and 7), or differences in the strength of perceptual grouping (Experiment 7). Combined, these results indicate that boundary features can be encoded and stored in visual short-term memory more efficiently than surface features of objects.

GENERAL METHOD

Participants

All the observers were between the ages of 18 and 35 years, gave informed consent, and were paid $10/h or were given 1 h of course credit for their participation. Ten observers participated in Experiment 1, and 8 observers participated in each of the other experiments.

Apparatus

All the experiments were run on Apple Power Macintosh computers, and displays were generated with custom software written in C, using the Vision Shell Graphics Libraries (Comtois, 2003).

Stimuli

Unless specified otherwise, the stimuli were 2.5°-diameter Gabor patches (high-contrast sine wave gratings with a spatial frequency of 1 cpd and contrast vignetted by a Gaussian envelope), bars (isolated black bars of a Gabor patch subtending 0.4° × 2.5°), or rectangles with blurred edges (variable size; see Experiments 1 and 2). The orientation of each object was set randomly to an angle between 0° and 165° (in steps of 15°). With 12 possible orientations, the displays tended to be heterogeneous, which minimized grouping effects. All the items were presented on a gray background (matching the average luminance of the Gabor patches). Finally, the items were presented in pseudorandom positions within a 4 × 4 grid subtending 26° × 22°. Each item was jittered ±1° from the center of the cell in which it was drawn, to reduce collinearity effects.

Procedure

In each experiment, we estimated the capacity of visual short-term memory for orientation (Experiments 1-3 and 5-7) or size (Experiment 4), using a change detection task. On each trial, several objects were presented for 500 msec (unless otherwise noted), followed by a 1,000-msec blank interval (luminance was equal to the mean luminance of the Gabor patch) and then by a second presentation of objects. On half of the trials, the two displays were identical, and on the other half of the trials, one of the objects changed on the target feature. The task was to remember the target feature of as many objects as possible and to indicate whether the two displays were the same or different by pressing the corresponding key on the keyboard. Responses were unspeeded, and no feedback was given.

Data Analysis

Capacity calculation

Capacity in terms of the number of objects stored was estimated from percent correct on the change detection task, using the following equation, which is equivalent to Cowan’s k (Cowan, 2001), except that it is expressed in terms of false alarms, instead of correct rejections, and can be reduced to this simple form:

$$C=(H-FA)\ast N.$$ (1)

C is capacity in terms of the number of objects stored in memory, H is the hit rate (rate of correctly reporting a change), FA is the false alarm rate (rate of incorrectly reporting a change), and N is the number of objects presented.

Estimating the storage capacity limit

The capacity limit was estimated for different stimuli as a function of the number of objects to be remembered. The average capacity estimate across all numbers of objects presented was taken as each observer’s capacity limit for a given stimulus. Note, however, that set sizes less than the capacity limit do not provide appropriate estimates. For example, perfect performance at set size 1 can yield a maximum capacity estimate of one object, even if the true capacity is four objects. Thus, after taking the average estimate over all set sizes, set sizes smaller than this average were dropped, and the average estimate from the remaining set sizes was taken as the capacity estimate. This process was iterated until the estimate did not exceed the minimum set size included in the estimate.

This method of estimating capacity is appealing because it allows the results to be interpreted in terms of the upper limit on the number of objects stored, which is an intuitive unit of capacity. However, we have previously demonstrated that visual short-term memory is limited not only by the number of objects that can be stored, but also by the total amount of visual information or detail that can be stored in memory (Alvarez & Cavanagh, 2004), and others have found that signal detection models account for change detection performance with greater accuracy than do high-threshold models, such as the capacity estimate we compute here (Wilken & Ma, 2004). Thus, to quantify capacity in terms of the number of objects stored is most likely an oversimplification and ignores the possibility that encoding partial information from multiple objects could give rise to the same level of performance as fully encoding a smaller number of objects. Therefore, it is important to note that the patterns of results reported here are qualitatively the same whether the data are analyzed in terms of percent correct or sensitivity measures, such as d’ (Green & Swets, 1966) or A’ (Grier, 1971) or in terms of the number of objects stored. For readers interested in these other performance measures, we have included tables with both raw accuracy data and d’ in the Appendix.

EXPERIMENT 1

Higher Storage Capacity for Bar Orientations Than for Gabor Orientations

The purpose of this experiment was to determine whether storage capacity for Gabor patch orientations is the same as storage capacity for bar orientations. The orientation of these Gabors is carried by the surface texture within a circular boundary, whereas the orientation of the bars is carried by the boundary. To estimate storage capacity, we used the change detection task shown in Figure 2 (see the General Method section). One potential limitation on performance in this task is the extent to which the orientation of the items can be accurately perceived. Figure 1 suggests that orientation is a reasonably salient feature for both the bars and the Gabors. This intuition is supported by visual search studies showing that the orientation of both types of stimulus is sufficiently salient to support pop-out when a single, oddly oriented item is present among a homogeneous set of distractors (for Gabors, see Joseph, Chun, & Nakayama, 1997; for bars, see Treisman & Gormican, 1988, and Wolfe, Friedman-Hill, Stewart, & O’Connell, 1992). Although these studies did not directly compare performance for Gabors and bars, the fact that both types of object support pop-out in visual search suggests that the orientation information in Gabors and bars is easily extracted. Moreover, we found, in a pilot study, that texture segmentation based on orientation differences is just as fast and accurate with Gabors as with bars.

Figure 2.

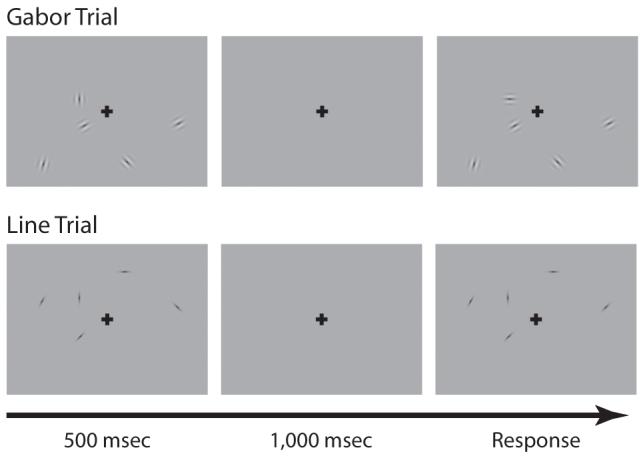
Display sequence in Experiment 1. On each trial, a fixation point was presented for 500 msec (not shown), followed by a 500-msec display of Gabors or bars, which was followed by a 1,000-msec blank interval and then by a second display of objects that was either identical or had a single object for which orientation had been changed by 90°. The second display remained present until the observer responded, indicating whether the two displays were the same or different.

Nevertheless, we ran a control experiment in order to verify that the orientation of Gabors and bars could be perceived equally well in our displays. The memory task required observers to discriminate between a remembered object and one that changed by 90° (if there was a change). Thus, this perceptual task measured how well a 90° difference in orientation could be perceived for Gabors and bars. To do so, we needed a task that did not require a comparison between items, either over space or over time, because such comparisons would require memory storage. Thus, we simply had observers judge the orientation of items that were presented for 500 msec and then were masked. A standard measure of visual sensitivity in psychophysics is the stimulus contrast necessary to make a discrimination judgment with 75% accuracy. Thus, in our control experiment, we measured the stimulus contrast necessary to discriminate vertical from horizontal for a single Gabor or bar as a function of the eccentricity and total number of items in the display. If orientation information is extracted equally well for Gabors and bars, and if 90° orientation differences are equally noticeable for Gabors and bars, the 75% threshold contrast should be comparable for both types of objects at each eccentricity and regardless of the total number of items in the display.

Provided the objects are matched in terms of the ability to perceive their orientation and discriminate an orientation difference, a memory system that uses a single abstract format to encode and store orientation information should store Gabor orientations and bar orientations equally efficiently. That is, once encoded, a single format for storing information in memory should require the same amount of “space” in memory, regardless of the form of the object from which that bit of information has been extracted. Any difference in storage capacity for Gabors and bars would then suggest that the orientation of Gabors and bars are encoded with different formats depending on differences in the physical appearance of the stimuli (i.e., the difference between surface orientation and boundary orientation illustrated in Figure 1B).

Method

Participants

A group of 10 observers participated in the main experiment, and a separate group of 8 observers participated in a perceptual saliency control experiment (author G.A.A. and 7 naive observers).

Stimuli

The stimuli in the main experiment were Gabor patches and bars (isolated black bars of a Gabor patch), as specified in the General Method section. The same stimuli were used in the perceptual saliency control experiment, except that stimulus contrast was varied and only vertical or horizontal items were presented.

Procedure: Capacity estimation

Memory capacity for orientation was estimated in separate blocks of trials for Gabors and bars, using the change detection task described in the General Method section (for set sizes 1, 3, 5, 7, and 9). On change trials, one item changed orientation by 90°. Each observer completed four blocks of 10 practice and 100 test trials, with the order of conditions counterbalanced across observers (Gabor, bar, bar, Gabor; or bar, Gabor, Gabor, bar).

Procedure: Contrast threshold

We measured the stimulus contrast necessary to discriminate vertical from horizontal with 75% accuracy separately for Gabors and bars, at three different eccentricities (4.6°, 10.2°, and 13.7°, corresponding to the four near, eight intermediate, and four far positions tested in the main experiment) and as a function of display size (one, five, or nine items, covering the full range of display sizes tested in the main experiment). On each trial, a cue (small red dot) was presented for 500 msec at a random location, followed by a 200-msec blank interval, a 500-msec presentation of one, five, or nine Gabors or bars, and then a mask (a random 30 × 30 grid of black and white dots, subtending 4.1° × 4.1°, presented at each item position). The task was to determine whether the cued item was vertical or horizontal. Stimulus contrast was varied by a staircase rule that converges on 75% correct (+2 steps for an incorrect response, -1 step for a correct response; Kaernbach, 1991). Eighteen independent staircases were interleaved (2 stimulus types × 3 eccentricities × 3 display sizes) until 20 reversals were obtained in each.

With such a large number of staircases, one condition could terminate much earlier than the others, and thus, the effects of fatigue or practice over the course of the experiment could exaggerate any small differences between conditions that terminate early versus ones that terminate late. Thus, the trial type was randomly selected from these 18, with each staircase weighted by the square of the number of reversals remaining. This procedure ensures that the staircase for each condition will terminate near the end of the session. The initial stimulus contrast was 1.00, and the step size initially was .2, decreasing by .02 over the first 10 reversals, and then was set at .01 for the final 10 reversals in each staircase. The 75% threshold was estimated from the average of the last 10 reversals. This task does not require memory storage and, thus, measures visual sensitivity to the orientation of Gabors and bars for the making of a 90° orientation discrimination (the same size as that in the memory experiment) and also tests whether there is any interaction between stimulus type and eccentricity or the number of items in the display.

Results

Capacity for bar orientations and Gabor orientations

As is shown in Figure 3, there was a large difference in the visual short-term memory capacity for bars and Gabors, with nearly twice as many bar orientations as Gabor orientations being stored in memory. Figure 3 illustrates estimated capacity (see the General Method section) versus the number of objects presented, or set size. If each object were stored perfectly, the capacity estimate would equal the set size. As set size increased, the estimated number of objects stored increased for both Gabors and bars, but performance was reduced from perfect by set size 3, and the asymptote for Gabors was lower than that for bars. These effects were confirmed by a 2 × 5 ANOVA on capacity estimates, with stimulus type (Gabor or bar) and set size (one, three, five, seven, or nine) as factors. Capacity was lower for Gabors than for bars [main effect of stimulus type, F(1,9) = 14.05, p < .01]. Capacity also increased significantly with the number of objects [main effect of set size, F(4,36) = 15.01, p < .01], and the interaction between stimulus type and number of objects was significant [F(4,36) = 6.84, p < .01], confirming the observation that capacity asymptotes at a lower number of objects for Gabors than for bars.

Figure 3.

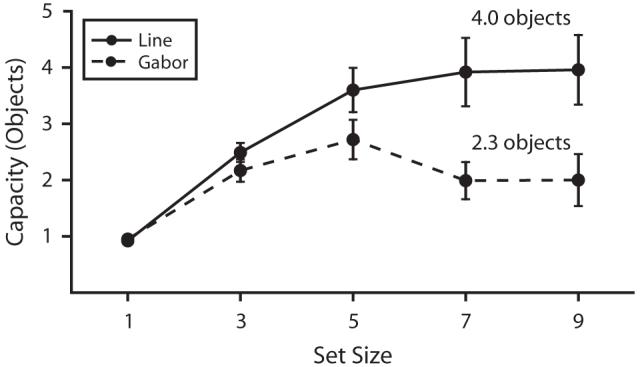
Storage capacity as a function of set size in Experiment 1. The solid line represents storage capacity for bars, and the dashed line represents storage capacity for Gabors (error bars show 1 SEM). Capacity estimates increase with set size until the maximum number of orientations that can be stored is reached. The limit (asymptote level) for Gabors (M = 2.3, SEM = 0.3) was lower than that for bars (M = 4.0, SEM = 0.6).

Asymptotic estimates of capacity were calculated separately for each individual observer and stimulus type, as specified in the General Method section. On average, approximately four bar orientations were stored in memory, but only two Gabor orientations were stored [t(9) = 3.75, p < .01].

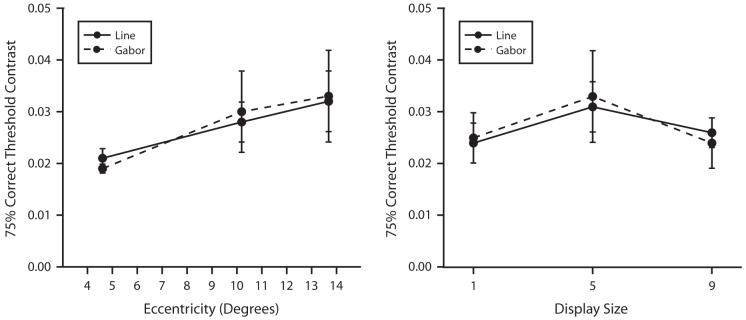
Contrast threshold for Gabors and bars

The observers were able to judge the orientation of Gabors and bars equally well at each eccentricity and regardless of the total number of items in the display (see Figure 4). A 2 × 3 × 3 ANOVA was run on the contrast threshold, with stimulus type (Gabor or bar), eccentricity (near, intermediate, or far), and display size (one, five, or nine) as factors. Overall, there was no difference in the contrast threshold for Gabors (M = 2.7%, SEM = 0.8%) and bars (M = 2.7%, SEM = 0.3%) [F(1,7) < 1, p = .89]. Although thresholds increased significantly with eccentricity [F(2,14) = 3.87, p < .05], there was no interaction between stimulus type and eccentricity [F(2,14) < 1, p = .71], as is shown in Figure 4A (collapsed across display size). The main effect of display size on contrast threshold did not reach significance [F(2,14) = 3.25, p = .07], and there was no interaction between stimulus type and display size [F(2,14) < 1, p = .60], as is shown in Figure 4B (collapsed across eccentricity). Finally, the three-way interaction between stimulus type, eccentricity, and display size was not significant [F(4,28) = 1.41, p = .26].

Figure 4.

Contrast threshold for judging the perceived orientation of Gabors and bars with 75% accuracy, as a function of eccentricity and display size in Experiment 1. In each figure, the solid lines represent the contrast threshold for bars, and the dashed lines represent the contrast threshold for Gabors (error bars show 1 SEM). (A) Contrast thresholds (collapsed across display size) increased as eccentricity increased, but there was no effect of stimulus type. (B) Contrast thresholds (collapsed across eccentricity) showed little effect of display size on contrast threshold and no effect of stimulus type.

Discussion

The results of the present experiment reveal that there is a dramatic difference in memory storage capacity for bars and Gabors: Nearly twice as many bar orientations as Gabor orientations can be stored in visual short-term memory. This difference cannot be attributed to differences in the ability to perceive the orientation of the objects or to detect orientation differences, since visual orientation sensitivity was equal for Gabors and bars at each eccentricity and across the range of display sizes tested in the memory experiment. Thus, the difference in the number of objects that can be stored in memory cannot be attributed to a difference in the fidelity with which a single object can be perceived. The results of this perceptual control experiment are consistent with previous research that has shown that memory for the features of sine wave gratings has a high fidelity, with little loss of detail, as compared with the directly perceived patterns (Magnussen, Greenlee, Asplund, & Dyrnes, 1990; Magnussen, Idas, & Myhre, 1998; Magnussen & Stein, 1994). Thus, it is clear that the orientation of gratings can be encoded and maintained in memory very accurately. However, the ability to store more than one such grating appears to be severely limited, as has been shown in previous work (Wright, Green, & Baker, 2000). In Experiments 2-4, we explored the possibility that the critical difference between Gabors and bars in the present experiment was that the Gabor orientation was a surface feature, whereas the bar orientation was a boundary feature.

EXPERIMENT 2

The Salience of Boundary Orientation Determines Storage Capacity

Why is the Gabor orientation stored less efficiently than the bar orientation? We propose that visual short-term memory operates more efficiently on boundary features than it does on surface features. On this view, the critical difference between Gabors and bars is that the outer envelope or boundary of the Gabor has no dominant axis of orientation, whereas the boundary of the bars has a clear dominant axis of orientation (see Figure 1B). The orientation of the Gabor is a surface property of the object, with the orientation information carried by a surface texture within a circular object boundary. In the present experiment, we tested whether this difference between boundary orientation and surface orientation plays a critical role in determining visual short-term memory capacity. We tested this by varying the aspect ratio (the ratio of the width divided by the height) of both the Gabors and the bars (see Figure 5). When the ratio of the width to height is 1, there is no dominant axis of orientation in the outer boundary of either stimulus type, and consequently, capacity for both Gabors and bars should be low. As the aspect ratio decreases, the orientation of the object boundary should become more salient, and storage capacity should increase for both Gabors and bars.

Figure 5.

Stimuli for Experiment 2. On the left are rectangles, and in the middle and right are Gabor patches. The aspect ratio (width divided by height) of each object decreases from top to bottom. As the aspect ratio decreases, the orientation of the object boundary becomes more salient. The Gabor patches in the middle column have the same spatial frequency (used in the main experiment), whereas the Gabor patches in the right column increase spatial frequency as the aspect ratio decreases, so that the same total number of cycles of the grating is visible at each aspect ratio. Note that the objects in this experiment changed orientation only by 45°, because an orientation change of 90° for a square results in exactly the same square.

Note that a 90° change of the target item used in the previous experiment was not an option for the bar stimulus here because, at an aspect ratio of 1.0, the bar would be a square and would look identical in a 90° rotation. For this reason, the rotation used for the Gabor and bar targets was 45°, which is the largest possible orientation change for a square.

The changing aspect ratios raise a different issue for the Gabor stimuli. As the aspect ratio decreases, the number of cycles of the grating that are visible decreases when the spatial frequency of the grating is constant (center column of Figure 5). The number of visible bars might be an important component of complexity for these stimuli, and thus, decreasing the aspect ratio would decrease the complexity of the Gabors. To control for this aspect of complexity, a control condition was included in which the spatial frequency of the Gabors increased as the aspect ratio decreased, so that the same number of cycles was present at each aspect ratio.

Method

Stimuli

In the main experiment, the stimuli were Gabor patches of 1.75 cycles per degree and bars (rectangles with blurred edges) with aspect ratios (ratio of width to height) varying from 1.0 (2.5° × 2.5°) to .75 (1.88° × 2.5°) to .50 (1.25° × 2.5°). The aspect ratio of the Gabor patch was varied by varying the standard deviation of the Gaussian window in the direction orthogonal to the orientation of the grating (see Figure 5). Note that the spatial frequency of the Gabors was higher in this experiment than in the previous experiments to ensure that several cycles of the Gabor were visible even at the smallest aspect ratio. The edges of the rectangles were blurred so that changes in orientation could not be detected by changes in the aliasing of the bars. In the complexity control experiment, the stimuli were identical, except that the spatial frequency of the Gabors varied with aspect ratio to ensure that the same number of cycles remained visible at each aspect ratio (1.75, 2.33, and 3.5 cpd for aspect ratio 1.0, .75, and .50, respectively).

Procedure

The same procedure was used in the main experiment and in the complexity control experiment. Memory capacity for orientation was estimated in separate blocks of trials for each combination of stimulus type (Gabor and bar) and aspect ratio (1.0, .75, and .50), using the change detection task described in the General Method section (with set sizes 1, 3, and 5 and changes of 45°). Each observer completed 12 blocks of 6 practice and 48 test trials, with the order of conditions counterbalanced across observers (ABCDEF FEDCBA, with each letter corresponding to one of the six conditions, determined randomly for each individual observer).

Results

Main experiment

Data for 1 observer were discarded because the observer appeared to press the wrong response keys for at least part of the experiment, resulting in capacity estimates of zero and well below chance performance in some conditions. Figure 6 shows estimated capacity as a function of aspect ratio for both Gabors and bars. As the aspect ratio decreases, making the boundary orientation more salient, the capacity estimate increases for both Gabors and bars. A 2 × 3 ANOVA was run on capacity, with stimulus type (Gabor or bar) and aspect ratio (1.0, .75, or .50) as factors. The main effect of aspect ratio was significant [F(2,12) = 8.46, p < .01]. Critically, both Gabors and bars behaved similarly as a function of aspect ratio (type × ratio interaction, F < 1, n.s.), and there did not appear to be any differences between Gabors and bars at any aspect ratio [main effect of stimulus type not significant, F(1,6) < 1, p > .05; aspect ratio 1.0, t(6) = 1.88, p > .05; aspect ratio .75, t(6) < 1, p > .05; aspect ratio .50, t(6) < 1, p > .05].

Figure 6.

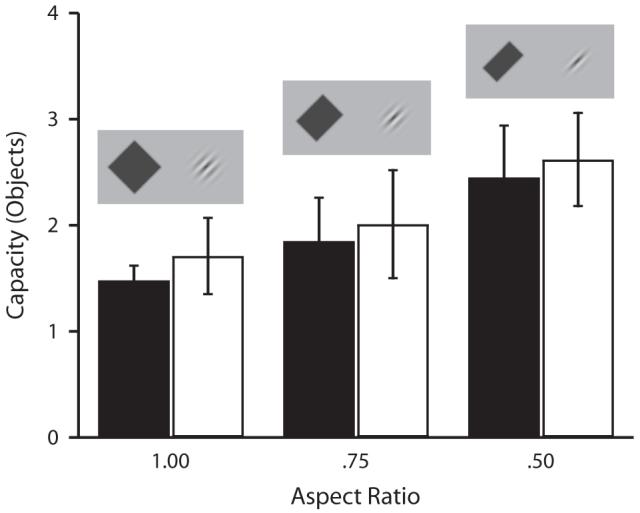
Storage capacity as a function of aspect ratio in Experiment 2. Capacity increases for both bars (black) and Gabors (white) as the aspect ratio decreases, and the orientation of the boundary becomes more salient (error bars show 1 SEM). There is no difference between bars and Gabors at any aspect ratio.

Visible cycles control experiment

Figure 7 shows estimated capacity as a function of aspect ratio for both Gabors and bars. The pattern of results obtained when the spatial frequency of the Gabors was varied with aspect ratio to keep the number of visible cycles of the grating constant was nearly identical to that observed in the main experiment (in which spatial frequency was held constant). A 2 × 3 ANOVA was run on capacity estimates, with stimulus type (Gabor or bar) and aspect ratio (1.0, .75, or .50) as factors. As the aspect ratio decreased (making the boundary orientation more salient), the capacity estimate increased for both Gabors and bars [main effect of aspect ratio, F(2,14) = 9.81, p < .01]. As in the main experiment, both Gabors and bars behaved similarly as a function of aspect ratio (type × ratio interaction, F < 1, n.s.), and there was little difference between Gabors and bars at each aspect ratio [main effect of stimulus type not significant, F(1,7) = 2.65, p > .05; aspect ratio 1.0, t(7) < 1, p > .05; aspect ratio .75, t(7) = 1.48, p > .05; aspect ratio .50, t(7) < 1, p > .05].

Figure 7.

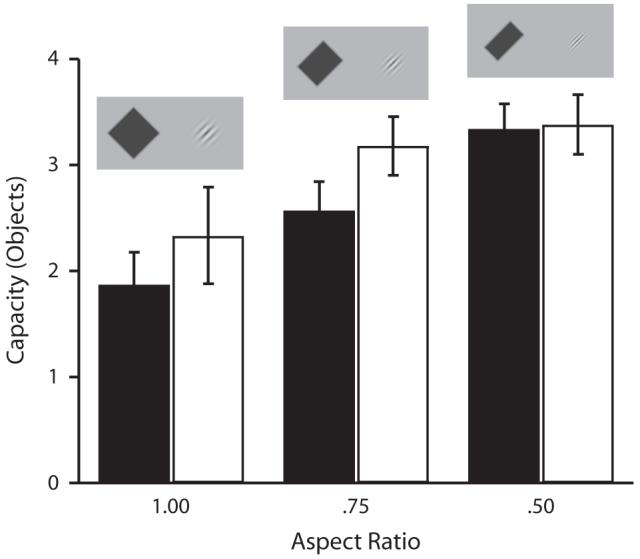
Storage capacity as a function of aspect ratio in the control condition of Experiment 2. Capacity increases for both bars (black) and Gabors (white) as the aspect ratio decreases, and the orientation of the boundary becomes more salient (error bars show 1 SEM). There is no difference between bars and Gabors at any aspect ratio, even though the number of visible cycles in the Gabor patch is the same at each aspect ratio.

Discussion

Experiment 1 demonstrated that visual short-term memory capacity for Gabor orientations was almost half the capacity for bar orientations. The results of the present experiment suggest that the critical difference between Gabors and bars in Experiment 1 was the saliency of the boundary orientation. In the present experiment, as the aspect ratio decreased, making the boundary orientation more salient, memory capacity increased for both Gabors and bars. Importantly, there was no difference in capacity for Gabors and bars when they had the same aspect ratio. The results suggest that visual short-term memory capacity for orientation depends on the salience of the object boundary orientation as set by the aspect ratio, rather than on the particular stimulus type. When the aspect ratio is 1, there is no dominant axis of orientation in the object boundary at all. However, as the aspect ratio decreases, the dominant axis of orientation within the boundary becomes more noticeable (for both Gabors and bars, see Figure 5), and thus, storage capacity increases.

One could argue that decreasing the aspect ratio in the main experiment decreases the complexity of the Gabors by reducing the number of visible bars. This reduction in complexity could explain the improvement in capacity for Gabor orientations as the aspect ratio decreases. However, in the complexity control experiment, the number of visible cycles in the Gabors was held constant with changes in aspect ratio (thus keeping one possible component of surface feature complexity constant), and performance still improved as aspect ratio decreased. Moreover, differences in surface feature complexity cannot explain why capacity for bar orientations increased as the aspect ratio decreased. The surface complexity of the bar did not change with aspect ratio, because the surface was always a homogenous black color, and yet storage capacity was dependent on aspect ratio. Finally, although the Gabor is presumably the more complex stimulus, if anything, there was a trend for capacity to be higher for the Gabors than for the bars at each aspect ratio. Thus, it does not appear that complexity of the surface texture was the limiting factor on performance in the present experiment.

Of course, this does not rule out a role for complexity in determining memory capacity. One can imagine that encoding more complex boundary descriptions requires more detail, or even that more complex surface textures require more detail. The important point for the present study is that complexity alone does not appear to account for these results. We propose that the present experiment supports the hypothesis that visual short-term memory operates more efficiently on object boundary features than on surface features of an object, even though those features can be perceived equally well for both types of object (see the perceptual control task in Experiment 1).

EXPERIMENT 3

A Test of the Boundary hypothesis

In this experiment, we further tested the hypothesis that the salience of the boundary orientation determines memory capacity. Here, the same physical object, a bar with an aspect ratio of .125, always carried the relevant orientation information. However, this bar was embedded within a higher level object, so that at the extremes, the orientation was either part of the object boundary or a surface feature of the object (see Figure 8). As is shown in Figure 8, we presented both oriented bars alone and oriented bars that had a circle of various sizes at the center. The salience of the object boundary orientation was estimated by taking the ratio of the bar length and the circle diameter, giving a relative-size ratio. As the size of the circles increased, the relative-size ratio decreased, making the object boundary orientation less salient. The boundary hypothesis predicts that storage capacity will gradually decrease as the relative size ratio increases, because the unoriented circle increasingly takes up the orientation of the bar, until, eventually, the bar orientation is a surface feature of the higher level object (the combined circle and bar).

Figure 8.

Stimuli for Experiment 3. As the circle grows larger, the boundary orientation becomes less salient, and the bar orientation goes from a boundary feature (on the left) to a surface feature (on the right).

Method

Stimuli

The stimuli were bars (rectangles with blurred edges) subtending 3.75° × 0.47° (aspect ratio = .125) and bars with circles drawn at their centers (diameter = 1.3°, 1.97°, or 3.75°), as shown in Figure 8.

Procedure

Memory capacity was estimated for the four stimulus types (in separate trials), using the change detection task with a display size of five items. There were 24 practice trials and 240 test trials.

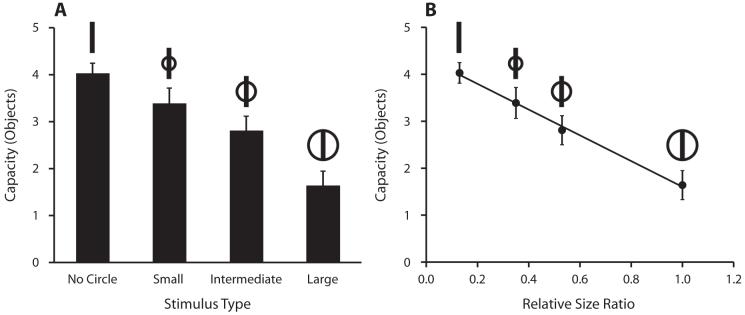
Results

As is shown in Figure 9A, memory storage capacity decreased as the relative size of the bars and circles approached 1 (as the boundary orientation became less salient). Overall, the effect of stimulus type was significant [F(3,15) = 33.06, p < .001]. With each increase in circle size, there was a significant decrease in capacity [none to small, t(5) = 3.64, p < .05; small to intermediate, t(5) = 3.60, p < .05; intermediate to large, t(5) = 3.71, p < .05]. As is shown in Figure 9B, there was also a strong linear correlation (r² = .996) between capacity and relative-size ratio (the aspect ratio of the bar alone, or the ratio of the bar length to the circle diameter), indicating that memory capacity is highly correlated with the saliency of the boundary orientation.

Figure 9.

Results of Experiment 3. (A) Storage capacity decreased as the circle size increased. (B) Storage capacity was correlated with the relative size ratio (aspect ratio for no circle, or the ratio of the bar length to the circle diameter; r = .996).

Discussion

Simply drawing a circle around a bar reduced memory capacity from four to two bar orientations, and in general, memory capacity was systematically related to the saliency of the object boundary orientation. Thus, consistent with the results of Experiment 2, it appears that the saliency of boundary orientation determines the efficiency of memory storage.

EXPERIMENT 4

Boundary Versus Surface Distinction and Memory for Size

It appears that visual short-term memory operates more efficiently on object boundaries than on the surface features of objects. The purpose of this experiment was to determine whether this distinction generalizes to other features—in this case, size. Here, we tested whether the ability to remember the size of an object is better when the relevant size is determined by the extent of an object boundary than when the size information is defined by the surface features within an object boundary (see Figure 10).

Figure 10.

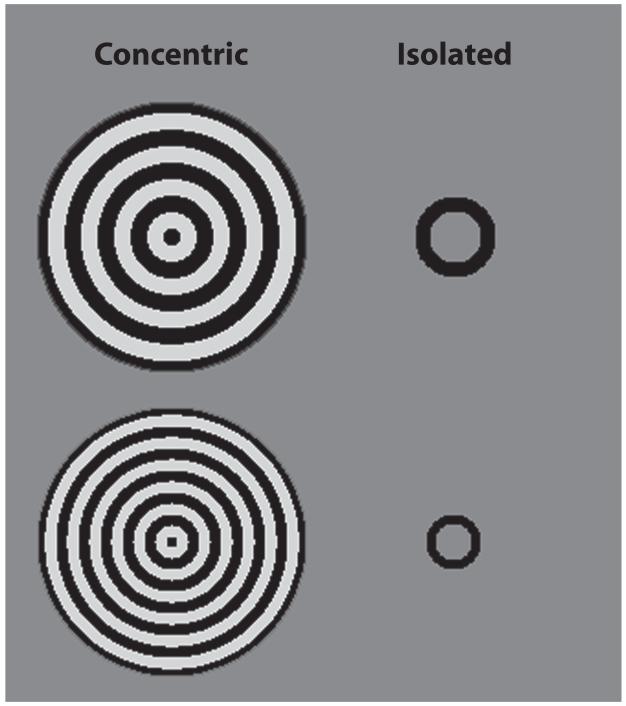
Stimuli for Experiment 4. On the left are concentric rings, and on the right are single isolated rings (identical to the center rings of the concentric rings to the left of each). The rings on top are bigger than the rings on bottom, but the difference in size is a difference in surface texture for the concentric rings and a difference in the size of the object boundary for the isolated rings.

Method

Stimuli

The stimuli were concentric rings and isolated rings (see Figure 10). Each of the concentric rings had an outer boundary with a 5° diameter. The ring thickness of each object was randomly set to one of eight sizes, including four large sizes (0.28°, 0.33°, 0.38°, and 0.42°) and four small sizes (0.19°, 0.22°, 0.25°, and 0.28°). Whenever a change occurred, small rings replaced large rings or large rings replaced small rings, so that the change always maintained a ratio of .67 between the small size and the large size. For example, in both a change from 0.42° (large) to 0.28° (small) and a change from 0.28° (large) to 0.19° (small) a .67 ratio is maintained between the small and the large sizes. Similarly, a change from 0.22° (small) to 0.33° (large) or from 0.25° (small) to 0.38° (large) maintains a ratio of .67 between the small and the large sizes. The isolated rings were identical to the innermost black ring of one of the eight concentric patterns. The same rule regarding a constant .67 ratio between the small and the large sizes was used for the isolated rings. Consequently, whether the size change was measured by the ring thickness or by the ring diameter, the change in size maintained a fixed ratio of .67 between the small and the large isolated rings. For example, a change from the small ring thickness of 0.28° to the large ring thickness of 0.42° would correspond to a change from a small boundary size, or ring diameter, of 1.38° to a large boundary size of 2.06°. Critically, the ratio of small to large ring thickness, as well as small to large boundary diameter, was approximately .67. Thus, change size was equated for different changes within and between classes of stimuli.

Finally, items were placed in pseudorandom positions within a 4 × 3 grid subtending 30° × 22°.

Procedure

Memory capacity for ring size was estimated in separate blocks of trials for concentric rings and isolated rings, using the same procedure as that in Experiment 1.

Results

As is shown in Figure 11, there was a marked difference in storage capacity for isolated rings and concentric rings, with nearly twice as many isolated ring sizes stored in memory than concentric ring sizes. As the number of objects increased, the estimated number of objects stored increased for both the isolated and the concentric rings, but the asymptote for the concentric rings was lower than that for the isolated rings. These effects were confirmed by a 2 × 5 ANOVA on capacity, with stimulus type (concentric or isolated) and set size (one, three, five, seven, or nine) as factors. Capacity was lower for concentric rings than for isolated rings [main effect of set size, F(1,7) = 25.52, p < .01], and capacity increased significantly with increases in the number of objects [main effect of number, F(4,28) = 17.05, p < .01]. The interaction between stimulus type and number of objects was also significant [F(4,28) = 5.31, p < .01], confirming the observation that capacity asymptotes at a lower number of objects for concentric rings than for isolated rings.

Figure 11.

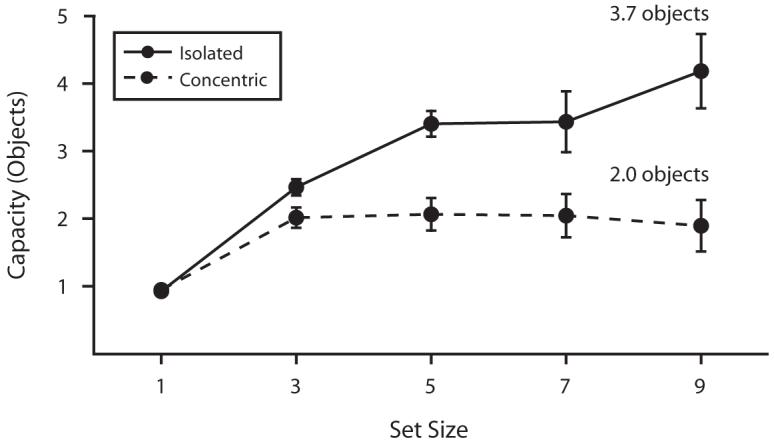
Storage capacity as a function of set size in Experiment 4. The solid line represents capacity for isolated rings, and the dashed line represents capacity for concentric rings (error bars show 1 SEM). Capacity estimates increase with set size until the maximum number of orientations that can be stored is reached. The limit (asymptote level) for concentric rings (M = 3.7, SEM = 0.4) is lower than that for isolated rings (M = 2.0, SEM = 0.2).

Asymptotic estimates of capacity were made as specified in the General Method section. On average, approximately 3.7 isolated ring sizes were stored in memory, but only 2.0 concentric ring sizes were stored [t(7) = 4.21, p < .01].

Discussion

Although the size of change was controlled for by maintaining a fixed ratio between large and small items, changes in boundary size were more easily detected than changes in the size of a surface texture, and estimated storage capacity for the size of the isolated rings was nearly double the storage capacity for the size of the concentric rings. Ring size is a boundary feature for isolated rings, whereas ring size is a surface feature for concentric rings. Thus, this finding provides converging evidence that visual short-term memory stores boundary features more efficiently than surface features of objects.

Any memory task can be divided broadly into three stages of processing: encoding, storage, and a retrieval or decision stage. Thus far, we have attributed the effects on change detection accuracy to differences in storage capacity, but it is possible that any of these three stages of memory processing can limit performance in the change detection task. For example, it is possible that surface orientation is not extracted as quickly as boundary orientation. If so, the duration of the initial presentation may have been too brief to fully encode multiple surface orientations (an encoding stage limit). It is also possible that the process of comparing multiple surface orientations in memory with those in the second display is more difficult than comparing multiple boundary orientations (a decision stage limit). In Experiments 5 and 6, we tested these possibilities.

EXPERIMENT 5

Increasing Encoding Time Beyond 500 msec Does not increase Storage Capacity for Boundary or Surface Orientations

It is possible that more time is required to encode the surface orientation of a Gabor than to encode the boundary orientation of a bar into memory. If so, it is also possible that the presentation time of 500 msec used in Experiment 1 is sufficient to encode a full memory load of bar orientations, but not Gabor orientations. The difference in estimated storage capacity would then be explained by an encoding stage limit, and not by differences in storage capacity. If this is the case, capacity estimates for Gabors and bars should converge as the presentation duration increases. In Experiment 5, we ruled out this possibility by varying the duration of the initial presentation from 200 to 950 msec and showing that, beyond 450 msec, there is no increase in capacity for Gabors (with an aspect ratio of 1.0) or bars (with an aspect ratio of .16).

Method

Stimuli

The stimuli were Gabor patches and bars (single isolated bars of a Gabor patch), as specified in the General Method section. A mask consisting of a 27 × 27 grid of squares, each subtending 0.125° × 0.125° (3.4° square overall) and each assigned a random luminance value between black and white, was used to mask the Gabors and bars.

Procedure

Memory capacity for orientation was estimated in separate blocks of trials for Gabors and bars, using a change detection task similar to that described in the General Method section, except for the initial presentation duration and mask presentation. On each trial, five objects were presented for one of four possible presentation durations (200, 450, 700, or 900 msec, mixed within blocks) followed by a 150-msec mask, by an 850-msec blank interval, and then by a second display of objects that remained present until the observer responded. Each observer completed four blocks of 8 practice and 56 test trials, with the order of conditions counterbalanced across observers (Gabor, bar, bar, Gabor; or bar, Gabor, Gabor, bar).

Results

Figure 12 shows capacity as a function of presentation time for both Gabors and bars. The most important finding of the present experiment is that increasing the presentation time beyond 450 msec did not improve performance for either Gabors or bars. Furthermore, beyond 450 msec, the estimated capacity was significantly greater for bars than for Gabors. Estimated capacity increased from 250 to 450 msec, but there was no increase in capacity beyond 450 msec for either Gabors or bars. A 2 × 4 ANOVA was run on capacity estimates, with stimulus type (Gabors or bars) and presentation time (200, 450, 700, or 950 msec) as factors. The increase in capacity with presentation time was significant [F(3,21) = 7.55, p < .01]. The difference between Gabors and bars, however, did not reach significance [F(1,7) = 4.79, p > .05] and the interaction between stimulus type and duration was not significant [F(3,21) < 1, p > .05]. It appears that both the effect of presentation time and the nonsignificant difference between Gabors and bars was driven by the lowest presentation duration of 200 msec. These observations were confirmed by a 2 × 3 ANOVA with the 200-msec presentation time excluded from the analysis. The results showed that the effect of presentation time was not significant in this upper range of presentation times [F(2,14) < 1, p > .05] and that the difference between Gabors and bars was significant [F(1,7) = 10.13, p < .05]. These findings indicate that after a presentation of at least 450 msec, there is no increase in capacity with increases in presentation time and that the difference in capacity between Gabors and bars is significant.

Figure 12.

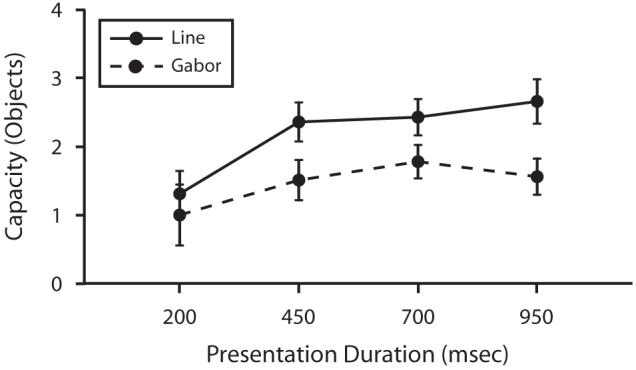
Capacity as a function of presentation duration in Experiment 5. The solid line represents capacity for bars, and the dashed line represents capacity for Gabors (error bars show 1 SEM). Capacity appears to increase for both Gabors and bars between 200 msec and 450 msec, but there is no increase in capacity beyond 450 msec for either stimulus type.

Capacity for both bars and Gabors appears to asymptote at levels lower than the estimates observed in Experiment 1 with a display size of five items. It is possible that this difference results from interference between the mask and to-be-remembered objects, even at longer presentation durations.

Discussion

Increasing presentation time beyond 450 msec did not improve storage capacity for either Gabors (with an aspect ratio of 1.0) or bars (with an aspect ratio of .16), and beyond 450 msec, there was an advantage in storage capacity for Gabors over bars. The results of the present experiment suggest that the difference in change detection accuracy for boundary and surface orientation does not reflect a difference in the amount of time required to encode items into visual short-term memory and are consistent with the results of previous research demonstrating that an encoding duration of 500 msec is sufficient to fully encode simple visual stimuli into visual short-term memory (Alvarez & Cavanagh, 2004).

EXPERIMENT 6

Cuing a Single Test item Does not increase Storage Capacity for Boundary or Surface Orientation

There are many ways in which performance in a memory task can be limited by the decision process, during which the test display is compared with the contents of memory. For example, it is possible that information in memory degrades during the comparison between objects in memory and the second test display and that the rate of degradation is greater for surface features than for boundary features. Alternatively, if we assume equal rates of degradation, it could still be the case that memory comparison takes more time for surface features than for boundary features. Consequently, the duration of the comparison process and the total degradation would then be greater for surface features than for boundary features. Moreover, previous work has shown that changes to a scene are often unnoticed, due to a failure to make the relevant comparison in the first place (Hollingworth, 2003; Mitroff, Simons, & Levin, 2004). Thus, it is also possible that observers are more likely to fail to make a comparison between surface features than to fail to make one between boundary features.

Each of these possibilities represents a retrieval or decision stage limit on performance, rather than a storage capacity limit. In this experiment, we addressed these possible issues by requiring observers to remember multiple objects but then cuing observers to make the same/different decision about a single item in the test display. This reduces the load of the comparison task by reducing the effects of information degradation during the test phase and ensuring that the relevant comparison is made. If information degradation during comparison, or a failure to make the relevant comparison, explains the lower capacity for surface orientation than for boundary orientation, this difference should be reduced or eliminated by cuing a single test item.

Method

Stimuli

The stimuli were Gabor patches and bars (single isolated bars of a Gabor patch), as specified in the General Method section. In the cue condition, a white frame (0.15° thickness) subtending 5.3° × 5.3° surrounded the location of a single test item. The minimum spacing between the cue frame and the cued test item was 1.25°.

Procedure

Memory capacity for orientation was estimated in separate blocks of trials for each combination of stimulus type (Gabors or bars) and cue condition (cue or no cue), using a change detection task similar to that described in the General Method section. On each trial in the no-cue condition, five objects were presented for 500 msec, followed by a 1,000-msec interval and then by a second display of objects that remained present until the observer responded. The presentation on cue trials was identical, except that a white frame appeared in the location of a single test item 200 msec prior to the presentation of the second display and remained present until the observer responded. On half of the trials, the two displays were identical, and on the other half, one of the objects changed orientation by 90°. In the cue condition, if there was a change, it always occurred at the cued location. The task was to indicate whether the two displays were the same or different in the no-cue condition and to indicate whether or not the cued test item was the same or different in the cue condition. Each observer completed eight blocks of 6 practice and 26 test trials, with the order of conditions counterbalanced across observers (ABCD DCBA, with the letters corresponding to one of the four conditions, as determined randomly for each individual observer).

Results

Figure 13 shows estimated capacity as a function of cue condition (cue or no cue) and stimulus type (Gabor or bar). Cuing a single item appeared to have little or no effect on capacity in this task, and storage capacity was significantly greater for bars than for Gabors, whether or not there was a cue. A 2 × 2 ANOVA was run on capacity, with stimulus type and cue condition as factors. The difference in capacity between Gabors and bars was significant [F(1,7) = 31.94, p < .01]. However, there was no effect of cue condition [F(1,7) = 1.60, p > .05], and the interaction between stimulus type and cue condition was not significant [F(1,7) < 1, p > .05].

Figure 13.

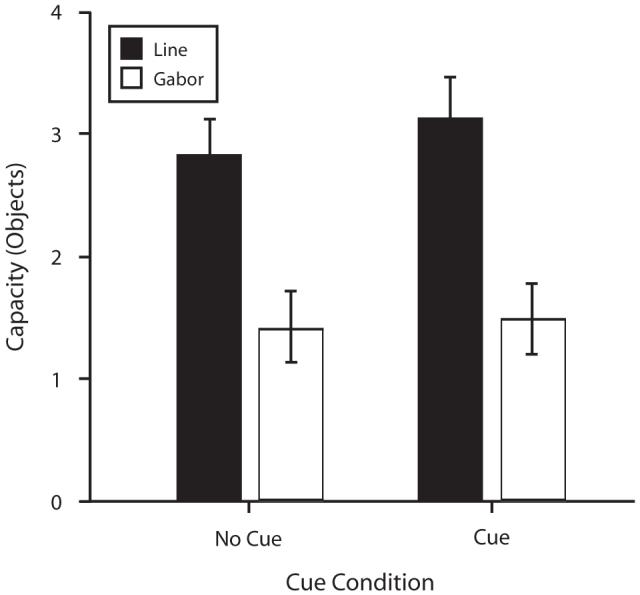
Storage capacity as a function of cue condition in Experiment 6. Capacity was nearly double for bars (solid black bars), as compared with Gabors (white bars), whether there was a cue or no cue in the second test display (error bars show 1 SEM). The cue had no effect on capacity estimates, and cue condition did not interact with stimulus type.

Discussion

The results of the present experiment suggest that the primary limit on change detection accuracy for Gabors (with an aspect ratio of 1.0) and bars (with an aspect ratio of .16) is a capacity limit on the amount of visual information that can be stored in short-term memory, rather than a limit on decision stage factors. Cuing a single test item did not improve performance for either Gabors or bars, with nearly twice as many bar orientations being stored in memory as Gabor orientations, with or without a cue. Thus, information loss during the comparison phase, or failure to make the relevant comparison between memory and the test array, did not impose a noticeable cost to performance in this task. This finding is consistent with other research that has shown that cuing a single item during the test display does not improve performance in the type of memory task used here (Vogel, Woodman, & Luck, 2001; Wright et al., 2000; but see Landman, Spekreijse, & Lamme, 2003).

EXPERIMENT 7

Advantage for Boundary Features Over Surface Features Without Perceptual Grouping

Previous research has suggested that items are not encoded into memory individually but that the spatial relationships between items is encoded and plays an important role in memory storage (Jiang, Chun, & Olson, 2004; Jiang, Olson, & Chun, 2000). For example, Jiang et al. (2004), demonstrated that memory for an item’s location is disrupted by changes to the scene context, such as changing the orientation of background items, even when that information is irrelevant to the task. Interestingly, they showed that the effect of orientation changes occurred when elongated bars changed orientation, but not when gratings similar to Gabors (with a circular boundary) changed orientation. They interpreted this in terms of the effect that changing orientation has on perceptual organization: When elongated bars change orientation, the layout of items changes, whereas changing the orientation of circular graings leaves the layout of items unchanged. It is possible that a difference in relational encoding or perceptual grouping accounts for the different storage capacities for boundary and surface orientations. Such relational encoding could occur either at a perceptual level or within memory after information has been perceptually encoded. Here, we rule out the possibility that such relational encoding or grouping at the perceptual level explains the boundary feature advantage.

In this experiment, items were presented one at a time for encoding into memory. Because no more than a single item was presented at a time, there was no perceptual grouping between the items. Thus, if perceptual grouping alone accounts for the difference between boundary and surface orientation, there should be no difference in storage capacity for Gabors and bars in this experiment. However, if perceptual grouping is not necessary to show a difference between boundary and surface features, the advantage for bars over Gabors should be observed even under these conditions.

Method

Stimuli

The stimuli were Gabor patches and bars (single isolated bars of a Gabor patch), as specified in the General Method section.

Procedure

Memory capacity for orientation was estimated in separate blocks of trials for Gabors and bars, using a change detection task similar to that described in the General Method section, with the following exceptions. On each trial, two or four items were presented sequentially, each at a different random location, for 250 msec each, with a 250-msec blank interval between items. After the last item was presented, there was a 1,000-msec blank interval, and then a single test item appeared. Each observer completed four blocks of 16 practice and 96 test trials, with the order of conditions counterbalanced across observers (Gabor, bar, bar, Gabor; or bar, Gabor, Gabor, bar).

Results

As is shown in Figure 14, the advantage for bars over Gabors was observed even under sequential presentation conditions that eliminated perceptual grouping. A 2 × 2 ANOVA was run on estimated storage capacity, with stimulus type and display size as factors. We observed significant main effects of stimulus type [F(1,7) = 21.6, p < .01] and display size [F(1,7) = 19.2, p < .01], as well as a significant interaction between stimulus type and display size [F(1,7) = 22.0, p < .01]. Thus, overall storage capacity was higher for bars than for Gabors, and capacity estimates increased with display size, but more so for bars than for Gabors. The difference between Gabors and bars was significant at both display sizes [display size 2, t(7) = 3.48, p < .05; display size 4, t(7) = 4.89, p < .01].

Figure 14.

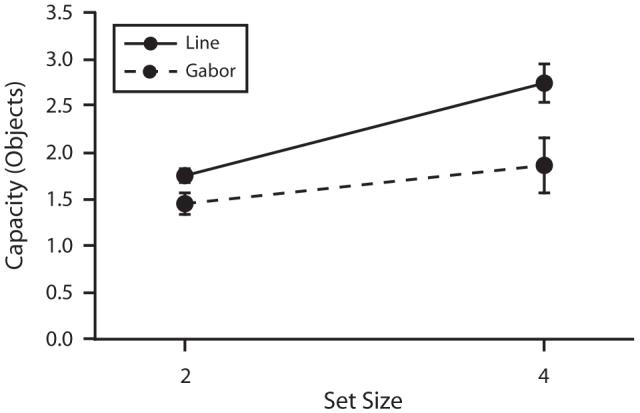
Storage capacity for sequentially presented items in Experiment 7. The solid line represents capacity for bars, and the dashed line represents capacity for Gabors (error bars show 1 SEM). The difference between Gabors and bars is observed under sequential presentation conditions.

Discussion

The present results provide two further bits of evidence supporting the conclusion that there is a difference in the number of individual surface and boundary orientations that can be stored in memory. First, only a single item was presented at test during the present experiment, limiting memory comparison to just a single item in memory, yet there was still a large difference in storage capacity for Gabors (with an aspect ratio of 1.0) and bars (with an aspect ratio of .16). This reinforces the findings of Experiment 6, which showed that limiting the comparison to just a single item, using a cue, did not improve performance for Gabors or bars and did not eliminate the difference in performance between stimulus types. Thus, even when the comparison demands are minimized, there remains a large difference in performance for Gabors with a circular aperture and bars with a clear boundary orientation.

Second, and more relevant to the present study, the boundary feature advantage could have been due to stronger perceptual grouping for boundary features. Many have argued that the efficiency of grouping or chunking information can determine working memory storage capacity (Miller, 1956; Simon, 1974), and subjectively, displays of multiple bars seem to form better perceptual groups than do displays of multiple Gabors. However, the present experiment demonstrates that even when items are presented sequentially, eliminating any role for perceptually grouping individual items, there is a large difference in storage capacity for Gabors and bars. Although this finding does not rule out the possibility that the bars benefited from stronger grouping in our previous experiments, it does show that such a grouping effect is not necessary to show a difference in storage capacity for boundary and surface orientation.

It remains possible that postperceptual memory operations encode relational information or form higher order groupings from individual elements and that these memory processes operate more efficiently on boundary features than on surface features. Such a memory-level account based on relational encoding or grouping processes would be consistent with our general claim that visual short-term memory operates more efficiently on boundary features than it does on surface features.

GENERAL DISCUSSION

In the present experiments, we investigated whether visual short-term memory capacity for a particular feature depends on the type of object to be remembered. A change detection task was used to estimate storage capacity for the orientation or size of different types of objects. The results were clear: Memory capacity for a particular feature depends on the type of object to be remembered. The critical difference for the objects tested here appears to be whether the to-be-remembered feature is part of an object boundary or the surface texture of an object, with boundary features being stored in memory more efficiently than surface features.

Experiment 1 showed that storage capacity for the orientation of Gabors (with an aspect ratio of 1.0 and no clear boundary orientation) was half the storage capacity for the orientation of bars (with an aspect ratio of .16 and a clear boundary orientation). The difference in the saliency of the boundary orientation appears to account for the advantage for bars over Gabors in Experiment 1. In Experiment 2, the aspect ratio of the objects (width divided by length) was varied, and the saliency of boundary orientation for Gabors and bars was matched. Critically, at any particular aspect ratio, storage capacity was identical for Gabors and bars. However, as the aspect ratio was increased for each type of object, making the orientation of the boundaries more salient, capacity increased for both Gabors and bars. This same result was observed when the spatial frequency of the Gabors was varied with aspect ratio, so that the same number of oriented stripes remained visible at each aspect ratio, keeping at least one component of the visual “complexity” of the Gabors constant for different aspect ratios. In Experiment 3, memory for the same physical object (a bar with an aspect ratio of .125) was higher when the bar orientation was part of the object boundary than when the bar orientation was part of the surface texture of a higher level object. Finally, Experiment 4 generalized the superiority of memory storage capacity for boundary over surface features to the size dimension.

The difference in change detection performance could not be explained by perceptual limits, given that a single Gabor orientation could be perceived as well as a single bar orientation (Experiment 1). Moreover, memory limits other than storage capacity did not appear to explain the difference in performance either. Increasing the presentation time beyond 450 msec did not increase capacity for Gabors or bars, indicating that the limit is not in the initial encoding stage, provided the stimuli are presented for 450 msec or more (Experiment 5). Furthermore, cuing a single test item during the test or presenting just a single test item to simplify the comparison process did not improve performance for Gabors or bars, indicating that limits in the decision process do not explain the difference in change detection accuracy for Gabor and bar orientations (Experiments 6 and 7). Finally, differences in the strength of perceptual grouping alone could not explain the difference, since the advantage for bars was observed even when the items were presented sequentially (Experiment 7). Thus, it appears that the difference in change detection performance reflects a true difference in the maximum number of individual orientations that can be stored in memory.

We have previously argued that visual short-term memory is limited by the total amount of information or detail that has to be stored for the memory task, so that storing more information per item reduces the maximum number of individual items that can be stored (Alvarez & Cavanagh, 2004). It is important to emphasize that we use the terms information, complexity, or detail not to refer to an intrinsic physical property of an object, but to refer to the efficiency with which an object can be encoded sufficiently to perform the memory task. Thus, if one makes exactly the same physical objects more difficult to encode—say, by rotating them into unfamiliar orientations—fewer of those objects can be stored in memory (Alvarez & Cavanagh, 2004). The present finding that visual short-term memory capacity for orientation and size depends on the type of object to be remembered adds to this previous work by demonstrating that a particular feature (e.g., left-tilted, or small) is not always encoded with the same efficiency. These features are encoded and stored more efficiently when they are part of the object boundary than when they are part of the surface texture of an object. In the remainder of this article, we will discuss the theoretical implications of the boundary/surface distinction for the structure of information storage in visual short-term memory, and we will discuss the generality of the distinction between boundary and surface features.

Structure of information in Visual Short-Term Memory

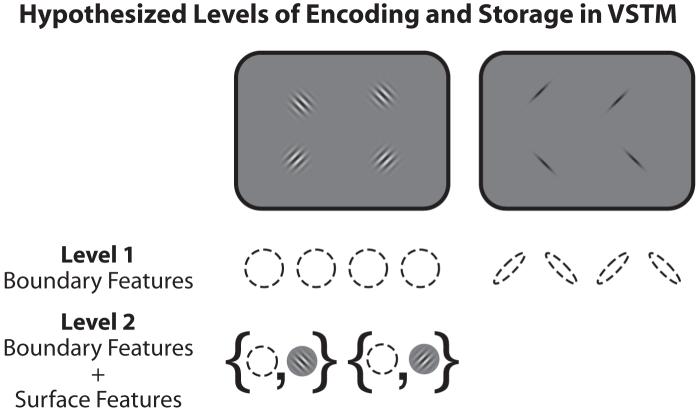
Here, we propose that there are at least two levels at which features are encoded and stored in visual short-term memory: One level includes boundary information, and the other level includes surface or texture details. Figure 15 illustrates how these different levels of description can be arranged hierarchically to explain the difference in storage capacity for boundary and surface features. The first level contains a description of each object’s boundary information. The second proposed level includes a boundary description plus surface features or details.

Figure 15.

Proposed levels of encoding in visual short-term memory. Two levels of encoding and storage for information in visual short-term memory (VSTM) are proposed. The first level is a description of each object’s boundary information. The second proposed level includes a boundary description plus surface features or details. Note that the first level of description is insufficient for encoding the orientation of these Gabors but that the boundary description alone carries all of the orientation information for the bars. Consequently, access to information in the second level of encoding is required for these Gabors, but not for bars.

Note that the first-level boundary description in Figure 15 is sufficient for encoding the orientation of bars but that the boundary description alone is not sufficient for encoding the orientation of the Gabors. Consequently, access to information in the second level is necessary to encode the orientation of Gabors, but not to encode the orientation of the bars. This proposed structure of encoding and storage provides two speculative explanations for why fewer Gabor orientations (with circular apertures) can be stored in memory than bar orientations. First, it is possible that the surface features of an object are optionally encoded and that encoding these additional details requires extra “space” in memory, so that the more surface-level detail that must be stored, the fewer the total number of objects that can be stored (see Alvarez & Cavanagh, 2004, for a demonstration of the trade-off between the amount of visual information or detail encoded per object and the maximum number of objects that can be stored in memory).

Second, it is possible that the boundary information serves as the memory-indexing feature that provides access to the subordinate-level surface features of stored objects. Before describing how this role for boundary features can explain the difference in capacity for boundary and surface features, we first will briefly describe how boundary features may serve as memory-indexing features.

Any form of lexical system requires a method of indexing the contents of the lexicon. For example, the Chinese dictionary indexes characters by the number of strokes. In the English dictionary, the first letter of a word is used as the indexing feature. In the domain of vision, Biederman (1987) has proposed that a certain structured set of geons (basic elements of shape) is used to access a particular object in the visual lexicon. For example, a chair is composed of a characteristic set of basic shapes, and it is this structured set of shapes that enables access to other information about chairs. In recent computer vision systems, boundary features have proven useful for searching large image databases (Mokhtarian, Abbasi, & Kittler, 1996; Wang, Khan, & Breen, 2002). In these systems, images are retrieved from a storage database based on boundary information, and once possible matches are retrieved from the database, other details about those images can then be accessed and scrutinized (e.g., color and texture information). Here, we propose that boundary features play a similar role for accessing information in visual short-term memory. According to this view, objects in memory are indexed by their shape or boundary description, and access to the subordinate level details of an object in memory proceeds by accessing the features associated with the encoded boundary description.

The possibility that boundary descriptions are the indexing feature for visual short-term memory provides the second speculative explanation for the lower storage capacity for surface features than for boundary features in the present experiments. For example, the difficulty in storing Gabor orientations could be due to the fact that the boundary description of each Gabor is identical. Thus, it could be the case that the surface orientation of each Gabor is fully encoded but that access to those details is not efficient, because none of the encoded objects has a unique indexing feature. In contrast, it was possible, but much less likely, that two bars would have the same boundary orientation. Therefore, the bars were much more likely to have a unique boundary description and, thus, a unique index in memory. Consequently, access to the relevant details in memory would be more efficient for bars than for Gabors. This would also explain why storage capacity increased as the aspect ratio increased for both Gabors and bars: As the aspect ratio increases, the similarity of the boundary of each object decreases. Thus, memory access improves as the probability that the memory-indexing feature addresses a unique object in memory increases.

We are not proposing that boundary features are the only features used to access information in visual short-term memory. Certainly, it is possible to use location or surface features to retrieve information from visual short-term memory. For example, in the typical change detection task for color (Luck & Vogel, 1997), all items have identical shapes, or boundary descriptions, and yet observers can remember the color of about four items. In this case, it would appear that location information provides the most reliable index to memory. However, even location information is not required, since observers can remember just as many colors if they are presented sequentially at a single spatial location (Shim, Alvarez, & Jiang, 2005). Given that neither location nor boundary information is necessary for memory access, we are proposing only that differences in boundary information can increase the efficiency of memory access, when present.

To summarize, we propose a model for the structure of information in visual short-term memory. Memory storage is object based, and each object in memory has at least two levels of description: The first level contains a boundary description, and the second level contains the subordinate-level surface features of the object. This proposed structure then provides two speculative explanations for the greater storage capacity for boundary features than for surface features. First, it is possible that the surface features are optionally encoded and that the greater the amount of surface feature detail that must be stored, the fewer the total number of objects that can be stored. Second, the boundary of an object may be the memory-indexing feature, leading to difficulty in accessing subordinate-level surface feature information when the boundaries of multiple objects in memory are identical. These possible explanations are not mutually exclusive, since both the cost for encoding additional detail and the difficulty of accessing subordinate-level detail could play a role in determining the capacity of visual short-term memory.

Other explanations are certainly possible. For example, it could be the case that observers can remember either the boundary features or the surface features of objects but that the surface is treated as a complex multipart object that takes more space in memory than does the boundary alone. This explanation assumes that observers remember the boundary when it is sufficient to perform the memory task, such as when the aspect ratio is less than 1 when orientation is remembered, and that the redundant surface details can be excluded from memory. In contrast, when the boundary alone is not sufficient, surface details must be remembered, but the surface is obligatorily treated as a multipart object and redundant details cannot be excluded (i.e., all of the surface details must be stored). Thus, storing the boundary is more efficient because irrelevant surface details can be excluded from storage, whereas storing the surface is inefficient because these irrelevant details are obligatorily stored. The important point for our purpose is that any explanation, including this complexity explanation, will have to propose a difference in the efficiency with which boundary features and surface features are encoded, stored, or retrieved from visual short-term memory.

Generalizability of the Boundary/Surface Distinction in Visual Short-Term Memory

We have found evidence that boundary orientation and size are stored in visual short-term memory more efficiently than surface orientation and size. However, it is important to consider why this is the case for these particular features and whether this distinction will generalize to other features as well.

Why have previous experiments shown that storage capacity for color is so high (about four objects; Luck & Vogel, 1997) if surface features are encoded less efficiently than boundary features? One possibility is that color is encoded more efficiently than the surface features tested in the present experiments. In previous experiments, we have shown that the information load for the surface color of objects is quite small. According to this view, the storage capacity for surface color (about four; Luck & Vogel, 1997) exceeds the storage capacity for surface orientation and size (about two in the present experiments) because surface orientation and size require more detail to encode than does color.

A more specific hypothesis of the nature of the boundary code gives an alternative account for the advantage of color. Specifically, if a boundary feature is a feature that is invariant along the length of the contour, color may be a boundary feature, whereas texture orientation cannot be. The color difference between a uniformly colored object and its background is the same along the entire length of the object’s boundary. The boundary of a textured patch is different. The patch differs in texture from the background, but the relation changes from point to point. The orientation of the texture is parallel to the border along part of the contour but is orthogonal to it at other locations. If color is part of the boundary code, it has the same advantage as the boundary shape for being coded in memory. This logic would then apply to any feature that is invariant along the length of the contour, such as luminance.

Will a complex boundary, such as the shape of a random polygon, be stored in memory more efficiently than a simple surface feature, such as color? The two-level architecture proposed here does not predict that the storage capacity for all boundary features will be greater than the storage capacity for all surface features. For example, it is undoubtedly the case that memory for fine detail in the object boundary will be less efficient than memory for a simple surface feature, such as color. For example, a small change in the size of an object is certainly less likely to be noticed than a change from red to green, even though the size change is a change in the object boundary and the color change is a surface feature change. However, the small size change can be perceptually matched to an equally small color change—say, by making a slight change in hue or saturation. Likewise, the magnitude of the size change can be increased to make it more noticeable than a slight color change. Thus, the relative storage capacity of a particular feature depends not only on whether it is a boundary feature or a surface feature, but also on the precision and detail with which each feature must be stored (see Palmer, 1990, for a demonstration of the trade-off between the number of objects encoded into visual short-term memory and the fidelity with which each individual object is encoded).

Conclusion

It is well established that visual short-term memory is limited to the storage of a small number of objects. Less is known about how visual information corresponding to a single object is packaged and stored as a unit in visual short-term memory. On the basis of the present results, we reject the possibility that visual short-term memory simply stores a single abstract code for a particular bit of information about an object. We find that storage capacity for a particular feature is much greater when that feature is part of the object boundary than when the feature is part of the surface texture of an object. Thus, we conclude that there are at least two levels of encoding and storage in visual short-term memory: one for the object’s boundary (the envelope surrounding an object) and another for the surface features of the object (the textural details of the surface within the object boundary). We propose that the boundary features of an object possibly serve as the indexing feature for retrieving the subordinate-level surface details of an object from memory. Given the primacy of boundary features in both perception and memory, future work should focus on the role of boundary features for indexing and localizing surface details both for perceptual access and for memory access.

APPENDIX

In all of the analyses in this article, we reported the estimated number of items held in visual short-term memory because it is an intuitive unit of capacity. In this appendix we include the raw hit rate (correctly reporting a change), false alarm rate (incorrectly reporting a change), and the standard sensitivity measure d’ for each experiment. The pattern of results in each experiment is qualitatively the same for overall percent correct andd’, and all of the major statistical results reported for estimated storage capacity are observed for both overall percent correct and for d’, with one exception. In the control condition in Experiment 2, the effect of aspect ratio did not reach significance when all display sizes were included in the analysis (p = .09). This appears to be due to the very high d’ values for display size 1, which leave no room for improvement as aspect ratio decreases. After eliminating display size 1 from the analysis, the effect of aspect ratio was again significant (p < .05). This ceiling effect for display size 1 did not have a similar effect on the analysis with capacity estimates, because the method for estimating capacity typically excluded display size 1 from the capacity estimate (see the General Method section for capacity estimation procedure).

Table A1.

Hit Rates, False Alarm Rates, and d’ As a Function of Display Size (1-9) and Stimulus Type (Gabor or Bar) in Experiment 1

	Hits				False Alarms				d’
Display Size	Gabor		Bar		Gabor		Bar		Gabor		Bar
	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM
1	.96	.03	.93	.03	.01	.01	.04	.01	4.5	0.3	3.7	0.3
3	.77	.06	.85	.05	.10	.03	.06	.02	2.6	0.5	3.1	0.4
5	.63	.04	.75	.07	.16	.04	.08	.03	1.5	0.2	2.6	0.4
7	.42	.03	.62	.08	.18	.04	.12	.02	0.9	0.2	1.7	0.3
9	.39	.04	.54	.06	.22	.05	.20	.03	0.7	0.3	1.0	0.3

Table A2.

Hit Rates, False Alarm Rates, and d’ As a Function of Aspect Ratio (1.0-.5) and Stimulus Type (Gabor or Bar), Collapsed Across Display Size in Main Experiment 2

	Hits				False Alarms				d’
Aspect Ratio	Gabor		Bar		Gabor		Bar		Gabor		Bar
	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM
1.00	.73	.04	.68	.03	.15	.03	.16	.03	1.9	0.3	1.5	0.1
.75	.74	.06	.74	.05	.13	.04	.12	.02	1.9	0.3	1.9	0.2
.50	.81	.07	.80	.05	.10	.02	.10	.02	2.6	0.5	2.6	0.4

Table A3.

Hit Rates, False Alarm Rates, and d’ As a Function of Aspect ratio (1.0-.5) and Stimulus Type (Gabor or Bar), Collapsed Across Display Size in the Control Condition in Experiment 2

	Hits				False Alarms				d’
Aspect Ratio	Gabor		Bar		Gabor		Bar		Gabor		Bar
	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM
1.00	.79	.04	.76	.03	.15	.04	.18	.02	2.1	0.3	1.7	0.2
.75	.85	.02	.81	.03	.11	.02	.15	.03	2.4	0.1	2.1	0.2
.50	.86	.03	.88	.02	.09	.02	.13	.03	2.7	0.2	2.6	0.2

Table A4.

Hit Rates, False Alarm rates, and d’ As a Function of Circle Size in Experiment 3

Circle Size	Hits		False Alarms		d’
	M	SEM	M	SEM	M	SEM
No Circle	.86	.05	.05	.02	2.99	0.70
Small	.82	.06	.14	.04	2.30	0.35
Medium	.64	.06	.08	.02	1.92	0.30
Large	.46	.04	.14	.04	1.20	0.34

Table A5.

Hit Rates, False Alarm Rates, and d’ As a Function of Display Size (1-9) and Stimulus Type (Concentric or Isolated Rings) in Experiment 4

	Hits				False Alarms				d’
Display Size	Concentric		Isolated		Concentric		Isolated		Concentric		Isolated
	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM
1	.95	.01	.94	.02	.07	.03	.05	.01	3.7	0.4	3.5	0.3
3	.74	.04	.84	.05	.17	.04	.10	.02	1.8	0.3	2.6	0.2
5	.55	.05	.71	.04	.23	.03	.08	.02	0.9	0.1	2.1	0.3
7	.43	.05	.57	.05	.19	.03	.16	.02	0.7	0.1	1.2	0.2
9	.40	.05	.56	.05	.24	.05	.19	.04	0.5	0.1	1.2	0.2

Table A6.

Hit Rates, False Alarm Rates, and d’ As a Function of Duration (in Milliseconds) and Stimulus Type (Gabor or Bar) in Experiment 5

	Hits				False Alarms				d’
Duration	Gabor		Bar		Gabor		Bar		Gabor		Bar
	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM
200	.42	.08	.44	.06	.31	.10	.26	.06	0.4	0.4	0.7	0.3
450	.38	.08	.56	.04	.13	.05	.15	.04	0.8	0.3	1.4	0.3
700	.50	.05	.55	.06	.21	.06	.14	.04	0.9	0.1	1.4	0.2
950	.44	.05	.57	.06	.18	.05	.08	.03	0.9	0.2	1.8	0.2

Table A7.

Hit Rates, False Alarm Rates, and d’ As a Function of Condition (no Cue or Cue) and Stimulus Type (Gabor or Bar) in Experiment 6

	Hits				False Alarms				d’
Condition	Gabor		Bar		Gabor		Bar		Gabor		Bar
	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM
No cue	.35	.06	.61	.05	.10	.04	.08	.02	1.1	0.3	1.9	0.3
Cue	.42	.05	.70	.05	.17	.03	.18	.03	0.8	0.2	1.6	0.3

Table A8.

Hit Rates, False Alarm Rates, and d’ As a Function of Display Size (2-4) and Stimulus Type (Gabor or Bar) in Experiment 7

	Hits				False Alarms				d’
Display Size	Gabor		Bar		Gabor		Bar		Gabor		Bar
	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM	M	SEM
2	.75	.05	.89	.04	.07	.02	.07	.02	2.4	0.3	3.1	0.4
4	.55	.06	.72	.05	.14	.02	.09	.02	1.3	0.2	2.0	0.2