OPTIMIZATION OF A MICROFLUIDIC DEVICE FOR DIFFUSION-BASED EXTRACTION OF DMSO FROM A CELL SUSPENSION

Abstract

This study considers the use of a two-stream microfluidic device for extraction of dimethyl sulphoxide (DMSO) from a cryopreserved cell suspension. The DMSO diffuses from a cell suspension stream into a neighboring wash stream flowing in parallel. The model of Fleming et al.[14] is employed to determine and discuss optimal geometry and operating conditions for a case requiring removal of 95% DMSO from suspension streams with volumetric flow rates up to 2.5 ml/min. The effects of Peclet number, flow rate fraction, and cell volume fraction are analyzed, and expansion of the analysis to other applications is discussed.

1. Introduction

Whereas microfluidics is traditionally defined as the science and technology of systems involving very small volumes of fluid (10⁻⁹ to 10⁻¹⁸ liters) [1], microfluidic environments are also used to manipulate larger volumes of liquids containing cells. For example, cells have been separated based on size or moved from one buffer to another using a combination of acoustic and flow fields [2, 3, 4]. Cells were also separated from the surrounding solution (i.e., blood plasma) using flow fields [5]. These studies demonstrated that populations of cells could be manipulated in a microfluidic environment. Conversely, the microfluidic environment can be used to control the transport of molecules in cell-containing samples. Yager and colleagues have designed microfluidic immunoassays for various biomedical applications including monitoring drug and hormone levels, diagnosing disease, and monitoring treatment [6, 7, 8]. These studies suggest that the microfluidic environment is well suited to control cell motion and to vary the concentration of the environment surrounding a cell.

One potential application for control of concentration and cell motion via microfluidics is cryopreservation. Specialized solutions consisting of a balanced salt solution supplemented with cryoprotective agents (CPA) are typically employed during cryopreservation to improve cell recovery following the freezing process. The most common cryopreservation protocols use a 10% dimethyl sulfoxide (DMSO) as a CPA [9, 10]. Cell preservation solutions are not physiological; a 10% DMSO solution is approximately 1.4 Osm (versus 0.27–0.3 Osm for isotonic solutions). When transferred from an isotonic solution to a solution containing DMSO, cells first exhibit a rapid efflux of water as each cell attempts to reduce the difference in chemical potential between intracellular and extracellular solutions. Slowly, the DMSO from the surrounding solution permeates the cell membrane and diffuses into each cell. Both the rate of volume change and the absolute volume changes experienced by the cell can result in cell lysis (see [11] for review). Cells also experience volumetric excursions upon dilution or removal from a cryopreservation solution. Transfer of a cell equilibrated with a cryopreservation solution into an isotonic solution will result in a rapid influx of water to decrease the chemical potential of the intracellular solution followed by a slow efflux of DMSO. Cells are much more sensitive to lysis upon expansion (versus dehydration), so post-thaw DMSO removal protocols are critical for preventing cell losses.

Conventional methods of removing cryoprotective agents from cell suspensions have changed little since the 1970s. Cells are centrifuged, and the supernatant is removed and replaced with a wash solution. Then, the process is repeated. This method of removal is labor intensive and results in significant cell losses. Further, the percentage of cell recovery depends heavily on the skill of the operator. For example, washing of umbilical cord blood (UCB), which takes approximately two hours, resulted in the loss of 27–30% of nucleated cells using either a centrifuge [12] or an automated cell washer [13]. It is important to note that these studies were performed with highly trained staff. Methods of post thaw processing that require little operator intervention (e.g, semi-automated) and minimize cell losses would represent a significant advance in cell preservation and directly benefit cell therapy, biotechnology, and biorepositories.

In a recent study by the authors, the feasibility of using a microfluidic device for removing cryopreservation solutions with minimal operator intervention and minimal cell losses has been demonstrated [15]. The design of this device was based on a theoretical model developed by Fleming et al. [14]. The model demonstrated the importance of the volume flow rate fraction of the cell stream, fraction of cells in the stream, and Peclet Number on the outlet concentration of the device. As a case study, the requirements for the removal of 95% of the DMSO from a hematopoietic stem cell product were determined. The results suggested that a microfluidic device with multiple washing stages would be required to achieve the 95% reduction needed. Further, the practical application of this device to clinical cell processing requires the device to process 2–3 ml/min. This paper demonstrates the use of the model to determine an optimal geometry and operating conditions for the 95% removal of DMSO from a clinical scale volume of cell suspension (150ml).

2. Model

The model by Fleming et al. [14] is used as the basis for the analysis. Two streams flow in parallel within a channel of constant rectangular cross section. The lower stream consists of a cryopreserved cell suspension, and the upper stream is a wash stream without cells or cryopreservative. In Fig. 1, δ and d denote the depths of the lower stream and the total channel, respectively. In this system, the cryopreservative DMSO diffuses from the cell stream to the wash stream. The x, y, and z coordinates correspond to the streamwise, cross-stream, and spanwise directions, respectively. Low Reynolds number (ρUd/μ) cases were studied such that the flow is laminar with a short entry length.

Figure 1.

Schematic of flow configuration as seen in Fleming et al [14]. Two streams enter at left and flow in parallel toward the right. The lower stream is a DMSO-laden cell suspension. The upper stream is a wash solution. Exploded view illustrates the flow of DMSO from the intracellular to the extracellular solution.

The model developed is based on the following assumptions:

• The flow is nominally two-dimensional and fully developed so that the streamwise velocity u_x is a function of the depth alone, and the cross stream velocity is zero.

• The viscosity is uniform across the entire depth so that the velocity profile is parabolic.

• The cells move with the local fluid velocity, and the possibility of cells settling due to gravity is ignored.

• The diffusion of DMSO from the intracellular solution to the extracellular solution in the cell stream is modeled as a source of additional extracellular concentration.

• Variations across the stream are much stronger than the variations along the stream (∂²/∂x²≪ ∂²/∂y²).

The equation for transport of DMSO in the wash stream is:

$$u_x\frac{\partial C_t}{\partial x}=D\frac{{\partial }^2{C}_t}{\partial y^2},$$ (1)

where D is the diffusion coefficient of DMSO and C_t denotes the number of moles of DMSO per unit total volume.

In the cell stream, the equations for transport of DMSO are:

$$\frac{\partial C_t}{\partial x}=\frac{D}{u_x}\frac{{\partial }^2{C}_t}{\partial y^2}+\frac{V_{i}B}{V_t{u}_x}(C_i-C_e),$$ (2)

$$\frac{\partial C_i}{\partial x}=\frac{B}{u_x}(C_e-C_i).$$ (3)

where C_e is the number of moles of extracellular DMSO per local extracellular volume V_e, C_i is the number of moles of intracellular DMSO per intracellular volume V_i, and B is the cell membrane permeability to DMSO. For the cell stream, C_t represents the number of moles of extracellular DMSO in the local volume V_t = V_i + V_e, V_i/V_t is the local volume fraction of cells, and C_t=C_e(V_e/V_t). The resistance of the cell membrane to transport of DMSO implies that a concentration difference between intracellular and extracellular compartments is required for transport of DMSO across the membrane. In the present application, diffusion of DMSO from the intracellular to extracellular compartments acts as a source of molecules of DMSO in the extracellular compartment. Zero flux boundary conditions were assumed at the channel walls.

When Eq. (2) is scaled using the mean channel velocity U, the total channel depth d, and the initial DMSO concentration C₀, three dimensionless parameters are found:

$$Pe=\frac{dU}{D},B\ast =\frac{Bd}{U},\text{and}\frac{V_i}{V_t}.$$

where Pe is the Peclet number, V_i/V_t is the cell volume fraction also known as the cytocrit, and B* is a dimensionless permeability parameter.

Another independent parameter found by scaling the initial inlet condition by the channel depth is δ/d. This depth ratio is directly related to the inlet flow rate fraction f_q, defined as:

$$f_q=\frac{q_c}{q_t},$$ (4)

where q_t is the total volumetric flow rate through the channel such that q_t = q_c + q_w. Here, q_c is the cell stream flow rate, and q_w is the wash stream flow rate. The flow rate fraction f_q, is related to δ/d through the parabolic velocity variation across the channel depth.

The analysis described assumes that the flow in the channel is laminar and fully-developed, and, therefore, considers cases of low Reynolds number (Re < 5) only. The values of D and B considered are 800 μm²/s and 10 s⁻¹ [16, 17]. The formulation of the model suggests that four independent parameters f_q, Pe, B* and V_i/V_t influence the diffusion of DMSO from the cell stream to the wash stream. We will discuss the influence of f_q, Pe and V_i/V_t within the body of this article. The range of Peclet number considered (250–2500) was limited on the upper end by the Reynolds number constraint. Below the lower end, the flow rate becomes too small to be practical. In this article, we consider a specific cell type with a known permeability to DMSO. For the range of B* possible under practical limits (0.5 < B* < 12.5), the diffusion across cell membranes characterized by this parameter occurs much more quickly than diffusion across the channel (see [14]). Therefore, variations in B* do not influence device design significantly and will not be considered in the optimization process. A more complete analysis of the influence of each parameter can be found in [14].

Considerations for channel scale-up and optimization

The scale-up analysis requires specification of the following geometric parameters: stage length, number of stages in series, and stage width. The length of a given stage will be set equal to the total useful length (TUL). As defined in [14], the total useful length is the streamwise distance after which the average cell stream concentration falls within 10% of the removal limit. The removal limit in a single stage is determined by the flow rate fraction [14]. For example, after an infinite streamwise distance, 95% of the DMSO can be removed from the cell stream when the flow rate fraction is 5%, resulting in a removal limit of 5%.

The authors’ previous analysis has demonstrated that a multi-stage device would be needed to achieve the desired outlet concentration for clinical scale volumes. A multistage device is shown schematically in Fig. 2 (in a real device, the sequential stages would likely be physically separated). The cell stream enters the first stage at the inlet and the wash stream enters at inlet A. The wash and cell streams flow in parallel over a set length, the TUL; then the wash stream is bled off through outlet B and a clean wash stream added into inlet C and run in parallel with the contaminant stream, with the cell stream leaving the device after the second stage through outlet cell and the wash stream leaving through outlet D. This bleeding off and addition of wash stream would continue for the necessary number of stages until the desired concentration removal is reached. The use of multiple stages in series permits enhanced diffusion-based removal from the cell stream by increasing chemical gradients in the device and thereby enhancing cross stream transport.

Figure 2.

Schematic of a two-stage device. Cell stream enters at lower left. Wash enters through inlet A, flows parallel to the cell stream for the total useful length, and exits through outlet B. A clean wash stream enters through inlet C, again flows parallel to the cell stream for the total useful length, and exits through outlet D. The cell stream exits at the lower right.

The model described can be used to estimate the number of stages needed for a given channel geometry and operating conditions. The number of stages in series can be estimated by using the average cell stream concentration at the stage outlet. For example, with f_q = 30%, the average cell stream concentration at the end of stage 1 is 40% of the initial concentration (assuming the stage length = TUL). A similar percent reduction in concentration will be experienced for any additional channels of the same geometry and flow condition. Therefore, at the end of stage 2, the average cell stream concentration is (0.4)² or 16% of the initial concentration entering the device, and at the end of stage 3 it is (0.4)³ or 6.4%. For this flow rate fraction, then, four stages in series are needed to reach less than 5% of the initial concentration.

The width of the device is determined by solving Eq. 5 after inserting the desired flow rate for the device:

$$w=\frac{q_c}{{\overline{u}}_c\delta }$$ (5)

where w is the channel width, q_c is fixed at the desired cell-processing rate (2.5 ml/min), δ is the depth of the cell stream and ū_c is the average cell stream velocity per cell stream depth δ. Note that ū_c and δ are functions of Pe and f_q.

Additional performance constraints are required to fully specify the problem. Conventional methods of DMSO removal from cells that have been frozen and thawed, i.e., centrifugation [12] and automated cell washers [13] described in the Introduction, result in roughly 95% removal. Thus, the device considered herein will be designed to remove 95% of DMSO from the cell suspension. The device also needs to process clinically relevant volumes of cells in a reasonable period of time. The device will be designed to process 2.5 ml/min, which would permit processing of a typical umbilical cord blood unit in less than 15 minutes and bone marrow or peripheral blood stem cell products in less than one hour. The manner by which different cell products are collected and processed can result in different cell volume fractions (e.g., cytocrit, V_i/V_t). After collection and processing, hematopoietic stem cell products can have V_i/V_t ranging from 2–20% [18]. Therefore, the influence of cell volume fraction on device scale up will also be determined.

The device is intended for use in a clinical laboratory setting. The footprint of the device, specifically the area of an individual stage, will be limited so that the device may be used on a laboratory bench top or at a patient’s bedside. (We assume that sequential stages could be stacked vertically). The stage footprint is calculated by multiplying the width (as determined above) by the total useful length of a given stage. The determination of the channel length, the total number of stages in series, device width and stage footprint allow for the scale-up of the single stage device considered in previous studies [14, 15] to clinical scale volumes. The device design should be as simple as possible to ensure ease of fabrication and assembly. This constraint implies the number of stages should be minimized where possible to decrease plumbing complexity. Finally, practical use of the device will require that the volume of wash stream be reasonable. The influence of device design on wash stream requirements will be discussed in Section 3.6.

3. Results and Discussion

3.1. Stage length

To generalize this analysis, the total useful length (e.g. stage length) was non-dimensionalized with the total channel depth. As described previously, the channel length is influenced by f_q, Pe, and V_i/V_t. For streams without cells, average concentration in the DMSO-laden stream at a given streamwise location is strongly influenced by f_q as shown in Fig. 3a. The TUL for a given f_q is also marked for each value of f_q by the circles on each curve. The quantity TUL/d increases with increasing f_q up to a maximum near f_q = 36.6%. Further increases in f_q result in a decreasing TUL/d. This relationship can be seen more explicitly in Fig. 3b. Fig. 3b also illustrates the influence of Pe on TUL/d. For a given f_q, TUL increases linearly with Pe. For example, at f_q= 23% and Pe=625, TUL/d = 65.6. Doubling Pe to 1250, results in TUL/d = 131 (for the same f_q).

Figure 3.

(a) Normalized average cell stream concentration versus normalized streamwise distance for f_q= 22.9%, 36.6%, 51.5%, and 63.3%. The ^○ symbol on each curve represents the TUL/d value for each flow rate fraction. (b) Flow rate fraction versus TUL/d for Pe = 250, 625, 1250, and 2500.

The inverted ‘u’ shape of the TUL/d curve and the location of the peak at f_q = 36.6% reflects the influence of two factors. First, for small values of f_q, the distance a DMSO molecule must diffuse before entering the wash stream is relatively small. The small distance implies that the residence time (and hence channel length) required for diffusion is low. As f_q increases, this distance and hence the required channel length increase. A similar situation is present at high values of f_q; the distance a DMSO molecule must diffuse to travel across the wash stream is small, so the residence time (and channel length) required to smooth the initial cross-stream concentration gradient is also small. The second factor influencing the curve shapes in Fig. 3B is the relationship between f_q and the removal limit. The removal limit increases linearly with f_q. Thus, for a larger value of f_q, the percentage of DMSO molecules needing to leave the DMSO-laden stream is smaller because the DMSO concentration associated with the removal limit for the stream is higher. Thus, TUL/d decreases for higher values of f_q. It is also noteworthy that at high values of f_q (> 40%), significant concentration gradients in the DMSO-laden stream can still exist even after the average concentration over the depth falls within 10% of the removal limit.

3.2. Number of Stages

The next step in optimizing the device design is to determine the number of stages needed to achieve the desired concentration removal. As described previously, the removal limit, and, therefore, TUL for each stage is a function of f_q. As described in the Model Section (Section 2), each stage is associated with a maximum level of concentration reduction. For example, based on our definition of TUL, a given stage will achieve a reduction in normalized concentration C_t/C₀ from 1 to (f_q + 0.1). The number of stages n required for a given value of fq must then satisfy (f_q + 0.1)ⁿ ≤ 0.05 to achieve an overall reduction in C_t of 95%. Increments in the required number of stages are represented by vertical lines in Fig 4a. In order to limit the overall system complexity, the maximum number of stages considered was four.

Figure 4.

Flow rate fraction versus TUL/d superposed with (a) the number of stages needed to achieve 95% removal of DMSO, (b) widths needed to achieve q_c = 2.5 ml/min.

3.3. Width

In addition to determining the stage length and the number of stages, the model facilitates selection of a stage width. For the application of interest, the flow rate for the device is specified as 2.5 ml/min. As described in Eq. (5), the stage width is a function of the specified flow rate, the average velocity U, and the depth of the DMSO-laden stream. δ. Based on this equation, the estimated width of a stage will be a function of Pe and f_q. As shown in Fig. 4b, contours of required stage width can be superposed on the TUL/d versus f_q relationship described previously to demonstrate the relationship amongst those parameters. The width scales inversely with Pe. For example, for f_q = 25.5% at Pe = 625, the width required to achieve 2.5 ml/min is 32.7 cm. If Pe is doubled (1250) for the same f_q, the width required is halved to 18.3 cm. While the influence of Pe on the width can been seen and scaled easily, the effect of f_q on channel width is more complex. Running the device at an extremely low flow rate fraction results in a very wide device (in order to achieve the desired flow rates), while a higher flow rate fraction decreases the width required. In a real device, it is desirable to limit the channel width because of the need to adapt between the round cross section associated with tubing and the channel cross section at the device inlet and outlet. For the current optimization, we will consider channel widths less than 10 cm as acceptable.

3.4. Stage Footprint and Overall Device Layout

Figure 5 shows a schematic of possible device geometries as a function of flow rate fraction for Pe = 2500. Note that a single stage device (f_q can be at most 4% to attain the desired removal limit) would require a very large width (55 cm), and for this reason is not shown. As demonstrated in the figure, increasing f_q increases the overall length of the device but reduces the device width. For a given f_q, increasing the number of stages decreases the total length required but does not change the width.

Figure 5.

Possible device footprints for four different flow rate fractions. Each box shows the width and length of a given stage in the device. Pe = 2500, V_i/V_t = 20%, and d = 0.5 mm.

3.5. Operating Conditions and Channel Depth

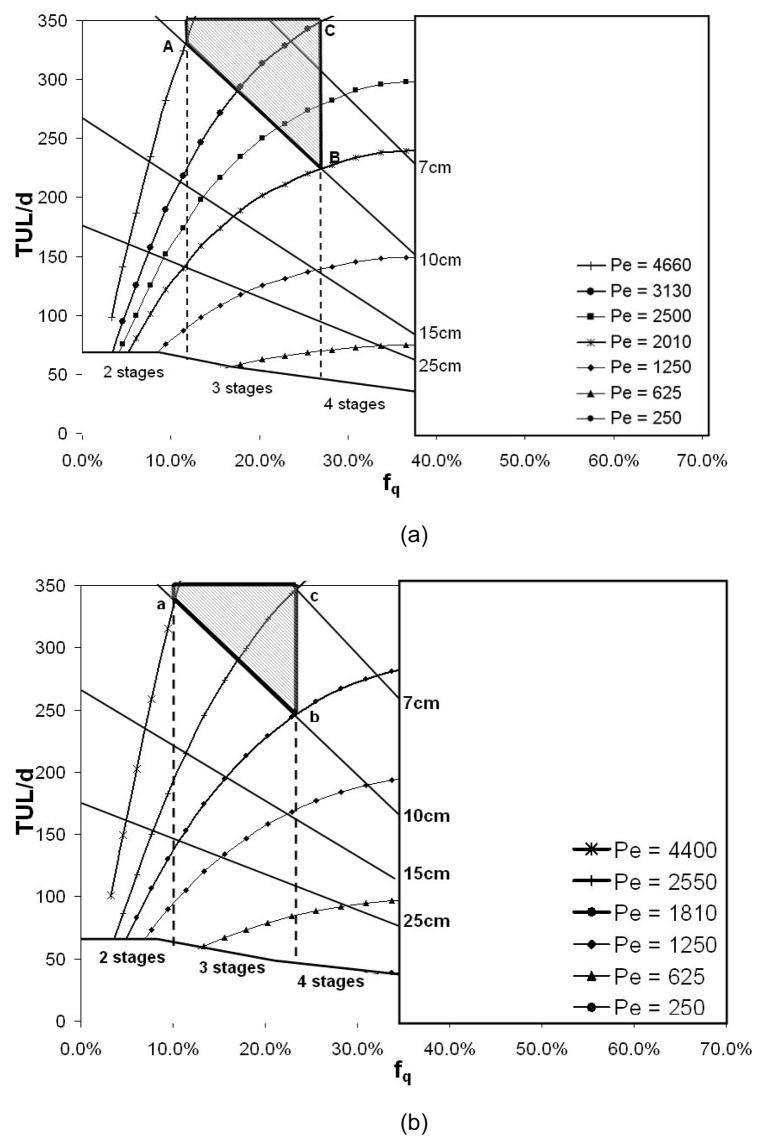
In addition to the selection of stage length, stage width, and number of stages, the model facilitates selection of operating conditions for the channel. Specifically, the range of operating conditions f_q and Pe can be bracketed. For a device with three stages and a width less than or equal to 10 cm, the window of possible operating conditions is illustrated in Fig. 6a by a thick black contour line and shading. The range of f_q in the operating window is 11–26%, and the range of Pe is 2040–5100. The corresponding range of Re in the operating window is 1.6–4.2, indicating that flow in the device remains in the desired regime.

Figure 6.

Flow rate fraction versus TUL/d superposed with the required widths and number of stages for (a) no cells and (b) V_i/V_t = 20%. The optimal operating window is marked with shading surrounded by a thick solid contour.

Thus far, channel depth has not been specified. Depths from 0.2 mm to 2.0 mm have been considered using the numerical model. Depths less than 0.5 mm result in large device widths that are impractical based on both plumbing considerations and overall size limitations. Depths from 0.5 to 2.0 mm result in acceptable device footprints and appropriate flow conditions (Re ≤ 4). Larger depths result in larger Pe and as demonstrated previously, increase TUL while decreasing the width. Thus, larger depth values result in unacceptably large stage lengths.

The total volume of the cell stream is constrained by the clinical application (e.g., 150 ml for hematopoietic stem cell products). The device design will influence the total volume of wash stream required for each run as the volume depends on both f_q and the number of serial stages. A single stage device, which requires f_q ≤ 4%, would require a large volume of wash (3600 ml). By contrast, for a case with f_q = 29%, Pe = 2045, w = 10 cm, and three wash stages, the total wash volume required is 3 × 367 = 1100 ml. Thus, the use of multiple stages not only decreases the overall device size, it also decreases the required wash volume.

Figure 7 shows ‘optimal’ device footprints assuming a depth of 0.5 mm and matching the corner conditions corresponding with the locations A, B, and C of the operating window in Fig. 6. At location A, a two-stage device is possible (perhaps less complexity in plumbing), although this design requires the highest local velocity (Pe = 4660, Re = 3.8) and volume of wash fluid (2430 ml). Locations B and C correspond with three-stage devices at reduced Pe, and wash fluid volume (1100 ml). Location C requires a smaller width (5.4 cm), greater stage length (17.5 cm), and higher Pe than location B.

Figure 7.

Footprints of devices corresponding with ‘optimal’ conditions in Fig. 6a and Fig. 6b and assuming d = 0.5 mm.

3.6. Cell Volume Fraction

Thus far, the analysis presented addressed DMSO diffusion between two streams without cells. The addition of cells will alter the extraction of DMSO from the cell stream as DMSO is present within the intracellular compartment and must diffuse through both compartments (intracellular and extracellular) to be removed. As described previously, hematopoietic stem cell products may be collected and frozen at cell concentrations ranging from 2–20%. Therefore, cases were considered that covered this range, and the discussion below focuses on the most extreme case of 20%.

A key difference in device performance caused by the presence of cells is a shift in the removal limit. In a cell-laden stream, the amount of DMSO available for cross-stream diffusion, as seen by neighboring volume elements, is reflected in the quantity C_t. The relation between the number of moles of extracellular DMSO in the total local volume C_t and the number of moles of extracellular DMSO in the extracellular volume, C_e can be expressed as C_t = C_e(1 − V_i/V_t). In previous studies that used centrifugation to remove DMSO, the separated liquid was tested to quantify DMSO concentration, and thus C_e was measured. Therefore, to reach C_e = 5% as in previous studies, C_t must reach 4% if V_i/V_t = 20%. The change in C_t causes the limits on stage numbers (such as those shown in Fig. 3A and 6A) to shift toward smaller values of f_q. Based on the description in Section 3.2, we must now satisfy (f_q + 0.1)ⁿ ≤ 0.04. For a two-stage device, the presence of cells at V_i/V_t = 20% causes the upper limit on f_q to shift from 0.12 to 0.10, and for a three-stage device, the upper limit on f_q shifts from 0.27 to 0.24.

Sample results are presented in Fig. 6b and Fig. 7 for a cytocrit V_i/V_t of 20%. In Fig. 6b, we use the same criteria as previously to delineate an ‘optimal’ window for device geometry and operating conditions. The window is marked by shading and surrounded by a thick contour. In this case, the shifts in the limiting values of f_q due to the presence of cells cause the size of the window to shrink. Also, the presence of cells increases TUL for a given condition, causing the Pe contours to shift upward and leftward in the plot. Therefore, if we consider the ‘optimal’ corner locations marked by a, b, and c in Figure 6B, the corresponding Pe values have decreased, and the stage sizes in Figure 7 have increased slightly. For example, the two-stage device corresponding with ‘a’ has a stage length of 17.1 cm vs. 16.5 cm for the case with no cells (the width has been held fixed at 10 cm) and Pe = 4400 vs. 4660 for ‘A’ with no cells. The three-stage devices at ‘b’ and ‘c’ show similar shifts in stage length (=TUL) and Pe values. Device ‘b’ has a length of 12.5 cm vs. 11.4 cm for Device B, and Pe decreases by about 10%. Device ‘c’ has length 17.6 cm vs. 17.5 cm for C and also an increased width (7 cm vs. 5.4 cm for C).

4. Conclusions

In this work, we have demonstrated the use of a numerical model to optimize geometry (stage length, width, and depth, and number of stages) and operating conditions for a microfluidic device designed to remove DMSO from clinical volumes of hematopoietic stem cell suspensions in a limited time. The stage length was influenced by the flow rate fraction f_q, Pe and the cell volume fraction. Also, the number of stages, stage width and operating conditions (Pe value) are linked. Increasing the number of stages decreases the overall length of the device. Increasing f_q in the device decreases the device width while increasing the device length. The Peclet number scales linearly with the length of the channel but inversely with the width. The presence of a cell volume fraction up to 20% was found to have only a small effect on the available operating window due to relatively small shifts in flow rate fraction limits associated with the number of device stages. The presence of cells also caused an increase in the TUL thus causing the optimal Pe numbers to decrease slightly.

The required volume of wash fluid was also considered, and it was demonstrated that designs with larger numbers of serial channel stages require smaller total volumes of wash fluid. As the cost of wash fluid is considered to be small compared with the ultimate cost of generating a viable volume of stem cells, designs with smaller numbers of stages may actually be preferable if they result in reduced plumbing complexity and smaller overall cell losses. The model described previously [14] has been verified experimentally using a small-scale experimental prototype [15]. Excellent agreement between theory and experiment was observed. The optimization strategy developed in this investigation will be used to finalize a prototype for processing clinical volumes.

Additives similar to DMSO designed to improve cell survival rates are required for cryopreservation of any type of cell. These additives are not physiological, and their introduction and removal must be performed properly, or significant cell losses can result [19]. The model and strategy described in this investigation can be employed to understand removal of relevant cryopreservation solutions from a variety of additional cell types. For example, red blood cells are frozen in solutions of glycerol ranging in concentration from 17.5–40%. When the cells are thawed for infusion into a patient, the glycerol concentration must be decreased to 1–3%. Thus, 87–97.5% of the glycerol must be removed, and our diffusion model could be employed to determine possible designs of multi-stream channels for this purpose. In this application, the membrane permeability parameter would be altered due to a decrease in the permeability of red blood cells to glycerol (B = 0.5 s⁻¹ for red blood cells [20]). In addition, the size of the glycerol molecule is larger and, therefore, the diffusion coefficient, D, would be smaller (D = 220–520 μm²/s for glycerol [21]). These changes suggest that diffusion across cell membranes may play a much more important role in determining the device length as compared to the case study for DMSO.

With slight modifications, the applicability of this model can extend beyond that of cryopreservation solution removal. For example, lab-on-a-chip applications may require the extraction of proteins and antibodies from a blood sample for analysis. Specifically, the diffusion coefficient for larger molecules such as proteins would be less (0.1 to 0.5 of the value of D for DMSO). In addition, the ‘source’ term in Eq. 2 could be eliminated as proteins do not passively diffuse through the cell membrane, and the kinetics of synthesis and active transport of most proteins is a much longer time scale (hours) than the residence time for the cells in the channel (seconds/minutes), implying that the contribution of protein secretion to the overall diffusion of protein in the channel would be negligible. Thus, the model described in this investigation is appropriate for understanding and characterizing the diffusion-based extraction of molecules from a cell stream.

Nomenclature

B

cell membrane permeability to DMSO

B*

non-dimensional permeability (Bd/U)

c_i

number of moles of intracellular DMSO per local intracellular volume

c_e

number of moles of extracellular DMSO per local extracellular volume

c_o

initial DMSO concentration

c_t

number of moles of extracellular DMSO per total local volume

D

molecular diffusion coefficient of DMSO

d

channel depth

f_q

flow rate fraction (qc/qt)

Pe

Peclet number (dU/D)

q_c

cell stream flow rate

q_t

total channel flow rate

q_w

wash stream flow rate

Re

Reynolds number (ρUd/μ)

TUL

total useful length

U

mean channel velocity

$\overline{u_c}$

average cell stream velocity

u_x

local streamwise velocity

V_e

extracellular local volume

V_i

intracellular local volume

V_i/V_t

volume fraction of cells

V_t

total local volume

x

streamwise direction

y

crossstream direction

z

spanwise direction

δ

depth of cell stream