DNA Sequencing By Denaturation: Principle and Thermodynamic Simulations

Abstract

We describe a new DNA sequencing method called sequencing by denaturation (SBD). A Sanger dideoxy sequencing reaction is performed on the templates on a solid surface to generate a ladder of DNA fragments randomly terminated by fluorescently-labeled dideoxyribonucleotides. The labeled DNA fragments are sequentially denatured from the templates and the process is monitored by measuring the change in fluorescence intensities from the surface. By analyzing the denaturation profiles, the base sequence of the template can be determined. Using thermodynamic principles, we simulated the denaturation profiles of a series of oligonucleotides ranging from 12 to 32 bases and developed a base-calling algorithm to decode the sequences. These simulations demonstrate that DNA molecules up to 20 bases can be sequenced by SBD. Experimental measurements of the melting profiles of DNA fragments in solution confirm that DNA sequence can be determined by SBD. The potential limitations and advantages of SBD are discussed. With SBD, millions of sequencing reactions can be performed on a small area on a surface in parallel with a very small amount of sequencing reagents. Therefore, DNA sequencing by SBD could potentially result in a significant increase in speed and reduction in cost in large-scale genome re-sequencing.

There is an increasing demand for genome sequencing technology for many applications such as genotyping, gene expression studies and genome sequencing for personalized medicine [1-4]. Current sequencing technology has enabled the sequencing of the human genome, but is still too slow and expensive for routine sequencing of individual human genomes. Gel electrophoresis-based Sanger dideoxy sequencing has been the conventional method for large-scale genome sequencing efforts. In the Sanger method, a DNA sequence is decoded by resolving the DNA fragments randomly terminated by fluorescently-labeled dideoxyribonucleotides in a polymerase reaction by gel electrophoresis. Because gel electrophoresis requires the spatial separation of the samples, to achieve the miniaturization and multiplexing required for genome-scale sequencing with a single miniaturized device has proven to be difficult [2, 5, 6].

Several next-generation sequencing technologies have become available to offer hundreds of times the throughput of traditional Sanger technology. While each utilizing different sequencing chemistries, including pyrosequencing in the 454-Roche GS-FLX [7], sequencing by synthesis in the Illumina 1G Analyzer [8-10] and the Helicos Heliscope[11], and sequencing by ligation by the Church group [12, 13] and in the Applied Biosystems SOLiD [14], as well as sequencing by synthesis recently reported by Guo et al. [15], and sequencing by hybridization by Pihlak et al. [16] and Sram et al. [17], there is a common trend towards providing a much greater throughput with short reads by sequencing in flow cells where reagents are brought in and washed away in multiple cycles [18]. Here we introduce a new sequencing method called Sequencing By Denaturation. This method utilizes a flow cell where millions of reactions can be carried out in parallel on a relatively small area on a surface in a single process without the cyclic delivery of reagents. It is based on the traditional Sanger reaction chemistry and melting curve analysis, but does not rely on gel electrophoresis. With SBD, sequencing speed and cost can potentially be improved by many orders of magnitude.

In DNA melting curve analysis, the denaturation profile of a double-stranded DNA molecule into two single strands is measured. The denaturation process can be effected by many means such as an increase in temperature or denaturant concentrations. The denaturation profile can be monitored by optical techniques such as absorption and fluorescence microscopy. For example, the interactions among stacked bases cause a decrease in UV absorption. Melting of double-stranded DNA at elevated temperature involves breaking the hydrogen bonds of the base pairs and a decrease of base stacking. This results in an increase in UV absorption, a hyperchromicity, which can be measured with a spectrophotometer [19]. Melting curve analysis has been used in many applications such as the detection of SNPs (single nucleotide polymorphisms) [20-22]. The melting behavior and melting temperature (T_m) of short oligonucleotides can be predicted quite well by the nearest-neighbor thermodynamic model which assumes that the stability of a DNA duplex depends on the identity and orientation of the neighboring base pairs [23-29]. In this study, we have extended this nearest-neighbor model to predict full melting curves of an extensive series of short oligonucleotides at various ionic strengths to provide a theoretical basis for SBD.

Denaturation is the reverse process of hybridization. A DNA sequencing method based on hybridization called sequencing by hybridization (SBH) was proposed many years ago as a high throughput sequencing method [30-32]. In SBH, a target sequence is interrogated by the hybridization of short complementary probes [30-36]. SBH has been difficult to implement primarily due to the complexity associated with the SBH process, particularly the cross-hybridizations of probes to incorrect but similar sequences in the context of a complex mixture of probes and target sequences. In contrast to hybridization, denaturation is a simple and relatively slow process which strictly depends on the thermodynamic properties of the DNA molecules [19]. Denaturation does not require the initial collision of single-stranded DNA species and thus is free of the complexity associated with the hybridization kinetics. Furthermore, it is not affected by cross-hybridization of mismatched probes to the target DNA. Therefore, we reason that melting curve analysis methods could be used for DNA sequencing.

Principle of SBD

The basic principle of SBD is illustrated in Figure 1. As shown in Figure 1A, first, a standard Sanger sequencing reaction is performed using fluorescently-labeled dideoxyribonucleotides on the templates immobilized on a surface. Instead of being resolved by gel electrophoresis, these randomly terminated DNA fragments are sequentially denatured and washed away by applying a denaturation force such as an increase in temperature and/or the concentration of a chemical denaturant. As each fluorescently-labeled dideoxy-terminated fragment denatures, the fluorescence in the corresponding channel on the surface decreases. The ensemble of these melting curves can be measured by monitoring the fluorescence from the fragments remained hybridized to the templates. A priori, single-base resolution can be obtained because the melting temperature of a DNA strand of certain number of bases is lower than that with one additional base. By analyzing the fluorescence intensity, which reflects the denaturation event, the sequence of the template can be determined. As shown in Figure 1B, the graph of the negative first derivatives of the denaturation curves with respect to temperature looks similar to a conventional electropherogram in Sanger dideoxy sequencing by gel electrophoresis. The sequence can be decoded from the order of the peaks in the graph.

Figure 1. SBD principle.

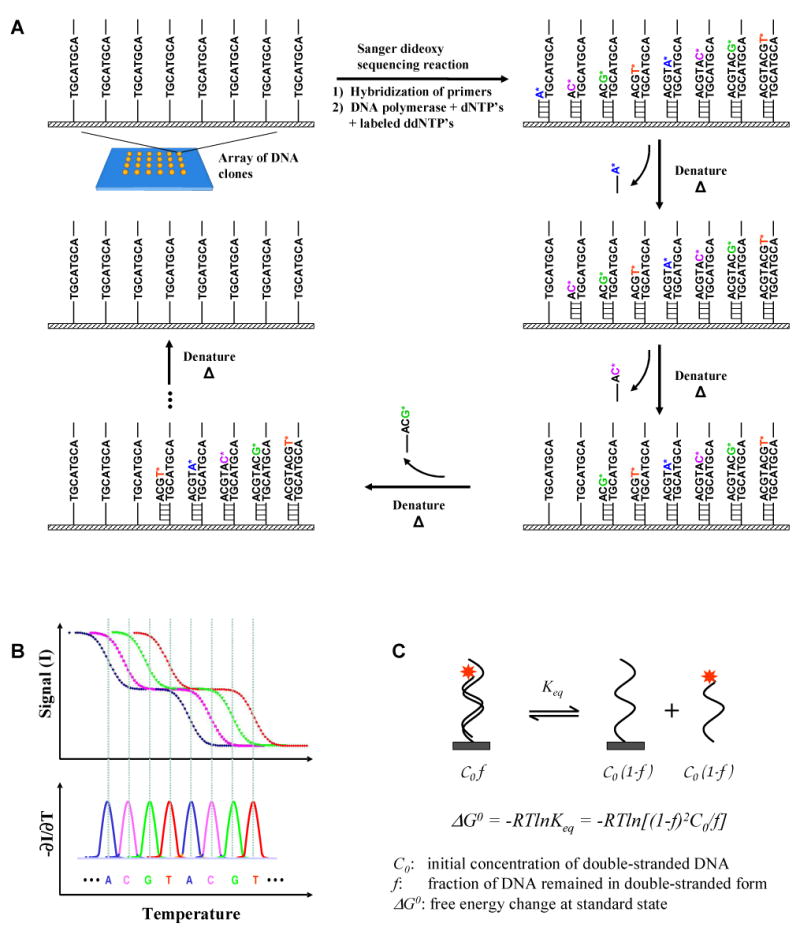
(A) The basic concept. Standard Sanger dideoxy sequencing reaction is performed on the templates immobilized on a surface. The dideoxyribonucleotides are incorporated randomly at each strand. The labeled dideoxy terminated fragments are then sequentially removed from the templates on the surface by gradually increasing the temperature or other degrees of denaturation. (B) If the denaturation process is monitored by measuring only the fluorescence from the molecules on the surface, sequence information can be obtained from the profile of signal intensity as a function of the degree of denaturation (in this example, temperature). The negative derivative of denaturation curve (-∂I/∂T) results in a graph similar to the conventional electropherogram in gel electrophoresis-based Sanger dideoxy sequencing. The sequence is decoded from the peaks in the graph. For clarity, the hypothetical denaturation curves of an 8-base sequence are shown. (C) The denaturation process is the reverse process of the hybridization reaction. At a given temperature, the equilibrium constant is determined by the change in free energy of the reaction (ΔG⁰), which is strictly determined by the thermodynamic properties of the double-stranded and single-stranded DNA molecules.

In this paper, we describe the basic the principle of SBD and provide a theoretical basis for it using a simple thermodynamic model. Melting profiles of a series of oligonucleotides that differ consecutively by one base are predicted and processed to simulate the SBD data. A base-calling algorithm is developed to decode the DNA sequence from these denaturation profiles. These simulations and experimental results demonstrate the feasibility of SBD.

Materials and Methods

Theoretical derivation

This section describes the theoretical basis for our simulations. In order to simulate the data obtained from SBD, we simulated the individual melting curves and ensemble denaturation profiles of short oligonucleotide series. The denaturation profiles of a double-stranded DNA were simulated by calculating the fraction of the DNA remained hybridized as a function of temperature.

Considering a double-stranded DNA with an initial concentration of C₀ that denatures and reaches equilibrium with two non-self-complementary single-stranded DNA molecules (Figure 1C), the equilibrium constant K_eq is related to the change of Gibbs free energy at standard state by:

$$\Delta G^0=-\mathrm{RT}ln{K}_{\mathrm{eq}}=-\mathrm{RT}ln\left(\frac{{(1-f)}^2{C}_0}{f}\right),$$ (1)

where f is the fraction of DNA remained hybridized in the double-stranded form, T is the temperature, R is the gas constant, and C₀ is the initial concentration of the duplex DNA. The denaturation profile can be represented by the fraction hybridized (f) as a function of temperature (T), when ΔG⁰ is known. Thermodynamic parameters such as the standard state enthalpy (H⁰) and entropy (S⁰) for DNA hybridization have been extensively studied and a nearest-neighbor model has been developed to predict these parameters from the sequence of the DNA [23-29]. The reported thermodynamic data of enthalpy (ΔH⁰) and entropy (ΔS⁰) for the nearest-neighbor pairs are the changes of these thermodynamic values in the binding (hybridization) process at standard state at 37 °C. Since denaturation is the reverse process of hybridization, the Gibbs free energy change used in our calculation is the negative of the ΔG⁰ calculated from the reported data. Therefore the ΔG⁰ in equation 1 is related to the ΔH⁰ and ΔS⁰ reported in the literature by ΔG⁰=-(ΔH⁰TΔS⁰). By combining this with Equation 1, we have:

$$\mathrm{RT}ln\left(\frac{{(1-f)}^2{C}_0}{f}\right)=\Delta H^0-T\Delta S^0.$$ (2)

By solving Equation 2, f can be expressed as a function of temperature (T) as follows:

$$f(T)=1+\frac{1}{2C_{0}exp\left(-\frac{\Delta H^0-T\Delta S^0}{\mathrm{RT}}\right)}\pm \sqrt{\frac{4C_{0}exp\left(-\frac{\Delta H^0-T\Delta S^0}{\mathrm{RT}}\right)+1}{4C_0^{2}exp\left(-\frac{2(\Delta H^0-T\Delta S^0)}{\mathrm{RT}}\right)}}.$$ (3)

For the solution with the “+” sign, the fraction f is greater than one. Since a fraction should not be greater than unity, out of the two possible solutions, the one with “-” sign is reasonable and was chosen as our solution.

Salt concentration has a significant effect on the denaturation process and must be taken into account. Monovalent cations such as sodium ions bind to both single- and double-stranded DNA causing conformational changes that affects the denaturation of DNA. The effect of salt concentration is accounted as an ensemble described by the denaturation reaction below.

$$D\rightleftarrows S_1+S_2+v{\mathrm{Na}}^{+},$$

where D represents the double-stranded DNA bound with monovalent counter cations (in this case Na⁺), S₁ and S₂ represent the two single-stranded forms, and ν represents the effective number of the sodium ions released during the denaturation process. The equilibrium constant then becomes:

$$K_{eq}=\frac{[S_1][S_2]{[{\mathrm{Na}}^{+}]}^v}{[D]}=\frac{{(1-f)}^2{C}_0{[{\mathrm{Na}}^{+}]}^v}{f}.$$ (4)

f expressed as a function of temperature (T) is then given by:

$$f(T)=1+\frac{1}{2C_0{[{\mathrm{Na}}^{+}]}^{v}exp\left(-\frac{\Delta H^0-T\Delta S^0}{\mathrm{RT}}\right)}-\sqrt{\frac{4C_0{[{\mathrm{Na}}^{+}]}^{v}exp\left(-\frac{\Delta H^0-T\Delta S^0}{\mathrm{RT}}\right)+1}{4C_0^2{[{\mathrm{Na}}^{+}]}^{2v}exp\left(-\frac{2(\Delta H^0-T\Delta S^0)}{\mathrm{RT}}\right)}}.$$ (5)

ν can be approximated by empirical methods described by Owczarzy and colleagues [37]. Since melting temperature (T_m) is defined as the temperature where 50% of the DNA remains hybridized, T_m can be determined from Equation 5 as:

$$T_m=\frac{\Delta H}{-Rln\frac{2}{C_0}+\mathrm{Rv}ln[N{a}^{+}]+\Delta S}.$$ (6)

Simulations of melting curves

The simulations were conducted with MATLAB. For each oligonucleotide, the ΔH⁰ and ΔS⁰ were calculated by the summation of all the nearest-neighbor pairs and the correction terms in the DNA sequence using the data reported by SantaLucia and colleagues [28]. From Equation 5, the fraction of DNA remaining in the double-stranded form f was simulated as a vector with each element corresponding to a temperature point in the temperature vector T, which ranges from 0 to 100°C. The initial concentration of the oligonucleotides C₀ used was 1 μM. We evaluated various salt concentrations ranging from 10 mM to 1 M and chose 10 mM for the example cases presented herein. The parameter ν was approximated by the derivative method described by Owczarzy and colleagues [37]. We performed simulations for 348 oligonucleotides provided in the accuracy benchmark developed by Panjkovich and Melo [38] to compare our predictions of melting temperatures to the previous studies and the experimental values. The results were used to confirm that the model provides a similar accuracy as reported.

Salt effects on melting curves

As described above, the concentration of monovalent salt influences the denaturation process. The relationship between melting temperature and salt concentration was determined by performing simulations on 1000 random sequences with sodium ion concentrations ranging from 10 mM to 1 M. Each sequence contains a common primer with the sequence ATTAAACCTTAA concatenated with 20 base sequences generated from a random number generator with uniform distribution. For each of these sequences, the ΔH⁰ and ΔS⁰ were calculated as each of the 20 bases was added to the primer generating 13- to 32-base long fragments. Then the melting temperature of each fragment was determined using Equation 6. In order to survey the melting temperatures of 13- to 32-base long oligonucleotides, an average over the 1000 randomly generated sequences for each fragment length was calculated. The average melting temperature for the DNA fragments was plotted versus salt concentration.

Thermodynamic simulations of SBD

Simulations of denaturation profiles

In SBD a DNA molecule is sequenced by measuring and analyzing the melting curves of the fluorescently-labeled DNA fragments generated by a Sanger dideoxy termination sequencing reaction. The measured fluorescence signal from each color/channel is the sum of the signals from all denaturation curves with sequences ended in the corresponding base type (A, C, G or T). We simulated the fluorescence intensity profiles accordingly. For a given DNA template, the denaturation curve for each sequence of all of the oligonucleotides, which consists of a common primer and the additional bases along the template, was simulated separately using the methods described in the previous sections. The curves from all the sequences ending at a particular base type were summed to give the overall fluorescence intensity profile for the channel corresponding to that base type. In order to account for noise and variations on sequencing data obtained from real experiments, a Gaussian noise was added to the simulated fluorescence intensity. The noise level was varied from 1% to 10% of the fluorescence signal.

Base-calling algorithm

The SBD simulated data were smoothed before and after taking the negative derivative curves to generate peaks that mimic the electropherograms generated by traditional Sanger sequencers. Because some peaks overlap and have different width properties from those of traditional electropherograms, an algorithm was developed to find the components of each peak for base-calling.

First, the peaks in each negative derivative curve were found if they are within certain width and height. Here we assume each Sanger fragment to be equally populated. Because neighboring peaks may overlap, each peak was fit to a sum of Gaussian curves to determine its components. The peak positions determined from the fit correspond to the melting temperature of the component Sanger DNA fragments. In some cases, two adjacent peaks, each containing two or more component peaks, may overlap at the ends of the peaks. A second fit was performed to correct for these cases. This was performed after subtracting the other components based on the first fit so that the fit can be improved. Finally, the peak positions were sorted to decode the DNA sequence.

The algorithm involves five steps which are described in detail as follows.

1. Take negative derivative from the smoothed SBD signal. The fluorescent intensity signal was smoothed using a moving average filter with window size spanning 3°C. After the derivative was taken, the signal was smoothed again with the same parameters.

2. Find all of the peaks. In the negative derivative curves, each peak was identified if its width and height were within reasonable boundaries to capture all of the legitimate peaks. In this step, each peak was characterized by the position, height, start and end of the peak. The peak position was determined by the local maximum in the second derivative of the negative derivative curve. The peak height was the value at the peak position. The start and the end of the peak were defined as the positions where the negative derivative reaches a threshold before and after the peak position, respectively. If two peaks overlap partially, the start or end between those peaks would be the local minimum. These parameters determined the range where each peak was located for fitting in the next step.

3. Fit each peak to a sum of Gaussians. The melting curves of some Sanger fragments overlap extensively forming a large combined peak. A fit to the sum of Gaussian curves was performed to deconvolve the individual components. The number of Gaussian components in each peak was determined by the area underneath the curve within this peak region. The initial coefficients and lower and upper bounds were chosen in order to achieve adequate Gaussian fits. The initial coefficients of the mean value for the Gaussian fits were equally-spaced values around the peak position within the region. The lower and upper bounds were determined so that the component melting temperatures do not overlap. In order to determine the bounds for the height and the standard deviation of the Gaussian curves, a set of statistical parameters was obtained by performing simulations on 20,000 negative derivatives of the melting profiles of random single DNA fragments fit to Gaussian curves. The height (A) was determined to relate to the mean position (μ) or melting temperature by the following quadratic equation:

   $$A=1.87\times {10}^{-5}{\mu }^2+2.41\times {10}^{-4}\mu +\mathrm{0.1017.}$$
   The standard deviation (σ) is linearly related to the mean or melting temperature:

   $$\sigma =-4.48\times {10}^{-2}\mu +\mathrm{5.67.}$$

   The initial coefficients for these parameters were set to the values determined by the above relationships at the corresponding starting point for the melting temperature. The lower and upper bounds of these coefficients were set to within 100% confidence value at the corresponding starting point for the mean position.

4. Subtract the interference from the neighboring peaks and refine the fit. In some cases, neighboring peaks overlap. For each peak, the contributions of the neighboring peaks were subtracted by the fitted curves of all the other peaks. Then, the corrected peak was fit again to the sum of Gaussian curves with the parameters determined using the same method as in step 3. The refined fit gives a more accurate presentation of the melting temperatures of each component because the interference from the neighboring peaks was eliminated.

5. Sort the component peaks for base-calling. Finally, the base sequence was called by sorting the melting temperatures of all of the components determined as the coefficients in the Gaussian fit. As we read from lowest melting temperature to the highest, the base sequence is called from the corresponding fluorescent channel.

Evaluation of the feasibility of SBD

Simulations were performed on one thousand 32-base long oligonucleotide sequences. All the sequences share a 12-base common primer with the sequence ATTAGACCTACG. The other 20 bases in each of the sequences were generated using a random number generation function with a uniform distribution in MATLAB. The salt concentration was fixed at 10 mM. The SBD signal was simulated by the summation of all melting curves ending at the base type corresponding to the fluorescence channel. By analyzing this signal with the base-calling algorithm described above, a resultant sequence is determined. The base-calling accuracy was evaluated by aligning the resultant called sequences to the original sequences. The error rate was defined as the total number of substitutions, insertions, and deletions divided by the number of bases called. The cumulative average error rate was calculated as the percentage of error for a given read length. The base-calling accuracy was evaluated for simulations with 0.1°C, 0.3°C, and 0.5°C sampling frequencies, and with simulated Gaussian noise values of 0%, 1%, and 5% of the total intensity.

Melting curve measurements

The melting curves of 8 oligonucleotide probes were measured with a UV-Vis spectrometer (PerkinElmer Lambda-20) by measuring the absorbance at 260 nm through time while the temperature is gradually increased. The samples were placed in a cuvette with a flow cell formed by thin walls around the sides of the cuvette. The water temperature in the flow cell was controlled to within ±0.1 °C using a Julabo F25-HE circulator with an external temperature probe in the cuvette. The 8 oligonucleotides each contain the first 21 through 28 bases of the sequence “CCATCAGTCATGTACGAAGTCAGTCATG”. These samples were prepared by combining 650 nM of each probe with 650 nM of a common template sequence “TAGCATGACTGACTTCGTACATGACTGATGGTCGA” in a 33 mM phosphate buffer, pH 7.2, which is equivalent to 49 mM of monovalent cation concentration.

In order to mimic the denaturation profile of Sanger products, the oligonucleotide probes that end in the same base type were combined to measure the SBD signals from an 8-base read: the 22mer and 26mer for A, the 21mer and 25mer for C, the 23mer and 28mer for G, and the 24mer and 27mer for T. In each solution, the two probe concentrations were 325 nM and the common template concentration was 650 nM so that each probe could hybridize to one template.

The melting curves were fit to sigmoid curves to determine its base-line and top-line for normalization. After normalization, the denaturation profiles that mimic SBD signal were analyzed by the base-calling algorithm described above.

Results

Melting curve analysis

Simulations of melting temperatures as well as melting curves were performed for the 348 sequences provided in the accuracy benchmark. The average error in melting temperature prediction was 3.1°C, which is similar to what has been reported [26, 27]. Shown in Figure 2A are the simulated denaturation curves of a series of 20 oligonucleotides each containing a common 12-base primer with the sequence “ATTAAACCTTAA” and additional bases from the first to the 20th bases of the sequence “GTCAGTCAGTCAGTCAGTCA”. Figure 2B shows the corresponding negative derivatives of the curves with respect to temperature. It is obvious that a shorter DNA denatures at a lower temperature than the one with one additional base longer. The longer the DNA strands are, the sharper the transitions become and the smaller the T_m differences between the neighboring bases. For clarity, the simulation results from a sequence with 4 base types evenly distributed along the sequence are shown. Simulations of the 1000 randomized sequences as described in the methods show that the T_m of the oligonucleotides increase monotonously as additional bases are added onto the primer sequence. These results demonstrate that in theory single-base resolution could be obtained for oligonucleotides up to 32 bases long.

Figure 2. Simulated denaturation curves and their negative first derivatives.

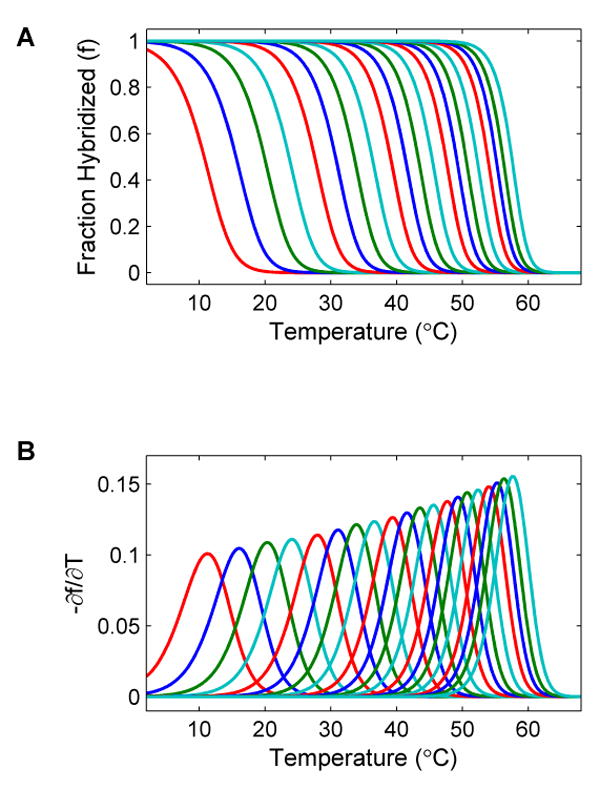
(A) Denaturation curves and (B) the corresponding negatives of the first derivatives of the curves of a series of 20 oligonucleotides each of which consists of a common 12 base primer with the sequence “ATTAAACCTTAA” and additional bases from the first to the 20th bases of the sequence “GTCAGTCAGTCAGTCAGTCA”. The leftmost curve is the simulated profile of the sequence with 13 bases. The rightmost curve is the profile of the full length sequence with 32 bases. A total of 20 curves are shown. As can be seen, the melting temperature increases monotonously as additional bases are added to the sequence.

Salt effects on melting curves

Figure 3 shows the effect of salt concentration on the melting temperature. The average melting temperatures of oligonucleotides with different lengths are plotted versus salt concentration. Each line represents the average of 1000 oligonucleotides with a common 12-base primer of sequence “ATTAAACCTTAA” and 1 to 20 additional bases. As shown, the melting curves have similar profiles but are shifted towards lower temperatures at lower salt concentrations in a non-linear relationship. This plot provides a comprehensive chart for determining the optimal salt concentration to use for experimental measurements of denaturation profiles in SBD. By using an optimal salt gradient, the observation window can be widened.

Figure 3. Salt concentration effect on SBD.

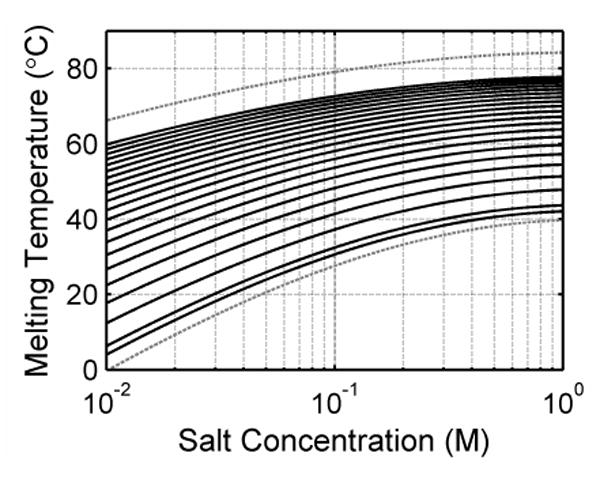
(A) The average melting temperatures of 1000 oligonucleotides with a common primer sequence of ATTAAACCTTAA and 1 to 20 more additional random bases are plotted versus sodium concentration. Note that the salt concentration is plotted on a logarithmic scale. The bottom dashed lines represents the average melting temperature minus two times standard deviation for the sequences with one base added to the primer. The top dashed line represents the average melting temperature plus two times standard deviation for the sequences with 20 bases added to the primer. In this figure, the melting temperatures of DNA become lower as the salt concentration is decreased. This plot is useful in determining the optimal salt concentration window for SBD measurements.

Thermodynamic simulations of SBD

Simulations were performed over 1000 randomized sequences to evaluate the feasibility of SBD. First the SBD signal was simulated for each sequence. Then the base-calling algorithm described in the methods section was used to find the base sequence. For illustrative purpose, two examples and the base-calling procedure are shown in Figure 4. Figures 4A & E show the fluorescent intensity signals, which are the sums of all Sanger fragments labeled in the corresponding channel. A 5% Gaussian noise was added in this case to simulate measurement error. This demonstrates the expected signal from SBD measurements. The signal was then smoothed and the negative derivative was determined and smoothed as shown in Figures 4B & F. Because some peaks overlap and combine into broader peaks, the original components in each wide peak were determined by fitting them to a sum of Gaussian curves. A second fit was performed after subtracting the contributions from the neighboring peaks determined from the initial fit. Figures 4C & G show the final fit results. Each corrected peak is plotted as a colored line. As compared to the one in Figures 4B & F, the line now extends to the base of the curve since the interference from neighboring peaks has been subtracted out. The fit to each peak is shown as a black dashed line. All fits overlay well with the corrected peaks. This indicates that the fit presents the data well.

Figure 4. Base calling algorithm.

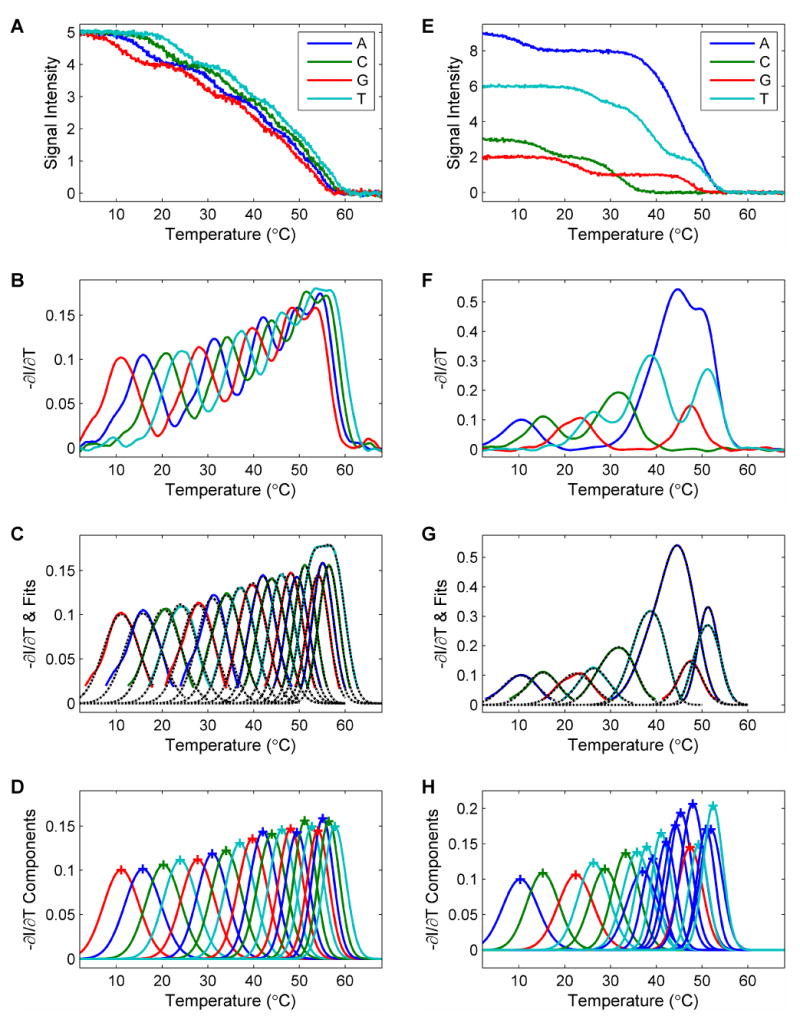
This figure illustrates the base-calling process with two examples. (A-D) A simple case is shown with the sequence “GTCAGTCAGTCAGTCAGTCA”, where the 4 different base types are distributed evenly along the sequence. All the bases are called correctly. (E-H) Another case is shown with the sequence “ACGTCCTATTAAAAGATAAT”. There are extensive overlaps between some of the curves. The called sequence is “ACGTCCTATATAAAGATAAT”. There is a pair of substitution errors in the call. (A) & (E) The simulated fluorescent signal is the sum of all the contributing melting curves in the corresponding channel. A 5% random Gaussian noise is added. (B)&(F) The smoothed negative derivatives of the curves. Some peaks are the combination of multiple melting curves. (C)&(G) Each peak is fit to a sum of Gaussian curves to deconvolve the components. These figures show the results from the correction fit where interference from neighboring curves have been subtracted. The black dashed lines show that each fitted curve overlaps with its colored solid original curve well. (D)&(H) The components from the fit. The peaks are labeled with a cross (+) for visualization. By reading from lower to higher melting temperature, the base sequence can be determined. Blue: A. Green: C. Red: G. Cyan: T. See text for more detailed description of the steps involved in the algorithm.

From the parameter of the fits, the Gaussian components of all peaks determined are plotted in Figures 4D & H. The peaks are marked with crosses to indicate the melting temperatures of the Sanger fragments. These curves mimic the electropherograms generated by traditional Sanger sequencing. The sequence was decoded by sorting these peaks from lower to higher temperature. An ideal case where the 4 different base types are spaced evenly along the sequence is shown in Figure 4D. As can be seen the height of the component peaks increases gradually as the melting temperature increases. In this case, all the peaks are well resolved and all the bases are called correctly. Figure 3H shows another case where there are extensive overlaps between some of the profiles. It is more difficult to resolve all the peaks. In this particular case, two call errors were made with the algorithm. Some of these cases could be better resolved by improving the separations between the neighboring curves. Experimentally, this can be achieved by using a combination of salt and temperature gradients.

After calling every sequence from the 1000 test sequences, the error rate was determined by dividing the number of errors by the number of bases called. Figure 5 shows the cumulative average error rate versus read length for SBD under 0.1°C sampling frequency, and 0% and 5% Gaussian noise levels. The error rate is about 4% with a read length of 20 bases. As expected, this error rate increases linearly with read length. However, added simulated noise level has very little effect on the error rate. This indicates that the base-calling algorithm is robust against noise which will be present in experimental data.

Figure 5. Error rate of SBD.

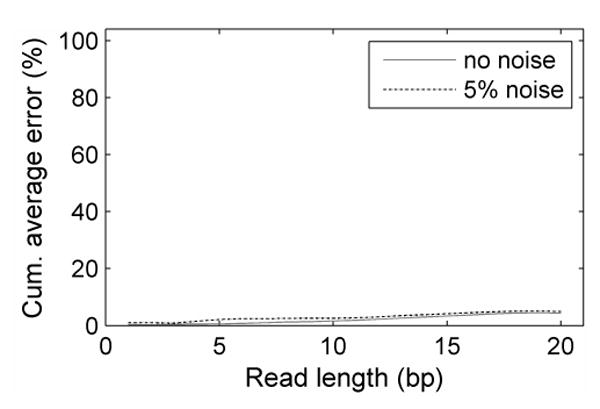
The cumulative average error rate is plotted versus read length under two different noise levels with 0.1°C sampling frequency. The error rate increases linearly with read length. With a read length of 20 the error rate is 4%. The increase in error rate resulted from 5% added simulation noise is not significant, indicating that SBD is robust against small measurement errors. Solid gray line: 0% noise. Dotted black line: 5% noise.

Melting curve measurements

As a simple test, we measured the denaturation profiles of eight oligonucleotides in solution. The melting curves of the 8 oligonucleotides are shown in Figure 6A. The shape of these curves overlap with the predicted melting curves very well. The melting temperatures of the oligonucleotides are shown in Figure 6B. The melting temperature of the oligonucleotides increases monotonously as the length of the oligonucleotide increases. The base-calling process is shown in Figures 6C to 6F. Figure 6C shows the denaturation profiles in 4 channels, each of which contains two component oligonucleotides. The corresponding negative derivatives of these denaturation profiles are shown in Figure 6D. The fit to a sum of Gaussian curves and the component peaks are plotted in Figures 6E & 6F. The shapes of the curves resemble those of the simulated negative derivatives. With the base-calling algorithm, the sequence was determined correctly.

Figure 6. Experimental measurements.

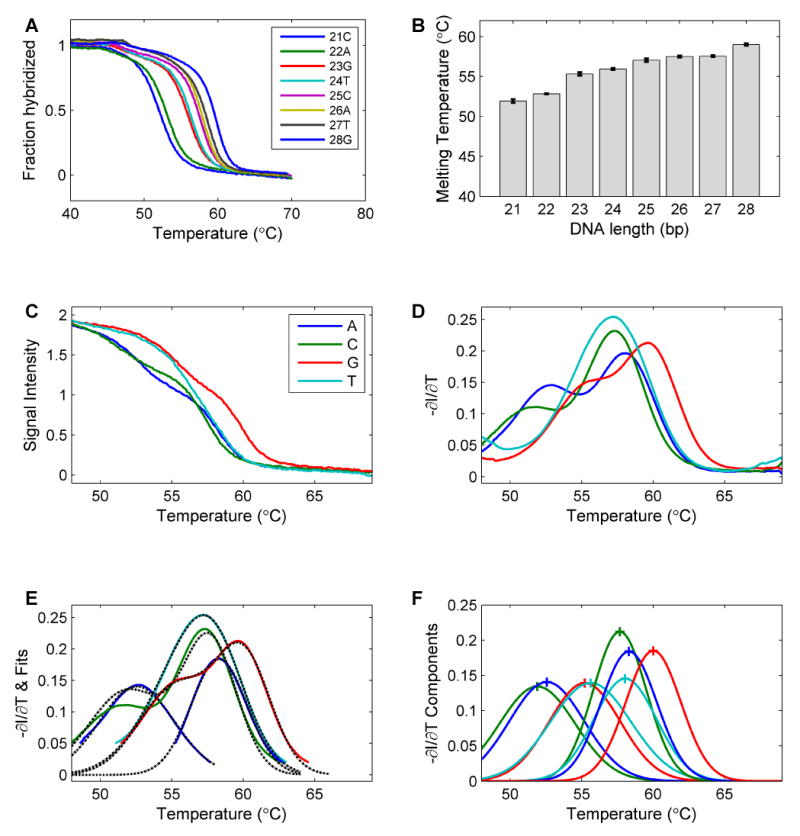
(A) The melting profiles of the 8 individual oligonucleotides with 21 to 28 bases from the sequence “CCATCAGTCATGTACGAAGTCAGTCATG”. (B) The melting temperatures of the oligonucleotides. It is obvious that the melting temperature increases as the length of the oligonucleotide increases. (C) Solution measurements mimicking the SBD process. To mimic the denaturation profile of Sanger fragments, the oligonucleotide probes that end in the same base type were combined to measure the SBD signals for an 8-base read: the 22mer and 26mer for A, the 21mer and 25mer for C, the 23mer and 28mer for G, and the 24mer and 27mer for T. (D) The negative derivative curves of the denaturation curves. These curves were used for the base-calling process. (E) The fitting of the profiles with a sum of Gaussian curves. (F) The resolved individual components used to determine the base sequence. Blue: A. Green: C. Red: G. Cyan: T.

Discussion

In this study, we have established the theoretical basis for SBD. The denaturation profiles of the DNA fragments generated by fluorescently-labeled dideoxyribonucleotides were simulated by melting curve analysis using thermodynamic principles and data. Melting curves and their negative first derivatives were plotted to show the melting temperatures as the peaks of the negative first derivatives. Both simulation and experimental results show that melting temperatures of oligonucleotides increase monotonously as each additional base is added. We have shown how this property can be used to determine the sequence. An algorithm for base-calling has been developed to decode the DNA sequence from the intensity data. The cumulative average error rates versus read lengths were estimated with different simulated noise levels and sampling rates. Within experimentally achievable sampling frequencies, the method is robust against noise. As a simple test, the sequencing of an eight-base DNA fragment was demonstrated in solution by measuring the denaturation profiles of a set of oligonucleotide hybridized to a common template. The results show that SBD data is well simulated by the model and the base sequence is correctly determined with the base-calling algorithm. We have demonstrated that different salt concentrations can be applied to modulate the melting curves of the DNA fragments (data not shown). This allows us to have a greater control over the denaturation temperature to achieve higher accuracy and longer read lengths.

The potential sources of sequencing errors have been investigated. The majority of the errors results from the imperfect fitting of the negative derivatives of the denaturation curves to a sum of Gaussian curves. The issues are more pronounced in certain sequences where a short repeat of one base type with lower binding strengths (A & T) is intercepted by another short repeat. For example, a sequence with “ATTAA” composition is more likely to produce an error with our calling algorithm. In addition, the denaturation event is subject to cooperativity and the negative derivative of a denaturation profile may be slightly skewed and not represented precisely with a Gaussian curve. Another major source of base-calling errors results from the difficulty in resolving the more extensive overlaps between the denaturation curves of longer fragments. An increase in read accuracy can be achieved by limiting the Sanger reaction to a certain length either by using a high concentration of dideoxyribonucleotides or terminating the reaction with a primer pre-hybridized a short distance from the sequencing primer. When terminating the reaction at a defined length, the interference from longer Sanger fragments is eliminated. This results in a clearer determination of the last few bases to sequence.

In the fitting process, we assume that each Sanger fragment is uniformly populated and its denaturation profile follows a normal distribution. In real experiments each Sanger fragment may be differentially represented during the sequencing reaction. However, this problem can be alleviated to some degree by using engineered DNA polymerases such as Sequenase version 2.0 or Thermo Sequenase to generate more uniformly represented DNA fragments. These enzymes have been shown to produce uniform bands in Sanger sequencing since they do not discriminate between dideoxyribonucleotides and deoxyribonucleotides and have much less sequence dependency [39-41]. The base-calling algorithm appears to be robust against potential noise in the measurement. We want to emphasize that the simple algorithm described here is sufficient to illustrate the principle of SBD but obviously is not the best one. The effects of fluorescent labels, dangling ends, and more complex secondary structures such as stemloops on the thermodynamic properties of the oligonucleotides in the denaturation process are more complex and have not been considered in our simulations. Most of the thermodynamic data used in our simulations with the nearest-neighbor model were derived with the assumption that the DNA fragments follow a two-state transition during the denaturation or hybridization process [28]. Therefore, we have not assessed the potential impact of these structures on the sequencing accuracy by SBD. Denaturation of sequences with complex structures such as palindromes, tandem repeats, hairpins and other secondary structures that denature in non-two-state transitions may be better predicted with a much more complex statistical model such as the one reported by Dimitrov and Zuker [29]. However the model is much more complex than the nearest-neighbor model that we used for this work. Higher sequencing accuracy can be achieved by further improvement in the base-calling algorithm, for examples, by optimizing the parameters with experimental data or by replacing the Gaussian fit with numerical methods such as higher-order derivatives to determine the component Sanger fragments. Further work is required to develop a more robust and better base-calling algorithm to reduce the base-calling errors. Unlike DNA hybridization process where kinetic factors play important roles and are difficult to control, the denaturation process is strictly determined by the thermodynamic properties of the double-stranded DNA molecules and is more predictable. We believe that highly accurate sequencing could be feasible with SBD.

When SBD is performed on a solid surface in a flow cell, there are several conditions that must be considered. First, in the simulations, the melting curves were generated using thermodynamic parameters derived from solution measurements. The denaturation process will not be at equilibrium while the denatured probes are washed away from the detection surface. Nevertheless, the washing of denatured probes prevents them from re-hybridizing to the sequencing template, which will result in a sharper transition in the melting curve. This effect may facilitate the unambiguous determination of the base sequence. Second, because multiple fluorescent images are required to monitor the denaturation profiles of a clone of the templates on a spot or captured on a microbead, photobleaching factor could be an issue. In our simulations, sampling frequencies of 0.1 to 0.5°C are used to monitor the denaturation profiles from 10 to 80°C, which generates 140∼700 images for sufficient representation of the denaturation curves. With about 50 ms of exposure time per image, the total exposure time is 7∼35 seconds, which is within the half-life of most organic fluorescent dye molecules. Experimentally, this effect and the effect of temperature on fluorescence quantum yield can be corrected by including proper control spots containing fluorescent molecules covalently bound to the surface or microbeads. Third, not only does the melting temperature of short DNA strands depend on the length of the DNA, but also on the base composition. Although the simulations have accounted for this condition by using nearest-neighbor parameters to estimate the melting profile of DNA strands, errors are encountered when the sequence contains many A and T's towards the end of the read. Experimentally, this issue can be resolved by adding a chemical such as tetramethylammonium chloride which is known to interact differentially with the A-T base pairs and increases their melting temperature to be the same as that of G-C base pairs. In the presence of such reagents, the effect of the base composition on melting temperature is neutralized so that the T_m is dependent only on the length of the DNA [42]. This will even out the melting curves and potentially eliminate the majority of the errors in SBD. Finally, the implementation of an experimental platform with integrated fluorescence detection, fluidics and temperature control must be established for continuous monitoring of fluorescence from the clones of templates either immobilized on a surface or microbeads in an array format [43] Such a system is being developed in our laboratory and will be reported in another manuscript.

Due to the limited resolution between the melting temperatures of longer DNA fragments, according to our simulations the practical read length of SBD is only around 20-30 bases. However, this read length can be extended to 40-50 bases by using a primer which can be cleaved off at the 3′ end of the first sequencing primer by, for example, using photochemically cleavable linkers [44, 45]. Even though the maximum read length is limited in SBD, with a potential read length of 40-50 bases, it can be used for genome re-sequencing and other applications where a short read is sufficient to identify the sequence unambiguously. If experimentally demonstrated, SBD could be competitive with the currently available sequencing platforms which can routinely provide extremely high-throughput short sequence data [8-11, 14]. SBD has many advantages as a sequencing method: (1) Ultra-high throughput. Millions of reactions can be performed in massive parallel on a single solid surface since electrophoresis is not required; (2) Simplicity. Denaturation can be carried out by a process as simple as heating; (3) Extremely low cost. Very little reagent is required for the sequencing reaction. As little as a few hundred microliters of the standard dideoxy sequencing reagents are needed for sequencing a human genome. Due to these advantages, multiple sequencing runs could be performed on the same templates in a flow cell, perhaps with a set of primers of different lengths, to significantly improve sequencing accuracy. With these capabilities, SBD technology has potential applications in genome re-sequencing, high-throughput SNP genotyping, and digital analysis of gene expression.