Effects of Sustained Interstitial Fluid Pressurization Under Migrating Contact Area, and Boundary Lubrication by Synovial Fluid, on Cartilage Friction

Abstract

Objective

This experimental study tests two hypotheses which address outstanding questions in cartilage lubrication: Can the friction coefficient remain low under sustained physiological loading conditions? How effective is synovial fluid in the lubrication of articular cartilage? Based on theory, it is hypothesized that migrating contact areas can maintain elevated cartilage interstitial fluid pressurization, thus a low friction coefficient, indefinitely. It is also hypothesized that the beneficial effects of synovial fluid stem from boundary lubrication rather than fluid-film lubrication.

Design

Five experiments were conducted on immature bovine femoro-tibial joints, to compare the frictional response under migrating versus stationary contact areas; the frictional response in synovial fluid versus saline; the role of sliding velocity and the role of congruence on the friction coefficient.

Results

Migrating contact areas could maintain a low friction coefficient under sustained physiological conditions of loading for at least one hour. Synovial fluid reduced the friction coefficient by a factor of ~1.5 relative to saline. However, interstitial fluid pressurization was far more effective, reducing the friction coefficient by a factor of ~60 relative to equilibrium (zero-pressure) conditions. It was confirmed that synovial fluid acts as a boundary lubricant.

Conclusions

These results emphasize the importance of interstitial fluid pressurization on the frictional response of cartilage. They imply that the mechanical integrity of cartilage must be maintained to produce low friction in articular joints. The more limited effectiveness of synovial fluid implies that intra-articular injections of lubricants in degenerated joints may have only limited effectiveness on their tribological properties.

2. Introduction

The main function of articular cartilage is to serve as a bearing material for diarthrodial joints, sustaining relatively large loads while providing low friction and wear. In recent years the mechanism of articular cartilage lubrication has been shown to depend significantly on the pressurization of the cartilage interstitial water ¹, which supports most of the joint contact load and helps to shift it away from the collagen-proteoglycan matrix, thereby producing a low friction coefficient ^1–4. This mechanism has been variously called ‘self-pressurized hydrostatic lubrication’ ² or ‘biphasic lubrication’ ³. A complementary mechanism considered in the literature has been the boundary lubrication of the articular surfaces by specialized molecules found in synovial fluid (SF) ⁵, such as lubricin ^6–9, hyaluronic acid ^10–13, surface-active phospholipids (SAPL) ^{14, 15}, or a combination thereof ^16–18. It has been proposed that molecules present in the superficial zone of articular cartilage may also contribute to boundary lubrication, such as superficial zone protein (SZP) ^19–22 which is homologous to lubricin ^{23, 24}, and the chondroitin sulfate of proteoglycans ^25–27.

From studies of cartilage mechanics ²⁸, it is known that interstitial fluid pressurization subsides over time under loading configurations of creep or stress-relaxation ^{29, 30}. Therefore, under these testing configurations, the friction coefficient of articular cartilage has been shown to increase progressively with time ^{1–3, 25, 26, 31}, reaching relatively elevated equilibrium values which may be detrimental to normal joint function. The time to reach this equilibrium value increases quadratically with the path length for fluid flow from high-pressure to low-pressure regions, thus linearly with the size of the contact area ³².

A question which remains unanswered is whether the friction coefficient might similarly rise to elevated values under in situ conditions, or whether physiological loading conditions in joints might promote sustained interstitial fluid pressurization that always maintains a low friction coefficient. In a recent study ³³, we explored the hypothesis that dynamic loading might repeatedly pressurize the tissue and sustain low friction indefinitely, but found from theory and experiments that the mean response of interstitial fluid pressurization eventually subsides, and the friction coefficient concomitantly rises; thus, sustained dynamic loading could not explain how the friction coefficient might remain low under physiological loading conditions. In the current study, we explore an alternative hypothesis motivated by our earlier theoretical study of rolling and sliding contact in diarthrodial joints ³⁴. According to this theory, a loading configuration which promotes migration of the contact area maintains elevated interstitial fluid load support indefinitely, as long as the migration speed is sufficiently high. On this basis, the friction coefficient should remain low under these conditions. To test this hypothesis, we conduct frictional measurements using testing configurations of glass against cartilage, where the contact area is either migrating or stationary. We also perform more physiologically relevant experiments of cartilage against cartilage, where the contact area is migrating.

While the influence of interstitial fluid pressurization on the frictional response of articular cartilage has been established unequivocally ¹, the relative contribution of boundary lubrication by various molecular constituents of synovial fluid remains unexplored. In the current study, we also test the hypothesis that synovial fluid contains a boundary lubricant that can significantly reduce the friction coefficient of articular cartilage, but that this reduction in friction is much less significant than that resulting from interstitial fluid pressurization.

3. Material and Methods

Five sets of experiments were performed in this study, to test the main hypotheses as well as two corollary hypotheses (Table 1). Experiments E1 and E2 served to test the first hypothesis by comparing the frictional response in migrating versus stationary contact areas. Experiment E3 served to test the second hypothesis regarding the role of synovial fluid, by comparing its effects to physiological buffered saline. E4 was used to test a corollary to the first hypothesis, that sub-physiological sliding velocities in a migrating contact area configuration defeat interstitial fluid pressurization and increase the friction coefficient. E5 was used to test another corollary, that decreasing congruence (smaller contact regions) compromises interstitial fluid pressurization by providing a shorter pathway for the fluid to escape from beneath the loaded region, thereby increasing the friction coefficient under a migrating contact configuration.

Table 1.

List of experiments and details of testing protocols. MCA: Migrating contact area. SCA: Stationary contact area.

Experiment	Lubricant	n	Test	Duration	Load	Translation	Velocity	Lens radius
E1	PBS	6	MCA: condyle on tibia	3600s	6.3 N	±10 mm	1 mm/s	N/A
			MCA: glass lens on tibia			±10 mm		18 mm
			SCA: condyle on glass slide			±4 mm		N/A
E2	PBS	6	MCA: condyle on tibia	3600s	6.3 N	±10 mm	1 mm/s	N/A
			MCA: glass lens on tibia			±10 mm		18 mm
			SCA: glass slide on tibial plug			±4 mm		N/A
E3	PBS	6	MCA: condyle on tibia	900s	6.3 N	±10 mm	1 mm/s	N/A
			SCA: glass slide on tibial plug*	7200s		±4 mm	1 mm/s*	N/A
	SF	6	MCA: condyle on tibia	900s		±10 mm	1 mm/s	N/A
			SCA: glass slide on tibial plug*	7200s		±4 mm	1 mm/s*	N/A
E4	PBS	6	MCA: condyle on tibia	4200s	6.3 N	±10 mm	0.005 mm/s	N/A
				420s			0.05 mm/s
				420s			0.5 mm/s
				420s			5 mm/s
E5	PBS	6	MCA: condyle on tibia	900s	6.3 N	±10 mm	1 mm/s	N/A
			MCA: glass lens on tibia					6.5 mm
			MCA: glass lens on tibia					13mm

^*Logarithmic time increments between sliding cycles

3.1. Testing Configurations

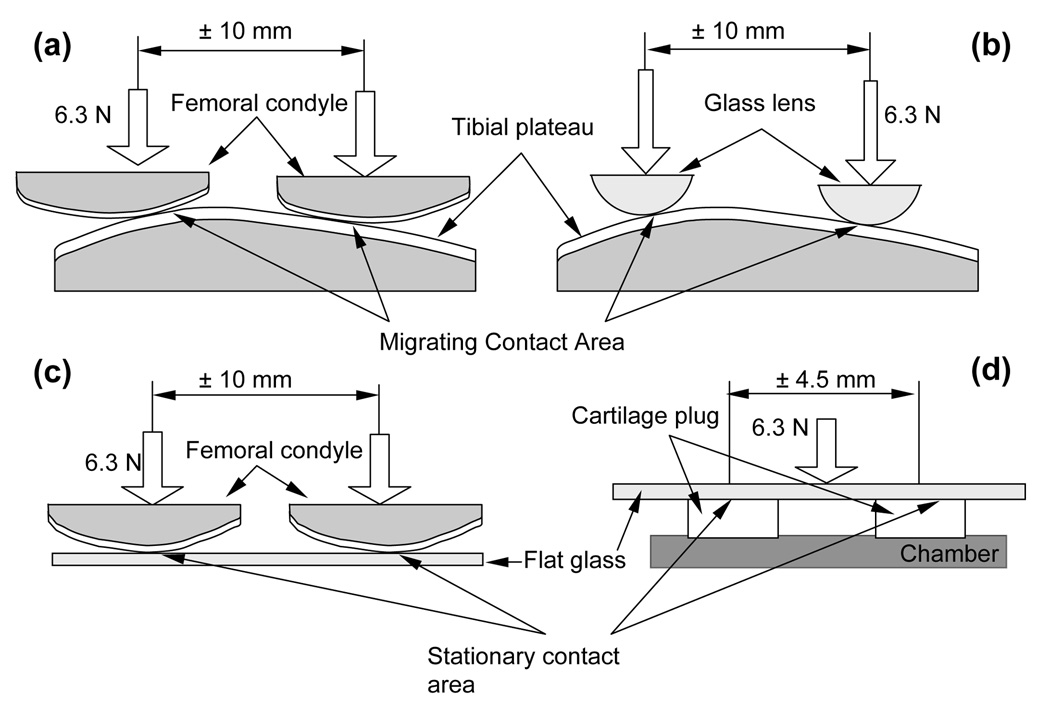
For MCA, a femoral condyle was slid against the matching tibial plateau of a meniscectomized immature bovine knee joint to produce a migrating contact area on both articular surfaces (Figure 1a). To preclude confounding interpretations from comparing cartilage-cartilage MCA results against cartilage-glass SCA results, cartilage-glass MCA tests were also performed by sliding a convex glass lens against the same tibial plateau (Figure 1b). Finally, to promote SCA, either the femoral condyle was slid against a flat glass slide (experiment E1, n=6 specimens, Figure 1c), or a cylindrical plug of cartilage was excised from the tibial plateau and slid against a flat glass slide (experiment E2, n=6, Figure 1d). These two alternatives were used to eliminate any confounding effects resulting from fluid-film lubrication, which may arguably occur in the condyle against glass and condyle against tibial plateau configurations.

Figure 1.

(a) Migrating contact area (MCA) - femoral condyle against tibial plateau; (b) MCA - convex glass against tibial plateau; (c) Stationary contact area (SCA) – femoral condyle against flat glass; (d) SCA – cartilage plug against flat glass.

To test the effect of synovial fluid (SF) versus physiological buffered saline (PBS) (experiment E3), two of the testing configurations used in experiment E2 (Figure 1a&d) were employed for samples tested with mature bovine SF, or with PBS. Separate specimens were used for the two lubricants (n=6 for each), to avoid lubricant cross-contamination.

According to our earlier theoretical study of rolling and sliding contact of articular layers ³⁴, the magnitude of interstitial fluid load support is predicted to be greatest when the rolling or sliding velocity is significantly greater than the characteristic diffusive velocity of interstitial fluid within the cartilage. This regime can be expressed as Pe ? 1, where Pe is the Peclet number representing the ratio of convective velocity (the velocity of the migrating contact area) to diffusive velocity (the velocity of interstitial fluid flow relative to the solid matrix). When Pe = 1, the interstitial fluid pressurization is negligible. In the transition regime, the interstitial fluid load support increases with increasing Pe. Consequently, a corollary to the first hypothesis is that the friction coefficient should increase as Pe decreases. This hypothesis is tested in Experiment E4 (n=6), using the condyle-on-tibia configuration of Figure 1a.

Another prediction of the theory is that interstitial fluid load support increases with increasing joint congruence, leading to the second corollary hypothesis that the friction coefficient should decrease with increasing congruence. This hypothesis is tested in Experiment 5 (n=6), using the natural condyle as well as convex lenses of various curvatures against the tibial plateau (Figure 1a&b).

3.2. Specimen Preparation

Fresh bovine calf knee joints (1–3 months old) were obtained from a local abattoir and dissected within 24 hours of sacrifice. The medial and lateral sides were separated, producing two specimen pairs. Specimens were stored in PBS containing protease inhibitors (PI) (Complete Cocktail Tablet, Roche Applied Science, Indianapolis, IN) at 4°C, refreshed daily, for no longer than 3 days before testing. For SCA tests, full thickness osteochondral plugs (4mm diam.) were harvested from the center of the tibial plateau, microtomed to remove the bony side, leaving a plug thickness of ~2mm with its articular cartilage intact.

Synovial fluid, needed in experiment E3, was aspirated from five adult bovine wrist joints, examined visually for potential blood contamination, and stored for no longer than 2 months at - 20°C.

3.3. Testing Apparatus and Protocol

The friction testing apparatus was described in detail in our previous study ³⁵. Briefly, friction measurements are performed using reciprocal translating motion via a computer-controlled translation stage. A constant normal load is applied on the specimen via load feedback control, using a voice coil actuator. The vertical and horizontal loads, F_z and F_x, are measured with a multi-axial load cell. The vertical displacement u_z of the load actuator is measured with a linear variable differential transformer (LVDT), while the horizontal displacement u_x of the translation stage is prescribed.

The duration of each test, applied load, range of motion of the translation stage, translation velocity, and lens radius (where applicable) are summarized in Table 1. As multiple tests were performed on the same specimen, a period of recovery from loading was allowed between consecutive tests, equal to the preceding testing duration.

When using PBS as the lubricant, the entire specimen was immersed in solution. When using SF, full immersion was feasible only when testing the cylindrical plug. When testing condyle on tibia, a layer of SF was initially laid on the contacting surfaces such that a meniscus of SF was clearly visible between the surfaces. Throughout the duration of the test (15 minutes), ~1 ml SF was injected in and around the contact region, at constant intervals (3 minutes), to ensure a constant presence of lubricant; this configuration is more representative of in situ conditions, since diarthrodial joints typically contain only a few ml of SF. The rest of the femoral condyle and tibial plateau were maintained moist using gauze soaked in PBS+PI, carefully placed not to interfere with the contact.

3.4. Calculation of the Friction Coefficient

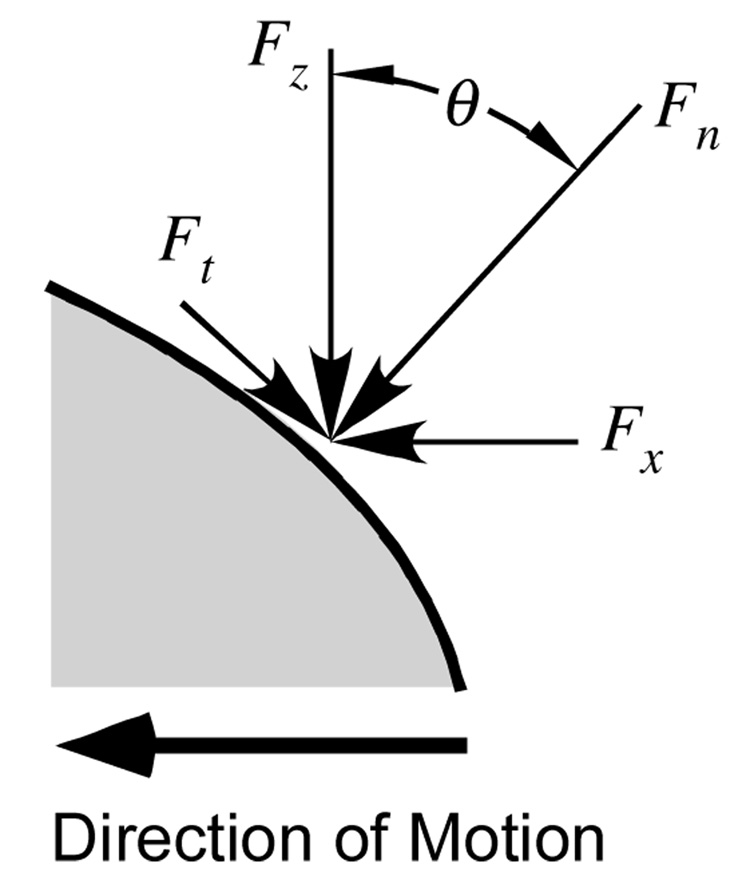
For the SCA tests the contact area was planar and perpendicular to the loading direction, so that the effective friction coefficient µ_eff could be calculated from the average of F_x/F_z over each reciprocating cycle. For MCA tests, the contact area was non-planar and its average unit normal vector deviated from the vertical throughout the reciprocating sliding motion. The vertical and horizontal forces measured by the load cell were transformed into normal ( F_n ) and tangential ( F_t ) forces using the trigonometric relations

$$\begin{array}{c}{F}_t=-F_x\text{cos}\theta +F_z\text{sin}\theta \hfill \\ F_n=F_x\text{sin}\theta +F_z\text{cos}\theta \hfill \end{array}$$ (1)

The angle θ (Figure 2) was obtained from the slope of u_z versus u_x, using suitable smoothing to minimize the noise inherent in numerical differentiation of raw data. The friction coefficient was then calculated from the average of F_t/F_n over each reciprocating cycle.

Figure 2.

Schematic detailing the components of the contact force in the load cell’s x – z frame, and in a normal-tangential frame to the contact interface.

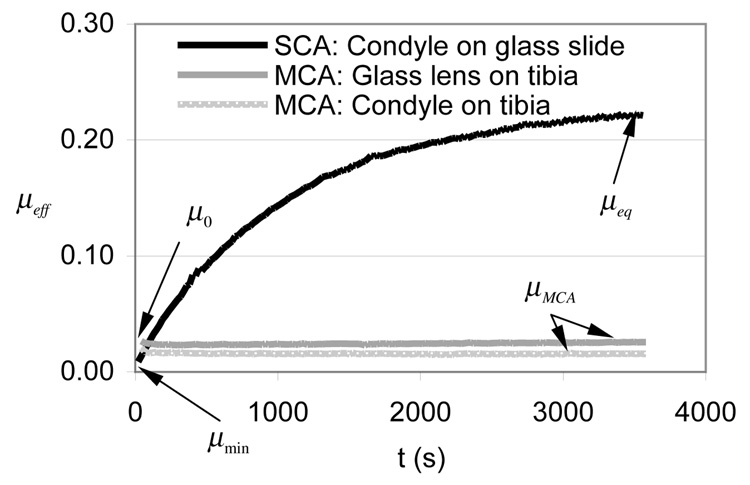
Two representative values were identified from µ_eff -versus-time curves (Figure 3) for the purpose of statistical analyses: The friction coefficient upon initial contact (called µ₀ for MCA tests and µ_min for SCA tests), and the steady-state friction coefficient (called µ_MCA for MCA tests and µ_eq for SCA tests).

Figure 3.

Time-dependent response of the effective friction coefficient, µ_eff, averaged over all specimens, in experiment E1, which compares the outcome of migrating versus stationary contact areas. All three testing configurations are shown. Standard deviations are reported in Table 2.

3.5. Statistical Analysis

Two-way analysis of variance (ANOVA) with repeated measures was used to compare values of the initial and steady-state friction coefficient (2 levels) among the testing configurations (3 levels) in experiments E1 and E2 (Table 1); repeated measures were used because the same joint specimen was involved in all measures. In experiment E3, three-way ANOVA was used to compare the initial and steady-state coefficients (2 levels, repeated measures), the testing configurations (2 levels, repeated measures) and lubricant (2 levels, non-repeated). One-way ANOVA was used to test the effect of velocity (4 levels, repeated measures) in E4 and the effect of congruence (3 levels, repeated measures) in E5. In all cases, α was set to 0.05 and statistical significance was accepted for p<0.05; post-hoc testing of the means was performed with Bonferroni correction (SAS 9.1, Cary, NC, USA).

4. Results

4.1. Experiment E1

When testing the femoral condyle against the tibial plateau (MCA configuration), the friction coefficient µ_eff was found to decrease slightly from its initial value µ₀, then remained constant for the entire duration of the test (3600 s) (Figure 3). This constant value was averaged to yield µ_MCA (Table 2). The same behavior was observed for the glass lens on the tibial plateau. In contrast, for the femoral condyle against the glass slide, µ_eff increases monotonically over time, from a minimum value µ_min to a (near-)equilibrium value µ_eq (Figure 3). µ_min was found to be significantly smaller than µ_eq in the SCA test (Table 2). When comparing MCA and SCA tests, µ_MCA was significantly smaller than µ_eq (Table 2).

Table 2.

Results for experiment E1.

µeff	Initial	Steady-state
MCA: condyle on tibia	0.024±0.012	0.016±0.011*
MCA: glass lens on tibia	0.034±0.005	0.024±0.010*
SCA: condyle on glass slide	0.014±0.005	0.214±0.039†

^*p<0.005 MCA vs SCA

^†p<0.005 initial vs steady-state.

4.2. Experiment E2

The results of E2 (Table 3) were nearly identical to those of E1, showing the same temporal behavior (Figure 3) for all three testing configurations. Though the SCA configuration in E2 measured friction between a glass slide and a cylindrical cartilage plug from the tibial plateau, the temporal response (not shown) and the values of µ_min and µ_eq were comparable to those for the femoral condyle against a glass slide (Table 2 versus Table 3).

Table 3.

Results for experiment E2.

µeff	Initial	Steady-state
MCA: condyle on tibia	0.018±0.003	0.015±0.003*
MCA: glass lens on tibia	0.028±0.004	0.030±0.003*
SCA: glass slide on plug	0.010±0.008	0.189±0.051†

^*p<0.005 MCA vs SCA

^†p<0.005 initial vs steady-state.

4.3. Experiment E3

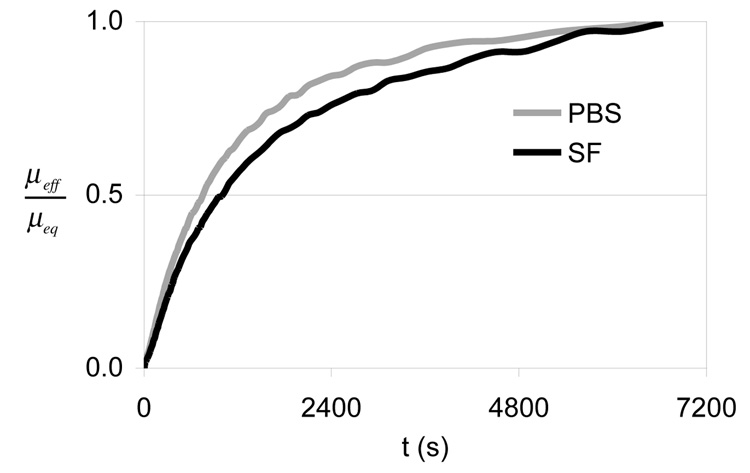
Based on the MCA results of E1 and E2, which showed a constant value of µ_eff after approximately one minute of loading (Figure 3), it was determined that the MCA tests of E3 could be conducted over a shorter duration (900 s) without compromising their value. When comparing lubricants, no statistical difference was observed in the MCA tests (p=0.085, Table 4). The SCA tests showed virtually the same temporal response for PBS and SF, as shown in the plot of µ_eff/µ_eq (Figure 4), though both µ_min and µ_eq were significantly smaller in SF than PBS (Table 5).

Table 4.

MCA results for Experiment E3.

Migrating contact area (MCA)	µ0	µMCA
PBS	0.038±0.017	0.022±0.010
SF	0.032±0.008	0.015±0.004
(µeff)PBS/(µeff)SF	1.2	1.5

p=0.085 SF vs PBS; p=0.58 µ₀ vs µ_MCA.

Figure 4.

Time-dependent response of the effective friction coefficient, normalized by its equilibrium value, µ_eff/µ_eq, in PBS versus SF, averaged over all specimens in experiment E3 which examines boundary lubrication by SF.

Table 5.

SCA results for experiment E3.

Stationary contact area (SCA)	µmin	µeq	$\frac{\mu {}_{\mathit{\text{eq}}}}{{\mu }_{\text{min}}}$
PBS	0.0027±0.0011	0.155±0.016 †	57
SF	0.0015±0.0003 *	0.088±0.008 * †	59
(µeff)PBS/(µeff)SF	1.5	1.8

^*p<0.05 SF vs PBS

^†p<0.005 µ_min vs µ_eq.

The effectiveness of lubrication by SF versus PBS was assessed from the ratios (µ_eff)_PBS/(µ_eff)_SF in the initial and steady-state conditions (Table 4 and Table 5). The effectiveness of lubrication by interstitial fluid pressurization was assessed from µ_eq/µ_min (Table 5), since it has been established experimentally that µ_min is achieved when the interstitial fluid load support is greatest, and µ_eq when the pressure has reduced to zero ¹.

The average creep deformation of the cartilage at steady-state was much smaller under the migrating contact area configuration (0.097±0.034 mm in SF , 0.083±0.036 mm in PBS) than the stationary contact area configuration (1.16±0.05 mm in SF, 1.25±0.20 mm in PBS). Note that the values for MCA represent the deformation of two juxtaposed articular layers, whereas those for SCA represent the deformation of a single cartilage plug, further emphasizing the disparity in creep deformation between the two testing configurations.

4.4. Experiment E4

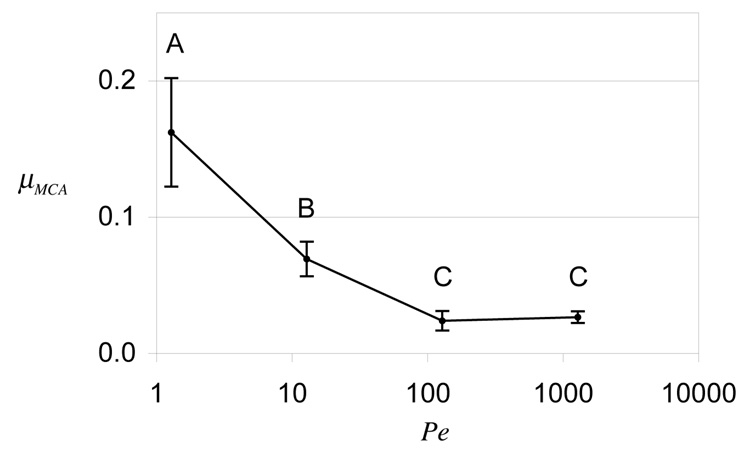
The duration of MCA tests in this experiment was suitably increased for the slower translation velocities (Table 1), in order to complete at least one full reciprocating cycle at the lowest velocity (5 µm/s). A plot of µ_MCA versus Pe is provided in Figure 5, along with statistical differences. The Peclet number was calculated from Pe = Vh/ H_+Ak ^{34, 36}, where h is the cartilage thickness (estimated at ~2 mm), H_+A is the tensile equilibrium aggregate modulus (estimated at ~13 MPa) ³⁶ and k is the hydraulic permeability (estimated at ~6×10⁻¹⁶ m⁴/N·s) ³⁶. µ_MCA was found to be lowest at the two highest values of Pe, and increased significantly with decreasing Pe (p<0.0001).

Figure 5.

Steady-state friction coefficient under migrating contact area, µ_MCA, as a function of the Peclet number, in Experiment E4 which examines the effect of sliding velocity. Significant differences are represented by distinct letters (p<0.0001).

4.5. Experiment E5

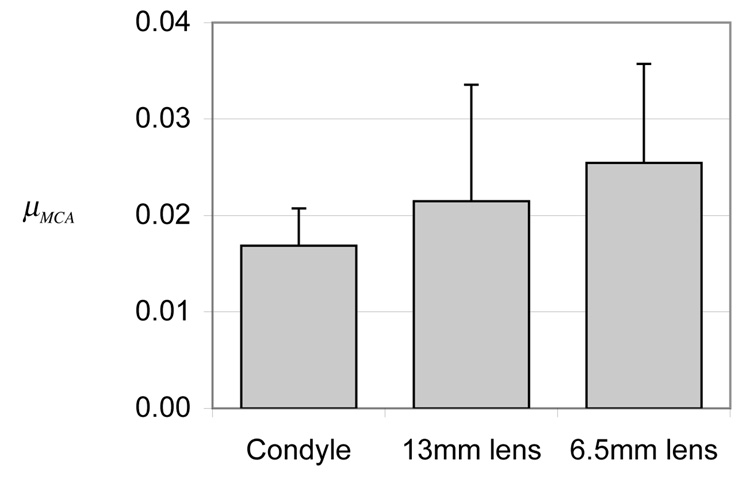
No statistical difference was observed in µ_MCA between the natural condyle and glass lenses of varying radii of curvature (p=0.24), though a trend of increasing friction with decreasing congruence was observed in the mean response (Figure 6).

Figure 6.

Steady-state friction coefficient under migrating contact area, µ_MCA, for condyle (~18 mm radius of curvature) against tibia, or glass lenses (13 and 6.5 mm radii of curvature) against tibia, in Experiment E5 which examines the effect of congruence. No significant differences were observed among the three cases (p=0.24).

5. Discussion

5.1. Migrating versus Stationary Contact

The first hypothesis of this study was that migrating contact areas can sustain a low friction coefficient for long durations, in contrast to earlier findings which have shown that the friction coefficient rises to elevated values over time. This hypothesis was motivated by our earlier theoretical study ³⁴ which showed that interstitial fluid pressurization remains elevated under steady-state rolling or sliding contact, and our experimental study which established that high interstitial fluid pressurization correlated with low friction ¹. Additional motivation for this hypothesis was the observation that the normal function of diarthrodial joints always promotes migrating contact areas, as demonstrated in experimental studies of articular contact during normal activities of daily living (e.g., the tibiofemoral ^{37, 38}, patellofemoral ^{39, 40}, glenohumeral ⁴¹, trapeziometacarpal ⁴², tibiotalar ^{43, 44}, and hip joints ⁴⁵).

The results of the current study strongly support this hypothesis, by showing that the friction coefficient under migrating contact areas remains low and essentially constant for at least one hour (Figure 3), with the data suggesting that this low value may be maintained nearly indefinitely. This outcome remains true whether testing cartilage against cartilage or cartilage against glass (Figure 3). The theoretical basis for this result is that a contact area which migrates at speeds significantly faster than the diffusive velocity of the interstitial fluid allows little time for the fluid in the loaded region to escape, and for the interstitial fluid pressure to subside. Therefore the interstitial fluid pressurization remains high at all times under the migrating contact area. This interpretation is supported by the observation that the steady-state creep deformation under MCA is much smaller than under SCA, implying that the interstitial fluid pressurization imparts a higher effective compressive modulus in the former configuration.

Further support for this mechanism comes from experiment E4 (Figure 6), which shows that the friction coefficient increases with lower values of the Peclet number, in excellent agreement with the theoretical prediction that the interstitial fluid load support decreases under these same conditions (see Figure 5 in our earlier theoretical study ³⁴).

In contrast, as reported in earlier studies, a stationary contact area produces a monotonic increase in the friction coefficient, with µ_eff reaching the relatively elevated value of ~0.2 (Table 2 & Table 3). This increase occurs because the same region of cartilage is constantly being loaded, allowing ample time for the pressurized interstitial fluid to escape (either to the external bath, in the case of the plug, or also to the surrounding unloaded tissue in the case of the condyle).

A novel outcome of the current study is that the SCA result remains true regardless of the contact geometry; whether testing an ovoid-shaped condyle or a flat cylindrical cartilage plug against a flat glass slide, the result is essentially unchanged. The fact that both produce the same frictional response suggests that fluid-film lubrication, which is normally promoted by a wedge-shaped contact geometry⁴⁶, is insignificant in these tests.

Though not statistically significant, the trend of increasing friction coefficient with decreasing congruence observed in experiment E5 (Figure 6) is also consistent with theoretical predictions; larger radii of curvature produce larger contact areas (relative to the cartilage thickness), which result in a longer path for the pressurized interstitial fluid to escape from the loaded region ³⁴. This weak trend between µ_MCA and congruence may also explain the (non-significant) trend of higher friction for glass lens-on-tibia versus condyle-on-tibia configurations in experiments E1 and E2, considering the smaller size of the lens used in these experiments (Table 1).

The hypothesis on the role of migrating contact areas tested here was first proposed in our earlier study of the frictional response of articular cartilage using atomic force microscopy (AFM) ⁴⁷. In that study it was found that the friction coefficient measured from AFM, using a spherical probe 5 µm in diameter under a MCA testing configuration, was comparable to µ_eq measured macroscopically on a cartilage plug under an SCA configuration. It was proposed from theory that the tiny contact area achieved with AFM resulted in a very small Peclet number, Pe = 1, thus producing negligible interstitial fluid pressurization. The current study confirms this hypothesis directly, as shown from experiment E4 (Figure 5). This same hypothesis was also investigated computationally by Pawaskar et al. in a recent study ⁴⁸, in support of earlier experimental findings from the same group ¹³.

5.2. The Role of Synovial Fluid

The second hypothesis of this study was that synovial fluid contains a boundary lubricant that can significantly reduce the friction coefficient of articular cartilage, but that this reduction in friction is much less significant than that resulting from interstitial fluid pressurization. When interstitial fluid pressurization subsides, all of the contact load across the joint is supported by the collagen-proteoglycan solid matrix, and the boundary lubricant serves to reduce the resulting solid matrix frictional interactions. The results of experiment E3 strongly support this hypothesis, as may be deduced from a number of observations. The most direct evidence for an effective boundary lubricant in SF is the reduction in the equilibrium friction coefficient relative to PBS (Table 5). Since µ_eq represents the friction coefficient in the absence of interstitial fluid pressurization, this reduction can only be attributed to the different lubricants. The second observation is that SF does not affect the temporal response of µ_eff relative to PBS in any fundamental way (Figure 4), which further reinforces our understanding that SF does not alter the nature of lubrication in cartilage. The fact that µ_eff/µ_eq is very similar in both lubricants (despite the fact that different specimens were used for each) is consistent with our validated friction model ¹, which predicates that the temporal response results from the time-varying interstitial fluid load support. Indeed, the effectiveness of SF relative to PBS remains approximately the same ( µ_eff in SF is 1.2 to 1.8 times smaller than in PBS, Table 4 and Table 5), whether examining results from the MCA or SCA tests.

No attempt was made in this study to identify the boundary lubricant in SF, though many candidates have been proposed in the prior literature, including lubricin ⁴⁹, surface-active phospholipids ⁵⁰, and hyaluronan ⁵¹; a recent study ¹⁸ suggests that the dominant contributors to SF boundary lubrication are superficial zone protein (which is homologous to lubricin ^{23, 24}) and hyaluronan. In a recent study ³⁵, it was shown that removal of the superficial zone of immature bovine articular cartilage, where SZP is localized, did not increase the friction coefficient of cartilage against glass, when all testing was performed in PBS. When combined with the results of the current study and more recent literature findings ¹⁸, it appears that the lubricin (and possibly other molecules) in synovial fluid contributes much more significantly to boundary lubrication than the SZP present in the superficial zone of immature cartilage.

It is also evident from the results of E3 that interstitial fluid pressurization is far more effective at reducing the friction coefficient of articular cartilage than the boundary lubricant found in SF. This observation is deduced from the fact that µ_min is nearly 60 times smaller than µ_eq, whether in PBS or SF (Table 5); this reduction is entirely due to interstitial fluid pressurization ¹.

This result has very significant ramifications in relation to our understanding of cartilage lubrication, as well as treatment modalities for osteoarthritic joints. The most obvious consequence of this observation is that the integrity of the cartilage layer is critical to its normal function as a bearing material. Any degradative mechanism which compromises cartilage interstitial fluid pressurization, such as enzymatic degradation ⁵² or matrix fibrillation, may significantly compromise its frictional properties ^{25, 26}. Once the cartilage has degraded, intra-articular injections of putative lubricants, such as hyaluronan, cannot practically compensate for the loss of interstitial fluid load support. Consequently, treatment modalities for degenerative joint disease should attempt to repair the articular cartilage using, for example, tissue engineering approaches which attempt to recover the mechanical properties of the native tissue.

Several earlier studies have shown that SF lubricates better than saline ^{3, 31, 53, 54}, though the effectiveness of SF reported in these studies has been somewhat variable. When testing cartilage against cartilage, Forster and Fisher ³ find an effectiveness of ~1.2 for their start-up coefficient after minutes of loading (similar to µ_eq ), consistent with the current study. Schmidt et al. ⁵⁴ find a higher effectiveness of ~5 in their measurement of the kinetic coefficient (comparable to µ_MCA ); this difference with the results of the current study can be attributed primarily to the higher value of their friction coefficient measured in PBS (~0.08 in their study versus ~0.02 here). This relatively minor discrepancy could be attributed to the difference in testing configuration or source of materials between the studies; it does not detract from the main conclusion that boundary lubrication by SF is far less effective than the effect of interstitial fluid pressurization.

5.3. Rolling Resistance

An interesting outcome of the experiments of this study is that the minimum friction coefficient achieved in SCA testing configurations, µ_min, can be significantly smaller than that achieved in MCA configurations, µ_MCA (see Figure 3, and for example µ_min in Table 5 versus µ_MCA in Table 4, p<0.0001). There is no theoretical basis to suggest that the peak interstitial fluid pressurization in these two configurations should differ substantially ^{34, 36}. Therefore the most likely mechanism appears to be the ‘rolling resistance’ ^55–57 arising from the flow-independent viscoelastic energy dissipation of the deforming cartilage layers ^58–62.

An interesting consequence of this observation is that the friction coefficient in situ may not be as low as intimated by the values of µ_min obtained here (as low as 0.0015 in SF). The more representative value is likely given by µ_MCA, ~0.015 in SF, a respectably low value for the friction coefficient, though ten times higher than µ_min.

6. Conclusion

From our perspective, this study settles two important outstanding questions in cartilage lubrication. First, it shows that a low friction coefficient can be sustained nearly indefinitely under normal physiological loading conditions where the contact area migrates along the articular surfaces. This finding assuages any concerns that might have arisen from examining testing configurations where a stationary contact area produces elevated friction under equilibrium conditions. It is now possible to ascertain that interstitial fluid pressurization is responsible for reducing the friction coefficient of articular cartilage under physiological conditions. Second, this study shows that the effectiveness of synovial fluid stems from a boundary lubricant, not from fluid-film lubrication. This boundary lubricant reduces the friction coefficient by a factor of ~1.5 relative to PBS. However, interstitial fluid pressurization is far more effective, reducing the friction coefficient by a factor of ~60 relative to equilibrium conditions. Therefore, the integrity of the cartilage layer must be maintained in order to produce low friction in articular joints, and intra-articular injections of lubricants may have only limited effectiveness on tribological properties.