Simultaneous bimanual dynamics are learned without interference

Abstract

Dynamic learning in humans has been extensively studied using externally applied force fields to perturb movements of the arm. These studies have focused on unimanual learning in which a force field is applied to only one arm. Here we examine dynamic learning during bimanual movements. Specifically we examine learning of a force field in one arm when the other arm makes movements in a null field or in a force field. For both the dominant and non-dominant arms, the learning (change in performance over the exposure period) was the same regardless of whether the other arm moved in a force field, equivalent either in intrinsic or extrinsic coordinates, or moved in a null field. Moreover there were no significant differences in learning in these bimanual tasks compared to unimanual learning, when one arm experienced a force field and the other arm was at rest. Although the learning was the same, there was an overall increase in error for the non-dominant arm for all bimanual conditions compared to the unimanual condition. This increase in error was the result of bimanual movement alone and was present even in the initial training phase before any forces were introduced. We conclude that, during bimanual movements, the application of a force field to one arm neither interferes with nor facilitates simultaneous learning of a force field applied to the other arm.

Introduction

Many studies have examined our ability to learn novel dynamics. When a novel state-dependent force field is applied to the arm during reaching movements, initial perturbations are large and then decrease over time (Shadmehr and Mussa-Ivaldi 1994; Brashers-Krug et al. 1996; Gandolfo et al. 1996; Conditt et al. 1997; Flanagan et al. 1999). Several studies have examined force fields which depend on the velocity of the hand and have demonstrated two key features of dynamic learning. First, an examination of generalization to novel areas of the workspace has shown that the CNS represents such a force field in intrinsic coordinates, for example a mapping from joint angular velocities to expected joint torques, rather than in extrinsic coordinates, such as a mapping from hand velocity to expected Cartesian forces (Shadmehr and Mussa-Ivaldi 1994; Shadmehr and Moussavi 2000). Second, when an opposing force field is subsequently applied to the same arm there is an initial decrease in performance compared to learning the opposing force field in isolation. Such interference is termed anterograde interference (Tong et al. 2002; Caithness et al. 2004; Miall et al. 2004).

Recently there has been interest in how dynamic learning transfers between the arms, and if transfer is seen whether it is in an intrinsic or extrinsic coordinate system. For a velocity dependent force field, Criscimagna-Hemminger et al. (2003) observed transfer of learning, but only from the dominant to non-dominant arm. Similarly in a study of adaptation to an inertial load, transfer was only seen from the dominant to non-dominant arm (Wang and Sainburg 2004). Neither study showed transfer from the non-dominant to dominant arm. While these studies agreed on the direction of transfer, there were differences in terms of the coordinate system which best accounted for the transfer. For the velocity-dependent force field the transfer was in an extrinsic coordinate system, whereas for the inertial load the transfer was in intrinsic coordinates. Recently it has been suggested that the transfer seen is cognitive in origin and it can be prevented by introducing the force field gradually (Malfait and Ostry 2004).

Whereas these previous studies examined unimanual learning in one arm followed by the other, a recent study by Nozaki et al. (Malfait and Ostry 2004) examined force-field learning by a single arm during bimanual movements. The results suggest that bimanual and unimanual movement tasks recruit partially separable neural resources. Learning of a force field on one arm while the other was at rest was shown to transfer only partly to a condition in which both arms moved. Transfer in this case was inferred based on a reduction in magnitude of catch-trial errors in a movement context that differed from the one in which the force field was learned. A further finding of the study was that it was possible to maintain learning of two conflicting force fields, if one was learned during bimanual movement and the other during unimanual movement. However, this study did not examine simultaneous learning of two force fields to test whether the bimanual neuronal population would interfere with or facilitate each other.

Here we examine simultaneous bimanual learning of two velocity-dependent force fields to investigate whether interference or facilitation occurs. In different groups of subjects, we examined bimanual learning when the two fields were identical in Cartesian space (extrinsic) or when the two fields were mirror symmetric and therefore the same in joint space (intrinsic). Learning in these conditions was compared to control groups who learned a single force field (applied to the dominant or non-dominant arm) while the other arm was either at rest or made similar movements in the absence of a force field (null field).

Materials and Methods

Subjects

After providing written informed consent, 36 right-handed subjects participated in the experiment (21 females and 15 males). The protocol was approved by the local ethics committee. All subjects completed an Edinburgh Handedness questionnaire.

Apparatus

Subjects were seated and held the handles of dual robotic manipulanda (see Figure 1). They made centreout-and-back movements to virtual targets located in a horizontal plane. The robotic manipulanda (vBOTs) are custom-built devices with two degrees of planar freedom consisting of a parallelogram constructed mainly from carbon fiber tubes (Kording et al. 2004). They are driven by rare earth motors via low-friction timing belts with high-resolution incremental encoders to permit accurate computation of the robot's position. Care was taken with the design to ensure it was capable of exerting large end-point forces while still exhibiting high stiffness, low friction, and low inertia. The motors were run from a pair of switching torque control amplifiers that were interfaced, along with the encoders, to a multifunctional I/O card on a PC using some simple logic to implement safety features. Software control of the robot was achieved by means of a control loop running at 500 Hz, in which position and velocity were measured and desired output force was set. Position was accurate to within 1mm. A virtual reality system was used that prevented subjects seeing their arm, and allowed us to present visual images in the plane of the movement (for full details of the setup, see Goodbody and Wolpert 1998). The positions of the left and right arms were displayed as red and green circles of diameter 1 cm respectively.

Figure 1.

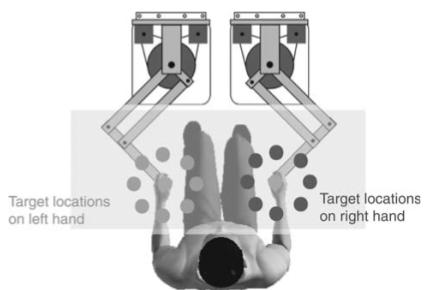
Top view of experimental setup. The dots surrounding the central home positions represent potential target locations that the subject must reach to before returning to the home position.

Procedure

The experiment was divided into 3 consecutive phases. In the first phase, the ‘pre-exposure period’, subjects performed the task with the motors of the vBOT inactive (null field). In the second phase, the ‘exposure period’, a force field was applied to one or both arms. In the third phase, the ‘post-exposure period’ subjects again made movements in a null field.

Each experiment involved either bimanual or unimanual out-and-back reaching movements (we describe here a typical bimanual trial – unimanual trials had only one arm moving). To initiate a trial, subjects positioned each arm within a 3 cm diameter circular disk – the ‘home’ position. The home position for each arm was approximately 30 cm below the head and 30 cm in front of the body. The two home positions were 30 cm apart, 15 cm either side of the mid-sagittal line. A tone sounded the start of the trial and two targets (2 cm diameter circular disks, red for the left arm and green for the right arm) appeared 10 cm from the home position. The locations of the target for each arm were independently selected from one of eight possible equally spaced target locations. Subjects were encouraged to move each arm to their respective target and back to the home position within 600 ms, as signalled by a second tone (timed from leaving the home position to returning to it). Subjects were alerted by text on the screen if they completed the movement in more than 600 ms but were not otherwise penalised and often did not complete the movement in time. To ensure simultaneous movements in the bimanual conditions a trial was repeated if subjects did not initiate movements of both arms within 100ms of each other. A new trial started 0.5 seconds after both arms had returned to the home positions. Subjects were encouraged by the experimenter to be accurate, but were only penalised when both arms moved to the wrong targets (based on the distance of the left arm to right target being smaller than the distance of the left arm to the left target or vice-versa), whereupon the trial was repeated.

Each phase of the experiment was further sub-divided into cycles which consisted of eight trials, where each of eight targets was presented once for each arm in a pseudo-random order, which differed for each subject. The order of targets for each arm was also independent so that on most trials the arms did not reach for targets in the same direction in Cartesian or joint space. A rest period of at least 30 seconds occurred every 10 cycles.

Six subjects participated in each of six conditions. Subjects carried out 35 and 15 cycles in the null field, during the first and third phases of the experiment respectively. In the second phase (50 cycles) each group experienced a different combination of force fields on the arms (Table 1). Either each arm did not move, moved in a null field or moved within a force field. The force field, with components F_x and F_y, could be one of two velocity dependent curl fields:

$$\left[\begin{array}{c}\hfill F_x\hfill \\ \hfill F_y\hfill \end{array}\right]=13\left[\begin{array}{cc}\cos \left(\theta \right)\hfill & -\sin \left(\theta \right)\hfill \\ \sin \left(\theta \right)\hfill & \cos \left(\theta \right)\hfill \end{array}\right]\times \left[\begin{array}{c}\hfill V_x\hfill \\ \hfill V_y\hfill \end{array}\right]\text{Newtons}$$

where V_x and V_y are the x and y component of the arm velocity in m/s and θ was either +90° for a counterclockwise field (CCW) or −90° for a clockwise (CW) field, as defined by the force experienced during the outward movement towards the target. For every cycle, one of the trials would be randomly selected as a catch-trial, in which the force field was switched off prior to movement onset. Catch-trials were used to measure learning independent of co-contraction.

Table 1.

Subject groups 1-6 described according to the condition they experienced and the type of field experienced by each arm.

Group	Condition	Field Experienced
		Left Arm	Right Arm
1	Unimanual: Right	No movement	CW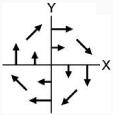
2	Unimanual: Left	CW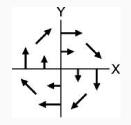	No movement
3	Bimanual: Extrinsic	CW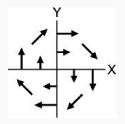	CW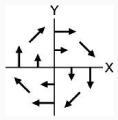
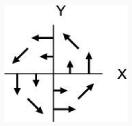
4	Bimanual: Intrinsic	CCW	CW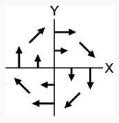
5	Bimanual: Right	Movement in Null Field	CW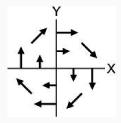
6	Bimanual: Left	CW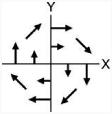	Movement in Null Field

The direction of the fields were balanced so that half the subjects in each group experienced the opposite fields to those shown.

Two groups made unimanual movements with either the right (Group 1) or left (Group 2) arm, with their other arm resting on their lap. Two groups made bimanual movements with forces on both arms. The force fields were either the same in extrinsic space (Group 3) or the same in intrinsic space (Group 4). The last two groups experienced forces only on one arm but still made bimanual movements, with their other arm moving in a null field. Group 5 experienced a force field on their right arm and a null field on the left arm. Conversely, group 6 experienced a force field on their left arm and a null field on the right arm. For each group the directions of the fields were balanced so that half the subjects in each group experienced the opposite fields to those shown in Table 1.

Analysis of task performance

Task performance was measured by how well subjects managed to compensate for the velocity dependent force field. For each trial, the peak perpendicular distance (PD) was defined as the error measure. It is the maximum perpendicular deviation from a straight line PD was averaged over the 7 field trials of a cycle (excluding the catch-trial) to give the cycle PD. For trials performed in a null field, the cycle PD was calculated using all 8 trials in each cycle. For each cycle, the mean PD over all subjects in the group summarises the performance for that group. These results are plotted as graphs, showing 5 cycles before the onset of the force field and 5 cycles after its removal (see figures 3 to 5).

Figure 3.

Performance during bimanual tasks with three different field types (extrinsic – green, intrinsic – red and null – yellow). A) shows PD for the right arm, B) shows PD for the left arm. PD was averaged over 7 trials per cycle and 6 subjects in the group, and is shown from 5 cycles before the onset of the field to 5 cycles after. The shaded areas show ±1 s.e. of the mean.

Figure 5.

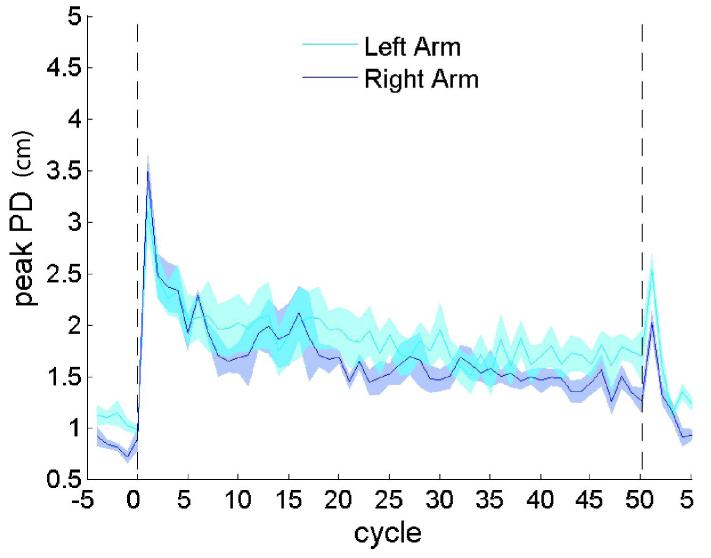
Performance of the left arm (cyan) compared to the right arm (blue) during a unimanual task. The shaded areas show 1 s.e. of the mean.

Catch-trials in the first three field cycles were averaged to give ‘early catch-trial’ PD, whilst the mean of the last three catch-trials in the field gave the ‘late catch-trial’ PD. The catch-trial PD were compared to each other to examine whether learning was achieved by compensating for the field (significant deviations on catch-trials, which increase over time) or by co-contraction (no significant deviations on catch-trials).

Two-way ANOVAs were computed with factors epoch and either group or arm (when comparing unimanual conditions). The levels of epoch were early and late, with early epoch defined as the mean of each subject's 2^nd and 3^rd cycle PD. The late epoch was defined as the mean of each subject's 49^th and 50^th cycle PD. When there was an improvement in the PD between early and late epochs, a main effect of epoch was taken as evidence of learning. A main effect of group indicates a difference in overall performance between groups, while a difference in learning between groups results in a significant interaction between group and epoch.

Results

All subjects completed the Edinburgh handedness inventory and the range of their laterality quotient was 33.3 to 100, where on a scale of -100 to 100, -100 is completely left-handed and +100 is completed right-handed (calculated using the same method as Oldfield 1971). Multiple t-tests between groups showed no significant difference in the laterality quotient (p's > 0.5).

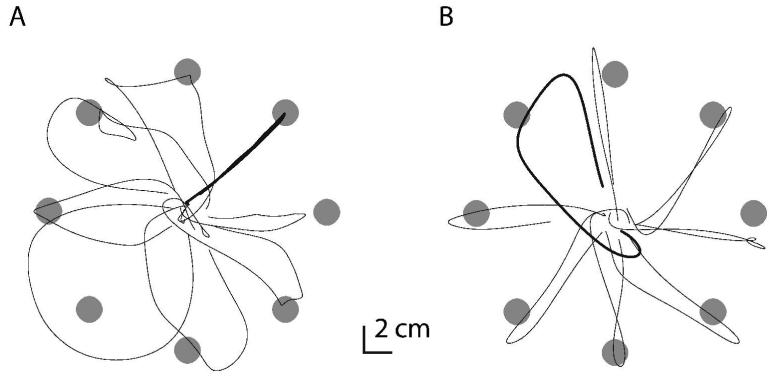
Subjects were not penalised for missing the target but nevertheless accurately reached the target with both arms in all directions (see Figure 2 for example hand-paths). For each subject accuracy was calculated as the mean minimum distance to the centre of the target across the last five trials in the pre-exposure period. Accuracy across subjects performing unimanual movements with the left arm was 0.38 ± 0.15 cm (mean ± standard deviation) and 0.34 ± 0.10 cm with the right arm. For bimanual movements, accuracy was relatively worse but was still within the 1 cm radius of the target at 0.78 ± 0.15 cm for the left arm and 0.60 ± 0.19 cm for the right. Subjects may have sacrificed speed for accuracy since the average duration of the movement was 0.69 ± 0.15 s for bimanual movements compared with 0.55 ± 0.02 s for unimanual movements of the left arm and 0.52 ± 0.01 s for the right.

Figure 2.

A) Hand-paths of a typical subject on first exposure to a CCW force-field B) Hand-paths of the same subject in the final cycle of the exposure period. Hand-path is shown in grey with 8 radial target positions shown at their correct size (radius 1 cm) and position in dark grey. Catch-trial paths are shown in black. It can be seen that peak perpendicular distance (PD) decreases from early to late cycles, whilst PD increases for late catch-trials, indicating that learning and not co-contraction took place.

Error during the pre-exposure period as measured by PD was very low, suggesting that the additional load of the robot was negligible. For the first pre-exposure cycle, the PD was 1.8 ± 0.5 cm for the left arm and 1.5 ± 0.1 cm for the right arm.

Performance in all force fields, as measured by PD, improved over the exposure period (see Figures 3-5). To test whether the groups learned to compensate for the force fields rather than simply co-contract we examined the catch-trials during force field learning. On these trials the force field is unexpectedly absent, so if a subject has learned to generate opposing forces to compensate for the force field, these will result in movement errors. We performed two two-way ANOVAs of catch-trial PD, separately for the right and left arms, with factors epoch (early vs. late) and group. Both ANOVAs showed a significant effect of epoch (right arm: F_(1,40) = 22.89, p < 0.001; left arm: F_(1,40) = 23.71, p < 0.001) and no significant effect of group (right arm: F_(3,40) = 0.8, p = 0.50; left arm: F_(3,40) = 0.43, p = 0.73) or interaction (right arm: F_(3,40) = 0.63, p = 0.60; left arm: F_(3,40) = 1.84, p = 0.16). On average, the PD of late catch-trials were greater than early catch-trials suggesting that the decreasing cycle PD during the course of the field trials was due to subjects learning to adapt to the force, rather than only increasing co-contraction to oppose the force.

Learning is independent of force field type

We focussed on two measures over the exposure periods: Performance which was the average PD of both the early (2^nd and 3^rd cycle) and late epochs (49^th and 50^th cycle), and learning which was the change in PD from early to late epochs. Figure 3 shows the PD for the right and left arms in all the bimanual tasks. On the introduction of a force field, PD increased sharply followed by an improvement over the course of the 50 field cycles. A two-way ANOVA was computed for each arm, with levels: extrinsic field, intrinsic field and null field (bimanual task) for the factor group, and levels early and late for the factor epoch. A main effect was present for epoch in both arms (F_(1,30) = 23.66, p < 0.001 for the right arm and F_(1,30) = 31.38, p < 0.001 for the left), which suggests that subjects in all groups were able to learn to compensate for the applied force field and reduce their errors (Figure 3). No main effect of group was found for either arm (F_(2,30) = 0.11, p>0.8 for the right arm and F_(2,30) = 0.89, p>0.4 for the left) showing that performance did not differ significantly as a result of the field applied to the other arm (intrinsic, extrinsic, or null). The interaction term was not significant for either arm (F_(2,30) = 0.02, p>0.95 for the right arm and F_(2,30) = 0.17, p>0.8 for the left) indicating that the learning did not differ between groups.

Bimanual versus unimanual tasks

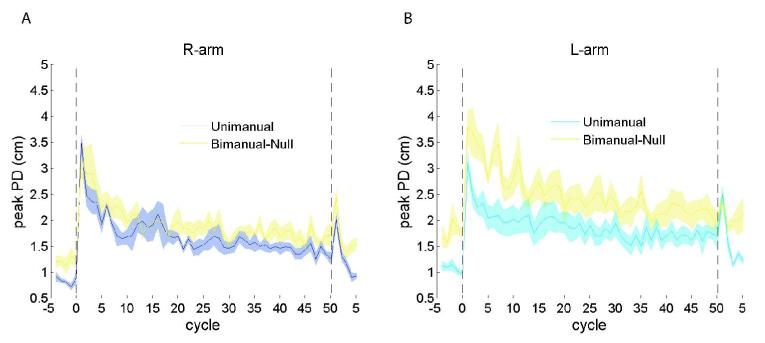
Figure 4 compares performance of the groups who experienced a force field on one arm during the bimanual movement task with groups who experienced the same field but did not make movements with the other arm. Results for the groups that experienced the force field in the dominant right arm only are shown in Figure 4A. A two-way ANOVA did not find a main effect of group for the right arm (F_(1,20) = 2.18, p = 0.16), whereas a main effect of epoch was found (F_(1,20) = 15.42, p < 0.001). The interaction was also not significant (F_(1,20) = 0.02, p = 0.89). Therefore both learning and performance in the dominant arm was unaffected by simultaneous movements of the non-dominant arm.

Figure 4.

Performance when a single force field was applied during a bimanual movement task (yellow), when the other arm moved in a null field, compared with adaptation when a single force field was applied during a unimanual movement task (right arm – blue, left arm – cyan). A) shows PD for the right arm, B) shows PD for the left arm. The shaded areas show 1 s.e. of the mean.

For the left arm, however, a similar analysis showed a main effect of group (F_(1,20) = 9.88, p = 0.005) as well as epoch (F_(1,20) = 22.16, p < 0.001). This suggests that although the left arm learned to adapt to the field in both groups, overall performance was not identical in the two conditions. This is evident in Figure 4B where the PD was greater for the group who made bimanual movements. Learning between the two groups was not significantly different (interaction term: F_(1,20) = 3.79, p = 0.07).

Comparison of learning in dominant and non-dominant arms

We examined unimanual conditions using a two-way ANOVA with factors arm and epoch. This showed only a significant main effect of epoch (F_(1,20)= 31.73, p < 0.001), confirming that there was learning over the exposure period (Figure 5). There was no main effect of arm suggesting that there was no difference in the performance between the two arms (F_(1,20) = 1.27, p = 0.27). Furthermore the interaction was not significant, which confirms that the learning did not differ between arms (F_(1,20) = 2.26, p = 0.15, respectively). Therefore, we found no evidence for differences between dominant and non-dominant arms in force field learning when the other arm was at rest.

Comparing Bimanual and Unimanual Tasks in the pre-exposure period

Figure 6 summarises the early and late epoch PDs for all groups and each arm during the exposure period. There is no clear difference between groups as a result of force-field type for both the right and left arm. Conversely, a bimanual movement task as opposed to a unimanual movement task shows an overall performance decrement in the non-dominant arm. To confirm that the performance decrement was not restricted to force field learning, we examined performance in the pre-exposure period, before the onset of the field (Figures 3 to 5, cycles -4 to 0). Here, in the absence of a force on either arm, PDs are higher in bimanual tasks compared to unimanual tasks. An unpaired t-test for each arm across all subjects in the bimanual and the unimanual conditions was performed comparing PD over cycles -4 to 0. This showed significant differences for both left and right arms (p < 0.001 for both arms). This analysis shows that the bimanual task alone results in a deficit in performance, irrespective of force field learning.

Figure 6.

Performance in the early and late epochs for the left and right arm for all groups. Early epoch performance was defined as the group average of the mean PD of the 2^nd and 3^rd cycle for each subject. Late epoch performance was defined as the group average of the mean PD of the 49^th and 50^th cycle for each subject.

Discussion

We found neither interference nor facilitation between the arms during simultaneous bimanual learning of velocity-dependent force fields. That is, learning in both dominant and non-dominant arms was the same regardless of whether the other arm was simultaneously exposed to the same or opposite force field or moved in the absence of a field. These results suggest that learning in the two arms is independent. However two previous studies of dynamic learning have observed intermanual transfer of learning. One observed transfer for a velocity-dependent force field, in the direction of the dominant to non-dominant arm and in an extrinsic coordinate frame (Criscimagna-Hemminger et al. 2003). The other observed transfer when learning to adapt to an inertial force field, again from the dominant to non-dominant arm, but in an intrinsic coordinate system (Wang and Sainburg 2004). These studies would suggest that the representation of learning in the two arms is not independent and we might have expected some competition during simultaneous force field learning. However there are two reasons why results from these unimanual studies may not be directly applicable to our results.

First, Nozaki (2006) found that during bimanual versus unimanual movement contexts, learning is represented by separate resources which only partially overlap. Therefore results from unimanual studies may not generalize to bimanual cases. In the current study the key result is that there is no change in either performance or learning when exposed to force fields applied to both arms compared to a force field applied to a single arm while the other moves in the null field. These comparisons were all made within a bimanual context and therefore examined the same representation.

Second, Malfait and Ostry (2004) argued that transfer of learning between the arms seen in the Criscimagna-Hemminger task (2003) relies on cognitive strategies. By preventing cognitive strategies, through the gradual introduction of the force field, they were able to remove transfer effects. In our bimanual task, the dual nature of the task is likely to prevent cognitive strategies being employed and thereby reveal independent learning. Furthermore a recent paper by Mazzoni and Krakauer (2006), suggests that in the case where both strategies were available, cognitive strategies would be overridden by the motor planning system, even to the detriment of performance. Another explanation as to why interference between the two arms was not observed stems from the model by Krakauer et al. (2006). Their Bayesian model of task context suggests that transfer is determined by the statistics of how a limb was previously used and would therefore not apply when learning in the limbs occurs simultaneously.

The same conflicting observations for transfer have been reported for another motor learning paradigm. Several studies have observed that learning a visuomotor transformation also transfers between arms (Cunningham and Welch 1994; Imamizu and Shimojo 1995; Sainburg and Wang 2002). Nevertheless, other studies have not observed such transfer (Kitazawa et al. 1997; Baizer et al. 1999), whilst earlier studies find that transfer may occur under certain conditions, such as whether the body and head are free to move (Hamilton 1964; Choe 1974). For motor tasks in general, Teixeira (2000) argued for greater intermanual transfer when tasks employed greater perceptual resources compared to motor resources. Although similar to the arguments put forward by Malfait and Ostry (2004), universal rules quantifying the levels of cognitive and motor skill any motor task may employ have yet to be defined.

Even though learning of a force field in one arm was not affected by the task performed by the other arm, there was an overall increase in non-dominant arm movement error when the dominant arm was performing a task. This performance decrement was independent of the presence or absence of a force field on the dominant arm. The decrement in a dual task compared to a single task is well known (see Swinnen and Wenderoth 2004 for a review). In particular, during bimanual coordination, there are strong interactions between the arms in terms of symmetry bias (Kelso 1984). Because the direction of motion of each arm was randomized and therefore the arms often had to move in different directions, symmetry bias could have led to the decrement in performance. Alternatively, it may be the result of other factors that differ between the unimanual and bimanual tasks, such as attentional deployment or trajectory planning.

In conclusion, learning of a force field applied to one arm is unaffected by whether the other arm is moving in a null field, moving in the same field or moving in the opposite field. These results suggest that force fields applied simultaneously to each arm are learned independently.