Actions and Consequences in Bimanual Interaction Are Represented in Different Coordinate Systems

Abstract

Moving one part of the body can generate interaction forces that tend to destabilize other parts of the body. However, stability is maintained by mechanisms that predict and actively oppose these interaction forces. When our body or environment changes, these anticipatory mechanisms adapt so as to continue to produce accurate predictions. In this study, we examine the acquisition of a novel predictive coordination between the arms, in a situation in which a force is produced on one hand as a consequence of the action of the other hand. Specifically, a force was applied to the left hand that depended on the velocity of the right hand. With practice, subjects learned to stabilize the perturbed left arm during right-arm movements by predicting and actively opposing the externally applied forces. After adaptation, we examined how learning generalized to a new joint configuration of the right or left arm to investigate the coordinate systems in which the internal transformation from movement to force is represented. This revealed a dissociation between the representation of the action of the right arm and the representation of its consequence, that is the force on the left arm. The movement is represented in extrinsic coordinates related to the velocity of the hand, whereas the force resulting from the movement is represented in a joint-based intrinsic coordinate system.

Introduction

Within a single limb, adaptation to novel relationships between movement and force has been investigated extensively (Shadmehr and Mussa-Ivaldi, 1994; Shadmehr, 2004; Lackner and DiZio, 2005). A common approach has been to apply a velocity-dependent force field to a subject’s hand during target-directed movements. On first exposure, the novel forces cause large deviations from the intended movement, but these movement errors decrease with practice. If the force field is then unexpectedly removed, deviations of the hand path (aftereffects) are observed in the opposite direction to the earlier errors. This implies that the subject’s motor control system generates a prediction of the expected forces during a movement and produces opposing forces to compensate.

When subjects subsequently make movements in a new workspace requiring a change in arm configuration, generalization is observed. An analysis of the forces the motor system expects to encounter in the new workspace can reveal the way in which the predictive mechanism represents the force field. Shadmehr and Mussa-Ivaldi (1994) considered two alternative coordinate systems in which the force field could be represented: “extrinsic,” related to the dynamics of the external environment, and “intrinsic,” related to the internal dynamics of the body. In an extrinsic representation, the force field is modeled as a transformation from the endpoint velocity of the hand to the force applied at the hand. When a movement is made in a new workspace, this model will predict the same forces on the hand as for the same Cartesian movement in the trained workspace. Alternatively, in an intrinsic representation, the force field is modeled as a transformation from the angular velocities of the joints of the arm to the torques experienced at those joints. For identical movements of the hand in external space, this model will predict different forces on the hand when the arm configuration is changed.

Based on an analysis of movement errors and aftereffects in the new workspace, Shadmehr and Mussa-Ivaldi (1994) concluded that the motor system had represented the force field in an intrinsic coordinate system. However, in the study by Shadmehr and Mussa-Ivaldi (1994), changing the arm configuration altered the joint coordinates of both the arm movement and the applied force. In this study, we used a bimanual task to dissociate the representation of the motion that determines the force from the representation of the force itself. Forces were applied to a subject’s left hand that depended on the velocity of their right hand. Based on examples of bimanual coordination (Gahery and Massion, 1981; Johansson and Westling, 1988; Massion, 1992; Blakemore et al., 1998; Witney et al., 1999; Witney and Wolpert, 2003), we expected that the motor system should adapt to the novel context, maintaining stability of the left arm during right-arm movements by predicting and actively opposing the forces applied to the left hand. After adaptation, we tested generalization to new joint configurations of the right and left arms, thereby separately examining the internal representations of the movement and of the force.

Materials and Methods

After providing written informed consent, six right-handed subjects (four males, two females; aged 23–32 years) participated in the experiment. The experimental protocol was approved by a local ethics committee. While seated, subjects held separately in each hand a handle of a vBOT force-generating robotic manipulandum that could be moved with minimal inertia in the horizontal plane (Fig. 1A) (for details, see Kording et al., 2004). The subjects’ arms were supported in the horizontal plane by slings. The positions and velocities of the hands were calculated on-line at 1000 Hz. The positions of the hands were displayed as spheres (white; 0.8 cm radius) in the plane of the arm via a reflected rear-projection system; subjects could not see their hands or arms.

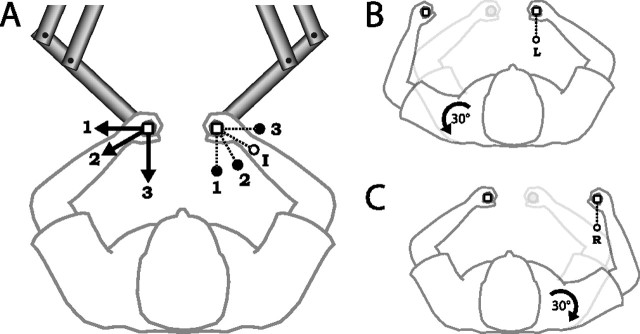
Figure 1.

Apparatus and task. A, Posture during the training session. Each trial began with the hands positioned in home positions (white squares) 43 cm in front and 8 cm to either side of the subject’s midline. Subjects made an out-and-back movement of their right hand to one of three target locations (1–3, filled circles). Forces were applied to the left hand determined by the motion of the right hand. Arrows illustrate the direction of force generated during a straight-line outward movement to each target. On intermediate target trials, subjects made right-hand movements to a fourth target location (I, open circle). B, Posture and target location (L, open circle) on left-arm rotation trials. C, Posture and target location (R, open circle) on right-arm rotation trials.

Procedure.

The experiment consisted of a series of trials in which the subject made out-and-back movements with the right hand to visually displayed targets while attempting to keep the left hand still. To begin each trial, subjects positioned their left and right hands in home positions displayed as blue cubes (1.6 cm side). A target sphere (magenta; 0.8 cm radius) was then presented at a distance of 10 cm from the right-hand home position. Subjects were instructed to move their right hand out to the target and back to the starting position in a single quick continuous motion. The right manipulandum was passive throughout the experiment and generated minimal resistance to the movement. An auditory signal was given 500 ms after the hand left the home position and subjects were told to time each movement so that they arrived back at the home position coincident with this signal. Subjects were instructed to keep their left hand as still as possible throughout each trial.

Subjects completed three consecutive experimental sessions. During the initial familiarization session (135 trials), subjects practiced making right-hand movements to all targets and in all limb configurations they would experience during the experiment (Fig. 1A–C) (for details, see below). No forces were applied to the left hand during the familiarization session, with the exception of occasional “catch” trials, described in detail below, in which the left manipulandum was locked in place to measure any forces generated by the subject.

The familiarization session was followed by a training session (360 trials) in which subjects were exposed to a novel force field generated by the manipulandum held in the left hand. Subjects made right-hand movements to three training targets situated at angles of 180°, 150°, and 90° (targets 1, 2, and 3, respectively) from the home position (in which 0° is the forward direction parallel to the subject’s midsagittal plane) (Fig. 1A, filled circles). In analogy to studies of unimanual motor learning (Brashers-Krug et al., 1996), the force applied to the left hand was proportional to the instantaneous velocity of the right hand and directed 90° clockwise to the velocity vector. Specifically, the force was given by the following:

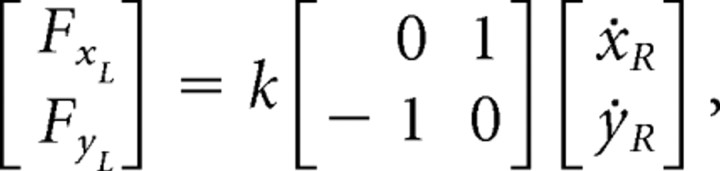where F_xL and F_yL are Cartesian components of the force applied to the left hand (respectively, perpendicular and parallel to the subject’s midline), ẋ_R and ẏ_R are Cartesian components of the velocity of the right hand, and k is 18 Ns/m. The direction of the force on the left hand resulting from an outward movement to each target is illustrated by the arrows in Figure 1A; the force during the return part of the movement is in the opposite direction.

Subjects completed 60 sets of six trials: within a set, each target was presented twice in a pseudorandom order. Five trials of each set were “field” trials in which the force field was applied to the left hand. The remaining trial was a catch trial, in which the manipulandum was locked in position at the start of the trial so that any forces generated by the subject’s left hand could be recorded. To achieve this, the left manipulandum simulated a stiff spring (2000 N/m spring constant) centered on the position of the handle at target onset. The high stiffness of this virtual spring meant that forces generated by the subject’s left hand on the handle were opposed by approximately equal and opposite forces from the manipulandum, resulting in very little movement. Visual feedback of the left-hand position was withheld on catch trials.

To encourage subjects to maintain control over left-hand posture, on field trials a circle (red; initial radius of 10 cm) was presented centered on the left home position. Subjects were told to try to keep their left hand within the circle at all times; if the left hand moved outside of the circle during a trial, the display flashed red to signal an error. The radius of the circle was adjusted on each trial to match the mean of the peak left-hand displacement on all previous field trials.

The training session was followed by a “generalization” session (225 trials). Two in every set of three trials was a field trial to one of the three training targets. The remaining trial was a catch trial in which forces generated by the subject’s left hand were measured. The catch trials in the generalization session were of three types: “intermediate target” trials, “left-arm rotation” trials, and “right-arm rotation” trials (25 trials of each in a pseudorandom order). On intermediate target trials, subjects made a right-hand movement to a target at 120° from the home position, intermediate between training targets 2 and 3 (Fig. 1A, open circle). On left-arm rotation trials, subjects began the trial by moving their left hand into a new home position. This position was calculated for each subject based on the position of the shoulder and lengths of the upper and lower arm to produce a 30° rotation about the shoulder, with no elbow rotation (Fig. 1B). The trial then proceeded as normal with a right-hand movement to a target at 180° (the same location as training target 1). On right-arm rotation trials, subjects began the trial by moving their right hand to a new home position, again calculated to produce a 30° rotation about the shoulder. A right-hand movement was then made to a target at 180° relative to this new home position (Fig. 1C).

Analysis.

All force, position, and velocity data from each trial were temporally aligned with the start of the right-hand movement, defined as the first time the velocity of the right hand toward the target exceeded 2.0 cm/s. To enable comparison between different target directions, force and velocity data were further separated into components parallel and perpendicular to the direction of the target from the right home position. Average time profiles were obtained by calculating mean forces and velocities for each time point across trials.

The direction and magnitude of forces generated by the subject on catch trials were assessed by calculating the left-hand force vector at the time of peak right-hand velocity toward the target. Because the left hand moved very little against the virtual spring (maximum deviation of 0.7 cm across all trials and subjects), the system could be considered to be in equilibrium and the force generated by the subject estimated by rotating the manipulandum force vector through 180°. For each subject, the mean force vector was calculated for each of the three training targets (averaged across catch trials in the second half of the training session) and for each of the three catch trial conditions in the generalization session. Comparisons of direction and magnitude between these mean force vectors were made using repeated-measures ANOVA.

Results

Adaptation over the training session

Subjects made out-and-back movements to targets with their right hand while attempting to keep their left hand still. Right-hand movements were predominantly accurate in magnitude, with a peak displacement toward the target of 10.7 cm (1.0 cm SD across all subjects and trials), and in direction, with a peak displacement perpendicular to the target direction of 0.9 cm (0.4 cm SD). Mean movement duration was 678 ms (131 ms SD).

The robotic manipulandum applied forces to the subject’s left hand proportional to the velocity of the right hand and directed at 90° to the direction of motion. Initially, these novel forces caused substantial deviations of the left hand during the right-hand movement: the peak displacement of the left hand from the home position on the first movement in the force field was 7.4 ± 1.1 cm (mean ± SE across subjects). However, these deviations reduced substantially in magnitude over the early part of the training session (Fig. 2A), falling to an average of 2.0 ± 0.3 cm over the second half of the session. This performance improvement can also be seen in Figure 2B, which shows the velocity of the left hand at the time of peak right-hand velocity toward the target: the time at which the first peak occurs in the force on the left hand. This velocity measure also fell over the course of the session from 26.7 ± 4.2 cm/s on first exposure to 9.4 ± 1.6 cm/s over the second half of the session, implying that subjects learned to minimize the acceleration caused by the forces on their left arm.

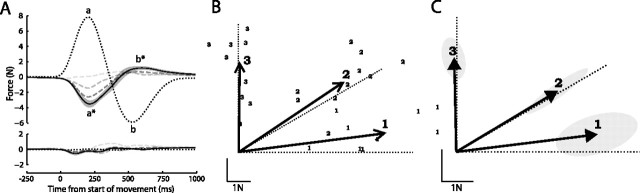
Figure 2.

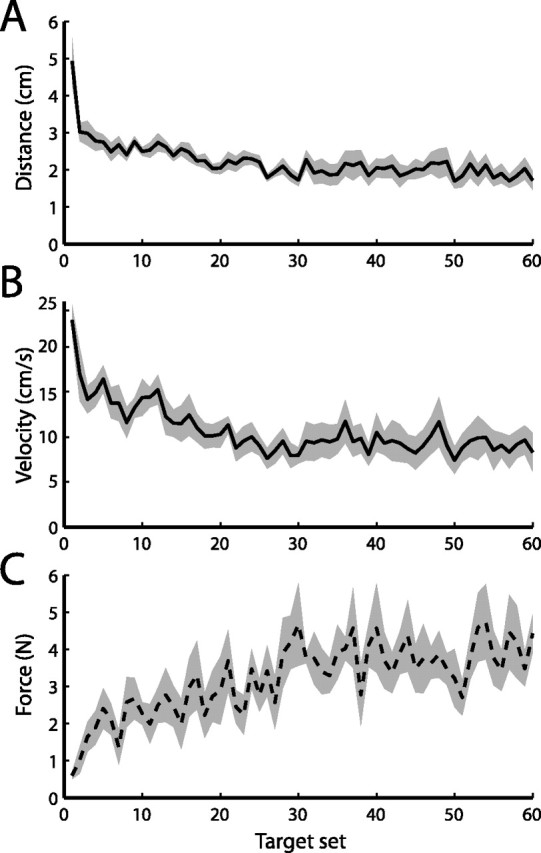
Adaptation over the training session. A, Peak distance of left hand from home position. Mean across each set of six trials; height of shaded area indicates ±1 SE across subjects. B, Magnitude of left-hand velocity at peak right-hand velocity toward target. Mean across each set of six trials; shaded area indicates ±1 SE. C, Mean magnitude of force generated by left hand on catch trials at peak right-hand velocity toward target. Shaded area indicates ±1 SE.

This improvement in stability of the left hand over the training session could result from an adaptation process in which subjects learned to anticipate the force from the manipulandum and generate an opposing force at the left hand to counter it. Alternatively, the improvement could be attributable to a nonspecific co-contraction strategy in which subjects increased the stiffness of the muscles of their left arm to minimize the movement caused by the imposed force. On occasional catch trials, the handle of the left manipulandum was unexpectedly locked in place and forces generated by the subject’s left hand were recorded. Before the training session, only very small forces were recorded on these trials (0.34 ± 0.05 N at peak velocity to target). Over the early part of the training session, the forces generated by all subjects on catch trials rapidly increased (Fig. 2C), reaching an asymptote at an average of 3.8 ± 0.4 N over the latter half of the session. This suggests that subjects learned to maintain the posture of the left hand by generating opposing forces to counter the expected force from the manipulandum.

Timing and direction of forces

The average time course of forces applied to the left hand by the manipulandum during field trials is shown by the dotted lines in Figure 3A. Movement of the right hand resulted in forces on the left hand perpendicular to the direction of movement and proportional to velocity. Therefore, on each trial, large forces were generated on the left hand in the direction perpendicular to the target direction (Fig. 3A, top), and very little force was generated parallel to the direction of the target (Fig. 3A, bottom). The magnitude of force reflects the velocity profile of the right hand, with an initial peak of 8.9 ± 0.6 N during the outward movement (labeled a), falling to 0 as the right hand reaches the target, followed during the return movement by a second force peak (labeled b; 8.8 ± 0.3 N) in the opposite direction to the first.

Figure 3.

Time course and direction of left-hand forces during the training session. A, Mean left-hand force perpendicular (top) and parallel (bottom) to the right-hand target direction as a function of time from right-hand movement onset. The dotted line shows mean force applied by the manipulandum on field trials. Mean forces generated by subjects are plotted for the first catch trial (light gray dashed line) and averaged across catch trials 1–10 (mid-gray dashed line), 11–30 (dark gray dashed line), and 31–60 (solid line; shaded area represents ±1 SE across subjects). B, C, Arrows indicate mean force vectors generated on catch trials 31–60 for each training target, for a typical subject (B; small digits indicate data points from individual trials) and averaged across all subjects (C; with 95% confidence ellipses). Dotted lines indicate direction of mean force vectors generated by the manipulandum on field trials for each target.

The solid line in Figure 3A shows the average time course of opposing forces generated by subjects on catch trials during the latter half of the training session [i.e., once the initial phase of rapid adaptation was complete (Fig. 3A, dashed lines)]. In the perpendicular direction (top), subjects produced opposing forces timed to counter the expected force from the manipulandum. An initial force peak (a*) was produced on average 231 ms after the start of the right-hand movement (77 ms SD across all subjects and trials). This closely matched the time of peak velocity to the target, at 248 ms (63 ms SD), when the first maximum in the force from the manipulandum would be expected. Although appropriately timed to counter the expected external force, the magnitude of this peak force (4.0 ± 0.4 N) represents only 46% of the expected force, suggesting that adaptation to the force field remained incomplete. The return movement of the right hand to the home position generated a second peak in the expected force at 549 ms (98 ms SD), which was again matched by a peak in the opposing force generated by the subject, also at 549 ms (282 ms SD) (b*). This second force peak was much more variable in timing than the first and weaker (2.1 ± 0.3 N, 23% of expected force). This may be because, by this stage of the movement, sensory feedback from the hand and arm had indicated that the force field was absent.

Very little of the subject-generated force recorded on catch trials was directed parallel to the target direction (Fig. 3A, bottom), suggesting that the direction as well as the timing of the force was well matched to oppose the expected force from the manipulandum. Results from a typical subject are shown in Figure 3B: arrows indicate, for each target, the mean opposing force vector at peak right-hand velocity, i.e., at the time the first peak in force from the manipulandum would be expected. Figure 3C shows mean force vectors across all subjects. The direction of the opposing force differed significantly between targets (F_(1,5) > 42.5; p < 0.002) and, for each target, did not differ significantly from a 180° rotation of the average force applied by the manipulandum on field trials to the same target (dotted lines) (F_(1,5) < 3.5; p > 0.12). This implies that subjects adjusted the direction of the opposing force for each target so as to counter the expected external force.

Some differences in force magnitude between targets are also apparent: this could reflect differences in the effort required to apply forces in different directions caused by the geometry of the arm and the lines of action of the muscles. The differing shapes of the confidence ellipses in Figure 3C indicate that there are also differences in intersubject variability between targets. This may reflect signal-dependent noise in force production: the variability is greatest for target 1, which is also the direction in which the force is largest.

Generalization of learning to new targets and postures

After the training session, subjects completed an additional session in which we tested the generalization of adaptation to targets and arm postures different from those on which they had been trained. Results from this session for a typical subject are shown in Figure 4A–C, and averages across all subjects are shown in Figure 4D–F. On intermediate target trials subjects made right-hand movements to a target situated at an angle intermediate between training targets 2 and 3. Opposing forces generated by the subject’s left hand were measured by locking the left manipulandum in place, as in the catch trials in the training session. Although subjects never experienced the force field during movements to this target, after training, they nonetheless generated substantial forces with the left hand. The mean opposing force on these trials (2.9 ± 0.2 N) did not differ significantly in magnitude from the mean opposing force for adjacent targets in the latter half of the training session (3.3 ± 0.4 N; F_(1,5) = 3.5; p = 0.12). Had the force field been active on these trials, right-hand movements toward the target (at 120°) would have resulted in forces on the left hand at an angle of 210°, requiring a 30° force from the subject to counter it. The actual direction of the mean opposing force vector on these trials (35 ± 4° at peak right-hand velocity) (Fig. 4D, black arrow) was not significantly different from this predicted direction (dashed line) (F_(1,5) = 1.9; p = 0.22) and differed significantly from the direction of forces generated on training targets 2 and 3 (F_(1,5) > 47.4; p < 0.001). This suggests that adaptation to the force field was not merely local to the training target movements, but that subjects had instead learned a mapping between right-hand movement and left-hand force that could generalize to new movement directions.

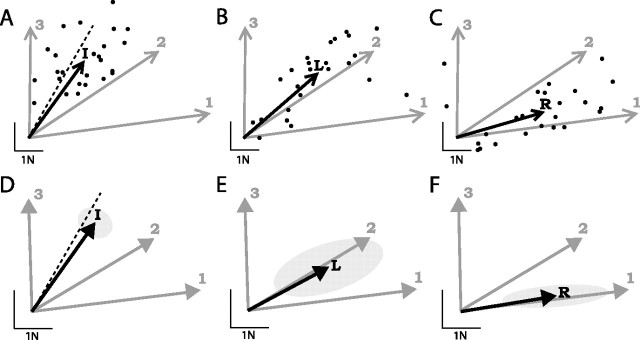
Figure 4.

Generalization of learning. Mean force vectors (black arrows) generated on generalization trials, for a typical subject (A–C; with data points from individual trials) and averaged across all subjects (D–F; with 95% confidence ellipses). Training target forces are replotted for comparison (gray arrows). A, D, Intermediate target trials. Dashed line indicates 30°. B, E, Left-arm rotation trials. C, F, Right arm rotation trials.

On left-arm rotation catch trials, subjects moved their left hand to a new position corresponding to a 30° rotation at the shoulder (Fig. 1B) before making a right-hand movement to target 1. Again, despite having never experienced the force field in this posture, subjects generated substantial opposing forces with the left hand (2.4 ± 0.6 N), although the magnitude was significantly reduced compared with movements to the same target during the training session (4.5 ± 0.5 N; F_(1,5) = 53.2; p < 0.001). The direction of force we expect subjects to generate on these trials depends on the way in which the motor system represents the structure of the force field. If the force applied to the left hand is represented in an extrinsic coordinate frame, then subjects should generate an opposing force in the same Cartesian direction as on movements to the same target in the training session. However, if subjects represent the force in an intrinsic reference frame related to the muscles and joints of the arm, for instance as joint torques, then the opposing force should remain constant relative to the joints and hence be rotated 30° counterclockwise. The mean opposing force direction on these trials (59 ± 7°) (Fig. 4E, black arrow) differed significantly from the opposing force to the same target in the training session (83 ± 3°; F_(1,5) = 12.0; p = 0.018) and did not differ from a 30° counterclockwise rotation of that force (F_(1,5) = 1.0; p = 0.37). This implies that the force on the left hand is represented in intrinsic coordinates.

On right-arm rotation catch trials, subjects moved their right hand to a new position corresponding to a 30° rotation at the shoulder (Fig. 1C) before making a right-hand movement to a target at 180°. As with the left-arm rotation trials, opposing forces generated by the left hand were substantial (2.5 ± 0.5 N) but less than those produced during the training session. Again, the force we expect subjects to generate on these trials depends on the way in which the motor system represents the force field. The required movement of the right hand on these trials was identical in Cartesian coordinates to a movement to target 1 in the training session. However, because of the shoulder rotation, the movement required the same changes to the joint angles of the arm as a movement to target 2 in the training session. Therefore, if the right arm movement is represented in extrinsic space, subjects should produce the same opposing force as for training target 1, and, if the movement is represented in intrinsic space, the opposing force should be the same as for training target 2. The mean opposing force direction on these trials (81 ± 2°) (Fig. 4F, black arrow) differed significantly from that generated on movements to target 2 in the training session (59 ± 2°; F_(1,5) = 170; p < 0.001) and did not differ from the force generated on movements to training target 1 (F_(1,5) = 0.6; p = 0.46). This result implies that the movement of the right hand is represented in extrinsic coordinates.

Discussion

Moving a limb or limb segment generates a perturbation that can have effects throughout the body attributable to interaction forces arising from the torques at the joints. When manipulating an object between the hands, activity of one hand will often result in a force on the other. In both cases, the motor system must actively generate opposing forces to maintain postural stability (Gahery and Massion, 1981; Massion, 1992). In this study, we investigated adaptation to a novel relationship between movement of the right hand and force on the left. The novel forces initially produced large deviations of hand position, but these errors decreased during an initial period of rapid adaptation as subjects learned to produce appropriate forces to oppose the external perturbation and maintain the stability of the left hand.

This finding is consistent with the results of previous studies that have examined the learning process involved when two hands act on each other through an object. A simple example is given by the unloading task: when one hand lifts a weight from the palm of the other hand, muscle activity in the load-bearing arm is decreased in parallel with the lift to minimize the change in posture (for review, see Massion, 1992). This anticipatory adjustment is thought to depend on a prediction of the change in load force based on the motor command, because it does not occur unless the lift is self-generated (Diedrichsen et al., 2003). Anticipatory responses in the unloading task are absent or inaccurate in young children (Schmitz et al., 1999, 2002) as are anticipatory grip force adjustments during object manipulation (Forssberg et al., 1991, 1992). This suggests that the prediction required for these tasks is acquired by experience during early life. Over shorter timescales, grip force responses have been shown to adapt to account for temporal delays between the force applied by one hand and the force experienced in the other (Witney et al., 1999) and to changes in the relative direction of the forces (Witney and Wolpert, 2003). These results imply that the underlying mechanism can rapidly adapt to novel contexts to continue generating accurate predictions. However, these studies have not addressed the issue of representation or the coordinate system in which learning takes place.

In contrast, several studies have investigated the internal representation of novel dynamics within a single limb. They have done so by examining how adaptation to a force field generalizes to new movements on which forces have not been previously experienced. For example, subjects trained to make reaching movements in a velocity-dependent force field subsequently show transfer of learning to circular movements in the same workspace (Conditt et al., 1997) and to reaching movements of different velocities and amplitudes (Goodbody and Wolpert, 1998). If subjects adapt to a force field for one direction of reaching movement, generalization is observed on movements to neighboring directions, decaying with angular distance from the trained direction (Gandolfo et al., 1996). These results imply that adaptation does not simply consist of learning a stereotyped pattern of muscle activations for each target, but rather involves the development of a more general representation of the force field. Generalization to neighboring directions is also observed for adaptation to novel inertial loads (Sainburg et al., 1999). Similarly, in the current study, learning was found to generalize to a new movement direction in which the force field had not been experienced. This suggests that the motor system had developed a model of the force field that could be used to predict the expected force on the left hand based on the parameters of the planned right-hand movement.

Shadmehr and Mussa-Ivaldi (1994) showed that unimanual force-field learning also generalizes to new joint configurations of the arm. Based on the pattern of generalization to the new arm configuration, they concluded that the force field was represented by the motor system in an intrinsic reference frame, related to the velocities and torques at the joints. In the current study, we also observed generalization of learning to new joint configurations of both the left and right arms. However, an analysis of the forces generated by subjects in these new arm postures revealed a dissociation in representation between the movement of the right hand and the force on the left.

When the left arm was rotated about the shoulder before a right-hand movement, the direction of the opposing forces generated by the subject remained constant relative to the joints of the arm. This implies that the motor system generates a prediction of the expected consequences of the movement in intrinsic coordinates, for instance, as expected joint torques. This is consistent with the results for unimanual learning. In contrast, when the right arm was rotated at the shoulder before movement, the direction of the opposing force generated by the subject was the same as on unrotated movements to the same location in Cartesian coordinates. This was the case, although the movements involved substantially different joint velocities, and implies that the motor system generates a prediction of the expected force based on a representation of the movement in an extrinsic coordinate frame.

Although substantial, generalization of learning to the new arm postures appears to have been incomplete, in that opposing forces were smaller than on the same movements in the training posture. Subjects generate opposing forces to counteract an expected force perturbation on the hand, but a perturbation was never applied when the arms were in their rotated configurations. The change in posture on these trials may therefore have acted as a cue before the movement, indicating that the perturbation would be absent. The fact that opposing forces were only reduced and not eradicated on these trials implies that subjects were only partially successful in using this cue. This change in force magnitude does not affect our assessment of the coordinate systems in which generalization occurs: this is reflected in the direction of force production and is therefore unaffected by global scaling.

This study examined a situation in which movement of the dominant hand produced forces on the nondominant hand. Although we would expect the results to be unaffected if the hands were reversed, some theories of handedness suggest that dominant and nondominant control systems are specialized for different roles (Bagesteiro and Sainburg, 2002, 2003). However, these theories do not make any explicit predictions about dynamic generalization.

Generalization in extrinsic coordinates has been observed previously in visuomotor learning. In studies of visuomotor learning, the normal relationship between the actual position of the hand and its visual location is altered, for instance, by prism glasses (Helmholtz, 1867; Welch, 1985), by a novel mapping between hand position and a screen cursor (Cunningham, 1989), or in virtual reality (Ghahramani et al., 1996). As with force-field learning, the visual perturbation initially causes movement errors that decay with practice, and aftereffects are observed if the perturbation is subsequently removed. Visuomotor learning has been shown to generalize to neighboring hand positions (Ghahramani et al., 1996) and joint configurations (Baraduc and Wolpert, 2002), implying that the motor system develops a model of the transformation, as with novel dynamics. Krakauer et al. (2000) trained subjects to make reaching movements to a single target under a 60° rotation of visual feedback and then tested generalization of learning to the same target in a new arm configuration. Subjects produced movements in the same direction across arm configurations, although this involved producing substantially different joint rotations and muscle activations. This result suggests that the motor system represents visuomotor perturbations in an extrinsic coordinate system.

In combination with the findings of Krakauer et al. the results of the current study could be taken to suggest a dissociation in representation between kinematic and dynamic planning, with trajectories represented by the motor system in extrinsic coordinates and forces represented in intrinsic coordinates. However, if this were the case, it would also be reflected in the generalization of unimanual force field learning. Although Shadmehr and Mussa-Ivaldi (1994) did not explicitly test the possibility of an extrinsic representation of movement combined with an intrinsic representation of force, their results are highly consistent with solely intrinsic representations. It therefore appears that the dissociation in representation demonstrated in the present study is specific to the learning of novel interactions between parts of the body. This implies an underlying mechanism partially or wholly independent of that involved in compensating for novel dynamics within a limb.