Spectral methods in machine learning and new strategies for very large datasets

Abstract

Spectral methods are of fundamental importance in statistics and machine learning, because they underlie algorithms from classical principal components analysis to more recent approaches that exploit manifold structure. In most cases, the core technical problem can be reduced to computing a low-rank approximation to a positive-definite kernel. For the growing number of applications dealing with very large or high-dimensional datasets, however, the optimal approximation afforded by an exact spectral decomposition is too costly, because its complexity scales as the cube of either the number of training examples or their dimensionality. Motivated by such applications, we present here 2 new algorithms for the approximation of positive-semidefinite kernels, together with error bounds that improve on results in the literature. We approach this problem by seeking to determine, in an efficient manner, the most informative subset of our data relative to the kernel approximation task at hand. This leads to two new strategies based on the Nyström method that are directly applicable to massive datasets. The first of these—based on sampling—leads to a randomized algorithm whereupon the kernel induces a probability distribution on its set of partitions, whereas the latter approach—based on sorting—provides for the selection of a partition in a deterministic way. We detail their numerical implementation and provide simulation results for a variety of representative problems in statistical data analysis, each of which demonstrates the improved performance of our approach relative to existing methods.

Spectral methods hold a central place in statistical data analysis. Indeed, the spectral decomposition of a positive-definite kernel underlies a variety of classical approaches such as principal components analysis (PCA), in which a low-dimensional subspace that explains most of the variance in the data is sought; Fisher discriminant analysis, which aims to determine a separating hyperplane for data classification; and multidimensional scaling (MDS), used to realize metric embeddings of the data. Moreover, the importance of spectral methods in modern statistical learning has been reinforced by the recent development of several algorithms designed to treat nonlinear structure in data—a case where classical methods fail. Popular examples include isomap 1, spectral clustering 2, Laplacian 3 and Hessian 4 eigenmaps, and diffusion maps 5. Though these algorithms have different origins, each requires the computation of the principal eigenvectors and eigenvalues of a positive-definite kernel.

Although the computational cost (in both space and time) of spectral methods is but an inconvenience for moderately sized datasets, it becomes a genuine barrier as data sizes increase and new application areas appear. A variety of techniques, spanning fields from classical linear algebra to theoretical computer science 6, have been proposed to trade off analysis precision against computational resources; however, it remains the case that the methods above do not yet “scale up” effectively to modern-day problem sizes on the order of tens of thousands. Practitioners must often resort to ad hoc techniques such as setting small kernel elements to zero, even when the effects of such schemes on the resulting analysis may not be clear (3, 4).

The goal of this article is twofold. First, we aim to demonstrate quantifiable performance-complexity trade-offs for spectral methods in machine learning, by exploiting the distinction between the amount of data to be analyzed and the amount of information those data represent relative to the kernel approximation task at hand. Second, and equally important, we seek to provide practitioners with new strategies for very large datasets that perform well in practice. Our approach depends on the Nyström extension, a kernel approximation technique for integral equations whose potential as a heuristic for machine learning problems has been previously noted (7, 8). We make this notion precise by revealing the power of the Nyström method and giving quantitative bounds on its performance.

Our main results yield two efficient algorithms—one randomized, the other deterministic—that determine a way of sampling a dataset prior to application of the Nyström method. The former computes a simple rank statistic of the data, and the latter involves sampling from an induced probability distribution. Each of these approaches yields easily implementable numerical schemes, for which we provide empirical evidence of improved performance in simulation relative to existing methods for low-rank kernel approximation.

Spectral Methods in Machine Learning

Before describing our main results, we briefly survey the different spectral methods used in machine learning, and show how our results can be applied to a variety of classical and more contemporary algorithms. Let {x₁,…, x_n} be a collection of data points in ℝ^m. Spectral methods can be classified according to whether they rely on:

Outer characteristics of the point cloud.

These are methods such as PCA or Fisher discriminant analysis. They require the spectral analysis of a positive-definite kernel of dimension m, the extrinsic dimensionality of the data.

Inner characteristics of the point cloud.

These are methods such as MDS, along with recent extensions that rely on it (more or less) to perform an embedding of the data points. They require the spectral analysis of a kernel of dimension n, the cardinality of the point cloud.

In turn, the requisite spectral analysis task becomes prohibitive as the (intrinsic or extrinsic) size of the dataset becomes large. For methods such as PCA and MDS, the analysis task consists of finding the best rank-k approximation to a symmetric, positive-semidefinite (SPSD) matrix—a problem whose efficient solution is the main focus of our article. Many other methods (e.g., refs. 1–5) are reduced by only a few adjustments to this same core problem of kernel approximation.

In particular, techniques such as Fisher discriminant analysis or Laplacian eigenmaps require the solution of a generalized eigenvalue problem of the form Av = λBv, where B is an SPSD matrix. It is well known that the solution to this problem is related to the eigendecomposition of the kernel B^−1/2AB^−1/2 according to

Notice that if A is also SPSD, the case for the methods mentioned above, then so is B^−1/2AB^−1/2. In the case of Laplacian eigenmaps, B is diagonal, and translating the original problem into one of low-rank approximation can be done efficiently. As another example, both Laplacian and Hessian eigenmaps require eigenvectors corresponding to the k smallest eigenvalues of an SPSD matrix H. These may be obtained from a rank-k approximation to H^ = tr(H)I–H, as Ĥ is positive definite and admits the same eigenvectors as H, but with the order of associated eigenvalues reversed.

Low-Rank Approximation and the Nyström Extension

Let G be a real, n × n, positive quadratic form. We may express it in spectral coordinates as G = UΛU^T, where U is an orthogonal matrix whose columns are the eigenvectors of G, and Λ = diag(λ₁,λ₂,…,λ_n) is a diagonal matrix containing the ordered eigenvalues λ₁ ≥ λ₂ ≥… ≥ λ_n ≥ 0 of G. Owing to this representation, the optimal rank-k approximation to G, for any choice of unitarily invariant* norm ∥·∥, is simply

In other words, among all matrices of rank k, G_k minimizes ∥G − G_k∥. We adopt in this article the Frobenius norm ∥G∥² := ∑_ijG_ij², but the results we present are easily transposed to other unitarily invariant norms. Under the Frobenius norm, the squared error incurred by optimal approximant G_k is ∥G − G_k∥² = ∑_{i = k + 1}ⁿ λ_i², the sum of squares of the n − k smallest eigenvalues of G.

The price to be paid for this optimal approximation is the expression of G in spectral coordinates—the standard complexity of which is O(n³). Although a polynomial complexity class is appealing by theoretical standards, this cubic scaling is often prohibitive for the sizes of modern datasets typically seen in practice. With this impetus, a number of heuristic approaches to obtaining alternative low-rank decompositions have been applied in the statistical machine-learning literature, many of them relying on the Nyström method to approximate a positive-definite kernel (7, 8), which we now describe.

Historically, the Nyström extension was introduced to obtain numerical solutions to integral equations. Let g : [0,1] × [0,1] → ℝ be an SPSD kernel and (u_i,λ_i^u), i ∈ ℕ, denote its pairs of eigenfunctions and eigenvalues as follows:

The Nyström extension provides a means of approximating k eigenvectors of g(x, y) based on an evaluation of the kernel at k² distinct points {(x_m, x_n)}_m ^k, _{n =1} in the interval [0,1] × [0,1]. Defining a kernel matrix G(m, n) ≡ G_mn := g(x_m, x_n) composed of these evaluations leads to the m coupled eigenvalue problems

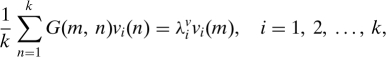where (v_i, λ_i^v) represent the k eigenvector-eigenvalues pairs associated with G. These pairs may then be used to form an approximation ${\tilde{u}}_i\underset{―}{\approx }{u}_i$ to the eigenfunctions of g as follows:

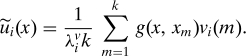The essence of the method is hence to use only partial information about the kernel to first solve a simpler eigenvalue problem, and then to extend the eigenvectors obtained therewith by using complete knowledge of the kernel. The same idea may in turn be applied to extend the solution of a reduced matrix eigenvalue problem to approximate the eigenvectors of an SPSD matrix G 8.

Specifically, one may approximate k eigenvectors of G by decomposing and then extending a k × k principal submatrix of G. First, let G be partitioned as

with A ∈ ℝ^k×k; we say that this partition corresponds to the multi-index I = {1, 2, …, k}. Now define spectral decompositions G = UΛU^T and A = U_AΛ_AU_A^T; the Nyström extension then provides an approximation for k eigenvectors in U as

In turn, the approximations $\tilde{U}\underset{―}{\approx }U$ and ${\Lambda }_A\underset{―}{\approx }\Lambda$ may be composed to yield an approximation $\tilde{G}\underset{―}{\approx }G$ according to

We call $\tilde{G}$ the Nyström approximation to G corresponding to I = {1, 2, …, k}; the extension of this definition to arbitrary multi-index I will be made formal below. We see from Eq. 2 that the main computational burden now takes place on a principal submatrix A of dimension k < n, and hence the Nyström extension provides a practical means of scaling up spectral methods in machine learning to very large kernels. From Eqs. 1 and 3 we deduce the resultant approximation error to be

where S_C(A) := C − BA⁻¹B^T is known as the Schur complement of A in G 9. The characterization of Eq. 4 ties the quality of the Nyström approximation explicitly to the partitioning of G; intuitively, this error reflects the loss of information that results from discarding submatrix C while retaining A and B.

Main Results

The Nyström method yields a means of approximating G conditioned on a particular choice of partition, hence shifting the computational load to determining that partition. To this end, we provide two algorithms for efficiently selecting from among all $\left(\begin{array}{l}n\\ k\end{array}\right)$ possible partitions of G while controlling the approximation error of Eq. 4. We first generalize the partitioning introduced above as follows. Let I,J ⊂ {1, 2, …, n} be multi-indices of respective cardinalities k and l that contain pairwise distinct elements in {1, 2, …, n}. We write I = {i₁, …, i_k}, J = {j₁, …, j_l}, and denote by $\bar{I}$ the complement of I in {1, …, n}. In order to characterize the Nyström approximation error induced by an arbitrary partition, we write G_I×J for the k × l matrix whose (p, q)-th entry is given by (G_I×J)_pq = G_ipjq, and abbreviate G_I for G_I×I.

Determining an optimal partition of G is thus seen to be equivalent to selecting a multi-index I such that the error

induced by the Nyström approximation $\tilde{G}$ corresponding to I is minimized. This naturally leads us to the algorithmic question of how to select the multi-index I in an efficient yet effective manner. In the sequel we propose both a randomized and a deterministic algorithm for accomplishing this task, and derive the resultant average or worst-case approximation error. To understand the power of this approach, however, it is helpful to first consider conditions under which the Nyström method is capable of providing perfect reconstruction of G.

Of course, if we take for I the entire set {1, 2, …, n}, then the Nyström extension yields $\tilde{G}$ = G trivially. However, note that if G is of rank k < n, then there exist multi-indices I of cardinality k such that the Nyström method provides an exact reconstruction: exactly those such that rank(G_I) = rank(G) = k, since this implies

We verify Eq. 6 presently, but the intuition behind it is as follows. If G is SPSD and of rank k, then it can be expressed as a Gram matrix whose entries comprise the inner products of a set of n vectors in ℝ^k. Knowing the correlation of these n vectors with a subset of k linearly independent vectors in turn allows us to reconstruct them exactly. Hence, in this case, the information contained in G_I is sufficient to reconstruct G, and the Nyström method performs the reconstruction.

Before introducing our two algorithms for efficient partition selection and bounding their performance, we require the following result, which gives an explicit characterization of the Schur complement in terms of ratios of determinants.

Lemma 1 [Crabtree–Haynsworth 10]. Let G_I be a nonsingular principal submatrix of some SPSD matrix G. Then the Schur complement of G_I in G is given element-wise by

We may use the Crabtree–Haynsworth characterization of Lemma 1 to deduce Eq. 6 as follows. First, notice that if rank(G) = k = |I|, then Eq. 7 implies that the diagonal of S_C(G_I) is zero. To wit, we have S_C(G_I)_ii = det(G_I∪{i})/det(G_I), with the numerator the determinant of a (k + 1)-dimensional principal submatrix of a positive-definite matrix of rank k, and hence zero. However, it is known that positive definiteness of G implies positive definiteness of S_C(G_I) for any multi-index I 9, allowing us to conclude that S_C(G_I) is identically zero if rank(G_I) = rank(G) = k.

Randomized Multi-index Selection by Weighted Sampling.

Our first algorithm for selecting a multi-index I rests on the observation that since G is positive definite, it induces a probability distribution on the set of all I : |I| = k as follows:

where Z = ∑_I,|I|=k det(G_I) is a normalizing constant.

Our corresponding randomized algorithm for low-rank kernel approximation consists of first selecting I by sampling I ∼ p_G,k(I) according to Eq. 8, and then implementing the Nyström extension to obtain $\tilde{G}$ from G_I and $G_{\bar{I}\times I}$ in analogy to Eqs. 2 and 3. This algorithm is well behaved in the sense that if G is of rank k and we seek a rank-k approximant $\tilde{G}$, then $\tilde{G}$ = G and we realize the potential for perfect reconstruction afforded by the Nyström extension. Indeed, det(G_I)≠0 implies that rank(G_I) = k, and so Eq. 6 in turn implies that $\parallel G_{\bar{I}}-G_{\bar{I}\times I}{G}_I^{-1}{G}_{I\times \bar{I}}\parallel =0$ when rank(G) = k.

For the general case whereupon rank(G) ≥ k, we have the following error bound in expectation:

Theorem 1. Let G be a real, n × n, positive quadratic form with eigenvalues λ₁ ≥ … ≥ λ_n. Let $\tilde{G}$ be the Nyström approximation to G corresponding to I, with I ∼ p_G,k(I). Then

Proof: By Eq. 5, we seek to bound

Denote the eigenvalues of S_C(G_I) as ${\left\{{\bar{\lambda }}_j\right\}}_{j=1}^{n-k}$; positive definiteness and subadditivity of the square root imply that

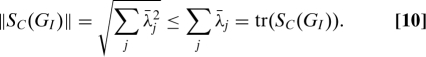The Crabtree–Haynsworth characterization of Lemma 1 yields

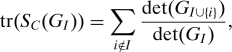and thus

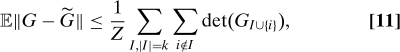where we recall that Z = ∑_I,|I|=k det(G_I).

Every multi-index of cardinality k + 1 appears exactly k + 1 times in the double sum of 11, whence

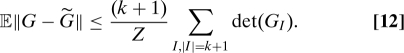As G is an SPSD matrix, the Cauchy–Binet Theorem tells us that the sum of its principal (k + 1)-minors can be expressed as the sum of (k + 1)-fold products of its ordered eigenvalues:

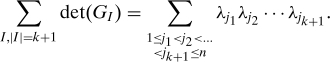It thus follows that

Combining the above relation with 12, we obtain

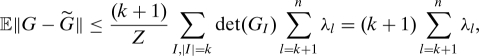which concludes the proof.

Deterministic Multi-index Selection by Sorting.

Theorem 1 provides for an SPSD approximant $\tilde{G}$ such that E$\parallel G-\tilde{G}\parallel$ ≤ $(k+1){\sum }_{i=k+1}^n{\lambda }_i$ in the Frobenius norm, compared with the optimal deterministic result ∥G − G_k∥ = (∑_i=k+1ⁿλ_i²)^1/2 afforded by the full spectral decomposition. However, this probabilistic bound raises two practical algorithmic issues. First of all, sampling from the probability distribution p_G,k(I) ∝ det(G_I), whose support has cardinality $\left(\begin{array}{l}n\\ k\end{array}\right)$, does not necessarily offer any computational savings over an exact spectral decomposition—a consideration we address in detail later, through the introduction of approximate sampling methods.

Moreover, in certain situations, practitioners may require a greater level of confidence in the approximation than is given by a bound in expectation. Although we cannot necessarily hope to preserve the quality of the bound of Theorem 1, we may sacrifice its power to obtain corresponding gains in the deterministic nature of the result and in computational efficiency. To this end, our deterministic algorithm for low-rank kernel approximation consists of letting I contain the indices of the k largest diagonal elements of G and then implementing the Nyström extension analogously to Eqs. 2 and 3. The following theorem bounds the corresponding worst-case error:

Theorem 2. Let G be a real positive-definite kernel, let I contain the indices of its k largest diagonal elements, and let $\tilde{G}$ be the corresponding Nyström approximation. Then

The proof of Theorem 2 is straightforward, once we have the following generalization of the Hadamard inequality 9:

Lemma 2 [Fischer's Lemma]. If G is a positive-definite matrix and G_I a nonsingular principal submatrix then

Proof of Theorem 2: We have from Eq. 10 that ∥G − $\tilde{G}$∥ ≤ tr(S_C(G_I)); applying Lemma 1 in turn gives

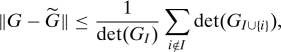after which Lemma 2 yields the final result.

While yielding only a worst-case error bound, this algorithm is easily implemented and appears promising in the context of array signal processing 11. Beginning with the case k = 1, it may be seen through repeated application of Theorem 2 to constitute a simple stepwise-greedy approximation to optimal multi-index selection.

Remarks and Discussion.

The Nyström extension, in conjunction with efficient techniques for multi-index selection, hence provides a means of approximate spectral analysis in situations where the exact eigendecomposition of a positive-definite kernel is prohibitively expensive. As a strategy for dealing with very large, high-dimensional datasets in the context of both the classical and contemporary statistical analysis techniques described earlier, this approach lends itself easily to a straightforward implementation in practical settings, and also carries with it the accompanying performance guarantees of Theorems 1 and 2 through the two algorithms presented above.

In considering the performance and complexity of these 2 algorithms, we first compare them with the only other result known to us for explicitly quantifying the approximation error of an SPSD matrix using the Nyström extension 12. This algorithm consists of choosing row/column subsets by sampling, independently and with replacement, indices in proportion to elements of {G_ii²}_i=1ⁿ, the squares of the main diagonal entries of G. The resultant probabilistic bound is written to include the possibility of sampling c ≥ k indices to obtain a rank-k approximation obeying (in Frobenius norm)

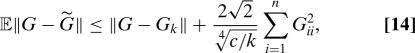an additive error bound relative to that of the optimal rank-k approximation G_k obtained via exact spectral decomposition.

Two important points follow from a comparison of the bounds of our Theorems 1 and 2 with that of 14. First, inspection of 13 (Theorem 2) and 14 reveals that a conservative sufficient condition for the former to improve upon the latter when c = k is that tr(G) ≥ n (also bearing in mind that the 13 is deterministic, whereas 14 holds only in expectation). A comparison of 9 (Theorem 1) and Eq. 14 reveals the more desirable relative form of the former, which involves only the (n − k) smallest eigenvalues of G and avoids an additive error term. Recall that Eq. 9 also guarantees zero error for an approximation whose rank k equals the rank of G.

A direct implementation of Theorem 1, however, requires sampling from p_G,k(I), which may be computationally infeasible. In the sequel we demonstrate that an approximate sampling is sufficient to outperform other algorithms for SPSD kernel approximation. Moreover, a sharp decrease in error is observed in simulations when k meets or exceeds the effective rank of G. This feature is especially desirable for modern spectral methods such as those described in the introduction, which yield very large matrices of low effective rank: whereas the number of data points n determines the dimensionality of the kernel matrix G, its effective rank is given by the number of components of the manifold M from which the data are sampled plus dim(M), a sum typically much smaller than n.

We also remark on similarities and differences between our strategies and ongoing work in the theoretical computer science community to derive complexity-class results for randomized low-rank approximation of arbitrary m × n matrices. Though our goals and corresponding algorithms are quite different in their approach and scope of application, it is of interest to note that our Theorem 1 can in fact be viewed as a kernel-level version of a theorem of ref. 13, where a related notion termed volume sampling is employed for column selection. However, in ref. 13, as in the seminal work of ref. 6 and others building upon it, approximations are obtained by applying linear projections to the approximand; although different algorithms define different projections, they do not in general guarantee the return of an SPSD approximant when applied to an SPSD matrix. The same holds true for approaches motivated by numerical analysis; in recent work, the authors of ref. 14 apply the method of ref. 15 to obtain a low-rank approximation termed an interpolative decomposition, and focus on its use in obtaining accurate and stable approximations to matrices with low numerical rank.

With reference to these various lines of work, we remark that a projection method applied to a matrix A can naturally be related to the Nyström extension applied to AA^T, though in our application setting it is of specific interest to work directly with the kernel in question. In particular, our results indicate how, by restricting to quadratic forms, one is able to exploit more specialized results from linear algebra than in the case of arbitrary rectangular matrices. We refer the reader to ref. 12 for an extended discussion of the various differences between projection-based approaches and the Nyström extension.

We conclude these remarks with a discussion of the computational complexity of the above algorithms for spectral decomposition. Recall that an exact spectral decomposition requires O(n³) operations, with algorithms specialized for sparse matrices running in time O(n²) 4. The deterministic algorithm of Theorem 2 requires finding the k largest diagonal elements of G, which can be done in O(n log k) steps. In analogy to Eq. 2, the subsequent spectral decomposition of G_I = U_IΛ_IU_I^T can be done in O(k³), and the final step of calculating $G_{\bar{I}\times I}{U}_I{\Lambda }_I^{-1}$ requires time O((n − k)k² + k²), as Λ_I is diagonal. The total running time of this deterministic algorithm is hence O(n log k + k³ + (n − k)k²), which compares favorably with previously known methods when k is small. The algorithm of Theorem 1 selects multi-index I at random, and thus the sorting complexity O(n log k) is replaced by the complexity of sampling from p_G,k(I) ∝ det(G_I). Below we describe an approximate sampling technique based on stochastic simulation whose complexity is O(k³), owing to the computation of determinants, with a multiplicative constant depending on the precise simulation method employed.

Numerical Implementation and Simulation Results

We now detail the implementation of our algorithms, and present simulation results for cases of practical interest that are representative of recent and more classical methods in spectral machine learning. Though simulations imply the adoption of a measure on the input space of SPSD matrices, our results hold for every SPSD matrix.

We first describe an approximate sampling technique adopted as an alternative to sampling directly from p_G,k(I) according to Eq. 8. Among several standard approaches 16, we chose to employ the Metropolis algorithm to simulate an ergodic Markov chain that admits p_G,k(I) as its equilibrium distribution, via a traversal of the state space {I : |I| = k} according to a straightforward uniform proposal step that seeks to exchange one element of I with one of $\bar{I}$ at each iteration. We made no attempt to optimize this choice, as its performance in practice was observed to be satisfactory, with distance to p_G,k(·) in total variation norm typically observed

Input: X = {x₁,x₂,…,x_n} ∈ ℝ^m // input dataset

k < m // desired dimension of the approximation

T > 0 // number of iterations for approximate sampling

Output: $\tilde{U}=\left\{{\tilde{u}}_1,{\tilde{u}}_2,\dots ,{\tilde{u}}_k\right\}$ ∈ ℝⁿ // approximant eigenvectors

$\tilde{\Lambda }=\left\{{\tilde{\lambda }}_1,{\tilde{\lambda }}_2,\dots ,{\tilde{\lambda }}_k\right\}$ // approximant eigenvalues

// Initialization: select a multi-index at random and build kernel

N ⇐ {1,2,…,n}

pickI⁽⁰⁾ = {i₁,i₂,…,i_k}⊂ N uniformly at random

G_I ⇐ EvaluateKernel(X,I⁽⁰⁾,I⁽⁰⁾)

// Sampling: attempt to swap a randomly selected pair of indices

for t = 1 to T do

pick s ∈ {1,2,…,k} uniformly at random

pick i′_s ∈ N \ I^(t−1) uniformly at random

I′ ⇐ {i′_s}∪ I^(t−1) \ {i_s}

G_I′ ⇐ EvaluateKernel(X,I′,I′)

with probability min (1,det(G_I′)/det(G_I)) do

I^(t) ⇐ I′

G_I ⇐ G_I′

otherwise

I^(t) ⇐ I^(t−1)

end do

end for

// Nyström approximation: obtain the eigenvectors and extend them

I ⇐ I^(T)

$\bar{I}\Leftarrow N\backslash I$

$G_{\bar{I}\times I}\Leftarrow \text{EvaluateKernel}(X,\bar{I},I)$

[U_I,Λ_I] ⇐ EigenDecomposition(G_I)

$\tilde{U}\Leftarrow \text{ConcatenateColumns}(U_I,G_{\bar{I}\times I}{U}_I{\Lambda }_I^{-1})$

$\tilde{U}\Leftarrow \text{PermuteRows}(\tilde{U},I,\bar{I})$

$\tilde{\Lambda }\Leftarrow \text{diag}({\Lambda }_I)$ to be small after on the order of 50|I| iterations of the chain. This approximate sampling technique yields a complete algorithm for low-complexity spectral analysis, as described in the algorithm above and implemented in subsequent experiments.†

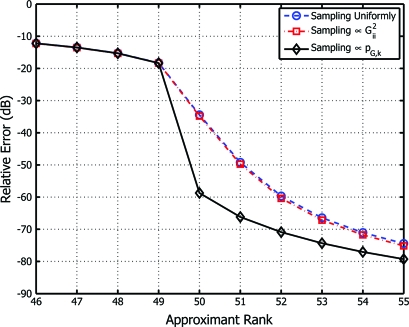
Our first experiment was designed to evaluate the relative approximation error 20 log₁₀∥G − $\tilde{G}$∥/∥G∥ incurred by the Nyström extension for the randomized algorithms of Theorem 1 and ref. 12. To do so we simulated G from the ensemble of Wishart matrices‡ according to G = G₁ + 5 × 10⁻⁷G₂, where G₁ ∼ _k (I, n) and G₂ ∼ _n (I, n); all generated matrices G were thus SPSD and of full rank, but with their k principal eigenvalues significantly larger than the remainder. We set n = 500 and k = 50, and averaged over 10,000 matrices drawn at random, with outputs averaged over 100 trials for each realization of G. A third algorithm indicating the Nyström extension's baseline performance was provided by selecting a multi-index of cardinality k uniformly at random. Fig. 1 shows the comparative results of these three algorithms, with that of Theorem 1 (implemented using the algorithm described above) outperforming that of 12, whose sampling in proportion to G_ii² fails to yield an improvement over the baseline method of sampling uniformly over the set of all multi-indices. Additionally, for approximants of rank 50 or higher, we observe a marked decline in approximation error for the algorithm of Theorem 1, as expected according to Eq. 6.

Fig. 1.

Relative approximation error of the randomized algorithms of Theorem 1 and 12 as a function of approximant rank, shown relative to a baseline Nyström reconstruction obtained by sampling multi-indices uniformly at random.

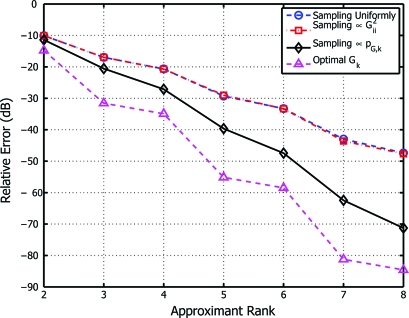
In a second experiment, we compared the performance of these 3 algorithms in the context of nonlinear embeddings. To do so we sampled 500 points uniformly at random from the unit circle, and then computed the approximate spectral decomposition of the 500-dimensional matrix required by the diffusion maps algorithm of ref. 5. Corresponding kernel approximation errors in the Frobenius norm were measured for each of the randomized algorithms described in the preceding paragraph, as well as for the optimal rank-k approximant obtained by exact spectral decomposition. We replicated this experiment over 1,000 different sets of points and averaged the resultant errors over 100 trials for each replication. As indicated by Fig. 2, the algorithm of Theorem 1 yields the lowest error relative to the optimal approximation obtained by exact spectral decomposition.

Fig. 2.

Diffusion maps kernel approximation error as a function of approximant rank, shown for the 3 randomized algorithms of Fig. 1, along with the minimum approximation error attained by exact spectral decomposition.

We also tested the performance of the deterministic algorithm implied by Theorem 2 in a worst-case construction of nonlinear embeddings. We proceeded by simulating positive-definite kernels for use with diffusion maps exactly as in the scenario shown in Fig. 2, but with 10,000 experimental replications in total. Then, rather than averaging over 100 trials for each replication, we instead took the worst of 10 different kernel approximation realizations for each randomized algorithm. As shown in Fig. 3, our deterministic algorithm consistently outperforms both the randomized algorithm of ref. 12 and the baseline method of uniform sampling in this worst-case scenario.

Fig. 3.

Worst-case approximation error over 10 realizations of the random sampling schemes of Fig. 2, along with the deterministic algorithm of Theorem 2.

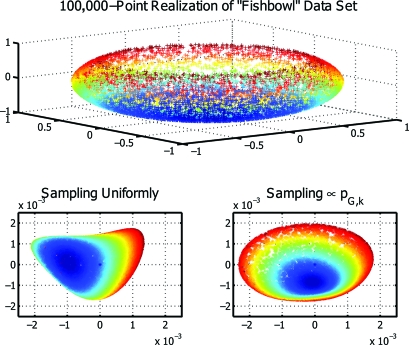
As a final example, we applied our randomized algorithm to realize a low-dimensional embedding via Laplacian eigenmaps 3 of a synthetic dataset containing 10⁵ points. The nearly 5 × 10⁹ distinct entries of the corresponding kernel matrix make it too large to store in the memory of a typical desktop computer, and hence preclude its direct spectral decomposition. As shown in the top portion of Fig. 4, the input “fishbowl” dataset—widely used as a benchmark—comprises a sphere embedded in ℝ³ whose top cap has been removed. The correct realization of a low-dimensional embedding will “unfold” this dataset and recover its 2-dimensional structure; to this end, Fig. 4 shows representative results obtained by choosing a multi-index I of cardinality 30 uniformly at random (Bottom Left) and in proportion to det(G_I) (Bottom Right). We see that the former realization fails to recover the 2-dimensional structure of this dataset, as indicated by the folding observed on the left-hand side of the resultant projection. The latter embedding is seen to yield a representation more faithful to the underlying structure of the data, indicating the efficacy of our method for kernel approximation in this context.

Fig. 4.

Recovery via Laplacian eigenmaps of a low-dimensional embedding from a 100,000-point realization of the “fishbowl” data set (Top), implemented using approximate spectral decompositions based on sampling multi-indices uniformly at random (Bottom Left) and according to the algorithm of Theorem 1 (Bottom Right).

Summary

In this article we have introduced two alternative strategies for the approximate spectral decomposition of large kernels, and demonstrated their applicability to machine learning tasks. We used the Nyström extension to transfer the main computational burden from one of kernel eigen-analysis to a combinatorial task of partition selection, thereby rendering the overall approximation problem more amenable to quantifiable complexity-precision trade-offs. We then presented 2 new algorithms to determine a partition of the kernel prior to Nyström approximation, with one employing a randomized approach to multi-index selection and the other a rank statistic. For the former, we gave a relative error bound in expectation for positive-definite kernel approximation; for the latter, we bounded its deterministic worst-case error. We also detailed a practical implementation of our algorithms and verified via simulations the improvements in performance yielded by our approach. In cases where optimal approaches rely on an exact spectral decomposition, our results yield strategies for very large datasets, and come with accompanying performance guarantees. In this way they provide practitioners with direct access to spectral methods for large-scale machine learning and statistical data analysis tasks.