Imaging brain vasculature with BOLD 3D microscopy: MR detection limits determined by in vivo two-photon microscopy

Abstract

Rat brain vasculature was imaged at 9.4 T with blood oxygenation level dependent (BOLD) microscopy. Data were acquired without exogenous contrast agent in < 35 min using 3D gradient-echo imaging with 78-μm isotropic resolution (N = 6). Detailed vascular patterns including intracortical veins and some branches were observed in simple magnitude-contrast data acquired at an experimentally-optimized echo time. The venous origin of the dark patterns was confirmed by oxygenation-dependent studies, and when the systemic arterial oxygen saturation level was < 80%, BOLD microscopy revealed additional intracortical vessels presumed to be of arterial orgin. Quantification shows a decrease of intracortical venous density with depth. The full width at half-minimum intensity was 90–190 μm for most intracortical venous vessels identifiable by BOLD venography. Since actual diameters are not directly quantifiable by BOLD, we also measured diameter-dependent intracortical venous density in vivo by two-photon excitation fluorescent microscopy (N = 5). Density comparisons between the two modalities, along with computer simulations, show that venous vessels as small as ~16–30 μm diameter are detectable with 9.4-T BOLD microscopy under our experimental conditions.

Introduction

Venous blood oxygenation level dependent (BOLD) contrast – originally described by Ogawa et al. (1,2) – relies on the magnetic susceptibility of paramagnetic deoxyhemoglobin (dHb). This endogenous contrast is the most commonly-used mechanism in functional MRI (3-5); neural activity induces a blood oxygenation increase (dHb concentration decrease) in capillaries, before draining to intracortical venous vessels, and finally to large pial veins. Since BOLD fMRI signal magnitude is closely related to baseline venous blood volume and oxygenation level, larger veins, which can be far from the sites of neural activity, often have larger BOLD signal changes relative to smaller venules and capillaries (6-9). High-resolution vascular imaging (capable of detecting extremely small veins) gives investigators a tool to examine the relationship between fMRI signal and vascular structures.

The first non-invasive depiction of vascular patterns with the BOLD effect was demonstrated in magnitude T₂*-weighted images of rat brain at high magnetic fields (1,2). But at the clinical field strength of 1.5 T, venous contrast in magnitude images is relatively poor, so venous contrast in the human brain has been enhanced by phase-contrast filtering to reveal detailed venous structure (10,11). When the phase difference between tissue and intravascular venous blood in T₂*-weighted images is 180°, this post-processing technique is most effective (10,11); however, the phase difference is a complicated function of several factors including venous oxygenation level, angle between vessel orientation and main magnetic field, magnetic field strength, and echo time (TE). Alternatively, at field strengths ≥ 7 T, simple magnitude T₂*-weighted images without phase-contrast filtering clearly have shown some venous discrimination in animal and human brain (1,2,12-15). At 9.4 T, T₂ of venous blood is much shorter than T₂ of tissue or systemic arterial blood (16), and this trend is also expected for T₂* values. Contrast between tissue and venous blood can therefore be enhanced in magnitude T₂*-weighted images at high field by setting TE sufficiently long relative to T₂* of venous blood. Additionally, longer TE values extend the susceptibility effect to greater distances in the surrounding tissue, causing the veins to appear larger (1,2), which increases their detectability.

In this paper, in vivo T₂*-weighted BOLD microscopy was performed using a 3D gradient-echo pulse sequence to obtain 78-μm isotropic scan resolution in rat brains at 9.4 T, as described in preliminary accounts of this work (17,18). Both signal to noise ratio (SNR) of tissue and contrast to noise ratio (CNR) between tissue and veins were maximized by experimental optimization of TE, which was compared with theoretical expectations. The levels of inspired oxygen were changed to confirm that the hypointense pixels in T₂*-weighted images were indeed of venous origin, and not magnetic susceptibility effects from sources other than venous dHb (e.g., arterial dHb, iron deposits, air/tissue/bone interfaces). Venous size-dependent density was quantified at selected cortical depths within the somatosensory area. Since intracortical venous diameters are not directly quantifiable by BOLD, the limits of detectability were determined by computer simulations and by density comparison with another imaging modality. Since vessel diameters measured by any histological techniques may differ from in vivo values and there are insufficient in vivo data, we determined diameter-dependent venous density in separate animals under similar in vivo conditions by 3D two-photon excitation laser scanning microscopy with intravenous injection of a fluorescent marker – an invasive, but “gold-standard” technique that can provide cortical depth-resolved measurements for all vessels between the cortical surface and 0.6-mm depth (19).

Methods

Animal preparation

Eleven male Sprague-Dawley rats weighing 260–450 g were used for MRI studies at the University of Pittsburgh (N = 6), and for two-photon microscopy studies at the National Institute of Radiological Sciences (Japan) (N = 5), with approval from the Institutional Animal Care and Use Committee (IACUC) at each respective institute. For all studies (MRI and two-photon), the rats were initially anesthetized by inhalation of 5.0% isoflurane in a 7:3 mixture of N₂O:O₂ or N₂:O₂, and then intubated for mechanical ventilation (RSP-1002, Kent Scientific, CT, USA and SAR-830AP, CWE, PA, USA). The isoflurane level was reduced to 2.0% for surgical preparation. The femoral artery and femoral vein were catheterized for blood gas sampling and for administration of fluid and/or fluorescent marker, respectively. Then the N₂O:O₂ mixture was replaced with an air:O₂ mixture in a ratio to attain a fraction of inspired oxygen (FiO₂) of 30% for MRI studies and 30-35% for two-photon studies, and the isoflurane level was adjusted to ~1.5% for MRI studies and ~1.3% for two-photon studies. These small differences in FiO₂ and isoflurane levels are unlikely to change physiological conditions and consequently vessel diameters. Rectal temperature was maintained at 37 ± 0.5 °C. Ventilation rate and volume were adjusted based on the blood gas analysis results (Stat profile pHOx; Nova Biomedical, MA, USA and i-Stat, Fusoyakuhin, Japan) to maintain carbon dioxide partial pressure levels within 30–40 mm Hg. Oxygen saturation levels were calculated using Hill’s equation with rat hemoglobin half saturation partial pressure (P₅₀) of oxygen = 38 mm Hg (20), Hill coefficient = 2.73, and measured partial oxygen pressure values. Note that the blood gas analyzers used human hemoglobin P₅₀ of ~26 mm Hg for calculation of oxygen saturation levels.

For MRI studies, the head of the animal was carefully secured to a home-built cradle by means of ear pieces and a bite bar. Reduced FiO₂ values of 21% and 15% were attained in oxygenation-dependent MRI studies by changing the gas mixture to air and air:N₂ mixtures, respectively. MR images were not acquired until at least 10 minutes after each target O₂ level was achieved.

For two-photon microscopy studies, the left skull was thinned (5 × 7 mm² area). In vivo cortical vasculature was imaged following a 0.2–0.4 ml intravenous bolus injection of 1-μM quantum dots (Qdot^® 605 ITK^TM Amino (PEG), Invitrogen, CA, USA), which remained in bloodstream and thus were used as a contrast agent for blood vessels.

MRI studies

Data collection

All experiments were carried out on a Varian 9.4 T / 31-cm MRI system (Palo Alto, CA) with an actively-shielded gradient coil of 12-cm inner diameter, which operates at a maximum gradient strength of 400 mT/m and a rise time of 130 μs. A home-built quadrature radiofrequency (RF) surface coil (inner diameter of each of 2 lobes = 1.6 cm) was positioned on top of the animal’s head and provided RF excitation and reception. Localized shimming was performed with point resolved spectroscopy (21) over a volume (~15 × 10 × 10 mm³) covering most of the brain to yield a water spectral linewidth of 30–50 Hz.

BOLD microscopy was performed with 3D RF-spoiled gradient-echo imaging. The pulse sequence similar to that presented by Reichenbach et al. (10), but flow compensation was performed on the readout and slab-select directions only. Slab selection (1.5 cm) is required in the anterior-posterior direction, since the sensitive volume of the surface coil exceeds the volume of interest (VOI). Also the inclusion of small TE values in the TE-dependent studies requires the shortest possible time between RF peak amplitude and start of data collection (T_delay). Therefore a minimum-phase Shinnar-Le Roux excitation pulse (22) was applied in the presence of a gradient, allowing T_delay to be fixed at 5 ms for all studies. The RF power level was adjusted to maximize subcortical signal. Imaging parameters were: repetition time = 50 ms, field of view = 3.0 × 1.5 × 1.5 cm³, corresponding matrix size = 384 × 192 × 192, voxel resolution = 78 μm (isotropic), and number of averages = 2. The largest field of view was along the readout direction (lateral-medial). Partial Fourier sampling (75%) was applied in both phase-encode directions (23). Each 3D venographic dataset was acquired in 34.5 min. In TE-dependent studies, the longest possible readout time (T_read) (corresponding to the narrowest possible acquisition bandwidth) was chosen to minimize the noise, while maintaining the relationship of TE = T_delay + T_read/2; however T_read was always ≤ 40 ms (i.e. TE ≤ 25 ms) to limit susceptibility artifacts. Consequently, datasets with TE values of 10, 13, 16, 20, and 24 ms, and corresponding T_read values of 10, 16, 22, 30, and 38 ms were acquired at FiO₂ = 30%. For the study of oxygenation dependence, additional datasets at FiO₂ = 21% and 15% were acquired with TE = 20 ms (T_read = 30 ms). Therefore, a total of seven 3D datasets were acquired for each animal; five TE-dependent datasets at FiO₂ = 30%, and one each at FiO₂ = 21 and 15%.

General venographic reconstruction, display, and SNR determination

Each 3D dataset was first zero-filled to a matrix size of 512×256×256 and then Fourier-transformed to yield datasets with nominal isotropic voxel dimensions of 59 μm. All displays and quantifications of data are based on magnitude data only.

To generate 2D views from any of the 3D datasets, a single-pixel (59 μm) plane or a 17-pixel (1 mm) slab was selected along one of the three orthogonal directions. Vessel detection within slabs was improved by minimum-intensity projection (11) or by averaging pixels across the slab thickness.

Lastly – for all displays and quantification of data (unless noted otherwise), intensity variation due to the inhomogeneous RF field of the surface coil was reduced with a 2D non-uniformity correction algorithm (24) after all other processing was complete. Intensity and contrast levels of images appearing within each figure were independently adjusted.

SNR values were determined in TE-dependent datasets both from signal within large VOIs containing vessels (7 × 7 × 7 mm³) at the brain center, and from signal within small cortical regions without prominent vessels (1.2 × 1.2 × 0.059 mm³) selected from coronal views, while noise for both was measured from 1.2 × 1.2 × 1.2 mm³ regions outside the brain. Rician distribution of intensity was accounted for by quantification as $\mathrm{SNR}=\sqrt{M^2-{\sigma }^2}/\sigma$, where M and σ represent measured signal (mean) and noise (standard deviation), respectively (25). Non-uniformity corrections were not applied when SNR was evaluated.

Reconstruction of flattened cortical planes

Cross-sectional views of vessels aligned perpendicular to the cortical surface were generated by performing cortical flattening along the lateral-medial dimension (minor anterior-posterior curvature was ignored). This procedure involved first manually defining a curve at a select cortical depth on a 59-μm thick coronal view containing the somatosensory area. At 59-μm intervals along this curve, pixel intensities were calculated by linear interpolation of the 4 nearest pixels to construct a flat line with 59-μm resolution, where distances along the line preserve the original distances along the curve. This entire process utilizing the same curve was repeated for each 59-μm thick coronal view from the 3D dataset, and each of these lateral-medial lines were then stacked in the anterior-posterior direction to compose a 2D cross-sectional view at the selected cortical depth.

Depth-dependent quantification of venous parameters

Venous pixel candidates were chosen and “identifiable veins” were assigned as follows. After comparison of coronal views with a stereotaxic atlas (26) for coordinate assignment, bilateral rectangular columns oriented perpendicular to the cortical surface were defined within the 3D dataset such that their centers intersected the surface at 1.0 mm posterior and ± 2.6 mm lateral to bregma. A column length spanned the entire cortical depth, with flattened cross-sectional areas of 1.8 × 1.8 mm². These columns incorporate as much somatosensory area as possible to reduce errors in venous quantification due to any potential tissue heterogeneity. Pixel intensities of each 1.8 × 1.8 × 0.059 mm³ section of a column (59-μm isotropic resolution) were calculated as previously described for cortical flattening. A VOI was then constructed consisting of all 1.8 × 1.8 mm² planes between cortical depths of 0.4 and 1.8 mm within the column; 2D planes with cortical depths < 0.4 mm were excluded due to extravascular signals from pial veins. Veins were identified within this VOI only if they passed criteria based on intensity threshold and depth contiguity. First, the intensity threshold for venous pixel candidates was determined by fitting a signal intensity histogram of each 2D plane within the VOI to a Gaussian curve, the center of which represents the average tissue signal intensity. Venous pixel candidates were assigned as those whose signal intensity did not exceed a threshold (default = 85%) based on the average tissue signal intensity. Venous pixel candidates below the intensity threshold were then tested for depth contiguity across each plane within the VOI. Since most intracortical veins are perpendicular and continuous to the cortical surface, an identifiable vein was assigned only if venous pixel candidates were also connected over a minimum number of contiguous planes, which by default was 4 planes based on a compromise between detection of vessels (as short as ~240 μm) vs. false assignment due to noise.

The density of identifiable intracortical veins and the apparent spatial extent of their cross sections were examined in equidistant 1.8 × 1.8 × 0.059 mm³ sections within the VOI, positioned 0.4, 1.0, and 1.6 mm from the cortical surface. For each of these sections, a binary map representing only the pixels that passed both criteria for identifiable veins was created. To minimize quantification problems associated with veins located at the edge of each plane, the measurements were performed only for veins whose minimum-intensity pixel was located within a smaller 1.4 × 1.4 × 0.059 mm³ region concentric with the 1.8 × 1.8× 0.059 mm³ region (gap between edges of these two regions = 3 pixels). Intracortical venous density vs. apparent size was determined at the select cortical depths after separating identifiable veins based on their in-plane contiguous pixels in these binary maps. Pixel locations of the same identifiable veins were also located on the 1.8 × 1.8 × 0.059 mm³ grayscale sections (linearly-interpolated and 2D RF non-uniformity corrected), from which full width at half-minimum intensity (FWHMin) values for the anterior-posterior and lateral-medial directions were averaged to yield one FWHMin value per vein.

Two-photon microscopy studies

Intracortical vasculature was three-dimensionally imaged in vivo with laser scanning microscope (TCS SP5 MP, Leica Microsysems, Germany). Injected quantum dots were excited with a Ti:sapphire laser (MaiTai Hp1020, Spectra-physics, CA, USA) at 900-nm wavelength with ~2.0 W output, and emitted orange-fluorescent light (605 nm). An image with 512 × 512 matrix size and 0.89-μm in-plane and 10-μm depth resolutions (0.456 × 0.456 mm² field of view) was obtained with the ×20 water-immersion objective lens (0.5 numerical aperture). Four adjacent images (2 by 2) were acquired by shifting the animal position relative to the microscope for coverage of a 0.91 × 0.91 mm² region of the primary somatosensory cortex relatively void of large pial vessels, centered 1.0 ± 0.4 mm posterior and 2.6 ± 0.5 mm left of bregma (mean ± SD). Vascular images were obtained from the cortical surface to a depth of ~0.6 mm, in 0.01-mm steps. Since pial arteries and veins were visually distinguished based on the differences in their color (artery is light vs. vein is dark red), intracortical venous network was identified by tracking from the pial vasculature. Intracortical venous density and cross-sectional diameter were measured within the four adjacent images (0.91 × 0.91 × 0.01 mm³) at cortical depths of 0.1 and 0.4 mm. For display purposes, images from contiguous planes were maximum-intensity projected.

Results

MRI studies

TE-dependent studies

Studies performed at FiO₂ = 30% with minimum acquisition bandwidths (10.1–38.4 kHz) show that the hypointense pixels become darker and more numerous as TE lengthens, due to increased susceptibility effects from dHb (Fig. 1a and b). Contrast between gray and white matter also improves at longer TE values, as can be seen by the darkening of the corpus callosum and internal capsule (Fig. 1b). SNR values from 7 × 7 × 7 mm³ VOIs in the center of the brain (Fig. 1c) and from 1.2 × 1.2 × 0.059 mm³ cortical regions without prominent vessels within coronal sections (Fig. 1d) were measured as a function of TE (N = 6). For the five conditions tested, SNR was highest when TE = 20 ms (T_read = 30 ms) for both regions, which is statistically significant (Wilcoxon signed rank test, p < 0.05). An echo time of 20 ms is ~3 times longer than T₂ of venous blood, resulting in negligible intravascular venous blood signal; therefore CNR between tissue and veins should also be near optimal when TE = 20 ms. Thus, further studies were restricted to TE values of 20 ms.

FIG. 1.

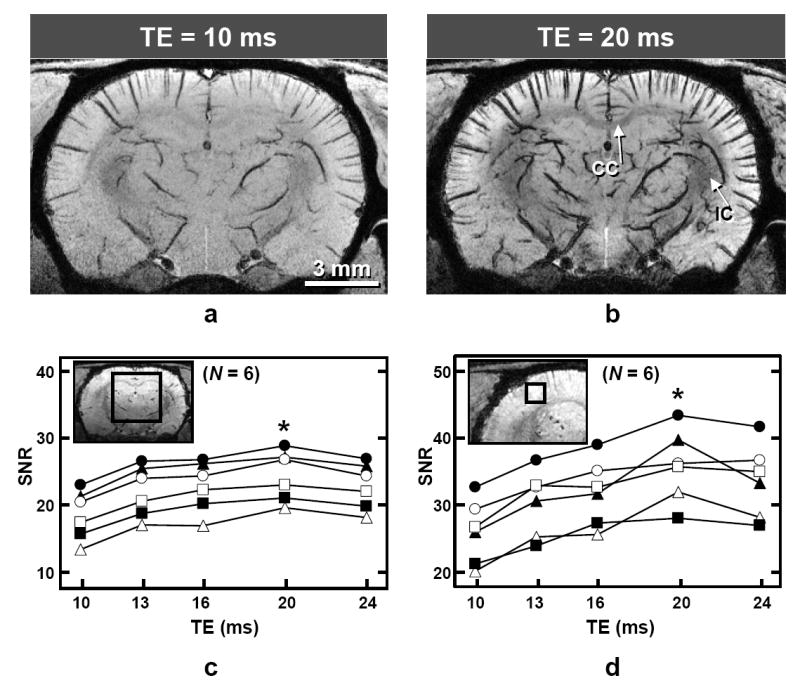
Dependence of image quality and signal to noise ratio (SNR) on TE with 9.4-T BOLD 3D microscopy (fraction of inspired oxygen = 30%). a and b: Images of one representative animal with TE = 10 ms (a) and 20 ms (b) after minimum-intensity projection of 1-mm thick coronal slabs from the 3D datasets (systemic arterial oxygen saturation level = 99%). CC = corpus callosum; IC = internal capsule. c and d: SNR values plotted as a function of TE for all studies (N = 6), where each line represents data from an individual animal; filled triangles represent data from a and b. Image insets are single-pixel thick (59 μm) coronal reconstructions (TE = 20 ms) from one study, where the signal spatial extent considered for each measurement is illustrated in two dimensions by the squares. The actual volumes for the signal measurement are 7 × 7 × 7 mm³ (c) and 1.2 × 1.2 × 0.059 mm³ (d), and the volume for noise measurement is 1.2 × 1.2 × 1.2 mm³ (not shown). SNR is statistically highest for both regions of signal measurement when TE = 20 ms; * p < 0.05.

Oxygenation-dependent studies

To confirm that the hypointense patterns are indeed of venous origin, BOLD microscopy was performed not only with an FiO₂ level of 30% but also with FiO₂ levels of 21% and 15%; corresponding systemic arterial blood oxygen saturation level (SaO₂) ranges were 90–97, 71–92, and 52–74% (95 ± 3, 85 ± 7 and 65 ± 8%), respectively, for six animals. Note that the SaO₂ calculated with human hemoglobin P₅₀ was 99 ± 1, 95 ± 3 and 85 ± 5% with FiO₂ levels of 30, 21, and 15%, respectively. Data from one oxygenation-dependent study are shown in Fig. 2. The dark lines observed at the highest FiO₂ level (Fig. 2a) thicken but do not lengthen as the FiO₂ levels are reduced (Fig. 2b and c), confirming that the dark patterns in data with FiO₂ = 30% are indeed of vascular origin. Notably, some new lines appear at the reduced FiO₂ levels (arrows in Fig. 2b and c), which are thin and appear with low contrast relative to other vascular patterns existing within comparable or shallower cortical depths. Even though it is not obvious from the 2D displays, careful evaluation of 3D data shows that these new vascular patterns appearing at reduced FiO₂ levels usually have increased contrast at deeper cortical regions, and some disappear near the cortical surface (example indicated by arrows in Fig. 2d), indicating that blood oxygenation level decreases with cortical depth. There was no continuation of these patterns in adjacent volumes, indicating that this aspect of their appearance is not due to a partial volume effect. When FiO₂ = 15%, these new vascular patterns were evident in all animals (N = 6, systemic SaO₂ = 65 ± 8%). When FiO₂ = 21%, some of these new vascular patterns were observed in half of the animals (N = 3, systemic SaO₂ = 80 ± 8%), while there was no evidence in the remainder (N = 3, systemic SaO₂ = 89 ± 3%). Based on these characteristics, the new vascular patterns are likely of arterial origin. To minimize any potential contamination of arterial vessels, only datasets with FiO₂ = 30% were used to examine venous patterns and quantify venous density and size characteristics.

FIG. 2.

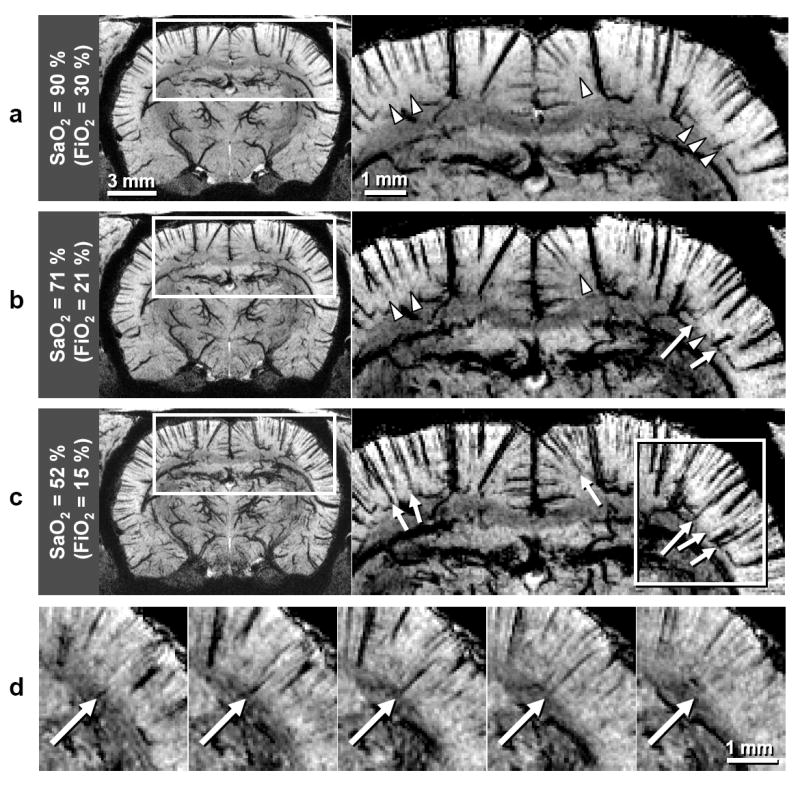
Oxygenation-dependent 9.4-T BOLD 3D microscopy study. Data were acquired with TE = 20 ms in an animal different from Fig. 1a and b (N = 6 total). Displays are minimum-intensity projections of 1-mm thick coronal slabs. SaO₂ and FiO₂ in a–c represent values for the oxygen saturation level of systemic arterial blood and the fraction of inspired oxygen, respectively. Note that SaO₂ was calculated with the half saturation partial pressure of oxygen appropriate for rat hemoglobin. Regions within the rectangles (left) are expanded (right), with intensity and contrast levels adjusted to emphasize the SaO₂ dependence of vessels presumed to be arteries. Arterial candidates are marked when they are visible (arrows) and not yet visible (arrowheads). An arterial candidate from within the rectangular region in c are better visualized in expanded views of five consecutive single-pixel thick (59-μm) planes, where the long arrow indicates a vessel with increased contrast at deeper cortical regions.

Visualization of veins

Venous patterns are clearly observed when TE = 20 ms and FiO₂ = 30% (Fig. 3). Key features are apparent even when venograms are displayed with only single-pixel thickness (Fig. 3a–c). When venous vessels (veins and venules) are oriented parallel to the plane, they appear as dark lines; this is clearly seen in a coronal view where most intracortical vessels are perpendicular to the cortical surface (Fig. 3a). When venous vessels are oriented perpendicular to the plane, they appear as dark spots, as seen in an axial view (Fig. 3b). Pial veins at the medial surface are especially prominent in the sagittal view (Fig. 3c). When signals were averaged across a 1-mm thick axial slab near the dorsal cortical surface, pial and intracortical veins were consistently detected (Fig. 3f). The 59-μm thick reconstructions also show detailed anatomical structure; gray to white matter contrast is sufficient to resolve corpus callosum and internal capsule (Fig. 3a and b), while ventricles appear hyperintense (Fig. 3a and c). Lateral ventricles also appear in a 59-μm thick axial view reconstructed ~0.3 mm ventral to the location of Fig. 3b (not shown).

FIG. 3.

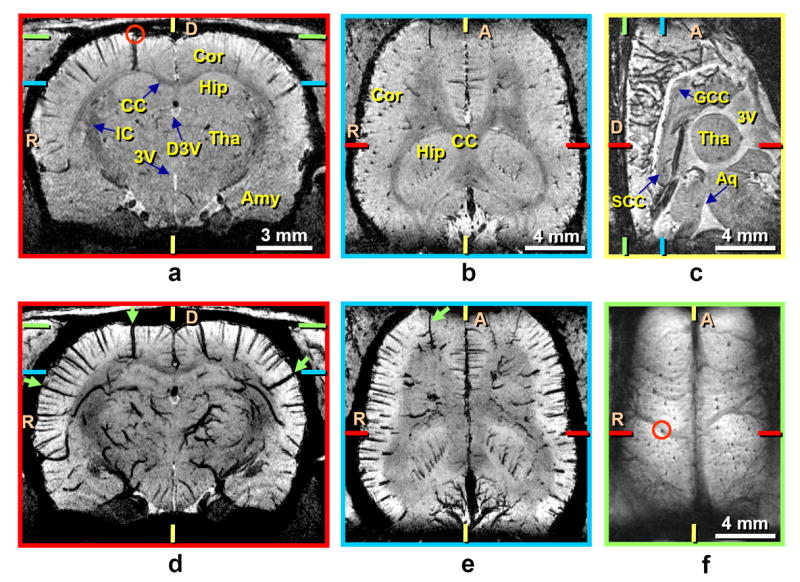
Endogenous BOLD-contrast venograms at 9.4 T demonstrating various 2D reconstructions from one 3D dataset. Data were acquired with TE = 20 ms and the fraction of inspired oxygen = 30% (systemic arterial oxygen saturation level = 90%) from the same animal shown in Fig. 2. Image reconstructions from single-pixel thick (59 μm) sections are shown along coronal (a), axial (b), and sagittal (c) directions. Minimum-intensity projections of 1-mm thick slabs are shown along coronal (d) and axial (e) directions, where projection slabs were centered at the planes of a and b, respectively. Images a and d are centered ~0.5 mm posterior to the reconstruction of Fig. 2a. Green arrows in d and e indicate intracortical vessels that have visible branches. For a reconstruction from the dorsal cortical surface (f), pixels across a slab thickness of 1 mm were averaged. Colored ticks represent slice or slab centers for reconstructions with borders of the same color. The same intracortical vein (marked by small red circles) is seen in a coronal view (a) and as it drains to the cortical surface (f). A = anterior; D = dorsal; R = right; Amy = amygdala; Aq = aqueduct; CC = corpus callosum; Cor = cortex; D3V = dorsal third ventricle; GCC = genu corpus callosum; Hip = hippocampus; IC = internal capsule; SCC = splenium corpus callosum; Tha = thalamus; 3V = third ventricle.

Venous patterns become even more conspicuous in displays where minimum-intensity projection was performed over 1-mm thick slabs (Fig. 3d and e) centered at the planes of Fig. 3a and b. Veins are then visible not only within the cortex, but also in subcortical regions, including the thalamus and hippocampus. Intracortical venous vessels draining the deepest cortical regions generally appear to have larger diameters in these images. A few intracortical branches can be seen along some large veins (arrows in Fig. 3d and e); this was consistently observed in all six animals.

Cortical depth-dependent venous distribution

The distribution of venous vessels as a function of cortical depth in data acquired with TE = 20 ms and FiO₂ = 30% is illustrated in Fig. 4. The manually-drawn yellow curve along the middle of the cortex (Fig. 4a) defined the location for reconstruction of a flattened plane (Fig. 4b), where intracortical venous vessels appear as small spots due to their perpendicular orientation. Cross-sectional views at select depths within the somatosensory cortex were also reconstructed for 1.8 × 1.8 mm² regions (red lines and square in Fig. 4a and b), and these are shown in Fig. 4c–f for cortical depths of 0.1, 0.4, 1.0, and 1.6 mm, respectively. Pial veins are observed in the plane near the cortical surface (Fig. 4c). Fewer intracortical venous vessels are visualized with increased cortical depth (Fig. 4d–f). A histogram of the 1.8 × 1.8 × 0.059 mm³ region at 0.4-mm depth (Fig. 4g) illustrates deviation from a Gaussian fitting for pixel intensities below ~85% of the average tissue signal intensity; histograms of the same regions in all animals (12 hemispheres) for cortical depths of 0.4, 1.0, and 1.6 mm appear similar, with deviations occurring for pixel intensities below 84 ± 2%, 86 ± 3%, and 86 ± 3%, respectively.

FIG. 4.

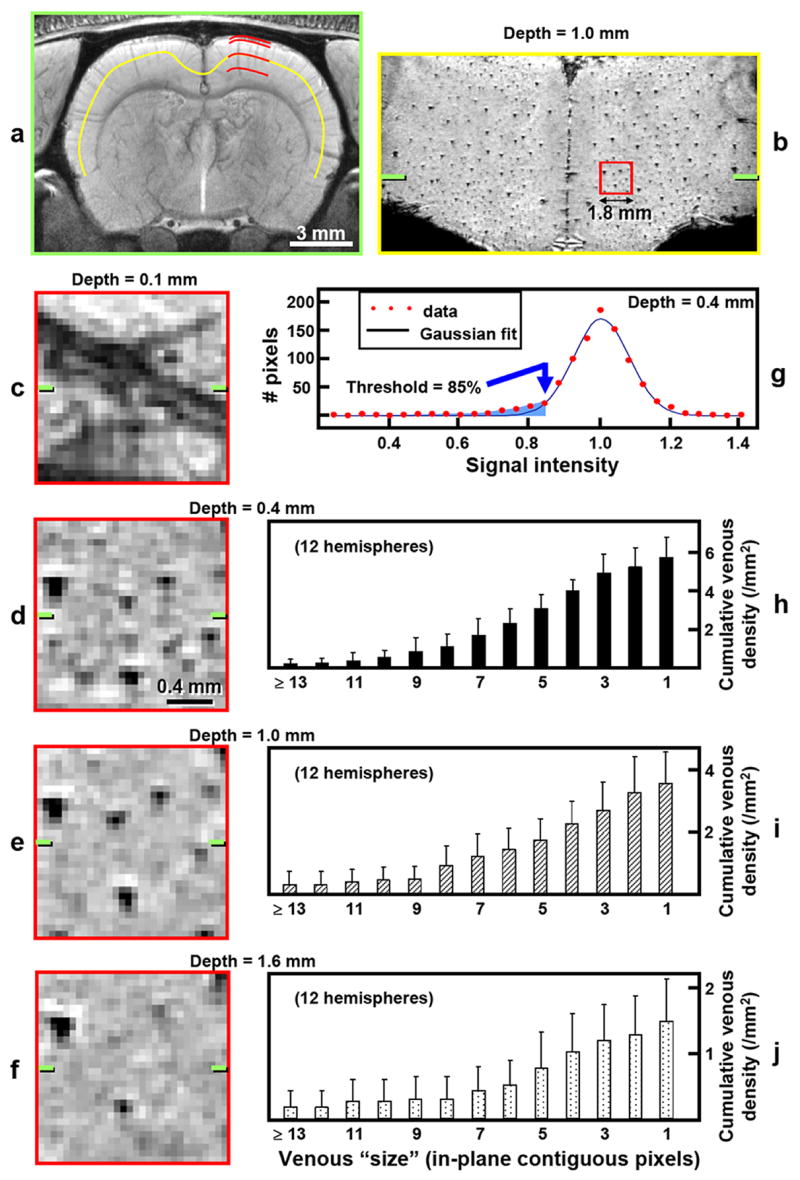
Reconstructions from a 9.4-T BOLD 3D venographic dataset and cortical depth-dependent quantification of venous distributions. Data were acquired with TE = 20 ms, and with the fraction of inspired oxygen = 30%. a–g: Data from one representative animal (different from Figs. 1-3) (systemic arterial oxygen saturation level = 95%). a: Coronal view reconstructed by averaging pixels across a 1-mm thick slab. Red curves are 1.8 mm in length and indicate cortical depths of 0.1, 0.4, 1.0, and 1.6 mm, within the somatosensory cortex. b: A single-pixel thick (59-μm) reconstruction at the location of the yellow curve in a (cortical depth of 1.0 mm). The red square in b represents a 1.8 × 1.8 mm² region within the somatosensory cortex.c–f: Expanded views of selected 1.8 × 1.8 × 0.059 mm³ regions at 0.1 (c), 0.4 (d), 1.0 (e), and 1.6 mm (f) from the cortical surface, as indicated by the red curves in a. The green ticks in b–f represent the slab center of a. g: Histogram of the 1.8 × 1.8 × 0.059 mm³ region at a cortical depth of 0.4 mm (shown in d) and its Gaussian curve fitting. Thirty discrete intensity bins were chosen based on minimum and maximum signal intensities within the region of interest. Venous pixel candidates (blue shading) are assigned as those with the intensity threshold = 85% of average tissue signal intensity (blue arrow). h-j: Cumulative intracortical venous densities vs. venous “size” (expressed as minimum in-plane contiguous pixels defining each identifiable venous vessel) at cortical depths of 0.4 (h), 1.0 (i), and 1.6 mm (j), for all studies (12 hemispheres). The right-most bar in each plot represents total venous density, which decreases with cortical depth (p < 0.05). Note the independent adjustment of vertical scales for better visualization. Measurements were performed within 1.4 × 1.4 × 0.059 mm³ regions concentric with the 1.8 × 1.8 × 0.059 mm³ regions illustrated in d–f, using default criteria for venous vessel identification (intensity threshold of 85% of average tissue signal intensity and depth contiguity of 4 pixels). The measurement error in cortical depth due to spatial variation of the cortical surface is ~0.1 mm (N = 6).

As cortical depth increases, the total density of intracortical venous vessels identified with the default criteria (intensity threshold of 85% of average tissue intensity, depth contiguity of four pixels) decreases (Fig. 4h–j, right-most bars); differences in the total identifiable venous densities of 5.7 ± 1.0, 3.5 ± 1.0, and 1.5 ± 0.6 / mm² (12 hemispheres) at cortical depths of 0.4, 1.0, and 1.6 mm, respectively, were statistically significant (Wilcoxon signed rank test, p < 0.05). The cumulative density patterns of Fig. 4h-j (all bars) represent distribution by venous size. Although the magnitudes are reduced, the overall pattern of the cumulative venous density plots for vessels with < 10 in-plane contiguous pixels is similar for the three cortical depths, indicating a proportionate reduction in density with cortical depth for all but the largest detectable vessels. Venous density is dependent on the choice of both intensity threshold and depth contiguity. Criteria-based quantification was therefore evaluated for the same regions at a cortical depth of 0.4 mm – a choice based on relatively high venous density, and potential for comparison with two-photon microscopy data. When the depth contiguity criterion was fixed at 4 pixels, but the intensity threshold varied from 80% to 90% of average tissue signal intensity, the density of identifiable venous vessels of all sizes was 4.4 ± 0.6 and 8.0 ± 1.6 / mm² (12 hemispheres), respectively. When the intensity threshold was fixed at 85%, but the depth contiguity criterion varied from 3 pixels (~180 μm) to 5 pixels (~300 μm), the density of identifiable venous vessels of all sizes was 6.4 ± 1.3 and 5.3 ± 0.9 / mm² (12 hemispheres), respectively.

Mean FWHMin values at cortical depths of 0.4, 1.0, and 1.6 mm were 128 ± 10, 131 ± 12, and 141 ± 14 μm, respectively, for veins identified with the default criteria. More than 95% of identifiable venous vessels within the regions measured at each cortical depth had FWHMin values between 90 and 190 μm. Quantities representing FWHMin and the number of in-plane contiguous pixels are not inter-convertible due to inherent differences in their properties. When small vessels are not fully contained within a pixel, the resulting artificial broadening is likely to more severely affect the FWHMin value to an unknown degree.

Two-photon microscopy studies

The SaO₂ ranges for five animals used for two-photon microscopy studies were 90–97% (92 ± 4%). Detailed intracortical vasculature including capillaries are visualized in the two-photon microscopy data (see Fig. 5a). Images obtained at cortical depths of 0.1 and 0.4 mm (Fig. 5b and c) represent details not detectable in the MRI data. Cross sections of intracortical venous vessels that are perpendicular to the cortical surface have round profiles (e.g., Fig. 5b and c, arrows), where diameters were measured. The slopes in the cumulative venous density plots for cortical depths of 0.1 and 0.4 mm (Fig. 5d-e) indicate a large population of relatively small venules (~10–30 μm diameter) compared to larger venous vessels in intracortical vasculature. At cortical depths of 0.1 mm and 0.4 mm, mean diameters of 23 ± 12 μm (96 venous vessels from 5 animals) and 17 ± 10 μm (59 venous vessels from 5 animals), respectively were statistically different (p < 0.05). Note that only vessels traceable to the cortical surface for venous/arterial assignment were measured and therefore the smallest vessels are greatly underrepresented. The total venous densities at cortical depths of 0.1 and 0.4 mm were 23.2 ± 2.9 / mm² and 14.2 ± 4.0 / mm² (Fig. 5d–e, right-most bars), respectively, which were also statistically significant (Wilcoxon signed rank test, p < 0.05). Mean venous densities for vessels with diameter > 10, 15, 20, 25, and 30 μm were 11.1 ± 3.9, 5.3 ± 1.8, 3.4 ± 1.6, 2.7 ± 1.6, and 1.5 ± 1.6 / mm² at a cortical depth of 0.4 mm (Fig. 5e), respectively.

FIG. 5.

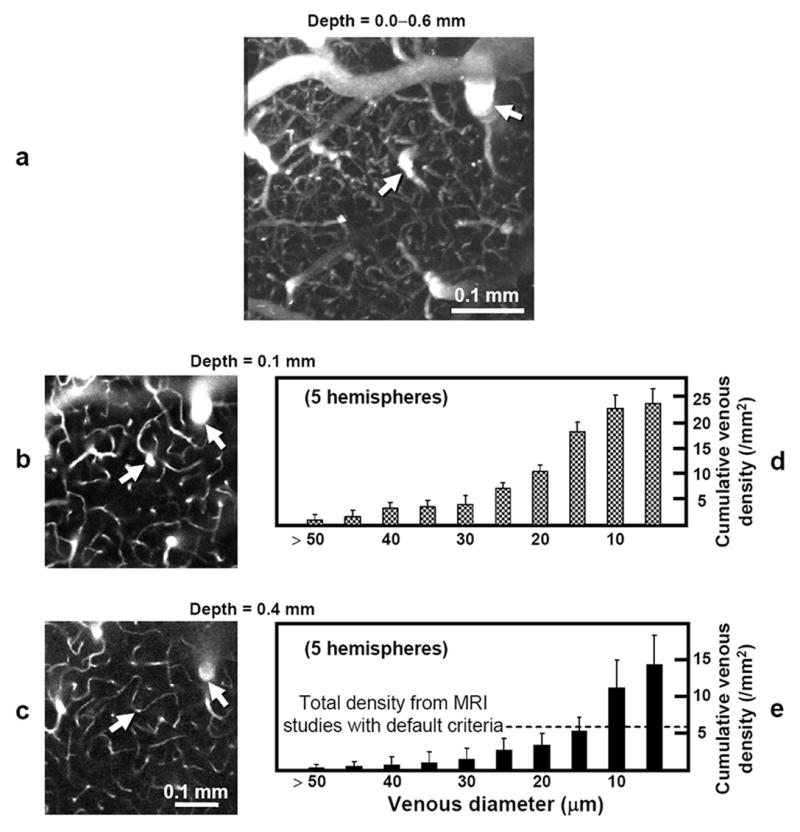
Images from a 3D in vivo two-photon angiographic dataset and cortical depth-dependent quantification of venous distributions. a–c: Data from one animal. The ability of this in vivo technique to resolve intracortical arteries and veins with much finer detail than by BOLD venography is illustrated in the maximum-intensity projected reconstruction (0.456 × 0.456 × 0.6 mm³) along the axial direction (a), where complete vascular networks including capillaries with ~5-μm diameter are observed. Two-dimensional single plane images (0.456 × 0.456 mm²) parallel to the surface at cortical depths of 0.1 mm (b) and 0.4 mm (c) show that relatively large sized vessels perpendicular to the cortical surface appeared as round shapes. Intracortical veins (and also arteries) can be traced between the surface and deep cortical regions, as seen in examples indicated by arrows. Note that these two-photon microscopy images (b and c) represent only ~1/16 the area as compared to the MRI venograms of Fig. 4c–f. Cumulative intracortical venous densities (expressed as minimum venous diameter) are plotted as a function of diameter at cortical depths of 0.1 (d) and 0.4 mm (e) for all studies (N = 5). The right-most bar in each plot represents total venous density, which decreases with cortical depth (p < 0.05). Vertical scales were independently adjusted for better visualization. The density of smaller-diameter venous vessels (10–30 μm) is higher than that of larger-diameter vessels at both cortical depths. Density at 0.4-mm depth for intracortical venous vessels with diameter ≥ 15 μm is 5.3 ± 1.8/ mm², which roughly corresponds to the venous density measurement of 5.7 ± 1.0 / mm² from our MRI data at the same depth using the default criteria (broken line). Note that due to a small field of view of two-photon microscopy, the two-photon densities were quantified for regions covering roughly half the area as compared to MRI data.

Discussion

Contrast in BOLD venograms

A longer echo time improved contrast in 9.4-T BOLD venograms, by limiting noise due to the correspondingly narrower acquisition bandwidth (i.e. enhancing SNR of tissue and thus CNR between tissue and blood) and by extending the susceptibility effect of dHb further into the surrounding tissue (Fig. 1). Empirical results of the TE-dependent studies also match theoretical expectations. Tissue signal intensity depends on exp(−TE/T_2,t*), where T_2,t* is the T₂* value from tissue, while the noise level depends on (T_read)^−1/2. Therefore tissue SNR is dependent on exp(−TE/T_2,t*)·T_read^1/2, where TE in our studies is (T_delay+T_read/2). Tissue SNR is highest when T_delay is minimized (5 ms) and T_read = T_2,t* (as seen by differentiation with respect to T_read). In our experiments, T_2,t* values were found to be 31.4 ± 1.5 ms (large brain region in Fig. 1c) and 35.0 ± 0.6 ms (small cortical region in Fig. 1d) (N = 6). Thus, optimal SNR will be achieved when T_read is 31.4–35.0 ms and the corresponding TE is 20.7–22.5 ms, which agrees with our experimental findings (Fig. 1c and d). Because the optimal TE value for 9.4-T BOLD microscopy is relatively long, the minimum-phase Shinnar-Le Roux RF pulse used here to test TE-dependence could be replaced with any RF pulse.

The effect of phase-contrast filtering (10,27,28) to enhance susceptibility weighting for 9.4-T BOLD microscopy was examined with our rat brain data obtained for all five TE values at FiO₂ = 30% after removing variations in the phase datasets due to static field inhomogeneity with a high-pass filtering algorithm (29). Contrast was enhanced for some venous patterns, but there was little improvement in their overall detectability with phase-contrast filtering, unlike the improvements seen at low fields (10,11,27). Phase-contrast filtering at 9.4 T also introduced significant susceptibility artifacts at regions near air/tissue/bone interfaces, which were more severe at longer TE values. These observations were consistent in all six animals. Although the effect of phase-contrast filtering at 9.4 T may be debatable, the lack of distortion in images without phase-contrast filtering appears to make them preferable. Further optimization and systematic analyses are required to determine the utility of high-field phase-contrast filtering.

Threshold level for venous identification

Our choice of 85% of the average tissue signal intensity as the threshold level for positive assignment of venous vessels was based on the following reasons. According to literature (30), a CNR value of ~5 is required for reasonable discrimination. CNR between tissue and venous blood can be expressed as ΔS/σ = (ΔS/S_t)·(S_t/σ) = (ΔS/S_t)·SNR, where ΔS represents the signal difference between venous blood and tissue, S_t is the average tissue signal intensity, and σ is noise, i.e. the standard deviation of signal. Since ΔS/S_t at an 85% threshold level is 0.15, and SNR of tissue in a region without prominent vessels at TE = 20 ms is 35.8 ± 5.4 (Fig. 1d), the resultant CNR is 5.37 (= 0.15 × 35.8), meaning our intensity threshold criterion is reasonable. Our choice of threshold level is also supported by the observation that histograms of the cortical depth-dependent 1.8 × 1.8 × 0.059 mm³ regions have a non-Gaussian distribution for signal intensities below ~85% of the average tissue intensity (example in Fig. 4g), which seems to indicate contributions from the hypointense pixels containing venous vessels.

Minimum-detectable vessel size in BOLD microscopy

Detectability of venous and arterial vasculature can be roughly estimated by comparing BOLD microscopy patterns to two-photon microscopy diameter measurements. Intracortical venous diameters measured by our two-photon microscopy studies were < 80 μm (data not shown). According to in vivo measurements of pial venous diameters, with every increase in venous branching order in the cortex, venous diameter decreases by a factor of ~2 (31). The analogous relationship indicates the first branches off from the largest intracortical veins (one increase in branching order) may have diameters of < 40 μm (i.e., half of < 80 μm). In our BOLD microscopy data, when systemic SaO₂ values are 90–97%, these branches were indeed detected (see Fig. 3d and e). Systemic venous oxygen saturation levels measured in separate animals under the same conditions were 50 ± 3% (N = 2) (equivalent to 71% with the human hemoglobin P₅₀ value for calculation). It is therefore reasonable to assume that venous vessels with diameter < 40 μm are detectable under our experimental conditions, when systemic venous and arterial oxygenation levels are ≤ 50 and 90%, respectively. Intracortical arterial diameters measured in our two-photon microscopy studies were < 40 μm (data not shown). In our BOLD venograms, new vascular patterns that were likely of arterial origin (arrows in Fig. 2c and d) appeared when systemic SaO₂ values were less than 80%, indicating that intracortical vessels with diameters < 40 μm may be detectable under these conditions.

To better assess detectability of venous vasculature, BOLD microscopy densities were compared with actual diameter-dependent densities measured by two-photon microscopy. Density for all venous vessels detected by BOLD microscopy for our conditions at 0.4-mm depth in the somatosensory cortex was 5.7 / mm² for default criteria for intensity threshold and depth contiguity and 8.0–4.4 / mm² over the range of criteria tested; comparison with two photon data at the same depths shows a venous detectability of ~15-μm and 10–20 μm, respectively. This correspondence implies that our BOLD microscopy may detect venous vessels at least as small as 20-μm diameter. But, since different animal groups were used for MRI and two-photon studies, there may be some errors in matching cortical depths between the two modalities. Inspection of two-photon microscopy data in Fig. 5d and e shows that cumulative density decreases for vessels of all sizes as cortical depth increases. Thus, a more conservative estimate of MR vessel detectibility can be obtained by comparing venous density from MRI studies measured at 0.4-mm depth with the cumulative densities from two-photon studies measured at 0.1-mm depth (Fig. 5d); BOLD microscopy venous densities of 5.7 /mm² for default criteria and 8.0–4.4 /mm² for the range of criteria tested then correspond to conservative detectability estimates of 25–30 μm and 20–30 μm, respectively.

FWHMin values of intracortical veins identifiable in our MRI studies were mostly 90–190 μm, indicating that the extended susceptibility effect of dHb into surrounding tissue makes veins appear to be more than triple their actual size under our experimental conditions. This exaggerated size compares favorably with previous blood-filled vascular phantom studies at 7 and 8.4 T by Ogawa et al. (1,2). It should be noted that the spatial extent of signal dephasing induced by the susceptibility effect of dHb is dependent on many parameters determined by experimental conditions (TE, magnetic field strength, and voxel resolution) and physiology (blood oxygenation level, hematocrit level, and vessel size and orientation).

To obtain further insight into vessel detectability at 9.4 T as a function of local oxygen saturation level and signal intensity threshold, computer simulations were performed based on a cylinder model of a single blood vessel perpendicular to both the main magnetic field and imaging plane (11,28,32,33). The area defined by in-plane resolution in these 2D simulations is denoted here as a “pixel”. Signal intensity of a pixel containing varying portions of a single vein (relative to pixel intensity without any venous contribution) was calculated for our experimental conditions as a function of vessel diameter, by considering magnitude and phase of both intra- and extra-vascular spins within the pixel. Signal intensity is dependent on the partial volume fraction of venous blood (which is related to the position of the vein within the pixel), and thus the condition with the lowest partial blood volume fraction (i.e., when the center of the venous vessel is located at a corner of the pixel) was chosen for our simulation of minimum detectability. Parameters for the simulation were T₁ of tissue and venous blood = 1.9 and 2.2 s, respectively (34); tissue T₂* = 35 ms; venous T₂* = 4.0, 4.9, 6.4, 9.0, and 15.2 ms for oxygen saturation levels of 50, 60, 70, 80, and 90%, respectively (16) (based on venous T₂ values measured in rat brain with different oxygen saturation levels calculated by human blood gas analyzer); relative spin density of tissue and venous blood = 0.89 and 0.86 (35); hematocrit level = 0.4; and susceptibility difference between fully oxygenated and deoxygenated blood = 0.2 × 10⁻⁶ in cgs units (32,36). For local oxygen saturation levels of 50, 60, 70, 80, and 90%, minimum-detectable vessel diameters for our conditions (e.g. TE = 20 ms, in-plane resolution = 78 × 78 μm², etc.) are 20, 22, 25, 30, and 48 μm when the intensity threshold is 85% of tissue signal intensity, respectively; the diameters are 23, 26, 30, 36, and 56 μm at the intensity threshold of 80%, respectively, and 16, 18, 20, 25, and 39 μm at the intensity threshold of 90%, respectively. Only systemic oxygen saturation levels were measured, but if it is assumed that local and systemic venous oxygen saturation levels are similar, then local venous oxygen saturation levels are 50 ± 3% (when measured systemic SaO₂ values were 90–97%). Our simulations therefore indicate that vessels with diameters as small as 16–23 μm can be detected in our venograms when the local oxygen saturation level is ≤ 50%.

In summary, both simulation results and density measurement comparisons between the two different imaging modalities (BOLD-based and two-photon microscopy) make it reasonable to conclude that venous vessels with diameters as small as ~16–30 μm are detectable by 9.4-T BOLD microscopy under our experimental conditions.

Conclusions

The detectability of intracortical vessels in BOLD microscopy depends on many physiological and imaging parameters including vessel diameter, oxygenation, hematocrit level, magnetic field, TE, voxel resolution, and SNR. When 9.4-T BOLD microscopy is performed with TE = 20 ms and isotropic scan resolution = 78 μm, the diameter of the smallest-detectable venous vessels is in the range of ~16–30 μm for FiO₂ of ~30%, as demonstrated by our two-photon microscopy studies and computer simulations. Lower oxygenation levels improve the detectability of vessels, including those presumed to be arteries. Higher spatial resolution may enable detection of even smaller vessels. Exploiting high-field advantages to obtain high-resolution venograms without exogenous contrast agent provides information which may be valuable in functional, developmental, and clinical studies of animals and humans. Indeed, functional maps obtained from MRI and from invasive optical imaging have already been coregistered using 9.4-T BOLD venograms (37,38).