Abstract
If a bar stimulus extends beyond a cell's receptive field, then alterations in binocular disparity parallel to the bar's orientation leave the portion of the stimulus within the cell's receptive field unchanged. This makes it hard for the cell to respond correctly to the bar's disparity. Likening the cell's receptive field to an aperture through which the cell views the world, this issue has been called the “aperture problem” and is a specific form of the more general stereo correspondence problem. We found no cells in macaque primary visual cortex (V1) that, when faced with this situation, were sensitive to the disparity of the bar. However, we did find a number of cells that showed sensitivity to parallel disparity shifts, but these cells responded only to the ends of the long bar. The ability to respond selectively to such tracking features could be the first step towards solving the stereo aperture problem. The second step would require either that the disparity information that in V1 is associated only with the ends of the stimulus be associated with the rest of the stimulus or that subsequent stages of visual processing respond preferentially to the end-selective cells. As this second step does not appear to occur in V1, we conclude that V1 only partially solves the stereo aperture problem.
Keywords: correspondence problem, depth perception, end-stopping, stereopsis, striate cortex, V1
Introduction
Because of the lateral offset of our 2 eyes, objects at different distances from the observer project to different relative positions on the 2 retinas. The difference in these positions, known as the object's disparity, can be used by the visual system to estimate the distance to the object, an ability known as stereopsis (Wheatstone 1838). The inputs from the eyes are first combined in the primary visual cortex (V1), and in this region disparity-sensitive cells are found (Barlow and others 1967; Nikara and others 1968; Clarke and others 1976; Poggio and Fischer 1977; Fischer and Kruger 1979; Ferster 1981; for a review see Cumming and DeAngelis 2001). Because V1 cells have small receptive fields, they should often suffer from the particular form of the stereo correspondence problem (Julesz 1971; Marr 1982; for a review see Howard and Rogers 2002) usually referred to as the aperture problem (Morgan and Castet 1997).
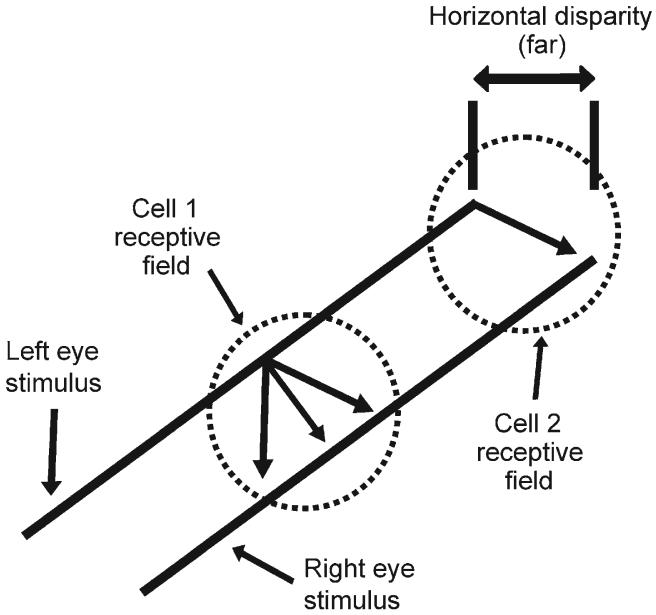
Figure 1, which shows the projection of a binocular bar stimulus onto 2 receptive fields, illustrates the issue. The information contained within Cell 1's receptive field is insufficient for the cell to determine which segment of the left-eye stimulus should be matched with which segment of the right-eye stimulus. The 3 arrows show 3 different possible matches, each of which would result in a different estimate of the bar's disparity. Conversely, Cell 2's receptive field contains the ends of the bar, and so this cell could signal the true disparity. Consequently, Cell 2 does not suffer from the stereo aperture problem.
Figure 1.
The stereo aperture problem. The receptive field of a cell can be thought of as an aperture through which the cell responds to the visual scene. The information contained within Cell 1's receptive field is insufficient for the cell to determine which segment of the left-eye stimulus should be matched with which segment of the right-eye stimulus, and so the cell suffers from the aperture problem. The 3 arrows show 3 different possible matches, each of which results in a different estimate of the stimulus' disparity. Conversely, Cell 2's receptive field contains the ends of the bar, and so this cell could signal the correct disparity.
The correspondence problem in general (e.g., Marr 1982; Lorenceau and others 1993; Rubin and Hochstein 1993) and the stereo aperture problem in particular (Bakin and others 2000; Cumming and Parker 2000) have attracted considerable attention. The latter 2 studies were physiological investigations and used grating stimuli that extended beyond each cell's receptive field. When the disparities of the gratings were altered, without altering the portion of the stimuli contained within the cells' receptive fields, it was found that V1 cells' responses were not affected. This suggested that cells in V1 cannot utilize stereoscopic information from outside their receptive fields. By using a different stimulus we were able to go one step further than these previous studies and show that some cells in V1 partially solve the stereo aperture problem. They do this by responding preferentially to the disparity of the ends of the stimuli. In other words, they combine disparity sensitivity with a kind of feature tracking.
Materials and Methods
All procedures were in compliance with National Institutes of Health (NIH) and Harvard University guidelines for the use of animals. In our experiments we used a modification (Livingstone and Tsao 1999) of the reverse-correlation technique (Jones and Palmer 1987; Ohzawa and others 1990) described in detail elsewhere (Livingstone 1998; Livingstone and Tsao 1999). In brief, these experiments used a male (R) and female (J) rhesus macaque monkey (Macaca mulatta). During the experiment the alert monkey was seated comfortably in a standard primate chair (Crist Instruments, Hagerstown, Maryland) with its head fixed and maintained foveation on a fixation point for a juice reward. We isolated approximately 315 single units but only 55 were both disparity sensitive and sufficiently stable to allow further study. The recordings were performed extracellularly using fine electropolished tungsten electrodes coated with vinyl lacquer (Frederick Haer, Bowdoinham, Maine) (Hubel 1957). The signals were amplified, band-pass filtered (1-10 kHz), and fed into a window discriminator (BAK Electronics, Germantown, Maryland). The isolation of the unit was confirmed by monitoring the size and shape of the spike as well as by verifying the existence of a refractory period. A GenuineIntel ×86 computer was used for stimulus generation and collection, using additional in-house software and hardware. Stimuli were presented on a 53 cm NEC multi-synch monitor 94 cm in front of the monkey. Eye position was monitored using a surgically implanted eye coil and magnetic field coils manufactured by DNI (Newark, Delaware) (Judge and others 1980). At the beginning of each recording session the eye monitor was calibrated by having the monkey follow a fixation spot that appeared randomly at each of the 4 corners and at the center of a 8° × 8° square on the monitor. Color filters and colored stimuli were used to stimulate each eye independently. The luminance of the monocular stimulus seen through that eye's filter was 3.6 cd/m2 and through the other eye's filter, less than 0.2 cd/m2. For each cell we generated 2 response maps in the manner described later. Because this process took a considerable amount of time, and because it was difficult to keep a cell well isolated, we did not perform further tests on the cells. In particular, we did not determine whether the cells were simple or complex.
Generating Response Maps
A continuous record of spike time (at 1 ms resolution), stimulus position, and eye position (at 4 ms and 0.03° resolution) was taken. For monkey J, the cells were recorded at an eccentricity of 5.7°-7.0° and for monkey R, 1.3°-1.8°. For each cell we determined the position, orientation, and length of a binocular bar stimulus, which always had a width of 0.07°, that elicited the largest response. To screen for disparity-tuned cells, an optimally oriented binocular bar was repeatedly flashed over the cell's receptive field (34 ms on, 34 ms off). Between flashes the position of each monocular component of the binocular bar was altered in a direction perpendicular to the orientation of the bar by an amount that was random but satisfied the constraint that each point in the stimulus range was visited equally often. Reverse-correlation binocular-response maps were generated by taking each spike, looking back in time by a given delay, and assigning that spike to the 2 monocular bar positions at that time. The delay was set to equal the time to peak of the poststimulus time histogram (PSTH) for stimuli in the receptive field. It was found that mapping resolution could be increased by continuously correcting the stimulus position for eye position. The maps were smoothed by convolving them with a 2-dimensional Gaussian of standard deviation of 0.10°. The background firing rate, which was defined as the average response at zero to 34 ms delay, was then subtracted.
Screening for Disparity-Sensitive Cells
The point of our study was to determine whether cells in V1 can solve the stereo aperture problem. To do this we had to find cells that were sensitive to disparity and then determine their preferred disparity and receptive field width. To do this we used the reverse-correlation technique with pairs of monocular stimuli that were translated perpendicular to their orientation. We call the resultant response maps “perpendicular binocular-response maps” to distinguish them from the response maps generated by moving the monocular stimuli parallel to their orientation, which we will refer to as “parallel binocular-response maps.”
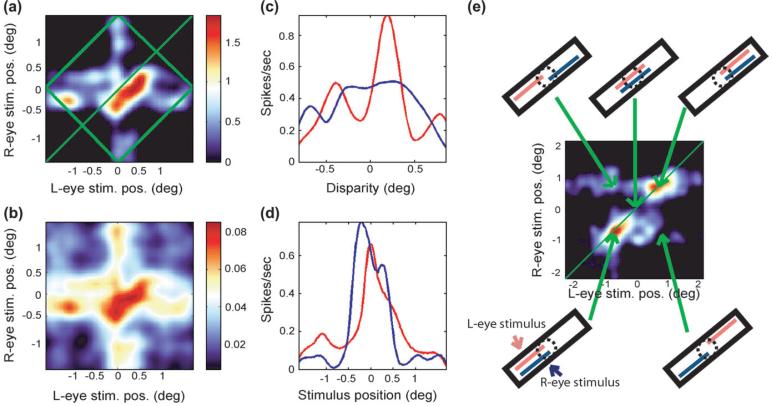
Figure 2a shows the perpendicular binocular-response map obtained from a cell that was sensitive to changes in disparity perpendicular to its optimum orientation. The map is centered on the cell's receptive field. The position of the left-eye bar, measured from the center of the bar to the left end of the stimulus range, is represented on the x axis, and the right-eye bar position is mapped on the y axis. The firing rate of the cell as a function of the position of each monocular component is indicated by a color code. Such binocular-response maps have been used in a number of previous publications to determine disparity tuning (Ohzawa and others 1990; Livingstone and Tsao 1999; Tsao and others 2003). The standard error associated with each point of this map is plotted in Figure 2b. Considering this subplot we see that for the region of highest activation in Figure 2a, the standard error was approximately 4.5%. All maps used in this study had a standard error of their maximum response of less than 6%.
Figure 2.
(a) The perpendicular binocular-response map with a color code representing spikes per second above the background firing rate. (b) The standard error associated with each point in the response map. (c) The cell's disparity-tuning curve (red) and the response range curve (blue). (d) The left (red) and right (blue) monocular response profiles. (e) A binocular-response map generated by stimulus translations parallel to its orientation. Insets surrounding the map show the stimulus positions for various points on the map. The cell responded only when the ends of the bar were within its receptive field and so has a high EE index.
Disparity Tuning
Superimposed on the map in Figure 2a is a green square that has been rotated by 45°. Because disparity is constant along lines parallel to the +45° diagonal, drawn in green, we can integrate the map parallel to this diagonal, within the square, to generate the cell's disparity-tuning curve. By integrating only within the square, we ensure that for each disparity we utilize the same number of data points (Tsao and others 2003). The peak of this curve represents the cell's preferred disparity.
Elongation Index for Perpendicular Disparities
Looking at the region of high activity in Figure 2a, we see that it is elongated parallel to the +45° diagonal. Because points that can be joined by a line parallel to this diagonal correspond to the same disparity but different stimulus positions, we can say that the cell in Figure 2a is more sensitive to changes in disparity than to changes in stimulus position. To quantify how sensitive a cell was for binocular disparity, we compared the cell's sensitivity to changes in disparity with its sensitivity to changes in stimulus position. To do this we first obtained the cell's disparity tuning by integrating the perpendicular binocular-response map parallel to +45° diagonal. Then we measured the response as a function of stimulus position along the receptive field by integrating the same map parallel to the -45° diagonal. We defined the width of these 2 curves to be their widths at half their respective maximum values. If the curve was multimodal, we would progress from one end of the curve toward the center until the curve increased beyond half its maximum value and then we would repeat this procedure starting from the other end. We defined the curve's width to be the separation of these 2 points. We defined the cell's disparity sensitivity to be the ratio of the width of the response curve to the width of the disparity-tuning curve. Because we are interested only in disparity-tuned cells, we studied only cells with a disparity sensitivity more than 1; that is, cells that were more sensitive to changes in disparity than to changes in stimulus position. Fifty-five of the 315 cells that we recorded from fit this criterion and were studied further.
Left and Right Monocular Receptive Field Widths
We also used this same perpendicular binocular-response map to estimate the width of the cell's receptive field. To do this we integrated the response map parallel to the y axis to generate the response profile drawn in red in Figure 2d. This curve shows the average activity of the cell as a function of the position of the stimulus visible to the left eye. We then integrated the response map parallel to the x axis to generate the response profile drawn in blue, which represents the average activity as a function of the stimulus visible to the right eye.
Results
Parallel Disparity Sensitivity: Does V1 Solve the Stereo Aperture Problem?
To measure the ability of cells to solve the aperture problem, we used bars that were considerably longer than the cell's receptive field width, which was on average 0.35° (standard deviation = 0.11°). Monocular stimuli were flashed as for the perpendicular binocular maps, but between flashes they were varied in position parallel to their orientation, with the perpendicular disparity always at the cell's optimum value. We used a stimulus range that was large enough that at some points during the stimulus train the ends of the stimulus fell within the cell's receptive field. This allowed us to measure the response of the cell both to the ends and to the center of the bar stimulus.
Figure 2e shows one of the parallel binocular-response maps that we obtained. It shows the response of a cell as a function of the positions of the left and right stimuli. Surrounding this map are diagrams that indicate the stimulus positions at 5 points in the map. This figure demonstrates that the cell responded selectively over a narrow range of parallel disparities.
End-Excitability
Figure 2e also shows that this cell responded better when the ends of the 2 monocular bars were in its receptive field than when the bars were centered on its receptive field, a characteristic we shall refer to as “end-excitability (EE),” to distinguish it from a closely related phenomenon known as “end-stopping.” End-stopping is measured by varying the length of a bar stimulus that is centered on a cell's receptive field and finding the degree to which the cell's response is suppressed. It is assumed that end-stopping arises because there are inhibitory end zones, at either or both ends of the receptive field, that produce response suppression when the stimulus extends into them (Hubel and Wiesel 1965; Bolz and Gilbert 1986). In our experiments we used only long bars, so at least one end zone was always activated, but for many cells we saw a big difference in response depending on whether the stimulus extended into one or both end zones. End-stopped cells are often selectively responsive to the ends of long bars, and the degree to which cells respond to the ends of flashed stimuli is highly correlated with their end-stopping (Pack and others 2003). We chose not to measure end-stopping because we could obtain the EE coefficient directly from the same map that was used to measure the sensitivity for parallel disparity, thus providing a direct comparison between these 2 parameters. To quantify each cell's EE we used the parallel binocular-response map to obtain the 2 monocular response curves as described previously. For each curve we estimated the EE coefficient using the following formula:
| (1) |
where Rend and Rcenter were the responses to the end and the center of the bar, respectively (i.e., the response when the end or the center of the bar was centered on the cell's receptive field). In the case that the response to one end was greater than the other, we used the larger value for Rend. This definition for EE can range from +1, for cells that respond to only the ends of bars, to -1, for those that respond only to the center. In practice all our EE coefficients ranged between +1 and 0, consistent with previous findings for end-stopping (DeAngelis and others 1994; Jones and others 2001; Sceniak and others 2001).
EE versus Parallel Disparity Sensitivity
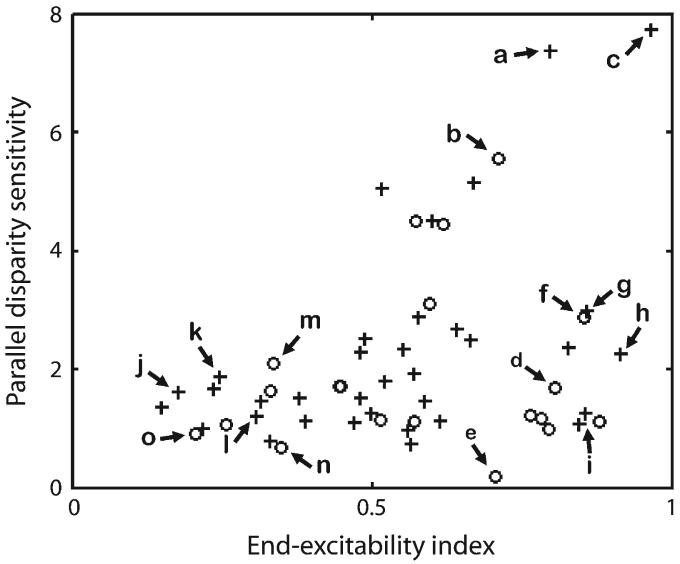
We defined each cell's parallel disparity sensitivity in terms of its elongation index for the parallel response map, which essentially compares the narrowness of the parallel disparity tuning with the sensitivity for stimulus position along the receptive field. The elongation index versus the EE index for the population of 55 disparity-tuned cells is shown in Figure 3. The cell labels refer to Figure 4. The figure shows that several cells were exquisitely sensitive to changes in disparity parallel to the bar's orientation. However, all these cells responded best when the ends of the stimuli were in their receptive fields, a fact that is demonstrated by their having a high EE index.
Figure 3.
The parallel binocular-response map elongation plotted as a function of the EE for the 55 disparity-tuned cells in this study. Crosses and circles indicate data points from monkeys R and J, respectively. Data points corresponding to the 15 cells of Figure 4 are labeled.
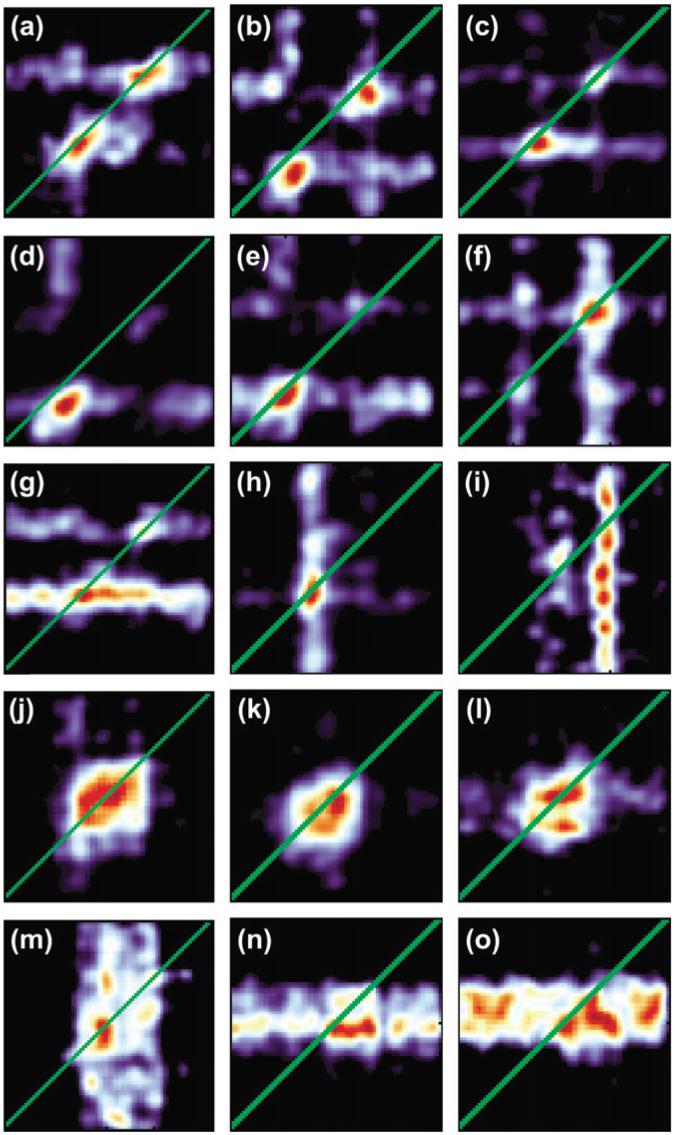
Figure 4.
Parallel binocular-response maps for 15 cells. These cells can be categorized naturally into 5 groups with each row representing a single group. The first 3 categories comprise cells with a high (>0.5) EE index whereas the last 2 comprise cells with low EE indices. The first, second, and fourth categories contain binocular cells whereas the third and fifth contain monocular cells.
The 5 Categories of Parallel Response Maps
We found that the parallel response maps could be naturally divided into 5 categories depending on their ocular dominance and the presence or absence of EE. This is shown in Figure 4 with each row corresponding to a single category. The cells in the first row, which we will refer to as Class One cells, responded preferentially to the ends of the long bar stimuli (cf., Fig. 2e). In particular, all these cells had an EE coefficient more than 0.5. Also these cells responded approximately equally to both left- and right-eye stimuli, with the peak values in the 2 monocular response curves differing by less than 50%. Finally, the peak responses to each end of the binocular bar were approximately equal in that they differed by less than 50%. Out of the 55 disparity-sensitive cells we recorded from, 11 fell into this category. The cells in Category One are the only ones with a high parallel sensitivity and so are the only ones likely to directly contribute to solving the aperture problem.
It is important to stress that many of these cells displayed a sensitivity to parallel disparities beyond that which would be caused solely by EE. Considering Figure 2e, which is an enlargement of Figure 4a, we see that the cell responded only if both the left ends or both the right ends of the 2 monocular stimuli were in its receptive field. Crucially, it did not respond if the left end of the left-eye stimulus and the right end of the right-eye stimulus were in its receptive field or if the right end of the left-eye stimulus and the left end of the right-eye stimulus were in its receptive field. In other words, it responded only if corresponding ends of the monocular stimuli were in its receptive field. These cells have therefore certainly solved a part of the correspondence problem, and for this reason we can describe them as disparity sensitive as opposed to merely having a high EE coefficient.
Cells in the second category, shown in the second row of Figure 4, were similar, except that their responses to the 2 ends of the long bar differed by more than 50%. Fourteen of the disparity-sensitive cells fell into this category. Pairs of these cells that respond to opposite ends could be combined to provide information similar to that carried by a single Category One cell.
Although the cells in the other 3 categories show low sensitivities to parallel disparities and therefore do not provide information that could be used to solve the stereo aperture problem, they do show distinct patterns of EE and ocular dominance. The cells in the third category were like ones in the first and second in that they responded primarily to ends of the stimulus, but unlike the cells in the first 2 categories, those in the third were dominated by either the right (Fig. 4g) or the left eye (Fig. 4h-i) in that the peak response in one monocular response curve was less than half the peak response in the other monocular response curve. For this reason the regions of high activity were elongated either horizontally or vertically. Six of the 55 cells fell into this category.
Cells in the fourth category had an EE coefficient of less than 0.5, meaning that they responded well when the bar was centered on their receptive fields and responded approximately equally to the left- and right-eye stimuli. The region of high activity in each response map was approximately square. Twenty of the cells fell into this category.
Cells in the fifth category also responded preferentially to the center of the stimulus but were strongly monocular, being driven primarily by the left (Fig. 4m) or right (Fig. 4n-o) eye. Four of our cells fell into this category.
Temporal Dynamics
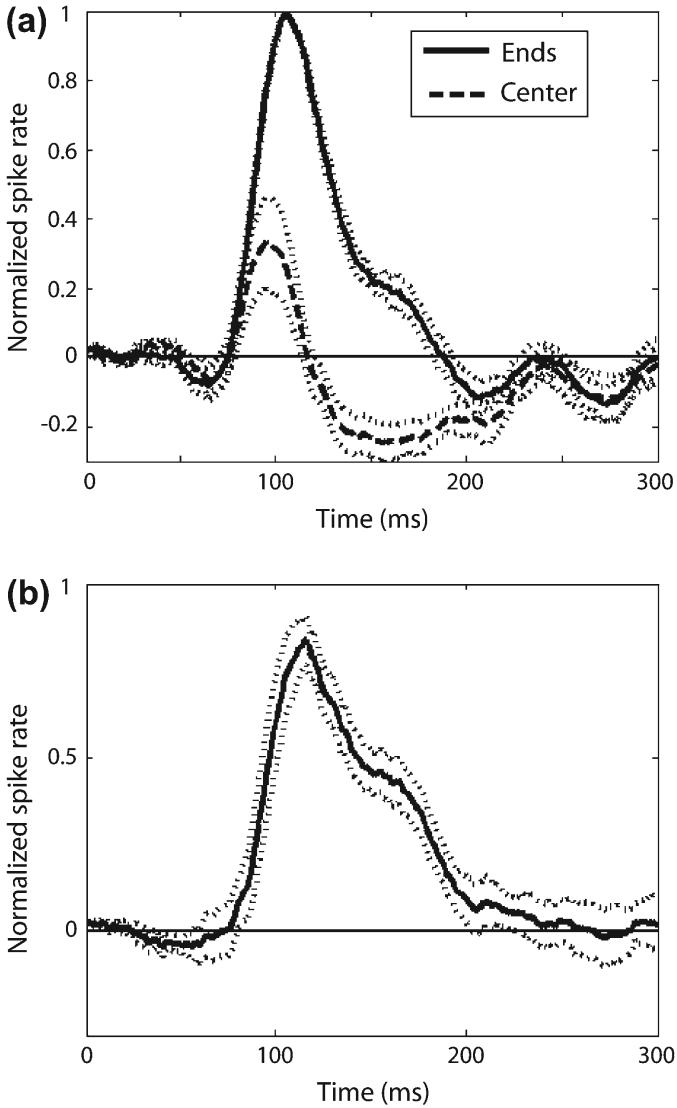
To further our understanding of the mechanisms underlying parallel disparity sensitivity in V1, we analyzed the temporal dynamics of the parallel response maps. For each cell we measured the PSTH for the response to the center and to the ends of the bar. We normalized the 2 PSTHs by the maximum spike rate and then translated both PSTHs along the time axis, each by the same amount, so that the maximum response to the ends of the bar always occurred at the average delay of the population. We repeated this procedure for each of the 8 neurons of Figure 3 that had an elongation index more than 4, because these were the cells that showed the greatest sensitivity to parallel disparity, and averaged the results (Fig. 5a). In this figure the dotted lines that flank the solid lines represent the standard error. The figure shows that initially the responses to the center and to the ends of the bar were similar. At 100 ms, the response to the center began to decrease and fell below the background firing rate at about 120 ms. The difference in the responses to the ends and to the center of the bar is shown in Figure 5b.
Figure 5.
Time course of end suppression. (a) The PSTHs for the responses to the ends and to the center of the bar. (b) The difference between the 2 PSTHs drawn in (a). In both (a) and (b) the dotted lines flanking the solid lines represent the standard error.
The relative time course of the end suppression in these responses is consistent with that reported for end-stopping in a psychophysical study (Yu and Levi 1999). In particular, Yu and Levi claim (p. 2064) that the perceptual correlates of end stopping first appear around 70-100 ms after stimulus onset. This is consistent with our observation that the responses to the center and ends diverge at about this time. Furthermore, Yu and Levi (1999) observed that the perceptual correlates of end stopping asymptote at full strength at 150-200 ms. This finding is consistent with our observation that the PSTH for the response to the center of bar has a minimum at this point.
Discussion
If a bar stimulus extends beyond a cell's receptive field, then alterations in disparity parallel to the orientation of the bar leave the portion of the stimulus within the receptive field unchanged, an issue known as the stereo aperture problem (Morgan and Castet 1997). In this study we asked whether any cells in V1 solved it. As Figure 3 shows, we found a number of cells that had a high elongation index (>4) for parallel disparities and were therefore highly sensitive to the disparity of the bar. Because all these cells responded preferentially to the ends of the stimuli (EE index > 0.5), they essentially avoided the aperture problem. If all disparity-sensitive cells responded only to the ends of stimuli, then this would amount to solving the aperture problem. However, many disparity-sensitive cells responded to the center of the bar (EE index < 0.5) and had a low elongation index, implying that they solved the aperture problem poorly if at all. Consequently, their responses do not accurately reflect the disparity of the stimulus and so must be discounted.
One way the brain could do this would be to propagate the unambiguous disparity information at the ends of the bar into the center of the bar and in this way overrule the ambiguous disparity information at the center of the bar (Grossberg and Mingolla 1993). Alternatively, the visual system could simply ignore the outputs of cells that do not respond selectively to the ends of the stimuli. Our laboratory has previously provided evidence that cells in the middle temporal area (MT), which evolve a solution to the motion aperture problem over about 100 ms (Pack and Born 2001), may do so by selectively responding to end-stopped directional V1 inputs (Pack and others 2003). We now suggest that the feature-tracking property provided by end-stopped V1 cells is the underlying mechanism for the solution to the aperture problem for both motion and disparity.
Notes
We thank Tamara Chuprina and David Freeman for technical assistance and Bevil Conway, Christopher Pack, and Doris Tsao for comments and discussion. This work was supported by a Helen Hay Whitney Foundation grant to PH and NIH grant EY 13135 to ML.
Funding to pay the Open Access publication charges for this article was provided by National Institutes of Health grant EY 13135.
Footnotes
Publisher's Disclaimer: The online version of this article has been published under an open access model. Users are entitled to use, reproduce, disseminate, or display the open access version of this article for non-commercial purposes provided that: the original authorship is properly and fully attributed; the Journal and Oxford University Press are attributed as the original place of publication with the correct citation details given; if an article is subsequently reproduced or disseminated not in its entirety but only in part or as a derivative work this must be clearly indicated. For commercial re-use, please contact journals.permissions@oxfordjournals.org.
References
- Bakin JS, Nakayama K, Gilbert CD. Visual responses in monkey areas V1 and V2 to three-dimensional surface configurations. J Neurosci. 2000;20:8188–8198. doi: 10.1523/JNEUROSCI.20-21-08188.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barlow HB, Blakemore C, Pettigrew JD. The neural mechanism of binocular depth discrimination. J Physiol. 1967;193:327–342. doi: 10.1113/jphysiol.1967.sp008360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolz J, Gilbert CD. Generation of end-inhibition in the visual cortex via interlaminar connections. Nature. 1986;320:362–365. doi: 10.1038/320362a0. [DOI] [PubMed] [Google Scholar]
- Clarke PG, Donaldson IM, Whitteridge D. Binocular visual mechanisms in cortical areas I and II of the sheep. J Physiol. 1976;256:509–526. doi: 10.1113/jphysiol.1976.sp011336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cumming BG, DeAngelis GC. The physiology of stereopsis. Annu Rev Neurosci. 2001;24:203–238. doi: 10.1146/annurev.neuro.24.1.203. [DOI] [PubMed] [Google Scholar]
- Cumming BG, Parker AJ. Local disparity not perceived depth is signaled by binocular neurons in cortical area V1 of the macaque. J Neurosci. 2000;20:4758–4767. doi: 10.1523/JNEUROSCI.20-12-04758.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAngelis GC, Freeman RD, Ohzawa I. Length and width tuning of neurons in the cat's primary visual cortex. J Neurophysiol. 1994;71:347–374. doi: 10.1152/jn.1994.71.1.347. [DOI] [PubMed] [Google Scholar]
- Ferster D. A comparison of binocular depth mechanisms in areas 17 and 18 of the cat visual cortex. J Physiol. 1981;311:623–655. doi: 10.1113/jphysiol.1981.sp013608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer B, Kruger J. Disparity tuning and binocularity of single neurons in cat visual cortex. Exp Brain Res. 1979;35:1–8. doi: 10.1007/BF00236780. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Mingolla E. Neural dynamics of motion perception: direction fields, apertures, and resonant grouping. Percept Psycho-phys. 1993;53:243–278. doi: 10.3758/bf03205182. [DOI] [PubMed] [Google Scholar]
- Howard IP, Rogers BJ. Seeing in depth: depth perception. Porteous; Toronto, Canada: 2002. [Google Scholar]
- Hubel DH. Tungsten microelectrode for recording from single units. Science. 1957;125:549–550. doi: 10.1126/science.125.3247.549. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields and functional architecture in two non-striate visual areas (18 and 19) of the cat. J Neurophysiol. 1965;28:229–289. doi: 10.1152/jn.1965.28.2.229. [DOI] [PubMed] [Google Scholar]
- Jones HE, Grieve KL, Wang W, Sillito AM. Surround suppression in primate V1. J Neurophysiol. 2001;86:2011–2028. doi: 10.1152/jn.2001.86.4.2011. [DOI] [PubMed] [Google Scholar]
- Jones JP, Palmer LA. The two-dimensional spatial structure of simple receptive fields in cat striate cortex. J Neurophysiol. 1987;58:1187–1211. doi: 10.1152/jn.1987.58.6.1187. [DOI] [PubMed] [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC. Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Res. 1980;20:535–538. doi: 10.1016/0042-6989(80)90128-5. [DOI] [PubMed] [Google Scholar]
- Julesz B. Foundations of cyclopean perception. Chicago University Press; Chicago: 1971. [Google Scholar]
- Livingstone MS. Mechanisms of direction selectivity in macaque V1. Neuron. 1998;20:509–526. doi: 10.1016/s0896-6273(00)80991-5. [DOI] [PubMed] [Google Scholar]
- Livingstone MS, Tsao DY. Receptive fields of disparity-selective neurons in macaque striate cortex. Nat Neurosci. 1999;2:825–832. doi: 10.1038/12199. [DOI] [PubMed] [Google Scholar]
- Lorenceau J, Shiffrar M, Wells N, Castet E. Different motion sensitive units are involved in recovering the direction of moving lines. Vision Res. 1993;33:1207–1217. doi: 10.1016/0042-6989(93)90209-f. [DOI] [PubMed] [Google Scholar]
- Marr D. Vision. W.H. Freeman & Co.; New York:: 1982. [Google Scholar]
- Morgan MJ, Castet E. The aperture problem in stereopsis. Vision Res. 1997;37:2737–2744. doi: 10.1016/s0042-6989(97)00074-6. [DOI] [PubMed] [Google Scholar]
- Nikara T, Bishop PO, Pettigrew JD. Analysis of retinal correspondence by studying receptive fields of binocular single units in cat striate cortex. Exp Brain Res. 1968;6:353–372. doi: 10.1007/BF00233184. [DOI] [PubMed] [Google Scholar]
- Ohzawa I, DeAngelis GC, Freeman RD. Stereoscopic depth discrimination in the visual cortex: neurons ideally suited as disparity detectors. Science. 1990;249:1037–1041. doi: 10.1126/science.2396096. [DOI] [PubMed] [Google Scholar]
- Pack CC, Born RT. Temporal dynamics of a neural solution to the aperture problem in visual area MT of macaque brain. Nature. 2001;409:1040–1042. doi: 10.1038/35059085. [DOI] [PubMed] [Google Scholar]
- Pack CC, Livingstone MS, Duffy KR, Born RT. End-stopping and the aperture problem: two-dimensional motion signals in macaque V1. Neuron. 2003;39:671–680. doi: 10.1016/s0896-6273(03)00439-2. [DOI] [PubMed] [Google Scholar]
- Poggio GF, Fischer B. Binocular interaction and depth sensitivity in striate and prestriate cortex of behaving rhesus monkey. J Neurophysiol. 1977;40:1392–1405. doi: 10.1152/jn.1977.40.6.1392. [DOI] [PubMed] [Google Scholar]
- Rubin N, Hochstein S. Isolating the effect of one-dimensional motion signals on the perceived direction of moving two-dimensional objects. Vision Res. 1993;33:1385–1396. doi: 10.1016/0042-6989(93)90045-x. [DOI] [PubMed] [Google Scholar]
- Sceniak MP, Hawken MJ, Shapley R. Visual spatial characterization of macaque V1 neurons. J Neurophysiol. 2001;85:1873–1887. doi: 10.1152/jn.2001.85.5.1873. [DOI] [PubMed] [Google Scholar]
- Tsao DY, Conway BR, Livingstone MS. Receptive fields of disparity-tuned simple cells in macaque V1. Neuron. 2003;38:103–114. doi: 10.1016/s0896-6273(03)00150-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheatstone C. Contributions to the physiology of vision—part the first. On some remarkable, and hitherto unobserved phenomena of binocular vision. Philos Trans R Soc Lond B Biol Sci. 1838;128:371–394. [Google Scholar]
- Yu C, Levi DM. The time course of psychophysical end-stopping. Vision Res. 1999;39:2063–2073. doi: 10.1016/s0042-6989(98)00263-6. [DOI] [PubMed] [Google Scholar]