Determination of Optical Properties of Superficial Volumes of Layered Tissue Phantoms

Abstract

Previously, we reported the design of a new diffusing probe that employs a standard two-layer diffusion model to recover the optical properties of turbid samples. This particular probe had a source-detector separation of 2.5 mm and performance was validated with Monte Carlo simulations and homogeneous phantom experiments. The goal of the current study is to characterize the performance of this new method in the context of two-layer phantoms that mimic the optical properties of human skin. We analyze the accuracy of the recovered top layer optical properties and their dependences on the thickness of the top layer of two-layer phantoms. Our results demonstrate that the optical properties of the top layer can be accurately determined with a 1.6 mm source-detector separation diffusing probe when this layer thickness is as thin as 1 mm. Monte Carlo simulations illustrate that the interrogation depth can be further decreased by shortening the source-detector separation.

I. Introduction

DIFFUSE OPTICAL SPECTROSCOPY (DOS) has been utilized to determine optical properties of deep tissues efficiently and noninvasively [2]. Time-domain and frequency-domain DOS usually employ source-detector separations larger than 5 mm, thus enabling the use of a standard diffusion model to accurately recover tissue optical properties [1], [3]. Since the source-detector separation is roughly proportional to the interrogation depth [4] in DOS, determination of the optical properties of superficial volumes of tissues requires a source-detector separation shorter than 3 mm in addition to improved theoretical models, such as or Monte Carlo methods [5], [6]. Recently, we reported a new DOS measurement geometry that uses a standard two-layer diffusion model to determine optical properties of homogeneous turbid samples at short source-detector separations. The new probe employs a highly scattering layer to diffuse photons emitted from a collimated light source before they enter the sample volume of interest. A modified two-layer standard diffusion model is then able to describe photon transport in this geometry at source-detector separations shorter than 3 mm. Monte Carlo simulations and homogeneous phantom studies demonstrated that the optical properties of samples can be recovered to within 5% of true values using this new diffusing probe with 2.5-mm source-detector separation [1].

The objective of this paper is to estimate the diffusing probe's interrogation depth and its ability to extract accurate optical properties from the top layer of a two-layer tissue phantom. We fabricated two-layer phantoms that consist of top layers of various thicknesses above much thicker substrates. The optical properties of top layers and substrates are similar to those of the epidermis-dermis and subcutaneous fat layer, respectively [7]. By carefully characterizing the two-layer phantoms, we expect to estimate the diffusing probe's sampling depth when it is employed to measure human skin, and thereby determine its applicability to quantify optical properties of in-vivo epidermis-dermis. In addition, we employed Monte Carlo simulations as a qualitative tool to analyze the dependence of interrogation depths on source-detector separations of the diffusing probe in support of our experimental observations.

II. Material and Methods

The frequency-domain photon migration instrument used to conduct our DOS measurements has been described in detail elsewhere [2]. A single laser diode at 785 nm was swept across a frequency range from 50 MHz to 300 MHz in 90 equal steps. Using multiple modulation frequencies enhances the robustness of the recovery of optical properties [8]. The diffusing probe geometry, illustrated in Fig. 1, is comprised of two optical fibers (3M, core diameter = 600 μm, NA = 0.37) for delivering and collecting photons, and a highly scattering layer (Spectralon Slab, Labsphere) to diffuse photons from the source fiber. A modified two-layer, diffusion-based model is employed to deduce the sample optical properties from measured phase delay and amplitude demodulation [1].

Fig. 1.

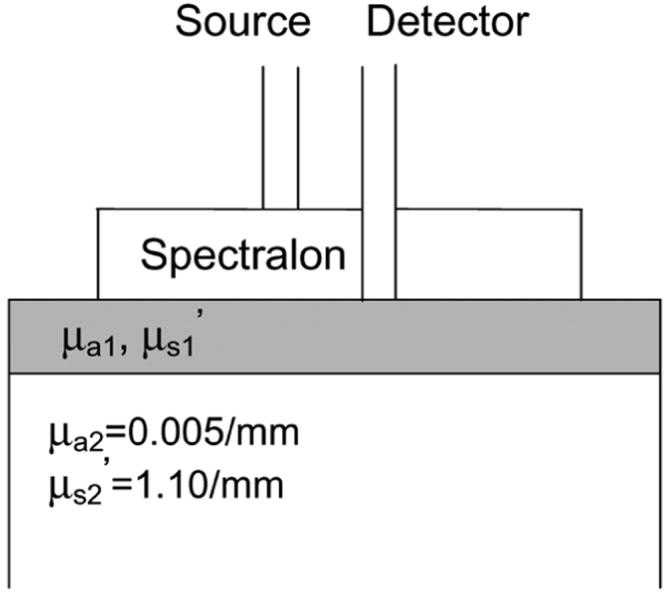
Diffusing probe on a two-layer phantom.

We designed our two-layer phantoms according to Simpson's ex-vivo measurement results [7]. The optical properties of the top layers are actually averages of epidermis and dermis layers. Ten two-layer and three homogeneous silicone phantoms were made by mixing polydimethylsiloxane (Eager Plastics, IL), catalyst, Titanium dioxide (scatterer), and India ink (absorber) in disposable polystyrene beakers. Ten “bulk” substrates having a thickness of larger than 50 mm were poured at the same time to ensure that all of them have the same optical properties. The substrates were designed to have optical properties similar to those of the subcutaneous fat of skin [7]. Two sets of “top-layer” phantoms, whose optical properties differ from those of the substrate, were then prepared. We designed the optical properties of the two sets of the top-layer phantoms to mimic those of light and dark skin epidermis-dermis [7]. Once the bulk substrate material had cured, the top layers of different thicknesses were poured and allowed to cure. This resulted in five different thicknesses, ranging from about 1 to 8 mm, for each set of top-layer material. The absorption coefficient of dark skin phantoms is 200% higher than that of light skin phantoms at the wavelength of 785 nm. Though we have done our best to make the reduced scattering coefficients of light and dark skin phantoms similar, there is a 10% difference. A single bulk substrate was left without a top layer as a control homogeneous phantom. In addition, a 50-mm-thick control homogeneous phantom of each top-layer material was left alone to cure in the absence of an underlying substrate.

III. Results and Discussion

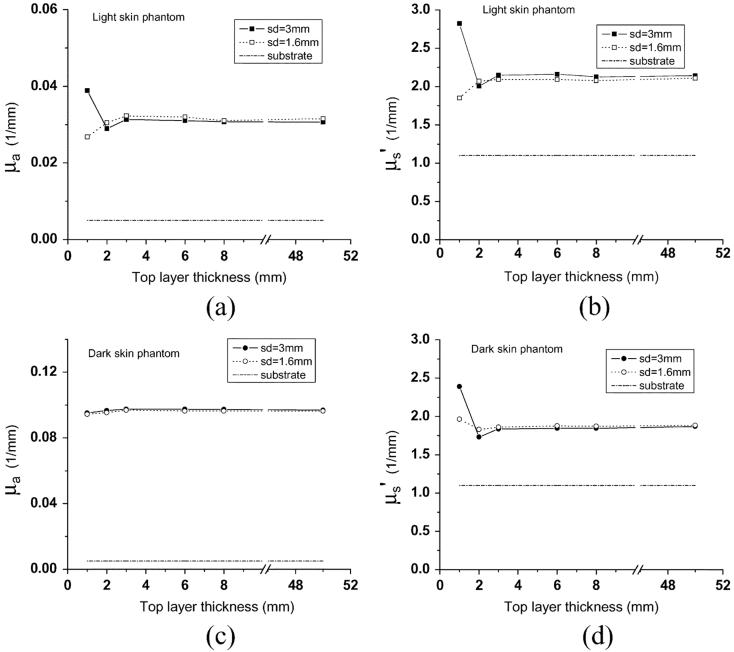
Measurements were carried out using two diffusing probes having source-detector separations of 1.6 mm and 3 mm. This allowed us to investigate the influence of source-detector separation on the probing depth of the diffusing probe. The source-detector separation of 1.6 mm is the shortest distance we can achieve with our current fabrication setup, but the distance can be further shortened by using fibers with smaller diameters. Spectralon slabs having a thickness of 1.5 mm and a diameter of 10 mm were employed for both probes. Fig. 2 illustrates the recovered absorption and reduced scattering coefficients versus top-layer thickness for the two sets of phantoms. Each symbol in the plot represents the average of three measurements, and deviations are all within 0.1%. Optical properties of samples having a 50-mm-thick top layer are actually results from measurements performed on the control phantoms. We take these results as the benchmark optical properties. Measurement results of the three control homogeneous phantoms are indicated in Table I.

Fig. 2.

(a) μ_aand (b)μ′_s recovered from light skin two-layer phantoms, and (c)μ_a and (d)μ′_srecovered from dark skin two-layer phantoms. The thickness of the top layer of the two-layer phantoms varies from 1 to 8 mm. Two diffusing probes having source-detector separations of 3 mm (solid squares and solid circles) and 1.6 mm (squares and circles) were employed. Dash-dot lines represent optical properties of the substrate of the two-layer phantoms.

Table I.

Optical Properties of Bulk Substrate and Two Bulk Top-Layer Materials at the Wavelength of 785 nm

	substrate	Low μa top layer	High μa top layer
μa (1/mm)	0.005	0.031	0.097
μs' (1/mm)	1.10	2.14	1.87

From Fig. 2, when the top layer is thicker than 2 mm, deviations of absorption coefficient μ_a and reduced scattering coefficient μ′_s from benchmark values for both source-detector separations are within 5% and 1% for light skin and dark skin phantoms, respectively. For the probe with a source-detector separation of 3 mm, as the top-layer thickness decreases to 1 mm, the deviations of recovered μ_a from benchmarkμ_a increase to 27% and 2% for light skin and dark skin phantom sets, respectively. The deviations of recovered μ′_s from benchmark μ′_s increase to 32% and 28% for light skin and dark skin phantom sets, respectively. On the other hand, employing the diffusing probe with a source-detector separation of 1.6 mm produced improved results in this region. The deviations of recovered μ_a from benchmark μ_a increase only to 15% and 2% for light skin and dark skin phantom sets, respectively. The deviations of recovered μ′_s from benchmark μ_s' increase to 12% and 4% for light skin and dark skin phantom sets, respectively.

Our measurement results suggest that deviations of recovered optical properties from benchmark values decrease as the source-detector separation becomes smaller. Decreasing the source-detector separation reduces the influence from the underlying substrate and ultimately increases the accuracy of the recovered optical properties. It is well known that source-detector separation is proportional to the interrogation depth for a DOS probe that has a source and detector in direct contact with samples [9]. We speculate that the interrogation depth of a diffusing probe, such as ours, that has a different source-detector arrangement from a conventional DOS probe, is also proportional to the source-detector separation.

To investigate this, we performed Monte Carlo simulations to estimate the interrogation depth of the diffusing probe. The Monte Carlo code we used was developed from Wang et al.,'S general multilayer, three-dimensional, weighted photon Monte Carlo code [10]. Our code employs a Henyey-Greenstein phase function and uses an anisotropy factor of 0.8 to reduce simulation time because using an anisotropy factor between 0.8 and 1 does not significantly influence the reflectance when μ′_s is constant [11]. The calculation of the interrogation depth of each simulation can be substantiated in the following manner. Construct a discrete probability density function (pdf) $p_i=W_i∕{\Sigma }_{i=1}^n{W}_i$, where W is the final weight of a detected photon packet and n is the number of photon packets launched, then ${\Sigma }_{i=1}^n{p}_i=1$. Using this pdf, the average interrogation depth of a simulation can be estimated as $\stackrel{‒}{z_{\max }}={\Sigma }_{i=1}^n{p}_i{\left(z_{\max }\right)}_i$, where z_max is the maximum penetration depth of a detected photon packet. The average of the maximum interrogation depths of a simulation provides a measure of the average depth photons would travel in a homogeneous sample. We designed the simulated sample to be homogeneous with optical properties n = 1.43,μ_a = 0.03/mm, and μ′_s = 2/mm for simulating the light skin, and = 1.43,μ_a = 0.09/mm and μ′_s = 1.8/mm for simulating the dark skin. The lateral extension and the thickness of the sample are set as 1 × 10⁸ mm. The Spectralon layer is 1.5 mm thick and has a diameter of 10 mm. Fresnel refraction introduced by index mismatch at the boundaries is taken into account. The optical properties of the Spectralon are n = 1.35,μ_a = 1 × 10⁻⁶/mm, and μ′_s = 35/mm. Source-detector separations used in the Monte Carlo simulations were 1, 2, 3, and 4 mm.

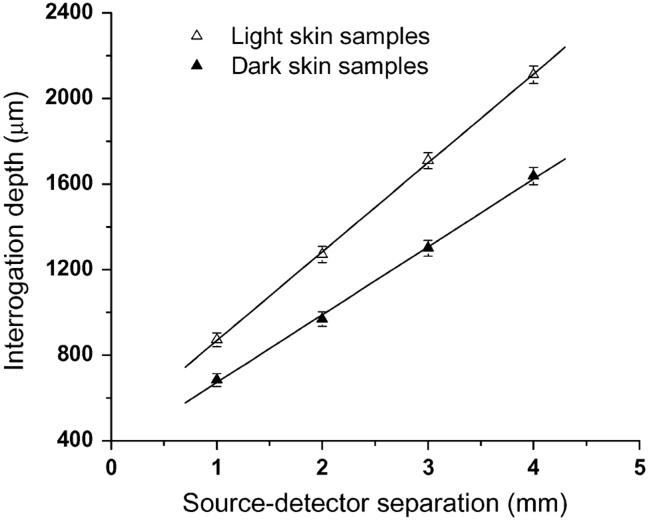
Simulated interrogation depth at the modulation frequency of 50 MHz versus source-detector separations is depicted in Fig. 3, and error bars indicate standard deviations. Increasing the modulation frequency from 50 MHz to 300 MHz can reduce the interrogation depth of the probe. Since the attenuation of the photon density wave is proportional to the modulation frequency, higher modulation frequency photon density waves tend to propagate in the sample in a shorter path length [12]. However, for the parameters employed in the simulations, the variation introduced by changing the modulation frequency is within 3%. Therefore, we present our data only at the modulation frequency of 50 MHz.

Fig. 3.

Interrogation depth versus diffusing probe's source-detector separation determined from Monte Carlo simulations. Samples have homogeneous semiinfinite geometry. Solid triangles and open triangles represent the interrogation depths of the probe-measuring samples having optical properties of light skin and dark skin, respectively. Please see the text for the parameters used in simulations.

Straight lines were fit to the simulated interrogation depths. The trend in interrogation depth versus source-detector separation shown in Fig. 3 indicates that the source-detector separation is proportional to the interrogation depth of a diffusing probe. In Fig. 2, we observed that the 1.6-mm source-detector separation diffusing probe can recover more accurate top-layer optical properties than the 3-mm source-detector separation diffusing probe, especially when the top layer of the two-layer phantom is 1 mm thick. The experiment results suggest that the interrogation depth decreases as the source-detector separation decreases. The Monte Carlo simulation results support our experimental observation.

In addition, the slopes of the two fit lines in Fig. 3 indicate that the source-detector separation has a higher impact on the interrogation depth in the light skin samples than in the dark skin samples. By interpolating simulated data shown in Fig. 3, the interrogation depth at 1.6-mm source-detector separation can be estimated to be 1111 μm and 865 μm for the light skin and dark skin samples, respectively. This decrease in simulated interrogation depth helps to explain the experimental results illustrated in Fig. 2. When a 1.6-mm source-detector separation diffusing probe is employed to measure two-layer phantoms having a 1-mm-thick top layer, the deviation of the recovered optical properties from the benchmark values is smaller for the dark skin phantoms than that for the light skin phantoms. On the other hand, although the simulated interrogation depth is 865 μm when the dark skin sample is measured with a 1.6-mm source-detector separation diffusing probe, we also observed 4% deviations of recovered optical properties from true values when a dark skin two-layer phantom of a 1-mm-thick top layer was measured with the probe. The deviation may be introduced by the small amount of detected photons that penetrate deeper than the calculated interrogation depth, and could also be a consequence of inherent differences between real experimental measurements and simulations, including probe contact, surface flatness, and the layer structure of real samples.

As illustrated in Fig. 2, when the two probes are applied to study the two-layer phantoms with 1-mm top-layer thickness, the recovered optical properties do not always fall in the region between the benchmark optical properties of the top layer and the substrate. In the data recovery, we used the MATLAB “lsqcurvefit” least-squares data-fitting algorithm. The recovered optical properties were obtained using an unconstrained optimization. The recovered unconstrained optical properties and the corresponding χ² values for the two-layer phantoms with a 1-mm-thick top layer are listed in Table II, We also constrained the optimization by requiring that optical properties lie in the range between the benchmark values of the top layer and the substrate. The recovered constrained optical properties and the corresponding χ² values are also found in Table II. From the χ² values shown in Table II, the unconstrained optical properties provide local minima. Based on a comparison of results obtained from constrained versus unconstrained optimizations, we believe that our unconstrained optimization produces optical properties that are not anomalous.

Table II.

Unconstrained and Constrained Recovered Optical Properties and the Corresponding χ²Values of Two-Layer Phantoms with 1-mm Thick Top Layer at the Wavelength of 785 nm. The Upper Bound and Lower Bound Were Set at the Optical Properties of the Top Layer (μ_a = 0.031/mm and μ′_s = 2.14/mm for Light Skin Phantoms, and μ_a = 0.097/mm and μ′_s = 1.87/mm for Dark Skin Phantoms) and the Substrate (μ_a = 0.005/mm and μ′_s = 1.10/mm), Respectively, When Determining Constrained Optical Properties

	3mm s-d separation probe				1.6mm s-d separation probe
	Light Skin Phantom (1mm)		Dark Skin Phantom (1mm)		Light Skin Phantom (1mm)		Dark Skin Phantom (1mm)
	unconstrained	constrained	unconstrained	constrained	unconstrained	constrained	unconstrained	constrained
Recovered μa (1/mm)	0.039	0.031	0.095	0.089	0.026	0.026	0.089	0.077
Recovered μs' (1/mm)	2.82	1.91	2.39	1.87	1.94	1.94	2.02	1.87
χ2	0.66	4.7	0.9	4.8	0.72	0.72	0.68	0.91

While it seems plausible that recovered optical properties would lie between the extreme values of the optical properties in both layers in this two-layer problem, we are aware of no rigorous argument that establishes this to be the case. To settle this issue would require taking measurements with shorter source-detector separations than can be achieved with our current probe, followed by validation studies such as those presented here. Based on the analysis that we have presented, however, we have no reason to conclude that the optical properties recovered through our unconstrained optimization are spurious.

Farrell et al., investigated the influence of layered tissue structures, such as that found in skin, on tissue optical properties obtained from a diffusion-based model which assumes tissues are semiinfinite and homogeneous [13]. They used multi source-detector separation steady state measurement apparatus and observed that the recovered tissue optical properties were not simply weighted averages of those of individual layers of tissues. Farrell et al., observed nonphysical optical properties when the optimization algorithm was not constrained in the case that the top-layer thickness is smaller than 1.5 mm. In our study, we used two probes which have source-detector separations of 1.6 mm and 3 mm. We can see from Fig. 2(a) and (b) that these two probes produce different results when the top-layer thickness is 1 mm. This inconsistency points to a need for additional refinement; in the future, we will investigate further reduction of the source-detector separation and development of a three-layer diffusion model as potential improvements to our approach.

IV. Conclusion

In conclusion, using our new diffusing probes, we have characterized two-layer silicone phantoms having various top-layer thicknesses. Measurement results indicate that the recovered top-layer optical properties μ_a and μ′_s deviate from true values within 5% when the top-layer thickness is larger than 2 mm. As the top-layer thicknesses decreases to 1 mm, the deviation of recovered optical properties is strongly dependent on the sourcedetector separation of the diffusing probe and the optical properties of samples under investigation. Our measurement results indicate that the errors of optical properties recovered from a 1-mm top-layer thickness two-layer phantom are less than 15% when a diffusing probe of 1.6-mm source-detector separation is employed. We observed that interrogation depth decreases as the source-detector separation decreases and as the absorption coefficient of the sample increases. Monte Carlo simulations support our experiment results qualitatively. Simpson et al.. indicated the dermis sample they used was from a human abdomen and breast and had a thickness in the range from 1.5 mm to 2 mm[7]. From our measurement and simulation results, it is reasonable to infer that the interrogation region is located primarily in the dermis layer if either the 1.6-mm or 3-mm source-detector separation diffusing probe were employed to measure skin sites at the abdomen and breast. Further reduction in interrogation depth can be achieved by shortening the source-detector separation of the diffusing probe. We will employ our diffusing probe to determine optical properties of in-vivo normal skin and abnormal skin, such as melanoma and port wine stain, in the near future.

Biographies

Sheng-Hao Tseng received the B.S. degree in electrical engineering from National Tsing-Hua University, Hsinchu, Taiwan, R.O.C, in 1997, the M.S. degree in electrooptical engineering from National Taiwan University, Taipei, in 1999, and the Ph.D. degree in electrical engineering with an emphasis on biomedical optics and spectroscopy from the University of California, Irvine, in 2006.

Currently, he is a Postdoctoral Scientist with Johnson and Johnson Consumer and Personal Products Worldwide, Skillman, NJ. His research interests include diffuse near infrared optical spectroscopy, development of methods for quantifying optical properties of superficial biological tissues, and probe design.

Carole K. Hayakawa received the Ph.D. degree in mathematics, specializing in Monte Carlo methods for the solution of transport problems, from the Claremont Graduate University, Claremont, CA.

Currently, she is a Project Scientist in the Department of Chemical Engineering and Materials Science at the University of California, Irvine. Her research is focused on the development of computational and analytical models to solve forward and inverse problems related to laser-induced radiative, thermal, and mechanical transport phenomena in turbid media.

Jerome Spanier received the Ph.D. degree in mathematics from the University of Chicago, Chicago, IL, in 1955.

Currently, he is a Researcher in mathematics at the Beckman Laser Institute (BLI) at the University of California, Irvine. His research concentrates on the development of mathematical models and computational algorithms based on these models for studying the interactions of light and tissue. He is Professor Emeritus of Mathematics from Claremont Graduate University (CGU), Claremont, CA, where most of his academic career was spent. Prior to his CGU appointment in 1971, he worked in the industry for 16 years. AT CGU, he helped to establish and direct the Mathematics Clinic, a practicum course for applied mathematics students. He is also the Founding Director of the Claremont Research Institute of Applied Mathematical Sciences, where he has been since 1998. His research focus is the theory and application of advanced Monte Carlo methods for biomedical problems.

Anthony J. Durkin received the Ph.D. degree in biomedical engineering with an emphasis on biomedical optics and spectroscopy from the University of Texas at Austin in 1995.

Currently, he is an Assistant Professor at the Beckman Laser Institute (BLI) at the University of California, Irvine. His research is focused on the development and application of optical spectroscopic techniques and analysis methods to interrogate superficial living tissues in-vivo.

Dr. Durkin has been a National Research Council Fellow with the Food and Drug Administration and Director of Bioscience with Candela Corp. He has eight issued patents. He serves on the editorial boards of Applied Optics (Optical Society of America) and Journal of Biomedical Optics (SPIE). He is the Past Chair of the Division of Optics in Biology and Medicine for the Optical Society of America.