Identification of direct residue contacts in protein–protein interaction by message passing

Abstract

Understanding the molecular determinants of specificity in protein–protein interaction is an outstanding challenge of postgenome biology. The availability of large protein databases generated from sequences of hundreds of bacterial genomes enables various statistical approaches to this problem. In this context covariance-based methods have been used to identify correlation between amino acid positions in interacting proteins. However, these methods have an important shortcoming, in that they cannot distinguish between directly and indirectly correlated residues. We developed a method that combines covariance analysis with global inference analysis, adopted from use in statistical physics. Applied to a set of >2,500 representatives of the bacterial two-component signal transduction system, the combination of covariance with global inference successfully and robustly identified residue pairs that are proximal in space without resorting to ad hoc tuning parameters, both for heterointeractions between sensor kinase (SK) and response regulator (RR) proteins and for homointeractions between RR proteins. The spectacular success of this approach illustrates the effectiveness of the global inference approach in identifying direct interaction based on sequence information alone. We expect this method to be applicable soon to interaction surfaces between proteins present in only 1 copy per genome as the number of sequenced genomes continues to expand. Use of this method could significantly increase the potential targets for therapeutic intervention, shed light on the mechanism of protein–protein interaction, and establish the foundation for the accurate prediction of interacting protein partners.

The large majority of cellular functions are executed and controlled by interacting proteins. With up to several thousand types of proteins expressed in a typical bacterial cell at a given time, their concerted specific interactions regulate the interplay of biochemical processes that are the essence of life. Many protein interactions are transient, allowing proteins to mate with several partners or travel in cellular space to perform their functions. Understanding these transient interactions is one of the outstanding challenges of systems biology (reviewed in ref. 1). The characterization of the molecular details of the interface formed between known interacting proteins is a requirement for understanding the molecular determinants of protein–protein interaction, the knowledge of which may be important for a variety of applications including synthetic biology, e.g., designing new specific interaction between proteins (reviewed in ref. 2), and pharmaceutics, e.g., protein interaction surfaces as drug targets (reviewed in ref. 3).

Experimental approaches to identify surfaces of interaction between proteins such as surface-scanning mutagenesis and cocrystal structure generation are arduous and/or serendipitous. Cocrystal structures provide the best molecular resolution but are particularly challenging to obtain for transient interaction partners. In addition, independent evidence is required to ensure that the structure reflects an accurate picture of the physiologically relevant interaction.

Given the challenges of these experimental approaches, it is clear that the comprehensive identification of interaction surfaces between a large number of cellular proteins may be significantly expedited by computational methods. Rapid increase in the number of sequenced bacterial genomes in the past decade [resulting in >700 completed genome projects to date (4)] has fueled the increasing use of covariance-based methods of sequence analysis for protein structure studies. Early on, these methods were largely applied to single proteins (5–9), e.g., in attempts to provide insight into tertiary structure. More recently, applications have also been made to identify interacting residues between proteins (10–13). Covariance methods rely on the premise that amino acid substitution patterns between interacting residues are constrained and hence correlated. To maintain protein function, the acceptance of a deleterious substitution at 1 position must be compensated for by substitution(s) in the residue(s) interacting with it (14). Traditional covariance methods identify interacting residue position pairs as those exhibiting correlated substitution patterns. Applying this idea to protein–protein interaction for which the structures of the individual protein partners are known (11), one would simply look for correlation in substitution patterns between residues of the interacting partners, and identify the surfaces defined by the covarying residues as the interacting surfaces.

However, the covariance approach has a number of shortcomings that may significantly affect its predictive power (15). One important problem stems from the fact that correlation in amino acid substitution may arise from direct as well as indirect interactions. For example, a substitution in 1 position of a protein may cause conformational changes of other residues in the same protein. Such a substitution may influence the interaction between 2 proteins without being directly at the interface and can even occur without being proximal to the interaction surface residue at all. A classic example of this type is the allosteric effect; but indirect correlations do not require large conformational changes and may result also from cumulative effects arising from a web of small direct interactions (see below).

Traditional covariance methods are unable to distinguish between direct and indirect correlation. A major focus of the present work is to develop a method to disentangle these correlations. Our approach is based on 2 premises: (i) the direct interactions are contained in the pairs of correlated residues as identified, e.g., by the covariance method, and (ii) all detected correlations in substitutions are generated by the set of direct interactions. One strategy to identifying the set of directly interacting residue positions would be to try out all possible subsets of correlated residue pairs as direct interactions. A formidable technical challenge with this approach is to work out the expected statistical correlation generated by a given set of trial direct interactions, because this itself is a very difficult global optimization problem [as exemplified by the notorious “spin-glass” problem (16)]. This challenge is dealt with here by applying a message-passing approach (17, 18). In recent years, insights from spin-glass physics have led to the development of generalized message-passing techniques, which have been applied successfully to a number of hard combinatorial problems such as K-SAT (19–21).

A further problem for inference is the sparsity of the information to be retrieved. The interaction surfaces constitute only a small subset of residues, each one being in contact with only a few surface residues of the interaction partner, and only a fraction of the interacting pairs exhibit covariance. Fortunately, for the many cases where the monomer structures of the interacting domains are already known, reliable information on even a limited number of interacting position pairs can already reveal the mode of interaction. The computational challenge is therefore to extract these few pairings from the large number of interprotein position pairs (≈10⁴ for typical protein domains) which constitute a substantial level of background noise.

In the absence of structure information, detection of correlation between variable positions in interacting proteins therefore requires a large set of homologous protein sequences with known interaction partners. The number of sequenced bacterial genomes will soon approach a number where such data could be extracted from protein pairs that are ubiquitously found in only a single copy per sequenced genome. At present, however, analyses are still limited to proteins that are highly amplified in individual genomes.

In this study, we will apply our method to reveal direct interactions within the prototypical signal transduction system in bacteria, the two-component signaling (TCS) system, which is highly amplified [≈10 per genome on average (22)] to regulate a flurry of adaptive responses to environmental and cellular cues; see ref. 23 for a recent review. Signal detection is achieved by the sensor histidine kinase (SK) and the cellular response is mediated by the response regulator (RR), which most commonly is a transcription factor (24). The signal between the 2 proteins is passed via the transfer of a phosphoryl group, from a histidine residue located on the so-called HisKA domain of the SK to an aspartate residue on the RR (25). The SK and RR proteins are believed to interact specifically in most cases, and the coupled pairs are often revealed by adjacency in chromosomal location (reviewed in ref. 26). More than 2,500 such coupled SK-RR pairs have been identified from ≈300 sequenced bacterial genomes, making this system ideally suited for statistical analysis (11, 12). In addition, a large base of existing genetic and structural information—including numerous RR (e.g., ref. 27), 2 HisKA (e.g., ref. 8), and an exemplary cocrystal structure (29)—allows for critical evaluation of the results of statistical sequence analysis.

We present here a detailed 2-stage analysis on TCS proteins. The covariance method is first used to identify the correlated residues, followed by a statistical message-passing approach to infer direct coupling between pairs of residue positions. Our method distinguishes interacting residues from noninteracting ones for both SK/RR heterodimer and RR/RR homodimer interactions, with vastly improved accuracy from a mutual information (MI)-based method without using any ad hoc tuning parameters. We propose that this method will be applicable for general protein interface determination given a sufficient number of homologous protein sequences, a requirement that should soon be met by proteins present at a single copy per genome.

Results and Discussion

Detection of Constrained Positions in Interacting Proteins.

A multiple sequence alignment of M = 2,546 homologue pairs was constructed for the HisKA domain of the SK and its partner RR domain by aligning with the respective hidden Markov models (see Materials and Methods). In the resulting database, chromosomally adjacent SK and RR sequences are concatenated to single sequences Ā^a = (A₁^a, A₂^a, …, A_NSK+NRR^a) for a = 1, …, M, such that positions i = 1, …, N_SK with N_SK = 88 correspond to the HisKA domain of SK, and i = N_SK + 1, …, N_SK + N_RR with N_RR = 124 to the RR domain. Alignment gaps are included as a separate letter, so entries A may assume 21 different values. Frequency counts f_ij(A_i, A_j) are introduced for the joint appearance of amino acids A_i, A_j in each intra- and interdomain pair of positions i and j, and f_i(A_i) for each single position i.

To identify correlated positions between the SK and RR proteins of the TCS system, every position in the SK was compared with every position in the RR, and their mutual information (MI) was evaluated. This raw MI was corrected for finite-sample size effects by subtracting the average MI in a null model; see ref. 11 and supporting information (SI) Text. The resulting MI between positions i and j, MI_ij = MI_ij^(raw) − MI_ij⁽⁰⁾, allows for comparison of different pairs with respect to the statistical correlation of their amino acid occupancies. Unconstrained position pairs are expected to have values close to zero.

The value of the score introduces a ranking of all pairs of positions between the 2 proteins. The histogram of scores allows for the self-consistent introduction of a threshold of MI^(t) separating relevant mutual information from an exponential background signal (Fig. S1). We find 32 correlated position pairs with MI > MI^(t). These pairs, involving 12 SK positions and 12 RR positions (listed in Fig. S2) constitute the starting point of our analysis. As will be shown below, the main results are nevertheless insensitive to the precise value of MI^(t) used. Also, very similar results (data not shown) are obtained when using other local pair-correlation measures, as e.g., a χ² test if residue frequencies in interacting and noninteracting protein pairs are drawn from the same distribution (13) and a likelihood ratio of the data under a correlated and a factorized model (12). Both measures identified almost the same pairings between the positions of the SK and RR domains as the high MI pairs (Fig. S2), and comparable even if slightly shuffled sets of high-ranking position pairs.

Disentangling Direct from Indirect Couplings.

The statistically correlated pairs are candidates for positions in contact at the protein–protein interface. However, statistical correlation does not automatically imply strong direct interaction. Imagine that position i is coupled directly to j, and j to k. Then i and k will also show correlation, without being directly coupled. The effect may become even more pronounced if there are multiple paths of weak couplings connecting i and k. A strong correlation may emerge without the existence of any strong direct coupling linking these positions to any other residues position.

The MI score introduced above is a local one, in that it considers only 1 residue pair at a time, and compares different pairs only at the end after scores are determined. This approach is therefore unable to disentangle direct from indirect couplings; the same is true for other local approaches, e.g., Refs. 12 and 13. To circumvent this problem, we infer a global statistical model P(A₁, …, A_{NSK + NRR}) describing the joint probability of the concatenated SK and RR sequence Ā_{NSK + NRR}. This statistical model is required to satisfy 2 key conditions.

(i) It has to be consistent with the statistics of the data up to the level of residue pairs, i.e., the marginal distributions of the model for 1 or 2 positions have to coincide with the frequency counts f_i(A_i) and f_ij(A_i, A_j) introduced above:

This condition has to hold for all intra- and interprotein pairs of positions (i, j), i, j = 1, …, N_SK + N_RR. Note that in principle higher correlations of 3 or more positions can be included in a similar way. However, the size of the available dataset does not allow for going beyond 2-residue correlations. The 21 × 21 elements of f_ij(A_i, A_j) have to be estimated from the M = 2,546 sequences in the database; frequency counts for >2 positions would be very imprecise because of insufficient sample size.

(ii) To avoid overfitting, the model has to show as few parameters as possible to meet condition i. Application of the maximum-entropy principle yields the simplest possible (i.e., least constraint) model satisfying these conditions (30):

Model parameters are direct couplings e_ij(A_i, A_j) between amino acid A_i in position i and amino acid A_j in position j, and local biases h_i(A_i) describing the preference for amino acid A_i at position i. Determining these parameters to meet Eq. 1 is an algorithmically hard task, and can be achieved by using a 2-step procedure. All technical details are explained in the SI Text:

1. Given a candidate set of model parameters, single- and 2-residue distributions P_i(A_i) and P_ij(A_i, A_j) are estimated from Eq. 2. This is computationally expensive, the exact summation over all possible protein sequences would require O(21^N−2N²) steps. Approximations can be achieved by MCMC sampling—which is expected to be very slow for 21-state variables—or more efficiently by a semiheuristic message-passing approach (31). We use the latter approach; it reduces the computational complexity to O(21²N⁴).

2. Once all P_ij(A_i, A_j) are estimated, we can use gradient descent to adjust the coupling strengths e_ij(A_i, A_j) [the h_i(A_i) can be treated in a more efficient way explained in the SI Text]:

   

   This equation can be derived variationally within a Bayesian approach, it maximizes the joint probability of the data under model 2 (compare SI Text). Because this probability is convex, it is guaranteed to converge to a single global maximum.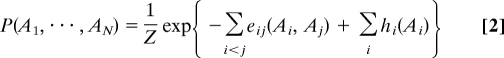

These 2 steps are iterated until Eq. 1 is satisfied within user-given precision. In the inferred model, matrices e_ij(A_i, A_j) describe the direct coupling between residue positions i and j. To compare different position pairs, we propose a scalar measure of the coupling strength. For technical reasons [invariance with respect to gauge symmetries of model 2 and robustness with respect to a pseudocount introduced to regularize inference (cf. SI Text)] a quantity called direct information (DI) is introduced. It measures the part of the mutual information of a position pair, which is induced by the direct coupling. Intuitively, it can be understood as the mutual information in a 2-variable model for positions i and j only, which has the correct statistics of the amino acid occupancy of single positions, and coupling e_ij(A_i, A_j) in between. The full technical definition is given in the SI Text.

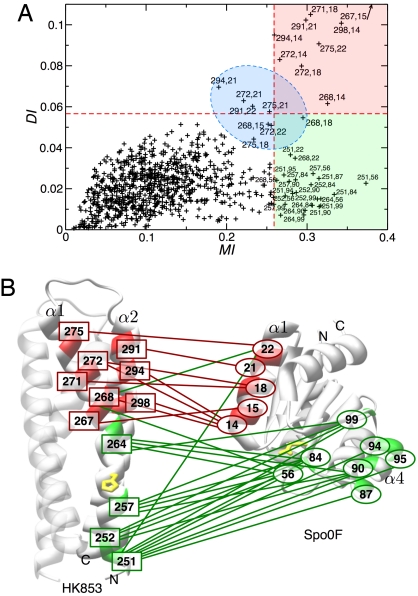
Because of the scaling of the algorithmic complexity, the method cannot be applied simultaneously to all 212 positions of the protein alignment. Therefore, the 60 positions of the protein alignment being involved in the 140 highest MI-ranking pairs (containing the 32 candidates for contact pairs identified before) are selected. The results are shown in Fig. 1A as a scatter plot of the full mutual information MI versus its direct contribution DI for the 1,770 considered position pairs (i, j). We observe that low MI implies low DI (Fig. 1A Lower Left), but high MI does not necessarily imply high DI. DI can thus be used to rank the 32 potential links previously identified by MI. This distinction allows us to identify 2 groups of position pairs:

Fig. 1.

The combined covariance/message-passing approach detects 2 groups of correlated pairs. (A) Scatter plot of direct mutual information (DI) versus total mutual information (MI) reveals 2 classes of covarying residue pairs, those with strong direct correlation found in the upper red quadrant (group I) and those with low direct correlation found in the lower green quadrant (group II). A group of pairings just around the border of the MI and/or the DI cutoff is highlighted in blue. (B) Direct and indirect interaction pairs depicted on exemplary structures of the HisKA and RR domain. All residues that appear in the network of pairings with MI > MI^(t) were mapped onto the structures of HK853 from T. maritima (HisKA domain) and Spo0F from B. subtilis (RR domain). Those pairings showing strong direct correlation are depicted in red and connected by a red line and those that show low direct correlation are depicted in green and connected by a green line. Green lines connecting red residues represent low direct correlation for that particular residue pairing. For orientation, the N and C termini and relevant structural elements are labeled. The phosphotransfer sites H260 in HK853 and D54 in Spo0F are shown in yellow.

Group I.

This group, including the 9 pairs in Fig. 1A Upper Right (red zone), has both high MI and large direct coupling DI. It connects 8 SK positions with 5 RR positions. The strong links there are expected to represent physical interactions, i.e., direct contacts in the interface of the SK/RR dimer.

Group II.

This group, including the 22 pairs in Fig. 1A Lower Right (green zone), is densely connected by weak direct couplings (i.e., low DI). High MI between these pairs emerge from the cooperation of a multitude of such weak links. The second group contains 4 SK and 7 RR positions. They would not be expected to be in direct contact in the dimer, but instead might have a collective influence on the functionality of the SK/RR phosphotransfer interaction.

An additional set of 8 pairings (including 1 of the 32 high-MI pairs) are found just below the thresholds set for MI and/or DI. This group lies in the blue zone in Fig. 1A. It is expected to contain both direct contact pairings and a few distant pairs.

The network defined by these residue pairs is shown in Fig. S2. Note that it contains many loops, so it cannot be found by dependence-tree-based inference methods (as used in ref. 12). Its structure is found to be robust with respect to the precise details of the algorithm: The values of DI as inferred from half of the dataset almost coincide with the values as inferred from the full dataset; a slightly smaller but similar degree of coincidence is found if 2 disjoint half-size datasets are used (Fig. S3). In particular, the high-scoring DI values are well reproduced.

Even though for each species only 1 sequenced strain was included in the database, sampling biases due to phylogenetic relations between the sequenced species exists. To evaluate whether DI values are sensitive to this phylogenetic misdistribution, a reweighting procedure for potentially oversampled regions in sequence space is introduced: For each interaction SK/RR pair $\overline{A^a}$, the number n_a of sequences having >80% sequence identity with $\overline{A^a}$ is determined, and the contribution of $\overline{A^a}$ to the frequency counts f_i and f_ij is assigned factor 1/(n_a + 1). Global model inference is applied to determine DI. The ranking by modified DI is found to reproduce the original ranking: In between the 10 highest-ranking position pairs, one finds 10 common pairs, in between the first 20 pairs 17, in between the first 30 ranks 25 common position pairs are found (Fig. S4). Only for reweighting with respect to 60% sequence identity did part of the information get modified (data not shown). This result illustrates that sampling has only small effects on the power of the proposed inference method in predicting contact pairs in interacting protein domains.

Interaction Surface of the SK/RR Phosphotransfer Interaction.

The validity of the above sequence-based predictions can be tested by using structural representatives of the SK HisKA domain [HK853 of Thermatoga maritima; PDB ID code 2C2A (28)] and of the RR domain [Spo0F from Bacillus subtilis; PDB ID code 1PEY (32)] as well as the cocrystal structure of Spo0F in complex with phosphotransfer protein Spo0B, both part of the sporulation phospho-relay in B. subtilis [PDB ID code 1F51 (29)]. Phosphotransferase Spo0B is a protein evolutionary related to the SK and features strong structural similarity, but is distinct in primary sequence (see below).

The HisKA domain exists as a homodimer of 2 helical hairpins, which form a 4-helix bundle. The conserved histidine residue (phospho-donor for the RR) lies on the α1-helix and faces away from the homodimer core. By using HK853 numbering (Fig. 1B), this residue (yellow) is at position 260. Approximately 20 residues downstream of H260 is a hairpin turn that terminates the α1-helix and initiates the α2-helix that runs antiparallel to the α1-helix. Positions of strong directly coupled residues (group I) predicted to form direct contacts are 267, 268, 271, 272, and 275 on the α1-helix and 291, 294, and 298 on the α2-helix, indicated by the red boxes in Fig. 1B. They are all found C-terminal to the active-site histidine, in the vicinity of the hairpin and are exposed to the exterior of the 4-helix bundle.

The RR domain forms an α/β-fold consisting of a 5-stranded β-sheet surrounded by 5 α-helices with the catalytic aspartate (receptor in phosphotransfer) nestled on the surface of 1 face of the fold, at position D54 by using Spo0F numbering (indicated in yellow). Group I residue positions are 14, 15, 18, 21, and 22, as indicated by the red ellipses in Fig. 1B. These are all situated on the α1-helix and exposed to the exterior of the RR domain.

SK residue positions belonging to the high-MI but low-DI group II are 251, 252, 257, 264 (green boxes in Fig. 1B). Residue positions 257 and 264 are on the same face of the helix as the phosphorylatable histidine residue 1 turn N- or C- terminal, respectively. Positions 251 and 252 represent partially buried residues located at the base of the 4-helix bundle. RR residue positions belonging to group II are 56, 84, 87, 90, 94, 95, and 99 (green ellipses); all but 1 (residue 56) are localized in or around the α4-helix.

Mapping these coupled positions to the exemplary individual structures, it becomes clear that group I pairings (red lines in Fig. 1B) define a mode of spatial interaction between the α1- and α2-helices of the SK and the α1-helix of the RR, bringing close together the catalytic site residues. It is, however, impossible to spatially align also the group II residue positions (green lines in Fig. 1B), consistent with the notion that these do not present direct interactions according to their DI ranking. [The high MI values of group II pairings likely reflect a dynamic role of these residues in arranging the active sites for phosphotransfer (33).]

The precise interaction mode predicted by group I coupled pairings is revealed by the Spo0B/Spo0F cocrystal structure (29), which provides a structural example to measure the distances of most coupled residues (see Fig. S5 for a structural representation and detailed data on residue pair distances).* All covarying residues of group I that can be mapped to the Spo0B structure are located in close proximity (≤6Å) at the interaction surface between Spo0B and Spo0F. Additionally, 5 of 6 pairings that just miss the set thresholds for DI_ij and/or MI_ij depicted in the blue zone in Fig. 1A are also within 6Å of each other.

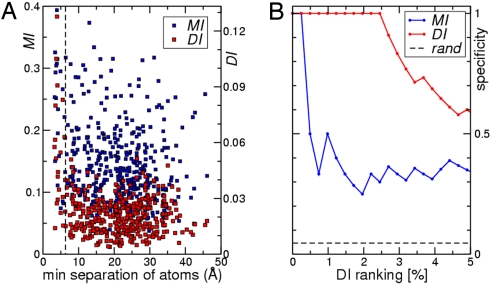
From the scatter plot of the distance between a pair of residues against their DI and MI for the 408 position pairs matched to the cocrystal structure (Fig. 2A), the DI values (red symbols) are clearly seen as anticorrelated with distance. Almost all strong direct interactions correspond to short distances. On the contrary, no strong correlation is observed between the distance and the MI values (blue symbols) alone. To be more quantitative, pairings were ranked according to their DI or MI values, and specificity (defined as the fraction of pairings with a minimal distance of <6 Å) was displayed as a function of scoring rank percentile (Fig. 2B). Whereas MI (blue line) produces the first false positive after only 1 true positive and rapidly drops to specificities of 30–40%, DI (red line) amazingly maintains specificity one for the top 2.5% of the 408 scoring pairs (= 10 true positives).

Fig. 2.

Direct Information is inversely correlated with residue distance of pairs in the Spo0B/Spo0F cocrystal structure. (A) Minimal atom distance for all 408 pairings that could be mapped to the Spo0B/Spo0F cocrystal structure was determined in Ångström and plotted either against direct information DI (red symbols) or total mutual information MI (blue symbols). (B) Specificity vs. rank percentile for predicting contact pairs via DI (red curve) and MI (blue curve). Specificity is defined as the fraction of pairings at the given rank percentile that are within 6Å in the Spo0B/Spo0F cocrystal structure.

It can then be concluded that the combination of covariance and message passing is capable of identifying direct surface interactions from sequence data alone and that DI is a much better indicator of proximity of residues than MI. This is particularly important in instances where no clear overrepresentation of high MI scores can be observed. In those instances the DI ranking alone can be used to infer proximity.

Interaction Surface of RR Homodimers.

Many proteins perform their function in bacteria as homooligomers, an example being transcription factors. Identifying their interaction surface poses considerable problems beyond the ones discussed above: statistical couplings of residue positions can result both from the role of a pairing as a residue contact inside the monomer structure, and as an intermonomer contact. It is not a priori clear that both mechanisms lead to comparable statistical correlations, i.e., that both of them can be simultaneously detected in analyzing large sample sets of dimer-forming proteins. Even if found to be comparable, there is no intrinsic way to distinguish intra- and intermonomer contacts. Only the knowledge of the monomer structure allows selecting candidate pairs for the interaction surface. However, the simultaneous detection of both types of statistical coupling would aid other methods in predicting tertiary and quaternary structures.

To test what kind of pairings are detectable, the global inference approach was applied to probe RR/RR interactions. Significant experimental support for a phosphorylation-dependent dimerization that increases transcription factor-DNA affinity in the largest class of RR proteins, the OmpR/PhoB class, has previously emerged (34). For probing of couplings within the phosphotransfer domains of RR proteins, the database construction was hence limited to proteins that contain both a RR phosphotransfer domain and a DNA binding domain of the OmpR/PhoB class (see Materials and Methods).

This search and alignment procedure identified >2,000 proteins. MI scores were calculated for the 123 × 124/2 possible combinations of RR/RR pairings. The distribution plot of MI scores does not result in a clear anomalous tail (data not shown), unlike what was observed for the SK/RR analysis (Fig. S1). Message passing was applied to calculate DI values for all pairings of the 60 positions contained in maximal MI scores, and the results were ranked according to their DI values (see Table S1 for the top 60 entries).

To evaluate the meaning of these DI rankings, the minimal atom distances of all pairs were determined by using 3 structural examples of OmpR class RR: those of Escherichia coli, ArcA [PDB ID code 1XHE (27)] and PhoP [PDB ID code 2PKX (35)], and Streptococcus pneumoniae MicA [PDB ID code 1NXW (36)]. For illustration, the 15 top-ranking pairs (excluding 3 pairs that were proximal in primary sequence) were mapped onto the ArcA structure (Fig. S6). As for the SK/RR analysis, a strong correlation between DI and minimal atom distance emerged (Fig. S7A), and the majority of the 60 top-scoring pairs (Table S1) are in close proximity within the monomer structures (i.e., within 6 Å). Four dimer contacts are also identified (ranks 1, 3, 26, and 40). False positives (i.e., pairings with distances >6Å) do not emerge until rank 24 and remain sparse within the top 60 pairs.^† Quantification of specificity was determined as for the SK/RR analysis and demonstrates again that DI impressively enhances the predictive power over MI alone (Fig. S7B).

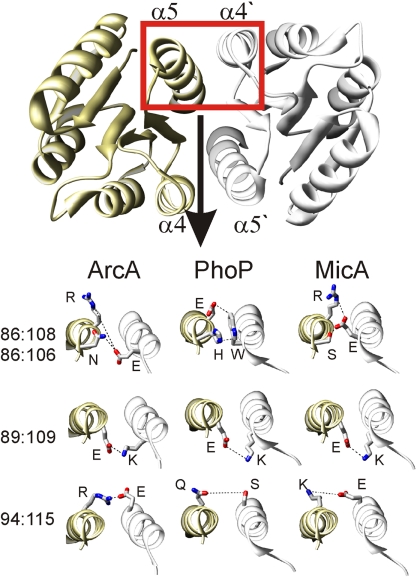
When mapping the 4 dimer contacts onto the 3 structural examples, it becomes apparent that the interactions formed by some individual contact residues are quite diverse (Fig. 3). The cluster involving pairings^‡ 86:106 and 86:108 demonstrates nicely the type of residue variation that is the foundation of the covariance-based method. As shown in Fig. 3, a salt bridge is formed between E86 and R108, and a hydrogen bond connects E86 and S106 in the MicA structure. In PhoP, an aromatic stacking interaction between a tryptophan and a histidine residue (W86 and H106) can be observed. The ArcA dimer is stabilized by a hydrogen bond between E86 and N106; an additional interaction (salt bridge) is predicted between E86 and R108.^§ Similar variations exist in the pairing of residues 94 and 115, whereas the pairing between residues 89 and 109 is always a salt bridge between E and K. Of course, the appearance of the pair 89:109 in the high DI list shows that E:K is not the conserved pairing between these positions among all RRs, but only one of the popular residue pairings at these positions (see Fig. S8). Information derived from such analysis may be exploited to design synthetic RR molecules with various degrees of cross-talk with the endogenous system.

Fig. 3.

Direct interaction between the identified dimer contact pairs. Four dimer contact pairings (red entries in Table S1) are localized to the α4- and α5-helices and are shown on the exemplary OmpR class RR structures of ArcA, PhoP, and MicA as a dashed line. Whereas contact pairing 89:109 (ArcA numbering, for PhoP and MicA numbering deduct 2) happens to represent a salt bridge in all 3 structural examples shown here, the pairing 94:115 and the cluster involving pairings 86:106 and 86:108 demonstrate nicely the type of residue variation that is the basis of the covariance method (see text). Detailed analysis of the covariance among the residues involved in these 4 pairings are given in Fig. S8.

In summary, inter- and intramonomer contacts lead to comparable statistical correlations. DI calculations provide constraints that could aid de novo structure prediction when applied to a single protein, or aid the verification or prediction of quaternary structure in cases where the monomer structure is available.

Concluding Remarks.

A computational method was introduced to infer structural details of protein–protein interactions based on primary sequence information. The method takes correlated residues from the covariance analysis as a starting point, and disentangles correlations arising from direct vs. indirect interactions by using a global inference approach implemented by a message-passing algorithm. The combination of covariance analysis and global inference impressively enhances the specificity of contact pair prediction compared with more traditional, purely local covariance-based approaches (e.g., MI). Currently, the applicability of the method relies on the existence of ≈10 structurally homologous protein sequences contained in a typical bacterial genome, due to the still limited number of sequenced genomes. With rapidly expanding genomic databases—including genes obtained via shotgun sequencing of environmental samples by the emerging field of metagenomics (reviewed in ref. 37)—the sample number should soon not be a limiting factor for the large majority of proteins that exist in a single copy in a genome, as long as they are widely occurring across the bacterial species.

The molecular details of the protein–protein interaction revealed may yield a large number of potential targets for antibiotic drug design in the absence of precise structural information. More broadly, the method of disentangling direct and indirect interactions presented here may also be valuable in aiding the interpretation of correlations observed in other large biological datasets, including mRNA and protein profiles, and neuronal spike activities.

Materials and Methods

Database Construction.

Domains were aligned and culled from the nonredundant refseq database (release 19) (38) using HMMER (39). Only genomic data from unique species were included to avoid oversampling of organisms with multiple sequenced strains in the database. Two overlapping sets of interacting domains, as defined by hidden Markov models (HMMs) in the Pfam database (40), were used in this study. For the SK/RR interaction study the accession numbers for the respective HMMs were PF00512 (SK) and PF00072 (RR). Functional association of these domains is inferred from chromosomal adjacency determined by GI numbers that differ by 1. For the RR/RR interaction the set of all proteins containing a PF00072 domain was restricted by requiring that the proteins also possess a specific DNA binding domain homologous to the OmpR-C domain (accession no. PF00486). All HMM searches used are detecting complete domains (in contrast to a search for fragments of domains).

Mutual information (MI) calculation.

MI was measured as described in ref. 11; see SI Text for a review.

Message Passing.

The computationally hard task in the suggested global inference is the estimation of marginal distributions for single positions and pairs of positions in the sequence alignment. We used the computationally efficient but semiheuristic message-passing approach (17, 18). This approach would be exact on tree-like graphs of couplings between positions, but it is known to work efficiently also for loopy graphs. The standard formulation of message passing in terms of belief propagation (17, 18) estimates only single-variable marginal distributions P_i(A_i). For estimating also 2-variable distributions P_ij(A_i, A_j) a recently proposed extension called susceptibility propagation (31) is used. Technical details are extensively exposed in the SI Text.

The computational cost of the approach is O(21²N⁴) and therefore not feasible for the full amino acid sequences having n = 212 positions. By using a cutoff in MI, a subset of up to ≈60 positions involved in high MI values is selected, and all pairs of these selected positions (intra- and interprotein pairs) are considered. The inference of the parameters of the reduced model requires ≈4 days of computational time on a single CPU of a Dell dual quad-core 2.33GHz Xeon processor. A selection of 100 residues would require >1 month of computation. However, smaller residue sets (n = 32, 40,50) demonstrate that the qualitative results given in Results and Discussion do not depend on the choice of the MI cutoff, as soon as all nodes contained in the network of coupled residues of Fig. 3 are included (data not shown).

Direct Information.

In the inferred statistical model, the direct information

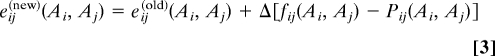is calculated by using the contribution P_ij^(dir)(A_i, A_j) of the direct coupling e_ij(A_i, A_j) between sequence positions i and j to the 2-residue distribution. This contribution can be calculated in a hypothetical system containing only the 2 positions i and j. They are coupled by e_ij(A_i, A_j) and have the correct single-variable marginals f_i(A_i) and f_i(A_j). DI measures the direct coupling strength between i and j; see the SI Text for a mathematical definition of P_ij^(dir)(A_i, A_j).