Genome rhetoric and the emergence of compositional bias

Abstract

Genomes exhibit diverse patterns of species-specific GC content, GC and AT skews, codon bias, and mutation bias. Despite intensive investigations and the rapid accumulation of sequence data, the causes of these a priori different genome biases have not been agreed on and seem multifactorial and idiosyncratic. We show that these biases can arise generically from an instability of the coevolutionary dynamics between genome composition and resource allocation for translation, transcription, and replication. Thus, we offer a unifying framework for understanding and analyzing different genome biases. We develop a test of multistability of nucleotide composition of completely sequenced genomes and reveal a bistability for Borrelia burgdorferi, a genome with pronounced replication-related biases. These results indicate that evolution generates rhetoric, it improves the efficiency of the genome's communication with the cell without modifying the message, and this leads to bias.

Living organisms exhibit a variety of statistical patterns of their genome composition (1), including species-specific codon usage bias (2, 3), GC content (4, 5), and asymmetry of nucleotide composition of leading and lagging strands (skews) (6). Despite many proposals, no single satisfactory explanation of skews and their diversity exists (7). Bacterial codon usage also seems complicated and multifactorial; there is evidence for translational selection resulting from uneven expression of the tRNAs (8, 9), optimization of tRNA pools to the existing codon usage (10, 11), and evidence for the primary role of neutral mutational pressure rather than selection (12, 13). Importantly, these mechanisms by themselves do not explain diversity. For example, if codon usage bias is a result of different tRNA pools or mutation pressure in different organisms, why are the tRNA pools or mutation pressure different in the first place?

We propose that a unified account of skews, GC content, and codon usage bias arises from multistability, which, we show, is inherent in the evolution of template-directed synthesis. Instead of treating the mechanisms described above as conflicting alternatives or trying to evaluate their relative importance, we model their coevolution: what happens when tRNAs adjust to codon usage and codon usage adjusts to the tRNAs; what is the outcome when the GC content and skews affect the pool of free nucleotides, and they in turn affect the nucleotide composition and mutation bias? As we will see, the answers to these questions help us integrate the accumulated knowledge about biases and, in addition, suggest bioinformatic tools for examining real genome data, demonstrating multistability and deducing the parameters governing the evolution of biases. As an example, we have determined that multistability of skews and GC content is consistent with the genome sequence of Borrelia burgdorferi.

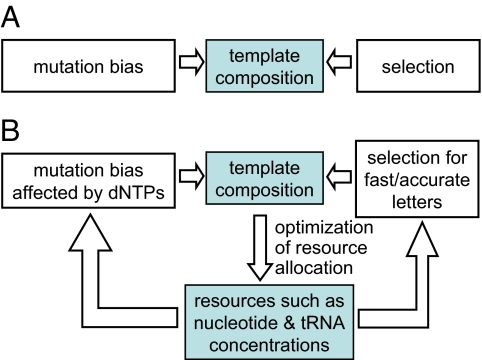
Fig. 1A shows schematically the conventional mutation–selection–drift framework (14), in which selection and mutation pressure are treated as static external variables governing the relaxation of the genome composition to a single state over evolutionary time. Our work describes how the mutation–selection–drift framework can be coupled to the notion of optimal resource allocation for processes of template-directed synthesis within cells (Fig. 1B). The feedback loops that are necessarily involved in such an extension generically lead to multistability (i.e., lack of uniqueness in the possible genome compositions that can arise over evolutionary time) and, as we show, generate a natural explanation of genome biases and their diversity. This framework opens the possibility of reconstructing patterns of genome bias diversity based on universal characteristics of information processing.

Fig. 1.

Contrasting frameworks for studying genome biases. (A) Mutation–selection–drift framework. Selection and mutation pressure are treated as static external variables, and for given values of these inputs the genome composition relaxes to a single state. The variety of genome biases must arise from exogenous mutation and selection pressures. (B) Coevolutionary framework of template-directed synthesis. Resource allocation is introduced as a dynamic degree of freedom. It is optimized to increase the speed, accuracy, and/or energy efficiency for a given template composition and in turn controls the mutation and selection pressures affecting template composition. The feedback loops lead to multistability and diversity of genome biases.

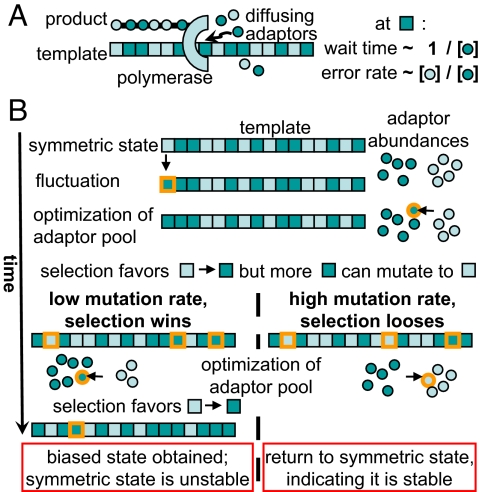
The notion of template-directed synthesis captures the common aspects of the central information processes of replication, transcription, and translation (Fig. 2A). During synthesis, a polymerase (DNA or RNA polymerase, ribosome) moves along a template and translates it to a product sequence by discriminating between competing adaptors (tRNAs for translation, dNTPs for replication, NTPs for transcription). The optimal allocation of different adaptors depends on template letter usage, as suggested for translation (10, 11, 15, 16), whereas selection and mutation pressure on letter usage depend on resource allocation (8, 9, 16).

Fig. 2.

Evolutionary instability of template-directed synthesis leading to genome biases. (A) Each template letter selects for an increase of its cognate (same color) adaptor concentration; for an optimal adaptor pool, more abundant cognate adaptors correspond to more popular letters. The time a polymerase waits for an adaptor to bind is inversely proportional to the adaptor concentration. The accuracy of synthesis also depends on the relative concentrations because the polymerase discriminates between correct and incorrect adaptors imperfectly. (B) Coevolution between regulation of adaptor abundance and genome composition leads to multistability at low mutation rates. Presented is a symmetric case with two synonymous template letters (dark and light squares) and their corresponding adaptors (dark and light circles). We follow the fate of the symmetric state after a fluctuation increasing the dark letters. The excess selects for an increase of dark adaptors (see A). This, in turn, selects for dark letters at all sites, whereas mutation tries to restore the letter balance. At low mutation rate, selection increases the dark letters, promoting a further increase of dark adaptors. The cycle continues until balanced by mutation pressure. Because of symmetry, there is an alternative state biased toward light letters and adaptors. The system is bistable: there is selection on the bias but not on its direction.

This interplay results in an evolutionary instability as heuristically explained in Fig. 2B. Consider two synonymous letters that have different cognate adaptors. If one of the letters is favored at some point, there will be an advantage in increasing the expression level of its cognate adaptor at the expense of the other adaptor because this will improve both the speed and accuracy of synthesis. As a result, the favored letter becomes even more favored. The cycle continues until the tendency of the disfavored letter to disappear is balanced by mutational pressure, or, if the letters are not synonymous at all genome sites, by functional constraints. The system is bistable: there is selection on the bias but not on its direction. The mechanism has different instantiations for translation, transcription, and replication, giving rise to different biases, summarized in Fig. 3.

Fig. 3.

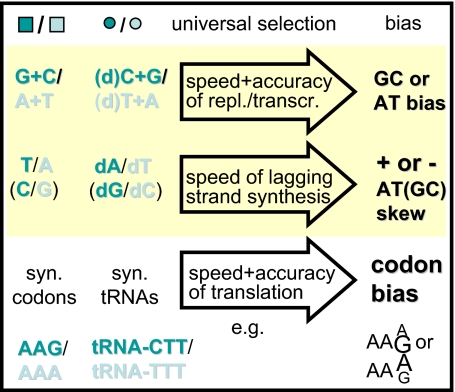
Different instantiations of genome biases emerging from the universal mechanism on Fig. 2B. The first two columns list the template letters and adaptors. dN denotes a dNTP, (d)N is dNTP for replication or NTP for transcription. The third column specifies an environmentally independent selection pressure that drives the optimization of resources and shapes letter usage. This picture is a simplification: GC content and skew evolution are coupled as reflected in the full model; nucleotide composition and codon biases also influence each other. More than two states are stable in general.

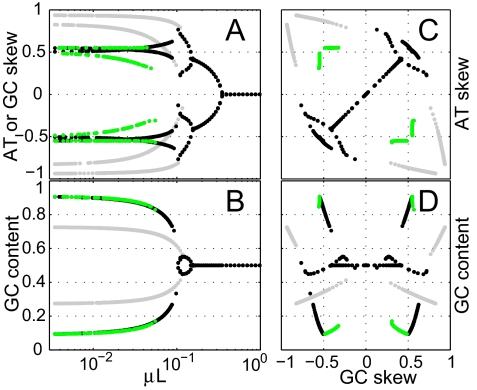
Multistability explains simultaneously the existence of certain intragenome patterns and their diversity among different genomes. The skews, an intragenome pattern, originate from selection on efficiency of replication through a coevolution between the nucleotide pool and strand-specific nucleotide usage. The two DNA strands are replicated in parallel by a single holoenzyme with two polymerase core units, but lagging-strand replication involves the additional step of primer synthesis. The leading-strand polymerase waits for its partner in Escherichia coli (17), and we expect this to be true in general. We suggest that the nucleotide pool is skewed to speed up the elongation of the lagging strand, and the letter usage of its template (the leading strand) evolved to use the complement of the more abundant nucleotides. Although the skews are generic, their orientations are not. All possible combinations of positive and negative GC and AT skews can be stable solutions of the coevolutionary dynamics, as shown in Fig. 4, in agreement with the observed diversity of microbial (18, 19) and mitochondrial (20) skews. The dynamics naturally allows for skews that are inconsistent with those predicted by mutation bias (21). Similarly, the multistability of the coevolution between synonymous codons and their cognate tRNAs leads to biased codon and tRNA usage. Again, although the bias is generic, its orientation is not. Different 3rd-codon position biases can result for different amino acids, an intragenome pattern that cannot be readily explained by mutation bias or environmental selection. The same multistability naturally accounts for the diversity of codon usage among organisms.

Fig. 4.

Pattern of equilibrium solutions reached using a fixed set of parameters and the same initial condition as a function of the mutation rate μ (M = I + μM⁽⁰⁾). The four panels present different projections of the same data. Outcomes are marked in black if GC and AT skews are in-phase (same sign) and in green if out-of-phase (opposite signs). Grayed out are solutions in which the lagging strand is no longer limiting (see SI Text). (A) Skew magnitude as a function of the mutations per genome per generation (same for the AT and GC skew because of parameter symmetry). (B) GC content as a function of the mutations per genome per generation. (C) Correlation between AT and GC skews. (D) Correlation between GC content and GC skew. The following parameters were used: symmetric mutation matrix M⁽⁰⁾ with transition transversion bias, k = 7, M_GC⁽⁰⁾ = M_GT⁽⁰⁾ = M_AC⁽⁰⁾ = M_AT⁽⁰⁾ = 1/(k + 2), M_AG⁽⁰⁾ = M_CT⁽⁰⁾ = k/(k + 2). Redundancy structure {R_si}: 9.09% fixed sites (evenly distributed to A, G, C, and T) and from the rest of the genome: 5% each of GC and AT redundant sites, 20% each of AG and CT redundant sites, 50% of GCAT redundant sites; genome length L = 110,000; α_i = 1, ϴ = 10⁶ = 9.09L. Δ_LAG = ϴ/2 was used to gray out solutions. Initial conditions: c_i = 1 and letter usage equilibrated to it.

Model.

To investigate multistability quantitatively, relate it to data, and examine its robustness to asymmetries, we constructed a model of selection on speed of template-directed synthesis. This model has two dynamic variables: the adaptor concentrations {c} and the frequencies u_si of different template letters i at genome sites of a given type s. A site type (22) is characterized by a vector R_si of the relative fitness values of different letters i at that site. For example, R_si = δ_i,A + δ_i,G describes a site type for which A and G are synonymous but C and T are lethal. The functional constraints on a genome are captured by the collection of its site types. The fitness of an organism increases with the speed of synthesis and decreases with the total adaptor concentration Σ_iα_ic_i; the weight factors {α} allow us to incorporate metabolic asymmetries in nucleotide or tRNA production. The mutation rate and biases are captured by a matrix M_ij, specifying the probability that letter i will mutate into letter j in one generation.

The dynamics iterates two steps. For given adaptor concentrations, and therefore given selection and mutation pressure, we solve for the equilibrium letter usage as prescribed by the mutation–selection–drift framework (relaxation step). Then we optimize the adaptor concentrations at fixed letter usage. A heritable change in the adaptor pool takes over if it is beneficial given the current letter usage. This step is not deterministic, different optimizations might be possible. Full details of the model are presented in Materials and Methods.

Other resource allocation decisions of the cell include the number of polymerases and investment in proofreading. However, an adaptor pool that enhances accuracy permits a decrease in resource allocation to proofreading or the time spent on error correction. Similarly, adaptor pool adjustment leading to faster elongation during translation allows the ribosome number to decrease for the same overall rate of protein synthesis. Thus, an effective theory focusing on the adaptor concentrations as the only resource allocation degree of freedom is a biologically relevant simplification.

Results from the Analytical Solution.

The equilibrium properties of the model are contained within a set of nonlinear algebraic equations. We solve explicitly and exactly the case of two synonymous letters [see supporting information (SI) Text]. The production asymmetries can be captured by α = α₂/α₁ and the mutation asymmetries by m = (M₁₂ − M₂₁)/M₁₂. The solution shows that selection on speed of template-directed synthesis leads to bistability at low mutation rates. The controlling parameter is the number of mutations per genome per generation. In the symmetric case, α = 1 and m = 0, there is a continuous-phase transition between states that are symmetric to genome biases (i.e., do not exhibit them at all) and states that break genome bias symmetry, as shown by the blue line in Fig. 5. This suggests an evolutionary scenario in which genome bias diversity emerged spontaneously as the accuracy of replication evolved above a certain threshold.

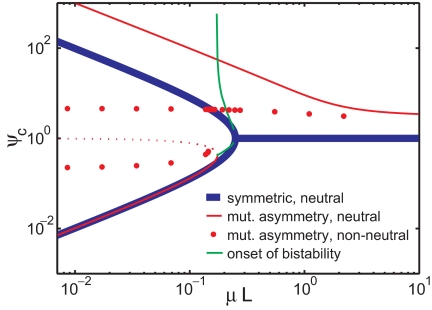
Fig. 5.

Bistability and robustness of adaptor bias (ratio of adaptor concentrations) for the two-letter model. The equilibrium adaptor bias, ψ_c, is plotted as a function of the number of mutations per genome per generation, μL, for different model parameters. All curves are for ϴ = 0. Thick blue line, exact solution of the symmetric case m = 0, α = 1, with the two letters being synonymous at all genome sites. Solid red line, same as the above except for the presence of strong mutational asymmetry, m = 0.9; the dotted red line indicates the unstable equilibria. Red balls, simulation of the previous case (m = 0.9), but 4.55% of the sites are fixed to letter 1, and 4.55% are fixed to letter 2. Green line, bias of the two solutions (Top and Bottom branches for the same μL) at the onset of bistability for different m >0 in the synonymous model.

Asymmetries in adaptor costs or mutation do not destroy the bistability (Fig. 5, red line), but lead to a nonzero minimal separation between the stable states (Fig. 5, green line). The transition point (expressed in terms of the larger mutation) is very insensitive to the degree of mutational asymmetry. The magnitude of adaptor pool or letter usage bias depends on the distribution of different site types. As illustrated by the red balls in Fig. 5, a small fraction of nonneutral sites regularizes the artifactual divergence apparent in the neutral cases so that biases are not extreme even at low mutation rates.

Discussion

A typical estimate for the mutations per genome per generation in bacteria is 10⁻³ (23), well below the transition point in our model when speed is limiting, suggesting that bacteria are typically in the bistable region. Care must be taken in interpreting this number because the effective population dynamics of bacteria might not follow exactly the selection–mutation model assumed here. The critical point value in our model is unlikely to be universal and is affected by the degree to which speed of synthesis is limiting and by the effective fitness cost of adaptor production. The first is likely to be high at high growth rates; the latter is likely to be high if resources are limiting. Both of these would promote multistability under a wide variety of ecological conditions. Finally, selection on speed of synthesis might be determined not only in relation to the overall growth rate but by molecular rate constants, such as the polymerase dissociation or slippage error rates. Increased speed of synthesis reduces the number of defective products, investment of time and energy in repairing interrupted replication forks, or collision rates between replication and transcription machineries. Again, we expect such benefits to be important for a variety of microbial life styles.

The model demonstrates that a universal selection pressure toward increase of efficiency of information processing can generate diversity of genome biases even if the individual molecular components, such as polymerases and tRNAs, are conserved. The genome bias diversity emerges at the systems level because of subtle changes in regulation. The different genome biases correspond to the different stable states of the coevolutionary dynamics. In addition to this mechanism, the individual molecular components can coadapt to the state of the coevolutionary dynamics. They can evolve asymmetries that reflect the asymmetries of the coevolutionary state. Such coadaptation is likely to reinforce the existing stable state and mask the multistability that generated it by moving the onset of multistability to lower mutation rates. It is therefore of great interest to see whether there are genomes that are multistable with their present-day molecular components and mutation rates.

Multistability of GC Content and Skews of Actual Genomes.

Ascertaining the possible multistability of actual genomes caused by selection on efficiency of replication is complicated by the lack of experimental data on mutation biases and the coevolution between replication and translation generated biases, which is not modeled here. We try to finesse these difficulties by considering a genome with a dominant replication-related bias and self-consistently deducing the mutation matrix from the known sequence, together with estimates of other model parameters. Specifically, we ask whether there is multistability of skews and GC content arising from the interplay between nucleotide concentrations and nucleotide composition at third codon positions while keeping the rest of the genome, the amino acid composition, and translational selection fixed. Further details are provided in Materials and Methods. This is a conservative test of multistability because the amino acid and tRNA usage are artificially kept adjusted to the existing skew and GC content and act to destabilize a state with an alternative 3rd-codon position skew.

We chose to analyze the main chromosome of B. burgdorferi, whose nucleotide usage at 3rd-codon positions is mostly determined by the strand, not the codon usage bias (Fig. S1). This is an indication that nucleotide composition is dominated by selection on replication or mutation and allows us to approximately treat translational selection pressures as static. It is possible that the dominance of replication is related to the large number of plasmids in this organism. In addition, the GC and AT skews have stable magnitudes along the chromosome and switch sign sharply near the origin and terminus. Thus, mutation and selection pressures appear independent of position along the chromosome.

We used the condition for optimality of the nucleotide concentrations and the total genome usage of the 4 nucleotides to determine the selection coefficients associated with replication as a function of the ratio κ of DNA elongation and total generation times (see Materials and Methods). Combining this with the approximation that translational selection is strand-independent and requiring mutation–selection equilibrium among synonymous groups of 3rd-codon positions on the same strand, we found the synonymous translation selection coefficients R_si and the mutation matrix via a least-square procedure. Overall, the only free parameters in our procedure are κ and the relative nucleotide asymmetries α.

We ran the stochastic coevolutionary dynamics many times and recorded the nucleotide composition of the reached stable states. Strikingly, we found that the simulations predict the existence of an additional stable state with skews of opposite sign and higher GC content (see Fig. 6). This behavior was observed for symmetric nucleotide costs and variations around it. We concluded that the existing data predict evolutionary bistability of the nucleotide composition of B. burgdorferi coming from selection on the speed of replication.

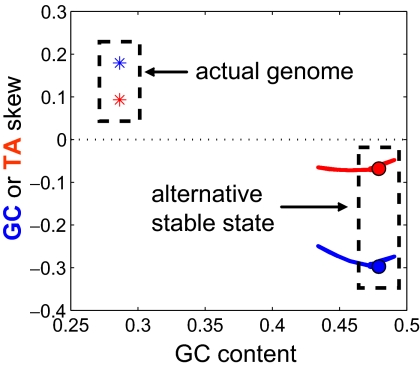
Fig. 6.

Predicted bistability of the genome composition of B. burgdorferi caused by selection on the speed of replication. The actual genome has GC and TA skews indicated by blue and red stars. Simulations reveal an additional stable state with skews of opposite sign and higher GC content. The location of the second stable state (but not its existence) depends on the free parameter κ∈ [0,1] (see Materials and Methods). Blue and red balls correspond to κ = 0.5; blue and red lines correspond to κ∈[0.001,0.99].

This bioinformatic procedure illustrates the possibility of integrating actual genome data with the coevolutionary framework. Other biological constraints can be incorporated.

Dynamic Mutation Model.

Many mutations are replication errors and thus affected by the nucleotide concentrations, as indeed has been observed experimentally (24). In this way, mutation turns into a dynamic degree of freedom, as indicated in the Left feedback loop of Fig. 1B. Different stable states have not only different adaptor concentrations and genome compositions but also different mutation biases. This finding has important implications for population dynamics. Perhaps paradoxically, even though mutation bias diversity is a consequence of selection on the efficiency of template-directed synthesis in this framework, the very fact that letter usage bias is partly channeled through mutational bias would make it difficult to detect the presence of selection at the redundant sites, as shown in Fig. S2. This helps to explain why certain types of statistical analysis appear to show dominance of mutation over selection (12).

Translational Coevolution.

Translation is by far the most complex instance of template-directed synthesis. We expect a rich set of patterns emerging from the coevolution of tRNA pools and codon usage, and even tRNA species and codon usage. Although in this article we have presented a model using selection on speed, selection on accuracy can be at least as important and may be naturally incorporated by turning the R_sis into dynamic variables dependent on the tRNA concentrations. The extension to translation would have to account for the fact that tRNAs are often coregulated as parts of operons and in fact might shed a new light on the diversity of the tRNA operon groupings among different organisms.

In addition to its implications for understanding contemporary patterns of codon usage and tRNA pools, the coevolution has implications for early life, when optimization of adaptor pools for speed and accuracy must have been even more important than in the present era because of the lack of compensatory mechanisms such as proofreading. Such models are relevant for understanding the evolvability of the genetic code and its evolution toward optimality (25).

Materials and Methods

Model Details.

A quasispecies is assigned a fitness

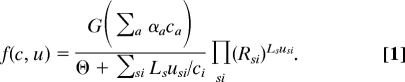Here, G is a decreasing function expressing the cost of production or maintenance of the adaptors. The denominator is the synthesis time T, and its functional form is justified below. (ϴ is a constant.) Site-specific selection pressures on letter usage and functional redundancies can be specified by the constants R_si ∈ [0,1]; they are important in connecting the model to actual genome data. u is normalized so that Σ_i u_si = 1, L_s is the number of sites of type s, and L = Σ_s L_s is the total genome length. Above, we restricted ourselves to one-to-one correspondence between adaptors and letters so that c_i is the cognate adaptor to letter i.

The exact interpretation of the denominator of Eq. 1 depends on detailed assumptions, but the functional form is rather generic. In the case of genome replication, we can imagine that cells accumulate resources for time ϴ and then replicate for a time that is the sum of the waiting times at each template letter. ϴ can also account for the replication time of the functionally conserved sites. Translation and transcription are parallel processes; the synthesis occurs at many sites simultaneously. However, because the elongation speed controls the fraction of busy polymerases and synthesis initiation rate is proportional to the concentration of free polymerases, we end up with the same functional form as in replication (14), but ϴ expresses the fraction of polymerases that are idle. The sum in the denominator of Eq. 1 could be weighted to incorporate different gene expression levels, but we do not discuss this extension here.

Dynamics.

To relax the letter usage at fixed adaptor concentration, we evolve an infinite asexual population, i.e., N_eμ ≫ 1,) until it reaches mutation–selection equilibrium. Specifically, let {g} be the space of possible genotypes. The abundance n_g of a genotype g with fitness f_g changes because of mutation and selection according to

where f̄ is the mean fitness of the population, and M̃ is obtained from M assuming independent point mutations. The next step in the dynamics is the optimization of adaptor concentrations at fixed letter usage. A heritable change in the adaptor pool {c′} takes over the population with adaptor pool {c} if f(c′; u) > f (c; u). This step is not deterministic; different optimizations might be possible. In the simulations we performed, each optimization is followed by a relaxation and each relaxation by an optimization. However, the average equilibrium properties will not depend on the relative rates of relaxation and optimization.

The model above can be directly applied to two-stranded DNA replication in the biologically relevant regime where the lagging strand is limiting the replication speed. However, in some regimes, it is possible to obtain solutions for which the lagging strand is no longer (solely) limiting (see SI Text).

Extracting Site Type Data from Genomes.

We determine the origin and terminus of replication from the GC skew and separate the protein-coding regions encoded on the leading and lagging strands. Each 3rd-codon position is assigned to a site type depending on the amino acid it encodes and the strand on which it is encoded. We compute the letter usage u_si at each site type s, specifying the frequency i of different synonymous nucleotides. For each strand, we end up with eight 4-fold degenerate site types, 12 2-fold degenerate ones and a 3-fold degenerate one (Ile) (6-fold degenerate amino acids are split into a 4-fold degenerate and a 2-fold degenerate site type). In addition, we record the total nucleotide usage vector (as read from the leading strand) of intergene regions U^inter, combined first and second positions U¹², and the total nucleotide usage U^tot. Fixed 3rd-codon positions coming from Trp and Met, stop codons, overlapping gene portions are added to U¹² and later treated as nonevolving sites.

Deriving Model Parameters from Genome Data.

Letters in the genome experience selection on efficiency of replication, specified by a vector of relative fitness values S_i, and site-specific selection R_si coming from functional constraints and selection on efficiency of translation and transcription. At mutation–selection equilibrium, the letter usage vector u_s at 3rd-codon positions of a given site type s is given by

or in more condensed form (MS)R_su_s = λ_su_s. The site type-independent part MS ≡ I + E is close to the identity matrix because the probability of a letter mutating is very small (<10−⁶) and the selection on efficiency of replication weak (S_is can be normalized to be close to unity). Correspondingly, (MS)−¹ ≈ I − E within an accuracy far greater than that coming from other assumptions and the mutation–selection equilibrium can be rewritten as

This choice of R_s (up to an arbitrary multiplicative constant) ensures not only that u_s is an eigenvector of the positive matrix MSR_s, but also, because of the Perron–Frobenius theorem, that it is the unique positive eigenvector corresponding to the largest eigenvalue.

r_si − r_sj specifies the relative selection coefficients of the letters i and j at a site of type s apart from selection on efficiency of replication. Therefore, for a pair of site types s and s′ that have the same functional constraints but are on different strands, we have r_si − r_sj = r_s′ı̄ − r_s′j̄ for all i and j, and ı̄ is the Watson–Crick complement of letter i. Here, to have the same MS operating on all site types, the letter usage is read from the same strand. Thus, for a pair of equivalent site types we have

Putting together the equations for all site type pairs and all i and j, we end up with a homogeneous, linear in the elements of E system of equations. Because Σ_iM_ij = 1, we have the additional nonhomogeneous constraint Σ_iE_ij = S_j − 1 ≡ s_j. Given S_i and the letter usage u_si of enough pairs of functionally distinct site types, we end up with an overdetermined linear system for E. (Although site types differ by 3 numbers, the nonlinear way in which they enter the equations provides linear independence.) By using an exponential G(), the condition for adaptor pool optimality ∂_cif(c, u) = 0 gives U_i^tot c_i⁻²α_i⁻¹ = T. Combining this with T = ϴ + ΣU_i^totc_i⁻¹ and s_i = −c_i⁻¹/T, we obtain

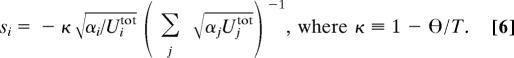To determine E, we minimize the sum of residuals of system 5 subject to the constraint that the actual genome is a stable steady state of the coevolutionary dynamics. To do so approximately, we solve a quadratic programming problem (minimizing the sum of the residuals of system 5) requiring that all off-diagonal elements of E are greater than ε. We look for the minimum ε (corresponding to least constraint and therefore the smallest residuals) that leads to E for which the observed genome composition is a stable state. For a given matrix E, we find R_si from Eq. 4; U¹²s are assigned to four evolutionary fixed sites types; U^inter are lumped into an effective site type with R obtained from Eq. 4. We ran the coevolutionary dynamics many times until an equilibrium was reached and determined whether (i) the actual genome is a stable state or not, and (ii) the system is multistable or not. (We used initial condition c_i = 10 for all simulations.) The results presented in Fig. 6 are for α_i = 1.