Simple prediction of interaction strengths in complex food webs

Abstract

Darwin's classic image of an “entangled bank” of interdependencies among species has long suggested that it is difficult to predict how the loss of one species affects the abundance of others. We show that for dynamical models of realistically structured ecological networks in which pair-wise consumer-resource interactions allometrically scale to the ¾ power—as suggested by metabolic theory—the effect of losing one species on another can be predicted well by simple functions of variables easily observed in nature. By systematically removing individual species from 600 networks ranging from 10–30 species, we analyzed how the strength of 254,032 possible pair-wise species interactions depended on 90 stochastically varied species, link, and network attributes. We found that the interaction strength between a pair of species is predicted well by simple functions of the two species' biomasses and the body mass of the species removed. On average, prediction accuracy increases with network size, suggesting that greater web complexity simplifies predicting interaction strengths. Applied to field data, our model successfully predicts interactions dominated by trophic effects and illuminates the sign and magnitude of important nontrophic interactions.

I would not give a fig for simplicity on this side of complexity, but I'd give my life for the simplicity on the other side of complexity.

Oliver Wendell Holmes, Jr.

One of the greatest challenges of environmental biology is to predict the effect of human activity on the complex webs of interactions among species. While there has been progress understanding how the extinction of one species may cause further extinctions of other species (1–5), understanding how extinctions may alter the abundances of every species in the web is critical for predicting community-wide responses to external perturbations (6, 7). Many species interactions involve the fundamental need to acquire energy, and well-documented allometric scaling rules describe relationships between body size, metabolism (8, 9), and food consumption (10, 11). Can these scaling rules at the level of individual trophic links help predict the effect of removing one species on others in a realistically structured food web? While nontrophic interactions among species (e.g., habitat modification, interference competition, behavioral modifications) (12, 13) can strongly affect species abundances, the fundamental physiological need for food may provide a null model (14) of species interactions against which the importance of other ecological processes can be assessed.

Some studies suggest that the multiple interaction paths connecting any two species in a realistically complex community will make it impossible to predict the influence of one on the other (15, 16). However, others argue that effects along longer paths should be weak and hence unlikely to interfere with prediction of extinction effects (17). Here, we report numerical experiments that explore how extinctions affect the mean abundances of all other species in models of complex food webs (see Materials and Methods). We simulated population dynamics and species removals in 600 food web models with 10–30 species and where all pair-wise consumer-resource trophic interactions are governed by simple allometric scaling rules (1, 18, 19). We explore two general questions: (i) How are per capita pair-wise rules modified by network dynamics? (ii) Is there a simple predictor of the dynamic effect of removing a species on the other species in a network governed by allometric scaling rules? While we focus on the consequences of species extinction, our approach may be extended to less dramatic changes in species abundance (e.g., over-harvesting).

The models are based on five simplifying assumptions: (i) autotrophs or “basal species” compete for fixed inputs of two primary limiting nutrients (20); (ii) the rate of metabolism and maximum per capita consumption (hereafter, “maximum consumption”) of all consumers scale with their body mass to the ¾ power (10, 21); (iii) consumer-resource body-mass ratios are log-normally distributed with mean 10 and standard deviation 100 (22); (iv) networks are structured according to the “niche model” (23); and (v) generalist consumers feed on different resources in proportion to the resources' relative biomasses (i.e., there is no complex foraging behavior). This Allometric-Trophic-Network (ATN) model simulates population dynamics within food webs following an allometric predator-prey model (18, 21) where:

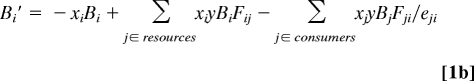describe changes in relative, dimensionless biomass densities of primary producer (Eq. 1a) and consumer species (Eq. 1b). In these equations, B_i is the biomass density of species i, r_i is i's mass-specific maximum growth rate, G_i describes the nutrient-dependent growth rate for all basal producer species i that compete for the same limiting nutrients (see SI Appendix), x_i is i's mass-specific metabolic rate, y is the maximum consumption rate of the consumers relative to their metabolic rate, e_ji is j's assimilation efficiency when consuming species i. The functional response, F_ij, is the fraction of i's maximum rate of consumption achieved when consuming species j (see Materials and Methods and SI Appendix). This ATN model makes it possible to explore how scaling relationships for bioenergetics and feeding interactions manifest in a network context.

We generated 600 food web models, ranging from 10 to 30 species, with realistic stochastic variation in the parameters that determine network structure and that drive species population dynamics. For each web, we simulated the effect of removing each species in turn (hereafter R, or “removed species”) on the biomass of every other species in the web (hereafter T, or “target species”). Simulated species' biomass and population density fluctuate indefinitely but their averages over moderate time windows stabilize after an initial transient phase (see Materials and Methods and SI Appendix). Removal effects are measured by these averages as either population-level interaction strengths (I = B_T⁺ − B_T⁻, where B_T⁺ is the biomass of T with R present, and B_T⁻ is the biomass of T without R) or per capita interaction strengths (per capita I = I/N_R, where N_R is the population density of R). For more details about this choice of I, see SI Appendix). Thus we focus here on the mean strength of dynamic coupling between R and T rather than on the variance in I (24–27) (SI Appendix). For each of these 254,032 possible interactions between R and T across all degrees of separation, we recorded 90 species, link, and network attributes that were then used to explain variation in I and per capita I (see Materials and Methods and SI Appendix).

Results

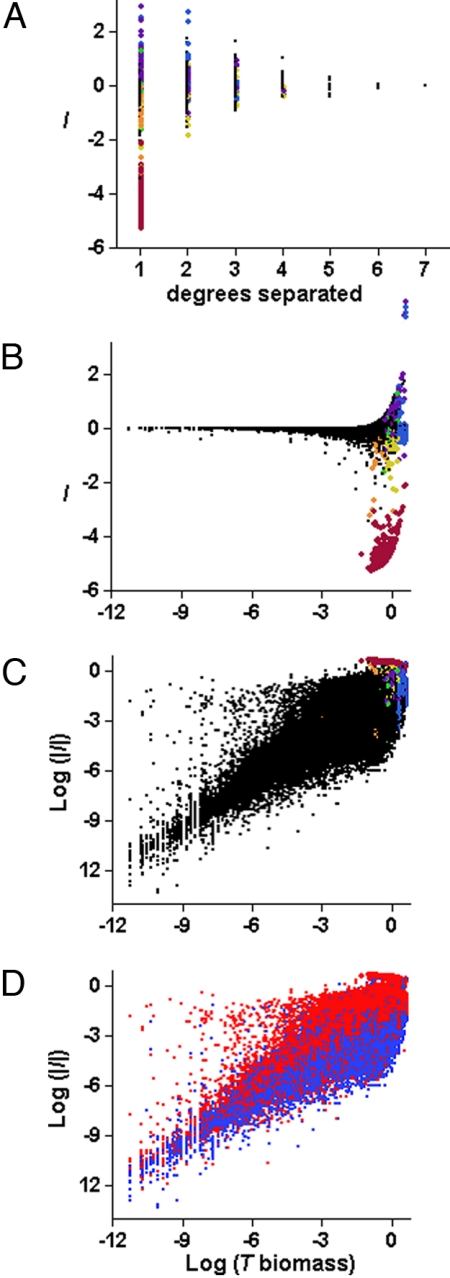
Of the interactions in these species-removal simulations, 45% were positive and 55% were negative. Consistent with empirical findings, the distributions of both positive and negative I and per capita I were all approximately log-normal (Fig. S1) (6, 28, 29); mean population density was roughly proportional to a negative power of body mass (8) (Fig. S2); and the maximum I decreased as the length of the shortest path (i.e., degrees of separation) between R and T increased (Fig. 1A) (12, 17).

Fig. 1.

Explaining variation in the magnitude and sign of I. Untransformed population-level I as a function of (A) the degrees of separation between R and T, and (B) log₁₀(B_T⁺). Colored symbols highlight all of the CART leaves whose mean was within the top 5% strongest I. Strong negative I included one degree, “simple” (one path) effects of R on basal T where R is T's only consumer (dark red) or one of two consumers (orange), or “diffuse” (multiple possible paths) effects of high biomass R on high biomass T where the weighted sum of path signs <0 (yellow). Strong positive I included simple and diffuse effects of high biomass R on high biomass T where the weighted sum of path signs ≥0 (purple, blue, and green). (C and D) The same data as B but with log₁₀|I| on the y axis. Color codes in C are the same as in A and B. Colors in D indicate upper (light red) and lower (blue) 50% quantiles of B_R. Multiple linear regression: log₁₀|I| = −1.34 + 0.71 log₁₀(B_T⁺) + 0.22 log₁₀(B_R), R² = 0.65 and 0.63 in the training and test data, respectively. B_T⁺ is the biomass of T with R present, and B_R is the biomass of R.

Predicting Population Interaction Strengths.

We explored how well a simple model based on a small subset of the attributes we tracked for each model run could predict the effect of removing one species on others. A Classification and Regression Tree (CART) algorithm using 7 of the 90 candidate variables explains 86% of the variance in I in a random sample of 300 of the 600 simulated networks (training data) and 89% in the remaining 300 networks (test data, see Materials and Methods and SI Appendix). The fit of the CART model for raw I is driven by a few large interactions (Fig. S1). We begin by discussing the variables CART selected to predict the strongest interactions (Fig. 1 A–C, colored symbols). The strongest negative interactions among these groups are one-degree effects of R on basal T that have R as their only consumers (Fig. 1 A–C, red symbols). A priori, these one-degree effects are not necessarily expected to be strong. For instance, if a basal T's sole herbivore is removed, it could still be suppressed by competition with other basal species for limited resources (SI Appendix).

More generally, strong positive and negative interactions are associated with some combination of: high biomass of R and T with R present (> 75th percentile), low degrees of separation, and “simply connected” species (species linked by only one path, excluding paths either through nutrients and through any species more than once) (Fig. 1). The majority of species are “diffusely connected” i.e., they are linked by multiple paths subject to the same exclusions. The sign of interactions is predicted best by a weighted sum of the signs of the shortest and next-shortest paths from R to T (SI Appendix). Species with low degrees of separation are often connected by longer paths as well, but our simulations suggest that for species extinction effects, longer paths may matter less than shorter paths (12, 17), even though these weak long paths may be dynamically important to overall web stability (30).

CART selected different variables to predict the magnitude and sign of I. Modeling log|I| instead of I reveals a simpler pattern that describes all of the interactions rather than just the strongest ones: log|I| varies approximately linearly with log(B_R) and log(B_T⁺) (Fig. 1D), where B_R and B_T⁺ are the biomasses of R and T with R present, respectively. CART explains 66% of the variance in log|I| in the training data and 63% in the test data. The strong interactions explained by the CART model for raw I (Fig. 1C, colored symbols) are part of a broader pattern among all interactions. A separate linear model for log|I | as a function of log(B_T⁺) and log(B_R) yields almost identical results—it accounts for 65% of the variance in log|I| in the training data and 63% in the test data (Fig. 1D). Including degrees of separation as an explanatory variable accounts for an additional 1% of the variance in log|I|. The other four variables CART used to model raw I (Fig. 1 A-C; the weighted sum of signs, simple vs. diffuse interactions, T trophic level, and the number of T's direct consumers) explain less than 0.5% more of the variance of log|I| in the linear model. Thus, the vast majority of the 90 explanatory variables that we tracked (see Materials and Methods and SI Appendix) contributed little to predicting the impact of R on T. Variables one might expect to be important, such as the functional response type, the consumer-resource body size ratio, or R's trophic generality, were not.

These results suggest that strong interactions are primarily associated with high B_R and B_T⁺ and secondarily with low degrees of separation. To test whether the strong correlation between log|I| and log(B_T⁺) is an artifact of the definition of I (I = B_T⁺ − B_T⁻), we randomly shuffled B_T⁺ and B_T⁻ pairings, computed I from the reshuffled data, and computed the correlation of those artificial values of log|I| and log(B_T⁺). The largest absolute Pearson correlation for 10,000 random permutations was 0.44, considerably smaller than the Pearson correlation of the original data, 0.77. One might expect that the largest negative effects would occur for rare T, but our simulations show the opposite.

Predicting Per Capita Interaction Strengths.

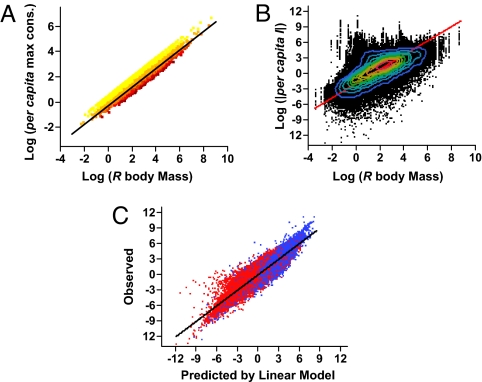
We expect from metabolic theory that per capita I would be tightly constrained by the power-law scaling of metabolism and consumption with body mass (29). Our ATN simulations follow this theory by linearly relating log maximum per capita consumption to log consumer body mass. The slope is ¾, and the intercept decreases with generality as a consumer divides its consumption among more resource species (Fig. 2A). Stochastic variation in species' generality yields an overall slope of 0.74 (Fig. 2A). Other theoretical studies have used a measure of “interaction strength” that is comparable to the maximum per capita consumption described here (11, 30, 31). To explore how this ¾ scaling of individual consumption manifests as per capita effects of removing R, we first regressed log₁₀|per capita I| on log₁₀(M_R), where M_R is the body mass of R. Simple, one-degree consumer-resource interactions (i.e., effects of specialist consumers on resources with only one consumer) preserve this allometric scaling relationship (slope = 0.74, R² = 0.32). However, for one-degree consumer-resource interactions that also have longer interaction paths (i.e., “diffuse” one-degree interactions), the slope increases to 1.30 (R² = 0.16). When all possible pair-wise interactions are included, the regression predicts 46% of the variance in log|per capita I| (Fig. 2B), but the exponent of this relationship, 1.38, is almost double the expected exponent of 0.74 (Fig. 2A). This particular value can be explained by the −1.38 exponent of the log(N_R) vs. log(M_R)relationship (Fig. S2B). Of the 89 other variables we tracked, B_R and B_T⁺ explain 61% of the remaining variance of log|per capita I|. Linear regression using log(M_R), log(B_R), and log(B_T⁺) accounts for 88% of the variance of log|per capita I| for both the training and test data (Fig. 2C). Including the B_R× B_T⁺ interaction accounts for less than 0.2% more.

Fig. 2.

Body mass scaling and per capita interaction strengths. (A) Maximum per capita consumption as a function of body mass (input parameters); colors indicate increasing consumer generality from yellow to red; RMA regression: slope = 0.74 ± 0.003 (mean ± 95% CI), R² = 0.90, n = 37,600 direct consumer-resource interactions. (B) Log₁₀|per capita I| depending on log₁₀(M_R), where M_R is the body mass of R._. Contour lines indicate 10% density quantiles from blue (low) to red (high). RMA regression model: slope = 1.38, R² = 0.46. (C) Observed log₁₀|per capita I| versus that predicted from the multiple linear regression: log₁₀|per capita I| = −1.14 + 0.88 log₁₀(M_R) + 0.71 log₁₀(B_T⁺) − 0.79 log₁₀(B_R), R² = 0.88. Colors are the same as in Fig. 1D.

Thus, ¾ allometric scaling of per capita I with R body mass is only preserved for the simplest possible consumer-resource interactions. In a network context, per capita interactions scale more steeply with R body mass and tend to be strongest between large bodied, low biomass R and high biomass T. Most of the 90 explanatory variables that we tracked, including the functional response type, predator interference, the consumer-resource body size ratio, or R's trophic generality, contributed little to predicting per capita I or I.

Application to Field Data.

Our ATN simulations characterize the behavior of a class of networks connected by metabolically constrained trophic interactions. When tested against empirical data, deviations from purely trophic behavior in natural communities should elucidate the importance of nontrophic interactions and nonmetabolic processes on species abundances. The variables that predict interaction sign and magnitude best in the ATN simulations can be measured easily in “intact” communities. This makes it possible to test empirically how well the model predicts the effect of removing one species on the biomass of another. Of course, if nontrophic effects are large, the model is unlikely to fit well. Thus, an initial empirical test of this general approach requires knowledge about the importance of trophic vs. nontrophic interactions. We illustrate this idea using a field experiment that disentangled trophic and nontrophic interactions in a rocky intertidal community (27, 32).

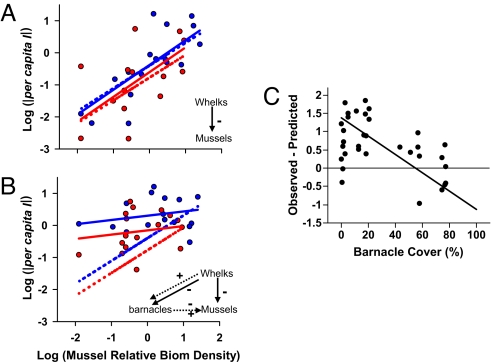
The experiment manipulated 3 species in a network of about 30 species that varied naturally over space and time (see SI Appendix), and separated primarily trophic effects of R on T from well-known, strong nontrophic effects mediated by a third species (Fig. 3A vs. B). In this system, R is a predatory whelk and T is its sessile mussel prey. Both positive and negative nontrophic effects of whelks on mussels are mediated by barnacles. Barnacles facilitate mussel recruitment: they are a preferred settlement substrate (27, 32). Whelks consume barnacles, but can also help them survive physical disturbances by thinning very dense colonies (27).

Fig. 3.

Empirical test of the metabolic baseline of interaction strengths. Log₁₀|per capita I| of predatory whelks (R) on mussels (T) depending on log₁₀(B_T⁺) for low (blue) and high (red) levels of R biomass with (A) or without (B) nontrophic influences of barnacles. ATN model predictions (dotted lines) are compared to separate linear regressions through the empirical data (solid lines). In the interaction web diagrams, solid arrows indicate trophic interactions, and dotted arrows indicate nontrophic interactions. Regression models for the empirical data (solid lines) for, A, R² = 0.48, log₁₀(|per capita I|) = −0.29 + 0.77 log₁₀(B_T⁺) − 0.47 log₁₀(B_R); B, R² = 0.22, log₁₀|per capita I| = 0.47 + 0.13 log₁₀(B_T⁺) − 0.96 log₁₀(B_R). (C) The difference between empirically observed log|per capita I| when nontrophic influences of barnacles are present and those predicted by the ATN simulations as a function of mean barnacle cover in paired plots without whelks or mussels. RMA regression: slope = −0.025, R² = 0.26.

When barnacles are excluded, the central tendency of per capita I of whelks on mussels (Fig. 3A, solid lines) is consistent with the linear model from our ATN simulations (Fig. 3A dotted lines). Both regressions explain 48% of the variation in log per capita I. However, when barnacles introduce nontrophic effects, our metabolic-trophic model under-predicts per capita I at low mussel biomass and over-predicts per capita I at very high mussel biomass (Fig. 3B). The difference between observed I and that predicted by our metabolic-trophic model is explained well by natural variation in barnacle cover (Fig. 3C). The observed negative effects of whelks on mussels were stronger than the model predicts when barnacles cover was low (< approximately 50%), and weaker than predicted when barnacle cover was high (> approximately 75%) (Fig. 3C). At low natural barnacle cover, the nontrophic effect of whelks on mussels is negative because whelks reduce the abundance of barnacles, impeding mussel recruitment. At very high barnacle cover, however, the nontrophic effect of whelks on mussels is positive because whelks stabilize barnacle abundance, which increases mussel recruitment. In sum, the ATN model accurately predicts the effect of whelks on mussels, absent nontrophic facilitation by barnacles. Deviations from the ATN model predictions reveal both the magnitude and sign of the important nontrophic effect. Results for population-level I are almost identical (data not shown). Thus, our simple empirical test of this ATN model successfully predicts a primarily trophic interaction and predictably fails when strong nontrophic effects were present. Similar tests in other systems will help evaluate the strength and generality of this approach.

Discussion

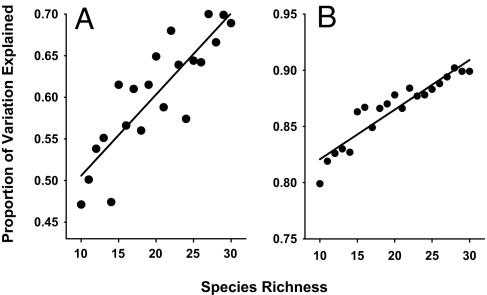
Our ATN simulations elucidate how very general metabolic constraints on trophic relationships play out in theory when consumer-resource interactions are embedded in realistically structured trophic networks. In a complex network, the response of one species to the removal of another does not scale the same way that direct per capita feeding interactions do. However, new simple patterns emerge. That distant effects of long interaction chains are generally weak tends to dampen difficult to predict and otherwise unexpected effects. Our results appear relatively independent of large variation in network structure, consumer-resource body mass ratios, consumer functional responses, and other species traits used to model species' population dynamics. These simulations also suggest that in trophic networks, static measures of interaction strengths based on simple species attributes (e.g., body mass and biomass) (6, 11) may be highly correlated with dynamic measures based on removing species. More complex networks had simpler behavior: the proportion of variation in both I and per capita I explained by the set of simple R and T attributes increased approximately linearly with species richness (Fig. 4).

Fig. 4.

More complex is more simple. The proportion of variation in (A) log₁₀|I| and (B) log₁₀|per capita I| explained by the most parsimonious multiple linear regressions described in Figs. 1D and 2C for different levels of species richness that each included a range of connectance values. The absolute magnitude of both I and per capita I explained increases with web size (R² = 0.74 and 0.88 for A and B, respectively).

|I| and per capita |I| in our simulations are predicted well by linear models that include the time-averaged biomasses of R and of T as explanatory variables. Predictions using the biomass at a single time would be less accurate if the biomass greatly fluctuates over time. Prior analyses of “keystone” species removal in complex networks (1) focused on one type of positive interaction where the removal of a consumer, R, causes a strong increase in a competitively dominant basal T that, in turn, causes other basal T species to go secondarily extinct. The group of red symbols in Fig. 1 A-C represent the small subset of cases where a dominant basal T increases greatly when its only consumer is removed. In cases of secondary extinction of T (1), I has been shown to depend strongly on local network structure with R present. In the more general case explored here, where B_T⁻ is nonzero, these local network properties do not help much to predict I: attributes of T and R suffice.

Our ATN simulations show how network effects transform a simple allometric rule for pair-wise feeding interactions. The approach could be extended to incorporate additional ecological factors (3, 33) to describe an energetic baseline of species interactions in ecosystems that vary in the importance of environmental stochasticity and spatial and subpopulation scale processes. The predictability of simulated interactions suggests that (i) studies of species interactions that focus on a simple subset of a natural community provide insights that are robust to variation in peripheral network structure; (iii) species' interactions known to be primarily driven by energetics may be predicted well by simple species and network attributes; and (iii) the characteristically variable, “context-dependent,” or “unanticipated” outcomes of species' perturbations in empirical studies (28, 32, 34) may not be due to inherently intractable network influences (15). Instead, this variability may point to other biotic mechanisms (e.g., behavior and nontrophic interactions) (12, 13) or abiotic factors regulating species interactions. Metabolic requirements are critical to all ecological networks, and the predictability of interactions mediated by these requirements makes it possible to assess the relative importance of other ecological processes by examining deviations from ATN predictions (14). More generally, our results suggest that the complexity of natural food webs is tractable and may simplify, rather than complicate, predicting the consequences of species loss.

Materials and Methods

General Approach.

We employ four steps to simulate ATN: (i) The niche model (23) generates network structures with random, uniformly distributed species richness (10 to 30) and connectance (0.1–0.2). (ii) Species' body masses are generated, starting with a basal species level of unity. Successively higher levels are generated using average consumer-resource body-mass ratios sampled from a log-normal distribution (mean = 10, SD = 100) (18, 22). (iii) A dynamic consumer-resource model (21) with nonlinear functional responses including random, normally distributed Hill exponents (mean = 1.5, SD = 0.25) and predator interference terms (mean = 0.5, SD = 0.25) is parameterized by random initial biomasses and ¾ power-law relationships between the rates of metabolism, maximum consumption, and production and body masses (1, 18) (see SI Appendix for model details). (iv) A plant-nutrient model (35) is assigned to the basal trophic level (1, 20). These steps were repeated independently 600 times to generate realistic variation in model parameters defining network structure, predator metabolism, maximum consumption, initial biomass, and functional response, and the nutrient uptake rates of basal species. To analyze the effect of removing each species on the biomass of every other species, each of the 600 dynamic network models was run once with all species present and subsequently with each species in the network removed in turn. Each species' average biomass per unit area and population density (number of individuals per unit area) from time step 50 to 200 was monitored to calculate I and per capita I (SI Appendix). For each removal, we tracked 90 attributes of the global network (e.g., connectance), the local network structure (e.g., the numbers of direct consumers of T and R), the species (e.g., body mass and biomass of T and R), and the pair (e.g., degrees separated) (SI Appendix). CART (36) was used to model the sign and magnitude of I and to select explanatory variables for Reduced Major Axis (RMA) regression and multiple linear regression models of log|I| and log|per capita I|. Models were developed using a random sample of half the webs and tested on the other half. Additional simulations of different length suggest that (i) secondary extinctions do not greatly alter the results, and (ii) the general patterns we observe are robust to different simulated times frames (Figs. S3 and S4, Table S1). Empirical data on interaction strengths in a rocky intertidal community were reanalyzed from previously published data (27, 32) [For more methodological details about the ATN model, the time frame of the simulations, the analysis of simulation data, and the application to field data, see SI Appendix]