Random walk in orthogonal space to achieve efficient free-energy simulation of complex systems

Abstract

In the past few decades, many ingenious efforts have been made in the development of free-energy simulation methods. Because complex systems often undergo nontrivial structural transition during state switching, achieving efficient free-energy calculation can be challenging. As identified earlier, the “Hamiltonian” lagging, which reveals the fact that necessary structural relaxation falls behind the order parameter move, has been a primary problem for generally low free-energy simulation efficiency. Here, we propose an algorithm by achieving a random walk in both the order parameter space and its generalized force space; thereby, the order parameter move and the required conformational relaxation can be efficiently synchronized. As demonstrated in both the alchemical transition and the conformational transition, a leapfrog improvement in free-energy simulation efficiency can be obtained; for instance, (i) it allows us to solve a notoriously challenging problem: accurately predicting the pK_a value of a buried titratable residue, Asp-66, in the interior of the V66E staphylococcal nuclease mutant, and (ii) it allows us to gain superior efficiency over the metadynamics algorithm.

In the past few decades, free-energy simulation has played a central role in computational chemistry and computational biophysics (1). Generally, free-energy simulation approaches can be categorized as alchemical free-energy simulation and conformational (chemical) free-energy simulation. In alchemical free-energy simulations (2), a 1-dimensional scaling parameter is required to bridge 2 chemical states (Γ_i and (Γ_f) in a hybrid potential function constructed as the following:

In Eq. 1, the boundary constraint should be set as U_r(0) = U_rⁱ and U_r(1) = U_r^f, which, respectively, stand for the energy terms that are unique in the corresponding end states. In conformational free-energy simulations, a low-dimension reaction coordinate is required to bridge the target conformational states; here, the original energy function can be rewritten as:

where U_r represents the energy terms involved in the reaction coordinate “ξ” description, and U_e represents the environmental energy terms. Based on the above energy functions, free-energy estimation can be performed based on the samples collected by means of a specially designed sampling scheme, which is usually in the framework of molecular dynamics (MD) simulation or Monte Carlo (MC) simulation. Traditionally, the efficiency improvement in free-energy simulation has been emphasized in 2 directions: (i) how to optimize the sampling design (3) and (ii) how to optimally employ the collected data for free-energy estimation (4, 5). It should be noted that these 2 issues are interrelated because the sampling strategy governs how the free-energy estimator should be optimally designed (6).

To understand the sampling optimization issue, let us first revisit a classical free-energy estimator: the thermodynamic integration (TI) method (7, 8). Based on TI, free-energy difference between 2 end states can be estimated by the following formula:

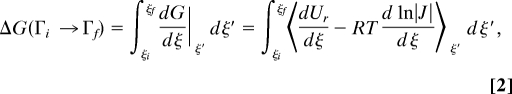where ξ_i and ξ_f, respectively, represent the order parameter values for the initial (Γ_i) and the final (Γ_f) states and ∣J∣ is the Jacobian term corresponding to the involved coordinate transformation. Here, dU_r/dξ − RTdln|J|/dξ can be called the generalized force F_ξ. For the alchemical transition where ξ is usually represented by the scaling parameter λ, dln|J|/dλ should be zero. To simplify the following discussion, we will use ξ to represent the order parameters for both the alchemical and the conformational changes. Eq. 2 indicates that there are 2 interrelated aspects of the sampling issues in free-energy simulation. First, the overlap sampling issue concerns whether all of the intermediate (ξ) states are under the sampling coverage for the mapping of their generalized force distributions. Second, the conformational sampling issue concerns how efficiently the generalized force distribution of each intermediate state can be accurately mapped for the estimation of the corresponding free-energy derivative dG/dξ|_ξ′. Apparently, for the complex systems that usually undergo slow structural transition during the order parameter move, the conformational sampling issue is particularly vital for free-energy convergence. As generally observed, the challenge of obtaining efficient free-energy simulation of complex systems usually lies in the fact that necessary structural relaxation cannot catch up with the move of the low-dimension order parameter. Consequently, the generalized force F_ξ, the value of which depends highly on the structure of the environmental portion, cannot efficiently move to the region expected for the instantaneous order parameter state; then the efficiency of free-energy convergence could be abolished. As identified by Kollman et al. (9), this so called “Hamiltonian lagging” issue has been a major factor responsible for the generally low efficiency of free-energy simulation methods.

Facing the Hamiltonian lagging problem, tremendous efforts have been made with the hope of accelerating the sampling of conformational transition during free-energy simulation. Among these efforts, the generalized ensemble methods, based on the strategy of the order parameter space random walk (OPSRW), have been extensively discussed. This general strategy has several variant forms; for instance, the widely used algorithms, including the adaptive umbrella sampling method (10), the metadynamics method (11), the adaptive force algorithm (12), etc., all belong to this category. In the OPSRW methods, the environmental relaxation can be sped up by a conformational “tunneling” mechanism (13). The major limitation of the OPSRW-based strategy lies in the fact that the sampling of conformational relaxation is a passive process, where the necessary conformational relaxation for the simulation of a state of interest cannot be robustly guaranteed from the simulation of other states; moreover, the order parameter random walking may greatly delay the transportation of the lead conformations to the target state. As a consequence, the OPSRW-based methods cannot guarantee robust solution of the Hamiltonian lagging problem.

Motivated by the above thought, in the present work, we propose an active sampling strategy by simultaneously flattening the free-energy surface in both the order parameter ξ space and its “generalized” force F_ξ space; thereby, the change of the generalized force can be efficiently synchronized with the order parameter move. By means of such an orthogonal space random walk (OSRW) strategy, besides the escape of the explicit free-energy minima projected along the order parameter space, the “hidden barriers” strongly coupled with the environmental relaxation process can also be overcome. As one would anticipate, the Hamiltonian lagging problem should then be naturally resolved. As demonstrated in both the model studies on the alchemical transition and the conformational transition, a leapfrog increase in free-energy simulation efficiency can be achieved by the present OSRW method. For instance, it allows us to solve a notoriously challenging problem: accurately predicting the pK_a value of a buried titratable residue in the hydrophobic protein interior; moreover, compared with the metadynamics method, the OSRW method permits superior efficiency.

Theoretical Design

Based on the above discussion, we would like to design a free-energy simulation scheme in which a random walk in orthogonal space (simultaneously along the directions of the order parameter ξ and its generalized force F_ξ) is realized. This goal can be achieved by iteratively applying a 2-dimensional biasing potential G(ξ, F_ξ). To obtain the adaptive potential G(ξ, F_ξ), we can implement a recursion strategy similar to the one in the metadynamics method (11). Specifically, the present OSRW can be obtained by repetitively adding a relatively small Gaussian-shaped repulsive potential:

which is centered at [ξ(t_i), F_ξ(t_i)], thereby discouraging the system from the often visited configurations. With this procedure repeated, the overall biasing potential

will build up and eventually flatten the underlying curvature of the free-energy surface along the orthogonal space. Then, as in traditional metadynamics simulations, the free-energy profile along the reaction coordinate [ξ(t_i), F_ξ] can be estimated as −G(ξ, F_ξ). It should be noted that the present OSRW method can be implemented in a straightforward manner for conformational free-energy simulation, where the move of the order parameter is naturally coupled with the system dynamics; for alchemical free-energy simulations, this technique can be realized based on the λ-dynamics method (14), where the coupling between the scaling parameter motion and the system dynamics is enabled via the extended Hamiltonian strategy.

Synergistically, the instantaneously obtained free-energy profile −G(ξ, F_ξ), as the byproduct of the conformational sampling design, has all of the information required for the estimation of target free-energy changes. For any intermediate state ξ′, the free-energy profile along its generalized force space can be estimated as −G(ξ′, F_ξ′); correspondingly, the generalized force distribution should be proportional to exp∣βG(ξ′, F_ξ′)∣. Then, the free-energy derivative can be obtained as the following:

Following the TI formula (Eq. 2), the free-energy change between the initial state with ξ_i and any target state with the order parameter ξ can unfold as the function of ξ:

The above implementation scheme seems sound for the target OSRW-based free-energy simulation algorithm. However, as discussed in earlier works (15, 16), the recursion efficiency should also be a critical factor because it determines the minimal simulation length before meaningful estimation of free-energy changes, which ought to cover the whole target order parameter range. Generally, the 2-dimensional recursion scheme is less efficient, in particular for the system that has a large free-energy gap between the free-energy minimum and maximum. For instance, if we employ the above OSRW implementation to compute the free-energy difference between leucine and asparagine in the gas phase (the details are provided below), the obtained orthogonal space free-energy profile −G(ξ, F_ξ) (Fig. S1A) shows that most of the early stage sampling has been concentrated near the state with the lowest free-energy value. Consequently, it takes ≈1-ns simulation for this model system to complete the first visit of the whole order parameter space. To overcome this recursion problem, we can adaptively add −ΔG(ξ) in the simulating potential to accelerate the free-energy surface flattening along the order parameter space. Herein, our used potential in the OSRW implementation can be summarized as:

where G(ξ, F_ξ) is updated via the metadynamics recursion, and ΔG(ξ) is updated according to Eqs. 3 and 4. Because the value of the term −ΔG(ξ) depends only on the used order parameter, the validity of Eqs. 3 and 4 should still hold. As a comparison, with this updated OSRW scheme, 1-ns simulation of the alchemical transition from leucine to asparagine allows the generation of uniformly distributed samples in orthogonal space as shown in Fig. S1B. Consequently, the updated scheme allows free-energy convergence to be reached within only 550-ps simulation (Fig. S1C).

Computational Details

The present OSRW method was implemented in the program CHARMM (17). To illustrate this method, 3 model studies are performed. Model system 1, the alchemical transition between the leucine and the asparagine molecules, was set up to demonstrate the importance of adding the −ΔG(ξ) term for the acceleration of the order parameter space recursion. The results of model study 1 are discussed above in Theoretical Design. To further demonstrate the superior sampling capability of the presently proposed method for both alchemical transitions and conformational changes, another alchemical free-energy simulation study was carried out to predict the pK_a value of a buried ionizable residue: Asp-66 of the V66D variant of staphylococcal nuclease (SNase) (18), and a conformational free-energy study was performed to compute the potential of mean force during the process of the separation of the ion pair of sodium and chloride in aqueous solution.

Alchemical free-energy simulation: Predicting the pK_a value of Asp-66 in the SNase V66D mutant.

This study tackles a long-standing biophysical problem: accurate prediction of the pK_a value of a titratable residue, Asp-66, which replaces the hydrophobic residue valine in the wild-type SNase (18). Following the traditional protocol of the pK_a shift prediction (19), 2 independent simulations were carried out to calculate the free-energy changes for the alchemical transition from the protonated to the deprotonated state of the aspartic acid molecule in the SNase V66D mutant and in aqueous solution, respectively. In this model study, the soft-core form (20) of the nonbonded interaction switching was used with the shifting parameter set as 6 Ų; a truncated octahedral water box was used to treat the whole system, and the particle-mesh Ewald (PME) method was applied to take care of the long-range Coulombic interactions, whereas the short-range interaction was switched starting at 10 Å and totally off at 12 Å. In Eq. 3, the height of the Gaussian function h was set as 0.01 kcal/mol; the widths of the Gaussian function, ω₁ and ω₂, were set as 0.01 and 4 kcal/mol, respectively. In the metadynamics recursion, G(ξ, F_ξ) was updated every 10 time steps. For the order parameter space recursion, ΔG(ξ) was updated every 100 time steps.

Conformational free-energy simulation: Mapping the free-energy profile for the separation of the ion pair of sodium and chloride.

Model study 3 demonstrates the use of the OSRW strategy in conformational free-energy simulation. In particular, we would like to compare the OSRW method with one of the most promising free-energy mapping techniques, the metadynamics method. Here, a classical model system, the separation of the ion pair of sodium and chloride in aqueous solution, was used. The order parameter was defined as the distance between the sodium ion and the chloride ion. Here, 2 ions are embedded in a cubic water box with the length of 48 Å. In Eq. 3, the height of the Gaussian function h was set as 0.02 kcal/mol; the widths of the Gaussian function, ω₁ and ω₂, were set as 0.1 Å and 1 kcal/mol/Å, respectively. In the metadynamics recursion, G(ξ, F_ξ) was updated every 10 time steps. ΔG(ξ) was updated every 100 time steps. In the reference metadynamics simulation, the height of the 1-dimensional Gaussian function h was set as 0.02 kcal/mol; the width of the Gaussian function was set as 0.1 Å.

Results and Discussion

Alchemical Free-energy Simulation: Predicting the pK_a Value of Asp-66 in the SNase V66D Mutant.

Accurate prediction of the pK_a values of the protein interior titratable residues can be of importance. The target system in the present model study is one of the representatives that may undergo simultaneous conformational transition during protonation and deprotonation (18); indeed, in recent years, the prediction of the pK_a value of Asp-66 in the SNase V66D has proven to be a great challenge to the computational community (21). We hope that this model study can convincingly demonstrate the superior efficiency of the present OSRW algorithm.

As described above in Computational Details, 2 independent free-energy simulations are needed to compute ΔG_AspH→Asp^solution and ΔG_AspH→Asp^protein, respectively, and then the pK_a shift of Asp-66 in the SNase V66D can be estimated based on the following ansatz (19):

Here, we use the solution study to illustrate the general feature of the OSRW method and then use the SNase V66D mutant study to show the superior sampling capability of the presently proposed algorithm.

Solution Study.

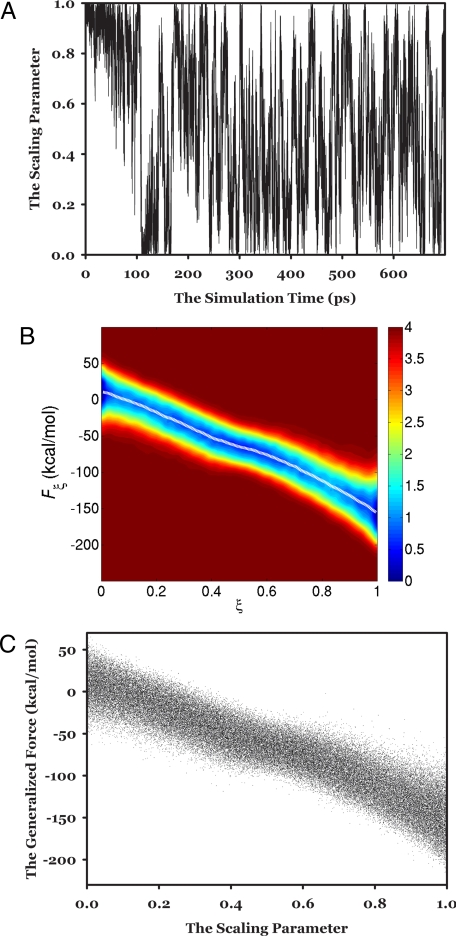
As shown in Fig. 1, because of our recursion design, the random walk in the scaling parameter can be quickly realized; the first complete 1-way trip in the scaling parameter space is achieved in ≈110 ps. Notably, at ≈110 ps, the estimated free-energy value is only 2.5 kcal/mol different from the target value (the solid line in Fig. 2A). This result indicates that in the OSRW simulation, decent free-energy estimation could be obtained even after a single 1-way trip in the order parameter space; this is different from the OPSRW simulations, in which even the location of the free-energy region (within 5–10 kcal/mol from the target value) alone may require many round-trip visits between the 2 end states (16). In the present OSRW simulation, after the first complete trip, further free-energy convergence is enabled by the refinement of the orthogonal space free-energy profile −G(ξ, F_ξ); to reach the final free-energy convergence (as shown by the time-dependent free-energy change in Fig. 2A), the refinement process takes only 1 other round-trip visit, occurring during the simulation from 120 to 280 ps.

Fig. 1.

The behaviors of the OSRW simulation on the solution system in model study 2. (A) The time-dependent scaling parameter change. (B) The free-energy surface along the orthogonal space produced by 300-ps OSRW simulation; in the middle, the white dash curve shows the estimated free-energy derivatives. (C) The distribution of the samples collected during the OSRW simulation in the orthogonal space.

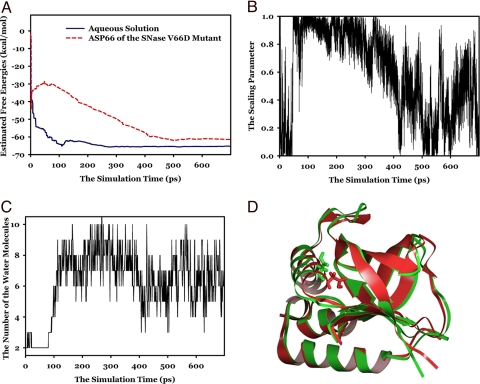
Fig. 2.

The free-energy simulation results and the behaviors of the OSRW simulation on the protein system in model study 2. (A) The time-dependent free-energy values. Dashed lines show the results on the protein (the SNase mutant) system; solid lines show the results on the solution system. (B) The time-dependent scaling parameter changes. (C) The time-dependent curve on the number of the water molecules that are exposed to Asp-66. (D) The structures of the SNase V66D mutant at the beginning and the end of the OSRW simulation.

Fig. 1B shows the orthogonal space free-energy profile −G(ξ, F_ξ) generated at 300 ps. As explained in Eq. 3, the cross-section of −G(ξ, F_ξ) for any order parameter ξ′ could lead to the estimation of the corresponding free-energy derivative dG/dξ|_ξ′. From the viewpoint of the overlap sampling, upon the complete generation of −G(ξ, F_ξ) in the whole target order parameter space, continuous sampling coverage is ensured; the white dashed line in Fig. 1B reveals the curve of free-energy derivatives produced at 300 ps. As the result of the continuous estimation of free-energy derivatives in the OSRW simulation, the scaling parameter-dependent free-energy change can be nicely obtained as shown by the solid line in Fig. S2. The finally converged free-energy value in the solution study is −65.3 kcal/mol. In classical free-energy simulations, reaching the same level of convergence usually takes tens of nanoseconds MD steps.

Besides the unique free-energy estimation scheme illustrated above, the synchronization between the order parameter move and the environment relaxation is also a major factor responsible for fast free-energy convergence in the OSRW simulation. For instance, in the present model study, the move in the scaling parameter space requires the solvent molecules to quickly adopt their relative positions so as to catch up with the change of the charge state of the solute molecule. In the traditional free-energy simulation schemes, the hidden barriers in the environment portion cannot be removed; as a consequence, the changes of the environmental “structures” are expected to fall behind the order parameter state transition, and the resulting lagging effect on the inaccuracy of the generalized force value will abolish the free-energy convergence. As a comparison, in the OSRW simulation, the simultaneous random walk in the generalized force space can speed up the required environmental response. This can be clearly shown in Fig. 1, where all of the samples are nicely distributed along the main channel of the expected generalized force change as the function of the order parameter switching.

Study on Asp-66 of the SNase V66D Mutant.

The OSRW simulation of Asp-66 in the SNase V66D mutant was initiated with the structure built on the wild-type conformation, in which the residue Asp-66 is buried in a hydrophobic core as shown by the red structure in Fig. 2D. One would expect that large conformational relaxation occurs so as to stabilize the Asp-66 residue. As shown in the previous free-energy simulation studies on the same target system, generating sufficient conformational relaxation for such stabilization has been very challenging, and the pK_a shift is usually overestimated (21).

At the beginning of the OSRW simulation of Asp-66, the order parameter was set as ξ = 0, which represents the state where Asp-66 is protonated. Because the target free-energy value is negative, before the energy term −ΔG(ξ) took adequate effect in flattening the free-energy landscape, the order parameter quickly moved to the other end with ξ = 1, which represents the deprotonated state (within 60 ps as shown in Fig. 2B). The time-dependent curve on the number of the water molecules that are exposed to Asp-66 (Fig. 2C) shows that a major conformational transition was not started until the end of 80-ps simulation, when a large free-energy value (approximately −30 kcal/mol as shown in Fig. 2A) was estimated; then in ≈150 ps (from 80 to 230 ps), the protein opened up the Asp-66 site and made this site accessible to the bulk water. It should be noted that completing such a large conformational change usually takes more than tens of nanosecond if no sampling enhancement is applied. The mechanistic reason for the OSRW method to quickly capture this event is that to realize the random walk in the generalized force space, the energy term G(ξ, F_ξ) can produce explicit forces that pull the nearby water molecules and other polar groups closer to Asp-66; as a consequence, the motion of these environmental species enslaved the protein dynamics and led to the opening of the protein cavity. Starting at 230 ps, the system started moving from the deprotonated state back to the protonated state (Fig. 2B); synchronously, the protein cavity became less water accessible. At ≈400 ps, Asp-66 was fully protonated; then the number of the accessible waters decreased to ≈4. Up to this point, −G(ξ, F_ξ) was well-developed throughout the whole order parameter space, and the estimated free-energy value is very close to the converged value (Fig. 2A). As the result of free-energy refinement (starting at 400 ps), during which −G(ξ, F_ξ) (Fig. S3) was further polished, free-energy convergence can be obtained at 530 ps with the estimated value of −60.2 kcal/mol. At 530 ps, the scaling parameter-dependent free-energy change can be nicely obtained as shown by the dashed line in Fig. S2.

Based on Eq. 6, the converged values of ΔG_AspH→Asp^solution and ΔG_AspH→As^pprotein allow us to predict the pK_a shift of Asp-66 in the SNase V66D mutant as 3.7 units. This result is in quantitative agreement with the experimental measurement (4.2-unit pK_a shift) (18). Such an unexpectedly small pK_a shift can be explained by the trajectory captured during the OSRW simulation; starting from a structure with the buried Asp-66 (colored in red in Fig. 2D), the helix where Asp-66 resides underwent a partially unfolding rotation (toward the green structure in Fig. 2D) so that the Asp-66 site became semiexposed. During this rotating process, the N terminus of the helix is partially unfolded, and the C terminus of this helix is bent from the ideal helix structure. This structural observation agrees also with the experimental measurement, which indicates the partial loss of the helix structure in the V66D mutant (18). Clearly, the present OSRW simulation captured 2 important components of the dielectric environment descriptions that lead to the observed ≈4-unit pK_a shift. First, the present OSRW simulation allows the Asp-66 site to be exposed to the bulk water. Second, the required conformational breathing can be synchronously obtained in the response to the move of the order parameter during the free-energy refinement stage (starting from 400 ps); as shown in Fig. 2 B and C, when the system moved to the deprotonated side, the protein cavity opened, with the accessible water number of ≈8; and when the system moved to the protonated side, the Asp-66 site became less open, with the accessible water number of ≈4.

Conformational Free-Energy Simulation: Mapping the Free-Energy Profile for the Separation of the Ion Pair of Sodium and Chloride in Aqueous Solution.

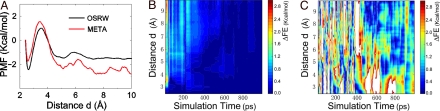
In this model study, we would like to illustrate the OSRW method for the mapping of free-energy surfaces in the conformational space. This study is on a classical model system, the separation of the ion pair of sodium and chloride in aqueous solution. As shown in Fig. S4A, we could obtain a decent order parameter space recursion within 20 ps, when the round-trip visits between 2 end states could be started; this is because the overall free-energy range is very narrow. As shown in Fig. S4B, within ≈250 ps, a nicely converged free-energy profile −G(ξ, F_ξ) along the orthogonal space could be obtained. According to Eq. 5, this free-energy profile allows us to generate the distance-dependent free-energy derivative curve as shown by the white line in Fig. 4B; by using the TI formula, the obtained free-energy derivative curve further gives rise to a well-converged potential of mean force curve represented by the black line in Fig. 3A. The potential of mean force curve is in quantitative agreement of the target result, which could be obtained from a long-time (50 ns) adaptive umbrella sampling simulation. As discussed earlier, a major advantage of the OSRW method lies in the fact that it allows the removal of the lagging of the generalized force behind the order parameter move. This orthogonal space synchronization can be clearly seen from Fig. 4C, where all of the samples are nicely distributed along the main channel of the expected generalized force change as the function of the order parameter change.

Fig. 3.

The free-energy simulation results in model study 3. (A) The distance-dependent potential of mean forces produced by 1-ns OSRW simulation (black) and 1-ns metadynamics simulation (red). (B) The time-dependent deviation of the estimated free-energy profiles produced by the OSRW simulation from the target result. (C) The time-dependent deviation of the estimated free-energy profiles produced by the metadynamics simulation from the target result.

Among the existing conformational free-energy mapping methods, the metadynamics algorithm has attracted a great deal of attention because of its impressive efficiency. As realized recently, the metadynamics method suffers from the “hidden barrier” problem as well (22); as a consequence, the error of estimated free-energy surface depends highly on the relaxation rate of the environmental portion after the order parameter move. To compare the present OSRW method with the metadynamics technique, for the same model system, we generated the time-dependent curves on the deviation of the estimated free-energy profiles from the target result. As clearly demonstrated in Fig. 3B, the OSRW algorithm shows intriguing convergence features: (i) a nice convergence could be obtained in <100 ps, and (ii) the convergence could be refined with the increase of the simulation time. As a comparison, the metadynamics simulation could not converge even after 1-ns simulation as shown in Fig. 3C.

Concluding Remarks

The hope of realizing efficient predictions of free-energy changes for various processes such as molecular binding, conformational change, chemical reaction, etc., has attracted many ingenious efforts in developing free-energy simulation algorithms. Unfortunately, achieving efficient free-energy calculation for the system that undergoes nontrivial structural transition during the switching between the target states has been challenging. As identified many years ago, the Hamiltonian lagging, which reveals the fact that necessary structural relaxation falls behind the order parameter move, has been a primary problem responsible for generally low free-energy simulation efficiency. In the present work, we propose a simulation algorithm by achieving a random walk in both the order parameter space and its generalized force space; thereby, the order parameter move and the required conformational relaxation can be efficiently synchronized. As demonstrated in both the alchemical transition and the conformational transition, a leapfrog improvement in free-energy simulation efficiency can be obtained; for instance, (i) it allows us to solve a notoriously challenging problem: accurately predicting the pK_a value of a buried titratable residue, Asp-66, in the interior of the V66E staphylococcal nuclease mutant, and (ii) it allows us to obtain superior efficiency over the metadynamics algorithm. Based on the present success of employing the OSRW method in dealing with nontrivial chemical and biochemical problems, we believe that this OSRW method may greatly catalyze the development of free-energy simulation in the near future. The refinement of this work, for instance, realizing a replica exchange scheme by having multiple OSRW copies to further improve its efficiency, remains to be completed.