Distinguishing between latent classes and continuous factors with categorical outcomes: Class invariance of parameters of factor mixture models

Abstract

Factor mixture models (FMM’s) are latent variable models with categorical and continuous latent variables which can be used as a model-based approach to clustering. A previous paper covered the results of a simulation study showing that in the absence of model violations, it is usually possible to choose the correct model when fitting a series of models with different numbers of classes and factors within class. The response format in the first study was limited to normally distributed outcomes. The current paper has two main goals, firstly, to replicate parts of the first study with 5-point Likert scale and binary outcomes, and secondly, to address the issue of testing class invariance of thresholds and loadings. Testing for class invariance of parameters is important in the context of measurement invariance and when using mixture models to approximate non-normal distributions. Results show that it is possible to discriminate between latent class models and factor models even if responses are categorical. Comparing models with and without class-specific parameters can lead to incorrectly accepting parameter invariance if the compared models differ substantially with respect to the number of estimated parameters. The simulation study is complemented with an illustration of a factor mixture analysis of ten binary depression items obtained from a female subsample of the Virginia Twin Registry.

Introduction

Factor mixture models provide a framework for a model-based approach to clustering. Variations of these models have been proposed by a variety of authors including Arminger, Stein, and Wittenberg (1999), Dolan and van der Maas (1998), Heinen (1996), Jedidi, Jagpal, and DeSarbo (1997), B. O. Muthén and Shedden (1999), Vermunt and Magidson (2003), and Yung (1997). Observed data within each cluster are assumed to have a multivariate normal distribution. The joint distribution is therefore a mixture of multivariate normal component distributions. Assuming that each object or subject belongs to only one cluster, the relative cluster sizes are the mixing proportions, which are modeled in terms of the parameters of a multinomial prior. The multivariate normal components are structured by imposing a factor model on their mean vector and covariance matrix. Different choices of the specific parameterization of the component distributions include the number of factors and cluster-specific parameters such as loadings, intercepts, and residual variances. These choices affect not only model fit but also the number of clusters needed to obtain the closest fit to the observed joint distribution (Lubke & Neale, 2006). A more restrictive within cluster parametrization will often result in choosing a model with more classes than a less restrictive parametrization. Hence, it is necessary to address the question of whether the correct model is chosen when fitting a set of different factor mixture models to observed data from a potentially clustered population. This question is especially relevant in an exploratory setting where neither the number of the clusters, nor their relative sizes, nor the pattern of relations between variables within a cluster is known, and different models are compared to investigate the underlying structure of the data.

In a previous simulation study, we investigated correct model choice for continuous data that were generated under different types of factor mixture models including latent profile models, factor models with 1 to 3 factors for a single homogeneous population, and factor models with 1 or 2 factors for a population consisting of 2 clusters (Lubke & Neale, 2006). The study showed that when comparing the fit of a set of different models it was possible to distinguish between latent profile models, which assume local independence within cluster, and models that allow for structured covariation within cluster. Furthermore, it was usually possible to use indices of model fit to identify the model with the correct numbers of factors and clusters. Not surprisingly, the results depended on the separation between clusters in the population and sample size. The study showed a trade-off between these two characteristics. For instance, a within cluster sample size of 75 was sufficient to choose the correct model in more than 95% of comparisons of a set of fitted models when the separation was large but needed to be increased to 200 for a smaller separation. Since the first study was limited to continuous data generated under factor mixture models without violating any of the model assumptions, the results of the first study should be regarded as a best-case scenario.

The aim of the current paper is again to investigate conditions under which a comparison of different mixture models leads to correct model choice. In this study, observed outcomes are ordered categorical, and not only different model types are considered, but also different types of constraints on the within class model parameters. The set-up of the simulation study is similar to the first. The data generating and the fitted models include a variety of factor models, latent class models, and factor mixture models with varying parameter constraints. The interest is in the proportion of correct model choice when fitting a series of different models. The simulation study is supplemented with an empirical example that illustrates some of the problems encountered when fitting a series of factor mixture models to collected test data. The data are scores on ten binary items designed to match the DSM-III-R criteria for depression. The data were collected in two separate but related studies of all-Caucasian female-female, male-male and male-female twins from the Virginia Twin Registry (Kendler & Prescott, 1999). For the illustration we used data from one female of each female-female or female-male twin pair.

The first part of the simulation study focuses on ordered categorical outcomes, which are very common in the social sciences. Lubke and Muthèn (2004) showed that when investigating multiple groups, incorrectly assuming normality in an analysis of Likert data is problematic and can lead to incorrect conclusions. Ordered categorical data can be modeled by assuming an unobserved multivariate normal response variable and imposing a threshold structure on the multivariate normal distribution (Agresti, 1990). Threshold parameters can be obtained by integrating over the normal variable. Due to the much longer computation time needed for the analysis of 5-point Likert items we did not fully replicate the first study. Nevertheless, the design of the current study permits an overall comparison of results. For a subset of the generated data, the proportion of correct model choice is directly compared for continuous, 5-point Likert, and binary versions of the outcome variables.

In the second part of the simulation study we take on the question whether model constraints such as class-invariance of regression intercepts or factor loadings can be tested by comparing increasingly restrictive models. These comarisons are important because (i) they test for measurement invariance of an instrument across latent classes, and (ii) for violations of the within class factor model.

Measurement invariance (MI) with respect to a grouping variable is said to hold if the measurement model relating items to underlying latent variables is invariant across groups (Meredith, 1993, for less technical presentations see Lubke, Dolan, Kelderman, & Mellenbergh, 2003, or Widaman & Reise, 1997). Dolan (2000) has shown that in a multi-group setting MI is a hypothesis that can be tested by fitting a series of models in which these parameters are subsequently constrained to be invariant. Focusing specifically on categorical outcomes, Millsap and Tein (2003) describe a more extended set of models that can be used to tests different levels of measurement invariance. It is unclear whether these approaches lead to correct results if the grouping variable is unobserved.

Violations of model assumptions (e.g., non-normality of the factors, non-linear item factor regressions, non-normality of the errors) result in deviations from multivariate normality of outcome variables within class ¹. Since mixture distributions can be used to approximate non-normal distributions, it is possible to specify mixture models that represent approximations of different types of model violations. Some of the tests of MI outlined by Dolan (2000) in the multi-group context involve the same tests of class-invariance of model parameters as some potential tests of model violations. This is obviously problematic because it might render the interpretation of results ambiguous.

The problem points to the more general question of how to interpret results from comparing mixture models with different numbers of classes and different types of constraints on within class model parameters. The next section addresses these questions, and also provides the rationale for the two parts of the current simulation study. The section is followed by a description of the general factor mixture model. To illustrate some of the problems, we present an analysis of ten binary depression items. Next, the methods and results of the simulation study are reported. In the final discussion an attempt is made to provide some guidelines for using factor mixture models to assess population heterogeneity.

Exploratory mixture models, indirect applications of mixture models, and the issue of interpreting results

Mixture distributions are a weighted sum of several component distributions (see later). A mixture model is a model that simultaneously specifies models for the different component distributions. Titterington, Smith, and Makov (1985) distinguish between direct and indirect applications of mixture models. In a direct application, the mixture components correspond to qualitatively or quantitatively distinct clusters of subjects or objects. In an indirect application, the mixture components are used to approximate a non-normal distribution. The degree of approximation depends on the number of components and the component specific parameters. For instance, McLachlan and Peel (2000) describe an example where models with class-specific variances required fewer classes than models with class-invariant variances.

In behavioral research, mixture models are often used to assess potential population heterogeneity (Greenbaum, Del Boca, Darkes, Wang, & Goldman, 2004, Hildebrandt, Langenbucher, Carr, & Sanjuan, 2007, Lubke et al., 2007, Neuman et al., 1999). The number of subgroups within a population is not known a priori, and it is common practice to compare models with an increasing number of classes. If the number of clusters is unknown, then it is unlikely that the exact structure within cluster, or the nature of the differences between clusters is known. In other words, analyses with mixture models are usually exploratory.

It is important to realize that the distinction between direct and indirect applications of mixture models is somewhat irrelevant when fitting mixture models in an exploratory setting. Even if the intention of the researcher is to distinguish between clusters of subjects in a population, the only information model comparisons may reveal is how well a given model serves to approximate the distribution of observed variables compared to some other model. Model comparisons do not reveal whether the specified latent classes actually correspond to meaningful clusters of subjects. One might even argue that in an exploratory setting, applications of mixture models are always indirect, and that the resulting cluster structure requires external validation (see Bauer & Curran, 2004, and comments). The situation is comparable to exploratory factor analysis (EFA) where the finding that three factors suffice to meet commonly used criteria (e.g. variance explained, eigenvalues > 1, etc.) does not necessarily imply that the three factors provide a description of the data that is meaningful on a conceptual level, or that the data generating process has three factors. It means that 3 factors ‘explain’ a large part of the common variance of the the observed variables. In the mixture setting, the mixture components correspond to areas of the observed distribution with similar response patterns. A better fit of model with 2 normal components compared to a model with a single component provides evidence that the response patterns in the population are not homogeneous and normally distributed.

However, the situation is slightly more complex when fitting mixtures than when carrying out an exploratory factor analysis. In EFA, the measurement model relating items to factors is extremely lenient. In the mixture setting, more constraints are usually imposed on model parameters. If population subgroups differ by a large number of parameters of the measurement model, then comparing models that constrain most of the parameters to be zero or class-invariant (e.g., local independence models, measurement invariant models) may lead to accepting a model with too many classes. The joint distribution of the scores from two groups characterized by many group-specific parameters differs from the distribution of two groups with locally independent or measurement invariant scores. The differences may concern location, shape, and/or higher order moments, and fitting local independence or measurement invariant models may require additional classes to capture these differences. To avoid choosing models with too many classes, one might want to fit multivariate normal mixtures without imposing any structure on the mean vectors and covariance matrices of the component distributions. Although such an approach might be feasible for very small numbers of items, it is usually impractical because the number of parameters increases dramatically when adding classes with unconstrained covariance matrices. In addition, fitting unconstrained models may lead to non-convergence. Hence, in practice, some compromise regarding the number of constraints needs to be found, which it turn means that there is always the possibility of accepting a model with too many classes. This is illustrated by the following example of skewed observed data.

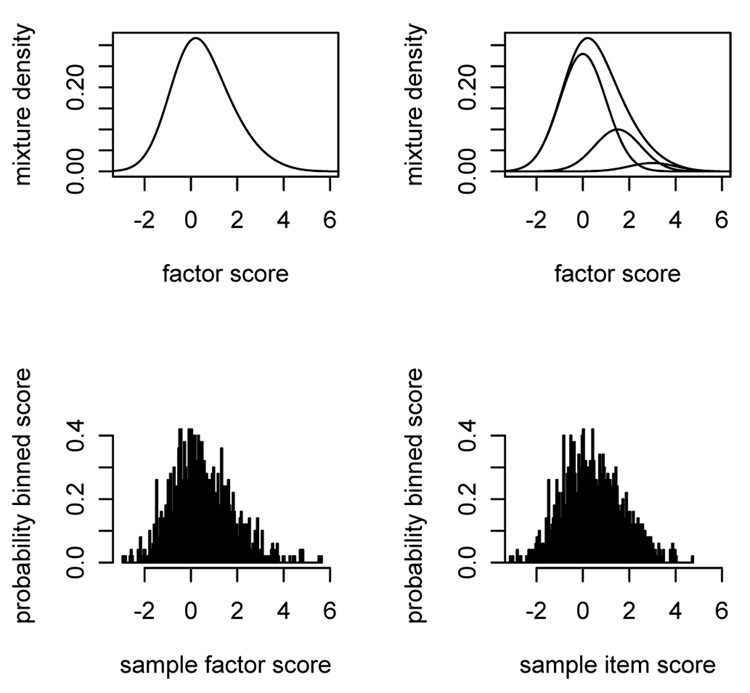
Skewed data can be generated in a variety of ways, including sampling from a distribution with non-zero skewness, transformation of a symmetric distribution, or sampling from a mixture of normal components. When fitting factor mixture models to skewed data, it should be expected that the number of mixture components needed to approximate the skewed observed data depends on the degree of skewness and the sample size, and not on the method of data generation. Hence, if data are generated from, e.g., a transformed univariate normal distribution, then fitting a mixture may lead to a solution with more clusters than the single cluster used to generate the data. If data are generated using a mixture, fitting mixtures may lead to under-, over- or correct estimation of the number of components used to generate the data depending on the power to detect mean differences between classes. Figure 1 illustrates this point.

Figure 1.

Factor and item distributions for a skewed factor

The upper left panel shows a distribution of a skewed factor score in the population. In this case the distribution was generated using a mixture of three normal component distributions as shown in the upper right panel (similar illustrations can be found in McLachlan and Peel (2000), among others). In Figure 1, components are separated by a Mahalanobis distance of 1.5, and class proportions decrease with increasing component means (ie., class 1=.7, class 2 = .25, class 3 =.05). The lower left panel shows a sample of N=1000 drawn from the factor distribution in the panel above, and the lower right panel depicts a sample distribution of an observed score that is created by adding a normally distributed error. If the sample size is much smaller than 1000, then it will depend on sampling fluctuation whether or not a mixture with more than one class would fit better than a single class model. A small sample might not contain a sufficient number of subjects in the second and third class to allow for class detection. However, with increasing sample sizes, mixtures with two or three classes will provide a better fit.

A very important issue in this context is the interpretation of the latent classes of the best fitting model. Whether or not it makes sense on a conceptual level to cluster the data shown in Figure 1 into two or three classes cannot be answered by comparing the fit of a set of mixture models. Model fitting approaches in general have to face the dilemma that affirming the consequent is a logical fallacy. Acceptable model fit does not allow one to deduct that the data generating process is in fact the one implied by the fitted model. The additional complication in the mixture context is that the set of alternative explanations include that mixture components can be used for a categorical approximation of continuous processes. As mentioned above, there are different processes that can generate skewed data, which include but are not limited to mixtures. Therefore, a good fitting mixture model with, say three classes can by definition not justify the conclusion that three distinct categories of subjects exist in the population from which the data are obtained. The distinction between ‘true clusters’ and a categorical approximation of a continuous process can not be made based on the comparison of mixture models. Whether this distinction is important depends of course on the context.

Models that allow for different types of class-specific parameters deserve additional attention regarding their interpretation. In a multi-group setting, models with intercept differences, or intercept and loading differences are directly related to the different types of measurement non-invariance (Meredith, 1993, Dolan, 2000, Widaman & Reise, 1997). If group membership is unobserved, the interpretation is less clear due to the indirect application of mixture models. For instance, factor loadings that increase as a function of the underlying factor score can be approximated using a model with several classes and class-specific loadings. Hence, the interpretation of mixture models with non-invariant parameters of the measurement models needs to be more cautious and includes more alternatives than in the multi-group setting. In the multi-group setting non-invariant loadings undermine a clear interpretation of the factors across groups. In the mixture setting one has to add the possibility that there is a single cluster with increasing loadings as a function of factor scores. In both settings, the interpretation of invariant models is much more straightforward.

It can be expected that detection of non-invariant parameters and even more severe misspecifications will depend on the separation between classes and sample size (Lubke & Neale, 2006). The present study investigates the conditions under which it is possible to select an appropriate model when comparing a series of different mixture models in case outcome variables have a 5-point Likert or binary response format. In the first part we address whether gross misspecifications of the within class model will be rejected in favor of the true model. Specifically, we investigate whether it is possible to distinguish between local independence models (i.e., classic latent class models), factor models with an increasing number of factors, and factor mixture models with factors and classes. The first part partially replicates a previous study that addresses the same question for normally distributed outcomes. In the second part, we investigate whether more specific misspecifiocations of the within class model can be detected. Here, we compare factor mixture models with and without class-invariant parameters and increasing numbers of classes.

The two parts of the study are interrelated. When comparing the different model types evaluated in the first part, a compromise needs to be found regarding the constraints on the within class models. As explained above, fitting unconstrained models is usually impractical. The second part of the current study is designed to provide an indication of the power to differentiate between different types of constraints.

Details of the data generation and design of the study are described below. First, a brief description of the general factor mixture model is provided followed by an empirical example.

The general model

The details of the general mixture model are described elsewhere (McLachlan & Peel, 2000, Lubke & Neale, 2006). In brief, the joint distribution of the latent class or clustering variable C and the observed outcome variable Y can be written as the product of the marginal (or prior) distribution of the class variable and the conditional distribution of the outcomes given class

$$f(c,\mathbf{y})=f(c)f(\mathbf{y}|\mathbf{c})$$ (1)

The class variable follows a multinomial distribution with parameters π₁,…,π_K where ${\mathrm{\Sigma }}_{k=1}^K{\pi }_k=1$ for k = 1;…;K classes (McCutcheon, 1987, Bartholomew & Knott, 1999). Conditional on class the observed outcomes have a multivariate normal distribution, which is structured according to the factor model. As a result, the marginal distribution of the outcomes is a sum of multivariate normal component distributions weighted by their class proportion π

$$f(\mathbf{y})={\displaystyle \sum _{k=1}^K{\pi }_k{f}_k(\mathbf{y};{\mu }_{\mathbf{k}},{\Sigma }_{\mathbf{k}})}$$ (2)

where

$${\mathbf{\mu }}_{\mathit{k}}={\mathbf{\nu }}_{\mathit{k}}+{\mathbf{\Lambda }}_{\mathit{k}}{\mathbf{\alpha }}_{\mathit{k}}$$ (3)

$${\mathbf{\Sigma }}_{\mathit{k}}={\mathbf{\Lambda }}_{\mathit{k}}{\mathbf{\Psi }}_{\mathit{k}}{{\mathbf{\Lambda }}_{\mathit{k}}}^t+{\mathbf{\Theta }}_{\mathit{k}}$$ (4)

Intercepts are ν, factor means are α, factor loadings are Λ, the factor covariance matrix is Ψ, and the matrix of residual variances is Θ. Note that not all parameters of the within class factor model can be estimated simultaneously as class-specific parameters for reasons of identification. Regarding the model for the means µ, the same restrictions apply as in multi-group models. In the context of this paper, residual covariances are assumed to be zero (i.e., Θ_k is diagonal), although this is not a necessary restriction.

Constraints on particular parameter matrices lead to specific submodels, for instance, fixing all loadings to zero results in a basic latent class model with local independence, setting the number of classes K equal to one results in conventional factor models, and letting K > 1 and loadings and factor variances be larger than zero leads to more complex factor mixture models.

Ordinal categorical outcome variables are derived by categorization of the normally distributed outcomes. The latter are now assumed to be unobserved and are denoted as Y*. The observed categorical outcomes are denoted as Y and are related to the unobserved Y* through threshold parameters τ. Assume that an observation y on a categorical outcome variable Y has m = 1,…,M response categories, then

$$y=m\text{if}{\tau }_{m-1}<y*\le {\tau }_m$$ (5)

Setting the lowest and highest threshold to −∞ and +∞, respectively, a categorical outcome variable with M response categories has M – 1 threshold parameters τ that can be class specific. The unobserved outcomes Y* are related to the factors through Equations 3 and 4. Consequently, each outcome Y* is related to an underlying factor by a single factor loading λ. In conjunction with Equation 5, this implies that the categorical outcomes are ordered. Note that holding all other parameters class invariant, increasing the number of classes of a model with class specific thresholds increases the number of estimated parameters by (M − 1) × P + 1 for P observed variables ². If loadings are also class specific, then the increase in the number of estimated parameters is MP + 1.

Illustration with empirical data

The data

Data for the illustration come from two separate but related studies of all-Caucasian female-female (FF) and male-male and male-female (MMMF) twins from the Virginia Twin Registry (Kendler & Prescott, 1999). The Virginia Twin Registry is a population-based register formed from a systematic review of all birth certificates in the Commonwealth of Virginia from 1918 onwards. Twins were eligible for participation in each of the studies if one or both twins were successfully matched to birth records and were born between 1940 and 1974.

Since genders differ with respect to the prevalence of depression, we limit the analysis to females. In addition, to avoid violations of independence of observations, we use data from one of the twins from each pair. This results in a sample of N=1093 females. The age ranged from 18 to 57. Lifetime prevalence for meeting DSM-IIII-R criteria for major depression (MD) was 36.7% for females.

The ten items are binary indicating presence (1) or absence (0) of symptoms such as fatigue/loss of energy, feelings of worthlessness, inability to concentrate, and recurrent thoughts of death. The endorsement frequencies of the items in our sample ranged between .60 and .95. A detailed description of the item and the data collection is given in Kendler and Prescott (1999).

Analysis

A preliminary exploratory factor analysis provided support for a single underlying dimension. Factor loading ranged between .68 and .9, and the RMSR was .048. Adding a second factor did not lead to a clear allocation of any of the items to one of the two dimension. The first two eigenvalues equalled 6.6 and 0.7, which can be regarded as further evidence for the unidimensionality of the ten items. Note that these results do not exclude the possibility that several ordered latent classes explain all covariation between items. Related to this, note also that the exploratory analysis is based on the potentially wrong assumption of a single homogeneous population.

The analysis plan consists of fitting latent class models, and three different types of factor mixture models (FMM’s). All models are fitted with an increasing number of classes. The FFM’s have a single within class factor. The first type imposes class invariance on all parameters of the measurement model, that is, only factor means and variance are allowed to differ across classes. The second type permits thresholds, τ in equation (5), to be class-specific. The third type has class-specifc loadings in addition to class-specific thresholds. Note that in this model we fix the factor variances to unity in all classes. Scale differences between classes are absorbed in the loadings (see for instance B. O. Muthén & Asparouhov, 2002). Models with class-specific loadings and class-invariant thresholds are not fitted since the thresholds τ in equation (5) and the residual variances θ in equation (4) are not independently identified (B. O. Muthén & Asparouhov, 2002, Millsap & Tein, 2003). Also, such a parameterization would not make much sense on a conceptual level.

The results of converged models are presented in Table 1.

Table 1.

Empirical example: Models fitted to depression items

	logL	# par	AIC	BIC	saBIC
F1C2t1	4409.738	23	8865.5	8980.4	8907.4
F1C3t1	4372.060	26	8796.1	8926.0	8843.5
F1C2t2	4386.512	32	8837.0	8996.9	8895.2
F1C2t3	4370.264	41	8822.5	9027.4	8897.2
F1C3t3	4336.729	62	8797.5	9107.3	8910.3
F1C4t3	4306.743	83	8779.5	9194.2	8930.6
F0C3	4397.108	32	8858.2	9018.1	8916.7
F0C4	4378.771	43	8843.5	9058.4	8921.8
F0C5	4358.129	54	8824.3	9094.1	8922.6
F0C6	4341.100	65	8812.2	9137.0	8930.5

Note. Abbreviations are as follows: AIC, BIC, saBIC and CAIC are information criteria (formulae see Appendix), models are denoted as FiCj where i indicates the number of factors and j the number of classes. Note that F0C3 indicates conventional 3-class latent class model, which can be conceptualized as a 2-class model without underlying factors. The additional extension tm for the single factor models refer to the type of factor mixture model (i.e, type 1, 2, or 3, see text).

Based on the BIC and the sample-size adjusted BIC, the measurement invariant single factor three class model, F1C3t1 in Table 1, is the best fitting model. The estimates of the factor variance show large differences across classes, and the variance in the highest scoring class is almost zero. The models with class-specific thresholds have a similar pattern regarding the factor variances. The 3-class version of the model with class-specific thresholds has estimates of class specific factor variances that do not seem to be trustworthy. The fit of this model is therefore not reported. The large factor variance differences in the measurement invariant model, and the inappropriate estimates of the factor variances in the model with class specific thresholds raise the question whether the constraint of class-invariant loading is appropriate. Based on the BIC, the models with class-specific loadings and thresholds have a worse fit than the measurement invariant models. The two-class model, F1C2t3, is the best fitting model among models with class specific loadings. In this model, the loading estimates in the higher scoring class show much more variability across items than in the lower scoring class. On a conceptual level this would mean that in the class of the participants with higher levels of depression, the ten items vary more with respect to how well they discriminate than in the class of unaffected participants. Since the two class model with class specific loadings has 41 parameters compared to 26 of the measurement invariant three class model, It is possible that the rejection of this model is due to lack of power.

The conventional latent class models have worse fit in general than the factor mixture models with comparable numbers of parameters. This seems to support the conclusion that the data support latent classes with continuous variation of depression within class. The first part of the simulation study addresses the general question of correct model choice in case of ordered categorical data, and focuses especially on the potential to discriminate between conventional latent class models and models with continuous variation within class. In the second part of the simulation we focus on the power of distinguishing between models with different constraints on the within class parameters.

Methods Simulation Part 1: Comparisons of different model types

Data generation

As in our previous study, data for the first part of the current study are generated under submodels of the general FMM described in Equations 2–4 without any model violations. Factor scores and error terms are generated under multivariate normal distributions, and items are linearly related to the factors with constant factor loadings. This results in multivariate normal outcomes conditional on class, which are subsequently categorized using Equation 5.

Due to much longer computation times when fitting models to categorical data (e.g., some models exceeded 24 hours), only 30 data sets are generated under each model. There are 5 data generating models, namely a two factor single class model (F2C1), a single factor two class model (F1C2), a two factor two class model (F2C2), a two class and a three class latent class model. Since LCA models can be concetualized in terms of zero factor models, these are abbreviated as F0C2 and F0C3. The number of outcome variables (i.e., 10) and the parameter values are the same as used for the data generation in the first study. Parameter values are listed in the Appendix. In the present study, data are generated under these five models for 4 different combinations of sample size and distance between classes. Total sample sizes of 300, 400 and 1500 are investigated at a multivariate Mahalanobis distance (MD) between equally sized classes of 1.5, and in the fourth combination, a sample size of 300 is combined with a distance of 2 (note that for the 3 class LCA, distances between classes 1 and 2 and classes 2 and 3 equals 1.5 whereas the distance between classes 1 and 3 is 3)³. The continuous data (i.e., Y*) are categorized with 4 equally spaced class-invariant thresholds, resulting in ordered categorical outcomes with 5 response categories. In addition, F2C2 data with 400 subjects and a distance of 1.5 are also categorized into binary items with a mean (i.e, p-value) of 0.5. The F2C2 5-point and binary data are used for a more detailed comparison with the continuous data investigated in the first study.

Fitted models

The standard set of fitted models includes one, two, and three factor models with a single class (F1C1, F2C1, F3C1), a two factor two class model (F2C2), and two, three, and four class LCA models (F0C2, F0C3, and F0C4). All fitted multi-class models have class-specific thresholds. Item mean differences are probably the most common violation of measurement invariance in practice. Fitting models with class invariant thresholds in a exploratory setting is therefore not advisable. For data with more than two ordered response categories, one might consider fitting models with intercept differences, ν in equation (3) rather than allowing thresholds to be class specific. Conceptually, this corresponds to a rigid shift where all thresholds of an item are shifted by a class-specific constant. Whether or not such a model makes sense on a conceptual level depends on the specific data. Furthermore, in case an item has also a class specific factor loading, this intermediate solution is not adequate since the metric of the latent response variable Y* is class specific. Generally, in an exploratory context for which this simulation is deemed relevant, thresholds should at least initially not be constrained.

In sum, seven models are fitted to the five different data types under 4 different settings of sample size and class separation. In addition, a direct comparison of correct model choice for continuous, 5-point and binary data is carried out. This is done only for the F2C2 data. In the first study, only exploratory factor mixture models were fitted to continuous outcomes. These are models in which loadings of all items on all factors are estimated except those fixed to achieve model identification. In addition to the models listed above, we also fit an exploratory F2C2 model to the 5-point and binary F2C2 data such that the set of fitted models is exactly the same as in the first study.

Model comparisons are based on information criteria (see Appendix) and the adjusted likelihood ratio test proposed by Lo, Mendell, and Rubin (2001). All models in this part of the simulation are fitted using the software program Mplus version 4.2 (L. K. Muthén & Muthén, 2007).

Results Simulation Part 1: Comparisons of different model types

First, results are presented for the 5-point Likert outcomes. This is followed by the comparison of correct model choice across different response formats.

The results for five different data generating models (F1C2, F2C1, F2C2, F0C2, and F0C3) are presented in Table 2 through Table 6. The total sample size in these Tables is 400 and the Mahalanobis distance equals 1.5.

Table 2.

Proportion of model choice: F1C2 data, N=400, Mahalanobis distance is 1.5

	aLRT	logL	AIC	BIC	saBIC	CAIC	entropy
F1C1	NA	0	0.53	1	0.93	1	NA
F2C1	NA	0	0.1	0	0.07	0	NA
F3C1	NA	0 1	0.13	0	0	0	NA
F1C2	0	0.9	0.23	0	0	0	0.17
F0C2	1	0	0	0	0	0	0.67
F0C3	0.87	0	0	0	0	0	0.03
F0C4	0.8	0	0	0	0	0	0.03

Note. Abbreviations are as follows: aLRT stands for adjusted Likelihood Ratio Test, AIC, BIC, saBIC and CAIC are information criteria (formulae see Appendix), models are denoted as FiCj where i indicates the number of factors and j the number of classes. Note tha F0C2 indicates conventional 2-class latent class model, which can be conceptualized as a 2-class model without underlying factors. The aLRT column contains the proportion of significant tests, the other columns show the proportion a given fitted model was the first choice.

Table 6.

Proportion of model choice: F0C2 data, N=400, Mahalanobis distance is 1.5

	aLRT	logL	AIC	BIC	saBIC	CAIC	entropy
F1C1	NA	0	0.8	1	0.97	1	NA
F2C1	NA	0	0.07	0	0.03	0	NA
F3C1	NA	0	0.03	0	0	0	NA
F1C2	0	0.03	0.03	0	0	0	0.07
F0C2	0.03	0	0	0	0	0	0.17
F0C3	0	0.1	0.03	0	0	0	0.13
F0C4	0	0.87	0.03	0	0	0	0.47

Note. Abbreviations are the same as in Table 2.

Table 2 shows the results for the F1C2 data generating model. Although the true number of classes is 2, the AIC indicated the need of a second class in only 23% of the model comparisons, and all other indices favor single class models. This is much lower that for continuous data. Under similar conditions, Lubke and Neale (2006) showed that the aLRT indicated the need of the second class in about 70% of the comparisons. An important difference between continuous and 5 point Likert outcomes concerns the fact that the difference in degrees of freedom when comparing models with k and k – 1 classes is much larger in the categorical than in the ordinal case. An additional class in the ordinal case has 42 additional parameters, where 40 of these parameters are the class specific thresholds for the ten 5-point scale items (the other two pertain to an additional factor variance and a class proportion). Researchers comparing different models for categorical data have to be sensitive to the difference in numbers of estimated parameters, which also affect the information criteria.

On a positive note, it is unlikely that a latent class model is incorrectly chosen when fitting data that are generated with an underlying factor within class. As shown in Table 2, information criteria for the latent class models are much higher on average. Note that the potential to discriminate between factor models and latent class models is not due to model parsimony: the F1C2 model with 91 estimated parameters has lower indices than the F0C2 model with 81 estimated parameters. Hence, a distinction between models imposing local independence and models that allow for structures within class covariation is easily made even if outcomes are categorical.

Regarding the power to detect the correct number of classes, the pattern of results for the other four data generating models with N=400 and MD=1.5 are very similar. The power of the aLRT to detect an additional class when it is present in the data is considerably lower than demonstrated in our previous study with continuous data. As mentioned above, this is most likely due to a larger differences in degrees of freedom when comparing k-class to k – 1-class models than when comparing models for continuous data.

Single class data with two factors (F2C1 data) are generally unproblematic to fit, which is most likely due to the fact that the incorrect two-class model is rejected because it has many more parameters. Table 3 shows that the correct F2C1 model would be chosen most of the time. The competing models are single and three factor single class models, however, the three factor model would probably be rejected in practice because the pattern of loadings is diffuse and the third factor adds little to the explained variance.

Table 3.

Convergence and average fit measures: Models fitted to F1C2 data, N=400, Mahalanobis distance is 1.5

	conv	aLRT	logL	npar	AIC	BIC	saBIC	CAIC	entropy
F1C1	1	NA	−3691.2	50	7482.5	7682.1	7523.4	7732.1	NA
F2C1	0.97	NA	−3685.1	59	7488.2	7723.7	7536.5	7782.7	NA
F3C1	0.8	NA	−3675.3	67	7484.6	7752	7539.4	7819	NA
F1C2	0.9	0.8	−3649.8	92	7483.6	7850.8	7558.9	7942.8	0.7
F0C2	1	0	−4106.9	81	8375.8	8699.1	8442.1	8780.1	0.9
F0C3	1	0	−3829.8	122	7903.6	8390.5	8003.4	8512.5	0.9
F0C4	1	0	−3715 6	163	7757.2	8407.8	7890.6	8570.8	0.9

Note. Abbreviations are the same as in Table 2. Additional abbreviations are conv which stands for converged and npar which indicates the number of estimated parameters.

The F2C2 data demonstrate that detecting two true classes is problematic when outcomes are categorical. As explained in the introduction, in an exploratory setting thresholds would be specified as class-specific parameters, leading to many additional parameters when adding a class. In the model comparison shown in Table5 the F2C1 model is the favorite. As with the single factor two class data, a researcher would not make the mistake of choosing one of the the latent class models as a favorite model.

Table 5.

Proportion of model choice: F2C2 data, N=400, Mahalanobis distance is 1.5

	aLRT	logL	AIC	BIC	saBIC	CAIC	entropy
F1C1	NA	0	0	0	0	0	NA
F2C1	NA	0	0.7	1	0.87	1	NA
F3C1	NA	0	0.3	0	0.13	0	NA
F2C2	0	1	0	0	0	0	0
F0C2	0.93	0	0	0	0	0	0.53
F0C3	0.9	0	0	0	0	0	0.2
F0C4	.53	0	0	0	0	0	0.13

Note. Abbreviations are the same as in Table 2.

The results for the latent class data with 2 and 3 classes are shown in Table 6 and Table 7). Even if information criteria are lower for the factor models, these would not be chosen in practice since loading estimates are close to zero, indicating the absence of an underlying factor. This is very similar to results with continuous data (Lubke & Neale, 2006). Taken together, Table 2, Table 5 and Table 6 show that the distinction between latent class models and models with factors within class is unproblematic no matter whether the true data are latent class or factor mixture models.

Table 7.

Proportion of model choice: F0C3 data, N=400, Mahalanobis distance is 1.5

	aLRT	logL	AIC	BIC	saBIC	CAIC	entropy
F1C1	NA	0	0	1	0.33	1	NA
F2C1	NA	0	0	0	0	0	NA
F3C1	NA	0	0	0	0	0	NA
F1C2	0.27	0	0.2	0	0.37	0	0
F0C2	0.83	0	0	0	0.03	0	0.3
F0C3	0.27	0.2	0.7	0	0.23	0	0.07
F0C4	0	0.8	0.1	0	0	0	0.57

Note. Abbreviations are the same as in Table 2.

Next, we consider results where the sample size is increased to N=1500. With continuous data it was shown that a total sample size of N=2000 resulted in a ceiling effect of 100% correct model choice at a Mahalanobis distance of 1.5. Additional results revealed that the percentage reached 98% for N=1500. For categorical data, results look much less positive. The proportions correct model choice are very similar to those with a sample size equalling 400. Decreasing the sample sample size to N=300, which had a clear detrimental effect in the continuous data, or increasing the distance between classes to MD=2.0 does not have a pronounced effect on correct model choice. Proportions of correct model choice remain approximately the same as for the N=400 and MD=1.5 setting.

As already noted, the decrease in power to distinguish between classes when comparing results for continuous and categorical outcomes can be due to the larger difference in numbers of parameters when adding a class. However, it can also be due to loss of information when categorizing outcomes. To disentangle these two effects we now compare continuous, 5-point scale and binary data. The loss of information should be the highest in binary data, whereas the difference in numbers of parameters when adding a class is highest in the 5-point scale data.

As can be seen in Table 7, the increase in loss of information when using binary rather than 5-point scale data does not lead to further deterioration of results. Apparently the smaller differences in number of estimated parameters in the comparisons of models for binary data compensate for the more crude categorization. This is even more evident when considering the aLRT, which performs much better for binary data where the test involves a difference of 30 degrees of freedom than for the 5-point data with a difference of 60 degrees of freedom. Although these results may depend to some extent on the specific settings in our simulation, it seems safe to conclude that when comparing a set of fitted models, one needs to be attentive to the difference in numbers of estimated parameters. Apparently, the penalties for the number of parameters of the commonly used information criteria BIC, sample size adjusted BIC and CAIC, and to a lesser extent AIC, are too great to be useful when comparing models for 5-point scale data because the different models of interest vary widely in parsimony.

Methods Simulation Part 2: Testing class invariance of model parameters

Lubke and Neale (2006) showed that in the absence of model violations and given adequate sample sizes and class separation, it is possible to choose the correct model when outcomes are multivariate normal. The first part of the current study showed that in the absence of model violations it is possible to distinguish between local independence models and models with factors within class. Detection of classes is more problematic due to a large increase in the number of parameters when adding a class with class-specific thresholds. The second part focuses on this question in more detail. Using data with and without class specific parameters, we investigate whether it is possible to detect non-invariance of model parameters.

Data generation and fitted models

Data were generated to investigate whether class specific thresholds or factor loadings can be detected when comparing mixture models. We chose thresholds and loading parameters to illustrate the power to detect more fine-grained differences between mixture models that nonetheless have quite different conceptual interpretations.

This part of the simulation is set up to test in how far the difference in numbers of parameters influences model selection when comparing k to k + 1 class models with and without constraints on measurement parameters. Testing the class invariance of thresholds with M-point Likert data and P items involves a model comparison where the k + 1 class model has (M − 1) × P + 1 more parameters than the k class model. Models where only the loadings are specified to be class-specifc have a difference of P + 1 parameters. Models with class specific loadings and thresholds have a difference of MP + 1 parameters.

One might consider fitting models with class specific intercepts, ν in equation (3), which would also involve a difference of P + 1, just as class specific loadings. Both models could therefore be used in the simulation to illustrate the impact of the difference in numbers of parameters on the power to reject models with invariant parameters when data are non-invariant. In the current simulation we use the model with class specific loadings rather than class specific intercepts.

It is important to realize that in an empirical setting it depends whether either of these two models (only intercepts ν or only loadings λ class specific) can be deemed appropriate. This is due to the fact that not all parameters in the model for categorical outcomes shown in equations (3) – (5) are independently identified (B. O. Muthén & Asparouhov, 2002). If loadings and factor variances are class invariant, then a model with class specific intercepts might be an interesting option. Conceptually, it corresponds to a situation where the width of the intervals between thresholds (i.e, the increase in underlying trait necessary to score in the next higher category) are class invariant. However, in case factor variances and/or loadings are class specific, this model looses its appeal. Similarly, the model with only class specific loadings might have limited practical value. As discussed in the section covering the empirical example, it is likely that in real data class specific loadings go together with class specific residual variances. Since residual variances and thresholds are not independently identified, models with class specific loadings should usually also allow for class specific thresholds.

The simulated data generated in this study have no class differences in residual variances, Θ in equation (4), and thresholds, τ in equation (5). Hence fitting models with class specific loadings and class-invariant thresholds is unproblematic. It is mainly meant to permit the investigation whether a smaller increase of parameters when fitting k + 1 class models has indeed substantially more power than when the k + 1 class models have a larger increase of parameters.

The first type of generated data has 2 factors and 2 classes (F2C2) and class specific intercepts, νk in Equation 3. Categorization with equidistant response categories results in class specific thresholds τk. We generate 30 data sets with a Mahalanobis distance of 1.5, and a sample size of 400. The 8 fitted models are single class factor models with 1–3 factors, 2 factor 2 class models with and without threshold invariance, and latent class models with 2–4 classes. We also use the F2C2 data generated for the first part of this study that have class invariant thresholds, and we fit the same models. This design allows us to investigate the power to detect class specific thresholds when data have this type of non-invariance, and to reject class specific thresholds when data have invariant thresholds.

The design to test class invariance of factor loadings is similar. The data generating model is again a 2 factor 2 class model, and we generate 30 data sets with class invariant loadings and 30 sets with class specific loadings. The Mahalanobis distance ν for the two types of data is kept at 1.5, and the sample size is 400. To both data types, we fit F2C2 models with class invariant or with class specific loadings.

Results Simulation Part 2: Testing class invariance of model parameters

Invariance of thresholds

When fitting the set of eight models to data with class specific thresholds, BIC and CAIC always point to the incorrect threshold invariant model. AIC and aBIC favor the 3 factor 1 class model (AIC in 73% and aBIC in 33% of the replications), the remaining replications also favor the incorrect F2C2 threshold invariant model. The correct threshold specific model did not have superior information criteria in any of the replications.

For data with class invariant thresholds, comparing the eight fitted models results in correct model choice approximately 98% of the time. It is interesting to compare this result to Part 1 Table 4 where different models were fitted to 2 factor 2 class data. Since Part 1 mimics an exploratory mixture analysis, the only fitted F2C2 model in Table 4 had class specific thresholds. The preferred model in part 1 was the F3C1 model. Including the more parsimonious model with the correct constraints on the within class thresholds leads to correct model choice. Even when decreasing the sample size to 300, the rate of correct choice remains above 80%. However, it is important to realize that the model comparisons based on information criteria are favoring the much more restrictive equal threshold model no matter whether the true data are threshold invariant or not. When testing measurement invariance it would be preferable to have a test with a higher power to reject the measurement invariant model.

Table 4.

Proportion of model choice: F2C1 data, N=400, Mahalanobis distance is 1.5

	aLRT	logL	AIC	BIC	saBIC	CAIC	entropy
F1C1	NA	0.03	0.03	0.03	0.03	0.03	NA
F2C1	NA	0.07	0.6	0.97	0.67	0.97	NA
F3C1	NA	0.57	0.33	0	0.3	0	NA
F1C2	0	0.33	0	0	0	0	0.03
F0C2	0	0	0	0	0	0	0.07
F0C3	0	0	0	0	0	0	0.13
F0C4	0	0	0	0	0	0	0.5

Note. Abbreviations are the same as in Table 2

Invariance of loadings

Results for tests of class invariance of factor loadings look more promising. When comparing the fit of models with class invariant and specific loadings to data with true class specific loadings, AIC and sample size adjusted BIC always select the correct model, and the BIC and CAIC in 83% and 77% of the comparisons. Fitting the same models to data with class invariant loadings shows that the AIC does not discriminate well between true class specific and true class invariant loadings. The AIC chooses the correct class invariant model in only 27% of the comparisons. The adjusted BIC performs better with 67% correct model choice. The BIC and CAIC always choose the the correct model. Taken together, the BIC provides the best compromise between false positives and false negatives (e.g., incorrectly accepting the invariant model when data class specific loadings and incorrectly rejecting the invariant model when the data have class invariant loadings). Compared to the results with class-specific thresholds, it is clear that power is less compromised when comparing models that do not involve large differences in the number of model parameters.

Discussion

The three main conclusions that can be drawn from the results of the current simulations concern (i) the dependence of model choice on response format, sample size, and class separation, (ii) the potential to use mixtures to test class invariance of model parameters, and, based on (i) and (ii), the necessity of contextualizing the results of any given mixture analysis.

Our previous simulation showed that in an exploratory analysis of continuous data, the comparison of different mixture models including latent class, factor and factor mixture models generally results in correct model choice given sufficient sample size and mean differences between classes (Lubke & Neale, 2006). Specifically, there was a trade-off between sample size and mean differences between classes very similar to what can be observed when testing mean differences between observed groups.

The current study similarly focuses on comparing mixture models in an exploratory context, but with categorical observed data. The first part of the current study shows that even for categorical data, it is easy to distinguish between latent class models that assume local independence within class, and models that assume a factor structure within class, although the number of classes in the absence of local independence may be underestimated. The first part of the simulation shows that factors explaining covariation of observed variables within a cluster are easily detected in data with true continuous variation, and rejected in data that are locally independent conditional on class. This result replicates the findings of the previous study with continuous data. The possibility to distinguish between latent class and factor mixture models is especially important in psychiatric research where it is a much discussed question whether a disorder should be described in terms of subtypes or continuous variability in severity (for a summary, see Pickles & Angold, 2003). Since data in psychiatric research are often Likert type data or binary symptom endorsements, replication of our previous findings concerning continuous data is encouraging.

The current study shows, however, a clear detrimental effect of response format on the power to detect additional classes. The effect is likely due to the larger difference in free parameters in models with additional classes. In an exploratory setting, in which the model comparisons we investigated would be relevant, thresholds should not be fixed to be class-invariant. Especially in settings where classes differ with respect to the variance of the underlying factors, it is usually unrealistic to assume that the increase in the score on the underlying factor(s) that is needed to score in the next higher response category, is the same for all classes. As a consequence, adding a class involves the estimation of P × (M − 1) + 1 additional parameters, where P is the number of items and M the number of response categories. Our simulation shows that this large increase in parameters is punished by the information criteria and the adjusted LRT regardless of the numbers of classes in the generated data. The penalties of the information criteria render model comparisons too conservative in favor of models with less classes especially in case of Likert data with 5 response categories. Binary data performed better when considering the aLRT, but very similarly to 5-point scale data when considering the information criteria. Apparently, the loss of information due to a much more crude categorization is to some extent canceled out by having smaller differences in numbers of estimated parameters between models with an increasing number of classes. Since calibrating new (versions of existing) indices is a tremendous task, it seems more realistic for researchers using mixture models to conduct a small scale simulation to assess the feasibility of detecting an additional class for their specific settings (e.g, class separation, sample size, numbers of items, numbers of response categories).

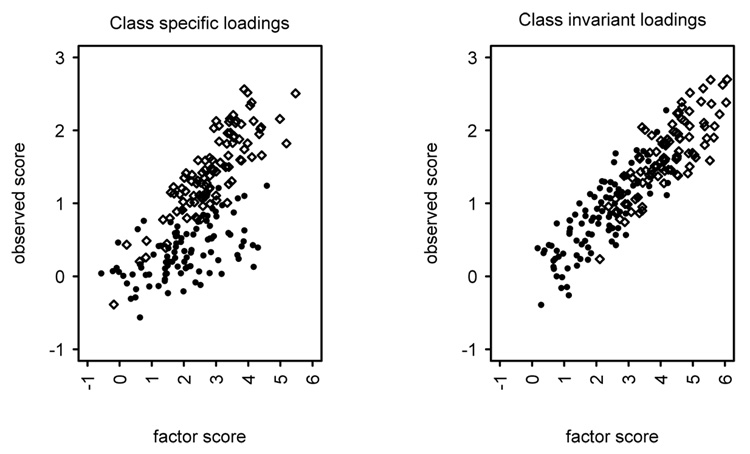
The second part of our study aims at testing class invariance of model parameters. We consider two forms of non-invariance, namely threshold invariance and factor loading invariance. Similar to the comparison of models with K and K −1 classes, the comparison of models with class invariant and class specific thresholds is characterized by a large difference in the number of estimated parameters. The more parsimonious models are favored regardless of whether they are correct or not. Researchers need to be aware that tests of measurement invariance of thresholds may incorrectly indicate absence of bias. The results are better when we compare models with a smaller difference of parameters, as was the case with data with and without invariant loadings. Especially the BIC emerged as a good index to detect non-invariant loadings. In addition to the fact that the difference in the number of parameters is smaller than in case of threshold differences with 5-point data, it is possible that the estimation of loading parameters (and hence detection of class differences with respect to these parameters) might be less problematic when the clusters in the population have specific loadings. This point is illustrated in Figure 2.

Figure 2.

Class specific and class invariant factor loadings

The contribution to the likelihood of a given subject is weighted by the probability of belonging to each of the clusters. Subjects whose response pattern does not place them in the area where clusters overlap belong with certainty to a particular cluster, and their response pattern contributes only to the estimation of the parameters of that cluster. Subjects in the area of overlap contribute less to either cluster. Figure 2 shows data with and without loading differences for the same underlying factor mean difference. For class invariant loadings (right panel), the two areas that contain the subjects outside the overlap of the clusters are the two clusters than in the case of data with class specific loadings (left panel). The topic of discriminating between classes that differ with respect to their factor structure, and the estimation of slope and regression coefficients in structural equation mixture models is covered in different study (Tueller & Lubke, submitted).

Contextualizing the results of any given mixture analysis is necessary because sample size, separation between classes, response format and the difference in numbers of free parameters between fitted models all influence the choice of best fitting model. Prior to any analysis it is therefore necessary to establish the power to discriminate between the fitted models by comparing different data generating processes. Essentially, this is not different from the necessity to compute the power in any other type of statistical testing procedure. It should become standard practice to accompany the comparison of different models with results from a parametric bootstrap showing the power to discriminate between models in a particular setting.

A second important issue when interpreting latent classes concerns the fact that favoring a multi-class solution may not be due to the presence of qualitatively or quantitatively distinct groups of subjects. As noted in the introduction, the distribution depicted in Figure 1 could have been derived using different data generating mechanisms, including skewed factor scores as well as a mixture of different clusters of subjects. Figure 2 equally illustrates this point. Data similar to those plotted in the first panel may also be generated using a single population in which the factor loadings increase as a function of the factor score. Consequently, the finding that a model with class specific loadings fits better than a model with invariant loadings can be interpreted not only in terms of absence of measurement invariance, but also in terms of a violation of the assumption that items are linearly related to the underlying factors. Mixtures can approximate systematic continuous variation using several component distributions that describe the characteristics of different areas of the joint distribution of the data. Mixture models do not necessarily settle the question of continuity vs. discontinuity, however, mixture models can provide a more or less detailed description of the different areas of the joint distribution of the data. This description can include guidelines as to which type of model is more adequate to describe the structure within a cluster, e.g., local independence or structured covariation within class. Whether a given clustering solution is useful on a conceptual level depends on the particular context of a study.

There are several limitations to the current study. First of all, all data in the simulation are artificially generated. This obviously has the advantage that the true cluster structure and within cluster models are known, but it also has the disadvantage that the data generating process is extremely simple compared to most real data. Fitted models in an analysis of real data are always more or less crude approximations of the data generating process. In addition, in a real data analysis the selection of fitted models, in particular, whether to include more exploratory or more confirmatory models, depends on how well the theory in a particular area is developed. The empirical example in this study illustrates the problem of choosing an adequate model due to potentially insufficient power to allow for class specific loadings and thresholds. The current simulation confirms this problem, and shows what to expect under a variety of other conditions. Base on the simulation results, the rejection of the conventional latent class models with local independence within class in the empirical example seems trustworthy. Other analyses of factor mixture analyses of real data that might serve as illustrations start to appear in the literature (Hildebrandt et al., 2007, Lubke et al., 2007).

The second limitation of the current study concerns an issue that is characteristic of simulations in general, namely that the design of the current study is limited by computation time. Computation times are substantial when analysing categorical data due to the computational burden of integrating over the unobserved continuous response variables Y *. As a consequence, only 30 replications were used to obtain rates of correct model choice and average fit measures. In addition, only a limited number of design factors were investigated. However, the main findings, namely that (1) it is possible to distinguish between latent class and factor mixture models, and (2) that the difference of the number of estimated parameters has a severe impact on the power to discriminate between two models, seem nonetheless convincing. Note that these results are valid for the investigated sample sizes and class separations. The latter reflect effect sizes that might be considered large in some areas of research although they are quite common for instance in psychiatric data. Smaller separations result in a decrease of power to distinguish between classes.

A third limitation of the current study is that we do not investigate the coverage of true parameters in the different fitted models. There is pilot evidence that coverage of factor variance parameters can be problematic when fitting models with class specific variances to data with considerable variance differences. A fourth and related limitation is that correct class assignment is not assessed in the current study. Rates of incorrect assignment depend to a large extent on how much the class specific distributions overlap, which is a function of mean and variance differneces. Parameter estimates and correct class assignment are addressed in detail in Tueller and Lubke (submitted).

Table 8.

Proportion of model choice: Models fitted to continuous, 5-point and binary F2C2 data, N=400, Mahalanobis distance is 2.0

	aLRT	logL	AIC	BIC	saBIC	CAIC	npar
continuous data
F1C1	NA	0	0	0	0	0	30
F2C1	NA	0	0	0	0	0	39
F3C1	NA	0.01	0.43	1	0.83	1	47
F2C2	0.83	0.99	0.57	0	0.17	0	59
F0C2	0.95	0	0	0	0	0	41
F0C3	0.57	0	0	0	0	0	62
F0C4	0.47	0	0	0	0	0	83
5-point scale data
F1C1	NA	0	0	0	0	0	50
F2C1	NA	0.03	0.57	1	0.87	1	59
F3C1	NA	0.43	0.2	0	0.13	0	67
F2C2	0.03	0.53	0.23	0	0	0	119
F0C2	0.93	0	0	0	0	0	81
F0C3	0.9	0	0	0	0	0	122
F0C4	0.53	0	0	0	0	0	163
binary
F1C1	NA	0	0	0	0	0	20
F2C1	NA	0	0.67	1	0.97	1	29
F3C1	NA	0.1	0.03	0	0	0	37
F2C2	0.67	0.9	0.3	0	0.03	0	59
F0C2	0.93	0	0	0	0	0	21
F0C3	0.93	0	0	0	0	0	32
F0C4	0.8	0	0	0	0	0	43

Appendix

The parameter values used for the data generation are largely the same as in the first study except for the thresholds used to categorize the data. Thresholds are differ slightly across data sets since the range of an item is categorized into five equidistant intervals. Thresholds for data with MD=1.5 and 2.0 are approximately

MD 1.5 [−1.73 − 0.16 1.41 3.0]

MD=2.0 [−1.64 0 1.67 3.32]

Two class latent class model

Class-invariant parameters:

residual variances [0.7 .5 .5 .5 .5 .5 .5 .5 .5 .5]^t

Class-specific parameters:

means class 2 [0.35 − .2 .6 − .75 0.35 − .2 .6 − .75 0.35 − .2]^t

Three class latent class model

Class-invariant parameters:

residual variances [0.7 .5 .5 .5 .5 .5 .5 .5 .5 .5]^t

Class-specific parameters:

means class 1 ν = [0 0 0 0 0]^t

means class 2 [.7 − .8 1.2 − 1.1 .7 − .8 1.2 − 1.1 .7 − .8]^t

means class 3 [1.3 − 1.2 1.2 − 1.3 1.3 − 1.2 1.2 − 1.3 1.3 − 1.2]^t

Two factor/single class model

factor loadings ${\left[\begin{array}{cccccccccc}1& .8& .8& .8& .8& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& .8& .8& .8& .8\end{array}\right]}^t$

factor covariance matrix $\left[\begin{array}{cc}1.2& .5\\ .5& 1.2\end{array}\right]$

residual variances [0.7 .5 .5 .5 .5 .5 .5 .5 .5 .5]^t

Single factor/two class model

Class-invariant parameters:

factor loadings [1 .8 .8 .8 .8 .8 .8 .8 .8 .8]^t

factor variance 1

factor mean in the second class MD=1.5 [1.57]

factor mean in the second class MD=2.0 [2.1]

residual variances [0.7 .5 .5 .5 .5 .5 .5 .5 .5 .5]^t

Two factor/two class model

Class-invariant parameters:

factor loadings ${\left[\begin{array}{cccccccccc}1& .8& .8& .8& .8& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& .8& .8& .8& .8\end{array}\right]}^t$

factor covariance matrix $\left[\begin{array}{cc}1.2& .5\\ .5& 1.2\end{array}\right]$

factor means in the second class MD=1.5 [1.37 1.37]

factor means in the second class MD=2.0 [1.85 1.85]

residual variances [0.7 .5 .5 .5 .5 .5 .5 .5 .5 .5]^t

Information criteria

All information criteria used in the present study are penalized log-likelihood functions with the general form −2L + f(N)p where L is the loglikelihood of the estimated model with p free parameters and f(N) is a function that may depend on the total sample size N (Sclove, 1987). The AIC does not depend on sample size, the penalty is f(N)p = 2p (Akaike, 1974, Akaike, 1987). The BIC, the CAIC, and the sample size adjusted BIC integrate N in different ways, the respective penalty terms are log(N)p, and (log(N) + 1)p for the BIC and the CAIC (Bozdogan, 1987, Schwarz, 1978). The sample size adjusted BIC uses (N* = (N + 2)=24) instead of N.