Modeling Mood Variation Associated with Smoking: An Application of a Heterogeneous Mixed-Effects Model for Analysis of Ecological Momentary Assessment (EMA) Data

Abstract

Aims

Mixed models are increasingly used for analysis of Ecological Momentary Assessment (EMA) data. The variance parameters of the random effects, which indicate the degree of heterogeneity in the population of subjects, are usually considered to be homogeneous across subjects. Modeling these variances can shed light on interesting hypotheses in substance abuse research.

Design

We describe how these variances can be modeled in terms of covariates to examine the covariate effects on between-subjects variation, focusing on positive and negative mood and the degree to which these moods change as a function of smoking.

Setting

The data are drawn from an EMA study of adolescent smoking.

Participants

Participants were 234 adolescents, either in 9th or 10th grade, who provided EMA mood reports from both random prompts and following smoking events.

Measurements

We focused on two mood outcomes: measures of the subject's negative and positive affect, and several covariates: gender, grade, negative mood regulation, and smoking level.

Findings and conclusions

Following smoking, adolescents experienced higher positive affect and lower negative affect than they did at random, non-smoking times. Our analyses also indicated an increased consistency of subjective mood responses as smoking experience increased and a diminishing of mood change.

Introduction

Linear mixed models (LMMs, aka multilevel or hierarchical linear models) have become a primary method for analysis of clustered data [1-2], where a cluster may be a subject observed on several occasions or a group of similar subjects. For data clustered within subjects, a basic characteristic of these models is the inclusion of random subject effects into linear models in order to account for the similarity among repeated observations taken from individual subjects. These random effects consist of unmeasured variables reflecting each person's influence on his/her data, and the variance of these random effects indicate the degree of between person variation (i.e., heterogeneity) in the population of subjects. Typically, the variance of the random effects is treated as homogeneous across groups of subjects or levels of covariates. However, these homogeneity of variance assumptions can be relaxed by modeling differences in variances across subject groups or attributable to subject covariates.

The study of individual variability has received increasing attention [3-6]; these articles describe many of the conceptual issues and some traditional statistical approaches for examining such variation. LMMs can be used to systematize and extend this work by assessing the determinants of inter-individual or between-subjects variation.

Modeling variances requires a fair amount of data. Modern data collection procedures, such as ecological momentary assessments (EMA, [7-8]), experience sampling [9-10], and diary methods [11], provide this opportunity. These procedures yield relatively large numbers of subjects and observations per subject, and data from such designs are sometimes referred to as intensive longitudinal data [12]. Such designs are in keeping with the “bursts of measurement” approach described by Nesselroade and McCollam [13], who called for such an approach in order to assess individual variability. As they note, such bursts of measurement increase the research burden in several ways; however, they are necessary for studying individual variation.

Mixed model analysis of EMA data is well-described in Schwartz and Stone [14]. Additionally, Moghaddam and Ferguson [15] analyzed EMA data using mixed models to examine smoking-related changes in mood. These articles focus on the effects of covariates, either subject-varying or time-varying, on the EMA mean responses. Here we extend this approach by examining the degree to which covariates influence the variation inherent in the EMA data. In this regard, a few articles have described approaches for examining determinants of between- and within-subjects variance from EMA studies. Penner et. al. [16] used basic descriptive statistical methods to examine relationships among within-subjects variation in several mood variables. More recently, Hedeker et. al. [17] and Hedeker and Mermelstein [18] have described mixed model approaches incorporating a log-linear structure for determinants of the within-subjects variance. In this article, we extend this by modeling the between-subjects variance, allowing covariates to potentially influence the variances associated with the random subject effects. In particular, we focus on the variation of mood that is associated with smoking, and the degree to which subject characteristics influence the mood variation. To aid in making this class of models accessible to researchers, we provide sample computer syntax and output at website www.uic.edu/:hedeker/long.html.

Adolescent smoking, mood, and variability

Many prominent models of cigarette smoking maintain that smoking is reinforcing, and that smoking can relieve negative affect [19-20]. Indeed, both adults and adolescents often claim that smoking is relaxing and reduces emotional distress [21-22]. However, although the relationship between mood and smoking has received substantial empirical attention for adult smokers, much less is known about the acute changes in mood with smoking among adolescents. The present study, with its focus on real-time assessments of mood and smoking among adolescents helps to shed light on this important topic.

Although there is substantial consensus among both smokers and researchers that smoking helps to regulate affect, most of the empirical work investigating the smoking-mood relationship has focused on the examination of changes in mean levels of mood with smoking. Surprisingly, although affect regulation inherently implies the modulation of variability in mood as well, the examination of variability in mood and smoking has largely been neglected. As Hertzog and Nesselroade [4] note, describing mean levels of variables is not always adequate for examining key features of developmental change. Variation also conveys important information about the phenomenon of interest. In the case of adolescent smoking and the development of dependence, variation in mood and mood changes may help to explain more the development of tolerance. Examining individual variability may enhance our ability to predict changes in smoking behavior above and beyond what can be achieved by examining mean information alone.

Important, too, in the examination of mood and smoking, is the distinction between within-person and between-person variability. Kassel and colleagues [19,22] have argued persuasively for the need to differentiate causal, within-person mechanisms from between-person data. Whether smoking relieves negative affect is essentially a within-person question, and thus analytic models need to similarly differentiate between within-subject and between-subject effects.

Much of the research on mood and smoking has also been limited to assessments of negative affect, while ignoring positive affect. This neglect is particularly problematic given the theoretical importance of differentiating between negative reinforcement models of smoking and positive reinforcement models, especially in the development of dependence among adolescents [23]. There is also considerable evidence to support the notion that positive and negative affect are distinct constructs, and not just opposite ends of a continuum [24-25]. Thus, in the current study, we assessed both positive and negative affect.

Finally, there may well be individual differences in the extent to which adolescents' moods vary, and whether they vary with smoking. Identifying potential moderator variables may also help in the prediction of smoking escalation among relatively novice smokers. Thus, the aims addressed in this study are: 1) to examine the variation in mood that is associated with smoking, and 2) to examine the degree to which subject characteristics influence the mood variation. We hypothesized that a key moderator of mood variability would be an individual's level of expectancies about their own ability to regulate negative moods – negative mood regulation (NMR; [26]). Individuals who hold high expectancies about their ability to cope with negative affect or stressors may show less variability in their mood states. In addition, we hypothesized that level of smoking would also affect mood variability and changes with smoking. Following along the lines of the development of tolerance with dependence, we hypothesized that as smoking level or experience increased, mood responses to smoking would decrease, as would variability in overall mood.

Methods

Subjects

The data for this paper come from a longitudinal study of the natural history of smoking among adolescents. The study uses a multimethod approach to assess adolescents at multiple timepoints (baseline, 6-, 9-, 15-, 24-, and 33-months). The data collection modalities include paper and pencil questionnaires, in-person interviews, and for subsets of participants, more intensive measurement modalities including family observations, psychophysiological assessments, and week-long time/event EMA sampling via hand-held palmtop computers (referred to as “Electronic Diary”). We report here on the data from the baseline EMA collection.

The design of the Electronic Diary study involved sampling 9^th and 10^th graders at baseline who had tried smoking at least once during the past 12 months, but who had not yet progressed to smoking five or more cigarettes a day; 461 adolescents completed the baseline assessment for this study. The majority (57.6%) had smoked at least one cigarette in the past month at baseline. Adolescents in the Electronic Diary study were recruited as part of the larger study of Social-Emotional Contexts of Adolescent Smoking Patterns (total N of 1,263). Active, written parental consent and adolescent assent were required for participation in the study.

Data collection occurred via hand-held palmtop computers, programmed specifically for our data collection needs, with all other residing programs disabled. Each data collection wave included 7 consecutive days of monitoring. Four types of interviews were programmed onto the Electronic Diary: random prompts, and three types of smoking-related event recordings. Random time prompts were initiated by the device approximately five times per day. Each random prompt was date- and time-stamped and recorded whether the interview was completed, missed, delayed, or disbanded. Compliance with responding to the random prompts was very good: approximately 71% of the random prompts were completed. No participants were excluded because of problems in using the devices. The random interviews asked about mood, activity, location, companionship (with whom or alone), presence of other smokers, and other behaviors. In addition to the random prompts, participants were trained to event record smoking episodes, as well as episodes when either they had the opportunity to smoke, but actively decided not to smoke, or when they wanted to smoke, but did not have the opportunity to do so. The “smoke” and “nonsmoking” interviews included the same questions as the random prompts, and in addition, asked about specific smoking-related items (e.g., how much smoked, how the cigarette was obtained, etc.). Random prompts and the self-initiated smoking records were mutually exclusive; no smoking occurred during random prompts.

Because of our interest in comparing mood from random prompts and smoking events, we only included in the analysis subjects who provided data from at least one smoking event during the EMA study phase. In all, there were 234 such subjects with data from a total of 8,179 random prompts and smoking events. The average number of random prompts was approximately 30 per subject (median = 30, range = 7 to 71), and the average number of smoking events was about 5 per subject (median = 3, range = 1 to 42). The Spearman correlation between the number of random prompts and number of smoking events was near-zero (-.08) and not statistically significant. This analysis sample of 234 participants included 54.3% female (N = 127) and 47.4% 9^th graders (N = 111). Their ethnic distribution was 59.8% white (N = 140), 21.8% Hispanic (N = 51), 12.8% African-American (N = 30), and 5.6% (N = 13) other. This subsample was not statistically different from those excluded in terms of gender, grade, or race. They also did not differ on psychosocial measures of perceived stress, life events, depressive symptomatology, or self-reported grades in school. However, as expected because of inclusion criteria, the adolescents who were included in the analyses smoked significantly more than those excluded; at baseline, adolescents who were included smoked an average of 1.3 cigarettes/day (SD = 2.36) in the past 7 days, whereas those excluded smoked an average of 0.03 cigarettes/day (SD=0.12; t = -8.36, df = 455, p < .0001). The adolescents included in the analyses, compared to those excluded, also had higher scores on a measure of alcohol problems (assessing frequency and amount of drinking, and consequences) at baseline (M = 4.6, SD = 1.50 compared to M = 3.5, SD = 1.49, t = -7.48, df = 459, p < .001).

Measures

Negative and Positive Affect

Two mood outcomes were considered: measures of the subject's negative and positive affect (denoted NA and PA, respectively) at each random prompt and at each smoking episode. Both of these measures consisted of the average of several individual mood items, each rated from 1 to 10, that were identified via factor analysis. Specifically, PA consisted of the following items that reflected subjects' assessments of their positive mood just before the prompt signal: I felt happy, I felt relaxed, I felt cheerful, I felt confident, and I felt accepted by others. Similarly, NA consisted of the following items assessing pre-prompt negative mood: I felt sad, I felt stressed, I felt angry, I felt frustrated, and I felt irritable. Subjects rated each item on a 1-10 Likert-type scale, with “10” representing very high levels of the attribute. For the smoking events, participants rated their mood right after smoking. Over all prompts and events, both random and smoking, and ignoring the clustering of the data within subjects, the mean of PA was 6.77 (sd=1.96), while the NA mean was 3.53 (sd=2.28).

Gender and Grade

To illustrate our approach, we selected a limited number of covariates. First, we considered gender and grade-level with the variables Male (coded 0=female or 1=male) and Grade10 (coded 0=9th or 1=10th grade).

Negative Mood Regulation Expectancies

We also examined a measure of negative mood regulation ( NMR) as a covariate because we hypothesized individuals' expectancies about their abilities to manage negative moods would be related to both their mean mood and level of variation. Negative mood regulation expectancies were assessed through the NMR Scale developed by Catanzaro and Mearns [26], which was designed to the measure the extent to which individuals believe they can do something to alleviate their own negative mood states. This 30-item measure asked the adolescents to indicate how much they agree or disagree (on a 5-point Likert scale) with statements beginning with the stem, “When I'm upset, I believe that …” On this unifactorial scale, higher scores indicate stronger beliefs about one's ability to regulate negative mood. Scores on NMR ranged from 1 to 5, with higher values indicating more negative mood regulation, and the sample mean was 3.5 (sd = .71).

Smoking Level

Finally, as a measure of a subject's smoking level, we used the number of cigarettes smoked per day in the last 30 days (denoted as SmkLevel). Based on the frequencies, we recoded this variable into six levels: 0 = did not smoke (n = 41), 1 = less than one cigarette per day (n = 37), 2 = one cigarette per day (n = 41), 3 = two cigarettes per day (n = 48), 4 = three to five cigarettes per day (n = 51), and 5 = more than five cigarettes per day (n = 16).

All covariates were measured at baseline and prior to the collection of the EMA data. This helps to explain why there were 41 subjects who, at baseline, indicated that they did not smoke in the last 30 days ( SmkLevel=0), but who did provide at least one smoking event during the EMA phase (our criterion for being included in the analysis dataset). Given the low and infrequent levels of smoking reported by this sample, and the selection criteria excluding more regular smokers, it is not surprising to see continued sporadic patterns of smoking between our baseline assessment week and the EMA assessment week. Of the covariates, there were only two significant positive correlations among them: Male with NMR (Spearman r = .26, p < .0001), and Grade10 with SmkLevel (Spearman r = .15, p < .02).

Data Analysis

Model I - standard LMM for changes in the level of mood associated with smoking events

Consider the following linear mixed model (LMM) for the mood measurement y of individual i (i = 1,2,…, N subjects) at occasion j (j = 1,2,…, n_i prompts and events), where SmkEvent represents a variable indicating whether the occasion is from a random prompt (=0) or a smoking event (=1):

$$y_{ij}=({\beta }_0+{\upsilon }_{0i})+({\beta }_1+{\upsilon }_{1i}){{\displaystyle \mathtt{\text{SmkEvent}}}}_{ij}+{\epsilon }_{ij}$$ (1)

Hereafter, we use the term and variable “ SmkEvent” to refer to this indicator variable which contrasts smoking events relative to random prompts. This model represents the regression of the outcome variable y on the independent variable SmkEvent, where β₀ is the overall population intercept, β₁ is the overall population slope, υ_0i is the intercept deviation for subject i, υ_1i is the slope deviation for subject i, and ε_ij is an independent error term distributed normally with mean 0 and variance ${\sigma }_{\epsilon }^2$. The errors are independent conditional on both υ_0i and υ_1i. With two random subject-specific effects, the population distribution of intercept and slope deviations is assumed to be a bivariate normal N(0,Σ_υ), where Σ_υ is the 2×2 variance-covariance matrix given as:

$${{\displaystyle \sum }}_{\upsilon }=\left[\begin{array}{cc}{\sigma }_{{\upsilon }_0}^2& {\sigma }_{{\upsilon }_0{\upsilon }_1}\\ {\sigma }_{{\upsilon }_0{\upsilon }_1}& {\sigma }_{{\upsilon }_1}^2\end{array}\right].$$

This model indicates the effect of SmkEvent both at the individual (υ_0i and υ_1i) and population (β₀ and β₁) levels. Specifically, the intercept parameters indicate the levels of mood during background random prompts, and the slope parameters indicate the degree of mood change associated with smoking events compared to random. The population intercept and slope parameters represent the random mood and mood difference associated with smoking for the population of subjects, whereas the individual parameters express how the individual deviates from the population in terms of their mood.

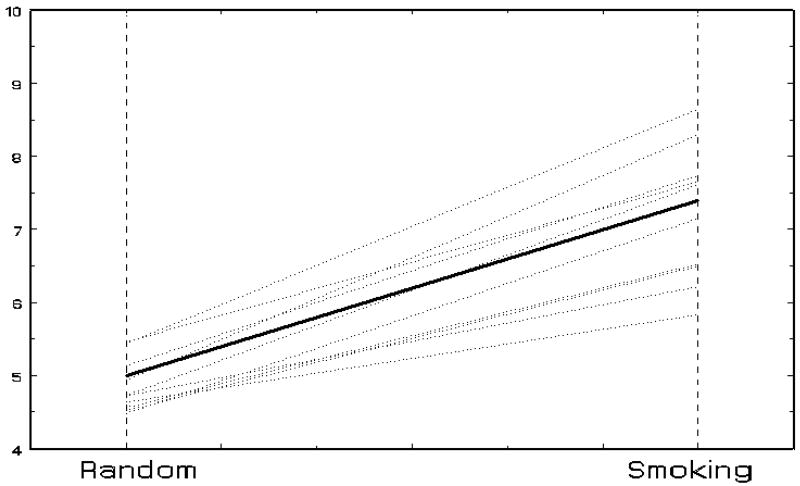
For a visual representation of the model, consider Figure 1 which illustrates the average change in mood attributable to smoking (the bold line) and trend lines (change in mood between random and smoking) of ten individual subjects who deviate randomly relative to the average trend. The average line is determined by β₀ (average mood for random prompts) and β₁ (average change in mood for smoking events). Similarly, the individual lines are determined by υ_0i (i.e., how different a person is relative to the random prompt average) and υ_1i (how different a person is compared to the average slope). The degree of individual mood variation for the random prompts is characterized by ${\sigma }_{{\upsilon }_0}^2$, and the degree of individual mood variation in the slopes (or mood changes for smoking, relative to random) is given by ${\sigma }_{{\upsilon }_1}^2$. Note that in Figure 1, there is a fair amount of individual variation for both: the ten individual lines do not equal the bold line in terms of the intercept or slope.

Figure 1.

Random intercept and slope model

To more fully model the effect of SmkEvent on mood, as described in Begg and Parides [27], we also included the subject's mean as a covariate. Notice that because SmkEvent_ij is simply a binary variable, taking on values of 0 or 1, 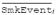simply equals the proportion of occasions (i.e., both random prompts and smoking events) that were smoking events for a subject. The model is now written as

$$y_{ij}=({\beta }_0+{\upsilon }_{0i})+({\beta }_1+{\upsilon }_{1i}){{\displaystyle \mathtt{\text{SmkEvent}}}}_{ij}+{\beta }_2{{\displaystyle \overline{\mathtt{\text{SmkEvent}}}}}_i+{\epsilon }_{ij}$$ (2)

Here, β₂ represents the subject-level effect of 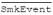, namely, the association of a person's proportion of smoking events with their average mood across both smoking events and random prompts. Conversely, β₁ is the within-subjects effect of SmkEvent, which indicates how a person's mood differs between a random prompt and smoking event, controlling for the proportion of smoking events that the person has. The subject-specific effects υ_0i and υ_1i indicate how subjects deviate from these overall effects. That is, υ_0i represents a subject's deviation in mood, adjusted for their proportion of smoking events, and υ_1i is a subject's deviation in the within-subject SmkEvent effect on mood (also adjusted for their proportion of smoking events), or in other words, how a given subject's reported mood differs following smoking a cigarette, relative to a random prompt.

Covariates can be added to the model to account for other determinants of mood. For example, to control for any mood-related changes attributable to day of week, one could include six indicator variables in the model. Let x_ij denote a vector of such covariates associated with subject i and occasion j. In general, this vector can include both time-invariant and time-varying covariates, as well as their interactions. The model is given as

$$y_{ij}=({\beta }_0+{\upsilon }_{0i})+({\beta }_1+{\upsilon }_{1i}){{\displaystyle \mathtt{\text{SmkEvent}}}}_{ij}+{\beta }_2{{\displaystyle \overline{\mathtt{\text{SmkEvent}}}}}_i+{{{\displaystyle \beta }}_x}^{\text{'}}{{\displaystyle x}}_{ij}+{\epsilon }_{ij},$$ (3)

where β_x is the (column) vector of coefficients associated with the additional covariates.

To be consistent with the generalization that will be described below (as Model II), let us re-express the random-effect variances associated with the intercepts υ_0i and SmkEvent slopes υ_1i as:

$${\sigma }_{{\upsilon }_0}^2=\text{exp}({\alpha }_{00}),$$ (4)

$${\sigma }_{{\upsilon }_1}^2=\text{exp}({\alpha }_{10}).$$ (5)

The reason for using the exponential function will become clear and be described in Model II below. For now, α₀₀ and α₁₀ simply represent the intercept and slope variance, respectively, on the natural log scale (since, taking logs, $\text{ln}{\sigma }_{{\upsilon }_0}^2={\alpha }_{00}$ and $\text{ln}{\sigma }_{{\upsilon }_1}^2={\alpha }_{10}$). Specifically, α₀₀ represents mood variation during random prompts (i.e., when SmkEvent_ij = 0) in natural log units, and α₁₀ represents the variation, in natural log units, of the mood changes associated with smoking events (i.e., when SmkEvent_ij = 1). Because the intercepts υ_0i and slopes υ_1i are allowed to be correlated (where σ_υ0υ1 is the covariance), the total mood variation during smoking events is given by exp(α₀₀) + exp(α₁₀)+2σ_υ0υ1. Notice that in Figure 1 the amount of variation for smoking events (horizontal spread around the bold line at Smoking) is greater than for random prompts (horizontal spread around the bold line at Random), and so in terms of the parameters, this figure depicts a situation where exp(α₁₀) + 2σ_υ0υ1 > 0.

Model II - heterogeneous LMM for modeling mood variation associated with smoking events

The LMM in equation (3), which we refer to as Model I, includes two random effects: one for a subject's intercept (υ_0i) and another for the within-subjects effect of smoking (υ_1i). It is very similar to the model described for EMA data in Moghaddam and Ferguson [15], who examined smoking-related changes in mood. In the proposed extended model, which we refer to as Model II, the variances associated with the random subject effects are also modeled in terms of covariates. To allow a subject-level covariate w_i (e.g., gender or grade) to influence these variances we utilize a log-linear representation, as has been described in the context of heteroscedastic (fixed-effects) regression models [28-29], namely,

$${\sigma }_{{\upsilon }_{0i}}^2=\text{exp}({\alpha }_{00}+{\alpha }_{01}{w}_i),$$ (6)

$${\sigma }_{{\upsilon }_{1i}}^2=\text{exp}({\alpha }_{10}+{\alpha }_{11}{w}_i).$$ (7)

A reason for using this representation is that the exponential function ensures that the variance being modeled will be greater than zero, as it should be. It is merely a convenient mathematical transformation that is used to yield logical results for these variances. Also, the variances are now subscripted by i to indicate that their values change depending on the value of the subject-level covariate w_i and its coefficients. This variable would typically also be added as a covariate in the regression model (i.e., in x_ij) to account for its effect on the mean of mood. Additionally, an interaction of w_i by SmkEvent_ij could be included to allow the covariate effect on the mean of mood to vary between random prompts and smoking events.

In equation (6), the random-prompt variance equals exp α₀₀ when the subject-level covariate w_i equals 0, and is increased or decreased as a function of the covariate w_i and its coefficient α₀₁. Specifically, if the coefficient α₀₁ > 0, then the random-prompt mood variance increases as w_i increases (and vice versa if α₀₁ < 0). The slope variance (i.e., the heterogeneity of the change in mood associated with smoking events) is modeled in the same way in equation (7). That is, this variance equals exp α₁₀ when the subject-level covariate w_i equals 0, and is increased or decreased as a function of this covariate and its coefficient α₁₁.

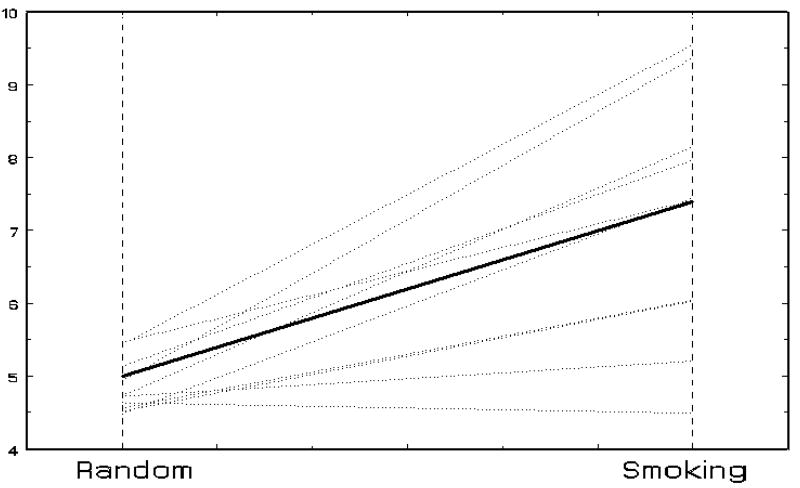
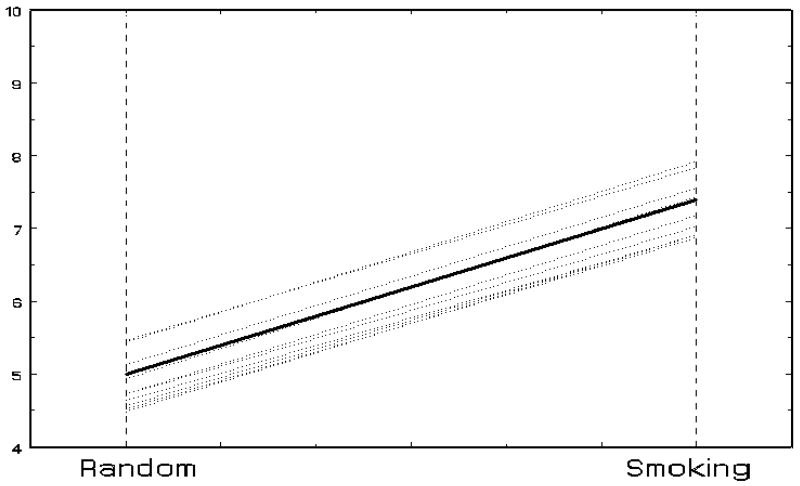
Figure 2 presents an illustration where there is considerable individual slope variation. If we consider w_i to be a dichotomous grouping variable (=0 or 1) and let Figure 1 represent the model for w_i = 0 and Figure 2 represent the model for w_i = 1, notice that the degree of variation around the random prompt average is the same, and so α₀₁ = 0. However the degree of slope variation is greatly increased in Figure 2, relative to Figure 1, and so α₁₁ > 0. Conversely, consider Figure 3 in which the slope variation is minimal. Here, if Figure 3 represents the model for w_i = 1, then α₀₁ = 0 (random prompt variance is the same), but α₁₁ < 0 (slope variance is decreased).

Figure 2.

Random intercept and slope model with increased slope variance

Figure 3.

Random intercept and slope model with decreased slope variance

To summarize, the proposed model has several avenues for examining the potential association of smoking and mood. First, β₂ (i.e., the coefficient for 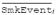) represents the association of individuals' level of smoking, as indicated by their proportion of smoking events, with their average mood. In other words, do adolescents who smoke more (less) have lower (higher) general mood? Second, β₁ (i.e., the coefficient for SmkEvent_ij), indicates the degree to which a person's mood differs after smoking (compared to random), controlling for their overall level of smoking and its effect on their overall mood. Interacting a subject-level covariate w_i with SmkEvent_ij indicates whether the covariate moderates any smoking-associated change in mood levels. Finally, the variance parameter α₁₁ is of particular interest. It indicates the degree to which the covariate w_i influences smoking-related change in mood variation. For example, it might be that heavier smokers experience greater mood stabilization when smoking than do light smokers. While several studies have examined the effects of covariates on the degree to which the mean of mood changes with smoking [15, 31-32], allowing covariates to influence the variance in mood, and not just the level of mood, associated with smoking is the unique feature of the proposed model. In this regard, in a recent review article, Parrott [33] suggested that mood vacillation and its relationship to nicotine dependency was an important topic for future research. The proposed model aims at providing a statistical tool for examining this suggestion.

Results

Table 1 lists the results for Model I applied to positive and negative affect. In addition to the SmkEvent-related variables, indicator variables are included in the analyses to account for day to day mood variation. Monday was selected as the reference day, and so these six day indicators (named Tuesday, Wednesday, …, Sunday) represent mood differences relative to Monday.

Table 1.

Positive and Negative Affect Model I estimates, standard errors (se), and p-values

	Positive Affect			Negative Affect
parameter	estimate	se	p <	estimate	se	p <
Intercept β0	6.713	.128	.0001	3.777	.149	.0001
SmkEventij β1	.432	.073	.0001	-.294	.078	.000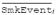2
β2	.088	.671	.90	-1.244	.780	.12
Tuesday βTue	-.053	.064	.41	-.041	.073	.58
Wednesday βWed	-.152	.064	.02	.106	.073	.15
Thursday βThu	-.140	.064	.03	.165	.073	.025
Friday βFri	.027	.064	.67	-.025	.073	.74
Saturday βSat	.110	.065	.09	-.096	.074	.20
Sunday βSun	.005	.066	.94	-.099	.075	.19
Intercept variance (ln units) α00	.414	.098	.0001	.752	.097	.0001
SmkEvent variance (ln units) α10	-.818	.269	.003	-.903	.322	.006
Intercept, SmkEvent covariance συ0υ1	-.303	.094	.002	-.431	.121	.0005
Error variance ${\sigma }_{\varepsilon }^2$	2.334	.038	.0001	3.045	.049	.0001

For the effect of SmkEvent on mood, the results are very consistent for positive and negative affect. Positive mood is significantly increased (β̂₁ = .432, p < .0001) and negative mood significantly decreased (β̂₁ = −294, p < .0002) for smoking events, relative to random prompts. These are within-subjects, rather than between-subjects, effects for both outcomes. Controlling for the proportion of smoking events a subject makes, and its effect on mood, subjects' moods are significantly different when they make smoking reports, relative to their random prompts. For the day effects, Thursday is observed to have significantly lower PA and significantly greater NA, relative to Monday (β̂_Thu = −.140, p < .03 and β̂_Thu = .165,p < .025, respectively). Wednesday is also significantly lower on PA than Monday (β̂_Wed = −.152, p < .20).

In terms of the variance parameters, it is first worth noting that comparing Model I to a simpler random-intercepts model (results not shown), which would assume that the SmkEvent variance and covariance parameters equal zero (i.e., α₁₀ = σ_υ0υ1 = 0), rejects the simpler model in favor of Model I (likelihood ratio ${\mathit{\text{X}}}_{(2)}^2$ = 39 and 30 for PA and NA, respectively, p < .0001 for both). Thus, in reference to our first study aim, there is strong evidence that changes in mood associated with smoking vary from subject to subject. Based on the Model I estimates, for PA, the between-subjects variance is exp(.414) = 1.513 for random prompts and exp(.414) + exp(−.818) + 2(−.303) = 1.348 for smoking events. By similar calculations for NA, the between-subjects variance equals 2.121 for random prompts and 1.665 for smoking events. Thus, between-subjects mood variation (i.e., subject heterogeneity), both positive and negative, is reduced under smoking reports, relative to random prompts. Additionally, the covariance parameters are both negative and highly significant (σ̂_υ0υ1 = −.303, p < .002 and σ̂_υ0υ1 = −.431, p < .0005 for PA and NA, respectively), indicating that higher PA and NA values during random prompts are associated with greater reduction in these moods with smoking events. This could be the result of a floor effect of measurement.

Next, we examined the role of covariates using Model II. As mentioned, the covariates we examined were Male, Grade10, NMR, and SmkLevel. Due to the complexity of the model these covariates were examined one at a time, rather than in one large model. We examined the effects of these covariates on mood as main effects and as moderators of the SmkEvent effect on mood, both in terms of the mean and variance of mood response. Specifically, in terms of the mean of mood, the model was augmented by including each covariate as well as its interaction with SmkEvent (e.g., the terms β₃ Male and β₄ Male×SmkEvent_ij were added to equation (3)). Similarly, in terms of variance, we added in the covariate effect on the random prompt variance and the SmkEvent-related variance (e.g., Male in place of w_i in equations (6) and (7)). Thus, the difference between Models I and II was the inclusion of four parameters for each covariate, and a likelihood ratio test can be used to test the significance of these four additional parameters. Table 2 lists the model deviance (i.e., -2 log likelihood) values and likelihood-ratio test results.

Table 2.

Positive and Negative Affect Model II Likelihood-Ratio Tests

	Positive Affect			Negative Affect
Model	deviance	$X_{(4)}^2$	p <	deviance	$X_{(4)}^2$	p <
Model I	30967			33129
Model II with Male	30966	1	.91	33117	12	.018
Model II with Grade10	30956	11	.027	33127	2	.74
Model II with NMR	30932	35	.0001	33089	40	.0001
Model II with SmkLevel	30956	11	.027	33111	18	.002

${\mathit{\text{X}}}_{(4)}^2$ = likelihood ratio test statistic for comparison to Model I

As can be seen, for PA, the significant covariates are Grade10, NMR, and SmkLevel. Similarly, Male, NMR, and SmkLevel are significant for NA. Table 3 lists the additional four parameter estimates of Model II for all covariates, though we will only interpret the estimates from models which were deemed significant by the likelihood-ratio test.

Table 3.

Positive and Negative Affect Model II estimates, standard errors (se), and p-values

	Positive Affect			Negative Affect
variable and parameters	estimate	se	p <	estimate	se	p <
Male: Gender (0=female, 1=male)
main effect β3	.087	.166	.60	-.519	.191	.007
interaction β4	-.120	.145	.41	.117	.157	.46
random prompt variance α01	-.020	.183	.92	-.358	.179	.05
SmkEvent-related variance α11	-.215	.498	.67	.484	.563	.40
Grade10: Grade (0=9th, 1=10th)
main effect β3	-.008	.168	.97	.044	.196	.83
interaction β4	.231	.140	.11	-.181	.154	.25
random prompt variance α01	-.418	.182	.03	.148	.179	.42
SmkEvent-related variance α11	1.017	.682	.14	-.105	.582	.86
NMR: Negative Mood Regulation (1 to 5)
main effect β3	.629	.110	.0001	-.790	.128	.0001
interaction β4	-.109	.105	.31	.054	.118	.65
random prompt variance α01	-.203	.150	.18	-.193	.133	.15
SmkEvent-related variance α11	-.300	.357	.41	-.105	.428	.81
SmkLevel: 30 Day Smoking Level (0 to 5)
main effect β3	-.025	.061	.69	.144	.072	.05
interaction β4	.068	.049	.17	-.105	.053	.05
random prompt variance α01	.099	.060	.11	-.007	.062	.92
SmkEvent-related variance α11	-.337	.140	.02	-.446	.153	.004

For PA, we see that the significant effect of Grade10 is in terms of the random prompt variance (α̂₀₁ = −.418, p < .03), with 10th graders having reduced PA mood variation, relative to 9th grade students. NMR has a highly significant positive effect on the mean PA response (β̂ = .629, p < .0001), such that subjects with higher negative mood regulation report significantly higher positive affect. SmkLevel significantly decreases the SmkEvent-related variance of positive affect (α̂₁₁ = −.337, p < .02). Thus, increased smoking level is associated with a reduced degree of positive affect change for smoking events, relative to random prompts. In other words, smoking-related positive affect mood response (i.e., the degree of difference in a subject's positive affect between smoking events and random prompts) is significantly less for more frequent smokers.

In terms of NA, Male has a significant effect on both the mean and variance; males are seen to have significantly lower negative affect scores (β̂ = −.519, p < .007) which are less variable (α̂₀₁ = −.358, p < .05). As for positive affect, NMR has a highly significant effect on the mean response, though for NA it is a negative effect (β̂ = −.790, p < .0001), such that subjects with higher negative mood regulation have lower negative affect. Finally, SmkLevel has significant mean and variance effects. In terms of the mean, higher smoking level is associated with higher negative affect scores during random prompts (β̂ = .144, p < .05). However, because the interaction is also significant and negative, this effect goes away during smoking events (β̂ = −.105, p < .05). Namely, the effect of SmkLevel on negative mood is essentially zero for smoking events (= .144 - .105 = .039). In terms of variance, the effect of SmkLevel on negative affect is very similar to its effect on positive affect. That is, increased smoking level is associated with a diminished degree of negative affect change for smoking events, relative to random prompts (α̂₁₁ = −.446, p < .004). Thus, smoking-related mood response (both positive and negative affect) is significantly decreased for more frequent smokers, relative to less frequent smokers.

Discussion

This article has illustrated how mixed models for EMA data can be used to model differences in variances, and not just means, across subject-varying covariates. As such, these models can help to identify predictors of between-subjects variation, and to test psychological hypotheses about these variances. While standard mixed model software (e.g., SAS PROC MIXED, SPSS MIXED, HLM, MLwiN) can easily estimate Model I (albeit not with the natural log scale conversion of the variance parameters that was used here), estimation of the heterogeneous LMM (Model II) goes beyond the capabilities of these software program. However, SAS PROC NLMIXED can be used for this purpose. At website www.uic.edu/:hedeker/long.html, we provide sample syntax and output for maximum likelihood estimation of Model II, making this class of models accessible to researchers.

Here, we focused on the degree of mood variation between random prompts and smoking events, and whether covariates influenced this variation among adolescent smokers. One of the key concepts in dependence is the development of tolerance, or the diminishing of effects of a substance with continued use. A common experience, reported by both adults and adolescents is mood change after smoking a cigarette, and the equally common notion is that these subjective feelings diminish over time as one's experience with smoking increases and tolerance may develop. However, heretofore, researchers have examined changes in these subjective experiences primarily through paper-and-pencil, retrospective questionnaire reports. Thus, it has been difficult to document adequately whether adolescents experience mood changes with smoking and also, how symptoms of dependence develop or with what level of smoking experience. Overall, following smoking, adolescents experienced higher positive affect and lower negative affect than they did at random, non-smoking times. However, our analyses also indicated an increased consistency of subjective mood responses as smoking experience increased and a diminishing of mood change. Our data thus provide one of the few ecologically valid examinations of the development of tolerance. Adolescents' self-reports, in real time, of the degree of their subjective response to smoking varied as a function of their smoking level. Importantly, too, these differences were relatively dramatic and were seen for both positive and negative affect. In fact, smoking level was the only covariate that influenced the variance of smoking-related mood response.

Our results also highlight the importance of examining both mean levels of mood and variability; each may convey important information about the development of nicotine dependence in adolescents. Indeed, in our own work (Weinstein, Mermelstein, Shiffman, & Flay, in press [38]), we have found that mood variability predicts smoking escalation even after controlling for mean levels of negative mood. Our results also indicated that adolescents who smoked more had higher background, random negative moods. We cannot, however, yet tease apart whether these affective states may reflect in part withdrawal distress, or general contextual or trait negative affectivity. Our study is one of the first to examine real-time subjective mood responses to smoking among adolescents who are still relatively early in their smoking careers and light or infrequent smokers (less than 7 percent of the sample smoked more than 5 cigarettes a day). As such, this study helps to add important information about the relatively early development of symptoms of dependence, a potential development of tolerance to the mood regulating effects of smoking. These analyses are limited, though, by their cross-sectional nature, and as such, we must take these results as only suggestive of longitudinal changes as smoking develops.

Our results are limited, too, by issues related to generalizability in terms of sampling and design characteristics. Our analysis sample was limited to adolescents who had recorded at least one smoking episode during a 7-day assessment week. In addition, we had excluded from this sample adolescents who had reported smoking more than 5 cigarettes/day at an initial screening survey. Thus, our sample represents relatively light and infrequent smokers. As such, we were unlikely to capture heavier smoking episodes among youth, which might show different patterns of mood variability and mean levels. Nevertheless, our data, with our focus on the earlier stages of smoking, may be important for shedding light on the development of dependence.

More potential applications of this class of models clearly exist in substance abuse and psychological research. For example, many questions of both normal development and the development of psychopathology address the issue of variability or stability in emotional responses to various situations and contexts. Often, an interest is with the variability of responses an individual gives to a variety of stimuli or situations, and not just with the overall mean level of responsivity. The models presented here also allow us to examine hypotheses about cross-situational consistency of responses as well.

In order to reliably estimate variances, one needs a fair amount of both within-subjects and between-subjects data. Modern data collection procedures, such as ecological momentary assessments (EMA) and real-time data captures, provide this opportunity. Such designs are in keeping with the “bursts of measurement” approach described by Nesselroade [34], who called for such an approach in order to assess individual variability. As noted by Nesselroade, such bursts of measurement increase the research burden in several ways; yet they are necessary for studying individual variation, and allow researchers to examine important research questions that were previously unanswerable. Nevertheless, it is not sufficient to have such data to address these questions, one must also have the appropriate statistical tools. This article has aimed at providing tools for this endeavor.

As this is a relatively new modeling technique, certain limitations and cautions should be mentioned. First, our model assumes that the errors and random effects are normally distributed, and it is unclear how robust this model is to violations of normality. Because of the focus on the variance of the dependent variable, the distributional assumptions might be more critical than in more typical models focusing on differences in means. Thus, use of variance stabilizing transformations could be very helpful and should be routinely explored as a preliminary to analysis. Also, it is unclear how well this model would behave for variables where the mean and variance are highly correlated. Again, transformation of the dependent variable could help this situation to some degree. In our analyses, we did note the possibility of floor/ceiling effects, and this would seem to be something to keep in mind for rating scale data. Finally, attention should be paid to outliers and influential observations, as these might have undue effects on estimation of the model parameters, especially the variance parameters. Admittedly, this is an emerging area for mixed models ([35]-[37]), and work needs to be done to further generalize these approaches, however a careful inspection for outliers in both the dependent and independent variables should accompany any sophisticated statistical modeling.