Abstract
ICP latency is defined as the time interval between the peak of QRS complex of the electrocardiogram (ECG) and the corresponding onset of intracranial pressure (ICP) pulse. Due to its inherent relationship with arterial pulse wave velocity, ICP latency may allow continuous monitoring of pathophysiological changes in the cerebrovasculature. The objective of the present work was to develop and validate a computerized algorithm for extracting ICP latency in a beat-by-beat fashion. The proposed ICP latency extraction algorithm exploits the mature technique of ECG QRS detection and includes a new adaptive peak detection methodology. The results were validated by comparing the performance of two human observers versus the algorithm in terms of locating the onset points of ICP pulses for 59 recordings extracted from 25 adult patients. The average ICP latency was 72.6 ± 19.5 milliseconds (range 40.0 – 159.8). The ICP pulse detection algorithm demonstrated a baseline sensitivity of 0.97 and a positive predictivity of 0.88. No difference was found in the mean location errors from comparing the results obtained by the two observers and those from comparing the results from algorithm to those from the two observers. Further investigation is needed to demonstrate the role of ICP latency in characterizing dynamic cerebral vascular pathophysiological changes in clinical states such as subarachnoid hemorrhage and traumatic brain injury.
Keywords: Intracranial pressure, pulse wave velocity, cerebrovascular resistance, cerebral blood flow autoregulation
INTRODUCTION
The study of ICP latency, defined here as the time interval between the cardiac contraction until the detection of the resultant intracranial pressure (ICP) waveform, offers an opportunity to investigate properties of the intracranial arterial system related to pressure pulse wave propagation. The state of the intracranial vasculature, such as arterial vasoconstriction or autoregulatory capacity, is difficult to assess on a continuous basis clinically because of practical limitations imposed by the bony skull. Because the initial phase of the ICP pulse wave is primarily generated by the forward-traveling arterial blood pressure pulse traversing the intracranial compartment, the timing of the ICP pulse inherently contains information about variables impeding or facilitating the ascending propagated pulse wave. The pulse wave velocity (PWV) in arteries is described by the Moens-Korteweg equation ; where E is the elastic modulus, ρb is the blood density, h is the thickness of the vessel wall, and R is the internal radius of the vessel. As ρb and h can be considered relatively constant, inferences can be drawn from PWV measurements about arterial elasticity and diameter.
Information regarding structural and functional changes of the cerebrovascular system is important in the management of several neurological conditions, including traumatic brain injury and subarachnoid hemorrhage. For example, pathological narrowing of cerebral arteries (vasospasm) that follows aneurysmal or traumatic subarachnoid hemorrhage can lead to cerebral ischemia and stroke if it is not treated in a timely manner (Harrod et al. 2005). ICP is routinely monitored in many of these patients, and therefore offers a unique opportunity to indirectly measure PWV via ICP latency. Inferences regarding changes in arterial constriction, based on ICP latency analysis, could result in earlier recognition of cerebral vasospasm.
There is precedence in utilizing PWV analysis to assess the state of the arterial vasculature (Davies and Struthers 2003). For example, the arterial augmentation index has been estimated based on PWV measurements (Nichols and Singh 2002). Sutton-Tyrrell et al. demonstrated that an elevated aortic PWV, a marker of arterial stiffness, predicted cardiovascular events in well-functioning older adults (Sutton-Tyrrell et al. 2005). Other studies have shown that increased PWV correlated with arterial stiffness in both healthy (Willum-Hansen et al. 2006) and diseased (Chang et al. 2006) adults. Even endothelial dysfunction has been inferred based on PWV measurements (Jadhav and Kadam 2005). To our knowledge, a PWV approach to the analysis of the intracranial arterial system was first investigated using the cerebral blood flow velocity pulse (Giller and Aaslid 1994). However, ICP pulse wave has not been studied for its role of in facilitating PWV analysis of cerebral vasculature.
The present work describes the technical details of a signal-processing algorithm capable of extracting beat-by-beat ICP latency relative to the QRS of the electrocardiogram (ECG). Beat-to-beat analysis of the ICP waveform is challenging due to a varying baseline, dynamically changing ICP waveform morphology, and superimposed signals (noise) or pressure influences (such as coughing and patient movement) that tend to lead to errors in automated algorithms. The linkage of each ICP pulse to a QRS was capitalized upon by leveraging the established ECG QRS detection techniques that have excellent immunity to the above distortions. This differentiates our algorithm from other pulse delineation algorithms (Aboy et al. 2005) that analyze the pressure signals in isolation. Furthermore, a novel adaptive algorithm was introduced to help detect misplaced QRS detection so that ICP latency extraction can be avoided for such cases. A subsequent manuscript will report the clinical utility of ICP latency measurement.
MATERIALS and METHODS
Subjects and Data Acquisition
The physiological data used for this analysis was obtained from patients undergoing continuous ICP monitoring as part of their clinical care at the UCLA Medical Center. ECG signals were recorded simultaneously with the ICP data. The data analyzed was derived from 25 patients with various diagnoses including: normal pressure hydrocephalus (n = 18), syringomyelia (n = 1), Chiari malformation (n = 1), slit ventricle syndrome (n = 3), pseudotumor cerebri (n = 1), and ventricular cyst (n =1). There were thirteen females and twelve males studied, with a mean age of 64 ± 22 years (range 18 to 92 years). The study was approved by the UCLA Institutional Review Board with informed consents from patients.
ICP was monitored using Codman intraparenchymal micro-sensors (Codman and Schurtleff, Raynaud, MA) situated in the right frontal lobe. Lead II of the ECG recording was used. Both the ICP and ECG signals were monitored using either an Eagle 4000 or a Dash 4000 beside monitor (GE Healthcare, UK), the analog output of which was transferred to the data collection computer. The ICP and ECG waveforms were sampled at 400 Hz using a PowerLab TM SP-16 data acquisition system (ADInstruments, Colorado Springs, CO).
In order to test the algorithm with the widest variety of ICP waveforms from an assortment of clinical conditions, ages, and intracranial dynamic states, data samples were selected in the following manner:
Periods of spontaneous large amplitude ICP oscillations (Lundberg B waves (Lundberg et al. 1965)) were detected in twelve patients. A representative six-minute recording during one of these ICP oscillatory episodes was visually selected from each patient. In addition, a six-minute recording was also selected during a stable ICP episode occurring between these oscillatory phases. A one-minute signal segment from each of these twenty-four episodes was randomly selected for validation.
A one-minute signal segment was randomly selected from recordings that were obtained from eight patients during a clinical assessment of cerebral blood flow velocity using Transcranial Doppler (TCD) without a priori selection of oscillatory versus stable ICP periods.
27 ICP segments were collected from nine NPH patients undergoing a CSF bolus injection test. The bolus test, which is a clinical study used to calculate the CSF outflow resistance (Marmarou et al. 1975), consisted of three consecutive 5-cc bolus intrathecal injections of Ringer’s lactate solution at the time of a lumbar puncture.
As a result, a total of 59 segments were collected for validating the proposed algorithm. They belonged to four groups: baseline ICP, oscillatory ICP, TCD ICP, and CSF injection ICP.
Brief introduction of the method
The input to the developed algorithm includes ICP and ECG QRS positions. As a general overview, the ECG QRS peak serves as a key reference point from which the ICP waveform analysis is performed. This one-to-one matching process helps promote the identification of the proper ICP waveform. There are four processing blocks in the proposed method. Utilizing the heart rate information, the first block processes raw ICP signals using a heart-rate dependent narrow band-pass filter. Then an adaptive peak detection algorithm is used at the second block to find the locations of ICP peak in each pulse. The third processing block then applies a moderate low pass filter on the raw ICP signals. This low pass filtered ICP is then combined with the peak locations of each ICP pulse to automatically determine the onset location for each identified ICP peak.
ECG QRS Detection
We chose the ECG QRS peak as the initial “reference point” for the latency measurement for several reasons. First, the ECG signal is easily obtainable and generally possesses an excellent signal-to-noise ratio. Other possible signals, such as radial artery blood pressure or pulse-oximetry waveforms, may not be measured routinely or have adequate reliability, and therefore would limit the broad application of our methodology. A second reason is that established and robust signal processing methods already exist for detecting the QRS complex (Nygards and Sornmo 1983; Afonso et al. 1999; Kohler et al. 2002), and therefore any uncertainty of the preciseness of the ICP latency measurement becomes primarily a sole function of the analysis of the ICP waveform.
ICP Pulse Detection Algorithm
It was assumed in the present work that an ICP pulse onset invariably follows a preceding ECG QRS peak. The first step was to identify the rising edge of ICP pulse. This was accomplished in the algorithm by identifying the peak of a band-pass filtered ICP pulse. Our algorithm incorporated band-pass filtering for simplifying the morphology of ICP pulse and an adaptive algorithm for robustly determining the band-pass filtered ICP peak.
Heart-Rate Dependent Band-Pass Filter
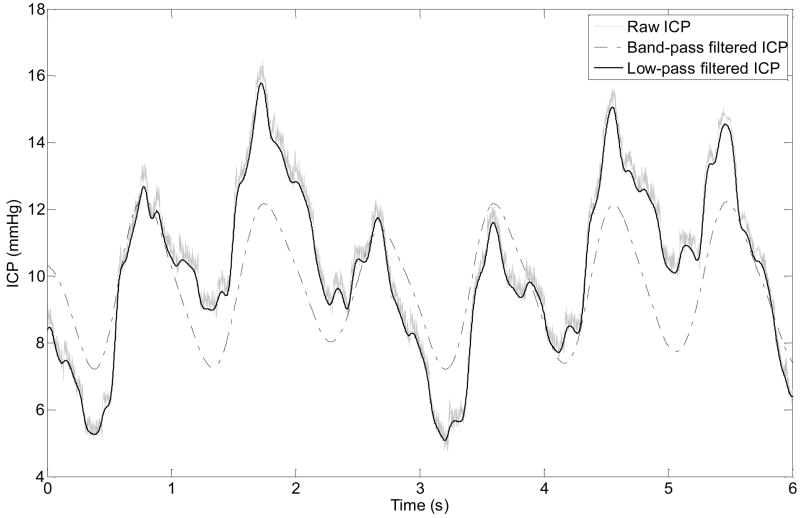
Due to the inherent noise and baseline variation in ICP signals, one cannot simply take the maximum of an ICP pulse for identifying the ICP rising edge. We instead chose to use a band-pass filter to pre-process raw ICP waveform to achieve: 1) the removal of both high-frequency noise and baseline wander in ICP, and 2) to reduce each complex ICP pulse morphology down to one representative peak (Fig. 1). The lower and upper cutoff frequencies of this band-pass filter were designed to adapt based on the heart rate such that its pass-band was 0.45 to 0.55 times the mean heart rate. A similar strategy of utilizing a noise reduction filter for maximally preserving only the pulsatile component was also used in a previously published pulse detection algorithm (Aboy et al. 2005).
Fig.1.
Illustration of a raw ICP recording, its low-pass filtered and its band-pass filtered versions. The band-pass filter was designed based on heart rate for the purpose of simplifying the morphology of ICP pulse so that only one peak is preserved in the filtered signal. The low-pass filter is a moderate 2nd order 5 Hz zero-phase Elliptic filter. It removes high frequency noise but has minimal influence on the onset location of ICP pulse.
Spurious ICP Peak Detection Using an Adaptive Interval Determination Algorithm
Two types of beat detection errors are usually encountered. The first type is missing beat detection. Our algorithm is inherently immune to this type of error because the above described ICP pulse onset is calculated for detected beats only. The second type of error is spurious beat detection where a spiky T wave, as an example, may be falsely detected as a QRS complex. These misplaced QRS peaks positions are problematic because they can result in incorrect ICP pulse delineation by splitting one ICP pulse into multiple ones. We addressed this by imposing a timing constraint on peak location of a filtered-ICP.
To proceed, suppose that the R wave position, in terms of sample number, of the ith heartbeat is ti. pi represents the interval to ti of a candidate ICP peak position. Besides the usual local maximum requirement for detecting peak, a timing constraint is imposed on pi such that βi ≤ pi ≤ αi, i.e., the timing difference between an ICP peak and ECG R wave should be within a physiological window. Note that both βi and αi can change from beat to beat. The adjustment algorithm for βi and αi was designed with the objective of maintaining a window of a constant length around pi for its robust detection, i.e., pi – βi ≡ Δ0 and αi – pi ≡ Δ1. Since pi can change from beat-to-beat, the requirement of a constant window length hence implies that βi and αi are adjusted beat-by-beat accordingly. This can be viewed as an adaptive interval determination such that the true but unknown pi is always trapped within the detection window. An equation for adapting αi from its value at previous beat αi − 1 in a beat-to-beat fashion can be implemented as
| (1) |
where λpos and λpre are weighting coefficient within [0, 1] that control adaptation rate. The correction added to αi − 1 consists of two parts: 1) the error between the desired window length and the actual window length at the previous beat; 2) the prediction of change of pi relative to pi − 1 based on the change from pi − 2 to pi − 1. Similar idea can be applied to derive βi as
| (2) |
A spurious beat can thus be detected if no ICP peak is found that satisfies the local maximum condition and the timing constraint.
Identification of the Location of the ICP Pulse Onset
The valid ICP pulse waveforms identified using the above described methodology were then subjected to an algorithm to identify the onset, or “foot,” of the ICP waveform. Of note, the band-pass filter used for identifying valid ICP pulses was not used in the ICP pulse onset algorithm due to the introduction of undesirable phase shifts in the signals (as can be seen in Fig. 1). Instead, a moderate 2nd order 5 Hz zero-phase elliptical low-pass filter was applied to the raw ICP waveform to remove high frequency noise while preserving the location ICP pulse onset.
The definition of ICP pulse onset location, illustrated in Fig. 2, was based on methods analogous to those described by Chiu et al. (Chiu et al. 1991) for the detection of arterial pulse wave signals. A tangential line (Line A in Fig. 2) was determined by a straight-line fitting of the rising edge of ICP pulse. This line fitting process takes two steps. The ICP sample having the maximal first derivative was first identified on the rising edge of the ICP pulse. Then centering at this ICP sample, additional neighboring ICP samples were added in the line fitting process until the fitted line failed to correlate with the original rising edge at a threshold above 0.999. A second line (Line B in the Fig. 2) was defined by the horizontal line passing the minimum of the ICP pulse. ICP pulse onset was then defined as the intersection of Lines A and B.
Fig.2.
Illustration of ICP pulse onset definition. ICP pulse onset is defined as the location where Line A intersects Line B. Line B is a horizontal line passing the minimum of a portion of filtered ICP pulse that lies between R wave of ECG and ICP peak. Line A is a straight line fitted to the rising edge of ICP pulse and passes the point of maximal first derivative of an ICP pulse.
Validation of the ICP Onset Detection Methodology
The described algorithm of automated determination of ICP waveform onset was tested against rote manual detection by trained observers. The time-aligned ECG and filtered ICP signals were digitally plotted using a custom-made computer program that had additional capabilities of adding and removing marks of various waveform landmarks including the QRS peaks and diastolic points of ICP pulse. ECG QRS detection results were visually inspected and annotated by one of authors (X.H.). Additionally, two human observers were trained to manually mark the minimum point of each ICP pulse that immediately followed the corrected ECG QRS complex. Low-pass filtered ICP was presented to the observers using the same low-pass filter adopted in the algorithm.
Two quality aspects of the proposed algorithm were assessed. The first aspect concerns the immunity of the algorithm to the misplacement of ECG QRS peaks. This is a highly relevant metric for the performance of the proposed algorithm. In its current form, the proposed algorithm does not attempt to calculate ICP latency for missed ECG QRS detection. The justification for doing so is the high sensitivity of QRS detection. However, the algorithm tries to reduce the effect of spurious ECG detection on ICP latency calculation. The relevant performance metrics for evaluating our algorithm are therefore false positive rate and false negative rate that can be achieved in avoiding spurious QRS detection. Particularly, a false positive is incurred if ICP latency calculation is skipped for a properly identified QRS peak and a false negative is incurred if ICP latency is calculated for a incorrectly identified QRS peak. This assessment was performed by first collecting the misplaced detections from ECG QRS detection and then investigating whether the calculation of ICP latency was skipped for these beats. Let N represent the total number of misplaced detections, NT the total number of correctly skipped ICP latency extraction, NM the total number of missed corrections, and NF the total number of incorrectly skipped ICP latency calculation. Two quantitative measures were then extracted:
The second quality aspect concerned the agreement of detection results between the two observers and those between the algorithm and two observers. This was assessed using a Bland–Altman plot. The compatibility of agreement statistics was assessed using a standard Z-test.
RESULTS
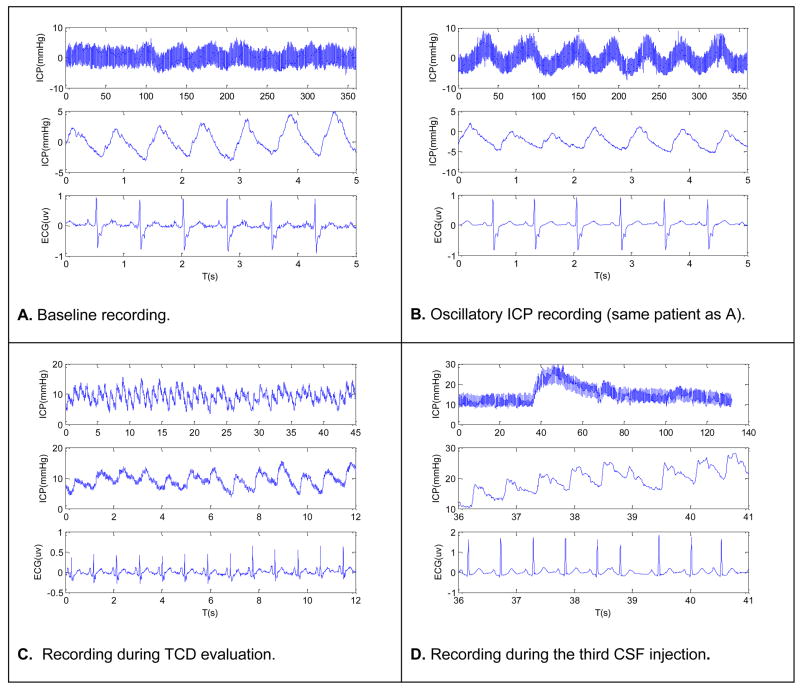
Four representative segments of ICP and ECG are shown in four panels of Fig. 3 corresponding to each of the four types of recordings we included in the validation. The top trace of each panel shows a long ICP recording to illustrate the key characteristic of the recording while the bottom two traces display a more focused view of ICP and ECG in terms of each ECG beat and ICP pulse.
Fig.3.
Four representative plots of ICP and ECG. Each plot corresponds to one of the four recording conditions that include baseline recording, oscillatory ICP state, recording during TCD evaluation, and recording during bolus CSF injection tests. The top trace of each plot shows a long ICP segment with the bottom two traces showing shorter segments of ECG and ICP, respectively.
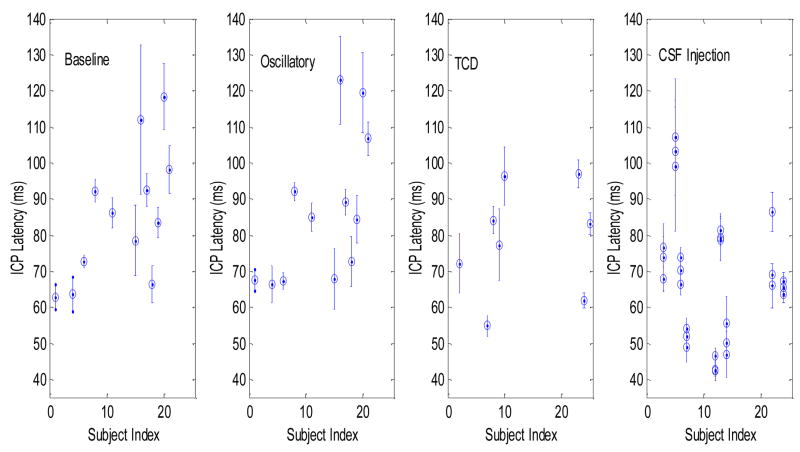
Mean ICP latency and its standard deviation calculated for each subject at a recording condition are presented in Fig. 4. This shows that a great variability of ICP latency exists at each recording condition and that the variability is more due to differences among subjects than to the four different recording conditions. Quantitative results are shown in Table 1 including the maximum and the minimum of the mean ICP latency of each recording as well as the indices of the patients for whom these extreme values were obtained. Large difference, approximately two-fold, existed between the maximal and the minimal values of ICP latency for all recording conditions. It can be also seen that extreme values were obtained from different subjects at different recording situations. This could be partly caused by the fact that not all subjects had recordings under the four conditions.
Fig.4.
Scatter plots of the mean ICP latency ± standard deviation for each subject under each recording condition.
Table 1.
Basic parameters summarizing the distribution of ICP, ICP latency, and heart rate of the subjects, in four groups, studied in the present work.
| BA | OC | TCD | CSF Injection | |||||
|---|---|---|---|---|---|---|---|---|
| ICP latency (ms) | Subject # | ICP latency (ms) | Subject # | ICP latency (ms) | Subject # | ICP latency (ms) | Subject # | |
| Max | 118.4 ± 9.2 | 20 | 122.9 ± 12.1 | 16 | 96.9 ± 3.9 | 23 | 107.1 ± 16.2 | 5 |
| Min | 62.9 ± 3.5 | 1 | 66.4 ± 5.2 | 4 | 54.9 ± 2.8 | 7 | 42.4 ± 2.7 | 12 |
There are 4305 true ECG beats in our validation data set. No ECG QRS beats were missed by the QRS detection process. However, there were 41 spuriously detected beats achieving a 99.05% positive predictivity of QRS detection. Figure 5 (lower panel) shows an example of illegitimate QRS detection that was recognized by the algorithm, resulting in a correctly skipped ICP pulse (upper panel). No ICP latency value was determined for this particular QRS-ICP couplet.
Fig.5.
One example showing a spuriously detected ECG beat and its influence on the ICP latency extraction. This spuriously detected ECG beat fragmented the ICP pulse such that the timing constraint on the ICP peak was not satisfied any more and hence no ICP latency extraction was done for the misplaced beat and the correctly identified beat prior to it.
As shown in Table 2, the ICP Pulse Detection Algorithm demonstrated a baseline sensitivity of 0.97 and a positive predictivity of 0.88. In order to assess the performance of the algorithm, individual algorithm parameters were modified (such as adaptation speed and/or fixed versus non-fixed band-pass filter) to determine the efficacy of correctly skipping ICP latency extraction for spuriously detected ECG beats. The analysis (Table 2) demonstrated that adaptively adjusting the initial window (λpos ≠ 0, λpre ≠ 0 ) was important, but an excessively large adjusting rate degraded the performance. Heart-rate dependent band pass filtering also contributed to the functioning of the algorithm as a fixed-band filter ([0.9 – 1.1] Hz) degraded the positive predictivity value.
Table 2.
| Parameter Combinations | Sensitivity | Positive Predictivity | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Description | HR-Dependent BP Filter | λpos | λpre | Δ0 (ms) | Δ1 (ms) | α0 (ms) | β0 (ms) | |||
| 1 | Baseline | Yes | 0.1 | 0.1 | 100 | 150 | 600 | 150 | 0.973 | 0.880 |
| 2 | Fast adaptation | Yes | 0.5 | 0.5 | 100 | 150 | 600 | 150 | 0.973 | 0.768 |
| 3 | No adaptation | Yes | 0 | 0 | 100 | 150 | 600 | 150 | 0.960 | 0.706 |
| 4 | Fixed band-pass filter | No | 0.1 | 0.1 | 200 | 300 | 600 | 150 | 0.973 | 0.794 |
| 5 | Fixed band-pass filter | No | 0.1 | 0.1 | 100 | 150 | 600 | 150 | 0.973 | 0.753 |
ms = Milliseconds, λpos , λpre = the weighting coefficient in Equations 1 and 2, Δ0 = the desired time interval between an ICP peak and its lower limit to the R wave of ECG, Δ1 = the desired time interval between an ICP peak and its upper limit to the R wave of ECG, α0 = initial value of the upper limit for the time interval between ICP peak and the corresponding ECG R wave, β0 = initial value of the lower limit for the time interval between ICP peak and the corresponding ECG R wave.
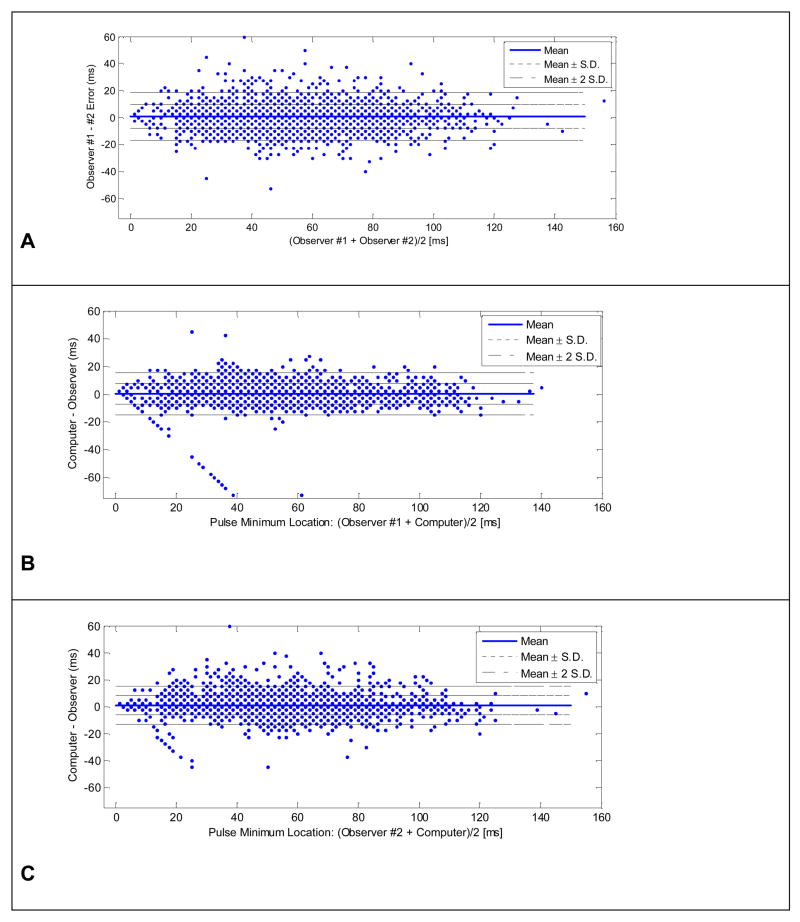
Bland–Altman plots (Fig. 6) were used to demonstrate the degree of the agreement between the location of the ICP onset points determined by different methods. Three combinations were compared: observer #1 versus observer #2; observer #1 versus the algorithm; and observer #2 versus the algorithm. Key measures of the agreement are summarized in Table 3. The mean location error between the manually marked points from the two observers was −0.67 milliseconds with a standard deviation of 9.2 milliseconds. This mean error was not significantly different from zero by a Z-test (p = 0.94). In addition, there was no systematic trend in the corresponding Bland-Altman plot indicating that human observers’ judgment of ICP onset locations were not influenced by the size of onset latency.
Fig.6.
Bland-Altman plots for assessing the agreement of locations of ICP pulse minimum marked by two observers and the computer algorithm. Panel A shows the Bland-Altman plot comparing two observers and Panels B and C display those comparing the algorithm and the first and the second observer, respectively.
Table 3.
Validation results for the computerized algorithm of identifying the location of minimum point in ICP pulse.
| Observer #1 vs. Observer #2 | Observer #1 vs. Algorithm | Observer #2 vs. Algorithm | |
|---|---|---|---|
| Error (ms) | −0.67 ± 9.24 | 1.13 ± 9.62 | 0.27 ± 10.44 |
| Slope of line fitting | 0.90 | 0.89 | 0.88 |
| Correlation Coefficient | [0.896, 0.908] | [0.892, 0.904] | [0.875, 0.889] |
Z-tests showed that there was no significant difference between the location error that existed between the two observers and those between the computer algorithm versus each of the individual observers (p=0.91 and p=0.98, respectively). The standard deviation of the differences of the three comparisons was similarly close to 10 milliseconds. This demonstrates that the proposed algorithm performed equivalently to rote localization performed by a trained human. However, a variation of 10-millisecond accounts for about 13% of the mean ICP latency value of 72.6 milliseconds. This degree of ambiguity was expected given the inhomogeneity and noise level of ICP waveforms recorded in the clinical setting.
There were a few outliers with an error greater than −50 milliseconds that existed in the Bland-Altman plots shown in Panels B and C (Fig. 6). Focused investigation of these specific points demonstrated that they appeared to be caused by the trained observers having uncertainty regarding the identity of the first versus the second ICP peak.
DISCUSSION
The latency of an ICP pulse, with regard to ECG, was first investigated several decades ago (Daley et al. 1982). This analysis, however, lacked computerized methodology and therefore was of limited clinical utility. Our algorithm exploited the mature technique of ECG QRS detection to aid in delineating individual ICP beats, plus incorporated an adaptive ICP peak detection step for locating spurious beat detections that would introduce erroneous ICP latency calculations. By adaptively defining a temporal window in which to look for the ICP beat, relative to a valid QRS peak, extraneous ICP data could be ignored. This approach was highly successful in correctly identifying valid QRS-ICP couplets in an environment complicated by different heart rates, ectopic beats, and an ICP waveform containing both high and low frequency noise plus a changing morphology. Clearly, alternative methodologies could have been developed and/or the algorithm parameters further refined. Although such improvements will evolve over time, we feel that the results shown in Table 2 demonstrate that our current algorithm (baseline setting) produces highly satisfactory results with a 97% sensitivity and 88% positive predictive rate in dealing with about 1% spurious QRS detection.
Based a human-versus-machine comparison paradigm and resultant three Bland-Altman plots, the computer algorithm performed equivalently well compared to human observers in locating the onset point on an ICP pulse, both in terms of average error and its variability. This success was attributed to the introduced adaptive peak location algorithm plus the heart rate dependent band pass filter, which improved the sensitivity, and positive predictivity of correctly identifying misplaced QRS beat detections. These validation results indicate that no significant bias of finding the ICP pulse location is introduced by the algorithm and that a variability of 10 milliseconds exists in locating ICP pulse onset. The 10-millisecond variability in the agreement among observers and the proposed algorithm is likely to be intrinsic to the recording and filtering conditions of ICP signals. It is possible that increasing the sampling rate and adopting more advanced noise reduction techniques might further decrease this variability.
Although the clinical correlation and application of ICP latency will be the subject of a subsequent paper, it is notable that a large variability existed among different subjects. Under any of the recording conditions, an approximate two fold difference could be found among this small cohort of patients. Pooling the data under all recording conditions, the third subject had the minimum ICP latency (42.4 ± 2.7 milliseconds) while the 14th subject had the maximum ICP latency (122.9 ± 12.1 milliseconds). If one assumes an average arterial PWV of 10 m/s (Nichols et al. 2005), this ICP latency range could not be explained solely by differences in patient anatomy (i.e. long neck) because it corresponds to a difference in distance of over one meter. Several other factors probably contribute to this wide range in ICP latency. The most likely factor is age, which strongly influences elastic properties of large arteries. The resultant effect on PWV (Sutton-Tyrrell et al. 2005; Chang et al. 2006; Willum-Hansen et al. 2006) should be directly apparent in ICP latency. The baseline caliber of the large arteries also will vary across patients and therefore influence the PWV. A further study to elucidate the influence of these factors on ICP latency is needed.
From a cardiac physiology standpoint, one might argue that the relationship between the ECG R wave and the aortic ejection, known as the interventricular mechanical delay, is variable across patients and therefore can account for differences in ICP latency. In a study of 316 patients with left ventricle systolic dysfunction, Perez de Isla et al. (Perez de Isla et al. 2006) found that the presence of a left bundle branch block correlated with an abnormally prolonged interventricular mechanical delay (> 40 milliseconds). We are therefore cautious in not over-interpreting the relationship between ICP latency and intracranial arterial state. Dynamic changes in ICP latency within subjects, however, is likely not explained by changes in cardiac electromechanical physiology, and therefore highlights the potential power and clinical usefulness of the ICP latency technique in assessing the vascular status. The limitations of ICP latency in assessing cerebrovascular changes will need to be established through further prospective studies and the assessment of different extracranial timing sources.
CONCLUSION
ICP latency relative to ECG QRS can be automatically extracted from clinical data using the proposed signal processing algorithm. Our methodology, which performed equivalently well compared to trained human observers, was able to accomplish this in a continuous, beat-by-beat basis. Further experimental and clinical studies are needed to investigate the theoretical projection that analysis of ICP latency may lead to continuous assessment of pathophysiological cerebral vascular changes.
Acknowledgments
The present work is supported by NINDS grants R21-NS055998, R21-NS055045, and R01-NS054881. We would like to thank biostatistician David McArthur Ph.D. for suggestion on an informative graphic presentation of variability of the latency data.
References
- Aboy M, McNames J, Thong T, Tsunami D. Ellenby M S and Goldstein B 2005 An automatic beat detection algorithm for pressure signals. IEEE Trans Biomed Eng. 52:1662–70. doi: 10.1109/TBME.2005.855725. [DOI] [PubMed] [Google Scholar]
- Afonso VX, Tompkins WJ, Nguyen TQ, Luo S. ECG beat detection using filter banks. IEEE Trans Biomed Eng. 1999;46:192–202. doi: 10.1109/10.740882. [DOI] [PubMed] [Google Scholar]
- Chang HK, Kim SK, Lee SS, Rhee MY. Arterial stiffness in Behcet’s disease: increased regional pulse wave velocity values. Ann Rheum Dis. 2006;65:415–6. doi: 10.1136/ard.2005.043430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiu YC, Arand PW, Shroff SG, Feldman T, Carroll JD. Determination of pulse wave velocities with computerized algorithms. Am Heart J. 1991;121:1460–70. doi: 10.1016/0002-8703(91)90153-9. [DOI] [PubMed] [Google Scholar]
- Daley ML, Gallo AE, Gehling GF, Isom JB, Mauch W, Kingsley PD. Fluctuation of intracranial pressure associated with the cardiac cycle. Neurosurgery. 1982;11:617–21. doi: 10.1227/00006123-198211000-00005. [DOI] [PubMed] [Google Scholar]
- Davies JI, Struthers AD. Pulse wave analysis and pulse wave velocity: a critical review of their strengths and weaknesses. J Hypertens. 2003;21:463–72. doi: 10.1097/00004872-200303000-00004. [DOI] [PubMed] [Google Scholar]
- Giller CA, Aaslid R. Estimates of pulse wave velocity and measurement of pulse transit time in the human cerebral circulation. Ultrasound Med Biol. 1994;20:101–5. doi: 10.1016/0301-5629(94)90074-4. [DOI] [PubMed] [Google Scholar]
- Harrod CG, Bendok BR, Batjer HH. Prediction of cerebral vasospasm in patients presenting with aneurysmal subarachnoid hemorrhage: a review. Neurosurgery. 2005;56:633–54. doi: 10.1227/01.neu.0000156644.45384.92. discussion 633–54. [DOI] [PubMed] [Google Scholar]
- Jadhav UM, Kadam NN. Non-invasive assessment of arterial stiffness by pulse-wave velocity correlates with endothelial dysfunction. Indian Heart J. 2005;57:226–32. [PubMed] [Google Scholar]
- Kohler BU, Hennig C, Orglmeister R. The principles of software QRS detection. IEEE Eng Med Biol Mag. 2002;21:42–57. doi: 10.1109/51.993193. [DOI] [PubMed] [Google Scholar]
- Lundberg N, Troupp H, Lorin H. Continuous recording of the ventricular-fluid pressure in patients with severe acute traumatic brain injury. A preliminary report. J Neurosurg. 1965;22:581–90. doi: 10.3171/jns.1965.22.6.0581. [DOI] [PubMed] [Google Scholar]
- Marmarou A, Shulman K, LaMorgese J. Compartmental analysis of compliance and outflow resistance of the cerebrospinal fluid system. J Neurosurg. 1975;43:523–34. doi: 10.3171/jns.1975.43.5.0523. [DOI] [PubMed] [Google Scholar]
- Nichols WW, O’Rourke MF, McDonald DA. McDonald’s blood flow in arteries: theoretic, experimental, and clinical principles. London New York, Hodder Arnold: Distributed in the U.S.A. by Oxford University Press; 2005. [Google Scholar]
- Nichols WW, Singh BM. Augmentation index as a measure of peripheral vascular disease state. Curr Opin Cardiol. 2002;17:543–51. doi: 10.1097/00001573-200209000-00016. [DOI] [PubMed] [Google Scholar]
- Nygards ME, Sornmo L. Delineation of the QRS complex using the envelope of the e.c.g. Med Biol Eng Comput. 1983;21:538–47. doi: 10.1007/BF02442378. [DOI] [PubMed] [Google Scholar]
- Perez de Isla L, Ortiz Oficialdegui P, Florit J, Angel Garcia-Fernandez M, Sanchez V, Zamorano J. Usefulness of clinical, electrocardiographic, and echocardiographic parameters to detect cardiac asynchrony in patients with left ventricular dysfunction secondary to ischemic or nonischemic heart disease. J Am Soc Echocardiogr. 2006;19:1338–44. doi: 10.1016/j.echo.2006.05.015. [DOI] [PubMed] [Google Scholar]
- Sutton-Tyrrell K, Najjar SS, Boudreau RM, Venkitachalam L, Kupelian V, Simonsick EM, Havlik R, Lakatta EG, Spurgeon H, Kritchevsky S, Pahor M, Bauer D, Newman A. Elevated aortic pulse wave velocity, a marker of arterial stiffness, predicts cardiovascular events in well-functioning older adults. Circulation. 2005;111:3384–90. doi: 10.1161/CIRCULATIONAHA.104.483628. [DOI] [PubMed] [Google Scholar]
- Willum-Hansen T, Staessen JA, Torp-Pedersen C, Rasmussen S, Thijs L, Ibsen H, Jeppesen J. Prognostic value of aortic pulse wave velocity as index of arterial stiffness in the general population. Circulation. 2006;113:664–70. doi: 10.1161/CIRCULATIONAHA.105.579342. [DOI] [PubMed] [Google Scholar]