High Intracellular Chloride Slows the Decay of Glycinergic Currents

Abstract

The time course of currents mediated by native and recombinant glycine receptors was examined with a combination of rapid agonist applications to outside-out patches and single-channel recording. The deactivation time constant of currents evoked by brief, saturating pulses of glycine is profoundly affected by the chloride concentration on the intracellular side of the cell membrane. Deactivation was threefold slower when intracellular chloride was increased from a low level (10 mm), similar to that observed in living mature neurons, to 131 mm (“symmetrical” chloride, often used in pipette internal solutions). Single-channel analysis revealed that high chloride has its greatest effect on the channel closing rate, slowing it by a factor of 2 compared with the value we estimated in the cell-attached mode (in which the channels are at physiological intracellular chloride concentrations). The same effect of chloride was observed when glycinergic evoked synaptic currents were recorded from juvenile rat spinal motoneurons in vitro, because the decay time constant was reduced from ∼7 ms to ∼3 ms when cells were dialyzed with 10 mm chloride intracellular recording solution.

Our results indicate that the time course of glycinergic synaptic inhibition in intact neurons is much faster than is estimated by measurements in symmetrical chloride and can be modulated by changes in intracellular chloride concentration in the range that can occur in physiological or pathological conditions.

Introduction

During fast synaptic transmission, receptors are activated by a brief exposure to high neurotransmitter concentrations (Clements et al., 1992; Maconochie et al., 1994). Rapid application techniques make it possible to mimic this synaptic transient, by producing concentration “jumps” of the order of 1 ms, with exchange times as short as 100 μs.

A limitation of this technique is that concentration jumps can be achieved only in outside-out patches, a recording configuration that inevitably disrupts the natural environment of the receptor by dialyzing intracellular solutes and by excising the cell membrane. A substantial effect of membrane excision on the properties of recombinant glycine receptors (GlyRs) was reported by Fucile et al. (2000), but the exact cause of such a change was never identified. In addition, it is commonly found that GlyR outside-out responses to concentration jumps decay much more slowly than the synaptic currents that they aim to mimic (Singer and Berger, 1999). A direct comparison is, however, complicated by many factors that may affect the time course of the IPSC, both postsynaptic (including differences between synaptic and extrasynaptic receptors) and presynaptic (most notably the corelease of GABA; Lu et al., 2008).

An alternative way to predict the deactivation time course of GlyRs in an intact cellular environment is to characterize the receptor activation mechanism by analyzing single-channel steady-state recordings in the cell-attached configuration (as we have done for recombinant α1 and α1β GlyRs and for rat native GlyRs) (Beato et al., 2004; Burzomato et al., 2004; Beato and Sivilotti, 2007). This quantitative modeling allows us to calculate the time course of a macroscopic response to a brief saturating agonist pulse and to compare it with data from outside-out patches containing the same GlyR subtype.

Here we show that our cell-attached estimates of single-channel reaction rates also show a discrepancy with outside-out data, because intact α1β GlyRs are predicted to deactivate much faster (∼8 ms deactivation time constant) than we see in outside-out experiments with the same receptors. For outside-out currents we measured a deactivation time constant of 20–25 ms, a value similar to that reported in the literature for native or recombinant GlyRs (Singer and Berger, 1999; Mohammadi et al., 2003).

The aim of our present work was to establish whether one or more of the experimental variables that differ in outside-out and cell-attached recording can account for this difference in GlyRs kinetic behavior. We show here that the major determinant for the time course of glycinergic currents was the concentration of intracellular chloride. GlyRs displayed fast deactivation in low intracellular chloride (10 mm), but this slowed appreciably even at 30 mm (from 7 to 11 ms for recombinant α1β GlyRs). Changes in the intracellular chloride concentration were also found to affect in a similar way the time course of evoked glycinergic IPSCs in juvenile rat motoneurons.

Materials and Methods

Heterologous expression of rat α1β glycine receptors in human embryonic kidney 293 cells.

Human embryonic kidney 293 cells (HEK-293) (American Type Culture Collection-CRL-1573; LGC Promochen) were maintained at 37°C in a 95% air/5% CO₂ incubator in DMEM supplemented with 0.11 g/L sodium pyruvate, 10% v/v heat-inactivated fetal bovine serum, 100 U/ml penicillin G, 100 μg/ml streptomycin sulfate, and 2 mm l-glutamine (all from Invitrogen) and passaged every 2–3 d, up to 20 times. Cells were plated and then transfected by a calcium phosphate-DNA coprecipitation method (Groot-Kormelink et al., 2002), with cDNA coding for the rat α1 and β GlyR subunits (GenBank accession numbers AJ310834 and AJ310839) at a ratio of 1:40 to minimize contamination by homomeric α1 receptors (Burzomato et al., 2004).

Spinal cord slices.

Spinal cord slices were obtained from P10 rats following UK Home Office regulations. Briefly, rats were anesthetized with urethane (1.8 g/kg, i.p. injection of 10% w/v solution, Sigma), decapitated, and the spinal cord was extracted in ice-cold solution composed of (in mm): 124 NaCl, 3 KCl, 25 NaHCO₃, 1 NaH₂PO₄, 2 CaCl₂, 2 MgCl₂, and 11 d-Glucose (pH 7.4, continuously bubbled with 95%/5% O₂/CO₂ mixture). The mid-thoracic and lumbar segments were glued to an agar block, and transverse slices (350 μm) were cut using a Leica VT1000 vibratome. Slices were cut in an ice-cold high potassium solution (Dugué et al., 2005) containing (in mm): 130 K-gluconate, 15 KCl, 0.05 EGTA, 20 HEPES, 3 kynurenic acid, and 25 glucose, with pH adjusted to 7.4 with NaOH. This solution mimics the intracellular medium and improves motoneuron survival. After 30 min incubation in normal extracellular solution at 37°C, slices were transferred to the recording chamber as needed and continuously superfused (5–7 ml/min) at room temperature (20°C).

Electrophysiological recording.

All single-channel recordings were obtained in the outside-out configuration, and four patches per glycine concentration (1 μm, 50 μm, and 1 mm) were selected for analysis. Cells were bathed in an extracellular solution containing (in mm): 102.7 NaCl, 20 Na gluconate, 2 KCl, 2 CaCl₂, 1.2 MgCl₂, 10 HEPES, 14 glucose, 15 sucrose, and 20 TEACl, pH adjusted to 7.4 with NaOH (osmolarity ∼320 mOsm). Glycine was bath applied via the perfusion system. Patch pipettes for outside-out single-channel recording were pulled from thick-walled borosilicate glass (GC150F; Harvard Apparatus), coated with Sylgard (Dow Corning), and fire-polished to a resistance of 5–10 MΩ. The intracellular high chloride solution contained (in mm): 107.1 KCl, 1 CaCl₂, 1 MgCl₂, 10 HEPES, 11 EGTA, 20 TEACl, and 2 MgATP. The same composition was used for experiments with 30 mm internal chloride, but with 101.1 mm K gluconate substituting for an equimolar amount of KCl. In the 10 mm chloride experiments, the composition of the internal solution was (in mm): 121.1 K gluconate, 1 CaCl₂, 1 MgCl₂, 10 HEPES, 11 EGTA, 6 TEACl, and 2 MgATP. In a subset of 10 mm chloride experiments, K methylsulphate was used as the replacement ion (121.1 mm). In some experiments phalloidin (10 μm) was added to the patch pipette. The pH was adjusted to 7.2 with KOH, and the osmolarity was corrected to 320 mOsm with sucrose when needed.

Single-channel recordings were made 14–24 h after transfection, at room temperature (20°C). Outside-out patches were voltage clamped at −100 mV with an Axopatch 200B amplifier. No correction for junction potential was applied. Recordings were prefiltered at 10 kHz with the amplifier four-pole Bessel filter and stored on digital audio tape (Bio-Logic Science Instruments). Recordings were replayed from the tape, filtered at 5 kHz with an eight-pole Bessel filter, and digitized at 50 kHz (Digidata 1322A; Molecular Devices) with Clampex software (Molecular Devices).

Perforated vesicle experiments (Levitan and Kramer, 1990) were performed by using either Amphotericin B (20 μg/ml) or gramicidin D (50 μg/ml). Seals in excess of 10 GΩ were routinely obtained without filling the tip of the pipette with antibiotic-free solution, provided that little or no positive pressure was applied when approaching the cell. Successful perforation was judged by a stable access resistance and was normally achieved within 10–15 min with Amphotericin B and 30–60 min with gramicidin D. Patches were pulled only if the access resistance was lower than 50 MΩ. The formation and stability of the vesicle was confirmed by monitoring the fluorescence at the tip of the pipette (see Figs. 2 and 3) throughout the experiment.

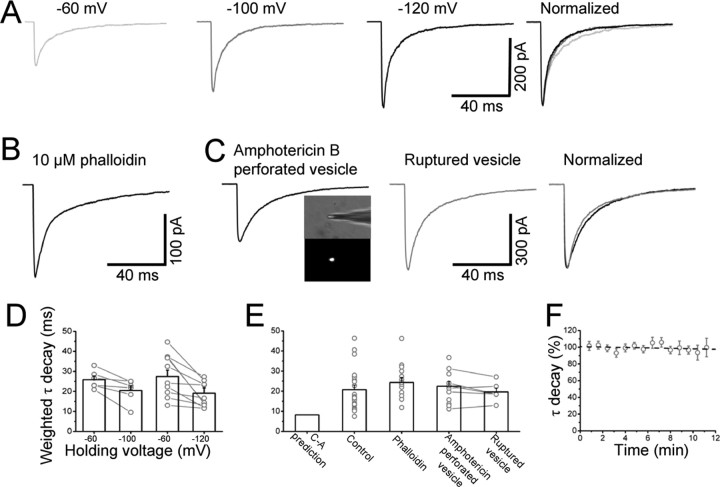
Figure 2.

Slower deactivation in outside-out patches cannot be accounted for by holding potential or cytoskeleton disruption or dialysis of intracellular constituents. A, Responses to 1 ms 3 mm glycine pulses of an outside-out patch held at 3 different holding potentials (averages of 15 sweeps each). The three responses are scaled to the peak response at −120 mV and superimposed in the right panel of A. Decay time is faster at more hyperpolarized potentials, as shown by the bars in D (average values for each condition). Dots joined by lines represent deactivation times obtained in the same patches at different voltages. Even at the highest voltage (−120 mV, D) the deactivation is slower then the cell-attached prediction (shown for comparison in the first column of E). Stabilization of the cytoskeleton induced by dialyzing the cell with 10 μm phalloidin before pulling the patch did not produce any change in the deactivation time (B, average of 15 sweeps and third bar in E). C, Example of a 1 ms 3 mm jump recorded from a vesicle perforated with amphotericin B (average of 12 sweeps). The inset in C shows that the integrity of the vesicle can be monitored by the fluorescence produced by the EGFP trapped inside the vesicle at the tip of the electrode. The time course of the evoked current is similar to that observed in control conditions (E). In pairs of recordings before and after spontaneous vesicle rupture, dialysis of the intracellular medium failed to affect deactivation (C, E). F, Deactivation is stable over time for at least 10 min after excision. Linear fit to the data points of F gave a slope of −0.2%/min and a correlation coefficient r = −0.21, suggesting that even during prolonged recording, such a small drift would not be sufficient to explain the differences in deactivation time.

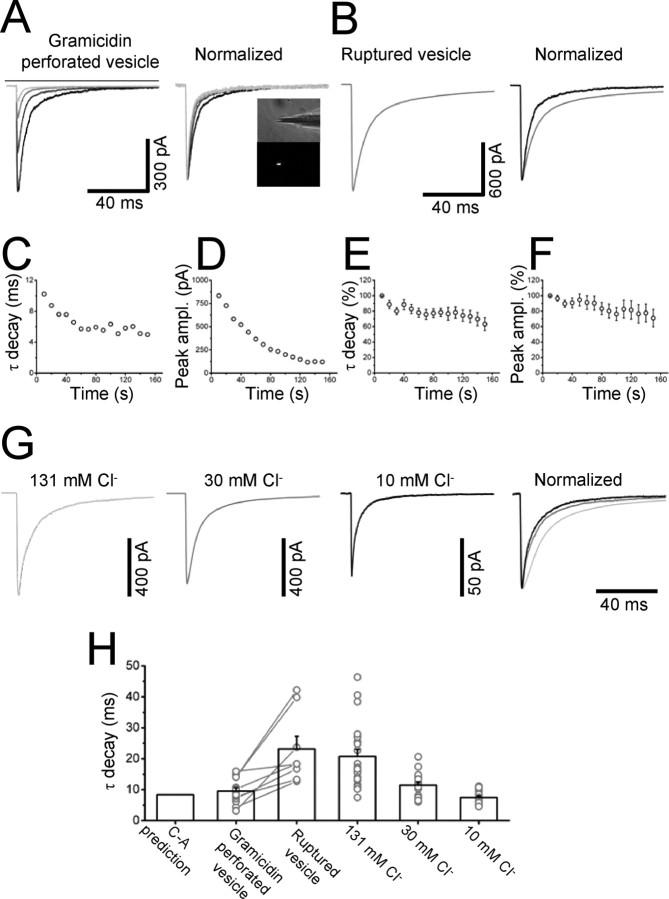
Figure 3.

Low intracellular chloride speeds up the decay time. A, GlyR-mediated currents recorded from perforated vesicles permeabilized with the cation-permeable antibiotic gramicidin D (4 individual responses to a 1 ms 3 mm glycine applications separated by 1 min; successive responses shown as progressively lighter gray lines). Note the gradual decrease in the peak amplitude and the speeding up of the response decay with chloride depletion, shown in C and D for the patch of A. When the vesicle ruptured spontaneously (B), the intracellular chloride concentration was restored and the decay time was prolonged (compare scaled traces before and after rupture on the rightmost panel). Individual values (dots) and their average (bars) are shown in H, by the side of the cell-attached prediction (first column). The average time course of the peak current and decay time for 14 patches is shown in E and F. The effect on both peak and decay was much larger and progressed faster in patches with an initially high current (like the one shown in A), hence the reduced effect on peak and decay when many patches were averaged. Further confirmation of the chloride modulation was obtained by substituting the intracellular chloride with varying amounts of gluconate. Three patches recorded with different intracellular chloride concentrations are shown in G. Average decay time constants at each chloride concentration are represented by the bars in H (dots are individual experiments). The time course of deactivation calculated from the cell-attached rates (first column in H) is between those observed with 10 and 30 mm chloride in the pipette.

Whole-cell and outside-out recordings from motoneurons were performed as described previously (Burzomato et al., 2004; Beato and Sivilotti, 2007). Low resistance electrodes (∼1 MΩ) for whole-cell recordings and high resistance ones (∼6–8 MΩ) for outside-out experiments were filled with an intracellular solution composed of (mm): 140 CsCl, 4 NaCl, 1 MgCl₂, 0.5 CaCl₂, 5 EGTA, 10 HEPES, 2 Mg-ATP, and 3 mm QX-314Cl (pH 7.3 with CsOH). In low-chloride experiments, CsCl was substituted by equimolar concentrations of Cs gluconate, giving a final concentration of 10 mm chloride. Cell-attached determination of the membrane potentials of intact motoneurons was performed by the method of Verheugen et al., (1999), using a high potassium pipette solution composed of (mm): 140 KCl, 2 CaCl₂, 2 MgCl₂, and 5 HEPES (pH 7.3 with KOH).

Recordings were filtered at 5 kHz and acquired online at a 50 kHz sampling rate. Motoneurons were visualized by using infrared differential interference contrast (IR-DIC) and identified by their size (>20 μm soma diameter) and location in the lateral motor column (Takahashi, 1992; Thurbon et al., 1998). Series resistance (4–10 MΩ) was compensated by 60–80%; the maximum uncompensated series resistance in these recordings was 3 MΩ, which would give a low-pass filtering of 265 Hz for an average whole-cell capacitance of 200 pF.

Minimal extracellular stimulation was used, and this was delivered by a constant current stimulator (DS-3 Digitimer Ltd.) through a patch pipette filled with extracellular solution and placed in the ventral region of Lamina VII at the border with the white matter, in which the density of Renshaw cells is highest, 200–400 μm from the recorded motoneuron (see Beato, 2008). Cells were held at −60 mV. Synaptic currents were recorded at −100 mV by delivering a 600 ms hyperpolarizing voltage step during the stimulation. For the experiments in which the same motoneuron was patched twice with different internal solutions, the pipette used for the first patch (either low or high chloride) contained Alexa-488 (50 μm) to enable unequivocal visualization of the patched cell. These pairs of recordings were accepted only if uncompensated series resistance was the same (within 10–20%) for the first and second recording.

Slices were continuously superfused with a combination of 40 μm AP5, 10 μm CNQX (or 5 mm kynurenic acid) and 3 μm SR-95531 to block fast glutamatergic and GABAergic transmission respectively.

All chemicals were from Sigma-Aldrich.

Analysis of single-channel recordings.

Time course fitting (with SCAN software) was used to idealize recordings (10000–15000 transitions per patch). After imposing the resolution (25 μs), dwell-time and fitted amplitude distributions were fitted with the appropriate mixture of exponential or Gaussian curves, respectively (EKDIST software). All of the programs used in our analysis can be obtained from http://www.ucl.ac.uk/Pharmacology/dcpr95.html.

The presence of sublevels in the outside-out configuration is well documented for both native (Bormann et al., 1987; Takahashi and Momiyama, 1991; Beato and Sivilotti, 2007) and recombinant (Bormann et al., 1993; Beato et al., 2002) glycine receptors.

To determine the relative frequency of the different conductance levels, we idealized the whole duration of the recording for each patch (5–20 min) after low-pass filtering at 100 Hz. This allowed us to increase the size of our sample of fitted amplitudes, because high resolution (5 kHz) idealization of 10,000–15,000 transitions correspond to only 5–15 s of single-channel activity.

Fitted amplitude distributions were analyzed only for openings that were long enough to reach full amplitude and not to be attenuated significantly by the filter, i.e., longer than 133 μs (twice the 10–90% risetime of our filter, calculated as 0.3321/f_c, in which f_c is the −3 dB frequency of the filter, here 5 kHz). Histograms of these distributions were fitted with mixtures of Gaussian curves. In all records, the main conductance level (∼40–45 pS) accounted for 96 ± 0.2% of the fitted amplitude distribution. A single sublevel (∼20–25 pS conductance) was detected in all patches and its frequency (5%, see Fig. 4B for a representative example) did not depend on the concentration of glycine. Only clusters and bursts corresponding to the main level were included in the kinetic analysis. All patches in which homomeric channels were detected (identified by their main conductance level of 90 pS) were discarded. For further details, see Burzomato et al. (2004).

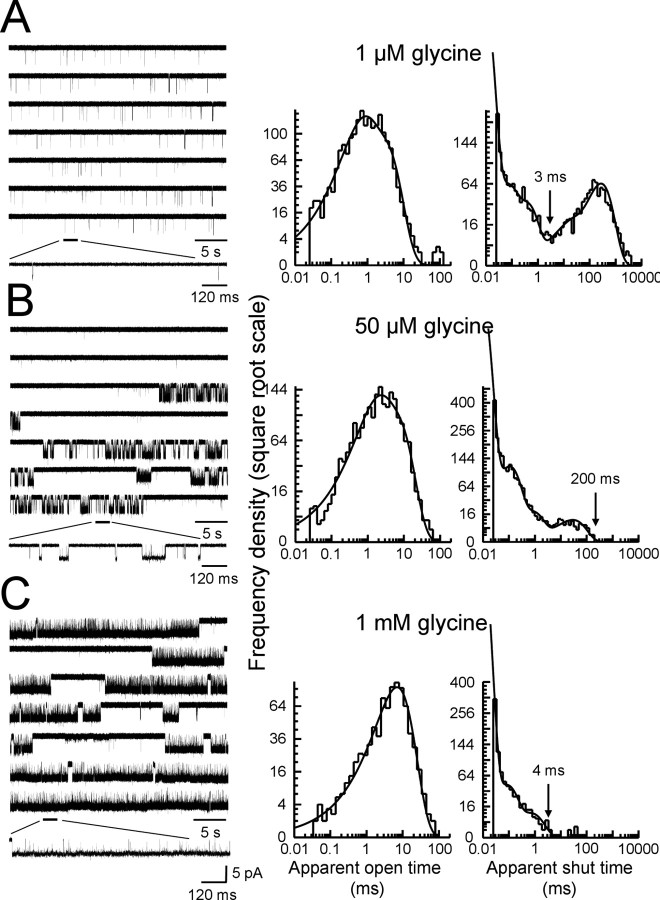
Figure 4.

Single-channel recordings of α1β channels from outside-out patches. The left column of A–C shows continuous sweeps of outside-out recordings at 1 μm, 50 μm, and 1 mm glycine (5 kHz filter, opening downward, holding potential −100 mV). The bottom traces in each block show channel activations on an expanded time scale. Bursts of openings are observed at 1 μm, whereas at higher agonist concentrations bursts group into clusters. Note in the traces in B (sixth row) a cluster of openings of low conductance (see Materials and Methods). The middle and right columns show the empirically fitted dwell-time distributions (apparent open and shut times). Distributions were fitted with a mixture of exponential probability density functions summarized in Table 1. The arrows shown above the shut-time distribution histograms correspond to the imposed value of t_crit for each experiment.

Maximum likelihood fitting.

Maximum-likelihood fitting for the estimate of kinetic rates was performed with the HJCFIT program (Colquhoun et al., 1996, 2003). Idealized recordings were grouped in four independent sets, with each set consisting of three experiments, one at each of the three glycine concentrations tested (1 μm, 50 μm, and 1 mm). All experiments in a set were fitted simultaneously.

Because it is impossible to estimate the number of channels in the patch for our sort of channel, the only data used for global mechanism fits were sequences of events that were likely to reflect the activity of one channel molecule. At high glycine concentrations (50 μm and 1 mm), this means selecting stretches of high P open data (i.e., desensitization clusters): these have to come from a single channel because the P open at these concentration is so high that we would have to see doubles if the activity came from more than one channel (Colquhoun and Hawkes, 1990). At the lower concentration (1 μm), openings occur in bursts. Here we selected (by examining shut-time distributions at different concentrations) a t_crit value such that shut times longer than the t_crit were classified as between burst. This divides the recording into activations (= bursts). These come from a single ion channel and are analyzed as such. The length of shut times that are between bursts is affected by the (unknown) number of channels in the patch, but we make use of some of the information in these shut times by using a special sort of vector (CHS) (Colquhoun et al., 1996) for starting and ending the likelihood calculation for the burst. Effectively these vectors use the fact that the true (one channel) length of the shut times between bursts has got to be at least as long as the one observed in our experiments, in which the possible presence of more than one channel in the patch may shorten them versus the ideal case.

In the fits we used the flip scheme shown in Figure 1C as the kinetic model (Burzomato et al., 2004; Lape et al., 2008). The flip scheme postulates that agonist binding favors a preopening conformational change that is associated with an increase in binding affinity. As described previously (Burzomato et al., 2004), we imposed the constraint that glycine binding affinity should be the same as long as the protein stays in the same conformation (either shut or “flipped”) regardless of how many other binding sites are already occupied (see Fig. 1C).

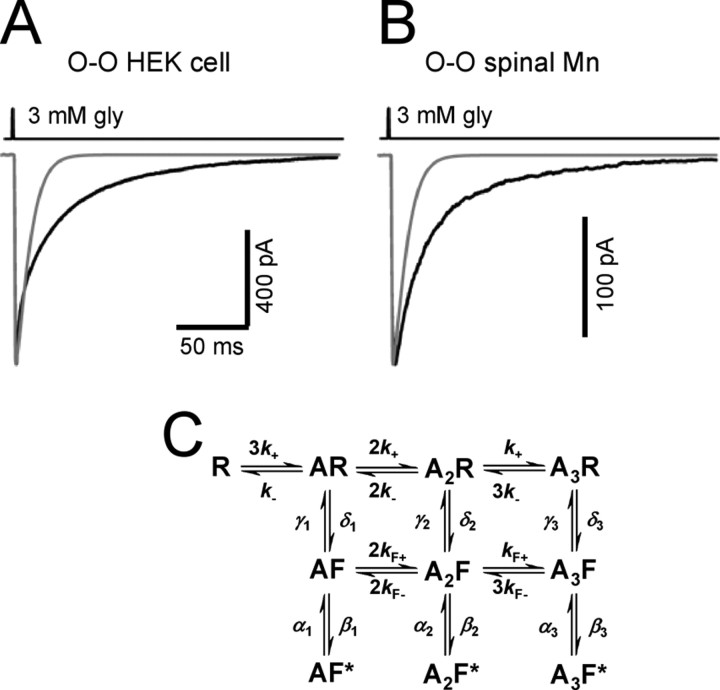
Figure 1.

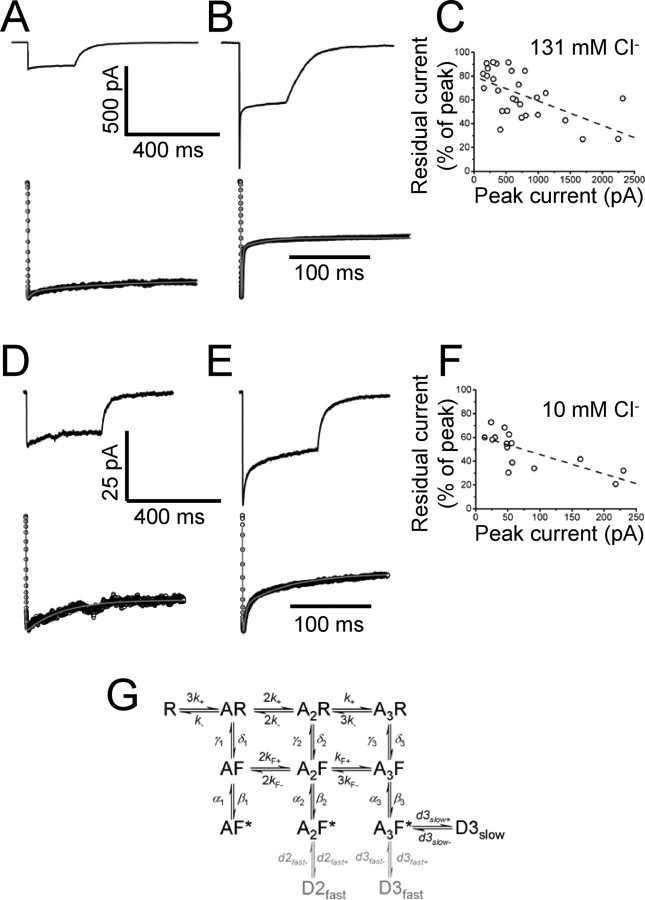
Glycinergic currents deactivate slowly in outside-out patches. The black traces in A and B are current responses to a 1 ms pulse of 3 mm glycine recorded from outside-out patches from HEK293 cell expressing rat recombinant α1β glycine receptors (A, average of 25 sweeps) or from a P10 juvenile rat motoneuron (B, average of 17 sweeps). The time course of glycine concentration (taken from the open tip potential recorded at the end of the experiment) is shown above each trace, and the holding potential was −100 mV. The gray line superimposed in A and B is the current predicted from cell-attached single-channel kinetic rates (Table 2) for the flip model shown in C for the same glycine pulse (1 ms, 3 mm). The flip scheme (adapted from Burzomato et al., 2004) has three equivalent binding sites. Each of the bound resting states R can switch to a flip conformation F, in which the pore is still shut, but agonist affinity (for all sites) is higher than for R states. The channel can open (to F* states) only from the flipped states. The scheme was fitted with the constraint that the affinity for the three binding sites remains the same as long as the protein stays in the same conformation (either shut or “flipped”), regardless of how many other binding sites are already occupied.

The rate constants estimated for the specified mechanism and the resolution were used to calculate the distributions of the apparent open and shut times [Hawkes-Jalali-Calquhoun (HJC) distributions]. The adequacy of the fit was judged by superimposing the distributions calculated from the optimized rate constants to the experimental dwell-times.

Fast concentration jumps and analysis.

All concentration jumps were performed using a theta tube (OD 2 mm, ID 1.7, septum 0.117, 14–072-01, Hilgenberg, Malsfeld, Germany) with the tip cut to a final diameter of ∼150 μm and driven by a piezo-stepper (Burleigh Instruments). Glycine (40 μm, 100 μm, and 3 mm) was washed in or out through the double-barrelled perfusion system. The exchange time was measured by application of a 20% diluted solution before each experiment (to optimize the position of the electrode) and after rupture of the patch. Only those patches in which the 20–80% exchange time was faster than 150 μs were included in the analysis.

Short synaptic-like pulses were obtained by applying to the piezo-stepper a 2 ms voltage command. The resulting fast transient was shorter than 2 ms, but its exact half-width varied for different theta tubes. The average half-width value for the duration of these brief applications for all patches was 1.20 ± 0.07 ms (n = 144, range, 0.6–2.1 ms) and for simplicity they will be referred to as 1 ms jumps.

For recombinant α1β glycine receptors expressed in HEK cells and native glycine receptors in motoneurons, a minimum of 10 individual responses, separated by at least 5 s, were used to generate an ensemble average (patch response). Only those experiments in which the run-down between the average of the first and last three responses in a series was <5% were included in the analysis. The time course of desensitization during long pulses of agonist (200 ms) and that of deactivation after short pulses were well described when fitted with a sum of two or three exponential components. For ease of comparison, weighted time constant values are reported for all of the deactivation responses to short agonist pulses in the text.

Rate constants were determined by using ChanneLab software (Synaptosoft), which optimizes rate constant values by a simplex algorithm. We used the open-tip potential measured at the end of each experiment (scaled appropriately), as an input for the concentration profile. Current traces in response to long glycine pulses (see Fig. 6) were fitted in three stages. First, the model (see Fig. 6 G) was fitted, leaving as free parameters all desensitization entry and exit rates and the association rate constant for binding to the resting states (R). Other rates were fixed to the values obtained in the outside-out single-channel experiments (gating rates) or were constrained by microscopic reversibility. Even if a patch had a fast desensitization component, this first stage adequately described only the slow desensitization, because this accounted for 90–95% of the data points in the fit. Because of that, the first 30 ms were refitted, this time fixing the slow desensitization rates to those from the first stage, to estimate rates for the fast desensitization components. The last stage of the fitting left only the association rate constant free and fitted the risetime of the glycine current. The calculated glycine response (gray in Fig. 6) was obtained from the model together with the rate constants obtained in the different stages and superimposed on the currents for a final check.

Figure 6.

Estimating desensitization in macroscopic patches. A and B show that there is a large patch-to-patch variability in the time course and extent of desensitization. A and B show two averaged current responses to a 200 ms application of 3 mm glycine (high chloride in the pipette, 12 sweeps in A and 17 in B). The response of the patch in A is a small current with little desensitization, whereas the patch in B has a larger current and a high level of desensitization. The plot of C shows the inverse correlation between the peak current amplitude and residual current at 200 ms. Responses in A and B were fitted to the scheme of G with 1 and 3 desensitized states, respectively. The fits are shown below each trace as gray lined superimposed to the experimental points (open circles). The same observations were done in recordings with low (10 mm) chloride in the pipette. D and E show the difference in desensitization among two patches with low (D) and high (E) current. The effect is summarized in the correlation plot of F. Fits with one (D) and two (E) desensitized states are shown below each trace.

All data are expressed as mean ± SD of the mean. For estimated rate constants, we report the mean of estimates obtained from different sets and the coefficient of variation (CV) of the mean across these different sets.

Results

Glycine receptors deactivate slowly in outside-out patches

The black traces in Figure 1, A and B, are the outside-out current responses of glycine receptors to the rapid application of 1 ms pulses of 3 mm glycine. The time course of these responses is very similar for recombinant and native receptors (Fig. 1A,B, respectively) because the weighted time constants were 20.7 ± 2.3 ms and 19.8 ± 1.6 ms for rat α1β receptors from HEK293 cells and for glycine receptors from P10 rat spinal motoneurons, respectively (n = 21 and n = 17; −100 mV holding potential).

The decay of the outside-out responses is nevertheless much slower than that expected on the basis of the activation mechanism that fits our cell-attached single-channel data for this receptor (Fig. 1C). This mechanism, together with the rates we obtained for recombinant or native GlyRs (Burzomato et al., 2004; Beato and Sivilotti, 2007), predicts a much faster exponential deactivation (8.4 ms, gray lines in Fig. 1A,B).

We proceeded systematically to test the effect of different experimental conditions on outside-out GlyR deactivation.

There are many experimental differences between the cell-attached and outside-out configuration. In the cell-attached mode, the environment of the receptor is intact, and we control only the solution and holding potential of the pipette. To obtain single-channel openings that are large enough to ensure good temporal resolution, the pipette holding potential was held at + 100 mV in our cell-attached experiments (Burzomato et al., 2004). This means that the inside of the patch was held at approximately −120 mV, given the normal resting potential of a HEK cell (−10 to −20 mV) (M. Beato, unpublished observations). This potential is more negative than that used for the outside-out experiments of Figure 1.

The row of traces in Figure 2A shows the effect of different holding potentials on the response of outside-out patches to 1 ms pulses of 3 mm glycine. When these responses are scaled to the peak response at −120 mV (black trace) and superimposed (right-hand panel in Fig. 2A), it is clear that the deactivation of glycine currents is faster at more negative potentials (as reported by Legendre, 1999). The extent of this effect is modest. In experiments in which the same patch was held at two different potentials, the weighted decay time constant decreased from 25.8 ± 1.8 ms at −60 mV to 20.4 ± 2.4 ms at −100 mV (n = 6, p = 0.02, paired t test, Fig. 2D) and, in a second set of experiments, from 28.4 ± 3.4 ms at −60 mV to 19.1 ± 2.6 ms at −120 mV (n = 10, p = 0.01, paired t test, Fig. 2D). The deactivation at hyperpolarized potentials, although clearly faster, is therefore still far slower than our cell-attached predictions.

One possibility is that in excised patches, receptor phosphorylation cannot be maintained at the normal, intact cell level. If that was the case, and phosphorylation controls receptor kinetics, we should observe a slow drift in deactivation with time from excision. However, during the lifetime of our outside-out patches (10 min on average), the deactivation time course was remarkably stable, as shown in Figure 2F (n = 19).

Another difference between outside-out and cell-attached patches is that membrane excision probably disrupts the cell cytoskeleton. We can test whether this affects deactivation by stabilizing the cytoskeleton before pulling the patch. When this was done (by dialyzing the cell with 10 μm phalloidin for at least 10 min in whole-cell mode) (Singer and Berger, 1999), there was no change in the deactivation time constant (24.3 ± 2.5 ms, n = 14, −100 mV holding potential) (Fig. 2B,E).

Alternatively, excision may cause the rapid loss of some intracellular diffusible factor from the environment of the receptor, as suggested by Fucile et al. (2000). To stop this process and preserve as much as possible the intracellular milieu, we therefore switched to the perforated vesicle configuration described by Levitan and Kramer (1990) for our concentration jumps.

In designing these experiments, we initially chose amphotericin B as the membrane permeabilizing agent, because it forms pores that are permeable to chloride and therefore can avoid the chloride depletion that would quickly occur in the vesicle with repeated glycine application. The change in intracellular chloride is expected to be substantial. A spherical vesicle with a diameter of 2 μm (the typical size of a recording pipette) would contain ∼80 × 10⁻¹⁸ moles of chloride (if intracellular chloride is 20 mm). A glycine current response with a 10 ms exponential decay and 0.5 nA peak amplitude would carry ∼50 × 10⁻¹⁸ moles of ions.

Glycine patch responses from amphotericin B-perforated vesicles had the same time course as normal outside-out patches (22.4 ± 2.4 ms, n = 12, −100 mV) (Fig. 2C,E). We checked that the vesicle was intact throughout the experiment by frequently monitoring the fluorescence at the electrode tip. EGFP in the cell cytoplasm is enough to make the vesicle interior fluorescent (inset of Fig. 2C), but fluorescence ceases suddenly as EGFP leaks out when either the seal is lost or the perforated side of the vesicle ruptures. In 6 experiments, the vesicle ruptured, turning into a normal outside-out patch. This allowed us to compare deactivation before and after dialysis of the intracellular medium in the same patch. Rupture of the vesicle had no effect on deactivation (20.8 ± 4.5 and 19.6 ± 1.9 ms before and after rupture, respectively n = 6, p = 0.58, paired t test) (Fig. 2C,E).

Intracellular chloride controls GlyR deactivation

In perforated vesicles, the only diffusible intracellular solute that can dialyze through the amphotericin B pores is chloride. Differences in intracellular chloride concentration between the intact cell and outside-out patches are the only candidate left to explain the differences in deactivation. Our outside-out recordings were obtained in symmetrical 131 mm chloride, but intracellular chloride is likely to be much lower in an intact cell. To maintain the intracellular chloride concentration at its physiological levels, one option is to record from vesicles perforated with the cation-permeable antibiotic gramicidin. The results of this experiment are shown in Figure 3A, in which the response to the first application is the black trace and subsequent responses (at 1, 2, and 3 min from the start) are shown as progressively lighter gray traces (−100 mV holding potential).

The response to the first application is much faster than any of the concentration jumps that we have recorded so far, with a weighted decay τ of 10 ms. The average value for this was 9.6 ± 1.1 ms (n = 14; Fig 3H), very similar to the 8.4 ms predicted by our cell-attached model. Most currents (10/14) were best fitted by a single exponential component, as opposed to the 2 or 3 observed in all our other experiments.

As expected, in the gramicidin vesicles, glycine response amplitude decreases with repeated applications, as chloride exits through glycine channels and the driving force for chloride decreases (see the plot of the peak amplitude for this patch in Fig. 3D). When the successive traces are normalized to the peak of the first and superimposed, it becomes obvious that later responses also decay much faster than the first, as the chloride concentration in the vesicle falls. For the vesicle in Figure 3A, the weighted τ of decay speeds up from 10 to 5 ms (Fig. 3C). This pattern was observed in all gramicidin-perforated vesicles (n = 14), and the average trajectory of the decay time and peak amplitude for the 10 perforated vesicles that were held for at least 3 min is shown in Figure 3E and F.

In 8 perforated recordings, the vesicle ruptured and turned into a normal outside-out patch. When this happens, the high chloride (131 mm) pipette solution diffuses into the fluorescent, low chloride content of the vesicle. There is complete loss of fluorescence, together with a sudden increase in the evoked current (as the chloride driving force increases, compare scale of Fig. 3A and 3B) and a dramatic slowing of the response decay, from 9.6 ± 1.7 to 23.1 ± 4.1 ms (n = 8) (Fig. 3B,H).

We next tested whether reducing the pipette chloride concentration in normal outside-out patches reproduced the faster deactivation observed with gramicidin-perforated vesicles. The traces of Figure 3G show three representative experiments: when these are scaled and superimposed (rightmost panel of Fig. 3G), it is clear that reducing the pipette chloride concentration substantially speeds up the decay of the patch response. As summarized in the bar chart of Fig. 3H, the weighted decay time constant decreases from its control value (20.7 ± 2.3 ms, 131 mm chloride) to 11.5 ± 1.0 ms with 30 mm chloride (n = 17) and to 7.5 ± 0.5 ms (n = 16) with 10 mm chloride (cf. the 8.4 ms decay calculated from our cell-attached rates). The nature of the ion used to substitute for chloride in the pipette solution did not appear to be important, because swapping potassium methylsulphate for gluconate (with 10 mm chloride in the pipette) left the decay time of currents unchanged (6.6 ± 0.6 ms, n = 13, data not shown).

These experiments show that differences in intracellular chloride concentration have a major effect on deactivation, speeding it by as much as threefold when chloride is reduced from 131 to 10 mm, i.e., from the high (symmetrical) chloride level often used for recording patch and synaptic currents, to a lower value, close to the intracellular concentration of chloride reported in mature neurons (Kaila, 1994; DeFazio et al., 2000; Coull et al., 2003).

Single-channel kinetics of α1β glycine receptors in the outside-out configuration

The time course of deactivation after a short pulse of saturating agonist is governed by the duration of the burst (Wyllie et al., 1998). In the kinetic scheme for glycine receptors (Fig. 1C), this means either the shutting rates (α), or the unflipping rates (γ) or the unbinding rate (k₋). Because macroscopic currents do not contain enough information to tell us which rates change in high chloride, we resorted to the analysis of outside-out single-channel recordings in the presence of high (symmetrical) chloride concentration.

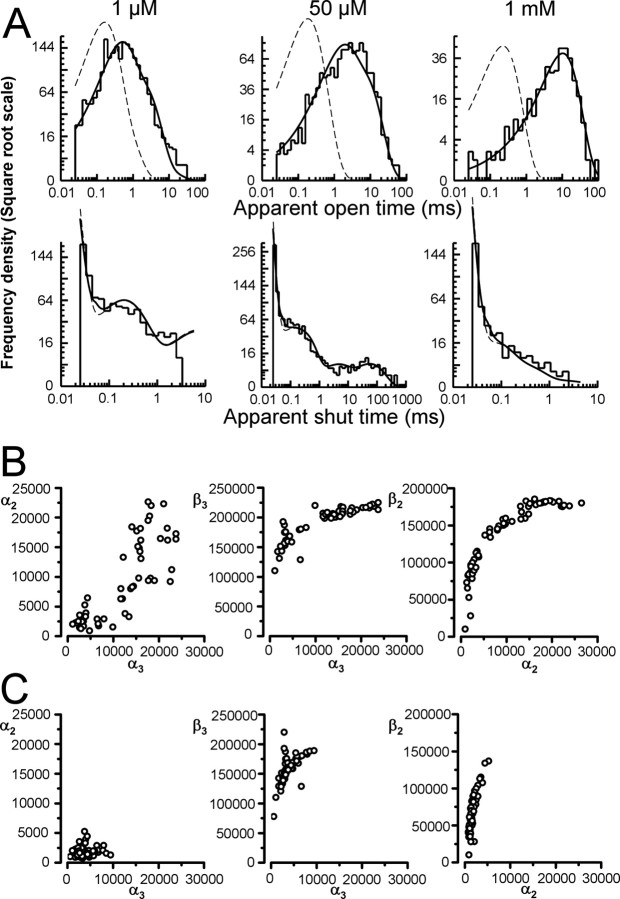
The outside-out recordings on the left of Figure 4 (A–C) are steady-state single-channel currents evoked by 1 μm, 50 μm, and 1 mm glycine (opening downward). The middle and right columns show the corresponding distributions of apparent open and shut times, fitted by mixtures of exponential probability density functions (summary in Table 1). The purpose of this stage of analysis is to identify stretches of events in the recordings that are likely to be the activity of one channel.

Table 1.

Dwell-time distributions

Gly (μm) (n)	τ1		τ2		τ3		τ4		τ5
	τ (ms)	Area (%)	τ (ms)	Area (%)	τ (ms)	Area (%)	τ (ms)	Area (ms)	τ (ms)	Area (ms)
Apparent open periods
1 (4)	0.59 ± 0.03	67 ± 8	2.8 ± 0.2	33 ± 8
50 (4)	1.1 ± 0.1	34 ± 3	5.7 ± 0.1	66 ± 3
1000 (4)			7.3 ± 0.1	100 ± 0
Apparent shut times
1 (4)	0.009 ± 0.001	74 ± 4	0.11 ± 0.01	7 ± 1	0.42 ± 0.03	4 ± 1	8.3 ± 2.6	2 ± 0.4	219 ± 23	16 ± 4
50 (4)	0.008 ± 0.001	91 ± 2	0.12 ± 0.001	7 ± 2	0.63 ± 0.03	1 ± 0.3			46 ± 9	1 ± 0.2
1000 (4)	0.006 ± 0.002	96 ± 1	0.06 ± 0.01	3 ± 1	0.44 ± 0.07	1 ± 0.2

Dwell-time distributions: time constants and relative areas of the exponential components fitted to the open and shut time distributions in the presence of increasing concentrations of glycine. The time constants and their relative areas are given as mean ± SD of the mean.

At the lowest agonist concentration (1 μm) (Fig. 4A, the expanded trace), openings were sparse and occurred in short bursts, each of which is the activation of one channel molecule. The shut time distribution was fitted with five exponential components. As the values of the three faster time constants were similar across different patches at the same concentration and across different concentrations (Table 1), they were classified as “within-burst.” The value of t_crit used to divide recordings into bursts was therefore chosen to be between the third and the fourth component. The criterion of minimizing the total number of misclassified events (Jackson et al., 1983) gave us t_crit values between 2 and 4 ms (arrow in Fig. 4A, right panel).

At higher concentrations of glycine (50 μm and 1 mm), openings occurred in clusters separated by long sojourns in desensitized states (Sakmann et al., 1980; Colquhoun and Ogden, 1988; Takahashi and Momiyama, 1991; Beato et al., 2004; Burzomato et al., 2004). These intervals were too few to be fitted, but were clearly distinct from the much shorter and more numerous intracluster shuttings (Fig. 4B,C). Shuttings longer than 200–500 ms at 50 μm glycine (arrow, Fig. 4B, right panel) or 3–4 ms at 1 mm glycine (arrow, Fig. 4C, right panel) were thus classified as “between clusters.”

The open-time distributions (Fig. 4A–C) were fitted well by one or two exponential components, and the mean apparent open time increased with glycine concentration (Table 1). At the highest concentration (Fig. 4C), when most openings are likely to come from fully liganded receptors, a single exponential fitted the data well. The maximum open probability of the clusters is very high.

Next, we fitted the idealized data with the “flip” scheme to estimate individual rate constants (Burzomato et al., 2004 and Fig. 1C). The results of a typical fit of the “flip” scheme to a set of three patches (one for each concentration, i.e., 1 μm, 50 μm, and 1 mm glycine) is shown in Figure 5A. The top two rows of Figure 5A show the apparent open-time and shut-time distributions: the predicted (HJC) distributions (continuous lines) are shown superimposed to the histograms of the data, to judge the adequacy of the fit (the dashed lines show the distribution predicted if no events were missed). We repeated the fitting procedure for the remaining 9 patches, also grouped in sets of three concentrations. The predicted dwell-time (HJC) distributions were in excellent agreement with the data for all of the four sets fitted.

Figure 5.

Fits of the flip mechanism to the outside-out single-channel data. A shows a simultaneous fit of the flip scheme to a set of outside-out single-channel data at 1 μm, 50 μm, and 1 mm glycine. The HJC distributions calculated from the optimized rate constants are shown superimposed to the experimental distributions of open (top row) and shut (bottom row) times (only shut times shorter than the t_crit are fitted and displayed). The distribution at perfect resolution is plotted as a dashed line. B shows the estimates of the shutting rates obtained from all of the possible sets of three patches (one per glycine concentration). Each of the 64 datasets was fitted with the flip model as shown in Figure 1C. The estimates of the shutting rates could be divided into two groups; high values of α₃ (>10000 s⁻¹) and low values of α₃ (<10000 s⁻¹). C shows the shutting rate estimates for all datasets that initially gave a low α solution combined with datasets that initially gave a high α solution that were refit and forced to converge to a low α solution. The initial guess for α₃ was 3000 s⁻¹, and the search in the parameter space was narrowed to force the values of α to converge to a likelihood peak close to their initial guesses.

For most rates, the values of the estimates from the fits were very consistent across the four sets, with the exception of the shutting rates α₂ and α₃. In three of the four datasets (including the one shown in Fig. 5A), the shutting rates were low, α₂ was 3000 s⁻¹ ± 52% and α₃ was 3300 s⁻¹ ± 14%, whereas the remaining dataset gave an estimate of α₂ and α₃ of 10000 s⁻¹ and 18000 s⁻¹, respectively. The degree of variability for the two shutting rates is larger than what would be expected for rates determined from single-channel records (Colquhoun et al., 2003).

It is possible that this discrepancy is because of a true difference in channel behavior across patches, i.e., that one or all of the three patches in the outlier “high α” set had channels that truly behaved differently, although the dwell-time distributions (as in Fig. 4) showed consistent properties across patches. Therefore, we reshuffled the grouping of the patches into different sets and fitted all possible combinations of three patches at each of the three concentrations (resulting in 64 combinations). The estimates of the shutting rates as shown in Figure 5B (each open circle corresponds to an individual set of three concentrations), could be divided into two groups: 60% of fits resulted in high values of α₃ (>10000 s⁻¹), and 40% resulted in low values of α₃ (<10000 s⁻¹). This was independent of which patches the dataset contained (data not shown). The estimates of α₃ and α₂ were positively correlated (Fig. 5B, left) so that low values of α₃ were associated with low values of α₂ and vice versa. This resulted in two distinct clusters that could be identified in the scatter plot of Figure 5B: one with slow shutting rates (low α solution) and one with fast shutting rates (high α solution). Note that estimates of α and β are also correlated and therefore a high α solution corresponds to higher values of β (Fig. 5B, middle plot and rightmost plot) (Colquhoun et al., 2003; Burzomato et al., 2004).

It has long been known that when events are missed, there are in general two solutions even for the simplest mechanism, i.e., one open and one shut state. Only one solution is real, but the two solutions are equivalent in terms of goodness-of-fit (Hawkes et al., 1990, 1992). In other words, the same simulated observations can be generated by two different sets of rate constants (the fast and the slow solution) (see Ball et al., 1990, and Colquhoun and Hawkes, 1995, p. 456). A similar behavior occurs for the muscle nicotinic receptor. When a realistic mechanism of the muscle nicotinic receptor is used to simulate data that are then fitted by HJCfit (Colquhoun et al., 2003), the fitting can converge to either the true solution or the fast solution and is sensitive to the initial guesses. If it is the two-solution phenomenon that is giving rise to the variability in estimates that we observe, altering the initial guesses should allow us to obtain good fits with a high α solution for each dataset that spontaneously gave a low α solution (and vice versa). All of the 64 combinations were refitted by using low α initial guesses for datasets that originally resulted in a high α solution and vice versa. To narrow the search in the parameter space and to encourage the values of α to converge to a likelihood maximum close to their initial guesses, the contraction factor of the Simplex search algorithm was reduced from the default value of 0.5–0.15 and the initial step size from 5–1.5 (logarithmic scale increment). With these settings, all of the datasets that had initially converged to the high α solution did converge to a low α solution and gave estimates of α₂ and α₃ similar to those obtained from the datasets that had spontaneously converged to a low α solution (Fig. 5C). In 80% of sets, a good agreement of the fit with the experimental data was observed. An example of fits of the same set of 3 experiments to the low and high α solution is shown in supplemental Figure 1, available at www.jneurosci.org as supplemental material.

Work with single-channel steady state simulations with a two-state model (Ball et al., 1990) shows that in those circumstances, the real solution could be distinguished by additional experimental observations (i.e., at a different concentration). We therefore wondered whether we could use the macroscopic data to help us establish the real solution. To our knowledge, this possibility has not been examined in theoretical papers. We proceeded to test whether either of the two sets of rates could give a better description of the outside-out current responses.

Estimating desensitization in macroscopic patches

Before we can integrate the information from concentration jumps with that from single-channel data, we need to characterize macroscopic desensitization, which is thought to affect the shape of current deactivation after even short (1 ms) agonist pulses (Legendre et al., 2002). Our single-channel work does not give us any information on desensitization, because sojourns in desensitized states are excluded from the analysis when records are divided into individual bursts or clusters and shut times longer than t_crit are discarded.

To determine the kinetics of desensitization, current responses to a long (200 ms) saturating (3 mm) glycine pulse were evoked in outside-out patches held at −100 mV in symmetrical chloride conditions (131 mm). In each experiment, a series of at least 10 trials separated by 5 s was used to generate an ensemble average for analysis. Figure 6A and B show that there was large patch-to-patch variability in the amplitude of the currents and in the time course and extent of desensitization. The smallest currents, such as the response in Figure 6A (peak amplitude 140 pA), had fairly modest desensitization that was well fitted by one or two exponential components (13/21 patches). However, the desensitization of larger currents was more substantial in extent and had two or three exponential components (8/21 patches), clearly visible in the response in Figure 6B (peak amplitude 890 pA, time constants of τ₁ = 1.3 ms, τ₂ = 7.4 ms, τ₃ = 83 ms, with relative amplitude of 60%, 24%, and 16%, respectively). As shown in Figure 6C, the extent of desensitization, plotted as the ratio between peak current and residual current at 200 ms, is strongly correlated with the size of the peak current, in agreement with the report that the extent and rate of desensitization of homomeric α1 glycine receptors increase with receptor density (Legendre et al., 2002).

Rate constants that describe the macroscopic currents were determined using ChanneLab software (see Materials and Methods), fitting the flip scheme with the addition of desensitized states (Fig. 6G). Although the slow desensitized state (D3_slow) was always included in the mechanism, the two fast ones (D2_fast and D3_fast, in gray in the scheme of Fig. 6G) were included only when a fast desensitization component was detected (as in the case of the trace of Fig. 6B). Binding and gating rates were fixed to those from single-channel outside-out data (either the low or the high α solutions), leaving only the desensitization rates as free parameters.

The gray lines superimposed to the expanded digitized current traces (open circles) in the bottom rows of Figure 6A and B show a typical fit for two patches with (right) and without (left) fast desensitization (rates fixed to the low α solution). The average entry and exit rates were 126 s⁻¹ ± 29% and 277 s⁻¹ ± 16% (n = 17) for the fully liganded fast desensitized state (D3_fast in Fig. 6G), 79 s⁻¹ ± 24% and 280 s⁻¹ ± 29% (n = 8) for the diliganded fast desensitized state (D2_fast in Fig. 6G). The rates for the slow desensitized state (D3_slow in Fig. 6G) were 11 s⁻¹ ± 21% and 20 s⁻¹ ± 14%. (n = 21). Similar desensitization rates were obtained if high-α solution rates were used to fix binding and gating rates in the mechanism.

Given that the number of channels in the patch is unknown, there is some uncertainty in our single-channel analysis in the determination of the agonist binding rate constant, k₊ (Colquhoun et al., 2003). Fitting the rising phase of long jumps to 3 mm, 100 and 40 μm glycine (see supplemental Fig. 2, available at www.jneurosci.org as supplemental material) gave another estimate of k₊ = 1.0 × 10⁶ s⁻¹·m⁻¹ ±2% (n = 4), a value slightly higher than that from single-channel analysis (0.7 × 10⁶ s⁻¹·m⁻¹ ± 28%, supplemental Table 1, available at www.jneurosci.org as supplemental material). By fixing the value of k₊ to that estimated from the concentration jumps and refitting our single-channel records, we verified that this small correction had no effect on the quality of the fits (supplemental Fig. 2, available at www.jneurosci.org as supplemental material).

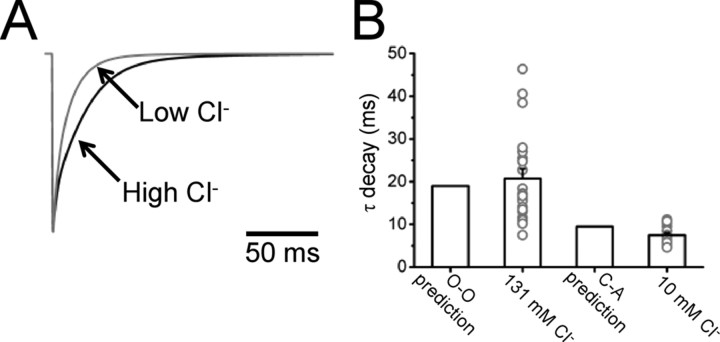
Having established the rates of entry and exit into desensitized states, we used them together with the rates from outside-out patches (in symmetrical chloride at −100 mV) to calculate the deactivation time expected for a brief jump to 3 mm glycine. The predictions obtained with the low and high α solutions were different, and high α solution rates predicted a current response with a decay of 14 ms, much faster than our observed value of 21 ms. However, this experimental value is in good agreement with the 19 ms prediction by the low α rates (see supplemental Fig. 3, available at www.jneurosci.org as supplemental material). This suggests that the solution with high shutting rates α₂ and α₃ is spurious, arises from missed events and was therefore discarded (see supplemental Fig. 3, available at www.jneurosci.org as supplemental material) (Hawkes et al., 1990, 1992; Ball et al., 1990; Colquhoun et al., 2003).

Next, we investigated whether desensitization is also different in low intracellular chloride and repeated the long 200 ms jumps to 3 mm glycine, with 10 mm chloride in the pipette. Two typical traces are shown in Figure 6D and E, one without fast desensitization and the other with. Again, we observed a strong correlation between peak current and the extent of desensitization at steady state (Fig. 6F), confirming the dependence of desensitization on channel density. As before, the flip scheme with the addition of desensitized states (in Fig. 6G) was used to fit the data, but this time the binding and gating rates were fixed to those determined from our cell-attached experiments. Fits of the experimental current traces without or with fast desensitization are shown in the bottom row of Figure 6, D and E. In all cases, one or two desensitized states were sufficient to describe the recorded currents. The average entry and exit rates for these two states were 143 s⁻¹ ± 33% and 198 s⁻¹ ± 22% (n = 13) for the fully liganded fast desensitized state (D3_fast in Fig. 6G). The rates for the slow desensitized state (D3_slow in Fig. 6G) were 9 s⁻¹ ± 22% and 27 s⁻¹ ± 31% (n = 14).

Fits of the rising phase of macroscopic currents using k₊ as a free variable were performed to check whether a correction in the binding rates was needed also for our single-channel cell-attached rates. The average value of k₊ was 0.7 × 10⁶ s⁻¹·m⁻¹ ± 14%. This value is in good agreement with our single-channel estimate (0.6 × 10⁶ s⁻¹·m⁻¹ ± 6%) and therefore no correction was applied to the rates (data not shown).

In both high and low chloride macroscopic currents, a fast desensitization component is always detected in patches with high receptor density and its magnitude increases with the peak current. However, our outside-out single-channel recordings were well described by a scheme that did not include any desensitized state. Dwells in the fast desensitized state have a lifetime of 4–5 ms and would be excluded from the analysis of our low and high glycine concentrations by our choice of a t_crit value of 3–4 ms, but would have been included in the analysis of our recordings at the intermediate concentrations, given the t_crit of 200 ms. The most likely explanation for the apparent contradiction is that recordings selected for single-channel kinetic analysis come from patches with low receptor density, because they are the only ones that allow us to identify isolated clusters (or bursts) of channel activity without double openings. As shown in Figure 6A and D, cells that have a low current and thus have a low receptor density show little or no fast desensitization, explaining the lack of this component in our steady-state single-channel recordings (see also supplemental Fig. 4, available at www.jneurosci.org as supplemental material).

We can now combine our data on desensitization with those from single-channel analysis to calculate the deactivation time course to brief glycine pulses in the presence of low and high intracellular chloride.

This is shown in Figure 7, in which panel A shows the current responses expected for low chloride (calculated from cell-attached rates and low-chloride desensitization; gray trace) (first column of Table 2) and for high chloride (calculated from outside-out single-channel rates and desensitization data with symmetrical chloride; black trace) (second column of Table 2). The expected weighted τ values for the two conditions match very well the experimental observations (see Fig. 7B), showing that steady-state single-channel data yield useful information on the receptor deactivation kinetics (Wyllie et al., 1998).

Figure 7.

Single-channel rates can predict the time course of patch current with both high and low chloride. A shows the response to a 1 ms 3 mm pulse of glycine calculated from the cell-attached rates (including the estimated desensitization rates, gray trace) and from the outside-out rates (including desensitization, black trace). The predicted decay time in the two conditions is compared side by side with the experimental values in the bar chart of B.

Table 2.

Kinetic rate estimates from single-channel fits

	Unit	Cell-attached low chloride (% coefficient of variation of the mean)	Outside-out high chloride (% coefficient of variation of the mean)
α1	s−1	3400 (13)	2000 (11)
β1	s−1	4200 (22)	2900 (51)
α2	s−1	2100 (12)	2400 (5)
β2	s−1	28,000 (17)	89,000 (4)
α3	s−1	7000 (18)	3900 (25)
β3	s−1	129,000 (4)	160,000 (8)
γ1	s−1	29,000 (10)	13,000 (51)
δ1	s−1	180 (24)	120 (11)
γ2	s−1	18,000 (14)	14,000 (10)
δ2	s−1	6800 (6)	4500 (10)
γ3	s−1	900 (26)	3500 (35)
δ3	s−1	20,900 (3)	17,000 (2)
k−	s−1	300 (6)	340 (9)
k+	m−1 · s−1	0.6 × 106 (6)	1.0 × 106(fixed)
kF−	s−1	1200 (12)	1300 (7)
kF+	m−1 · s−1	150 × 106 (5)	160 × 106 (30)
d3slow+	s−1	9 (22)	11 (21)
d3slow−	s−1	27 (31)	20 (14)
d3fast+	s−1	140 (33)	130 (29)
d3fast−	s−1	198 (22)	280 (16)
d2fast+	s−1		79 (24)
d2fast−	s−1		280 (29)
E1		1.3 (21)	1.3 (49)
E2		13 (9)	37 (9)
E3		20 (16)	50 (21)
F1		60 × 10−2 (18)	3 × 10−2 (50)
F2		0.40 (15)	0.30 (16)
F3		27 (31)	8 (33)
KR	μm	520 (12)	350 (9)
KF	μm	8 (14)	13 (46)

Kinetic rate estimates from single-channel fits: Average rate constants (±coefficient of variation of the mean) from the fit of the flip mechanism (Figure 1C) (Burzomato et al., 2004) to four independent sets of single-channel experiments (three concentrations per set) in the outside-out configuration are compared with the rates from Burzomato et al. (2004) (first column). Desensitization rates are estimated from the fits of 200 ms jumps to 3 mm glycine with low or high chloride in the pipette. The efficacies, the equilibrium constants for the flip states (F_n = δ_n/γ_n), and the dissociation equilibrium constants are reported at the bottom of the table.

Intracellular chloride levels affect the time course of glycinergic IPSCs

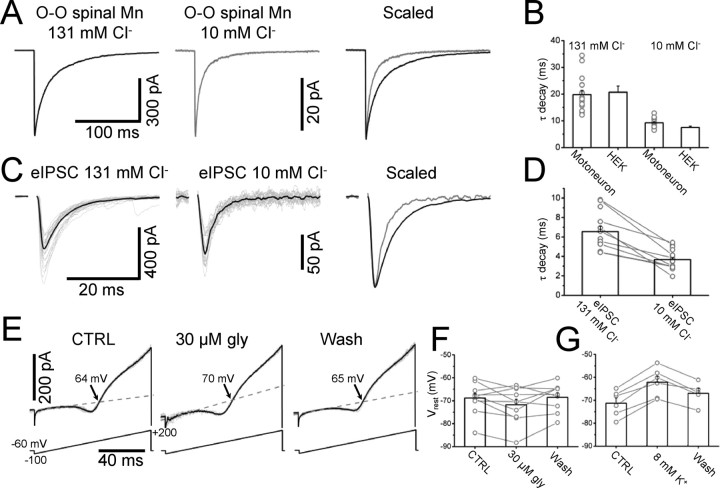
Our data show that the intracellular chloride concentration has a profound impact on the deactivation kinetic of recombinant heteromeric GlyRs. Switching from a near-physiological level (10 mm) to symmetrical chloride conditions (131 mm) slowed deactivation by almost threefold. We proceeded to establish whether intracellular chloride has the same effect on native GlyRs. This is shown in Figure 8A, in which the left and middle traces are responses to fast concentration jumps on patches from spinal motoneurons with high or low chloride, respectively. Comparing the scaled currents shows that, with 10 mm chloride in the pipette, the decay is much faster than at 131 mm chloride, with weighted τ of 9.2 ± 0.4 ms and 19.8 ± 1.6 ms (n = 15 and 17, respectively). These values are very similar to those measured for recombinant receptors (see the bar chart in Fig. 8B), suggesting that native and recombinant receptors behave similarly in this respect.

Figure 8.

The kinetics of both synaptic and extra-synaptic native glycine receptors is modulated by intracellular chloride. Current responses to 3 mm glycine concentration jumps were obtained from outside-out patches excised from P10 rat spinal lumbar motoneurons with high (left) or low (right) chloride in the pipette (A, −100 mV). The decay of the response is much faster when the chloride concentration is low, as shown in B, which also shows that the time constant values measured for native and recombinant receptors are almost identical. C shows that synaptic glycine receptors undergo a similar modulation by intracellular chloride: the same motoneuron was whole-cell clamped first with high chloride then with low chloride solutions in the electrode (left and middle traces, respectively; stimulation artifacts blanked for clarity). The decay time of the evoked IPSCs was almost halved when the cell was dialyzed with 10 mm chloride (bars in D, in which pairs of values from the same cell are shown as circles connected by lines); motoneurons were held at −60 mV and the voltage was stepped to −100 mV for 600 ms as the IPSC was evoked. The resting membrane potential of motoneurons was measured in the cell-attached configuration before and during bath application of glycine. E, Current responses to voltage ramps (in the presence of 0.5 μm TTX). The dashed lines are the extrapolation of the linear fit of the leak current and arrows indicate the reversal potential of the voltage-activated potassium current. Glycine shifted the resting membrane potential to more hyperpolarized values. The normal resting potential was restored after wash (bars in F). The sensitivity of the cell-attached method was confirmed by bath applying 8 mm potassium: the resulting depolarization was detected in all of the cells tested (G).

The final question is whether the intracellular chloride concentration can influence the time course of glycinergic synaptic currents. In symmetrical chloride (131 mm), glycinergic currents from spinal motoneurons decay with a time constant of ∼7 ms at −70 mV (Beato, 2008).

With low intracellular chloride (10 mm), glycinergic IPSCs decay much faster than that, with a time constant of 3.7 ± 0.2 ms (n = 21). With low chloride, eIPSCs had to be recorded at −100 mV, to increase the driving force for chloride, so we repeated our high chloride controls at the same holding potential and confirmed their much slower time course (6.6 ± 0.5 ms, n = 13, p = 16 × 10⁻⁵, unpaired t test).

In a subset of cells (n = 9), we succeeded in obtaining two consecutive whole-cell recordings from the same motoneuron with pipettes containing different internal chloride concentrations. This was done without altering the position of the stimulation electrode or the intensity and duration of the stimulation required to elicit the eIPSC (the initial chloride concentration was low in 6/9 recordings, high in the remaining 3/9). An example of two such recordings from the same cell is shown in Figure 8C for high and low chloride, in which the gray traces are representative individual evoked events and the black trace is the average over >35 sweeps. The scaled and superimposed traces on the right show a striking within-cell difference in the decay time. The bar chart in Figure 8D shows the results of individual experiments. Within this subset of double experiments, the average decay time in high chloride was 6.7 ± 0.7 ms, significantly different from its counterpart in low chloride (3.6 ± 0.4 ms, paired t test, p = 46 × 10⁻⁵).

We also attempted to record eIPSCs in motoneurons using the gramicidin-perforated whole-cell configuration to preserve the physiological concentration of intracellular chloride. The best access resistance that was achieved was 40 MΩ, which with 50% compensation gives a filter cutoff frequency of 40 Hz, too slow for our purposes.

No estimates of the intracellular chloride concentration are available for P10-P14 rat spinal motoneurons. In the dorsal horn of adult animals, the anion reversal potential determined by perforated patch recording is approximately −70 mV (Coull et al., 2003), corresponding to an intracellular chloride concentration of 5–10 mm. We verified that glycine hyperpolarizes juvenile intact motoneurons by measuring their membrane potential by the cell-attached method of Verheugen et al. (1999). Figure 8E shows the current responses to cell-attached voltage ramps: these elicit a potassium current whose reversal potential (arrows) matches the motoneuron potential. The average resting potential (−69 ± 2 mV; n = 10) was slightly hyperpolarized by bath application of 30 μm glycine (to −72 ± 2 mV). This effect was reversed on wash of glycine (to −68 ± 2 mV, bars and individual points in Fig. 8F). As shown in Figure 8G, this method consistently detected the depolarization produced by bath-applied 8 mm potassium (from −71 ± 2 to −62 ± 3 mV, n = 6, some cells different from those used for the glycine experiments). This effect was partly reversed on washout (V_m after wash was −67 ± 2 mV).

With our extracellular solution, a hyperpolarizing effect of glycine can be explained only if the intracellular chloride is lower than 10 mm. Consequently, in an intact neuron, the time course of glycinergic inhibition is faster than is observed in normal whole-cell recordings, in which the cell is usually patched with high chloride internal solution.

Discussion

Recording of current responses to brief saturating agonist applications shows that GlyR deactivation is slower at higher intracellular chloride concentrations. A clear effect is seen when intracellular chloride is increased from 10 to 30 mm, and currents become three times slower in 131 mm (“symmetrical”) chloride. This effect is identical for recombinant heteromeric α1β GlyRs and for native GlyRs from rat juvenile motoneurons. In whole-cell recordings from neurons, the choice of chloride concentration in the pipette internal solution affects the time course of decay of glycinergic synaptic currents.

Concentration jumps are a common tool for studying the kinetic properties of synaptic ligand-gated channels in a more controlled environment. However, the outside-out configuration has the disadvantage that it disrupts the intracellular environment.

We have previously shown that the rates of activation determined for GlyRs from cell-attached experiments, in which the environment of the receptor should be intact, predict a fast decay time constant (∼8 ms) after a short pulse of agonist. This is in sharp contrast with the ∼20 ms observed in outside-out experiments for both recombinant (Mohammadi et al., 2003, present study) and native (Singer and Berger, 1999) receptors.

The perforated vesicle configuration is a particularly useful technique for addressing these differences because it allowed us to perform fast applications to patches in which the intracellular medium was unaltered, except for the ions that go through the pores formed by the perforating antibiotic. When amphotericin is used, anions are free to diffuse into the vesicle from the high-chloride pipette solution, and the time course of glycine currents is as slow as in normal outside-out recordings. In contrast, when cation-permeable gramicidin is used, at the beginning of the experiment the chloride concentration in the vesicle is close to that in the intact cell and the deactivation we measured is very similar to that predicted by our cell-attached experiments.

All of the other factors, such as exact transmembrane voltage, level of phosphorylation, or cytoskeleton proteins, had little or no effect compared with intracellular chloride.

The site of action of chloride

Observing such a large effect of chloride on the kinetic properties of GlyR was an unexpected finding, and there is little in the literature that examines chloride other than as a permeant ion for this channel.

From our data it is impossible to tell whether chloride acts by binding directly to GlyRs or by modulating the activity of another target upstream of the receptor, such as a G-protein. Chloride concentrations in the physiological range are known to modulate the activity of G-proteins (Higashijima et al., 1987), an effect that may explain the reduction in I_h currents and GABA_B responses produced by high intracellular chloride in hippocampal neurons (Lenz et al., 1997).

A direct effect of chloride on the channel protein itself is also possible. Modulation by chloride of a ligand-gated ion channel was recently described for kainate receptors (Plested and Mayer, 2007; Plested et al., 2008), in which the GluR6 extracellular domains contain binding sites for chloride and sodium, whose occupancy affects receptor desensitization. As Plested and Mayer (2007) point out, binding of chloride is necessary for the appropriate function of retinal red and green pigments (G-protein linked receptors, Wang et al., 1993). Structural binding motifs and apparent affinities for chloride are very different in these proteins, and this makes it difficult to guess where a putative binding site may be in GlyRs. It is nevertheless interesting to note that the intracellular loops of GlyR α subunits (and other nicotinic superfamily receptors) contain many positively and negatively charged amino acids in adjacent positions, resembling the Arg-Asp-X-X-Thr motif that complexes chloride in GluR6.

The effect of chloride on channel kinetics

Our single-channel analysis reveals that gating is profoundly affected by high chloride, whereas agonist binding is unaltered. The main change is a twofold slowing of the shutting rate. This is associated with a smaller increase in the opening rate and is somewhat (but not totally) balanced by an increase in the unflipping rate, which leads the channels away from their activated states. The overall effect of high chloride on the maximum P_open (when the receptor is saturated by glycine) is a slight increase (from 0.95 to 0.98), negligible given the very high maximum P_open of this channel. The twofold change in the shutting rate has nevertheless major consequences on the kinetics of deactivation, a process that determines the time course of synaptic currents (Wyllie et al., 1998).

Intracellular chloride and the IPSC time course

Our results show that the decay time constant of the evoked glycinergic IPSCs slows from 3 to 7 ms when we increase intracellular chloride in a single motoneuron by whole-cell recording with increased chloride in the pipette solution. The slower time constant of 7 ms is in agreement with reported measurements for evoked or spontaneous IPSCs, values that were obtained with high pipette chloride, which is used to increase the driving force at the normal holding voltage between −60 and −70 mV. Surprisingly, we show that when physiological concentrations of chloride are used, the decay of glycinergic synaptic currents can be as fast as 3 ms. This is still considerably faster than expected from the time course of patch responses to brief agonist application in 10 mm chloride (7 ms). Possible explanations for this discrepancy include subtype differences between synaptic GlyRs and the extrasynaptic GlyRs sampled by outside-out patches (as seen for GABA by Mellor and Randall, 1997; Banks and Pearce, 2000; Farrant and Nusser, 2005; Schofield and Huguenard, 2007) and the presence of anchoring proteins at the synapse. It is also possible that transmitter transients in the cleft are much shorter than the 1 ms that can be achieved by fast application techniques (as suggested for GABA by Mozrzymas et al., 2007). Note, however, that the glycine transient at motoneuron synapses is not faster than 0.6 ms (Beato, 2008). Finally, the decay of midbrain glycinergic synaptic currents is now known to be speeded up by corelease of glycine and GABA, because GABA acts as a low affinity, weak partial agonist of GlyRs (Lu et al., 2008), and a similar phenomenon could occur in the spinal cord.

Our findings indicate that in intact neurons, GlyR-mediated IPSCs have a much faster time course than is generally believed. This is because intracellular chloride in adult neurons is low, as demonstrated by the fact that in most mature systems the reversal potential for chloride is very close to the resting potential of the cell or slightly hyperpolarized (Staley and Smith, 2001; Ben-Ari, 2002).

The time course of the synaptic current is important because it determines the duration of the time window during which glycine inhibition is effective on the neuron. Indeed, the network dynamics of neuronal circuits depends on both the relative strength of synaptic excitation and inhibition and their relative speed, namely the decay time of the synaptic currents (Brunel and Wang, 2003).

Our data also show that a slowing in the GlyR deactivation time constant is detectable for smaller changes in intracellular chloride (from 7 to 11 ms when chloride was increased from 10 to 30 mm). This opens the possibility that glycinergic inhibition is affected also by increases in intracellular chloride associated with short-term changes in neuronal activity or with pathological conditions such as epilepsy and neuropathic pain (Kaila, 1994; Staley and Smith, 2001; Cohen et al., 2002; Coull et al., 2003; Lamsa and Taira, 2003).