Properties of Two Human Atrial Cell Models in Tissue: Restitution, Memory, Propagation, and Reentry

Abstract

To date, two detailed ionic models of human atrial cell electrophysiology have been developed, the Nygren et al. model (NM) and the Courtemanche et al. model (CM). Although both models draw from similar experimental data, they have vastly different properties. This paper provides the first systematic analysis and comparison of the dynamics of these models in spatially extended systems including one-dimensional cables and rings, two-dimensional sheets, and a realistic three-dimensional human atrial geometry. We observe that, as in single cells, the CM adapts to rate changes primarily by changes in action potential duration (APD) and morphology, while for the NM rate changes affect resting membrane potential (RMP) more than APD. The models also exhibit different memory properties as assessed through S1–S2 APD and conduction velocity (CV) restitution curves with different S1 cycle lengths. Reentrant wave dynamics also differ, with the NM exhibiting stable, non-breaking spirals and the CM exhibiting frequent transient wave breaks. The realistic atrial geometry modifies dynamics in some cases through drift, transient pinning, and breakup. Previously proposed modifications to represent atrial fibrillation-remodeled electrophysiology produce altered dynamics, including reduced rate adaptation and memory for both models and conversion to stable reentry for the CM. Furthermore, proposed variations to the NM to reproduce action potentials more closely resembling those of the CM do not substantially alter the underlying dynamics of the model, so that tissue simulations using these modifications still behave more like the unmodified NM. Finally, interchanging the transmembrane current formulations of the two models suggests that currents contribute more strongly to RMP and CV, intracellular calcium dynamics primarily determine reentrant wave dynamics, and both are important in APD restitution and memory in these models. This finding implies that the formulation of intracellular calcium processes is as important to producing realistic models as transmembrane currents.

Introduction

Mathematical modeling of the electrophysiology of cardiac cells and simulation of isolated and coupled myocytes have become an increasingly important approach to studying the electrical dynamics of cardiac cells and tissue. Although models have been used for several decades, the number of mathematical models of cardiac cell electrophysiology has grown rapidly over the past decade. Using currents measured from whole cells or ion channels, it has been possible to formulate models for individual species and specific regions of the heart. However, the growth in the number of available models has resulted in the independent development of multiple models for the same species and heart region, such as canine ventricular (Winslow et al., 1999; Fox et al., 2002; Cabo and Boyden, 2003; Hund and Rudy, 2004; Greenstein et al., 2006), human ventricular (Priebe and Beuckelmann, 1998; Iyer et al., 2004; Ten Tusscher et al., 2004, 2006), and human atrial models (Nygren et al., 1998; Courtemanche et al., 1998).

In this manuscript, we focus on the two models of human atrial cell electrophysiology, the Nygren et al. (1998) model (NM) and the Courtemanche et al. (1998) model (CM). The two models include formulations of the same 12 transmembrane currents and were derived largely from similar human atrial current data. A central question is the degree to which the two models show similar properties. This issue has been addressed in detail for isolated myocytes (Nygren et al., 2001; Cherry et al., 2008). However, thorough tissue-level comparisons have not yet been performed, although it is well known that electrotonic effects in tissue can alter isolated cell behavior, and new properties, such as propagation and reentry, emerge only in tissue and currently cannot be predicted from properties of isolated cells. Simulations of spiral waves using the two models have been performed and have found that the NM gives rise to stable spiral waves (Nygren et al., 2001; Biktasheva et al., 2002), but dynamics reported for the CM have been in disagreement, with rapid extinction, stable spirals, and breakup all having been reported (Nygren et al., 2001; Biktasheva et al., 2002; Xie et al., 2002).

To assess the degree of similarity between the NM and the CM, we analyze the emergent tissue-level properties of action potential duration (APD) and conduction velocity (CV) restitution, memory, and reentry in one, two, and three dimensions. We analyze the original models as well as variants previously proposed to improve agreement of the model in single cells. We also address the behavior of the models when channel conductances are modified to simulate the electrophysiological remodeling accompanying long-term atrial fibrillation. Finally, we investigate the effects of interchanging the transmembrane current formulations of the two models and discuss the implications of these results for the roles of ionic currents and intracellular calcium dynamics on the dynamic properties of these models.

Methods

Model implementation

The two models incorporate the same twelve transmembrane currents (the ultra-rapid delayed rectifier K⁺ current I_Kur of the CM and the sustained K⁺ current I_sus of the NM are derived from similar data and thus for consistency will be referred to as I_Kur throughout), but include structurally different formulations for intracellular calcium dynamics, with that of the NM based on the Lindblad et al. (1996) rabbit atrial model and that of the CM based on the Luo-Rudy 2 model (Luo and Rudy, 1994). The basic NM and CM were implemented as described by Nygren et al. (1998) and Courtemanche et al. (1998), with a few minor exceptions. For the NM, the voltage differential equation was corrected to include the rapid and slow components of the delayed rectifier current (I_Kr and I_Ks), the calcium diffusive current I_di in the differential equation of the subsarcolemmal space calcium concentration [Ca²⁺]_d was corrected to have a positive sign, and the value of the parameter k_Ca was corrected to 0.025 mmol/L. In addition, as discussed by Cherry et al. (2008), the electroneutral Na⁺ influx term Φ_Na,en of the original model was not used and instead the stimulus current was assigned a charge carrier, as suggested by Hund et al. (2001), to reach ionic homeostasis at a pacing frequency of 1 Hz (the current integral of Φ_Na,en was equal to that of the stimulus current). For the CM, the concentrations [Na⁺]_i and [K⁺]_i both drifted slowly over time in a linear fashion without reaching a steady state, and assigning a charge carrier for the stimulus current did not eliminate the drift. Thus, these concentrations were held fixed throughout all simulations. The capacitance was set to 1 µF/cm2 in all cases to minimize effects of cell size.

Model variants

Along with the original specifications of the models, several variants are used. For the NM, in one variant all ionic concentrations except for intracellular calcium [Ca²⁺]_i are held fixed to a constant value; this model is referred to as the NMf. Another set of variants is created by implementing a set of changes proposed by Nygren et al. (2001) to produce in the NM a spike-and-dome action potential similar to the CM. In these variants, the currents I_Ca,L, I_to, I_Kur, I_Kr, and I_Ks are multiplied by factors of 1.33, 2, 0.4, 3, and 3, respectively, producing the NM-C and NMf-C when ionic concentrations are allowed to vary or held fixed as specified above. The inverse of these changes applied to the CM results in the CM-N variant. A later set of changes proposed by Syed et al. (2005) to reconcile the two models is also investigated. In this variant, concentrations are held fixed as described above and the current magnitudes are multiplied by the following factors: I_Na, 0.938; I_Ca,L, 1.37; I_to, 2.07; I_Kur, 0.196; I_Kr, 1.56; I_Ks, 1.50; I_K1, 1.07, I_Na,b, 1.02; and I_Ca,b, 1.02. This variant is referred to as the NMf-C2.

Changes to simulate electrophysiological remodeling as a result of atrial fibrillation also can be included in the models by modifying the conductances of several currents, as described by Courtemanche et al. (1999). Specifically, I_Ca,L is multiplied by 0.3, and both I_to and I_Kur are multiplied by 0.5. The resulting variants are referred to as the CM-AF, NM-AF, and NMf-AF.

A final set of variants is implemented by exchanging the transmembrane current formulations of the two models, specified as current densities. Thus, the CM-X uses the intracellular calcium handling of the CM combined with the transmembrane current descriptions of the NM. Likewise, the NM-X and NMf-X combine the transmembrane currents of the CM with the NM calcium handling and, for the NM-X, intracellular and cleft space ionic concentration descriptions. In the CM-X, the extracellular concentrations were used in place of the extracellular cleft space concentrations, and the intracellular Ca²⁺ concentration was used in place of the restricted subsarcolemmal space Ca²⁺ concentration, because the CM (and hence the CM-X) does not include this concentration. In the NM-X and NMf-X, the extracellular cleft space concentrations were used for the extracellular concentrations.

Table 1 lists the different model variants and brief descriptions for each. The published initial conditions for the CM (Courtemanche et al., 1998) were used for the CM, CM-N, and CM-AF, while the published initial conditions for the NM (Nygren et al., 1998) were used for the NM, NMf, NM-C, NMf-C, NMf-C2, NM-AF, and NMf-AF. Initial conditions for the CM-X, NM-X, and NMf-X were obtained after pacing for several minutes in a single cell with a CL of 1 s.

Table 1. Abbreviations and descriptions of the model variants used.

Abbreviation	Model Variant Description
NM	Nygren et al. model
NMf	Nygren et al. model with the following concentrations held constant: [K+]i, [K+]c, [Na+]i, [Na+]c, [Ca2+]c
NM-C	Nygren et al. model with ICa,L multiplied by 1.33, Ito by 2, IKur by 0.4, IKr by 3, and IKs by 3 (from Nygren et al., 2001)
NMf-C	Nygren et al. model with ICa,L multiplied by 1.33, Ito by 2, IKur by 0.4, IKr by 3, and IKs by 3 (from Nygren et al., 2001) and with the following concentrations held constant: [K+]i, [K+]c, [Na+]I, [Na+]c, [Ca2+]c
NMf-C2	Nygren et al. model with INa multiplied by 0.938, ICa,L by 1.37, Ito by 2.07, IKur by 0.196, IKs by 1.50, IKr by 1.56, IK1 by 1.07, INab by 1.02, and ICab by 1.02 (from Syed et al., 2005) and with the following concentrations held constant: [K+]i, [K+]c, [Na+]i, [Na+]c, [Ca2+]c
NM-AF	Nygren et al. model with ICa,L multiplied by 0.3, Ito by 0.5, and IKur by 0.5 (from Courtemanche et al., 1999)
NMf-AF	Nygren et al. model with ICa,L multiplied by 0.3, Ito by 0.5, and IKur by 0.5 (from Courtemanche et al., 1999) and with the following concentrations held constant: [K+]i, [K+]c, [Na+]i, [Na+]c, [Ca2+]c
NM-X	Nygren et al. model formulations of ionic concentrations and calcium handling combined with the 12 transmembrane currents of the Courtemanche et al. model
NMf-X	Nygren et al. model formulations of calcium handling combined with the 12 transmembrane currents of the Courtemanche et al. model and with the following concentrations held constant: [K+]i, [K+]c, [Na+]i, [Na+]c, [Ca2+]c
CM	Courtemanche et al. model with [K+]i, [Na+]i held fixed
CM-N	Courtemanche et al. model with ICa,L divided by 1.33, Ito by 2, IKur by 0.4, IKr by 3, and IKs by 3 (from Nygren et al., 2001) and with [K+]i, [Na+]i held fixed
CM-AF	Courtemanche et al. model with ICa,L multiplied by 0.3, Ito by 0.5, and IKur by 0.5 (from Courtemanche et al., 1999) and with [K+]i, [Na+]i held fixed
CM-X	Courtemanche et al. model formulations of calcium handling combined with the 12 transmembrane currents of the Nygren et al. model and with [K+]i, [Na+]i held fixed

APD restitution curve measurement

Both steady-state and S1–S2 APD restitution curves are calculated using one-dimensional cables and rings. Steady-state restitution curves (also known as dynamic restitution curves (Koller et al., 1998)) are obtained by pacing at each of a range of CLs for a fixed amount of time (30 seconds) and recording the last APD and the preceding DI (or the last two APDs and their preceding DIs when stable alternans are present). S1S2 restitution curves are computed by pacing for 30 seconds at a fixed CL (S1) and then introducing a single subsequent stimulus over a range of intervals (S2); the APD following each S2 stimulus and the preceding DI are recorded to generate a curve that in general is dependent on S1. The S1S2 protocol therefore produces a family of curves for different values of S1 and can be used to quantify memory (Cherry and Fenton, 2007). Measurements were performed in tissue to account for electrotonic currents, to obtain the minimum DI for propagation, and to avoid the influence of the stimulus current magnitude, as explained further in Cherry and Fenton (2004) and Bueno-Orovio et al. (2008).

Because the resting membrane potential and action potential amplitude (APA) can vary substantially among the models and as a function of cycle length (CL) (Cherry et al., 2008), specific model-dependent voltage thresholds are used to measure APDs and DIs. For the steady-state restitution curves, the threshold is set to the voltage value that defines 90 percent of repolarization for each CL used. For the S1S2 restitution curves, the threshold is set to the voltage value that defines 90 percent of repolarization for the S1 CL. In this way, the specific voltage threshold is allowed to vary in response to changes in CL that affect APA.

For the NM and its variants, a true steady state generally was not reached within 30 seconds or longer, as described previously (Cherry et al., 2008). Thus, for consistency, the initial conditions were set to the original initial conditions specified by Nygren et al. (1998) for each CL tested, and the APDs and DIs obtained after 30 seconds of pacing were recorded.

CV restitution curve measurement

CV restitution curves are measured using the same protocols as for the APD steady-state and S1S2 restitution curves. In each case, CV is measured between adjacent points using a fixed voltage threshold during the AP upstroke. The resulting CV values are plotted as a function of the DIs computed for the APD restitution curves obtained using the same CL. Differences in S1S2 CV restitution curves depending on the S1 CL indicate the presence of memory in CV (Bueno et al., submitted).

Spiral and scroll wave initiation and trajectory tracking

Spiral and scroll waves were initiated using a cross-stimulation protocol. Spiral waves and their trajectories were then tracked for 60 s in all cases except for the NM-AF and NMf-AF, where they were tracked for 90 s. In the three-dimensional realistic anatomy, scroll waves were always initiated in the left atrial free wall and were tracked for a minimum of 10 s or until termination. Trajectories were tracked using the zero-normal velocity method of Fenton and Karma (1998) with voltage contours between −65 and − 30 mV, depending on the model. In the realistic human atrial geometry, the thin atrial wall kept endocardial and epicardial dynamics nearly identical, and thus filament trajectories are shown only as their projections on the epicardial surface.

Numerical methods

The equation solved in tissue was the monodomain formulation ∂_tV = Δ(DΔV) −I_ion / C_m, where V is the transmembrane voltage, D is the diffusion tensor (here equivalent to a constant coefficient as the tissue was isotropic), C_m is the membrane capacitance, and I_ion is the ionic current specified by the model formulation used in each case. The diffusion coefficient was set to 0.001 cm²/s, following Xie et al. (2002), which also produced a conduction velocity for the NM similar to that shown by Nygren et al. (2001).

Spatial resolution generally was 0.025 cm, the same as that of Xie et al. (2002) and slightly coarser than that of Nygren et al. (2001) and were verified not to change significantly with increased resolution; some two-dimensional simulations were performed with finer spatial resolution to investigate whether wave dynamics were affected by resolution. The human atrial anatomy developed by Harrild and Henriquez (2001) was implemented on a uniform mesh at a spatial resolution at 0.025 cm using the phase-field method (Fenton et al., 2005). The equations for voltage and ionic concentrations in the models were computed using forward Euler, and the scheme of Rush and Larsen (1978) was used to integrate the gating variables. Precomputed lookup tables were created for exponentials and other time-consuming functions of a single variable (such as voltage or calcium) to improve computational efficiency ( et al., 1985).

Results

Restitution, memory, and propagating delayed afterdepolarizations

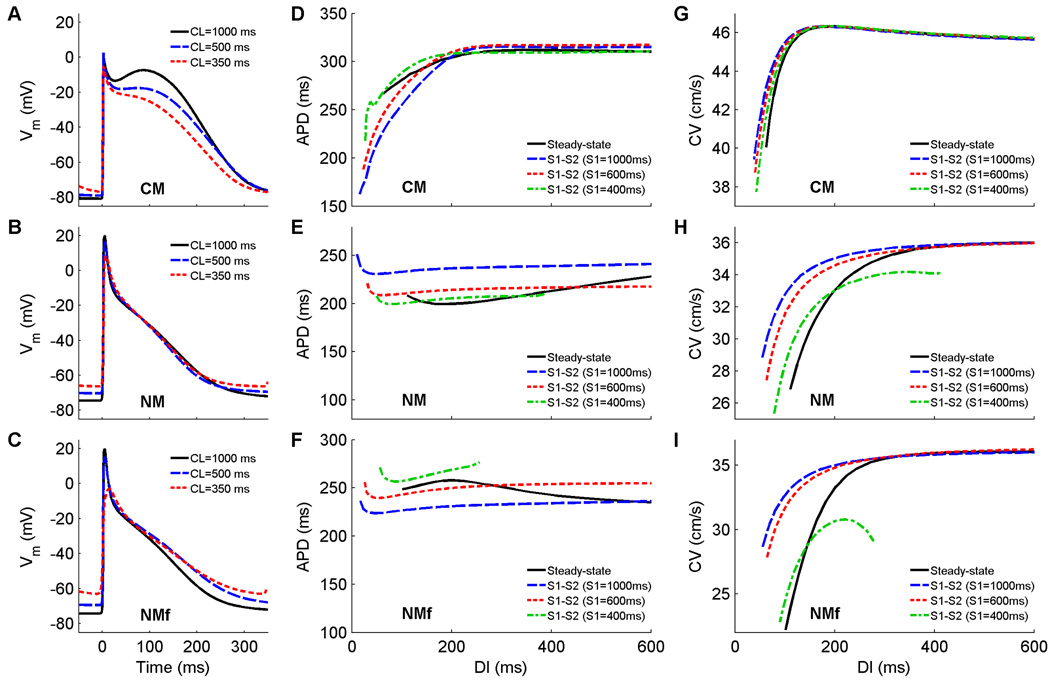
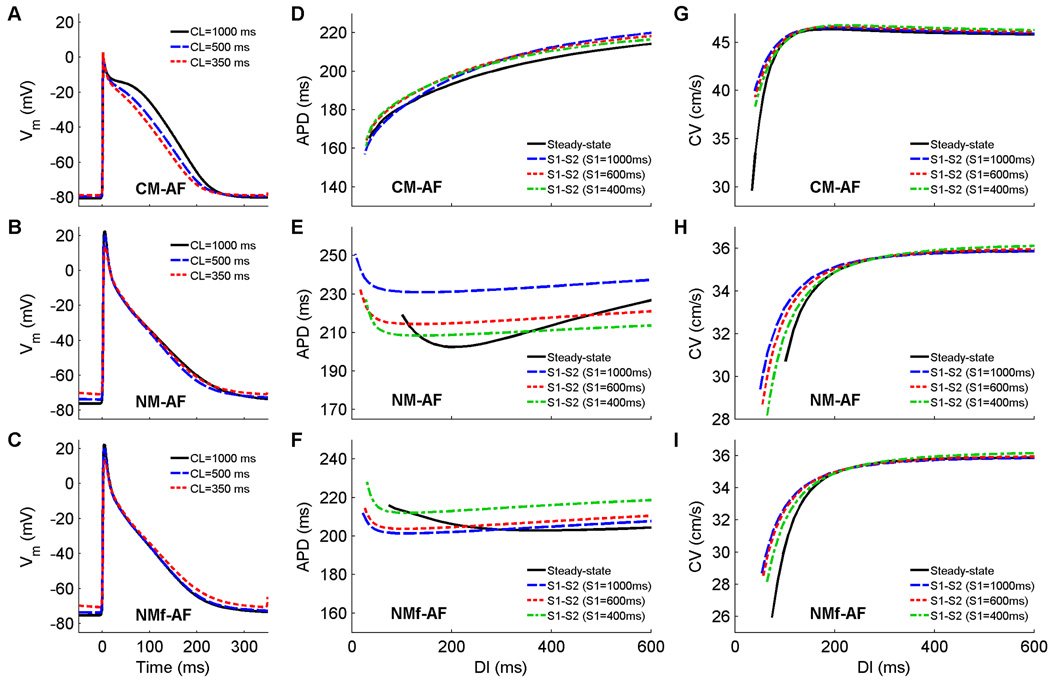
The CM and NM from the beginning assume different action potential morphologies: the NM uses a triangular shape, while for the CM spike-and-dome APs occur for long CLs and transition to triangular when paced more rapidly. Figure 1A–C shows action potentials at three different CLs for the CM, NM, and NMf. As expected, the CM shows a pronounced notch at a CL of 1000 ms, while the notch essentially disappears when the CL is decreased to 500 ms and a triangular shape is present at 350 ms (Fig. 1A). Despite substantial differences in plateau voltage, the durations of the APs do not vary much, although the maximum APD of the CM is around 300 ms, much longer than the maximum APDs of the NM and NMf.. The NM and NMf both exhibit triangular action potentials whose durations remain nearly constant with changes in CL. However, the NMf exhibits a slight prolongation of APD as the CL is decreased from 1000 ms to 350 ms. Both the NM and NMf show a moderate increase in resting membrane potential (RMP) as the CL is decreased from 1000 ms to 350 ms (8 and 11 mV, respectively), an effect that is much smaller for the CM (4 mV).

Figure 1.

A–C Action potentials at cycle lengths of 1000, 500, and 350 ms using the CM, the NM, and the NMf. Compared to isolated cell APs, the upstroke amplitude is decreased about 30 mV owing to electrotonic effects. All APs have been shifted in time slightly so that the upstrokes align at time=0 ms to allow better comparison. All traces are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm). D–F Restitution of APD₉₀ measured in a 1d cable for the CM, the NM, and the NMf. Steady-state restitution curves (solid lines) obtained after pacing for 30 seconds at each CL until 2:1 block was reached are shown along with S1–S2 restitution curves obtained after 30 seconds of pacing at three different S1 CLs over a range of premature S2s. Note that although the ranges of APDs vary among the curves, the scaling used is identical. Data points are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm). G–I. Restitution of conduction velocity measured in a 1d cable for the CM, the NM, and the NMf. Both steady-state restitution curves (solid lines) and S1–S2 restitution curves are shown and indicate little CV memory for the CM but more substantial memory for the NM and NMf.

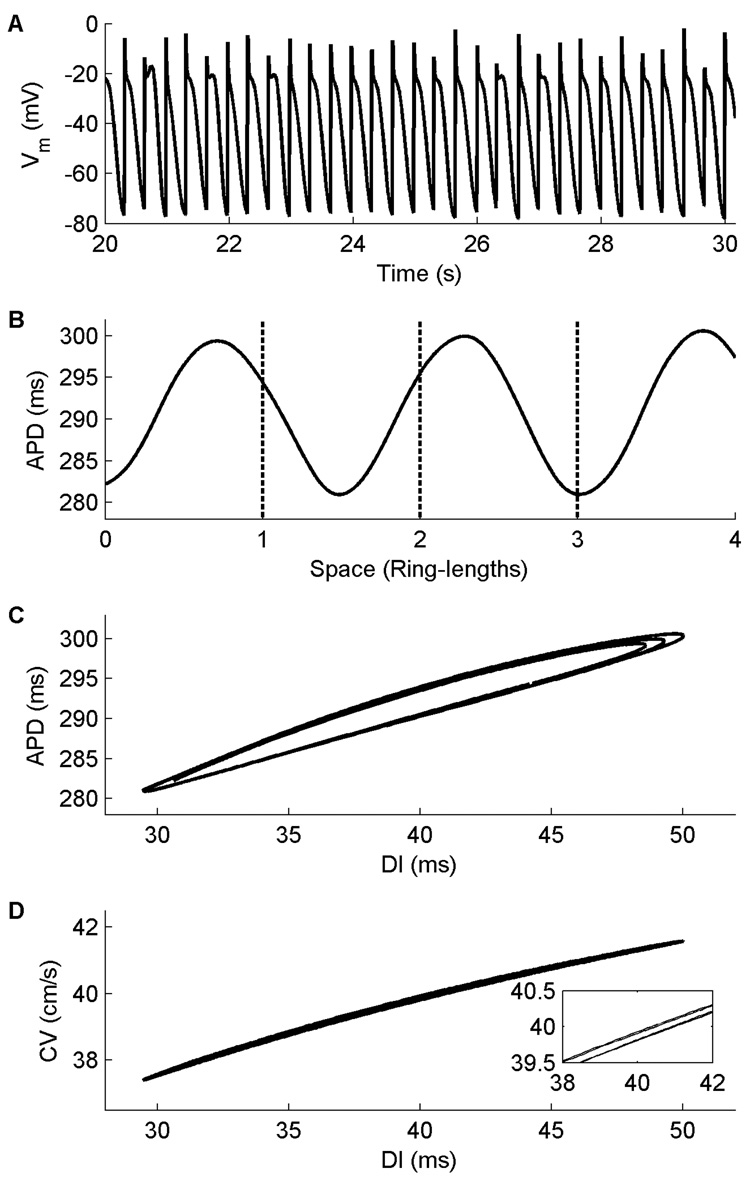
The steady-state restitution curves for these models both show little rate adaptation (Fig. 1D–F, solid lines), with an APD range of no more than 50 ms. This stands in contrast to the case in isolated cells (Cherry et al., 2008), where very short APDs could be produced when pacing was extremely rapid. In tissue, APDs at these short DIs cannot propagate and are blocked, causing the restitution curves to terminate at larger minimum DI values and thus excluding the shortest APDs. All of the steady-state restitution curves are biphasic, with global maxima occurring at DIs of 370 ms and 200 ms for the CM and NMf, respectively, and a global minimum occurring at a DI of 180 ms for the NM. The slopes of all steady-state restitution curves are less than one over all DIs, and no alternans is present in the cables. However, in a ring geometry the CM does exhibit alternans over a small range of ring sizes. Figure 2 shows APD alternans using the CM in a ring that is 13 cm long, with variations in APD and AP morphology arising because the period associated with the ring length and the period of the alternans are incommensurate (Frame and Simson, 1988). The geometry of the ring allows electrotonic effects to become more important (Cherry and Fenton, 2004), because the wavefront can continuously adjust its velocity as it interacts with its tail. The alternans arises in conjunction with splitting of the APD restitution curve (Watanabe et al., 2001; Cherry and Fenton, 2007), as shown in Fig. 2C. The CV restitution curve also exhibits a small degree of splitting (Fig. 2D) (Chen et al., 2005) that contributes to alternans formation in the ring.

Figure 2.

Alternans in the CM in a ring 13 cm long. A. Action potentials at one location 20 s after initiation of the reentrant pulse at this length. Variations in APD and AP morphology can be seen. B. Consecutive APDs measured at all points along the ring during four successive beats (27–30). The APD varies with a period incommensurate with that associated with the ring length (indicated by dashed lines). No alternans is observed in cable geometries. C. APD restitution curve obtained from the same four beats shown in A. Splitting of the curves can be observed. D. CV restitution curve obtained from the same four beats shown in A. A small degree of splitting is also present here as well, as magnified in the inset.

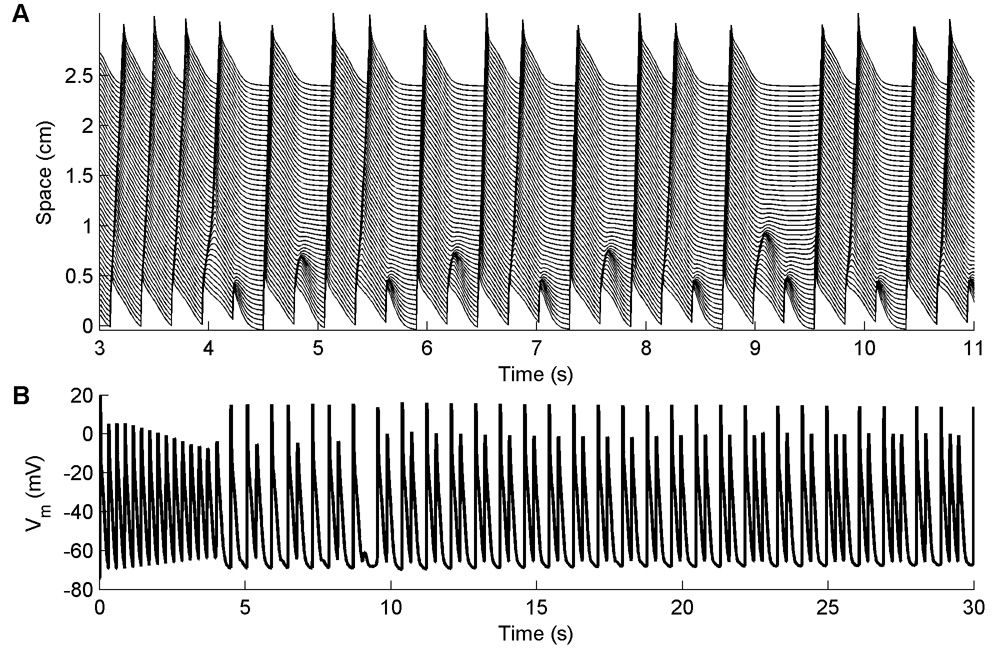
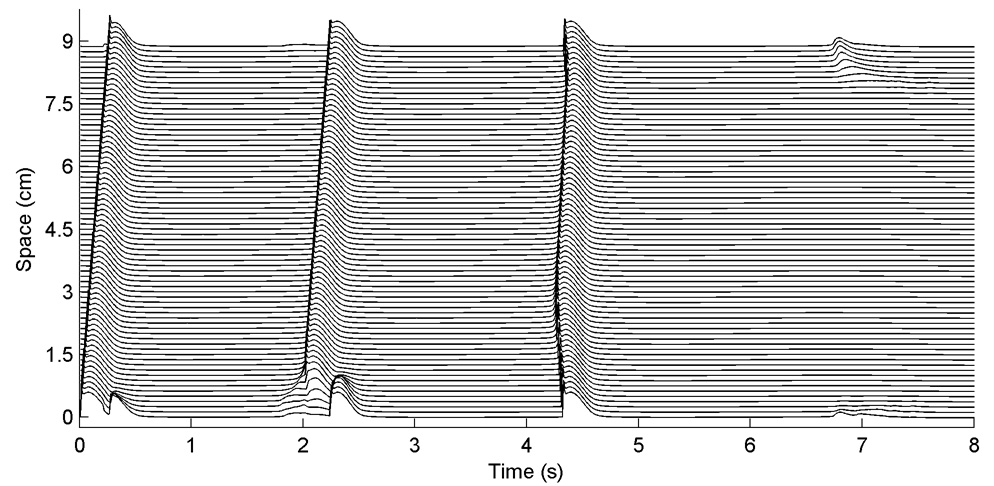
Oscillations in the action potential amplitude, such as those shown in Fig. 3, occur in cables at fast pacing rates for the NM and all its variants and make meaningful measurements of steady-state APDs and DIs impossible at short CLs. The oscillations arise because although the stimulus site conducts every beat, 2:1 block occurs along the cable, as shown in Fig. 3A, giving rise to variations in AP amplitude and frequency along the cable, as shown in Fig. 3B. The CL at which 2:1 block arises away from the stimulus site varies between 280 and 440 ms in all variants except for the NM-X and NMf-X, where the onset occurs at a CL of 100 ms as a result of their much shorter APDs.

Figure 3.

A. Block occurring along a one-dimensional cable using the NM. A. Space-time plot of propagating waves at a CL of 300 ms. Because there is little time for the tissue to recover after a previous beat, some waves propagate slowly, causing block away from the stimulus site on the subsequent beat. The precise location where 2:1 block occurs is variable, as is the number of successfully propagating beats between occurrences of block. No meaningful steady-state measurement of APD can be obtained after 30 seconds of pacing. This form of 2:1 block occurs for all variations of the Nygren et al. model in a 1d cable for short CLs, although the CL corresponding to the onset of oscillations varies between 280 and 440 ms (except for the NM-X and NMf-X, which have much shorter APs and consequently begin to show oscillations at a much shorter CL of 100 ms). B. Oscillations in membrane potential resulting from 2:1 block for the same case shown in A. Here the voltage is shown 1 cm away from the stimulus site.

S1–S2 restitution curves for the CM, NM, and NMf obtained using different S1 CLs do not overlie each other and thereby indicate that the models have memory. The S1–S2 curves of the CM show APDs increasing with decreasing S1 CLs for short DIs, as do those of the NMf, while for CM at longer DIs and the NM this is reversed. Because of the occurrence of delayed afterdepolarizations in the NM and NMf after cessation of rapid pacing, S1–S2 restitution data in some cases cannot be obtained for long DIs, and the maximum usable DI generally decreases with decreasing S1 CL. Thus, some of the S1–S2 curves shown do not span the full DI range, and S1–S2 curves from shorter S1 CLs produced even fewer restitution curve data points and are not shown. S1–S2 restitution curves have slopes greater than one in absolute value only for a few of the S1–S2 curves, and only at the smallest DIs, below 60 ms.

Conduction velocities (Fig. 1G–I) for the models are also different, with a maximum of 46 cm/s for the CM and 36 cm/s for the NM and NMf. The steady-state CV restitution curves for the NM and NMf are monotonically decreasing, but that of the CM is biphasic, with its maximum occurring at a DI of approximately 200 ms, the same DI as for the maximum APD using the steady-state protocol. The range of CVs is small for the CM (6 cm/s) but larger for the NM (9 cm/s) and especially for the NMf (14 cm/s). The S1S2 curves are nearly identical for the CM, indicating little memory in CV, although at short DIs the CVs increase slightly with increasing S1 CL, and a smaller minimum DI can be attained with the S1S2 protocol. Delayed afterdepolarizations in the NM and NMf prevent CV measurements for short S1 CLs and for long DIs, just as they prevent APD measurements, so that full curves cannot always be obtained. Nonetheless, memory in CV is more pronounced for the NM and NMf, which both show a dependence on S1 CL.

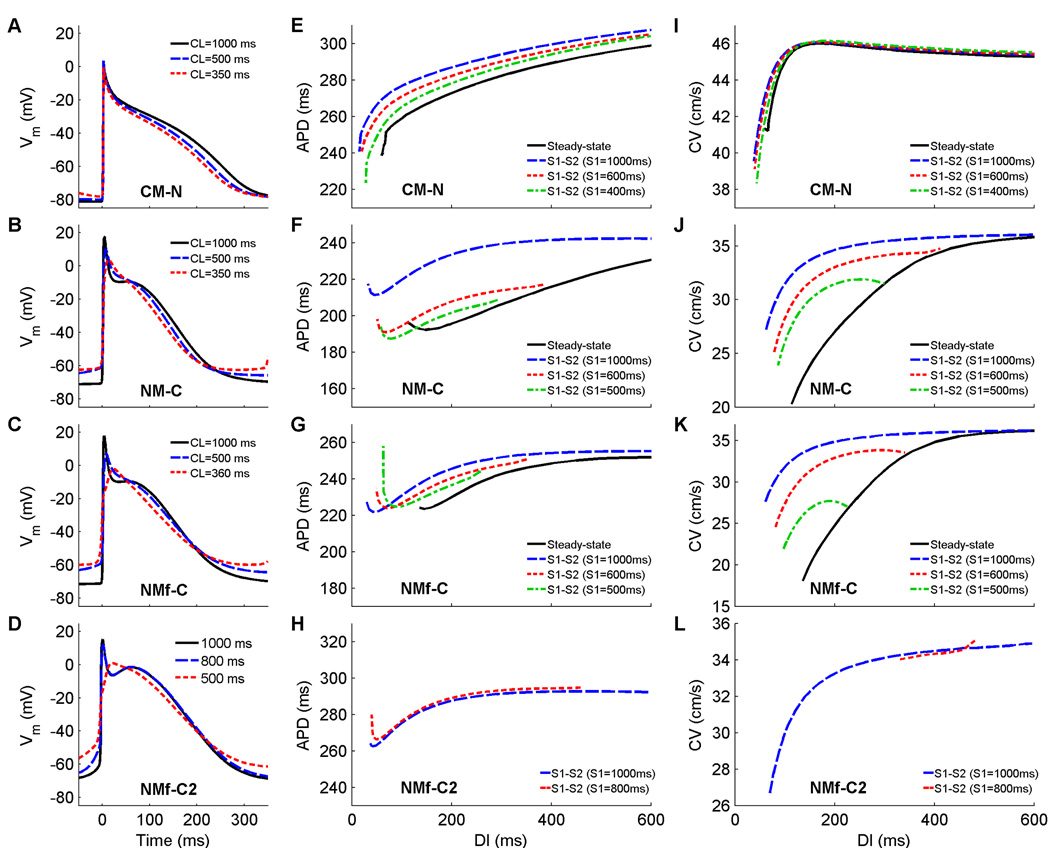
Overall, the models display many differences including AP morphology; adaptation of APD, RMP, and CV to rate changes; and memory of APD and CV. One study of the current formulations of the two models (Nygren et al., 2001) found few differences in the current dynamics and proposed adjustments to current magnitudes to the NM that could produce a spike-and-dome AP like that of the CM (specific changes are described in the Methods and in Table 1). The APs obtained by applying these changes to the NM and NMf and applying their inverse to the CM are shown in Fig. 4A–C. The changes have the desired effects of producing triangular APs in the CM-N even at long CLs and producing spike-and-dome APs for the NM-C and NMf-C at long CLs. However, a number of other properties are minimally altered. All of the models continue to exhibit little rate dependence of APD, but the rate dependence of RMP is decreased to 2 mV in the CM-N and slightly increased to 9 and 12 mV in the NM-C and NMf-C. Action potentials resulting from a different set of proposed changes (Syed et al., 2005), the NMf-C2, are shown in Fig. 4D. As with the NM-C and NMf-C, spike-and-dome action potentials are produced, but the increase in RMP with decreasing CL is about 12 mV, similar to the NMf-C.

Figure 4.

A–D Action potentials at cycle lengths of 1000, 500, and 350 ms using the CM-N, the NM-C, the NMf-C, and the NMf-C2. All APs have been shifted in time slightly so that the upstrokes align at time 0 to allow better comparison. All traces are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm). Because the NMf-C exhibits oscillations arising from 2:1 block at a CL of 350 ms, the action potential shown was obtained using a CL of 360 ms, a CL that did not exhibit oscillations. E–H Restitution of APD₉₀ measured in a 1d cable for the CM-N, the NM-C, the NMf-C, and the NMf-C2. Steady-state restitution curves (solid lines) obtained after pacing for 30 seconds at each CL until 2:1 block was reached are shown along with S1–S2 restitution curves obtained after 30 seconds of pacing at three different S1 CLs over a range of premature S2s. The NMf-C2 exhibits oscillations during the steady-state restitution protocol, leading to a gap at mid-range DI values as well as for CLs of 440 ms and below. Similarly, different values of S1 are used because the NMf-C2 and other model variants exhibit pronounced oscillations or DADs at short CLs. Note that although the ranges of APDs vary among the curves, the scaling used is identical. Data points are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm). I–L. Restitution of conduction velocity measured in a 1d cable for the CM-N, the NM-C, the NMf-C, and the NMf-C2. Both steady-state restitution curves (solid lines) and S1–S2 restitution curves are shown (using the same S1 values as in E–H) and indicate little CV memory for the CM-N but more substantial memory for the other models.

The steady-state restitution curves for the CM-N, NM-C, NMf-C, and NMf-C2 variants, as shown in Fig. 4E–H, are relatively flat, like the original models. The CM-N steady-state curve does not have a biphasic portion, while those of the NM-C and NMf-C increase slightly at small DIs. The NMf-C also has a global maximum APD at a DI of 600 ms, with slight decreases for longer DI values (not shown). The NMf-C2 has a discontinuous steady-state curve (not shown) because delayed afterdepolarizations give rise to oscillations at intermediate DIs and no useful APD and DI data can be obtained. Minimum steady-state DI values remain the same for the CM and CM-N, as well as for the NM and NM-C; the minimum DI is increased by 35 ms and 70 ms for the NMf-C and NMf-C2, respectively, compared to the NMf. Memory is most pronounced for the NM-C, although the CM-N and NMf-C also show a dependence on S1 CL, while the two S1S2 curves shown for the NMf-C2 are almost identical. However, the CM-N and the NMf-C show decreasing APDs with decreasing S1 CL, in contrast to the CM and NMf. Regions with slope greater than one occur only for the CM-N steady-state curve and for some S1S2 curves of all the models, but only for DIs below 70 ms. Slightly larger values of S1 CL give rise to delayed afterdepolarizations for the NM-C and NMf-C than for the NM and NMf, so that the minimum S1 CL shown is slightly higher than for the CM-N. The NMf-C2 is even more prone to afterdepolarizations, and S1–S2 curves can only be obtained at long S1 CLs, such as those shown in Fig. 4H, which is a possible reason for the small memory effects observed for this variant.

Figure 5 shows the effects of the delayed afterdepolarizations (DADs) in the NMf-C2. DADs arise after a period of quiescence. In Fig. 5, a one-dimensional ring too short to support reentrant propagation is shown. An initial paced beat is constrained to propagate unidirectionally along the ring, but it blocks at the the original stimulation site because of the short length. However, the cells using this model variant depolarize slightly over time and in the absence of external pacing can produce DADs (Cherry et al., 2008). In this ring, sub-threshold depolarizations are produced after about 2 seconds close to the original stimulus location, with DADs of increasing amplitude occurring further from the stimulus site and the first full-amplitude action potential arising around 0.8 cm away. This initial DAD propagates unidirectionally around the ring. After another 2 seconds pass, another DAD arises about 3 cm from the stimulus site and propagates bidirectionally around the ring. A third DAD occurs about 2.5 seconds later, but it does not reach full amplitude and is unable to propagate.

Figure 5.

Space-time plot of propagating DADs in a ring using the NMf-C2 model. The ring length is 9 cm, too short to support propagation of a reentrant impulse. Instead, because pacing is effectively ceased after the first paced beat, DADs occur spontaneously at various sites and propagate bidirectionally around the ring until they are blocked by refractory areas or self-annihilate on the opposite side of the ring. Electrotonic effects alter the locations of the two propagating DADs as well as the location of a third DAD, which does not trigger a full-amplitude action potential and is damped out as it propagates. Other parameter variations, including the NM-AF, NM-C, and NMf-C, also exhibit propagating DADs for rings just short enough to cause propagation failure.

Figure 4I–L shows the CV restitution curves for the CM-N, NM-C, NMf-C, and NMf-C2, which are generally close to those of the original models. The CV values are about 0.5 cm/s slower for the CM-N than for the CM, and the range of CVs also is decreased to 5 cm/s. The NM-C and NMf-C, in contrast, show broader ranges of CVs of 16 and 18 cm/s, respectively. While useful steady-state values of the CV cannot be obtained for long DIs for the NMf-C2, the S1–S2 CV values are similar to those of the NMf and reach a minimum CV close to that of the NMf-C. Little memory in CV is displayed by the CM-N and by the NMf-C2, although the impossibility of obtaining S1S2 data from shorter S1 CLs likely contributes to the lack of memory displayed by the NMf-C2. For the NM-C and NMf-C, like the NM and NMf, CVs vary noticeably at shorter DIs depending on the S1 CL used.

When the models are altered to reflect electrophysiological changes that arise after prolonged AF, all of the action potentials are shortened, are triangular in shape, and continue to exhibit limited adaptation to rate (Fig. 6A–C). Rate adaptation of RMP also decreases to 2, 5, and 5 mV for the CM-AF, NM-AF, and NMf-AF, respectively. All of the steady state APD restitution curves are relatively flat (see Fig. 6D–F), with maximum slopes below one. In addition, the minimum DI decreases from 60 to 35 ms for the CM-AF, from 110 to 100 ms for the NM-AF, and from 101 to 74 ms for the NMf-AF. Memory is reduced, with the S1S2 restitution curves clustering more closely together, and all the S1S2 curves increase or decrease with decreasing S1 CL in the same manner as those of their corresponding original models. As shown in Fig. 6G–I, maximum CV values also are not altered, but the range of CV values is increased for the CM-AF compared to the CM by 10 cm/s and is decreased for the NM-AF and NMf-AF compared to the NM and NMf by 4 cm/s in each case.

Figure 6.

A–C Action potentials at cycle lengths of 1000, 500, and 350 ms using the CM-AF, the NM-AF, and the NMf-AF. All APs have been shifted in time slightly so that the upstrokes align at time=0 ms to allow better comparison. All traces are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm). D–F Restitution of APD₉₀ measured in a 1d cable for the CM-AF, the NM-AF, and the NMf-AF. Steady-state restitution curves (solid lines) obtained after pacing for 30 seconds at each CL until 2:1 block was reached are shown along with S1–S2 restitution curves obtained after 30 seconds of pacing at three different S1 CLs over a range of premature S2s. Note that although the ranges of APDs vary among the curves, the scaling used is identical. Data points are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm). G–I. Restitution of conduction velocity measured in a 1d cable for the CM-AF, the NM-AF, and the NMf-AF. Both steady-state restitution curves (solid lines) and S1–S2 restitution curves are shown and indicate reduced CV memory for the NM-AF and NMf-AF compared to their non-AF versions and consistently small CV memory for the CM-AF compared to the CM.

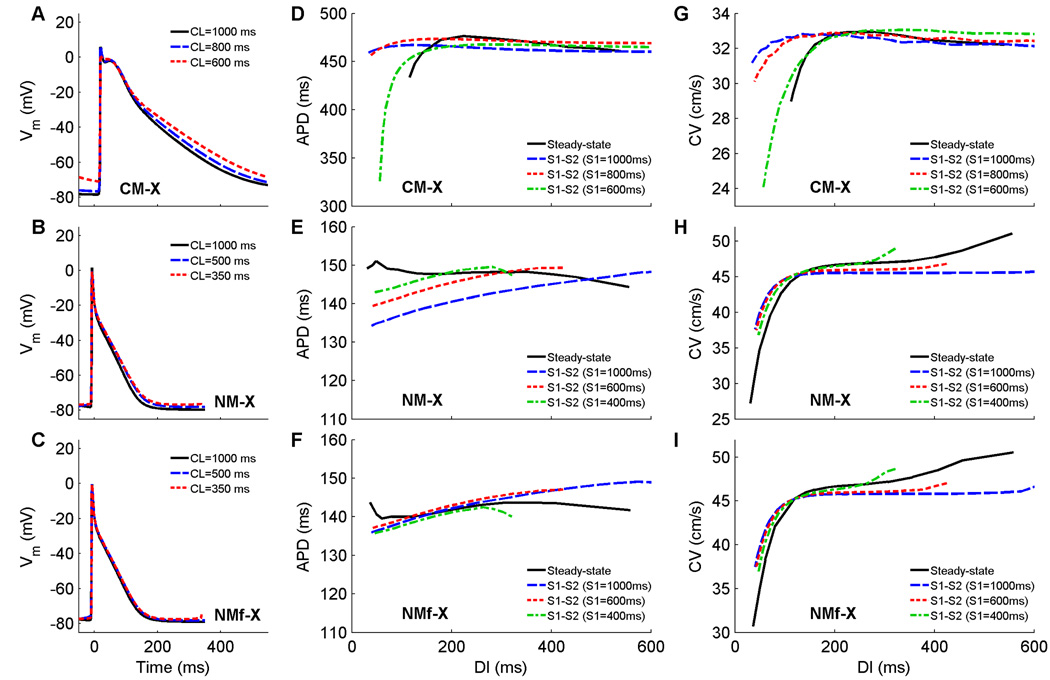
In the final set of modifications, where the models’ transmembrane current formulations have been exchanged, more significant changes can be seen as shown in Fig. 7. The APs of the CM-X are substantially longer than those of the CM, while the APs of the NM-X and NMf-X are substantially shorter than those of the NM and NMf (see Fig. 7A–C). None of the steady-state or S1S2 restitution curves have slope greater than one, but the CM-X does develop discordant alternans at a CL of 530 ms, with block along the fiber occurring at a CL of 440 ms. The minimum DI of the steady-state restitution curve has increased to 112 ms for the CM-X and has decreased to 31 and 36 ms for the NM-X and NMf-X, respectively. Memory effects, as observed through the ordering of S1S2 restitution curves, have become more complex for all three model variants, as the APDs first increase and then decrease for a given DI value as the S1 CL is decreased. The range of CVs is similar to the original models (4, 8, and 14 cm/s for the CM-X, NM-X, and NMf-X, respectively), but the maximum CV value for the CM-X is closer to that of the NM and the maximum values for the NM-X and NMf-X are closer to that of the CM. Furthermore, the differences in CV values associated with different S1S2 restitution curves indicate increased memory in CV in the CM-X (compared to the CM), especially for short DIs, but decreased CV memory for the NM-X and NMf-X (compared to the NM and NMf, respectively).

Figure 7.

A–C Action potentials at cycle lengths of 1000, 500, and 350 ms using the CM-X, the NM-X, and the NMf-X. All APs have been shifted in time slightly so that the upstrokes align at time=0 ms to allow better comparison. All traces are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm). D–F Restitution of APD₉₀ measured in a 1d cable for the CM-X, the NM-X, and the NMf-X. Steady-state restitution curves (solid lines) obtained after pacing for 30 seconds at each CL until 2:1 block was reached are shown along with S1–S2 restitution curves obtained after 30 seconds of pacing at three different S1 CLs over a range of premature S2s. Data points are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm). G–I. Restitution of conduction velocity measured in a 1d cable for the CM-X, the NM-X, and the NMf-X. Both steady-state restitution curves (solid lines) and S1–S2 restitution curves are shown and indicate increased CV memory for the CM-X compared to the CM and reduced CV memory for the NM-X and NMf-X compared to the NM and NMf.

Spiral wave stability and trajectories

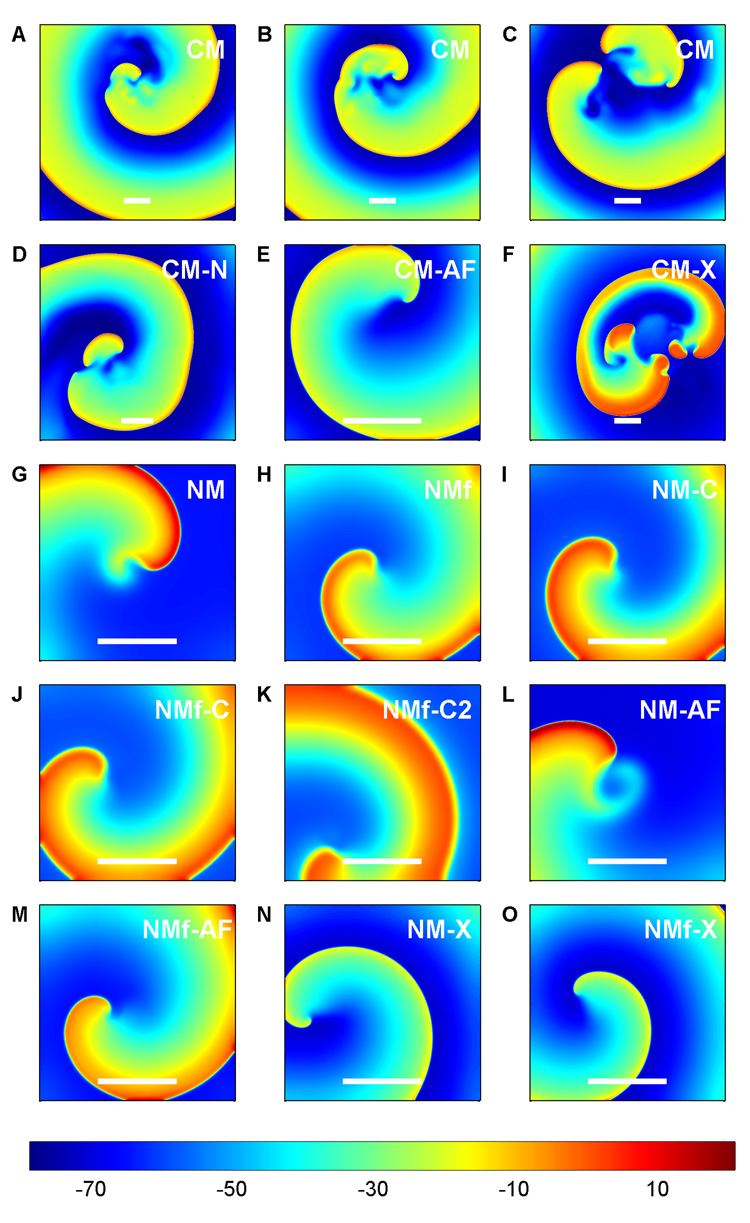
Reentrant spiral waves initiated in the models exhibit different behaviors, as shown in Fig. 8. For the CM, true sustained spiral wave breakup was never observed, even in large domains up to 30 cm × 30 cm and with a spatial resolution as fine as 0.01 cm. Instead, as shown in Fig. 8A–B, a spiral wave in the CM frequently encountered refractory regions that cause a transient wave break. In most cases, the wave healed quickly, within several milliseconds. However, in some cases, a wave break resulted in additional, longer-lasting spiral waves. These spirals sometimes persisted for tens or hundreds of ms, but in large domains where boundary effects play a minimal role, multiple spirals typically lasted no more than one to three rotations. The CM-N (Fig. 8D) showed similar behavior, with transient breakups that generally healed quickly. The CM-X, on the other hand, did show sustained breakup (Fig. 8F). The NM and all its variants in two dimensions show non-breaking spiral waves that can be maintained in relatively small domains (see Fig. 8G–O). The CM, on the other hand, shows a stable spiral wave only for the CM-AF variant (Fig. 8E), which, like the NM variants, never exhibits spiral wave breakup.

Figure 8.

Representative dynamics of the models in a 2D homogeneous tissue slice. Stable spiral waves are exhibited by all of the NM variants and by the CM-AF, while the other CM variants all exhibit wave break. Colorbar indicates voltage in mV. Scales bars represent 4 cm.

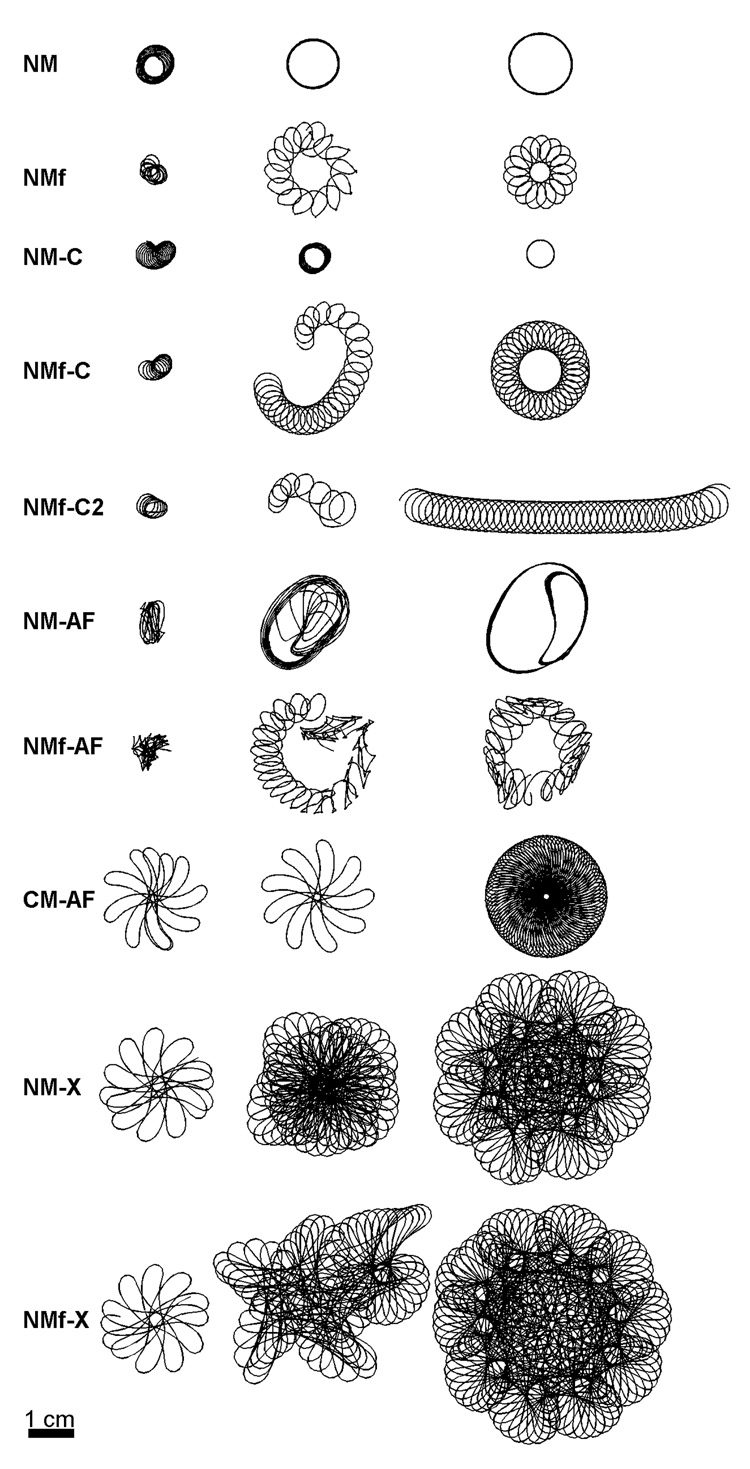
The non-breaking spiral waves showed a number different trajectory shapes, with transient trajectories often observed as the spiral waves settled into steady-state behavior that could take up to tens of seconds to achieve. Transient and steady-state trajectories for the ten model variants with stable spiral waves are shown in Figure 9. Circular trajectories were obtained for the NM and NM-C, hypocycloidal for the NM and NMf-C, and cycloidal for the NMf-C2. The trajectory of the NM-AF is elliptical with an inner loop that arises as a result of propagation within the core occurring on every other beat, and the NMf-AF is a complex hypocycloidal trajectory in which the size and shape of the petals also modulates. The CM-AF exhibits a linear-petal trajectory that slowly precesses, and the NM-X and NMf-X exhibit similar trajectories with an additional frequency that gives rise to petals within the petals. Table 2 lists the frequencies associated with the spiral waves for all the model variants, except for the CM-X, for which sustained breakup prevented obtaining a meaningful frequency.

Figure 9.

Transient and steady-state spiral wave trajectories found using all variants of the NM and the CM-AF. The last trajectory shown for each variant represents steady-state at the end of the simulation except for the NMf-C2, which followed a cycloidal trajectory that changed direction whenever it hit the boundary. Thus, the longest nearly straight portion of the trajectory is shown after a rotation for visualization purposes. Scale bar represents 4 cm. Times for the three trajectories shown for each model are as follows. NM: 7.5–12.5 s, 30–35 s, 55–60 s. NMf: 1.5–4.5 s, 7.5–12.5 s, 55–60 s. NM-C: 1.2–5.2 s, 10.2–14.2 s, 50.2–60 s. NMf-C: 1.2–3.7 s, 4.2–14.2 s, 46.7–60 s. NMf-C2: 0.7–2.7 s, 3.2–6.2 s, 26.7–47.7 s. NM-AF: 6.7–9.2 s, 29.2–34.2 s, 85.2–90 s. NMf-AF: 1.2–4.2 s, 5.2–14.2 s, 80–90 s. CM-AF: 0.6–1.8 s, 15.8–16.8 s, 50–60 s. NM-X: 0.5–1.7 s, 5.2–15.2 s, 42.3–60 s. NMf-X: 0.5–1.6 s, 15.2–25.3 s, 35.3–60 s.

Table 2. Important periods for the two-dimensional spiral waves.

Descriptions are provided for cases where multiple periods are present. For the CM and CM-N, average values during the longest two windows of stability are given.

Model	Period (ms)
NM	350
NMf	5400 360	Outer loop Single petal
NM-C	340
NMf-C	12000 390	Outer loop Single petal
NMf-C2	480
NM-AF	370 710	Single petal Double-petal motif
NMf-AF	10000 290 610	Outer loop Single petal Modulation of single petal size/shape
NM-X	20000 190 600	One full loop Single petal Medium loop
NMf-X	30000 190 600	One full loop Single petal Medium loop
CM	330
CM-N	330
CM-AF	200 1000	Single petal Single rotation
CM-X	N/A

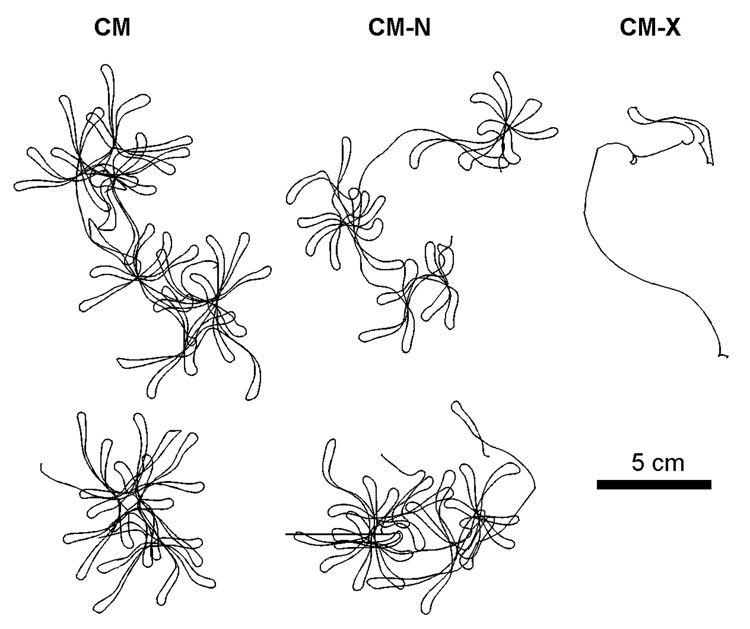
Although the spiral waves of the CM, CM-N, and CM-X gave rise to breakup, representative trajectories during stable periods within the overall dynamics can be obtained and are shown in Fig. 10. In all cases, the stable motif is a linear, hypermeandering trajectory. The CM-X, because of its sustained breakup, did not have a long window of stability, but the type of linear trajectory shown in Fig. 10 for the CM-X is similar to the trajectories of the CM and CM-N in terms of shape and size.

Figure 10.

Spiral wave trajectories during windows of stability during the quasi-stable dynamics of the CM, CM-N, and CM-X. Two trajectories are shown for the CM and CM-N, while only one trajectory is shown for the CM-X, which was particularly prone to breakup. All the models produce meandering linear core trajectories approximately 4–6 cm in length.

Scroll waves in a realistic human atrial anatomy

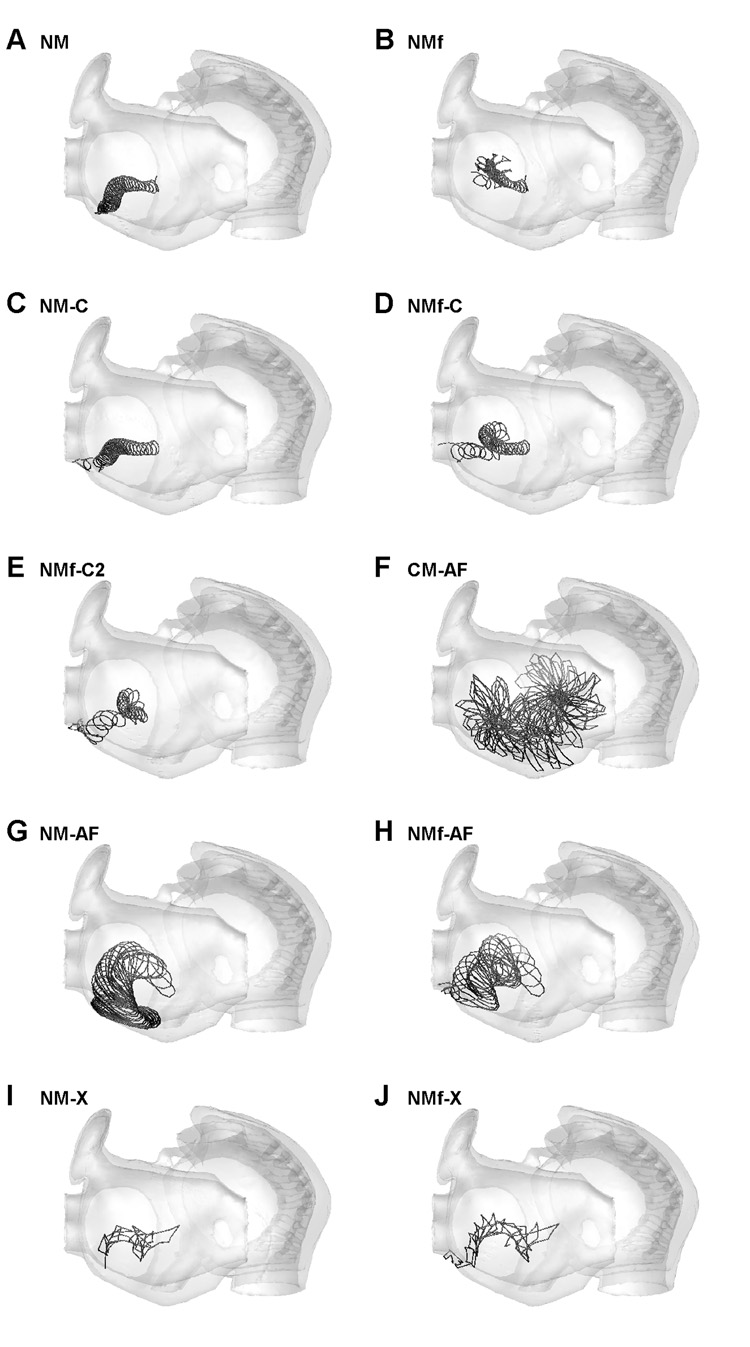
To understand how the models behave in a realistic human atrial anatomy, the structure of Harrild and Henriquez (2000) was used. Scroll waves were initiated in the left atrium for each model variant and although results similar to the two-dimensional sheets were obtained in many cases, several new phenomena emerged. Figure 11 shows surface projections of the scroll wave filament trajectories for the ten model variants that did not produce breakup (these are the same variants that were stable in two dimensions as well). In this realistic anatomy, only the scroll waves of the NMf, CM-AF, and NM-AF remained after 10 s; in all other cases significant trajectory drift arising from anatomical effects pushed the scroll waves toward the left pulmonary veins, where the scrolls were extinguished. In the remaining cases (NMf, CM-AF, and NM-AF, in Fig. 11B, F, and G), drift was still observed, but it was not substantial enough to move the scrolls to a boundary where termination would occur.

Figure 11.

Surface trajectories of scroll waves in a three-dimensional realistic anatomical structure of the human atria for all variants of the NM and the CM-AF. Trajectories last until scroll wave extinction or for a maximum of 10 s. All scroll waves were initiated in the same location on the left atrium free wall. Because the atria are thin, the trajectories on the exterior and interior are nearly identical. The view shows the left atrium on the left and the right atrium on the right. In all cases, translational drift is seen that was not seen for spiral waves in two-dimensional sheets (see Fig. 7). Extinction occurred at the pulmonary vein ostia within 10 seconds for the NM, NM-C, NMf-C, NMf-C2, NMf-AF, NM-X, and NMf-X.

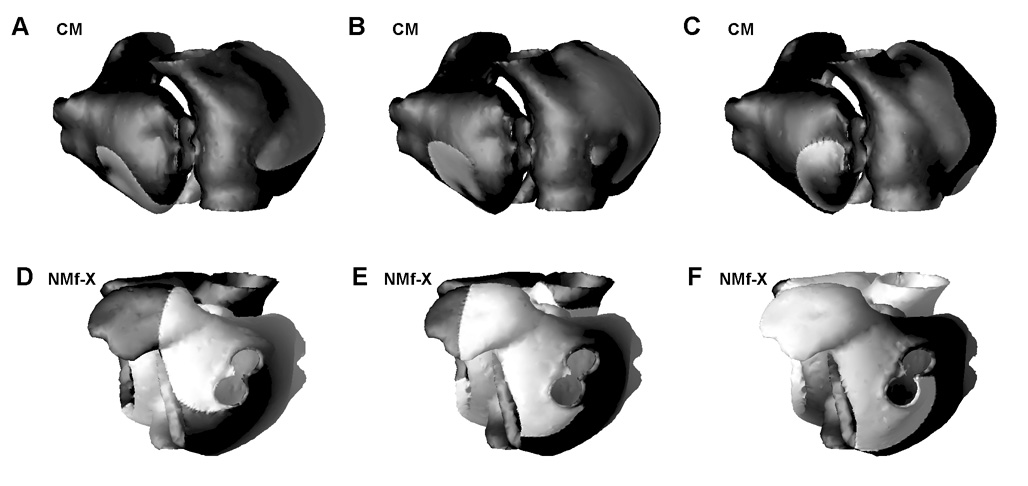
In the CM, anatomical effects gave rise to sustained breakup that resulted in the presence of scroll waves in both atria, as shown in Fig. 12A–C, with the CM-N producing similar results (not shown). The long action potentials and associated long wavelength of the CM-X did not allow scroll wave initiation in this model using the same protocols as for all the other model variants and is not shown.

Figure 12.

Complex dynamics in a three-dimensional realistic anatomical structure of the human atria, with scroll waves initiated on the left atrium free wall. The views show the left atrium on the left and the right atrium on the right. A–C. The CM meanders throughout both atria and quickly establishes multiple reentrant waves. Transient breakup and recombination occurs in the right atrium near the crista terminalis and caval veins. Transient pinning to the right pulmonary veins also occurs, as shown in C, but because the period of the reentrant wave is longer than the time it takes to circulate around the vein ostia, the wave cannot remain pinned. Times are (A) 10.47 s, (B) 10.64 s, and (C) 12.48 s. D–F. The scroll wave initiated using the NMf-X terminates at the left pulmonary veins, where it becomes largely pinned. Transient unpinning occurs because the period of the reentrant wave is slightly longer than the time to travel around the ostia, but the wave soon re-pins to the veins and the process repeats. Times are (D) 3.09 s, (E) 3.12 s, and (F) 3.15 s. Grayscale indicates membrane potential in mV as in Fig. 8.

An additional effect that occurred in the three-dimensional anatomy is pinning of the waves to various edges of the tissue corresponding to valves and vessels, especially the pulmonary veins. The CM exhibited transient pinning to the right pulmonary veins, as shown in Fig. 12C, while retaining complex scroll wave activity throughout both atria. Certain variants of the NM, especially the NMf-X, exhibited sustained pinning although all other wave activity had ceased. In the NMf-X, the wave front pinned to the left pulmonary veins (Fig. 12D), but because the time required to circulate around the vein ostia was shorter than the wavelength, transient unpinning occurred (Fig. 12E). When the tissue became quiescent again, the wave re-attached to the ostia (Fig. 12F). This pattern, once initiated, was sustained for several seconds until the end of the simulation.

Discussion

Agreement of the original models

Comparison of the CM and NM/NMf shows a number of differences in many important properties. While both models exhibit little adaptation of APD to rate changes, the CM shows a greater range of APDs along with alteration in AP morphology. The NM and NMf, on the other hand, show fairly constant APDs with consistently triangular shapes, but show much greater rate adaptation of RMP than the CM. The APDs of the CM are substantially longer than those of the NM and NMf at all but the shortest DIs. The steady-state APD restitution curves of all the models are biphasic, with the NM showing increased APDs at the shortest DIs and the CM and NMf showing the maximum APD at intermediate DI values (although the biphasic nature of the CM restitution curve is quite slight). Both models show some memory in APD as assessed through families of S1S2 restitution curves, although the CM exhibits noticeable differences in APD for a given DI as the S1 CL is changed only at the smallest DIs. In addition, the S1S2 restitution curves with the longest S1 CLs produce the longest APDs for the NM and for the CM at long DIs, while the ordering is reversed for the NMf and for the CM at shorter DIs. The maximum CV of the CM is about 28 percent faster than that of the NM and NMf, and although there is limited memory present in the CV restitution curves of the CM, those of the NM and NMf show more substantial dependence on the S1 CL used.

During reentry, the changes are even more dramatic, with the NM and NMf exhibiting stable spiral waves in tissue with circular and hypocycloidal trajectories, respectively, while the CM produces a hypermeandering trajectory together with largely transient breakup and rapid healing of wave breaks occurring frequently. Spiral waves have been simulated previously for both the NM and the CM by Nygren et al. (2001), who similarly found the NM to exhibit stability and the CM to be hypermeandering but non-sustained in small domains up to 4 cm × 10 cm. Xie et al. (2002) found that larger domains could sustain reentry using the CM and, if large enough, could support sustained wave break as well. However, Biktasheva et al. (2002) also analyzed the stability of spiral waves for the NM and CM and found that while the NM was highly stable, the stability of the CM depended on spatial resolution: at fine resolutions of at most 0.01 cm, induced spiral waves were stable, while for coarser resolutions of 0.02 cm or more (such as that of Xie et al.), breakup occurred. We found that wave break occurred even at a spatial resolution of 0.01 cm, although most breaks healed quickly and multiple waves were present only for several rotations at the longest. The differences with the findings of Biktasheva may be explained in part by their phase distribution protocol for spiral wave initiation, in which the initial conditions of an action potential were distributed radially in a symmetric fashion that may limit wave break. In addition, larger domains and longer times, such as those used here, may be necessary to observe the presence of multiple waves because it occurs infrequently.

In a realistic anatomical model of the human atria, initiated scroll waves produced different results for the CM, NM, and NMf. Wave breakup and multiple waves were observed only for the CM. The NM maintained a primarily circular trajectory, but anatomy induced a drift that caused the scroll wave to terminate at the left pulmonary veins. Drift also occurred for the NMf, but to a lesser degree, and the single initiated scroll wave remained present for the full 10 seconds simulated. Given that fibrillation induced in healthy human atria quickly self-terminates, the NM appears to be the closest at reproducing normal atrial tissue in this regard, although it is not clear whether drift would cause termination of scroll waves initiated in different locations.

Feasibility of reproducing the dynamics of one model by modifying conductances of the other

As discussed, two different sets of changes have been proposed to improve the agreement between the CM and NM. One set of changes (Nygren et al., 2001) was focused on producing a spike-and-dome AP morphology using the NM, resulting in the NM-C and NMf-C. Compared to the NM, the NM-C exhibits a spike-and-dome morphology at long CLs and a decreased steady-state range of CVs. Similarly, the NMf-C shows a spike-and-dome morphology at long CLs, an increased minimum DI (136 vs. 101 ms), and an increased CV range (18 vs. 14 cm/s) compared to the NMf. However, compared to the CM, the NM-C/NMf-C have much less pronounced plateaus, a much greater rate dependence of RMP (9/12 vs. 4 mV between CLs of 1000 and 350 ms), increased minimum DI (113/136 vs. 60 ms), decreased maximum APD (230/252 vs. 310 ms at a DI of 600 ms), increased APD and CV memory, decreased maximum CV (36/36 vs. 46 cm/s), and increased steady-state CV range (16/18 vs. 6 cm/s). For reentrant waves, the differences are more striking, with the NM and NM-C exhibiting stable waves with circular trajectories and the NMf and NMf-C producing stable waves with hypocycloidal trajectories, compared to the hypermeandering quasi-stability of the CM.

Applying the inverse of the changes of Nygren et al. (2001) to the CM, resulting in the CM-N, leads to similar findings. Compared to the original CM, the CM-N exhibits a triangular morphology and a different dependence of APD restitution curve on S1 CL. However, the differences compared with the NM/NMf are more significant, including decreased rate dependence of RMP (2 vs. 8/11 mV between CLs of 1000 and 350 ms), decreased minimum DI (60 vs. 110/101 ms), increased maximum APD (299 vs. 228/235 ms at a DI of 600 ms), decreased APD and CV memory, increased maximum CV (46 vs. 36/36 cm/s), and decreased steady-state CV range (5 vs. 9/14 cm/s). Again, reentrant waves show pronounced differences as well, with the CM-N exhibiting hypermeander and quasi-breakup similar to that of the CM, while the NM and NMf show stable rotating waves.

The other set of changes (Syed et al., 2005) was based on matching the AP shapes and durations of the CM over a range of CLs, producing the NMf-C2. While a spike-and-dome morphology is produced at long CLs and the maximum APD is significantly increased to better match the CM, the NMf-C2 has a serious problem with depolarization during phase 4, resulting in the generation of DADs over a wide range of CLs, a phenomenon not seen in the CM and seen only to a lesser extent in the NM and NMf. Compared to the CM, there is also a significant increase in RMP rate adaptation (12 vs. 4 mV) and a significant decrease in maximum CV (36 vs. 46 cm/s). Reentrant spiral waves also show differences, with the NMf-C2 producing a stable but cycloidal trajectory compared to the hypermeandering and quasi-stability characteristic of the CM.

Although Syed et al. (2005) found good agreement between their modified model (NMf-C2) and the original CM, we have identified a number of differences. Several factors contribute to the different findings, as discussed elsewhere (Cherry et al., 2008). Perhaps the most important difference is that the fitting was obtained using only ten beats at the different CLs, whereas the NM continues to exhibit action potential changes beyond ten beats, especially at short CLs. Other differences, including the manual aligning of RMPs by Syed et al. and differences in restitution protocols, also may be involved.

Effects of atrial fibrillation-induced electrophysiological changes

Electrophysiological changes induced by atrial fibrillation are produced by modifying current magnitudes following Courtemanche et al. (1999), as described. These changes result in some effects common to all the model variants, including decreased rate adaptation of RMP, decreased minimum steady-state DI, decreased APD (at a DI of 600 ms), and decreased CV memory. All spike-and-dome morphologies are abolished as well. APDs are decreased overall in the CM-AF compared to the CM, but remain similar for the NM-AF/NMf-AF and their non-AF-modified counterpart variants. Maximum CV and the directionality of the dependence of APD on S1 CL for a given DI remain essentially unchanged. APD restitution curve slopes are also decreased for the steady-state curves and are never greater than one, and are also decreased for most of the S1S2 curves.

In spiral wave dynamics, the changes are more striking for the CM-AF, where breakup no longer occurs and a stable spiral wave results instead. The NM-AF and NMf-AF also have stable spiral waves. In the realistic human atrial anatomy, scroll waves using both the CM-AF and NM-AF are stable and remain in the atria after 10 seconds, while a scroll wave using the NMf-AF drifts toward the pulmonary veins and is terminated.

Comparison with experimental rate adaptation and restitution data

A number of studies examining AF have found reduced rate adaptation of APD after chronic AF (Boutjdir et al., 1986; Franz et al., 1997; Kamalvand et al., 1999; Manios et al., 2000; Osaka et al., 2000) and provide both control and AF data. In healthy atria, the range of APDs seen over a range of different CLs is in general broader than what is observed for the models, with ranges generally around 60–70 ms (Manios et al., 2000, right atrial appendage (RAA); Osaka et al., 2000, right atrial (RA) wall), but sometimes more than 140 ms when longer CLs are included (Franz et al., 1997, average of high and low RA sites; Boutjdir et al., 1986, isolated RAA tissue). Only Kamalvand et al. (1999) find a smaller range of 23 ms, for the RAA, with APDs between 236 and 259 ms. The NMf produces a very similar range of 20 ms with APDs between 235 and 255 ms. However, the NM and CM produce ranges larger than Kamalvand et al. of 40 ms but nonetheless smaller than the other data. Thus, the model data in general does not match experimental values, with the exception of an excellent fit between the NMf and the RAA data of Kamalvand et al. (1999).

After chronic AF, the APDs reported experimentally are generally somewhat shorter and the range of APDs also decreases (Boutjdir et al., 1986; Franz et al., 1997; Kamalvand et al., 1999; Manios et al., 2000; Osaka et al., 2000). Again, differences in the ranges found experimentally are apparent, with some finding small ranges around 20–25 ms (Kamalvand et al., 1999, RAA; Manios et al., 2000, RAA; Osaka et al., 2000, RA wall) and others finding broader ranges of 70–75 ms (Franz et al., 1997, high/low RA average; Boutjdir et al., 1986, isolated RAA). The ranges of the NM-AF and NMf-AF are close to the former, especially the data of RAA Kamalvand et al. (1999), in both APD range (10/15 ms vs. 17 ms) and APD values (200–220/200–215 ms vs. 208–225 ms). The CM-AF agrees more closely with the atrial flutter, rather than chronic AF, data of Franz et al. (1997) in both APD range (55 ms vs. 60 ms) and APD values (165–220 ms vs. 160–220 ms).

Little published data on electrical restitution in human atrial tissue is available, but one study by Kim et al. (2002) found increased APD restitution in chronic AF patients, in contrast with the decreased rate adaptation observed more generally. One possible explanation for the difference is that Kim et al. tested much smaller DIs than most other studies, which may produce a small region with very steep restitution over the smallest DIs. Although Kim et al. measure data at four different sites, none of the control APD ranges (between 50 and 75 ms) agree well with those of the CM, whose range is too large (120 ms), or with the NM or NMf, whose ranges are too small (10–15 ms). The chronic AF data of Kim et al. also does not agree well with the CM-AF, NM-AF, or NMf-AF, all of which have much smaller APD ranges (10–35 ms) compared with the experimental findings (60–90 ms).

Conduction velocity values appear to be similar to observed values of 30 cm/s for muscle cells and 45 cm/s for specialized conducting cells (Gelband et al., 1972). However, significantly higher human atrial conduction velocity values of 60–115 cm/s during sinus rhythm and 45–105 cm/s during pacing have been reported as well (Hansson et al., 1998; Kanagaratnam et al., 2002; Smits et al., 2005). The value of the diffusion coefficient used here is identical to that of Xie et al. (2002) and results in conduction velocities and spiral periods similar to those shown by Nygren et al. (2001) (note that the period of a spiral wave in the NM lengthens over time and is initially around 270 ms). Faster velocities can be achieved by increasing the conductance of the sodium current I_Na (Nygren and Giles, 2000) or by increasing the diffusion coefficient. Supernormal conduction, such as that exhibited by the CM, also has been observed in some cases (Brorson and Olsson, 1977).

Effects of exchanging transmembrane current formulations

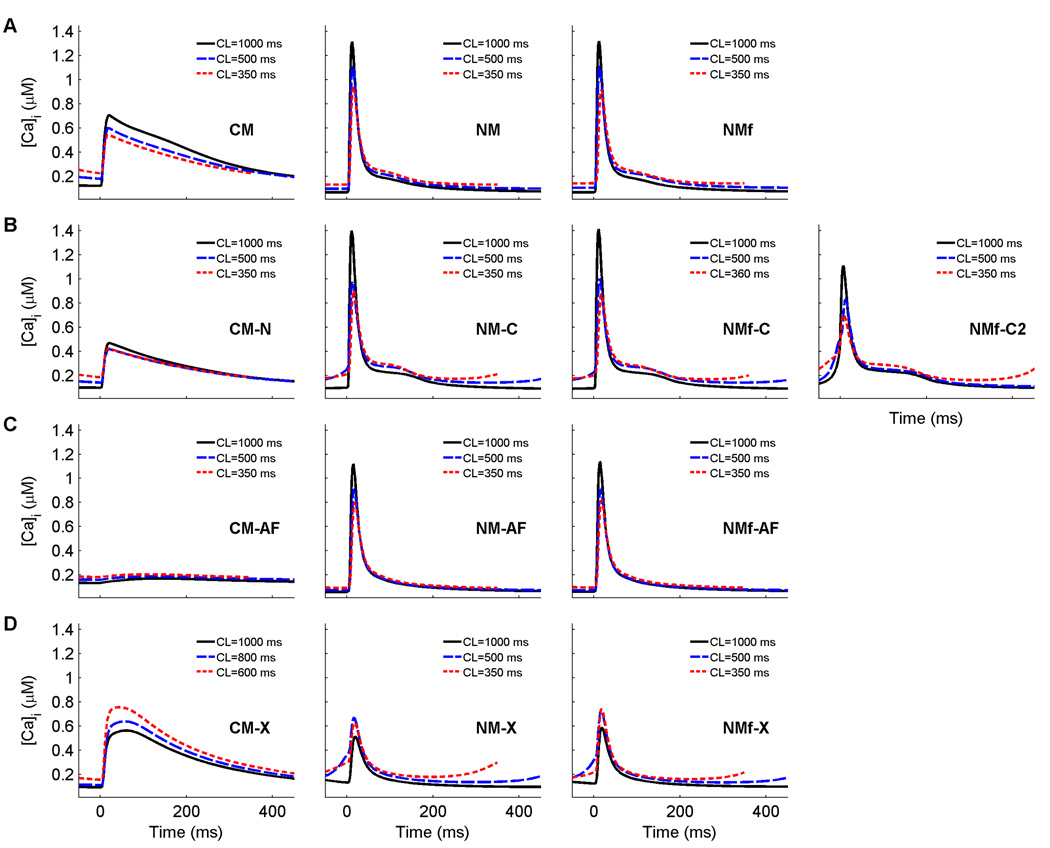
As can be seen by the changed APDs of the CM-X, NM-X, and NMf-X, exchanging model current formulations can have serious effects on the action potentials. The long APDs of the CM-X, and the short APDs of the NM-X and NMf-X, are explained primarily by the differences in the calcium transients of the original models, which are shown at three different cycle lengths for all the model variants are shown in Fig. 13. In the CM, the calcium transient is long-lasting, with a rapid upstroke but a slow decay. The NM, in contrast, has a larger peak transient but a much more rapid decay. The calcium currents of the models were designed to work in conjunction with transients of these shapes. Thus, using the NM calcium transient with the CM calcium current results in an abbreviated calcium current and shortened APD, as in the NM-X and NMf-X, and using the CM calcium transient with the NM calcium current produces the elongated APD of the CM-X, as can be seen in Fig. 13D.

Figure 13.

Calcium transients for each of the 13 model variants analyzed for three different cycle lengths. The CM and its variants have longer-lasting transients than the NM and its variants, except in the case of the CM-AF, where the transient amplitude is greatly reduced. All traces are taken from node 80 along a one-dimensional cable with 100 nodes (Δx=0.025 cm) after pacing for 30 s at the given CL.

Other effects can be observed. The rate dependence of RMP is increased for the CM-X compared to the CM (7 vs. 4 mV between CLs of 1000 and 350 ms), but is reduced for the NM-X (1 vs. 8 mV) and the NMf-X (1 vs. 11 mV). The slopes of all steady-state and S1S2 APD restitution curves are less than one for the CM-X, NM-X, and NMf-X. The minimum DI is also altered, with an increase for the CM-X compared to the CM (112 vs. 60 ms) and decreases for the NM-X (31 vs. 110 ms) and NMf-X (36 vs. 101 ms). The maximum CV values are essentially reversed, with a decreased maximum for the CM-X and increased maxima for the NM-X and NMf-X (although some degree of DAD propagation may be partly responsible for the increases in CV at long DIs). In addition, the CM-X has a greater degree of CV memory than the CM, and the NM-X and NMf-X have reduced CV memory compared to the NM and NMf. Reentrant spiral waves initiated using the CM-X progress to sustained breakup, while spirals initated using the NM-X and NMf-X produce complex but stable trajectories featuring three frequencies, resulting in the appearance of small petals within the large-petal trajectories.

Importance of intracellular calcium handling in determining model properties

The CM-X, NM-X, and NMf-X provide a unique means of assessing the importance of transmembrane currents compared to intracellular calcium handling in generating the observed characteristics of the models. Properties present in the CM (or NM/NMf) that remain present in the CM-X (or NM-X/NMf-X) are likely to arise from the details of intracellular calcium handling, while those present in the CM and NM-X/NMf-X or in the NM/NMf and CM-X are likely to occur because of characteristics of the transmembrane currents.

Rate dependence of RMP is strong in the NM/NMf but reduced in the NM-X and NMf-X, and also is increased in the CM-X compared to the CM, and thus is likely an effect of the transmembrane currents. Because of the differences in APD of the CM-X and NM-X/NMf-X compared to the original models, it is difficult to assess whether currents or calcium dynamics contributes more to the maximum APD, shape of the APD restitution curve, minimum DI, and APD memory. However, the currents appear to affect minimum DI, since the current reductions associated with AF decreased the minimum DI in all cases, while APD memory was only slightly decreased in magnitude (if at all) and the shapes of the restitution curves were largely unaffected by the AF modifications. In determining CV and CV memory, the influence of the currents appears to be stronger, an association which seems logical given the close connection between CV and the sodium current.

In determining the stability of spiral waves, however, calcium dynamics, and specifically the shape and magnitude of the calcium transient, appear to have a dominant effect. The effect of the calcium dynamics is not seen through independent calcium behavior, such as destabilization via calcium transient alternans, but rather through the interrelationship between calcium and the transmembrane currents, especially the L-type calcium current. The calcium dynamics of the NM never lead to spiral wave breakup in any of the model variants, including the NM-X and NMf-X. Although it is possible that different parameter sets not tested could lead to breakup, it seems likely that the NM calcium dynamics play an important role in promoting spiral wave stability, given that all ten of the stable parameter variants tested used these calcium dynamics. In contrast, the calcium dynamics of the CM were associated with breakup or quasi-breakup in three of the four cases tested. Only the CM-AF, with its greatly reduced calcium current (see Fig. 13C), produced a stable spiral wave. Trajectories similar to that of the CM-AF were generated by the NM-X and NMf-X, which also had reduced calcium current because of their more rapid calcium transients that hastened calcium channel inactivation. However, the NM-X and NMf-X over time developed additional frequencies in their rotation, whereas the CM-AF did not. For the other NM model variants, holding the ionic concentrations fixed as described earlier appeared to promote spiral wave meander, while allowing the concentrations to vary freely promoted more circular trajectories.

Implications of model differences

There are a number of potential explanations for the differences in properties between the CM and the NM. It is possible that the two models represent spatial heterogeneity that is present natively in the human atria. Differences in APDs and rate adaptation have been found at different sites in the human right atrium (Kamalvand et al., 1999; Kim et al., 2002). Other properties also may underlie the differences, including the effects of age (Jeck and Boyden, 1992) and gender (Tanabe et al., 1999; Xiao et al., 2006).

However, the problem with assuming the models reflect existing spatial heterogeneity is that the currents formulated from human atrial cell data drew largely on the same experimental data, leaving differences in model development as the most likely explanation. One possibility discussed to some extent may be the differences in intracellular calcium handling. While the CM drew from the calcium description of Luo and Rudy (1994), the calcium handling in the NM is based on that of Lindblad et al. (1996). We have shown here that the calcium description used can have profound effects on dynamics. In addition, although the descriptions of the transmembrane currents may be similar in many ways, as analyzed by Nygren et al. (2001), there are clearly differences in the current formulations, or else the CM and CM-X would behave similarly, for instance. It is possible that some of the differences may arise because of the inclusion of current formulations not based on human atrial data. The remaining differences must be attributed to choices involved in model creation, including underlying AP and calcium transient shapes, curve fitting, and setting relative conductance values.