Exploration dynamics in evolutionary games

Abstract

Evolutionary game theory describes systems where individual success is based on the interaction with others. We consider a system in which players unconditionally imitate more successful strategies but sometimes also explore the available strategies at random. Most research has focused on how strategies spread via genetic reproduction or cultural imitation, but random exploration of the available set of strategies has received less attention so far. In genetic settings, the latter corresponds to mutations in the DNA, whereas in cultural evolution, it describes individuals experimenting with new behaviors. Genetic mutations typically occur with very small probabilities, but random exploration of available strategies in behavioral experiments is common. We term this phenomenon “exploration dynamics” to contrast it with the traditional focus on imitation. As an illustrative example of the emerging evolutionary dynamics, we consider a public goods game with cooperators and defectors and add punishers and the option to abstain from the enterprise in further scenarios. For small mutation rates, cooperation (and punishment) is possible only if interactions are voluntary, whereas moderate mutation rates can lead to high levels of cooperation even in compulsory public goods games. This phenomenon is investigated through numerical simulations and analytical approximations.

Evolutionary game dynamics describes how successful strategies spread in a population (1, 2). Individuals receive a payoff from interactions with others. Those strategies that obtain the highest payoffs have the largest potential to spread in the population, either by genetic reproduction or by cultural imitation. For example, from time to time, a random focal individual could compare its payoff with another, randomly chosen role model. The role model serves as a benchmark for the focal individual's own strategy. Depending on the payoff comparison, the focal individual either sticks to its old strategy or it imitates the role model's strategy. We focus here on the simplest choice for a payoff comparison, which is the following imitation dynamics (3): If the role model has a higher payoff, the focal individual switches to the role model's strategy. If the role model has a lower payoff, the focal individual sticks to its own strategy. If both payoffs are identical, it chooses between the 2 strategies at random. The imitation dynamics can be obtained from other dynamics with probabilistic strategy adoption in the limit of strong selection (4). When only 2 strategies are present, the dynamics becomes deterministic in following the gradient of selection. In infinite populations, it leads to deterministic dynamics closely related to the classical replicator equation (5, 6). In both cases, the dynamics remains stochastic if the payoff differences vanish. For large populations and in the absence of mutations, the replicator dynamics is a useful framework to explore the general dynamics of the system. However, because it does not include any stochastic terms, it is not necessarily a good approach to describe the dynamics in behavioral experiments. In finite populations, the system is affected by noise, which can trigger qualitative changes in the dynamics.

Although imitation dynamics are a common way to model evolutionary game dynamics, they do not include the possibility to explore the available strategies. Thus, we allow for random exploration (or mutations) in addition to the imitation dynamics. In our model, mutations occur with probability μ in each update step. In genetic settings, mutations change the strategy encoded in the genome. In such a setting, the mutation probabilities μ are expected to be small. In contrast, according to behavioral experiments (8, 9), the willingness of humans to explore strategic options implies much higher mutation rates. In such settings, people not only imitate others but also act emotionally, attempt to outwit others by anticipating their actions, or just explore their strategic options (7–9). As a first approximation for a system with few strategies, we subsume the occurrence of such behavior by a large exploration rate, which leads to the continuous presence of all strategic types. For example, in compulsory public goods games without punishment, ≈ 20% of the players cooperate (M. Milinski, personal communication), even though defection is dominant. Therefore, it seems reasonable to consider mutation rates even greater than 10%.

Thus, 2 limiting cases can be considered: Either random exploration represents a small disturbance to a pure imitation process (μ ≪ 1) or imitation is a weak force affecting a purely random choice process (1 − μ ≪ 1). This second limit is a simple way to incorporate effects that cannot be captured by imitation. For both cases, we present analytical approximations.

To make our analysis more concrete, we focus on the evolution of cooperation, which is a fascinating problem across disciplines such as anthropology, economics, evolutionary biology, and social sciences (10, 11). In public goods games among N players, cooperation sustains a public resource. Contributing cooperators pay a cost c to invest in a common good (12, 13). All contributions are summed up, multiplied by a factor r (1 < r < N) and distributed among all participants, irrespective of whether they contributed or not. Because only a fraction r/N < 1 of the focal individual's own investment is recovered by the investor, it is best to defect and not to contribute. This generates a social dilemma (14): Individuals that “free ride” on the contributions of others and do not invest perform best. Such behavior spreads, and no one invests anymore. Consequently, the entire group suffers, because everyone is left with zero payoff instead of c(r − 1) (15). This outcome changes if individuals can identify and punish defectors. Punishment is costly and means that one individual imposes a fine on a defecting coplayer (7, 16–21). The establishment of such costly behavior is not trivial (22, 23): A single punishing cooperator performs poorly in a population of defectors. Moreover, punishment is not stable unless there are sanctions also on those who cooperate but do not punish. Otherwise, such “second-order free riders” can undermine a population of punishers and pave the way for the return of defectors. Recently, Fowler (24) has proposed that punishment is easily established if the game is based on voluntary participation rather than compulsory interactions. However, for infinite populations and vanishing mutation rates, the dynamics of the resulting deterministic replicator equations are bistable as well as structurally unstable (25). Nevertheless, Fowler's intuition is confirmed for finite populations and small mutation rates (22). In this case, the initial conditions determine the outcome of the process.

Methods

Here, we focus on the effect of random exploration and demonstrate that the mutation rate can trigger qualitative changes in the evolutionary dynamics (26–30). To illustrate how increasing mutation probabilities affect the evolutionary dynamics, we address the evolution of cooperation and punishment in N-player public goods games in finite populations. A group of N individuals is chosen at random from a finite population of M individuals. If interactions are not mandatory, individuals can choose whether they participate in the public goods game (as cooperators C or defectors D) or refuse to interact (14, 31, 32). The public goods game represents a risky but potentially worthwhile enterprise. If it fails, nonparticipating loners (L) relying on a fixed income σ are better off. However, if it succeeds, participation is profitable. Thus, the loner payoff σ is larger than the payoff in a group of defectors but smaller than in a group of cooperators, 0 < σ < (r−1)c. Loners affect the average number of participants S (S ≤ N). Whenever only a single cooperator or defector joins the game (S = 1), he acts as a loner. The introduction of loners generates a cyclic dominance of strategies: If cooperators abound, defection spreads. If defectors prevail it is better to abstain and the average S decreases. For S < r investments in the public good yield a positive return, and hence, cooperators thrive again. However, the increase of cooperators also increases S and thus reestablishes the social dilemma. This rock–paper–scissors like dynamics has been confirmed in behavioral experiments (8). Here, we consider also a fourth strategic type, the punishers (P) who cooperate and invest but, in addition, punish the defectors (22, 25). Punishing a defector costs γ and reduces the defector payoff by β > γ. We consider a generic choice of parameters leading to nontrivial dynamics: Punishment is less costly to the punisher than to the punished player, β > γ. Furthermore, r < N, such that defection dominates cooperation. In addition, our analysis makes the weak assumption that a population of only punishers and defectors is bistable, i.e., punishers cannot invade a defector population, and defectors cannot invade a punisher population. This is a weak requirement, because otherwise punishment is either trivial (for vanishing costs, P dominates D) or impossible (if the costs exceed the fines, D dominates P), see supporting information (SI) Appendix.

Our analytical approach works as follows: First, we calculate the payoffs of each strategy in one particular interaction with i_C cooperators, i_D defectors, i_L loners, and i_P punishers. Next, we compute the probability that an interaction group has a certain composition, i.e., that it includes a particular number of each type. This determines the average payoffs of the 4 strategies, π_C, π_D, π_L, and π_P, which depend on the composition of the population X = (X_C, X_D, X_L, X_P). Details of these calculations can be found in the SI Appendix. The average payoffs form the basis of the evolutionary dynamics, because they determine the probability, T_j→k(X), to choose a type j individual and transform it into type k. The dynamics of the system in infinite populations has been discussed before in detail (25, 31, 32). It turns out that if all 4 strategies are available, the dynamics is bistable as well as structurally unstable. The system either converges to cycles of cooperators, defectors and loners, such that no punishers are present, or to a neutral mixture of cooperators and punishers, such that no loners and defectors are present (25). Thus, we focus on finite populations and consider 2 different analytical approaches: (i) For small mutation rates, a mutant goes extinct or takes over the population before the next mutation occurs. In this case, the dynamics can be described by an embedded Markov chain based on the transitions between pure states, where all players use the same strategy. (ii) For large mutation rates, the Master equation determining the evolutionary dynamics of the system can be approximated by a Fokker–Planck equation, which governs the stationary distribution.

For the technical details of these 2 analytical approaches, we refer to the SI Appendix. Here, we concentrate on the qualitative features of the resulting dynamics.

Results and Discussion

First, we turn to the evolutionary dynamics of finite populations for small mutation rates, μM² ≪ 1 (22, 33). In this case, the time scales of mutation and imitation are separated. The system is homogeneous most of the time, i.e., all individuals use the same strategy, and only occasionally a mutation occurs. The mutant will either reach fixation or extinction before the next mutant arises. Thus, we can restrict our analysis to a pairwise comparison of pure strategies, where all individuals use the same strategy. The full Markov chain of the system on a large state space can be approximated by an embedded Markov chain between the pure states. Interestingly, for imitation dynamics the transition probabilities—and thus the fixation probabilities—are completely independent of the interaction parameters (see SI Appendix). For imitation dynamics, this is a generic result for any game unless a stable coexistence of at least 2 strategies exist. In our case, stable fixed points on the edges appear only for parameters violating our “generic” assumptions. In contrast to many other types of selection dynamics with weaker selection (22), only the population size M enters in the transition probabilities. Thus, the stationary distribution only depends on the population size (see SI Appendix).

In the standard public goods game, defectors naturally dominate cooperators: A defector can take over a cooperator population, but a cooperator cannot invade a defector population.

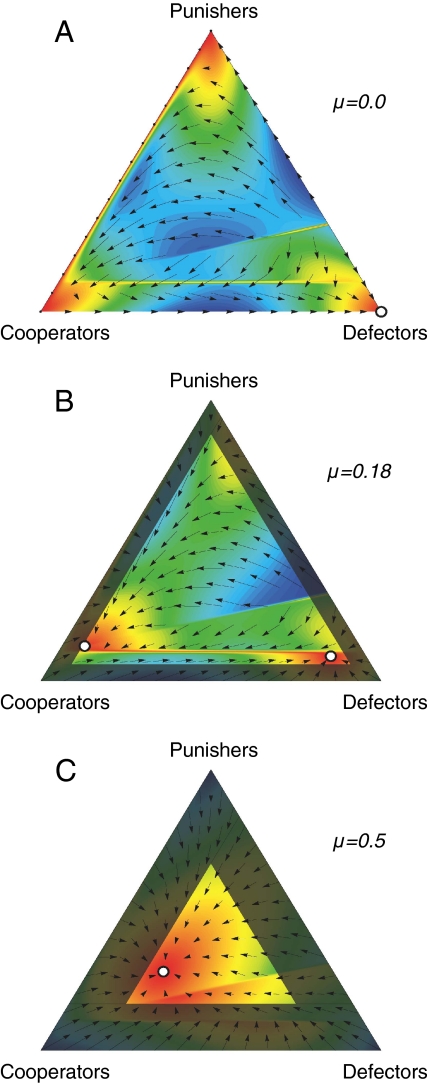
In public goods games in which cooperators have the option to punish defectors, the resulting dynamics can be characterized as follows: In the state with punishers only, no deviant strategy obtains a higher payoff. However, the situation is not stable, see Fig. 1A: Cooperators obtain the same payoff and can thus invade and replace punishers through neutral drift. Once cooperators have taken over the whole population, defectors are advantageous and take over. Thus, this evolutionary end state is observed regardless of the availability of the punishment option, see Fig. 2 A and B: For μ → 0, defectors prevail.

Fig. 1.

Dynamics of the system with cooperators, defectors and punishers in the simplex S₃ for different mutation rates. The arrows show the drift term 𝒜_k(x) of the Fokker–Planck equation, white circles are stable fixed points in the limit M → ∞. The discontinuities are a consequence of the strong selection. Blue corresponds to fast dynamics and red to slow dynamics close to the fixed points of the system. The system does typically not access the gray shaded area, because the minimum average fraction of each type because of mutations is μ/3. (A) For vanishing mutation probability (μ → 0), there is only 1 stable fixed point in the defector corner. (B) For μ = 0.2, there are 2 stable fixed points, one close to the cooperator corner and one close to the defector corner. The population noise can drive the system from the vicinity of one of these points to the other, which makes an analytical description of the dynamics difficult. (C) For μ = 0.5, there is only a single stable fixed point, which is closest to the cooperator corner—thus, cooperators prevail for high mutation rates. We use the position of this fixed point as an estimate for the average abundance of the strategies, see Fig. 2 [parameters: M = 100, N = 5, r = 3, c = 1; β = 1, γ = 0.3; σ = 1, graphical output based on the Dynamo software (37)].

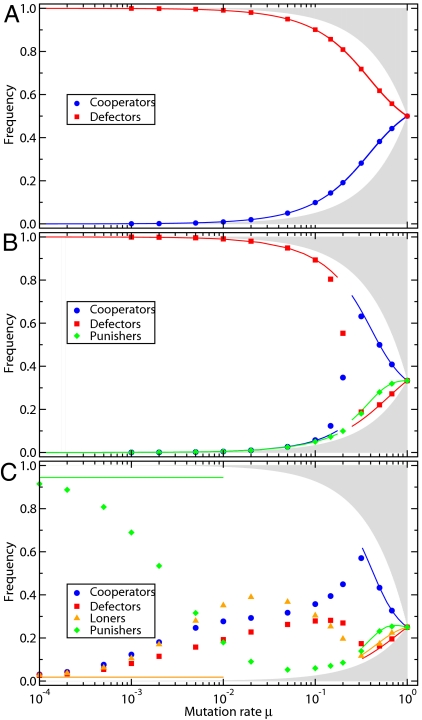
Fig. 2.

Imitation dynamics for different mutation rates. Symbols indicate results from individual-based simulations (averages over 10⁹ imitation steps), and solid lines show the numerical solution of the Fokker–Planck-equation, corresponding to a vanishing drift term 𝒜_k(x), see SI Appendix. Because a fraction μ of the population always mutates, the minimum fraction of each type is μ/d (for d strategies) and the gray shaded areas are inaccessible to the process. Although previous approaches have focused on small mutation rates, large mutation rates change the outcome significantly. (A) In compulsory public goods interactions, defectors dominate cooperators for all mutation rates. (B) In compulsory public goods interactions with punishment, defectors only dominate for small μ. For high mutation (or exploration) rates μ, cooperators dominate, see Fig. 1 for details. Despite their small abundance, punishers are pivotal for the large payoff and high abundance of cooperators for μ > 0.2. (C) In voluntary public goods games, cooperators dominate for high mutation rates as well. Although this effect does not depend on the presence of loners, these are essential for the success of punishers for small mutations. The horizontal lines for small μ, to which the symbols converge for μ → 0, is the stationary solution of the Markov chain, see SI Appendix (parameters: M = 100, N = 5, r = 3, c = 1; β = 1, γ = 0.3; σ = 1).

In voluntary public goods games without punishment, there is cyclic dominance. In finite populations, it manifests itself as follows: When defectors dominate, taking part in the game does not pay, and the loners that do not participate have the highest payoff. When there are no participants, a single cooperator does not have an advantage (because there is no one to play with). However, as soon as the second cooperator arises by neutral drift (which happens with probability $\frac{1}{2}$), cooperators take over, and the cycle starts again. Thus, in the long run, the system will spend 50% of the time in the loner state and 25% in the cooperator and defector states, respectively (see SI Appendix).

If we combine all 4 options, the loner option provides an escape hatch out of mutual defection: As soon as loners take over, they pave the way for the recurrent establishment of cooperation, either with or without punishment (22): In the vicinity of the loner state L, the dynamics is neutral as long as, at most, a single participant is present (S = 1). A second participant arises by neutral drift with probability $\frac{1}{2}$. Both cooperators and punishers are advantageous as soon as S ≥ 2 and ultimately take over. If cooperation without punishment is established, defectors are advantageous and can invade. However, if punishers take over, it may take a long time before nonpunishing cooperators take over via neutral drift, because, on average, M invasion attempts are necessary before fixation occurs. A detailed analysis of the transition matrix of the system shows that the system is in state C, D, or L with probability p = 2/(8 + M), see SI Appendix. With the remaining probability 1 − 3p = (2 + M)/(8 + M), the system is in state P. Because lim_M→∞p = 0, punishers prevail for large M. Even though the system spends vanishingly little time in the loner state, they are pivotal to tip the scale in favor of cooperation (and punishment), see Fig. 2 (22).

The small mutation rates are fully justified under genetic reproduction, but this approximation seems to be less appropriate to model cultural evolution or social learning. For high mutation rates, the previous analytical approximation fails, because the time scales between imitation and mutation are no longer separated. For high mutation or exploration probabilities and large populations, Mμ ≫ 1, all strategies are always present in the population. Thus, mutations generate a fixed background of all strategic types. Additionally, the dynamics is also affected by noise arising from the finite population size M. To describe the system analytically, we can approximate the underlying master equation of the system by a Fokker–Planck equation. The drift term captures the deterministic part of the dynamics. The diffusion term takes stochastic fluctuations into account that arise from the finite population size M. For μ → 1, there is no imitation, and the only equilibrium is equal abundance of all strategies. For smaller μ, several stable equilibria may exist, but the stochastic noise preferentially leads to the equilibrium with the largest basin of attraction. This approach works best for large M, because in this case, the noise is too weak for the system to switch repeatedly between equilibria. In addition, we need large μ, such that only 1 or very few equilibria exist. For M → ∞ and μ → 0, this approach essentially recovers the replicator equation again (34, 35).

The continuous presence of all strategic types for large μ is reflected by a drift away from the boundaries of the simplex, see Fig. 1. If only cooperators and defectors are present, this leads to a nonvanishing fraction of the dominated cooperators, see Fig. 2A. If also the punishment option is available, large μ implies that defectors are always punished and cannot take over, whereas punishers suffer from the persistent need to sanction defectors. Consequentially, cooperators perform best, because they can rely on the punishers to decrease the payoff of defectors, see Figs. 1 and 2B. In agreement with behavioral experiments (36), punishers bear the costs of punishment and do not win. Nonetheless, the punishment option is often chosen (21, 36). The option to abstain has no qualitative influence for large μ and barely changes the outcome, see Fig. 2C. The pivotal role of loners to promote cooperation for small μ falls to punishers for large μ: Even though the average fraction of punishers is barely higher than that of defectors, punishers are responsible for the success of cooperators. Thus, large exploration rates can lead to a significant increase of cooperation.

To summarize, we have shown that for rare mutations, the imitation dynamics in a finite population of size M becomes independent of the parameters r, N, β, γ, and σ, because the fixation probabilities depend only on the ranking of payoffs and not on their detailed values. For rare mutation rates, the average abundance of the strategy is entirely governed by the fixation probabilities. Interaction parameters are relevant only when the mutation rate μ increases. Most importantly, however, the magnitude of μ can have crucial effects on the qualitative features of the dynamics. For low mutation probabilities cooperation (and punishment) gets established only in voluntary public goods interactions. If participation is compulsory, cooperation is not feasible at all, even with punishment. In contrast, high mutation or exploration probabilities lead to the prevalence of cooperators irrespective of whether individuals have the option to abstain from the public enterprise. Thus, large exploration rates can lead to a significant increase of cooperation.

In evolutionary game theory, it is common practice to assume small mutation rates. This is, of course, justified by the small probabilities of genetic mutations. However, when turning to imitation dynamics, social learning or cultural evolution, exploration probabilities may be high and may turn into an important and decisive factor for the evolutionary fate of the system.