Height, health, and inequality: the distribution of adult heights in India

This paper explores the relationship between adult heights and the distribution of income across populations of individuals. There is a long literature that examines the relationship between mean adult heights and living standards. If adult height is set by the balance between food intake and charges to disease in early childhood, it is informative about economic and epidemiological conditions in childhood. Because taller populations are better-off, more productive, and live longer, the relationship between childhood conditions and adult height has become an important focus in the study of the relationship between health and wealth. Here I follow one of the tributaries of this main stream. A relationship between income and height at the individual level has implications for the effects of income inequality on the distribution of heights. These relationships parallel, but are somewhat more concrete than, the various relationships between income inequality and health that have been debated in the economic and epidemiological literatures, Richard G. Wilkinson (1996), Angus Deaton (2003).

If height is an increasing but concave function of income, average height will be negatively related to income inequality, Richard Steckel (1995). Income inequality will also have implications for the dispersion of height, so that inequality in height might serve as an indicator of inequality of income in the absence of data on the latter, just as mean height might serve as an indicator of mean income, Aravinda M. Guntupalli and Joerg Baten (2006) and Alexander Moradi and Baten (2005). Differences in height between subpopulations, such as lords and vassals, or highlanders and lowlanders, may also provide information on the distribution of resources between such subpopulations,Carles Boix and Frances Rosenbluth (2006). In Section 2 below, I present a theoretical discussion of what to expect. In Section 3, I provide an analysis of adult heights in India, where I can look at the relationship across states between (a) mean heights and expenditure inequality, (b) inequality in height and expenditure inequality, (c) men’s and women’s heights. The difference in heights between men and women is of considerable importance in its own right. India has one of the highest rates of child malnutrition in the world with around 55 percent of young children stunted. A leading explanation for this is health discrimination against women, Vulimiri Ramalingaswami,Urban Jonsson and Jon Rohde (1996). If discrimination starts in early childhood, and since all evidence suggests that there are regional differences in the treatment of women, there should be clear traces in spatial patterns of relative heights between men and women.

I. Income inequality and the distribution of heights

Suppose that each person’s adult height is an increasing and concave function of income. Then mean population height will depend, not only on mean income, but on the distribution of income, Steckel (1995). For example, if the underlying individual relationship is quadratic, mean height will be a positive function of mean income and a negative function of the variance of income. This proposition depends only on the existence of a concave relationship between height and income, albeit between adult height and childhood income. It does not require that income be the only determinant of height and it is indeed consistent with an account in which the epidemiological environment in childhood is the dominant factor.

A relationship between inequality in income and inequality in heights is relatively easy to establish in the case of two groups, for example men and women, or boys and girls. This is parallel to the historical case, where groups born in better times were taller as adults, though as always the effects may be overridden by variations in disease. To the extent that boys and girls of the same cohort experience the same epidemiological environment, variations in the differences in adult height of men and women will reflect nutritional differences or differences in access to healthcare in their childhood. There is also a biological theory of sexual dimorphism, according to which males of a species become larger in response to the need to compete with other males for females so that, for example, males are relatively larger in species that are relatively more polygamous. In the Indian context, this suggests the hypothesis that males will be relatively taller in places where the ratio of females to males is lowest and where more women are “missing.” Such an effect would reinforce the effects of nutritional or health discrimination against women; men are larger in order to compete with other men for the relatively small pool of women, which itself comes about because of the nutritional and health advantage of boys over girls.

The relationship between income inequality—as in standard measures such as the gini coefficient—and inequality of heights is harder to establish with any generality. The argument in the literature is an intuitive one that parallels the argument about groups—if height indicates income, then inequality in income should show up in inequality in heights—but this will not hold in general. If height is a concave increasing function of income, second-order stochastic dominance in the distributions of income will be inherited by the distribution of heights. But when we compare the inequality of distributions, we look at distributions scaled by their means and use Lorenz dominance, not second-order stochastic dominance, and Lorenz dominance will typically not be passed from the income to the height distribution. Taking again the example where height is a quadratic function of income, the variance of heights depends on the second, third, and fourth moments of the income distribution, and if we measure inequality independently of the mean by using the coefficient of variation—as we would do for incomes—we obtain an expression that depends on the first four moments of income and so is not a function of any standard measure of income inequality. And even this takes no account of distribution of other components of adult heights, most obviously genetic effects, and their possible covariance with income.

However, there are special cases that yield relatively simple results. For example, if the logarithm of height is a linear function of the logarithm of income, so that

$$\ln h_i=\alpha +\beta \ln y_i+{\epsilon }_i$$ (1)

for height h of individual i, with income y_i and other factors ε_i including genetics, as well as the effects of idiosyncratic childhood disease. Under the (strong) assumption that these other factors are distributed independently of the logarithm of income, we

$$\mathrm{var}(\ln h)={\sigma }_{\epsilon }^2+{\beta }^2\mathrm{var}(\ln y)$$ (2)

so that the two inequality measures are linearly related across populations, at least provided that the genetic and other variation is constant. But this result is clearly fragile. For example, if in (1) we replace the logarithm of height by its level, the variance of height itself will have the form (2), but the coefficient of variation will also depend on the mean of log y.

II. Height, gender, and inequality in India

My data come from the third round of India’s National Family Health Survey, (NFHS) conducted in 2005–2006 throughout the country. The NFHS is India’s version of the Demographic and Health Survey. The 2005–2006 survey is the first to collect data on men’s as well as women’s heights; these are directly measured by the enumerators, not self-reported. I merge the NFHS data at the state level with data from the National Sample Survey (NSS), which collects extensive household expenditure data. (Merging at finer disaggregation than the state level is impossible because there are no district identifiers in the NFHS data, as a result of the human subjects protocols associated with the measurement of HIV prevalence in that survey; and the restriction to the state level is one of the main weaknesses of my analysis.) The 1983 round of the NSS, which sampled 115,529 households, is my main source because it is the oldest survey currently available, and because we would ideally like to match individual heights to living conditions in their year of birth; this is not possible, and using the 1983 survey is as close as I can get. I also use the 2004–2005 NSS, which sampled 124,560 households, to document living conditions at the time of the NFHS survey. Although living conditions in 2004–2005 played no role in setting contemporaneous adult heights, there is a possible reverse causality from heights to living standards, and there is a good deal of persistence in living standards over time. For the 34 states for which I have observations, the interstate correlation between the average of the logarithms of per capita total household expenditure (PCE) in 2004–2005 and 1983 is 0.89, while for the standard deviation of the logarithm of PCE , the correlation is 0.57. There are three new states, Chhattisgarh, Jharkhand, and Uttaranchal, that appear in the NFHS and in the 2004–2005 data from the NSS but did not exist in 1983; in order to maximize the number of observations, I “created” them in the 1983 data from the appropriate regions of the parent states.

An immediate issue with the measurement of heights is to account for the relationship between height and age. In India, as in historical data from Europe, people attain their adult height only in their twenties, several years later than in contemporary rich countries. Figure 1 shows the relationship between mean height and age for men and women in India in 2005–2006; the two scales differ only by a shift of 10 cm, so that the slopes of the two curves are in the same units. The sharp rise on the left to a peak shows that people reach adult height in the early 20s. The mean difference between men and women between ages 20 and 54 is 12.5 cm, a little less than the 14.2 cm difference in measured heights in the U.S. for men and women 20 or older, but the extent of sexual dimorphism in heights, defined here as the difference in mean heights divided by the average of mean heights, is 8.1 percent, as opposed to 8.4 percent in the U.S., much closer than the average heights themselves (176.5 and 162.2 cm in the U.S.)

Figure 1.

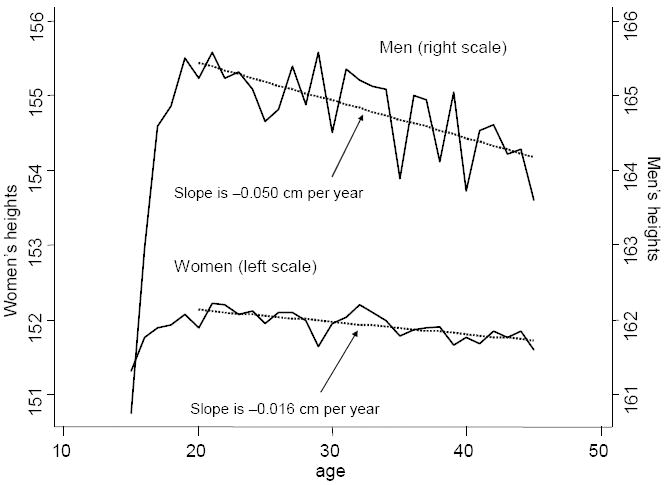
Heights and age

After the mid-20s, heights decline with age, which is typically interpreted as a cohort effect, that later born people, who in a growing economy experience better nutritional and epidemiological environments in childhood, and perhaps even better health care, are taller. However, it is also possible that there is some shrinkage with age, though this is thought to be unimportant prior to age 50. There may also be height-selective mortality, with shorter people more likely to die as adults than taller people. Yet mortality rates among young adults are low, especially among men, who show the sharpest decline with age. On the most likely interpretation, then, that of cohort effects, Figure 1 shows that Indians—who are among the shortest people in the world, Deaton (2007)—are getting taller, but that Indian men are doing so at more than three times the rate of Indian women. (The two dotted lines are regressions of height on age for people aged 20 or more.) Sexual dimorphism in height has increased from 7.8 percent in the cohort born between 1960 and 1965 to 8.2 percent in the cohort born between 1975 and 1980. I do not know how to explain this change other than through differential access to whatever improvements there have been in health or food or both.

If discrimination against girls or women is one of the causes of sexual dimorphism in heights in India, or of its increase over time, sexual dimorphism should also be related to other measures of sex discrimination. The differential trend in adult heights is consistent in direction with the century long decline in the female to male ratio (FMR) in India, from 0.97 in 1901 to 0.93 in 2001, see P. N. Mari Bhat (2002, Figure 6) and Jean Drèze and Amartya Sen (2002, Chapter 7). Since 1951, this decline in the FMR has been mainly driven by a decline in the FMR at ages 0–14, at least some of which has come from a decline in the FMR at birth. However, it may also reflect (different sources are inconsistent) a decrease in the survival rate of girls relative to boys against a background of increasing survival rates for both. If so, the general improvement in morbidity in early childhood may be larger for boys than for girls, leading to differential trends in adult heights, in much the same way as temporal and spatial variations in post-neonatal mortality in Europe after 1950 led to inverse patterns of adult height, Carlos Bozzoli, Deaton, and Climent Quintana-Domeque (2007).

We can also make interstate comparisons of sexual dimorphism in height to the ratio of males to females in the population which I measure here in a comparable way to the height dimorphism, as the difference between the population of males and females as a percentage of their average. Note that this measure could also be motivated by the biological literature that links sexual dimorphism in size to the competition by males for mates. Figure 2 presents a mixed but suggestive picture. The correlation over the 29 states is −0.065. However, this gives the same weight to all states and the figure shows that much depends on the five very small north-eastern states, Sikkim, Meghalaya, Nagaland, Mizoram, and Arunachal Pradesh, where sexual dimorphism is low. If the correlation is calculated weighted by state populations, it rises to 0.33, and if Delhi is excluded on the grounds that the high ratio of men to women has more to do with migration than discrimination, the correlation is 0.44. Of course, by this point we are resting on a small number of states, which is the best that can currently be done given the lack of finer geographical disaggregation in the NFHS3.

Figure 2.

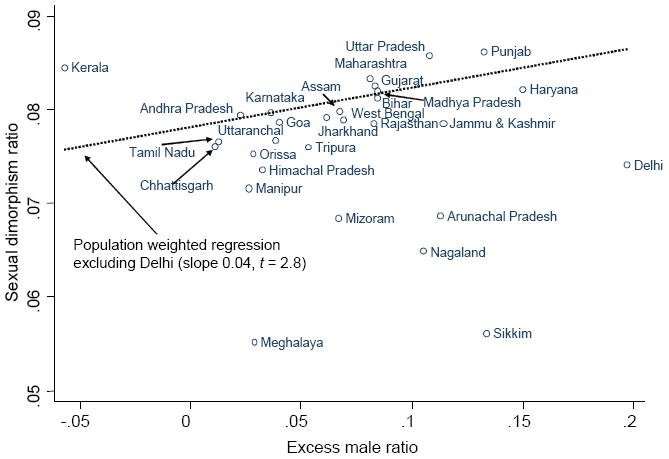
Sexual dimorphism and missing women

Table 1 shows the populations, age-adjusted heights, and decadal rate of change of heights by sex and state. The age-adjustment is carried out by running a regression for each sex in each state of height on age minus 20 using those aged 20 to 45. The intercepts of these regressions, predicted height at age 20, are the age-adjusted heights, and the slopes—with the sign changed and multiplied by ten—are the decadal increases in height. The estimated standard error of the regression is used as an age and trend-adjusted measure of the dispersion of heights.

Table 1.

Indian heights and growth in heights, by state and sex

	Population (millions, 2001)	Height at 20 (cm)		Cm increase per decade
		Men	Women	Men	Women
Jammu & Kashmir	10.14	168.3	154.9	1.09	0.38
Himachal Pradesh	6.09	167.1	153.9	1.31	0.18
Punjab	24.36	168.6	154.6	−0.04	−0.04
Uttaranchal	8.49	165.4	153.1	0.41	0.35
Haryana	21.14	168.1	154.8	−0.04	−0.10
Delhi	13.85	165.8	153.6	−0.05	−0.37
Rajasthan	56.51	167.5	154.6	0.25	0.02
Uttar Pradesh	166.20	164.6	150.7	0.33	−0.04
Bihar	83.00	163.8	150.4	0.40	−0.17
Sikkim	0.54	160.7	151.7	0.74	0.45
Arunachal Pradesh	1.10	160.5	151.0	−1.06	0.06
Nagaland	1.99	163.1	152.5	0.10	−0.22
Manipur	2.29	163.5	152.3	0.18	0.31
Mizoram	0.89	163.3	152.0	0.77	0.24
Tripura	3.20	161.6	150.2	−0.09	0.28
Meghalaya	2.32	157.2	149.1	−0.57	−0.19
Assam	26.66	163.6	150.6	0.42	0.01
West Bengal	80.20	164.6	151.1	1.13	0.19
Jharkhand	26.95	162.7	150.2	0.18	0.12
Orissa	36.80	163.0	151.0	0.15	−0.04
Chhattisgarh	20.83	163.9	151.8	0.37	0.30
Madhya Pradesh	60.35	165.7	152.5	0.01	−0.08
Gujarat	50.67	166.3	152.9	0.48	0.29
Maharashtra	96.88	166.1	152.5	0.79	0.49
Andhra Pradesh	76.21	165.0	152.3	0.64	0.58
Karnataka	52.85	166.0	152.7	0.60	0.07
Goa	1.35	166.2	152.4	1.07	−0.05
Kerala	31.84	168.3	154.6	1.29	1.16
Tamil Nadu	62.41	165.8	153.4	0.84	0.66

Notes: Population from Census of India 2001, http://www.censusindia.gov.in/Census_Data_2001/Census_data_finder/A_Series/Total_population.htm accessed December 22^nd, 2007. Other columns from author’s calculations using NFHS3 of 2005–2006. Using data on men and women aged 20 to 45 (inclusive), regressions were run of height on age by state and sex. Height at 20 is predicted height at age 20 and the increases are (minus) ten times the coefficient on age.

In most states, both men (23 states) and women (19 states) have grown taller over time, and men have grown more than have women (24 states). Men’s and women’s heights are correlated across states, 0.86 unweighted and 0.90 population weighted, as is the growth of heights, 0.55 unweighted and 0.70 weighted. Regressions of the rate of change of men’s and women’s heights on the change in the logarithm of PCE from 1983 to 2004–2005 have coefficients of 0.233 (t = 3.6) (men) and 0.222 (t = 4.1) (women); the differential rate of growth is uncorrelated with the growth of PCE. These results appear to suggest that some catch up growth is possible—contrary to much of the literature—or they may reflect long-run persistence in economic growth of Indian states.

Table 2 turns to the relationship between the distribution of heights an the distribution of per capita expenditure. It shows cross-state population-weighted regressions of (adjusted) height and its (adjusted) standard deviation on the state averages and standard deviations of the logarithm of total household per capita expenditure (lnpce) from the NSS for 1983. The regressions on heights at age 20 show a consistent positive effect of lnpce on heights, somewhat larger for women than men, but statistically significant in both cases. However, the effect of inequality in lnpce has the opposite sign from that predicted by a concave relationship between height and income; conditional on the level of living, more unequal places have taller men and women, though the estimated effects are barely significant. (The regressions on unadjusted height are very similar, so the age-adjustment is not very important in these regressions.

Table 2.

Means and dispersion in heights

	Height at 20 (cm)		Adjusted s.d. of height
	Men	Women	Men	Women
ln pce in 1983 (t-value)	5.34 (3.4)	5.85 (4.6)	0.36 (1.5)	0.85 (3.6)
sd ln pce in 1983 (t-value)	7.26 (1.7)	7.65 (2.2)	−0.40 (0.6)	1.72 (2.7)
Number of states	29	29	29	29

Notes: based on the same statewise regressions described in Table 1. The first two columns regress the predicted heights at 20 across the 26 states on the state average of the logarithm of household total expenditure per capita (lnpce) and on the state standard deviation of lnpce. The last two columns report the regressions with the same independent variables but with the regression standard error as dependent variable; these choices of adjusted dependent variable are intended to remove the effects of different age structures in different states. All regressions are weighted by total state population.

The regressions in the last two columns explore the possibility of using dispersion in adult heights as a measure of income—here expenditure—inequality. I include the mean of lnpce as well as its dispersion because, as discussed in Section 2, inequality of heights may depend on both the mean and dispersion of expenditure, depending on the functional form linking heights and expenditures. Once again, the results are quite mixed. For men, neither lnpce nor its standard deviation predicts the standard deviation of heights. For women, both do so, though it is hard to take much encouragement from this last result in the absence of a parallel result for men, and in the absence of any theoretical reason why inequality in women’s height should indicate income inequality, while inequality in men’s heights does not. We are almost certainly looking at some other phenomenon here, though at this stage it is unclear what it might be. Indeed, even the link between mean height and income is far from established, see particularly the analysis of global heights and income in Deaton (2007), where there is no relationship between mean height of women and GDP in the year of birth across poor countries in Asia, Africa, and Latin America.