Metric Learning Using Iwasawa Decomposition

Abstract

Finding a good metric over the input space plays a fundamental role in machine learning. Most existing techniques use the Mahalanobis metric without incorporating the geometry of positive matrices and experience difficulties in the optimization procedure. In this paper we introduce the use of Iwasawa decomposition, a unique and effective parametrization of symmetric positive definite (SPD) matrices, for performing metric learning tasks. Unlike other previously employed factorizations, the use of the Iwasawa decomposition is able to reformulate the semidefinite programming (SDP) problems as smooth convex nonlinear programming (NLP) problems with much simpler constraints. We also introduce a modified Iwasawa coordinates for rank-deficient positive semidefinite (PSD) matrices which enables the unifying of the metric learning and linear dimensionality reduction. We show that the Iwasawa decomposition can be easily used in most recent proposed metric learning algorithms and have applied it to the Neighbourhood Components Analysis (NCA). The experimental results on several public domain datasets are also presented.

1. Introduction

In many machine learning, pattern recognition and data mining problems, the distance measures (or metrics) used over the input data space play a fundamental role. For example, the nearest neighbor algorithms, multi-dimensional scaling and clustering algorithms such as K-means, all depend critically on whether the metric used truly reflects the underlying relationships between the input instances. The problem of finding a good metric over the input space has attracted extensive attention recently. Several recent papers have focused on the problem of automatically learning a distance function from examples or training sets [2, 6, 7, 10, 11, 13–15]. Most existing metric learning methods assume the metrics to be quadratic forms parameterized by positive (semi-) definite (PSD) matrices, which leads to a constrained optimization problem.

In this paper we address the difficulties and problems associated with various techniques which are used in previous work towards learning a PSD matrix. We introduce the Iwasawa decomposition which leads to a unique and effective parameterization of the space of (n × n) SPD matrices denoted by _n. We derive the analytical Jacobian of this parameterization and point out that in most cases the original complicated constrained optimization problem can be transformed to a smooth convex nonlinear optimization problems with much simplified constraints. A modified Iwasawa coordinates is also introduced in order to parameterize the rank-deficient PSD matrices, which can be used to perform metric learning and dimensionality reduction simultaneously. Finally, we investigate the combination of Iwasawa decomposition and a recent proposed metric learning algorithm, namely, Neighbourhood Component Analysis (NCA), and present comparisons with several other techniques in clustering and classification tasks.

2. Previous Work

In general, finding a universally “good” metric suitable for different tasks and datasets can be difficult if not impossible. Usually, in order to learn a data-dependent or context dependent metric, some auxiliary data, or side-information, which is in addition to the input data set, must be made available. Our current work belongs to the research theme that focuses on learning a “good” metric using equivalence constraints. More specifically, the prior knowledge on (dis)similarity from small groups of data is assumed to take the form of (i, j, v) ∈ Ω × Ω × {+1, −1}. Each example is composed of an instance pair (i, j) and an equivalence flag v equals +1 if i and j are considered similar and −1 otherwise. Note the pair with flag +1 only implies that the two objects associated with this pair are known to originate from the same class (or with large possibility), although their own labels are still unknown as in a clustering or classification problem. The positive relation is transitive while the negative relation is not. Obviously the supervised classification problem with labeled training sets can be formulated in terms of the equivalence constraints but not vice verse. Now the goal is to learn a distance (semi)metric d(i, j) over Ω which respects the given side-information. Most existing methods assume the metric to be in the form of Mahalanobis distance, i.e., as the square root of a quadratic form $d_{\text{A}}=\parallel x-y\mid {\mid }_{\text{A}}=\sqrt{{(x-y)}^{\text{T}}\text{A}(x-y)}$ where A ≽ 0 is a symmetric positive (semi)definite matrix. Examples of previous work in this area include [2, 4, 8, 14].

Let 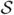denote the set of similar pairs and 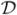the set of dissimilar pairs. A natural way of defining a criterion for the desired metric is to demand that pairs in 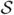, have, say a small distance between them, while pairs of 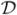have distance as large as possible. For example, Xing et al. [14] defines the criterion to be the sum of squared distances between the similar pairs and solves the optimization problem:

$$\underset{\text{A}\succcurlyeq 0}{min}\sum _{(i,j)\in \mathcal{S}}\parallel x_i-x_j\mid {\mid }_{\text{A}}^2\text{s}.\text{t}.\sum _{(i,j)\in \mathcal{D}}\parallel x_i-x_j\mid {\mid }_{\text{A}}\ge c$$ (1)

The inequality constraint has to be added in order to prevent A from shrinking to 0. Here c is an arbitrarily chosen positive number since most applications of metric learning algorithms do not depend on the scale of the metric. Note the sum of distances but not the sum of squared distances is used in the inequality constraint, otherwise the optimization problem is trivially solved by a rank-1 matrix (see [14]).

Instead of using the side in the form of pairwise constraints as in [14], Relevance Component Analysis (RCA) method [2] introduces the concept of so called chunklet whose elements are similar to each other by making use of the the transitivity of the pairwise positive constraints. Then the sum of within chunklet distances is minimized and the closed-form minimizer is shown to be the the average of the within-class covariance matrices under the assumption of Gaussian model. Neighbourhood Components Analysis (NCA) introduced in [7] directly maximizes a stochastic variant of the leave-one-out score on the training set. The corresponding optimization problem is: max_A≽0 Σ_{(i, j)∈S}p_ij where, 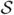is formed by the k-nearest neighbors and p_ij is defined as the softmax over the Mahalanobis distance:

$$p_{ij}=\frac{exp(-\parallel x_i-x_j\mid {\mid }_{\text{A}}^2)}{{\sum }_{k\ne i}exp(-\parallel x_i-x_k\mid {\mid }_{\text{A}}^2)}.$$ (2)

An alternative objective function proposed in [7] is based on the maximum likelihood estimation: max_A≽0 Σ_i log(Σ_{(i, j)∈S} p_ij) and is also used in the follow-up work [6] where an interesting algorithm called Maximally Collapsing Metric Learning (MCML) tries to map all points in a same class to a single location in the feature space via a stochastic selection rule.

Though there are different choices of metric learning criteria and the employment of side information, the key common issue here is to enforce the positivity constraint of A during the optimization. Both the objective functions in [14] and [13] can be reformulated as semidefinite programming (SDP) problems, however, due to the poor scalability of general-purpose SDP solvers in the number of constraints, special-purpose solvers have to be used. For example, Xing et al. [14] combine the gradient descent and iterative projections. Based on our experience with the implementation of [14], the iterative projections between two oppositive constrained sets usually result in only a few updates even during a large number of iterations, which makes the final results highly depend on the initial seting. Weinberger et al. [13] choose a more efficient alternating projections [12] which speedup the updates. However, as in [14], the positiveness needs to be checked at each step by performing a spectral decomposition and forcing the negative eigenvalues to 0.

To simplify handling the positivity constraints, Yang et al. [15] fix the eigenspace of the matrix A by taking a few top eigenvectors from the pairwise correlation matrix of the training set, then attempt to find the positive eigenvalues by maximizing a similar cost function used in [7]. Note this approach is equivalent to finding a diagonal metric matrix in a linearly transformed space and hence the finding of optimal solution is greatly limited. In addition, as pointed out in [3], the eigenvalue reformulation of the semidefiniteness constraint creates a non-smooth problem due to the multiplicity of eigenvalues.

Several recent studies [6, 7, 10, 13] on Mahalanobis metric learning use the factorization A = L^TL which interprets the Mahalanobis distance metric by performing a linear transformation on the input. Two problems accompany this approach. First, since L^TL = (RL)^T(RL) for any orthogonal matrix R, there are infinitely many L satisfying A = L^TL, if no additional constraint is put on L; Second, as pointed out in [6], the factorization A = L^TL turns a convex problem (in A) into a non-convex problem (in L). Both the infinitely many extrema and the non-convexity can cause serious concerns in the practical optimization.

Tsuda et al. [11] introduce the matrix exponential gradient update which preserves symmetry and positive definiteness due to the fact that the matrix exponential of a symmetric matrix is always a symmetric positive definite matrix. However, taking matrix exponential can be computationally expensive for the large scale problems.

3. Proposed Method

Here we propose a novel method which enables the optimization of the aforementioned cost functions to be carried out directly on the curved space 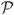_n as opposed to the Euclidean space. A significant feature of our method is the use of Iwasawa decomposition, which leads to an easy and effective parameterization of 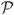_n. By choosing this parametrization, the constructed matrices will always stay on 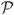_n and hence there is no need to further enforce the positivity constraint during the optimization via projections as in other approaches.

3.1. Iwasawa coordinates

As an analogue of the rectangular coordinates of Euclidean space, the so-called Iwasawa coordinates [9] is defined as follows for Y ∈ 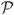_n:

$$Y=\left(\begin{array}{cc}V& 0\\ 0& W\end{array}\right)\left[\begin{array}{cc}{I}_p& X\\ 0& I_q\end{array}\right],$$ (3)

where V ∈ 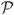_p, W ∈ 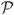_q, X ∈ ℝ^p×q and Y [g] denotes g^TY g. We shall emphasize this bracket notation of “[]” since it is heavily used in the text below. Note the above decomposition can always be solved uniquely for V, W, X once p, q and Y ∈ 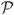_n are given. Hence, for any matrix Y = V_n in 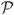_n with n > 1, by representing V_n as a tuple (V_n−1, x_n−1, w_n−1) and repeating the following partial Iwasawa decomposition:

$$V_{n+1}=\left(\begin{array}{cc}{V}_n& 0\\ 0& w_n\end{array}\right)\left[\begin{array}{cc}I& {\mathbf{x}}_n\\ 0& 1\end{array}\right]$$ (4)

where V_n ∈ 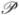_n, w_n > 0 and x_n ∈ ℝⁿ, we finally get the following vectorized expression iwasawa(V_n):

$$V_n\mapsto (((w_0,{\mathbf{x}}_1^{\text{T}},w_1),{\mathbf{x}}_2^{\text{T}},w_2),\dots ,{\mathbf{x}}_{n-1}^{\text{T}},w_{n-1})$$ (5)

which we term full Iwasawa coordinates. Note that the diagonal element w_i−1 at i(i + 1)/2-th position in Iwasawa coordinates should be positive, while off-diagonal elements x_i can be any real numbers. The full Iwasawa actually leads to the well known “LDU” factorization by Gaussian elimination. It is worth noting that any positive definite matrix has a unique Iwasawa decomposition, in contrast to a non-unique spectral decomposition. Actually, one key advantage of Iwasawa coordinates over other parameterizations is that it is closely related to the geometry of the symmetric space formed by SPD matrices (see [9]).

3.2. Smooth Convex NLP Reformulation

More importantly, the convexity of the problem can be preserved using Iwasawa decomposition according to the work presented in [3] where canonical SDP problems are expressed as smooth convex nonlinear programming (NLP) problems by replacing the semi-definiteness constraint A ≽ 0 with constraints on the diagonal entries of D (the w_i in Iwasawa coordinates) from LDU factorization. The key fact is that diagonal entries of D are twice differentiable w.r.t A and concave on 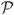_n. The resulting positive constraint on w_i can be much more easily handled. For example, − Σ log(w_i), the usual self-concordant function in convex programming, can be used here as a barrier function.

Furthermore, the one-to-one property of Iwasawa coordinates and the existence of analytical Jacobian (see below) enable the direct use of efficient gradient-based optimization techniques and make the expensive eigenvalue checking at each update unnecessary. Let vec(A) be the column vector created from a matrix A by stacking its column vectors and vech(A) be the compact form with the upper portion excluded when A is symmetric. We further define a row vector symm() for symmetric matrix such that symm(i) = vech(i) for diagonal entries otherwise symm(i) = 2vech(i). Then the jacobian of the one-to-one transformation in (5) can be easily derived from (4) in a recursive fashion:

$$J_{n+1}=\left(\begin{array}{ccc}{J}_n& 0& 0\\ (x_n^{\text{T}}\otimes I)S_n{J}_n& V_n& 0\\ \text{symm}(x_n{x}_n^{\text{T}})J_n& 2x_n^{\text{T}}{V}_n& 1\end{array}\right)$$ (6)

where S_n is the duplication matrix such that vec() = S_n vech() and ⊗ denotes the Kronecker product.

For a cost function f of A, let J_A be the gradient of f w.r.t A written in the form of a symmetric matrix, the new gradient w.r.t the Iwasawa coordinates can be easily computed as (symm(J_A))J_n where J_n is computed in (6). Hence, with this Iwasawa coordinate system, the gradient-based techniques can be used to optimize cost functions like (1) or other forms. A generic metric learning algorithm using Iwasawa coordinates is outlined in Algorithm 1.

Algorithm 1.

A simple gradient-based algorithm for minimizing the cost function f(A)

To prevent A from shrinking to 0, one can simply put constraints on those diagonal elements in the Iwasawa coordinates: e.g. 0 < c_l < w_i < c_u. Note that this bound can also be used to regularize the resulting matrix.

3.3. Dimensionality Reduction

In scenarios where the dimensionality of input data is very high, even kNN classification or k-means clustering is prohibitively expensive in terms of storage and computational costs. The traditional solution is to first reduce the dimensionality of input data and then perform subsequent learning tasks in the resulting low-dimensional subspace. Although most of the recent efforts have focused on nonlinear dimensionality reduction methods, linear techniques (which apply a low-rank linear mapping to the original data) are popular because of their simplicity, efficiency and topology preserving feature.

Recent studies [2, 7, 10] address the problem of performing metric learning and linear dimensionality reduction simultaneously by learning a low rank positive semidefinite matrix. Relevant component analysis (RCA) [2] implicitly assumes a Gaussian distribution for each class; however, this assumption is rarely true. To get a low rank matrix A, both [7, 10] employ the A = L^TL factorization and restrict L to be a non-square matrix of size r × n where r < n is the desired dimensionality. This approach, however, still suffers the non-uniqueness and non-convexity problems.

Unlike the SPD matrix, a low rank PSD matrix does not have the unique Iwasawa decomposition/coordinates. In this subsection, we introduce a modified Iwasawa decomposition to parametrize the n×n PSD matrices with prescribed rank r inspired from the non-square LDU decomposition for PSD matrices. Starting from the Iwasawa coordinates (5) with two additional conditions, namely, (1) w_i−1 = 0 for i > r; (2) x_j (i) = 0 for i > r, we can construct a PSD matrix of rank r using (4). The effective number of this modified Iwasawa coordinates is nr−(r²−r)/2, which corresponds to the dimension of the space of PSD matrices of rank r. Note the first r leading principal minors of any PSD matrix constructed using the modified Iwasawa coordinates are always positive definite. Because of this, only with permutations on both rows and columns, the modified Iwasawa coordinates can cover the entire space of PSD matrices of rank r. However, similar to the modified Cholesky decomposition [5], it can be shown that a small perturbation can be added to any PSD matrix such that the perturbed matrix can be expressed using the modified Iwasawa coordinates. For example, The corresponding Jacobian of the resulting matrix w.r.t the modified Iwasawa coordinates can be obtained by simply eliminating the columns in original Jacobian matrix (6) corresponding to the additional zero conditions.

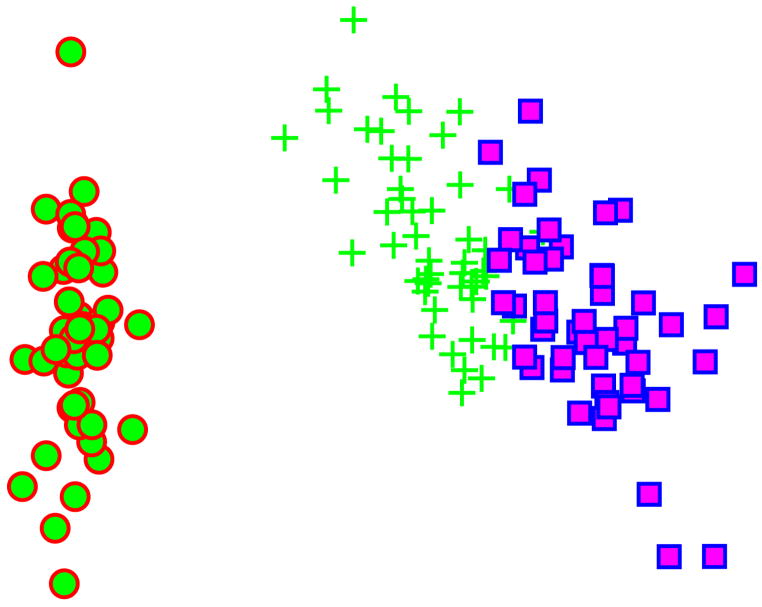
As an illustration, Figure 1 visualizes the clustering of “iris” dataset from UCI machine learning repository [1]. The 2-dimensional show is reduced from the original 4-dimensional space using the modified Iwasawa coordinates combined with the NCA method. (See section 4 for more experiments on high dimensional datasets.)

Figure 1.

Visualization of “iris” dataset after applying NCA with the modified Iwasawa coordinates for rank-2 PSD matrices.

4. Experiments

The Iwasawa decomposition technique can be used in most of the aforementioned metric learning algorithms. In our experiments, we choose the NCA method [7] as the cost function for learning Mahalanobis metrics since it has been reported that NCA is able to produce quite good classification results on several public domain datasets in comparison with other competing algorithms.

We first evaluated the NCA method on the four low-dimensional datasets (Bal, Wine, Iris and Diabetes) from the UCI repository [1] and compared the performance of unsupervised clustering tasks with the default Euclidean distance, the “whitening” transformation and the RCA method. For each run of the algorithms, we randomly split the dataset into training (approximately 70%) and testing (approximately 30%) subsets. After the metric was learned, the K-means clustering algorithm was run on the linearly transformed datasets. Following [14], we compute the error rate of the resulting clustering {ĉ_i} with respect to the ground truth clustering {c_i} using the following measure:

$$\text{error}=1-\sum _{i>j}\frac{1\{1\{c_i==c_j\}==1\{{\widehat{c}}_i=={\widehat{c}}_j\}\}}{0.5m(m-1)}$$

where 1{·} is the indicator function (1{True} = 1, 1{False} = 0) and m is the size of dataset. All results reported in Figure 2 used K-means with multiple restarts and were averaged over 40 runs. It can be observed that the results of NCA and RCA on these datasets are roughly comparable (i.e. better in some cases, worse in others) but are both consistently better than those of using Euclidean distance and the “whitening” transformation. Similar patterns were also observed in previous work.

Figure 2.

K-means clustering errors on low-dimensional UCI datasets.

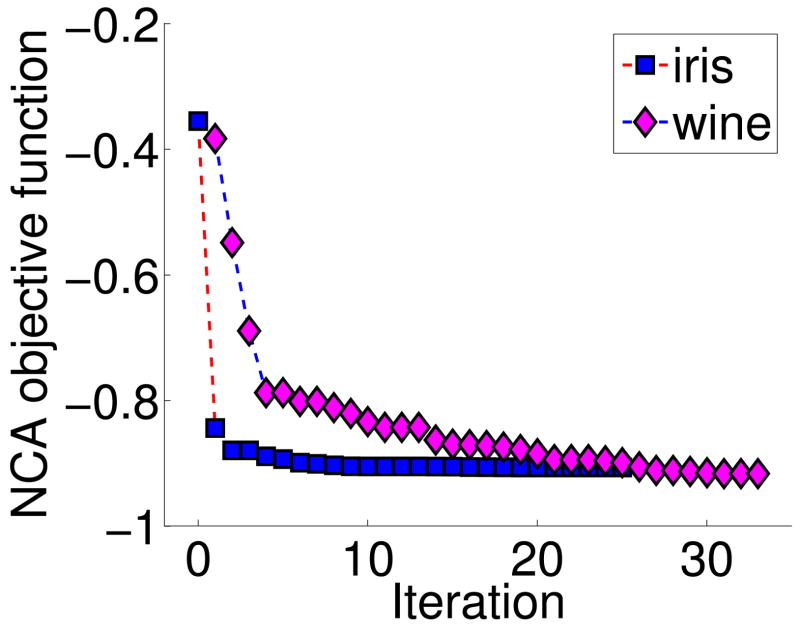
Since the original semidefinite programming problem can be reformulated to a smooth convex nonlinear programming problem with much simpler constraints by using Iwasawa coordinates, one can directly apply the “fmincon” function in MATLAB optimization toolbox which further calls some efficient and powerful optimization algorithms accordingly. It would be a big convenience especially for machine learning practitioners who are not familiar with those complicated special purpose solvers. In Figure 3, we show the two converging procedures of optimizing the NCA objective function. These two examples were taken from two sample runs on the “iris” and “wine” datasets. It is evident from this figure that the Newton method quickly drives the objective function to the global minima close to −1, which indicates that the numerator part in (2) quickly becomes dominant. This observation actually implies that the optimization of NCA objective function tries to collapse all example in same class to a single point and push examples in other classes sufficiently faraway such that the corresponding denominator part in (2) will be truncated.

Figure 3.

The iterations of two NCA runs on the iris and wine datasets obtained using MATLAB optimization toolbox.

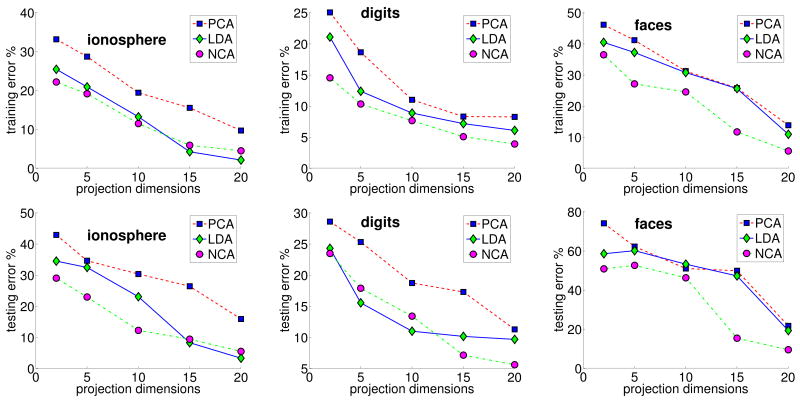
We have also investigated the use of modified Iwasawa coordinates for performing linear dimensionality reduction as well as metric learning on the following datasets: (1) the UCI “ionosphere” dataset, which consists of 351 points with 34 properties labeled into 2 classes; (2) the UPSP dataset of handwritten digit images, which consists of 1100 grayscale images of each digit from “0” to “9”; (3) the AT&T faces database, which contains 10 grayscale face images of each of 40 distinct subjects taken at different times, with varying illumination, facial expressions and poses. The following preprocessing steps were carried on the digit images and face images prior to the dimensionality reduction. The digit images were downsampled from 16 × 16 to 8 × 8 pixel resolution, corresponding to 64 input dimensions. The face images were downsampled from 64 × 64 to size 16 × 12, resulting 192 dimensions. As in [10, 13], the ratio of training subsets and testing subsets was 70/30. For each dataset, we tried 5 lower projection dimensions (d = 2, 5, 10, 15, 20). The performance of the NCA was compared with the PCA and LDA using the KNN classification on the reduced space. Figure 4 shows that both the training and testing error rates of NCA are consistently lower than those of PCA and LDA, especially in the very low dimensional representations as reported in previous work. Unlike the original NCA approach in [7] where a nonconvex optimization is performed on a non-square matrix of size d×D, we directly worked with a smooth convex optimization problem using the modified Iwasawa coordinates with dD − (d² − d)/2 free parameters.

Figure 4.

Training and testing error rates for KNN classification after linear dimensionality reduction using various methods.

5. Conclusions

The metric learning problem plays an important role in many pattern recognition applications and is an active research topic in the filed of machine learning. Based on a review of several recent studies on learning a Mahalanobis metric represented by a positive semidefinite matrix, we summarize some difficulties and problems on dealing with the semidefiniteness constraint usually encountered in the optimization procedure. One major contribution of this paper is the introducing of the Iwasawa decomposition, which to the best of our knowledge, has not been exploited in the machine learning literature, though as a unique and effective parameterization of the positive definite matrices. The significant feature of this Iwasawa decomposition relevant to the Mahalanobis metric learning problem is in that many original complicated semidefinite programming problems formulated in previous work can be reformulated as smooth convex nonlinear optimization problems with much simplified constraints by employing Iwasawa decomposition. The existence of analytical Jacobian also enables the use of the efficient general purpose nonlinear optimization techniques. We also introduce a novel modification to the original Iwasawa coordinates for parameterizing rank-deficient PSD matrices and show that it can be used to perform metric learning and dimensionality reduction simultaneously. As an example, we apply the proposed Iwasawa decomposition technique to the Neighbourhood Component Analysis (NCA) and present comparisons with several other techniques in clustering and classification tasks. Finally we shall point out that the (modified) Iwasawa coordinate system, as a natural parametrization of positive (semi)definite matrices, and the general approaches described in this paper, can be used in many other applications which involve the learning of a positive (semi)definite matrix.