AN OPTIMAL-PATH APPROACH FOR NEURAL CIRCUIT RECONSTRUCTION

Abstract

Neurobiologists are collecting large amounts of electron microscopy image data to gain a better understanding of neuron organization in the central nervous system. Image analysis plays an important role in extracting the connectivity present in these images; however, due to the large size of these datasets, manual analysis is essentially impractical. Automated analysis, however, is challenging because of the difficulty in reliably segmenting individual neurons in 3D. In this paper, we describe an automatic method for finding neurons in sequences of 2D sections. The proposed method formulates the problem of finding paths through sets of sections as an optimal path computation, which applies a cost function to the identification of a cell from one section to the next and solves this optimization problem using Dijkstra’s algorithm. This basic formulation allows us to account for variability or inconsistencies between sections and to prioritize cells based on the evidence of their connectivity.

1. INTRODUCTION

Models of neural circuits are central to the study of the central nervous system. However, relatively little is known about the connectivities of neurons and state-of-the-art models are insufficiently informed by anatomical ground truth. Serial-section microscopy can provide the data necessary for the reconstruction of large-scale neural circuits. However, the complexity and vast size of these images make human interpretation an extremely labor intensive task. A number of researchers have undertaken extensive electron microscopy imaging projects in order to create detailed maps of neuronal structure [1] and connectivity [2]. Research on the reconstruction of neural circuit diagrams has focused on the worm species c-elegans which has 302 neurons and is one of the simplest organisms with a nervous system. This manual reconstruction effort is estimated to have taken more than a decade. Newer imaging techniques are providing larger volumes from more complex organisms, further complicating the circuit reconstruction process. Hence, there is a need for the automated analysis methods for these large data sets.

The strategy for reconstructing neural circuitry is to identify neurons and the synapses that connect them in microscopic imagery. Serial-section transmission electron microscopy (TEM) is a desirable modality for achieving this because it offers a relatively wide field of view—sufficient to identify large sets of cells that may wander significantly as they progress through the sections—and has an in-plane resolution that is sufficient for identifying synapses. In creating images from TEM, sections are cut from a specimen and suspended so that an electron beam can pass through it creating a projection. The projection can be captured on a piece of film and scanned or captured directly as a digital image (Fig. 1). A trade-off occurs with respect to the section thickness. Thinner sections are preferable from an image analysis point of view because structures are identified easier due to less averaging. However, from an acquisition point of view, thinner sections are harder to handle and impose a limit on the area of the section that can be cut. To gain an understanding of neural connectivity patterns, scientists need to study sections with relatively large areas such as 200μm × 200μm. Thus, there is a need for algorithms that are sufficiently robust to trace neurons through a stack of hundreds or thousands of sections under conditions where the in-plane resolution, contrast, noise, etc., are not ideal.

Fig. 1.

Example of images from a serial-section TEM. (a) Labeled neurons in section 1 and (b) labeled neurons on section 28, identified through the optimal path finding algorithm.

The extremely anisotropic resolution of TEM, 2-5 nm in-plane compared to 90 nm out-of-plane, poses two image processing challenges. First, the cell membranes can range from solid, dark curves for neurons that run approximately perpendicular to the cutting-plane to grazed, grey swaths for others which run more obliquely and suffer more from the averaging effect. Consequently, segmentations of neurons in these 2D images, although generally good, are not entirely reliable. Second, due to the large physical separation between sections, shapes and positions of neurons can change significantly between adjacent sections. In order to successfully track neurons across a large number of sections, it is important to use an approach that can account for these challenges. In the proposed approach, images are first segmented in 2D followed by a novel correspondence identification approach that identifies correspondences between neurons across the third dimension.

In related work, Jain et al. uses supervised learning to classify pixels as membrane or non-membrane in specimens prepared with an extracellular stain [3]. This stain shows only the cell boundaries and results in simpler structures. However, neural circuit reconstruction requires the detection of synapses, which is only possible when intracellular structures are also observed. Our neuron segmentation method works in the presence of intracellular structures as demonstrated in Section 3. Tracking methods that use active contour based tracking models [4, 5] work well for identifying features that contain small amounts of variation between sections and individual structures with little variability. Probabilistic frameworks [6, 7] use tracking in the more traditional sense to identify features in time lapse light microscopy. The problems we address in this paper is also different from cell tracking in light microscopy Properties of light microscopy images are very different than TEM images; therefore these methods do not apply to the problem discussed in this paper. Furthermore, neither approach completely addresses the problem of identifying and tracking data with high amounts of variation of movement and texture between sections.

2. METHODS

2.1. 2D Segmentation

The first step of the algorithm is to segment the individual neurons in the 2D images. First, a contrast limited adaptive histogram equalization (CLAHE) is applied to the raw data, improving the contrast of the neuron membranes and fixing the contrast variation. Furthermore, many of the cell membranes appear to contain gaps. To address this problem, a directional diffusion filter is applied [8] to enhance the neuron boundary. To isolate the membranes, the image is thresholded and a connected component filter is applied to remove components that are small in size and do not correspond to neuron membranes. This results in a binary image of the neuron membranes, which we then blur with a Gaussian filter to obtain a fuzzy edge map. The final step applies a watershed segmentation using the implementation from ITK [9]. A perfect 2D segmentation is not possible because of the problems with grazed membranes, as described in Section 1, and the presence of intracellular structures.

2.2. Optimal-Path-Finding Algorithm

We will formulate the problem of identifying correspondences between segmented 2D regions across the third dimension as a optimal path finding problem in a graph structure. We begin with the construction and processing of the graph in the basic algorithm, and then describe the extensions to the graph that make the algorithm significantly more robust in Section 2.3. Let R_s,i be the i’th region from the 2D segmentation in section s. Next we construct a directed graph containing a set of nodes that correspond to the set of segmented regions in section s. The set of directed edges on the graph is between all nodes in adjacent sections. That is,

$$E=\left\{\bigcup _{s,i,j=1}^{N,Q_s,Q_{s+1}}{E}_{s,i,j}\right\}\text{where}{E}_{s,i,j}=[R_{s,i},R_{s+1,j}],$$ (1)

N is the total number of sections, and Q_s denotes the number of segmented regions in section s.

We define a path through the graph as a sequence of nodes connected by edges. We are interested in paths that span all sections P = (R_1,i1, R_2,i2, … , R_N,iN), and we define the cost of the path as the sum of the costs of the edges

$$K\left(P\right)=\sum _{s=0}^{N-1}W\left(E_{s,i_s,i_{s+1}}\right),$$ (2)

where i₁, … i_N is the set of indices that the path follows on each section; because of the directed nature of the graph, paths cannot cross back to previous sections.

For biologists, the identification of neurons between sections relies on texture, shape, and proximity. These properties motivated our construction of the edge cost as the negative of the log-product of the correlation between regions and a Gaussian penalty on in-section displacement. That is:

$$\begin{array}{cc}\hfill W\left(E_{s,i,j}\right)=& -\log [C(R_{s,i},R_{s+1,j})\hfill \\ \hfill & \exp (-D{(R_{s,i},R_{s+1,j})}^2{\sigma }^{-2})],\hfill \end{array}$$ (3)

where C is the maximum value of the normalized cross-correlation of the two segmented regions, and D(R_s,i, R_s+1,j) is the distance between region centers in the x — y coordinates of the section. For computational efficiency, we compute the normalized cross-correlation in the Fourier domain. The log is used so that the formulation is equivalent to a product through the section (there is a probabilistic interpretation), and the system avoids seeking out very good connections at the expense of very bad ones—i.e. cell identity is lost if a connection between sections is not sufficiently strong. Finally, the log-product , which can be seen as an edge connection weight, is negated to create a cost function.

Finally, Dijkstra’s algorithm, which finds a minimum distance path in a directed graph is used to find the optimal connectivity for each neuron (region) in the first section. If we run Dijkstra’s with a zero cost for all the regions in the first section, we find the region with the best cost on the last section, and trace the solution backwards, we have the optimal path (best cell) for the whole data set. Of course in this solution, cells can share paths, which is not normally what we want for this particular application. To account for this, we enforce uniqueness iteratively, in a greedy optimization strategy. That is, we solve for the best path, remove those nodes from the graph, and repeat, producing a sequence of cells associated with a decreasing degree of evidence for connectivity.

2.3. Extension to Robust Optimal-Path-Finding

The algorithm described in Section 2.2 is moderately effective, but fails in cases where the 2D segmentation fails or the quality of a section is particularly bad. We can make the method more robust with two additional features. The first is to account for over-segmentation by inserting extra nodes in the graph that correspond to merged regions. Let

$$M_{s,i}=\{j:R_{s,j}\text{is adjacent to}{R}_{s,i}\},$$ (4)

represent the indices of all regions that are neighbors of R_s,i (i.e. they contain adjacent pixels). Next, we define a subset of M_s,i corresponding to those neighbors of R_s,i whose union with R_s,i will be considered as additional nodes in the graph:

$${\tilde{M}}_{s,i}=\{j\in M_{s.i}\text{and}g(R_{s,i},R_{s,j})>T\}.$$ (5)

The function g(R_s,i, R_s,j) measures the boundary strength between any two adjacent regions in the same section. Because boundaries are dark, we use the negative of the maximum value of the intensities along the boundary that separates the two regions. If the edge strength is less than a threshold T, these regions become part of M̃_s,i in (5). We define the set of new regions in a section as

$${\{R_{s,i}\bigcup R_{s,j}\}}_{j\in {\tilde{M}}_{s,i}},$$ (6)

and augment the set of nodes, edges, and edge costs accordingly. The inclusion of these merged regions as well as their individual constituent regions provides our approach the flexibility to correct 2D over-segmentation problems, but does not address 2D under-segmentation problems.

Another other important extension to the basic framework is to allow paths to skip sections, in order to avoid poor quality sections (which happens regularly) or to overcome a segmentation problem that is not corrected by the merging strategy. To do this we add edges to the graph that allow connections up to M sections away:

$$E=\left\{\bigcup _{k,s,i,j=1}^{M,N,Q_s,Q_{s+k}}{E}_{s,i,j,k}\right\}\text{where}{E}_{s,i,j,k}=[R_{s,i},R_{s+k,j}]$$ (7)

In this paper, we use M = 2, thereby allowing connections between sections separated by at most a single intermediate section. This choice gives Dijkstra’s algorithm a choice in calculating the best path in the case where an immediately adjacent section does not have the best match. We must be careful in how we construct the costs for these edges, because we want to avoid cost functions that favor skipping sections when there is sufficient data to support a path through a section. We adjust the cost function penalizing the correlation term to account for the missed sections (factor of α^k—1 multiplying correlation), but allow for more displacement (factor of k^-2 multiplying displacement). Generally we have

$$\begin{array}{cc}\hfill W\left(E_{s,i,j,k}\right)=& -\log \left[{\alpha }^{k-1}C\right(R_{s,i},R_{s+k,j})\hfill \\ \hfill & \exp (-D{(R_{s,i},R_{s+k,j})}^2{\left(k\sigma \right)}^{-2})],\hfill \end{array}$$ (8)

where α is the typical correlation between a cell in two adjacent sections, which was found empirically to be about 0.6.

3. RESULTS

This method for tracking neurons through sections was applied to a mouse retinal dataset with a resolution of 2.5 × 2.5 × 90 nm. As a preprocessing step, the dataset is registered and assembled using displacement histograms [10], which accurately aligns all the individual sections from the microscope and creates a volume. Each section is segmented in 2D, using the method described in 2.1, to create a series of regions through the volume. Fig. 2 shows regions identified as the best path for 4 neurons across 28 sections using the proposed method. The top right image illustrates the hand segmented regions. The following sections are segmented automatically and identified using the optimal-path-finding algorithm. The labels for these regions are found to be correct when compared to data labeled by an expert after the system parameters were set. The quality and the consistency of the neuron boundaries can change dramatically between sections. For example, in Fig. 2-Section 3, the lower right portion of the boundary for region C is not captured and therefore undersegmented. As a result, the edge cost from region C in section 2 to region C in section 4 is much smaller when compared to the edge costs from region C in section 2 to any regions in section 3. This causes section 3 to be skipped for region C. It is possible this neuron is splitting, as indicated by the abrupt change in region shape. This is an important area of future research, since splitting indicates the beginning of other neurons. Also in section 3, region D is over-segmented. As a consequence, the algorithm prefers a merged alternative region over all of the single regions directly obtained from the 2D segmentation. The boundaries between the two regions that were merged are shown as dashed lines in Fig. 2. Region A in section 14 and region C in section 28 are also merged in Fig. 2. Over the 28 sections, regions A, B, C and D skipped a total of 9 sections and performed 6 merges.

Fig. 2.

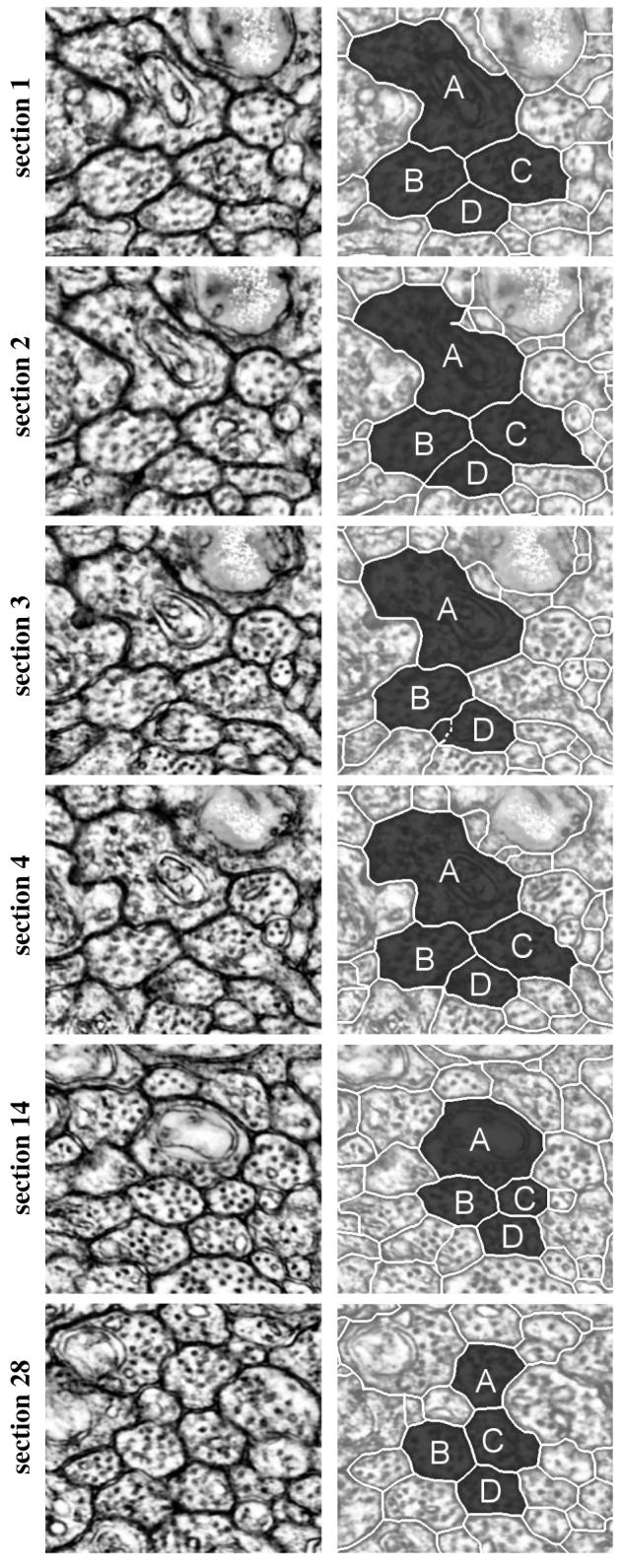
Sequence of images showing the result of tracking 4 neurons over 28 sections. The left column is the CLAHE enhanced raw data and the right column is the corresponding segmentation for the tracked neurons. Sections 1, 2, 3, 4, 14, and 28 are shown from top to bottom. Letters correspond to matching regions between sections.

This paper demonstrates an effective method for tracking neurons through serial section TEM images. This is a significant step in bridging the gap between image acquisition and the reconstruction of neural circuitry. Individual sections are segmented into sets of regions, a connecting graph is built in 3D, and a version of Dijkstra’s algorithm to used to calculate a unique path through the graph. To account for over and undersegmented regions, this method can merge regions within a section or skip regions between sections. Failure to correctly identify a sequence of neurons can still occur when an accurate segmentation of a neuron is missing for more than one section or more than two regions need to be merged for the best possible correlation. Both of these cases will most likely result in diverting the optimal path to a different path, with a higher correlation. Future work will address these problems, including region splitting, and focus on tracking larger numbers of neurons over longer sequences of sections.