Summary
There has been a recent surge of interest in modeling and methods for analyzing recurrent events data with risk of termination dependent on the history of the recurrent events. To aid the future users in understanding the implications of modeling assumptions and modeling properties, we review the state of the art statistical methods and present novel theoretical properties, identifiability results and practical consequences of key modeling assumptions of several fully specified stochastic models. After introducing stochastic models with noninformative termination process, we focus on a class of models which allows both negative and positive association between the risk of termination and the rate of recurrent events via a frailty variable. We also discuss the relationship as well as the major differences between these models in terms of their motivations and physical interpretations. We discuss associated Bayesian methods based on Markov chain Monte Carlo tools, and novel model diagnostic tools to perform inference based on fully specified models. We demonstrate the usefulness of current methodology through an analysis of a data set from a clinical trial. In conclusion, we explore possible future extensions and limitations of the methodology.
Keywords: Gibbs sampling, Frailty, Mixed Poisson process, M-site model, Semiparametric Bayes
1 INTRODUCTION
Modeling and analysis of recurrent event times data in many applications range from clinical trials, engineering product testing, reliability analysis of repairable systems and so forth. References include Kuo and Yang (1995, 1996) in software reliability and reliability analysis of repairable systems, Oakes (1992), Wei and Glidden (1997), Scheike (2000), Lin et al. (2000), Wang et al. (2001) and Miloslvsky et al. (2002, 2004) in clinical trials and medical applications. In this article, we investigate the theoretical properties and implications of key modeling assumptions of recently developed fully specified stochastic models of recurrent events data with dependent termination. We will demonstrate how some of the important classes of models, particularly with associated Bayesian analysis tools, can be used analysis of such data including model selection and diagnostics for adequacy of modeling assumptions.
To illustrate with a typical data example, we consider a study involving heart-transplant patients who are at risk of recurrent events of transplant rejection (treated effectively by drug therapy) as well as the non-recurrent terminal event of death. The # of recurrent rejection events to a patient by time t is N(t) = Σj 1[Yj≤t], where Y1 < Y2 < · · · are the ordered rejection times. In this situation, the non-recurrent event of death terminates/censores the observation of the recurrent event process {N(t)}, and the termination time T is not determined via the design of the study. We make a practical distinction between the terms “termination” and “censoring”. The censoring due to loss of follow-up, end of study, etc., when they occur before death, is treated as a case of typical noninformative censoring of the termination/death time T. In general, N(C) is informative of N(T) even when a termination time T is non-informatively censored at C.
A simplifying assumption for modeling recurrent events data subject to termination (e.g. Sinha, 1993, Hougaard, 2000) is that given the history of of right-predictable covariates x(s) and the history of recurrent events of the subject, the risk of termination at any time point t is independent of the history , that is,
| (1.1) |
In practice, one usually uses ordinary survival analysis methods for the termination time T using {N*(t-), x(t)} as time-dependent covariates, where N* (u) is a prespecified vector of function of . If there are no significant effects of N* (t-) found, then the data on recurrent events can be analyzed under the assumption of (1.1). However, assumption (1.1) may not be valid in many practical examples. For example, in a organ transplant trial, the intensity of recurrent graft rejection episodes is considered an indicator of the unobservable health-state of the patient, whereas the risk of termination due to death, an important outcome by itself, is also very much related to the unobservable health-state. For an organ-transplant trial, both types of events are negative outcomes. For a product testing study of repairable systems, each system may experience recurrent failures leading to detection of faults (recurrent negative outcomes signifying unobservable quality of the product) until it is terminated (positive outcome related to unobservable quality) with the final release of the product.
In the frequentist literature, most of the statistical methods for recurrent events data, with noninformative termination, use partially specified models for robust estimation of the regression parameters associated with either the marginal hazard of Yj (the j-th recurrent event of the subject) or E[dN(t)], where dN(t) = N[t, t + dt). These models are defined conditional only on a subset of the history (e.g. Sun and Wei, 2000, Wang, Qin and Chang, 2001). The interpretations of the regression parameters are strictly restricted to the subset of the history the model is conditionally defined on. For example, , and can be very different from each other. It is not possible to automatically derive the regression parameters of one partially specified model from those of another partially specified model. We refer interested readers to the detailed and excellent reviews by Miloslavsky et al. (2002, 2004) regarding frquentist inference for recurrent events data under noninformative termination using different partially specified models. The same problems arise when partially specified models for gap times Uj = Yj - YJ-1 are used conditional on , a subset of the history up to (j - 1)-th recurrent event times Yj. We also loose a sense of the progression of the process over calendar time from origin when we use models based on gap times. For some studies, it is desirable to have a fully specified unifying model such that conclusions about different components conditional on different subsets of observed history are compatible with each other. This helps to fully comprehend the data generation process of the experiment at hand. A fully specified model can be also used for prediction, model diagnostics, simultaneous inference on multiple parameters, etc.
In Section 2, we begin with different fully specified stochastic models for recurrent events data with noninformative termination. We discuss the physical interpretations, new stochastic formulations and the relationships among the following models of recurrent events data: the frailty model (Oakes (1992), Sinha 1993 and Hougaard (2000)), the M-site model (Gail et al., 1980) and the time-varying correlated frailty model (Herdersen and Shimakura, 2003). Despite the recent interest and research activity in Bayesian survival analysis (e.g., Sinha and Dey (1998), Walker, et al. (1999), Dey, Mueller and Sinha (1998) and Ibrahim, Chen and Sinha (2001)), the current Bayesian literature on recurrent events data is very limited. One goal of this paper is to review the current state of Bayesian methodologies for recurrent events data and demonstrate the use and advantages of the Bayesian paradigm for such problems.
In later Sections, we examine extensions of these recurrent events models to recurrent events with informative termination. The extensive simulation study of Miloslavsky et al. (2002) demonstrates the issue of bias in the regression estimates of the marginal rate and marginal intensity functions when informative termination is ignored during estimation. We focus on fully specified stochastic models where the recurrent events and as well as the termination are considered as important responses. In presence of two different types of event processes of interest, to comprehend the effects of covariates and the data generation process, we need to evaluate the effects of covariates separately on two processes as well as the effect of the joint process. For example, in a transplant study, we are interested in as well as when can be equal to either or . A careful examination of the regressions functions in all three functions can only reveal the true nature of the effects of covariates on two types of outcomes.
Methods of estimation in the presence of informative termination are presented and reviewed by Miloslavsky et al. (2002, 2004) using the CAR (Coarsening At Random) assumption, (e.g., Heitjan and Rubin, 1991; Gill et al., 1997; Robbins, 1993), which implies that the risk of termination hT has the following property:
| (1.2) |
where , and (0, τ] for τ > t is either the study-interval or the time-interval of interest. When termination is, say, the event of death for the transplant example, it is not possible to either define or conceptualize a hazard hT(t) of death at t < τ given the history of recurrent events and covariate at an interval (t+, τ] beyond time t. One can only observe a history of recurrent rejections in (t, τ] only when the patient is alive beyond time t. The CAR assumption is difficult to understand and verify unless a bigger class of joint stochastic models of {N(·), T} is defined and then the validity of CAR assumption is verified. The CAR assumption is applicable when termination event is not of interest and it is precisely treated as a non-informative censoring. In such a case, the focus is on understanding dN(t) given and we only need to take care of inferential problems raised by the observed data under informative censoring. Even after having the CAR assumption, one needs to correctly specify and , where N+(t) = N(Min(t, T)). To obtain the regression parameters of from , we need additional set of assumptions (beyond CAR) whose validity cannot be evaluated solely from observed data. We will investigate what key assumptions of fully-specified stochastic models of the joint process can give rise to CAR and related assumptions.
Recent work by Lancaster and Intrator (1998), Sinha and Maiti (2004), and Liu, Wolfe and Huang (2004) offer several new fully specified models for recurrent events data with dependent termination describing {dN(t), d1[T≤t]} sequentially unfolding over time. However, no theoretical investigations of relationships among these models and their properties have been examined in current literature. The relationships (or the lack there of) these models with CAR assumption based models have not been investigated yet. In general, a fully specified stochastic model may not even satisfy the CAR assumption. In this work, we consider novel theoretical explorations of three major aspects of modeling: (1) theoretical properties and practical consequences of key modeling assumptions on the observable quantities; (2) relationships among different models; and (3) identifiability of model parameters and distributional assumptions from observable data. For each model with dependent termination, we explore in detail different consequences resulting from modeling assumptions because these important consequences may not be reasonable in various biological and engineering applications. For example, we show that for some of the existing models, when termination times are subject to noninformative right-censoring, the induced censoring of the number of recurrent events until termination is bound to be noninformative (contrary to what we expect to see in most real-life data examples). We investigate the relationships and comparisons of related models existing in the recurrent events literature to help the user to make informed selection of the models most appropriate for the study/experiment in hand.
In Section 3, we discuss a comparison of a full Bayesian analysis (with the help of sampling based algorithms) versus a semiparametric likelihood-based analysis. A full Bayesian approach is one of the natural choices of inference based on fully specified stochastic models, and we argue that it is the most appropriate one in this case. In Section 4, we present details regarding the Bayesian computational tools used in this problem. Then, a typical Bayesian analysis of recurrent events data with informative termination is illustrated with the analysis of recurrent events data from a heart transplant study.
One important component of any model-based methodology is the development of appropriate tools for evaluating model adequacy, outlier detection and influential observations. In Section 5, we demonstrate the Bayesian case-influence diagnostics and residual analysis appropriate for the proposed models. Recurrent events data with a terminating event is also related to various other applications such as cumulative medical costs data (e.g., Lin, et al., 1997; Etzioni et al., 1999), cumulative repair/warranty costs data (e.g., Nelson, 1995), and quality-adjusted survival data (e.g., Zhao and Tsiatis, 1997). In Section 6, we explore the relationship between recurrent events data and cumulative cost process data. We conclude our article with some closing remarks and exploring further extensions of our models and methods.
2 MODELS
2.1 MPP Models Under Non-informative Termination
We first describe models for {Ni(t)} under the non-informative termination assumption of (1.1) (e.g., Oakes, 1992; Sinha, 1993). The Mixed Poisson Process model (MPP model) for recurrent events data in Oakes (1992) and Sinha (1993) assumes that for subject i = 1, · · · , n with Ti > t, the probability of a new recurrent event in [t, t + dt) is given by
| (2.1) |
and , where μ0(t) is the baseline cumulative intensity and β1 is the regression parameter of the covariate effect on the conditional intensity. The time-constant frailty random effects, w1, · · · , wn, are assumed to be i.i.d. with common cdf F(w|η) with EF [Wi] = 1 (to assure identifiability of the model parameters). Hougaard (2000) calls this the shared frailty model. The use of a finite mean frailty distribution is warranted here to ensure the expected number of events within any finite time interval to be finite. For simplicity of notation, we will present our models and the results assuming fixed time-constant covariate x(t) = x thoughout. Extending the following discussion and results to accommodate time-dependent x(t) is quite straightforward. The results which are not valid for time-dependent predictable covariate x(t) will be mentioned separately in this paper.
In practical applications, we only observe the process {N+(t) = N(t)1[T ≥ t]}, and the conditional intensity of {N+(t)} given should be defined, however, with the non-informative termination assumption of (1.1), we can use the simplified conditional intensity of (2.1). In Section 6, we discuss the extension of the MPP model using a non-proportional intensity for N(t). One main consequence of the mixed Poisson process assumption in the MPP model is P [dNi(t) > 1|xi] = o(dt), indicating that the MPP model is not suitable when the recurrent events within a subject tend to cluster together within a small time-interval. The number N(t) carries all the predictive information of the history for the conditional risk of a new event (Oakes, 1992), because
| (2.2) |
where x is the vector of fixed covariates. The expression in (2.2) shows that the MPP model is a subclass of the dynamic covariate model discussed by Aalen et al. (2004) and Fosen et al. (2006), where the model is specified via , where is a pre-specified subset of . There are many choices for a dynamic covariate model, and only a careful investigation of the underlying structure (performed in this paper) can give the user some understanding of the implications of the assumptions of a particular dynamic covariate model.
Even when μ0(t) is left unspecified, the frailty distribution F (w|η) is identifiable from the observed recurrent events data (Oakes, 1992). This implies that the observed recurrent events data can be used via appropriate goodness-of-fit plots for identifying a suitable F(w|η) among various choices of frailty distributions. In susequent Sections, while discussing the recurrent events model under dependent termination, we will address whether the frailty density is identifiable from the observable data. Use of a Gamma frailty distribution with F(w|η) assumed to be a Ga(η, η) cdf with variance η-1, is fairly commonplace due to its convenience and theoretical properties. However, choices other than a Gamma frailty can be considered. The frailty random effect accommodates heterogeneity among subjects due to their variable proneness to the recurrent non-fatal events via the unknown variance η-1 of the Gamma frailty .
2.2 M-site Models
The popular M-site model of carcinogenesis (e.g., Whittemore and Keller (1978) and Gail et al. (1980)) is based on the premise that recurrent detectable tumors (or cancers) in a finite interval of interest (0, τ) arise from proliferation of clones derived from each of M progenitor cells or tumor-sites within a patient with i.i.d. promotion times Z1, · · · , ZM (times to recurrent detectable tumors in cancer context) with common density g(t). When the unknown and unobservable Mi given the frailty wi and time-constant xi has a Poisson distribution with mean E[Mi|wi, Ti; xi] = μi = wi exp(β1xi)γ0, the resulting process {Ni(t)} in (0, τ) is same as the MPP model of (2.1) with dμ0(t) = γ0g(t)dt (Oakes, 1992). This result gives a strong biological justification for the use of the MPP model in cancer. In product testing, Mi can represent the unknown number of undetected faults/bugs in product i at the onset and i.i.d. Zi1, · · · , ZiMi are the detection times of these faults.
A new modification of the M-site model assumes that [Mi|Ti] is Poisson with mean μi = γ0 exp(β1xi) (free of the patient-specific random effects) and the patient specific piecewise exponential promotion time density gi(t) = Uij e-Uij for t ∊ (aj-1, aj) with a pre-specified grid 0 = a0 < a1 < · · · < aJ = τ. When the vector of patient-specific rates Λi = (Ui1, · · · , UiJ) follows a multivariate Gamma density of Griffiths (1984), we get the serially correlated Gamma frailty model of Henderson and Shimakura (2003). We call this model the HS M-site model. This model can be used when we believe that the effect of among subjects heterogeneity on the rates (Ui1, · · · , UiJ) of latent activation times is more than its effect on number of latent tumors/faults Mi. The original work of Henderson and Shimakura uses a composite likelihood method to analyze only discrete panel count data (instead of continuous time recurrent events data) under the HS M-site model. Extensions of the composite likelihood method to analyze data based on actual recurrent event times are not trivial. To analyze continuously monitored recurrent events data with this kind of time-varying frailty model, we recommend using a multivariate log-normal density for Λi, instead of the multivariate gamma density of the HS M-site model. Our major concern is non-identifiability of the density g(t| Λi) and the multivariate density of Λi from recurrent events data when both densities are left unspecified.
2.3 L-I Model for Informative Termination
In many data examples and studies, the non-informative termination assumption of (1.1) will not be valid. Lancaster and Intrator (1998), in what we call here the L-I model, formulated the association between and the risk termination at time t via the shared frailty wi and replaced the assumption of (1.1) with the assumption
| (2.3) |
where β2 is the regression parameter of the covariate effect on the conditional risk of termination, and the baseline intensity is the derivative of μ0(t). The parametric L-I model allows only a certain type of association between and risk of termination T, and has some important consequences of its modeling assumptions (discussed below).
We now present a way of viewing the L-I model as a process that unfolds over time. This alternative description and a series of theoretical results will facilitate a better understanding of the consequences of the key assumptions. Let us assume that all events are generated via a latent nonhomogeneous mixed Poisson process (Ross, 1983) N*(·) with conditional (given frailty w) intensity wμ*(t; x), where . When dN*(·) = 1, there are two possibilities for the new event-either a non-fatal event (Type I) with probability P[dN(t) = 1, T > t + dt|dN*(t) = 1, T > t, w; x] = ϕ(x) or a termination event (Type II) with probability P[T < t + dt, dN(t) = 0|dN*(t) = 1, T > t, w; x] = 1 - ϕ(x), where 0 ≤ ϕ(x) = exp(β1x)\[exp(β1x) + γ exp(β2x)] ≤ 1 for some γ ≥ 0. Because the recurrent events and termination are essentially coming out of a single event process N*, the L-I model implies that any subject with a history of higher than usual rate of N(t) will be at a higher than usual risk of termination. As an important consequence of being an extension of MPP model, the L-I model has properties similar to (2.2). More precisely, following calculations similar to Oakes (1992), we can show that
| (2.4) |
The expectations denoted by EW in (2.4) are taken with respect to the frailty distribution F(w|η). We can also show that , and
| (2.5) |
These results imply that , i.e., given the history , the risk of a new recurrent event is proportional to the risk of termination and both risks depend on the observed history only via number of past events N(t-). When F(w|η) is Ga(η, η), then and . The L-I model can be also expressed as an extension of the M-site model with the additional assumption that N*(t) within interval (0, τ] is generated via the extended M-site model of the promotion of a random number (Poisson distributed) of sites. The following consequences of the L-I model are less obvious. However, they have a major practical significance.
Theorem 2.1
Under the L-I model, the number of recurrent events before termination N(T) is geometric, that is, P[N(T) = k; x] = {ϕ(x)}k{1 - ϕ(x)} for k = 0, 1, · · ·.
The proof of Theorem (2.1) is given in Appendix I. It is important to note that the marginal distribution of N(T) is free of μ*(t). In practice, it is often a reasonable assumption to allow the termination time T to be subjected to the possibility of noninformative right censoring at C, that is, , P[T > t + u|T > t, C > t; x] = P[T > t + u|T > t; x] for all t, u > 0 (Cox and Oakes, 1984). In the transplant study, the the termination time of death is subjected to on-informative censoring due to drop-out. Theorem (2.1) implies that the L-I model is a very special class of models for recurrent events where the induced censoring of N(T) by N(C) is also non-informative, since P[N(T) > u + v |N(C) > u, T > C] = P[N(T) > u + v |N(T) > u] = (1 - ϕ)v. The proof of this result follows directly from Theorem (2.1). This restrictive property of the L-I model limits its application in most real data setting. As it is argued by Lin et al. (1997), the induced censoring of N(T) by N(C) should not be noninformative in general. We mention that these results are valid irrespective of the form of F(w|η). An extension of the L-I model suggested by a reviewer assumes time-varying ϕt(x) = exp(β1x)/[exp(β1x) + γ(t) exp(β2x)], where γ(t) is a function of time t. In this case, the assumption of (2.3) and the result of Theorem (2.1) are not valid. The resulting model is a special case of another competing model introduced in a subsequent section.
One important question is whether the unknown and unspecified frailty distribution F(w|η) is identifiable from the observed data under the L-I model. In absence of the covariate x, we can show that
| (2.6) |
where ψ(u) = E[exp(-uW)] is the Laplace transform of F(w|η) with first and second derivatives ψ’ and ψ”. Writing this ratio as a function ζ(v) of v = P[T > t, N(t) = 0] = ψ(μ*(t)), we get
| (2.7) |
where χ is the inverse function of the Laplace transform ψ(u). The solution of the above differential equation is {χ’(v)} = exp[-cA(v)], where c is a constant of integration and . By using the boundary condition based on the assumption that E(W) = ψ’(0) = 1, we can show that the function χ(v) is uniquely determined by ζ(v) even when ϕ is unknown. Note that knowing χ(v) is the same as knowing the unique Laplace transform ψ(u) = E[exp(-uW)] of F(w|η). This proves that when the observed data contain some subjects at risk of termination after their first recurrent events (i.e., hT (t|N(t-) = 1) and hT(t|N(t-) = 0) are estimable), the frailty distribution F(w|η) is identifiable. Using similar calculations, we can also demonstrate that we can obtain the same differential equation of χ(v) using λN(t|N(t) = 1, T ≥ t) and λN(t|N(t) = 0, T ≥ t). Without giving any rigorous arguments, we claim that the L-I model is somewhat under parameterized when we expect to have a substantial amount of information on the risk of T given N(t) ≥ 2.
2.4 GMPP Model
The generalized MPP model (GMPP model), recently introduced by Sinha and Maiti (2004) and Liu et al. (2004) (only for analysis of grouped panel count data), assumes that the hazard of Ti at time t depends on via the subject specific unobservable frailty wi (an assumption similar to L-I model). In the GMPP model, the assumption of (1.1) is replaced by the assumption
| (2.8) |
where β2 is the regression parameter of the covariate effect on the conditional hazard of termination. For the analysis of data example in Section 4, the form of the conditional hazard hT in (2.8) will be further generalized by the introduction of an additional regression parameter to adjust for the direct effect of Ni(t-) on . Unlike the L-I model, the conditional baseline hazard of termination h0(t) is, in general, not related to μ0(t). However, similar to the property of the L-I model, the conditional risk of termination and the conditional risk of a new recurrent event , depend on the recurrent events history only through the current cumulative count Ni(t-). The proof of this result is very similar to the proof of (2.2) given in Oakes (1992). This property indicates that, when the actual gap-times between past events in history are very informative about the risk of T in [t, t + dt), the GMPP model will not be very applicable. In this case, it is not prudent to use a model where depends on only through N(t-).
The parameter -∞ < α < ∞ quantifies the nature of the dependence between and the hazard of Ti. When α = 0, we have non-informative termination, that is, is free of . When α = 1, we obtain the extension of the L-I model with time-varying ϕt(x). The theorems presented below explicitly describe the role of α, and they investigate some useful and desirable properties of the GMPP model.
Theorem 2.2
When the frailty distribution is Ga(η,η), the hazard hT (t|Ni(t-); xi) can be expressed as where H(t; x) = H0(t) exp(β2x); μ(t; x) = μ0(t) exp(β1x); and V ∼ Ga(Ni(t) + η; μ(t; xi) + η). For the special case α = 1, we obtain a further simplified expression
| (2.9) |
The proof of Theorem 2.2 is given in Appendix I. Equation (2.9) shows the role of α in describing the predictive effect of N(t) on the risk of termination. We see that hT(t|Ni(t); xi) is an increasing function of Ni(t-) for α > 0; and is a decreasing function of Ni(t-) for α < 0. We can get a crude approximation of the relationship in (2.9) as
| (2.10) |
Further, for the Ga(η, η) frailty, λN(t|Ni(t-), Ti ≥ t; xi) is expressed via
| (2.11) |
where H(t; x) = H0(t) exp(β2x); μ(t; x) = μ0(t) exp(β1x); VN+1 ∼ Ga(1 + Ni(t-)+η; μ(t; xi) + η) and VN ∼ Ga(Ni(t-)+η; μ(t; xi)+ η). For the special case α = 1, we have
| (2.12) |
Equation (2.11) shows that the value of plays a very moderate role on the effect of N(t-) in the risk of a new recurrent event, compared to the corresponding role of α for the effect of N(t-) on the conditional risk for termination. Because VN+1 and VN are very similar in distribution when N(t-) is sufficiently large, we can get a crude approximation of the relationship in (2.11) as
| (2.13) |
where V0 ∼ Ga(1 + η; μ(t; x) + η) and V1 ∼ Ga(η; μ(t; x)+ η). Equations (2.10) and (2.13) describe the essence of the role of α in the marginal hazard of T and the risk of new recurrent events given the history . The proof of (2.11) is similar to the proof of Theorem (2.2), and is omitted here for brevity. The properties in (2.9) and (2.12) demonstrate that the GMPP model is very different from the modulated renewal process of Oakes and Cui (1994).
The following theorem shows how α affects the relationship between the distribution of number of past recurrent events N(t) and the information on whether a subject has been terminated at t. The proof is given in Appendix I.
Theorem 2.3
For the GMPP model with Ga(η,η) frailty,
| (2.14) |
where V is distributed as Ga(m + η; μ(t; x) + η). When α > 0, equation (2.14) is an increasing function of m and when α < 0 it is a decreasing function of m.
One consequence of (2.14) is that E[N(t)|T > t] < E[N(t)|T = t] when α > 0 and E[N(t)|T > t] > E[N(t)|T = t] when α < 0.
The GMPP model can be also motivated via an extension of the M-site model by introducing the additional hazard (2.8) for termination as a competing risk with promotion times Z1, · · · , ZM of M sites. If we know that for a subject at risk of termination at time t < τ, the number of past recurrent events is m (that is, m of M sites have already been promoted to recurrent events), then we expect these past event times to be i.i.d. with density g*(u; t) = g(u)/G(t) where G(t) = P (Z < t). The following theorem shows this, and the common distribution of the past event times does not depend on whether the subject has been terminated at t.
Theorem 2.4
The joint conditional distribution of the recurrent event times given {N(t) = m, T > t, x} is same as the joint conditional distribution of the recurrent event times given {N(t) = m, T = t, x}. The common joint density is given by
| (2.15) |
where μ(t; x) = exp(β1x)μ0(t).
Theorem 2.4 is another consequence of the mixed Poisson process assumptions of the GMPP model, and the proof is given in Appendix I. Theorem 2.4 implies that, if we compare a subject terminated at time y with another terminated after y, there will be no difference in their times of occurrences of past recurrent events after adjusting for their respective numbers of past events. If one believes that the termination is invariably followed by a marked change (e.g., big clustering) in the occurrences recurrent events, then this property will not hold for a given study. For example, for a study involving heart patients with recurrent acute angina, the number of past recurrences of angina as well as the exact timings and gaps between these anginas are important predictors of death. For such a study we need to explore alternative modeling strategies via directly formulating , were at least the time of most recent angina YN(t-) has to be included as a predictor.
For the GMPP model, the distribution of the variable N(T), which is the total number of recurrent events until termination, does not have a simple closed form expression. However, in some studies including the transplant study, E[N(T)|x] summarizes the expected total quality of life experience over a lifetime. For a GMPP model, E[N(T); x] can be computed using the marginal expectation of N(T) given by
| (2.16) |
where EF means the expectation is taken with respect to the frailty distribution F(w|η). The proof of (2.16) follows from the fact that E[N(T)|x] = EG[E{N(T)|W, x}] and the property that N(t) given {T = t, W, x} is Poisson distributed.
2.5 CAR Model
Models based on CAR assumption in (1.2) are popular, since with this assumption, it is possible to make inference using proportional risks models for and , where N+(t) = N(Min{t, T}). For examples, we can consider a model with and , where qk is known function of with unknown parameter γk for k = 1, 2. These models are special cases of the multiplicative risk Andersen-Gill class of models for recurrent events (Andersen and Gill, 1982). Motivated by the expressions of the risk of new recurrent event and of the risk of termination for GMPP model obtained in previous section, we can use a CAR model with a conditional density
| (2.17) |
similar to conditional density in (2.10), and a conditional hazard of termination
| (2.18) |
similar to the hazard in (2.12).
The main motivation behind using such proportional intensity and proportional hazards models of (2.17) and (2.18), is to take advantage of partial likelihood based inference (if it is justified) since we do not need to mention the baseline functions h0(t) and λ0(t) to estimate the parameters β1, β2, α and η. However, a straight-forward partial likelihood based inference for a CAR model with these proportional intensity and proportional risk models cannot be used, since the risk-set is a biased sample of . Works by Miloslavsky et al. (2002, 2004) propose an inverse probability of censoring weighted estimator to deal with this problem. Under the assumption of CAR, the regression parameters of can be obtained via estimating the Anderson-Gill like intensity model . However, if one uses a proportional rate model for E[dN+(t)|x], then the corresponding regression estimates for E[dN(t)|x] under CAR assumption will require further assumptions about termination risk given history. In subsequent sections, we will present a Bayesian (based on full likelihood) analysis of a transplant study under a CAR model with assumptions in (2.17) and (2.18).
There are some important differences between the CAR models and the GMPP models. First of all, a GMPP model does not satisfy the CAR assumption of (1.2) when α ≠ 0 in (2.8). We omit the proof of this result. We can further show that if we define any model (either GMPP or an extension of GMPP) based on the conditional intensity and conditional hazard , then we can satisfy the CAR assumption of (1.2) only when is free of the subject-specific random effect w. Hence, the assumption of CAR implies that there is no common unobservable random-effects affecting the two responses {N(t)} and T given x. This suggests that we should not use CAR assumption when we think that there is a latent unobservable patient-specific factor (random effect) which affects the risk of new recurrent events as well as the risk of termination. For example, in a transplant study, a CAR assumption may not be very appropriate since a patient’s unobservable disease status can affect both the risk of rejection and risk of death.
3 LIKELIHOODS AND PRIORS FOR GMPP MODELS
The observable data Y can be split into three component vectors, Y = (D1, D2, X), where D1 = {Nio: i = 1, · · · , n} where is the data from the observed recurrent events times, D2 = {ti, δi : i = 1, · · · , n} is the data from the observed termination times subject to possible censoring (δi is the indicator for censoring for subject i), and X = {xi : i = 1, · · · , n} is the data on observed covariates.
Using the conditional intensity of in (2.1), the likelihood contribution from the sampling distribution of D1 is
| (3.1) |
where means that the product is taken over the set of mi observed recurrent event times of subject i. Similarly, based on the sampling distributions of D2 in (2.8), we get
| (3.2) |
The observed data likelihood Lo(β1, β2, μ0, h0, α, η|Y) of the GMPP model is obtained via multiple integration,
| (3.3) |
where θ = (β1, β2, α, μ0(·), h0(·), η), and g(w|η) is the joint density of w = (w1, · · · , wn) given the frailty parameter η. The semiparametric maximum likelihood estimator of θ can be obtained via maximizing Lo(θ|Y) via a Monte Carlo EM (see Liu et al., 2004) algorithm. The E-step of each iteration requires Metropolis-Hasting simulations from the conditional density , making the computation too intensive. The algorithm is also heavily dependent on the starting values, since it needs to estimate (using Breslowtype non-parametric MLEs) two nonparametric functions and at the M-step of each iteration. We note that the asymptotic justifications and convergence issues for the EM algorithm in semiparametric maximum likelihood estimation of this model are not available.
In recent years, there has been remarkable progress and growing interest in Bayesian methods for event history analysis and survival analysis (e.g., Ibrahim, Chen and Sinha (2001) and the references therein). We advocate using a semiparametric Bayes approach with an independent increments gamma process prior (Kalbfleisch, 1978; Walker, Damien, Laud and Smith, 1999; Ibrahim, Chen and Sinha, 2001) for specifying the prior distribution on the unknown function μ0(·) and the rest of the parameters. In practice, for many of the studies, when the available covariates are important well-studied variables such as treatment, race and gender, one can use informative priors on β1 and β2 to balance both the skeptical and the enthusiastic views about the benefits/effects of the covariates. It is also a common practice in Bayesian survival analysis to assume that priors on parameters associated with baseline functions μ0 and h0 be independent of the rest of the parameters. The mutual independence between the set of parameters associated with nonfatal events and the set of parameters associated with termination is also justifiable, as we can expect to have independent expert opinions about these two different types of events. Similarly, the prior belief for α, which quantifies the association between the two types of events, can be obtained independently from the others. Thus the joint prior of the parameter vector θ is often assumed to be
| (3.4) |
The joint posterior for the GMPP model is given by
| (3.5) |
where and π(θ) is given in (3.4). It is obvious that we need to use MCMC tools to sample from (3.5), and then use those MCMC samples to carry out the Monte Carlo integrations (Chen, Shao and Ibrahim (2000) and Robert and Casella (1999)). At each iterative stage of the MCMC algorithm, we only need to sample the full conditional distributions of the parameters and the frailty random effects.
For a semiparametric Bayesian analysis of GMPP model, we need to express the prior opinions about λ0(t) and h0(t) (baseline functions) using prior processes. The gamma prior process GP(γ(t), c) for μ0(t) is determined by the known prior mean Eπ[μ0(t)] = γ(t) and the known prior precision c of μ0(t) (with prior variance V arπ[μ0(t)] = γ(t)/c). It is possible to put another level of hierarchy in this model using an unknown c and a functional form of γ(t| γ0) with some unknown γ0. For a parametric model of h0(t) in (3.2), we suggest a Weibull hazard h0(t) = h0(t|λ,ν) = λ νtν-1 with a prior distribution (possibly noninformative) on ψ = (λ,ν) using a product of two independent Gamma densities (with known small mean and large variance). The Weibull assumption allows for a very wide class of choices for h0(t). However, one can also use a nonparametric h0(t) with, say, a nonparametric Gamma process on H0(t).
We need to choose the forms of the priors π(β1), π(β2), π(α) and π(η), that are flexible, yet they facilitate easy to sample conditional posteriors. In particular, we use N(β10, σ1) for π(β1) and N(β20, σ2) for π(β2). The π(α) is assumed to be N(0, σ3), when we are not sure whether the association between the two classes of events should be either positive or negative. The hyperparameters of the priors are specified via a careful prior elicitation procedure. We would like to emphasize that the sampling based MCMC computational technique can handle more complicated prior structures including a π(θ) which induces prior dependencies among the parameters.
For MCMC sampling, we need to derive the exact full conditional distributions of each of the model parameters and random effects. Using the expression of L1(β1, μ0, w|D1, X) in (3.1) and the property of the Gamma process prior of μ0(t), we obtain the full conditional of μ0(t) as
| (3.6) |
where N+(t) = Σ{i:ti>t} Ni(t), R+(t; β1, w) = Σ{i:ti>t} wi exp(β1xi) The full conditional in (3.6) can be derived following the arguments similar to previous work on recurrent events data using the Gamma process prior (e.g., Sinha (1993), Ibrahim, Chen and Sinha (2001)). We note that for computational purposes, we only need to sample from the increments of μ0(t) in between consecutive observed recurrent event times and termination times when N+(t) and R+(t) (two step functions) change their values.
The expressions of the full conditionals for all parameters used in the MCMC chain are given in Appendix II. Except for μ0(t), all other full conditional distributions are not in standard form. The full conditional for β1, β2, h0j, α and η are log-concave. Thus, the adaptive rejection sampling algorithm of Gilks and Wild (1992) can be used to sample from these log-concave densities. We use the Metropolis-Hastings algorithm to sample wi.
4 Applications
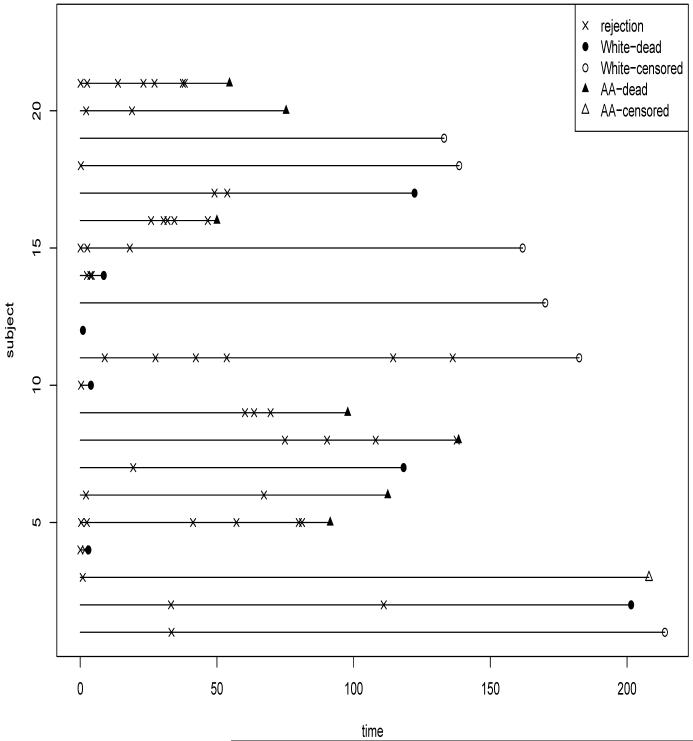
To illustrate the use of Bayesian methodology for the analysis of recurrent events with dependent termination, we use a subset of the cardiac transplant data from the Medical University of South Carolina. Cardiac transplant recipients may experience non-fatal recurrent graft rejections after the transplants. By modeling the intensity of non-acute graft rejections and risk of death, we can understand the roles of the risk factors for death and graft rejection, and predict a patient’s risk of death/rejection given history of rejections, thus it can help clinicians to make decision on patients’ schedule of biopsy (a very invasive monitoring plan with potentially serious side-effects) given the history of graft rejections. The main aims of the actual study also included investigation of the effects of the time-independent covariates race and gender on the risk of recurrent graft rejections and risk of death. For this article, we are going to only analyze the data from 21 female patients from certain ages and years of entry (the details are withheld because the results of the analysis of the entire study have not been published yet). The numbers of recurrent events among these women vary between 0 to 7. The time-independent covariate available for each patient is a binary variable of race (1 for non-Caucasian women and 0 for Caucasian women). It is often argued in the transplant literature that non-Caucasian women are somewhat at higher risk of graft rejections compared to Caucasian women, and marginally, non-Caucasian women are also at higher risk of death. However, the effect of race on death for such transplant patients may be confounded by the effect of history of graft rejections on death. The complex relationship among transplant rejections, death and race are not very well-understood. A graphical representation of the data is given in Figure 1. From this figure, it is difficult to immediately comprehend the relationship of race with the observed data of these two types of responses.
Figure 1.
Plot of the rejection times and death for African American (AA) and Caucasian (White) females from transplant study
A Cox partial likelihood analysis based on the response variable termination time shows that the effects of both race and the time-dependent covariate consisting of the number of previous rejections, are statistically highly significant (indicating increased risk of death for non-Caucasian women). This confirms that we have informative termination in this example. Analyzing the recurrent transplant rejections using either the methods of Sun and Wei (2000) or Wang et al. (2001) shows that the race effect is statistically significant. However, these analyses fail to explain the complex relationship of gender, rejections and death. They do not explain whether the effect of gender on death is only via its effect on rejection followed by rejection’s effect on death. We also emphasize that the CAR assumption of (1.2) is clearly not physically interpretable in this situation.
For this data example, we consider following two models. (1) Model-0: a GMPP model for the {N(t)} process with conditional intensity and hazard (respectively for recurrent rejections and death) given in (2.1) and (2.8), with a time-independent covariate xi (gender) and patient-specific frailty wi; (2) Model 1: an extension of the GMPP model with the conditional hazard of the termination Ti given in (2.8) replaced by
| (4.1) |
where β3 is an additional regression parameter measuring the direct effect of number of previous rejections Ni(t-) on the risk of termination. The baseline hazard is assumed to be monotone h0(t) = λνtν-1. A credible interval of α in Model-1 can be used to evaluate the justification for a CAR assumption, since Model-1 gets reduced to a CAR model for α = 0. It is of particular interest to know whether ν < 0 and the actual value of ν to decide whether the baseline risk of death after adjusting for effects of race and history of rejections decrease over time, and how much the risk can decrease over a certain interval, say, on interval of 3 years. The frailty density is assumed to be Ga(η, η) with η-1 as the variability of the frailty.
For Gibbs sampling, we use the publicly available popular software WinBUGS. We follow the recommendations of Gelman and Rubin (1992) to monitor convergence. In particular we used 10 Gibbs chains with 50,000 iterations in each chain. We checked that the estimated scale reduction factor R̂ of the Gelman and Rubin statistic is less than 1.2 for each of the parameters. We also checked several other convergence criteria using CODA (Best et. al., 1995).
We used zero means and large variances for the hyperparameters of the prior distributions of the regression parameters β1, β2 and β3 to reflect prior opinions of no direct regression effects on the rejection intensity as well as on the risk of termination. For the gamma priors for λ, ν and η, we used small scales and shapes so that the prior distributions are diffuse. We observed that our analysis is not sensitive to these choices, as long as the priors remain sufficiently diffuse. In this analysis, another crucial elicitation step is to choose the hyperparameters τ = 1/c and γ0(t) associated with the gamma process of μ0(t) in (3.6). We take γ0(t) = λ0tα0 with λ0 = .01, α0 = .5 and τ = 5.0. The rationale behind choosing α0 is that a plot of the prior baseline intensity over the time intervals reduces approximately according to a square root scale. We also use a very diffuse gamma process for μ0(t) to represent low confidence in our prior guess γ0(t) of μ0(t).
The results of our Bayesian analysis using Model-0 suggest that there is good evidence for a direct race effect on the intensity of recurrent graft events with 95% credible interval (0.5133, 1.55) for β1. The 95% credible interval (0.828, 2.99) of α lies above zero indicating strong evidence that patients who are more prone to recurrent graft rejections are at higher risk of death because a higher unobservable patient-specific frailty increases the risk of recurrent rejections as well as death. The evidence for the direct race-effect on the increased risk of death is also significant, since the 95% credible interval (0.6, 2.93) for β2 is also above zero, and the posterior median is 1.74. This suggests that the race effect on risk of death may not be explained adequately by the effect of race on death via the intermediate variable of the history of past rejections. The variance parameter η of the frailty density has a credible interval of (0.6,2.9) indicating evidence of high level of patient-heterogeneity for frequency of graft rejections.
For the extension of the GMPP model (Model-1), the corresponding credible intervals of β1 and β2 are (0.29,1.6) and (0.8,3.9). They are slightly wider than the credible intervals obtained from Model-0. The credible interval of β3 (direct of number of past rejections N(t-) on risk of death) is (0.16,1.17) supporting the anticipated effect of past number of rejections for increasing the risk of death. The posterior analysis of this model does not support the CAR assumption for this study, since the credible-interval of α for this model turns out to be (1.23,503), which is way above zero. In a subsequent section, we discuss about how to decide about the most appropriate model (based on observed data) among these two competing models. One of the major advantages of a Bayesian analysis is that one can compute the predictive distributions of the future event process for different races. We have omitted the predictive distributions here for brevity.
5 MODEL DIAGNOSTICS
Model validation diagnostics are very important components of Bayesian survival analysis (Sinha and Dey (1997); Ibrahim, Chen and Sinha (2001)). We present a method for Bayesian model validation for recurrent events data via the conditional predictive ordinate (CPO) (Gelfand, Dey and Chang, 1992). For subject i, the cross-validated posterior predictive probability evaluated at the observed data point is given by
| (5.1) |
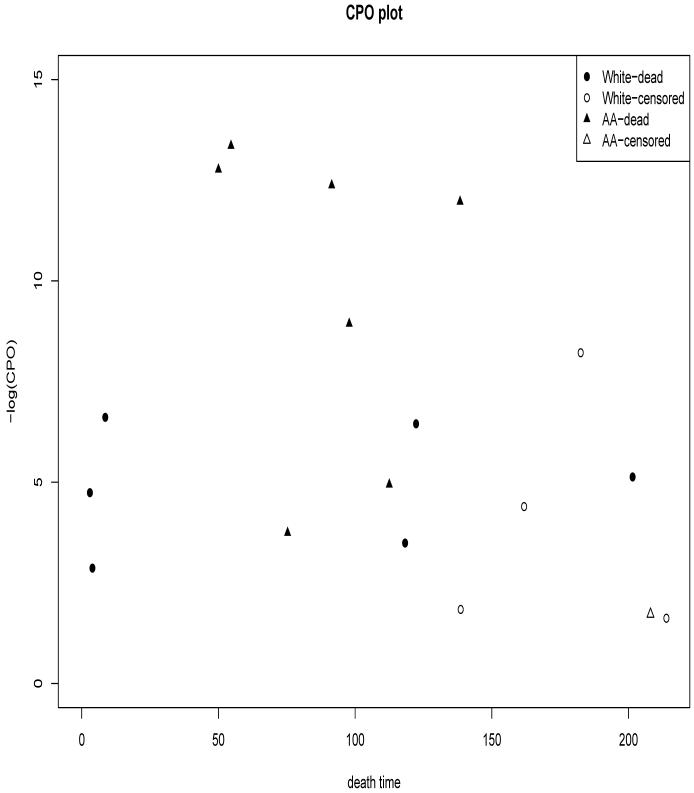
where Y(-i) is the observed data with subject i removed, θ is the vector of model parameters, and Ni,obs is the observed recurrent events history data for subject i. Using a result of Gelfand, Dey and Chang (1992), we have CPO(i) = {E[P(Ni = Ni,obs, Ti = ti|θ)-1 |Y]}-1, which can be computed using MCMC samples from the full posterior p(θ|Y). The method for calculating the CPO(i)’s is particularly simple within WinBUGS. In WinBUGS, we need to specify n additional ‘nodes’ (which are treated as posterior quantities to be computed) for i = 1, · · · , n. After computing the posterior means of these n nodes, the CPO(i)’s are obtained as inverses of these posterior means. Typically, the CPO(i)’s (treated like Bayesian residuals) are plotted against either xi or ti (or even Ni,obs) to check whether the CPO(i)’s values have any relationship with the covariates and observed data values. From this plot, we can identify possible outliers and possible evidence of a covariate dependence pattern. A plot of - log(CPO(i) vs xi can evaluate whether these cross-validated residuals depend on certain ranges of the covariate values. For the transplant data under Model-0, we found that non-Caucasian women tend to have lower CPO(i)’s values compared to African American Women, indicating a poorer fit of Model-0 to the data from Aferican American as compared to Caucasian women. This suggests that, in future, race should be treated as stratification variable instead of a binary covariate for the analysis of such data. A plot of CPO(i) vs ti can evaluate whether the posterior analysis has any unusually small prediction capabilities for certain values of the termination times. For the transplant data under Model-0, we found no association between CPO(i) and ti in Figure 2.
Figure 2.
Plot of the -log(CPO) under Model-0 versus the observed time of death yi for each patient
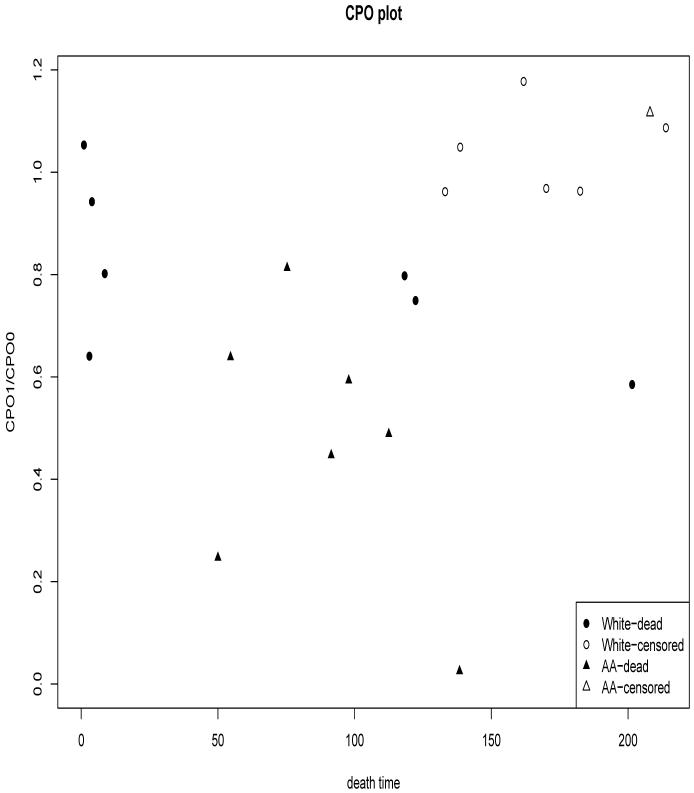
Ratio of CPO(i) under two competing models (e.g., ratio of Model-1 and Model-0 for transplant data) evaluates the relative support of observation i to Model-1 compared to Model-0. Figure 3 presents a plot of these ratios of CPO from two competing models (CPO of Model-1 divided by CPO of Model-0) versus the times of death. The ratio of greater than 1 indicates the observation from the patient prefers Model-1 against Model-0 (and vice-versa). Most observations have the ratios below 1 indicating a strong data support for Model-0 (GMPP model) over Model-1. The plot uses different symbols for races to help us evaluate whether the degree of data-support to a particular model depends on the covariate value and observed death-time. The figure suggests that support to Model-0 compared to Model-1 from observations from African American patients is somewhat stronger than the support form most of the observations from Caucasian patients. All the observations favoring Model-1 over Model-0 come from Caucasian women indicating an association between model preference and race.
Figure 3.
Plot of the ratio of Model-1 CPO and Model-0 CPO versus the observed time of death yi for each patient
6 COMMENTS AND FUTURE RESEARCH
We have proposed a comprehensive Bayesian model for recurrent events data with dependent termination whose parameters are fully interpretable. We have provided theoretical justifications for each part of the model and established relationships with other existing models. The novelty of this research is to view the recent developments of recurrent events with dependent termination data models in an unified and theoretically valid Bayesian model. Bayesian model diagnostics are also provided. The advantage of the Bayesian methodology is the ability of predicting future observations. Below, we mention some of the immediate extensions and future developments.
6.1 Cumulative Medical Care Costs Data
The inference problem of recurrent events data described here is very related to other important statistical problems such as the estimation of the mean of quality adjusted lifetime (Zhao and Tsiatis, 1997) and lifetime medical costs data. For simplicity, we focus here on the latter to identify its relationship with our models and methods. Studies of medical costs often focus on estimating the cumulative costs of care over a specified time interval, say, time of diagnosis to the time of a terminating event such as death or cure (e.g., Etzioni et al., 1996; Lin et al., 1997; Etzioni et al., 1999). For such experiments, for patient i, we can let Ni(t) denote the continuous variable of cumulative cost at time t and Ti is the time to the terminating event. Our main interest is in the distribution of Ni(Ti), the cumulative medical cost at the termination time Ti. The extension of the GMPP model to cumulative medical cost data is achieved via the assumption that {N(t) : t ≤ T} given the frailty random effect w, is a realization of an independent-increment nonnegative process with conditional characteristic function
| (6.1) |
where μ0(t) is a non decreasing function and ψ(y) is the characteristic function of an infinitely divisible distribution function with unit mean. One example of such an N(t) is the Gamma process where ψ(y) = {ρ/(ρ - iy)}ρ and the resulting distributions of the disjoint increments in N(t) given w are independent and N(u+Δ)-N(u) ∼ Ga(ρ(μ0(u+Δ)-μ0(u)), ρ). We obtain discrete Poisson distributed increments of recurrent events data when we use ψ(y) = exp{1 - exp(iy)}.
For the medical costs data problem, two important quantities of much practical interest are the expected lifetime cost CT = E[N(T)|x] and the rate of cost accumulation over the lifetime RT = E[N(T)/T* |x]. Here, we define T* as the minimum of the last inspection time aJ and the termination time T. The posterior means and credible intervals of CT and RT given x are useful posterior summaries of a Bayesian analysis for such data. For our model, the general simplified expression of E[N(T)|x] in (2.16) is valid even for this case. The posterior mean of E[N(T)|x] can be computed using MCMC samples from the posterior distribution p(w,θ|Y).
6.2 Extensions of the Model
One key assumption of the GMPP model is the proportional intensity of N(t) given {w, x, T > t}. A possible criticism of this assumption can be addressed by extending the model to a nonproportional intensity for N(t) given {w, x, T > t}. We address two ways of extending the model to a nonproportional intensity—(1) nonproportional with respect to w, and (2) nonproportional withrespect to x. We now discuss possible computational difficulties and challenges in extending our Bayesian methodology to these two cases.
The accelerated time intensity model is given by replacing the assumption in (2.1) by
| (6.2) |
where μ0(t) is the baseline cumulative intensity and its prior is modeled by an independent increment Gamma process similar to what was described in Section 3.
It is important to note that, now, L1(β1, w, μ0|D1, X) in (3.1) involves μ0(wi ti) and dμ0(wi ti). For the GMPP model, at each iteration of MCMC chain, we need to only sample from the joint full conditional distribution of n increments μ0(t(i)) - μ0(t(i-1)) in between two consecutive events, and this set of increments are independent given w. On the other hand, for the accelerated intensity model, in each iteration of the MCMC chain, after we sample the vector w, we now need to sample from the joint full conditional distribution of the n2 increments of μ0(t) at time-points ti wk for i = 1, · · · , n and k = 1, · · · , n. For the accelerated intensity model, the increments {μ0(wi t(k)) - μ0(wi t(k-1)) : i = 1, · · · , n; k = 1, · · · , n} are not independent. This is increases the dimensionality of the MCMC algorithm and results in slow convergence of the MCMC chain, because now the full conditional involves the entire sample path of the function μ0(t) instead of its increments at fixed time points t1, · · · , tn.
Another possible extension is to use the transformation intensity model (Lin, Wei and Ying, 2001) to replace the assumption of (2.1) as
| (6.3) |
where ψ is a known link with (possibly) unknown parameters. One example is ψ(μ0(t), x) = log[μ0(t)eβ1x + 1]. For this case, the MCMC based Bayesian methodology described in Section 3 can be (in principle) extended to the transformation intensity model. Details of these methods are yet to be explored.
6.3 Interval Censoring
In some real data settings, a continuous termination time T is monitored through scheduled inspections at a1, · · · , aJ, and it gives rise to interval censoring of the termination time within the inspection intervals. For example, patients within a trial can be monitored through monthly clinic visits and a patient’s termination time is recorded only up to the last month’s clinic visit before termination (death). Therefore, for each subject i, we only observe that Ti ∈ Iji+1 for some inspection interval Iji+1 = (aji, aji+1], and the observed counts Nik for k = 1, · · · , ji. Thus, similar to Lin et al. (1997) and Lin (2000), here N(aji) is informatively censored for N(T). In practice, if our modeling assumptions of the GMPP model of Section 2.4 are correct, we can make correct inference on the model parameters using a likelihood based on P(Ti ∈ Iji+1, Ni1, · · · , Niji|θ). This likelihood will be similar to the likelihood in Section 3, except that now, , where . However, from this available interval-censored data, it is not possible to check whether our modeling assumptions are valid. To be more specific, if our assumptions fail within a very short interval around Ti, then we will not be able to detect that using the available data, because the available data has no information about the relationship between N(T) - N(ak) and T - ak where ak < T < ak+1. Even if we have available data on N(T) - N(ak), but no available data on T - ak, then we cannot check the validity of our modeling assumptions.
Acknowledgments
Dr. Sinha’s research was partially supported by NCI grant #R01-CA69222. Dr. Maiti’s research was partially supported by NSF grant SES-0318184. Dr.Ibrahim’s research was partially supported by NCI grant 74015 and GM 070335. The authors are grateful to the Editor and the referees for suggestions that considerably improved this paper.
APPENDIX I
Proof of Theorem (2.1)
We simplify the following equations by suppressing the covariate x from the expressions. We begin with the conditional distribution of N(T) given the frailty w. Under the L-I model, we can show that
| (6.4) |
Also, note that
Using the above two results, we get
| (6.5) |
This completes the proof of the theorem.
Proof of Theorem (2.2)
To simplify the expressions, we suppress the covariate x and the subscript i and use the abbreviated notation h(t) = h(t; xi) = h0(t) exp(β2xi); μ(t) = μ(t; xi) = μ0(t) exp(β1x); . Using properties of a mixed Poisson process, we have
where f(w|η) is the density of the univariate frailty random variable w and V has a Ga(m + η; μ(t) + η) distribution. Using the same argument, we can show that
Dividing P[T ∈ (t, t + dt), N(t) = m] with P[T > t, N(t) = m], we can obtain the limiting expression for hT(t|N(t-); x). For the case α = 1, using the formula for the Gamma integral, we can further show that
| (6.6) |
which completes the proof.
Proof of Theorem (2.3)
Using the modeling assumptions in (2.1) and (2.8), we can show that
| (6.7) |
and
| (6.8) |
where the expectations are taken with respect to the Ga(η, η) distribution of the frailty W.
Proof of Theorem (2.4)
Using the property of a non-homogeneous Poisson process (Ross 1983), from (2.5) and (2.6) we get
| (6.9) |
and
| (6.10) |
where H(t|x) = H0(t)eβ2x. From the above two equations, we can show that
| (6.11) |
Using the nonhomogeneous Poisson process property of N(t)|T > t, w; x and conditional independence of N(t) and T ∈ (t, t + dt) given w, we get
| (6.12) |
and
| (6.13) |
Dividing these two quantities, we can show that
| (6.14) |
This result completes the proof.
APPENDIX II
The conditional posterior distributions for the Gibbs sampling steps for discrete termination time (panel count) data are given as follows. Define
We denote the full conditional distribution of θ given all other parameters by [θ|rest].
Contributor Information
Debajyoti Sinha, Department of Statistics, Florida State University.
Tapabrata Maiti, Department of Statistics, Iowa State University.
Joseph G. Ibrahim, Department of Biostatistics, University of North Carolina
Bichun Ouyang, Department of Biostatistics, Medical University of South Carolina.
REFERENCES
- Aalen OO, Fosen J, Weedon-Fekjr H, Borgan, Husebye E. Dynamic analysis of multivariate failure time data. Biometrics. 2004;60:764–773. doi: 10.1111/j.0006-341X.2004.00227.x. [DOI] [PubMed] [Google Scholar]
- Best NG, Cowles MK, Vines SK. CODA Manual version 0.30. MRC Biostatistics Unit; Cambridge, UK: 1995. [Google Scholar]
- Chen M-H, Shao Q-M, Ibrahim JG. Monte-Carlo Methods in Bayesian Computation. Springer-Verlag; NY: 2000. [Google Scholar]
- Cox DR. Regression models and life tables. Journal of the Royal Statistical Society, B. 1972;34:187–220. [Google Scholar]
- Cox DR, Oakes DO. Analysis of survival data. Chapman & Hall Ltd; London; New York: 1984. [Google Scholar]
- Dey DK, Mueller P, Sinha D, editors. Practical Nonparametric and Semiparametric Bayesian Analysis. Springer-Verlag; New York: 1998. [Google Scholar]
- Etzioni R, Feuer EJ, Sullivan SD, Lin D-Y, Hu C-C, Ramsey SD. On the use of survival analysis techniques to estimate medical care costs. Journal of Health Economics. 1999;18:365–380. doi: 10.1016/s0167-6296(98)00056-3. [DOI] [PubMed] [Google Scholar]
- Fosen J, Borgan, Weedon-Fekjr H, Aalen OO. Dynamic analysis of recurrent event data using the additive hazard model. Biometrical Journal. 2006;48:381–398. doi: 10.1002/bimj.200510217. [DOI] [PubMed] [Google Scholar]
- Gail MH, Santner TJ, Brown CC. An analysis of comparative carcinogenesis experiments based on multiple times to tumor. Biometrics. 1980;36:255–266. [PubMed] [Google Scholar]
- Gelfand AE, Dey DK, Chang H. Model determination using predictive distributions with implementation via sampling-based methods. In: Bernardo JM, Berger JO, Dawid AP, Smith AFM, editors. Bayesian Statistics. 4, Ed. Oxford University Press; 1992. pp. 147–167. [Google Scholar]
- Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences (with discussion) Statistical Science. 1992;7:457–472. [Google Scholar]
- Gilks WR, Wild P. Adaptive rejection sampling for Gibbs sampling. Applied Statistics. 1992;41:337–348. [Google Scholar]
- Griffiths RC. Characterization of infinitely divisible multivariate gamma distributions. Journal of Multivariate Analysis. 1984;15:13–20. [Google Scholar]
- Heitjan DF, Rubin DB. Ignorability and coarse data. The Annals of Statistics. 1991;19:2244–2253. [Google Scholar]
- Henederson R, Shimakura S. A serially correlated gamma frailty model for longitudinal count data. Biometrics. 2003;90:355–366. [Google Scholar]
- Hougaard P. Analysis of Multivariate Survival Data. Springer; NY: 2000. [Google Scholar]
- Ibrahim JG, Chen M-H, Sinha D. Bayesian Survival Analysis. Springer-Verlag; 2001. [Google Scholar]
- Ibrahim JG, Chen M-H, Sinha D. Criterion based methods for Bayesian model assessment. Statistica Sinica. 2001b;11:419–443. [Google Scholar]
- Kalbfleisch JD. Nonparametric Bayesian analysis of survival time data. Journal of Royal Statistical Society, B. 1978;40:214–221. [Google Scholar]
- Kuo L, Yang TY. Bayesian computation of software reliability. Journal of Computational and Graphical Statistics. 1995;4:65–82. [Google Scholar]
- Kuo L, Yang TY. Bayesian computation for nonhomogeneous Poisson processes in software reliability. Journal of the American Statistical Association. 1996;91:763–773. [Google Scholar]
- Lancaster T, Intrator O. Panel data with survival: hospitalization of HIV-positive patients. Journal of the American Statistical Association. 1998;93:46–51. [Google Scholar]
- Lin DY, Feuer EJ, Etzioni R, Wax Y. Estimating medical costs from incomplete follow-up data. Biometrics. 1997;53:419–434. [PubMed] [Google Scholar]
- Lin DY. Proportional means regression for censored medical costs. Biometrics. 2000;56:775–778. doi: 10.1111/j.0006-341x.2000.00775.x. [DOI] [PubMed] [Google Scholar]
- Lin DY, Wei LJ, Ying Z. Semiparametric transformation models for point processes. Journal of the American Statistical Association. 2001;96:620–628. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis With Missing Data. Wiley; New York: 1987. [Google Scholar]
- Liu L, Wolfe RA, Huang X. Shared frailty model for recurrent events and terminating event. Biometrics. 2004;60:747–756. doi: 10.1111/j.0006-341X.2004.00225.x. [DOI] [PubMed] [Google Scholar]
- McCulloch RE. Local model influence. Journal of the American Statistical Association. 1989;84:473–478. [Google Scholar]
- Miloslavsky M, Keles S, Van der Laan MJ, Butler S. U.C. Berkeley Division of Biostatistics Working Paper Series. 2002. Recurrent Events Analysis in the Presence of Time Dependent Covariates and Dependent Censoring. Working Paper 123. [Google Scholar]
- Miloslavsky M, Keles S, Laan, Mark J, Butler S. Recurrent events analysis in the presence of time-dependent covariates and dependent censoring. (Series B).Journal of the Royal Statistical Society. 2004;66:239–257. Series B. [Google Scholar]
- Nelson W. Confidence limits for recurrence data - Applied to cost or number of product repairs. Technometrics. 1995;37:147–157. [Google Scholar]
- Oakes D. A model for association in bivariate survival data. Journal of the Royal Statistical Society, B. 1982;44:414–422. [Google Scholar]
- Oakes D. Frailty models for multiple event times. In: Klein JP, Goel PK, editors. Survival Analysis: State of the Art. Kluwer Academic Publisher; Netherlands: 1992. pp. 371–379. [Google Scholar]
- Oakes D, Cui L. On Semiparametric Inference for Modulated Renewal Processes. Biometrika. 1994;81:83–90. [Google Scholar]
- Robert CP, Casella G. Monte Carlo Statistical Methods. Wiley; New York: 1999. [Google Scholar]
- Robins JM. Information recovery and bias adjustment in proportional hazards regression analysis of randomized trials using surrogate markers. ASA Proceedings of the Biopharmaceutical Section. 1993:24–33. [Google Scholar]
- Ross SM. Stochastic Process. Wiley; New York: 1983. [Google Scholar]
- Scheike TH. Comparison of non-parametric regression functions through their cumulatives. Statistics & Probability Letters. 2000;46:21–32. [Google Scholar]
- Sinha D. Semiparametric Bayesian analysis of multiple event time data. Journal of the American Statistical Association. 1993;88:979–983. [Google Scholar]
- Sinha D, Dey DK. Semiparametric Bayesian analysis of survival data. Journal of the American Statistical Association. 1997;92:1195–1212. [Google Scholar]
- Sinha D, Maiti T. Analyzing panel-count data with dependent termination: a Bayesian approach. Biometrics. 2003;60:34–40. doi: 10.1111/j.0006-341X.2004.00140.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Wei LJ. Regression analysis of panel count data with covariatedependent observation and censoring times. Journal of the Royal Statistical Society, B. 2000;62:293–302. [Google Scholar]
- Tanner MA. Tools for Statistical Inference. Third Edition Springer-Verlag; New York: 1996. [Google Scholar]
- Walker, Stephen G, Damien P, Laud PW, Smith AFM. Bayesian Nonparametric Inference for Random Distributions and Related Functions (with discussion) Journal of the Royal Statistical Society, B. 1999;61:485–509. [Google Scholar]
- Wang M-C, Qin J, Chang C-T. Analyzing recurrent event data with informative censoring. Journal of the American Statistical Association. 2001;96:1057–1065. doi: 10.1198/016214501753209031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei LJ, Glidden DV. An overview of statistical methods for multiple failure time data in clinical trials (with discussion) Statistics in Medicine. 1997;16:833–839. doi: 10.1002/(sici)1097-0258(19970430)16:8<833::aid-sim538>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- Whittemore A, Keller JB. Quantitative theories of carcinogenesis. Society for Industrial and Applied Mathematics Review. 1978;20:1–30. [Google Scholar]
- Zhao H, Tsiatis AA. A consistent estimator of the distribution of quality adjusted survival time. Biometrika. 1997;84:339–348. [Google Scholar]